(理想流体动力学5-8)
工程流体水力学第四章习题答案
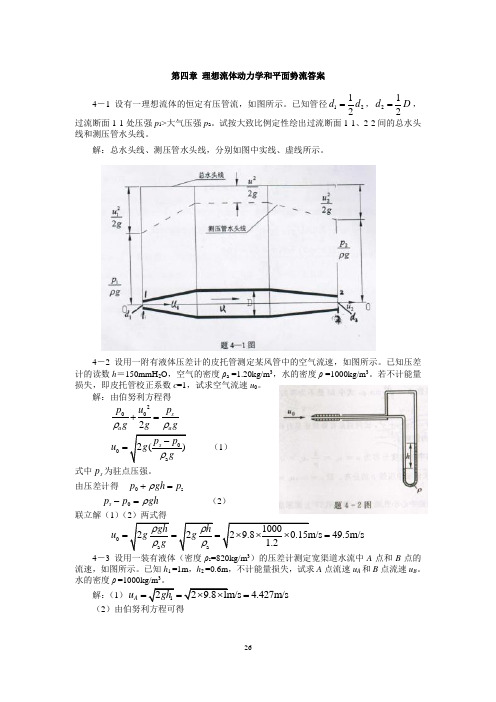
第四章 理想流体动力学和平面势流答案4-1 设有一理想流体的恒定有压管流,如图所示。
已知管径1212d d =,212d D =,过流断面1-1处压强p 1>大气压强p a 。
试按大致比例定性绘出过流断面1-1、2-2间的总水头线和测压管水头线。
解:总水头线、测压管水头线,分别如图中实线、虚线所示。
4-2 设用一附有液体压差计的皮托管测定某风管中的空气流速,如图所示。
已知压差计的读数h =150mmH 2O ,空气的密度ρa =1.20kg/m 3,水的密度ρ =1000kg/m 3。
若不计能量损失,即皮托管校正系数c =1,试求空气流速u 0。
解:由伯努利方程得2002s a a p u p g g gρρ+= 00a 2()s p p u g gρ-=(1) 式中s p 为驻点压强。
由压差计得 0s p gh p ρ+=0s p p gh ρ-= (2)联立解(1)(2)两式得0a a 10002229.80.15m/s 49.5m/s 1.2gh h u gg g ρρρρ===⨯⨯⨯= 4-3 设用一装有液体(密度ρs =820kg/m 3)的压差计测定宽渠道水流中A 点和B 点的流速,如图所示。
已知h 1 =1m ,h 2 =0.6m ,不计能量损失,试求A 点流速u A 和B 点流速u B 。
水的密度ρ =1000kg/m 3。
解:(1)1229.81m/s 4.427m/s A u gh ==⨯⨯= (2)由伯努利方程可得22A AA u p h g gρ+= (1)22B BB u p h g gρ+= (2)式中A h 、A p 和B h 、B p 分别为A 点和B 点处的水深和驻点压强。
由(1)、(2)式可得2222A B A BA B p p u u h h g g gρ-=+-- (3) 由压差计得,22ρρρρ--++=A A s B B p gh gh gh gh p ,所以220.82A BA B p p h h h h gρ-=+-- (4) 由(3)式、(4)式得2222 4.427(10.82)0.6(10.82)0.8922229.8B A u u h g g =--=--=⨯ 29.80.892m/s 4.18m/s B u =⨯⨯=。
流体力学简介

设环流速度为u,机翼远前方气流的速度和压强可视为
常量,与位置无关,分别设为v和p0,机翼上部的压强为 p1,下部为p2,则由伯努利方程,有
p0
1 2
v2
p1
1 2
(v
u)2
由此得
p0
Байду номын сангаас1 2
v2
p2
1 2
(v
u)2
p2
p1
1 2
[(v
u)2
(v
u)2 ]
2uv
a1 b1
因为时间t极短,所以 p1 S1
v1
a1b1和a2b2是两段极短的 位移,在每段极短的位
移中,压强p、截面积S
h1
和流速v都可看作不变。
a2 b2
h2 p2
v2 S2
设p1、S1、v1和p2、S2、v2分
a1 b1
别是a1b1与a2b2处流体的压 强、截面积和流速,则后方
p1 S1
v1
根据伯努利方程,在等 高(水平)流管中,有
p 1 v2 常量
2
即,流速大处压强小,流速小处压强大.
例题1 水电站常用水库出水管道处水流的动能来发 电.出水管道的直径与管道到水库水面高度h相比为 很小,管道截面积为S.试求出水处水流的流速和流 量。
解:把水看作理想流体.在 水库中出水管道很小,水 流作定常流动.如图所示, 在出水管中取一条流线ab. 在水面和管口这两点处的 流速分别为va和vb.在大水 库小管道的情况下,水面 的流速va远比管口的小,可 以忽略不计,即va=0.
网球、乒乓球中的”弧 圈球”以及足球中的” 香蕉球”偏离原运动方 向的现象,就是由于这一 效应造成的.
流体力学第四章

• 在每一个微元流束的有效截面上,各点的速度可认为是相同的 总流:无数微元流束的总和。
38
2016/12/26
流体运动学和动力学基础(Fluid Kinematics and Dynamics)
均匀流与非均匀流·渐变流和急变流
均匀流——同一条流线上各空间点上的流速相 同的流动,流线是平行直线,各有效截面上的 流速分布沿程不变 非均匀流——同一条流线上各空间点上的流速不 同的流动,流线不是平行直线,即沿流程方向速 度分布不均
迹线· 流线 1、迹线 1)定义:某一质点在某一时段内的运动轨迹 线。 2)迹线的微分方程
dx dy dz dt ux u y uz
烟火的轨迹为迹线
流体运动学和动力学基础(Fluid Kinematics and Dynamics)
流体运动学和动力学基础(Fluid Kinematics and Dynamics)
25
2016/12/26
流体运动学和动力学基础(Fluid Kinematics and Dynamics)
一维、二维和三维流动
三维流动:流动参数是x、y、z三个坐标的函数
的流动。
二维流动:流动参数是x、y两个坐标的函数的
流动。
一维流动:是一个坐标的函数的流动。
26
2016/12/26
流体运动学和动力学基础(Fluid Kinematics and Dynamics)
x= x (t)
dux ux ux dx ux dy ux dz ax dt t x dt y dt z dt
(1)当地加速度(时变加速度):流动过程中流体 由于速度随时间变化而引起的加速度; (2)迁移加速度(位变加速度):流动过程中流体 由于速度随位置变化而引起的加速度。
工程流体力学(粘性流体动力学基础公式推导)

2h
u
x
vw0
U 0
不可压连方
u v w 0, u 0, u u( y)
x y z
x
运动方程
u t
u
u x
v
u y
w
u z
1
p x
2u ( x 2
2u y 2
2u z2 )
26
运动方程
u t
u
u x
v
u y
w
u z
1
p x
2u ( x 2
2u y2
2u z 2
)
简化为
2u y 2
1
p x
13
px
py
pz
3 p
2 ( vx
x
vy y
vz z
)
(8--9)
问题:上式括号内表示什么?
对于不可压缩流体,故有:
p
1 3
(
px
py
pz
)
(8-10)
即对于粘性不可压缩流体,三个互相垂直的法
向应力的算术平均值恰好等于理想流体的压力。
14
将切向应力和法向应力关系式代入(8--5)式得
vx t
vx
Dt
x
y
z
DVz Z 1 ( zx zy pzz )
Dt
x
y
z
(8-5)
单位质量流体的惯性力
单位质量流体的应力
单位质量流体的质量力
这就是应力形式的粘性流体运动微分方程 8
讨论
1.式(8-5)中未知函数:三个速度分量和六个 应力分量;加上连续性方程,只有四个方程,
2.若要求解,需补充方程。
将(d)式代入(a)式,经移项后可得
流体力学
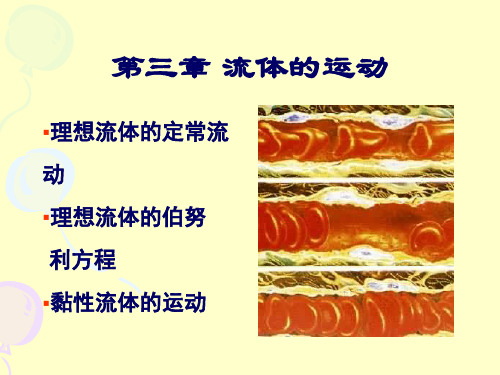
表明流速不变或流速的改变可以忽略时,理
想流体稳定流动过程中流体压强能与重力势
能之间的转换关系,即高处的压强较小,低处 的压强较大. 两点的压强差为
p1 p2 g (h2 h1 )
空吸原理
SB SA SC
S AvA SB vB
S A SB
vB vA
1 1 2 2 P vA P vB A B 2 2
vB 2 gh
管涌
铜壶滴漏 “寸金难买寸光阴”是再熟 悉不过的诗句了,其中揭示 了计量时间的方法.我国古 代用铜壶滴漏计时,使水从 高度不等的几个容器里依次 滴下来,最后滴到最低的有 浮标的容器里,根据浮标上 铜壶滴漏 的刻度也就是根据最低容器 说明其计时原理. 里的水位来读取时间.
(三) 压强与流速的关系 在许多问题中,所研究的流体是在水平或接近 水平条件下流动.此时,有 h1=h2或 h1≈h2,伯 努利方程可直接写成 1 2 1 2 p1 v1 p 2 v 2 2 2 1 2 p v 常量 2 平行流动的流体,流速小的地方压强大,流速 大的地方压强小(例).
(2)求虹吸管内B、C 两处的压强. 解:水面为参考面,则 有A、B点的高度为零,
C 点的高度为2.50 m, D点的高度为-4.50m.
(1)取虹吸管为细流管,对于A、D 两点,根据伯 努利方程有 1 2 1 2 ghA v A p A ghD vD pD 2 2 由连续性方程有
1 2 1 2 p A v A pB v B 2 2
1 2 PB P0 vB 2
根据连续性方程可知,均匀虹吸管内,水的速率
处处相等,vB=vD.
1 2 PB P0 vB 5.7 10 4 Pa 2 结果表明,在稳定流动的情况下,流速大处压强
流体力学ppt课件-流体动力学

g
g
2g
水头
,
z
p
g
v2
2g
总水头, hw 水头损失
第二节 热力学第一定律——能量方程
水头线的绘制
总水头线
hw
对于理想流体,总水
1
v12 2g
2
v22 2g
头线是沿程不变的,
测压管水头线
p2
为一水平直线,对于
g
实际流体,总水头沿 程降低,但测压管水
p1 g
头线沿程有可能降低、
z2
不变或者升高。
z1
v2 A2 e2
u22 2
gz2
p2
v1A1 e1
u12 2
gz1
p1
微元流管即为流线,如果不 可压缩理想流体与外界无热 交换,热力学能为常数,则
u2 gz p 常数
2
这个方程是伯努利于1738年首先提出来的,命名为伯努利 方程。伯努利方程的物理意义是沿流线机械能守恒。
第二节 热力学第一定律——能量方程
皮托在1773年用一根弯成直角的玻璃管,测量了法国塞纳河 的流速。原理如图所示,在液体管道某截面装一个测压管和 一个两端开口弯成直角的玻璃管(皮托管),皮托管一端正 对来流,一端垂直向上,此时皮托管内液柱比测压管内液柱 高h,这是因为流体流到皮托管入口A点受到阻滞,速度降为 零,流体的动能变化为压强势能,形成驻点A,A处的压强称 为总压,与A位于同一流线且在A上游的B点未受测压管的影 响,其压强与A点测压管测得的压强相等,称为静压。
第四章 流体动力学
基本内容
• 雷诺输运公式 • 能量方程 • 动量方程 • 流体力学方程应用
第一节 雷诺输运方程
• 前面解决了流体运动的表示方法,但要在流 体上应用物理定律还有困难.
流体动力学

3)按照液体流动方向列出伯努利方程的一般形式;
4)忽略影响较小的次要参数,以简化方程; 5)若未知数的数量多于方程数,则必须列出其它辅助 方程,如连续性方程、静压力方程等联立求解。
伯努利方程应用举例
例1:如图示简易热水器,左端接冷水管,右端接淋浴莲蓬头。 已知 A1=A2/4 和A1、h 值,问冷水管内流量达到多少时才能 抽吸热水? 解:沿冷水流动方向列A1、A2截面的伯努利方程
2 1 1 2 2
注意: 1)截面1、2应顺流向选取,且选在流动平稳的通流截面上。 2)z和p应为通流截面的同一点上的两个参数,一般将其定在 通流截面的轴心处。
应用伯努利方程解题的一般步骤
1)顺流向选取两个计算截面:一个设在所求参 数的截面上,另一个设在已知参数的截面上; 2)选取适当的基准水平面;
伯 努 利 方 程 应 用 举 例
泵吸油口真空度
分析变截面水平管道各处的压力情况
求水银柱高度?
管中流量达多少时才能抽吸?
判断管中液体流动方向和流量?
动量方程
动量方程是动量定理在流体力学中的具体应用,可用来计算 流动液体作用在限制其流动的固体壁面上的总作用力。
∑F = Δ(m u)/Δt = ρq(u2 - u1)
例1:如图所示,进入液压缸的流量Q1是否等于缸排
出的流量Q2?
d1
d2
Q2
解: ∵油液是不连续的,不可用连续性方程。
Q 1≠ Q 2
例2 如图所示,已知流量 q1= 25L/min,小活塞杆直径d1=20mm,小活塞
直径D1=75mm,大活塞杆直径d2=40mm,大活塞直径D2=125mm,假设没有泄 漏流量,求大小活塞的运动速度v1,v2。
25 L / min
5第五章流体动力学(微分方程)

上式减此式: 上式减此式: 定义状态参数焓: 定义状态参数焓: ,则能量方程又可表示为: 则能量方程又可表示为:
关于理想流体假设应用范围的讨论:粘性作用,速度梯度,边界层。 关于理想流体假设应用范围的讨论:粘性作用,速度梯度,边界层。 一般气体的粘性系数和导热系数值都很小, 一般气体的粘性系数和导热系数值都很小,只是在速度梯度和温度梯度 很大的区域中才起作用。 很大的区域中才起作用。
这一方程说明,对于理想流体,在质量有势( 这一方程说明,对于理想流体,在质量有势( 的条件ห้องสมุดไป่ตู้有: 压流场 的条件下有:
),流场为正 ),流场为正
ur ur r 流场如果一开始无旋,Ω ( x , 0) = 0 ,则: DΩ ≡ 0 ,流场将永远无旋。 流场如果一开始无旋, 流场将永远无旋。
上式说明,对于理想流体,在质量力有势、流场正压的条件下, 上式说明,对于理想流体,在质量力有势、流场正压的条件下,
一、应力张量的建立
我们首先讨论表面应力怎样随着受力面的方位变化而变化,并 我们首先讨论表面应力怎样随着受力面的方位变化而变化, 证明可以表示成受力面的外法线单位向量与某个张量的乘积, 证明可以表示成受力面的外法线单位向量与某个张量的乘积,而这 个张量只是空间点的位置和时间的单值函数。 个张量只是空间点的位置和时间的单值函数。 为此我们取一个四面体作为控制体, 为此我们取一个四面体作为控制体,该控制体的三个面是迪卡 尔坐标系中坐标轴构成的三个面,如同在流体静力学中所取一样。 尔坐标系中坐标轴构成的三个面,如同在流体静力学中所取一样。
Dt
我们知道,无旋流动是有势流动,由此可知, 我们知道,无旋流动是有势流动,由此可知,理想流动如果一开始是 有势的,则将一直是有势的。 有势的,则将一直是有势的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3. 涡 束
涡管内充满着作旋转运动的流体称为涡束,微元涡管 里的涡束称为微元涡束。
表征速度场和旋涡场的常用概念
速 速度
度
场v
流 流线的微分方程 流管 流束 过流
线
dx dy dz
vx vy vz
断面
旋 旋转角 涡 涡线的微分方程 涡管 涡束 涡管
涡 场
速度
线
dx dy dz
x y z
断面
二、涡通量和速度环量
球坐标系(R,θ,β)与直角坐标系(x,y,z)的转 换关系:
x=Rsinθcosβ y=Rsinθsinβ z=Rcosθ
2、空间点源(点汇) 建立球坐标系(R,θ,β) ,在坐标原点处放置一个 空间点源(点汇),流量为q,则速度分量为:
q
vR 4R2
v 0 v 0
由于球坐标系下势函数Φ的梯度公式为:
vr vz
b
dr dz
b
有
rb
4
l (z )q( )d
0
3
[rb 2 (z )2 ]2
{v
1
4
l 0
(z [r 2
)q( (z
)d
3
)2 ]2
}
drb dz
同样,利用数值解法求近似解。
当源(汇)强度q(ζ)确定后,就可以得到势函 数、流函数,继而计算出任意轴对称的零攻角 绕流场的速度分布和压强分布。
第五节 空间势流
一、空间势流的势函数 二、轴对称流动的流函数 三、几个基本轴对称流动的流函数 四、圆球绕流 五、轴对称体绕流
一、空间势流的势函数
势函数Φ与速度之间的关系式为:
vx x
vy y
vz z
将上述等式代入不可压缩流体的连续性方程:
v x v y v z 0 x y z
得到势函数的拉普拉斯边界方条程件::
证明:
先证明微元封闭曲线的斯托克斯定理。
d vABxdx vBCydy
vCDxdx vDAydy
证明: 通过回转面的流量为
B
Q A v n2rdl
B
2 A (vr nr vz nz )rdl
因为
nr
dz dl
vr rz
nz
dr dl
vz
rr
所以
Q 2 B (1 dr 1 dz)rdl A r r dl r z dl B 2 A d
2 ( B A )
三、几个基本轴对称流动的流函数
l 0
子的强度或偶极矩
q
偶极子的势函数为:
11
lim lim
l 0
q1 1
4 ( R1 R2 )
l 0
ql 4
R1 R2
l
q
q
1
M
4
d( ) R dl
M
4R 2
dR dl
M cos 4R 2
二、轴对称流动的流函数 轴对称流动:指流体在过某空间固定轴的所 有平面上的运动情况完全相同的流动。 因此,只需要研究其中一个平面上的流动就 可以知道整个空间内流体的运动情况。 常见的轴对称流动有:圆管流动、沿轴向流 经回转体的流动、水轮机叶轮内的流动。
M sin2 4R
四、圆球绕流
奇点法:通过将简单势流如均匀流、点源 (汇)、偶极子等进行叠加来处理较复杂的势 流问题的方法。
均
偶
1 2
v
R
2
- M sin2 4R
零流线方程为:
1 2
v R2
-
M
4R
0
0,
球面方程 R 3 M
2v
球面的半径 a 3 M
2v
偶极子的强度 M 2a 3v
vz
v R cos
柱坐标系(r,θ,z)与直角坐标系(x,y,z)的转 换关系:
x=rcosθ y=rsinθ z=z
/ / / / / / / / / / / / / / / / / //http ://// / / / / / // / / / / / / / / /
第六节 理想流体的旋涡运动
如流体微团的旋转角速度ω≠0,则是有旋运动, 也称为旋涡运动。 理想流体的流动可以是有势的,也可以是有旋的。 但粘性流体的流动一般是有旋的。 第六-八节讲述理想不可压缩流体的旋涡运动,涉 及的基本概念及定理有:涡线、涡管和涡束;涡 通量和速度环量;斯托克斯定理;汤姆逊定理; 亥姆霍兹定理;毕奥-沙伐尔公式;卡门涡街。
2
整个OA段的源(汇)在P点处的势函数和流函数分别为
1
1
4
l 0
q( )d
r 2 z 2
1
1
4
l
0
q( )z d r 2 z 2
均匀流在P点处的势函数和流函数分别为
2 vz
2
1 2
v
r
2
势流叠加后的流场的势函数和流函数分别为
1
2
v z
1
4
l 0
q( )d r2 (z )2
q>0,表示源 q<0,表示汇 建立柱坐标系(r,θ,z),流动参数与无关。 在对称轴的OA段上连续布置源(汇),设单位长度 上的源(汇)强度为q(ζ),则微元段dζ的强度为
dq q( )d
微元段dζ的源(汇)在P点处的势函数和流函数分别为
d1 4
q( )d
r 2 z 2
d1
q( )d z 4 r 2 z
R
eR
1 R
e
1
R sin
e
得到
对应方向的单位矢量
vR R
v
1 R
因此
q
R 4R2
v
1
R sin
q 4R
3、空间偶极子
依据势流叠加原理,P点处的势函数为
q q q ( 1 1 ) 4R1 4R2 4 R1 R2
满足下面关系式才能构成偶极子流,即
lim ql M M为常数,称为偶极
①式对R积分,得到
v R2 sin2 f ( )
2
将上式对θ求导,得到
v R2 sin cos
f '( )
与②式比较,得到 f '( ), 0即
f ( ) C
令 f ( ) ,0最终空间均匀流的势函数为
v R2 sin2
2
2、空间点源(点汇)
设速在度坐矢标量原为点v有一点源,强度为q。空间点P (R,θ,β)的
程为:
(R2 sinv R ) (R sinv ) 0
R
定义流函数Ψ (R, θ),满足
R
R
sinv
R2
s inv R
v
1
R sin
R
vR
1
R2 sin
3、流函数的性质
1)等流函数线就是流线;
2)在通过包含对称轴线的流动平面上,任意两点 的流函数值之差的2π倍,等于通过这两点间的任 意连线的回转面的流量。
1、柱坐标系(r, θ, z)的流函数Ψ (r, z)
柱坐标系中,不可压缩流体轴对称流动的连续性方
程为:
(rv r ) (rv z ) 0
r
z
定义流函数Ψ (r, z),满足
r rvz
z
rvr
vz rr
vr
rz
2、球坐标系(R,θ,β)的流函数Ψ (R,θ)
球坐标系中,不可压缩流体轴对称流动的连续性方
圆球绕流的表面速度的最大值 圆柱绕流的表面速度的最大值
v
max
3 2 v
v max 2v
球面压强分布,由伯努利方程求出
p v2
p
v2
2 2
压强系数
Cp
p p
1 2
v
2
1
v v
2
1 9 sin2
4
压强对称分布,因此球面所受的合力为零。
五、轴对称体(回转体)绕流 依然采用奇点法分析,需要寻找适当的基本势流, 使之与均匀流叠加后的势函数和流函数能满足物面 和无穷远处的边界条件。
量沿闭曲线的线积分,即为沿该闭曲线的速度环
量。
l v dl
v dl v cosdl
vxdx vydy vzdz
第七节 理想流体旋涡运动 的基本定理
一、斯托克斯定理 该定理将速度场和旋涡场之间联系起来。 斯托克斯(Stokes)定理: 沿封闭曲线的速度环量 等于该封闭曲线内所有涡通量的和。
1 2
1 2
v
r
2
1
4
l q( )(z )d 0 r2 (z )2
现需要确定q(ζ)使得上述函数满足物面和无穷远 处的两个边界条件。其中,由于无穷远处源(汇) 的速度为零,自动满足无穷远处边界条件,而要 满足物面边界条件,需进行计算。
方法1:
物面上的流函数值等于零,即 ( )b 0
求解方程
1、均匀流
有一速度为v∞的空间均匀流,取z轴为流动方向,在 球坐标系(R,θ,β)中为一轴对称流动,流动参数与β无关。
v R v cos
v v sin
R
R sinv
v R sin2
R2
sinv R
v R2
sin
cos
R
R sinv
v R sin2
①
R 2 sinv R v R 2 sin cos ②
因此,流函数为
1 2
v
R
2
[1
-
a
3
]sin2
R
势函数为
均
偶
v Rcos
M
4R 2
cos
v R[1
1 2
a 3 ]cos
