第4章理想流体动力学
合集下载
4工程流体力学 第四章流体动力学基础
因为 F 沿 y 轴正向，所以 Fy 取正值
Fy F V•n dS = -V0 dS
= =
=
ρ vV n dS ρ vV n dS ρ vV n dS ρ vV n dS
CS
S0
S1
S2
v = -V0 sin
0
0
§4-2 对控制体的流体力学积分方程（续18）
由于V1，V2在y方向上无分量，
忽略粘性摩擦力，控制体所受表面力包括两
端面及流管侧表面所受的压力，沿流线方向总压
力为：
FSl
pS p δpS δS
p
δp 2
δS
Sδ p 1 δpδS 2
流管侧表面所受压力在流 线方向分量，平均压强
§4-2 对控制体的流体力学积分方程（续27z）
控制体所受质量力只有重力，沿流线方向分
Q2
Q0 2
1 cosθ
注意：同一个问题，控制体可以有不同的取法，
合理恰当的选取控制体可以简化解题过程。
§4-2 对控制体的流体力学积分方程（续23）
微元控制体的连续 方程和动量方程
从流场中取一段长度为l 的流管元，因
为流管侧面由流线组成，因此无流体穿过；流 体只能从流管一端流入，从另一端流出。
CS
定义在系统上 的变量N对时 间的变化率
定义在固定控制 体上的变量N对 时间的变化率
N变量流出控制 体的净流率
——雷诺输运定理的数学表达式，它提供了对
于系统的物质导数和定义在控制体上的物理量
变化之间的联系。
§4-2 对控制体的流体力学积分方程 一、连续方程
在流场内取一系统其体积为 ，则系统内
的流体质量为：
根据物质导数的定义，有：
Fy F V•n dS = -V0 dS
= =
=
ρ vV n dS ρ vV n dS ρ vV n dS ρ vV n dS
CS
S0
S1
S2
v = -V0 sin
0
0
§4-2 对控制体的流体力学积分方程（续18）
由于V1，V2在y方向上无分量，
忽略粘性摩擦力，控制体所受表面力包括两
端面及流管侧表面所受的压力，沿流线方向总压
力为：
FSl
pS p δpS δS
p
δp 2
δS
Sδ p 1 δpδS 2
流管侧表面所受压力在流 线方向分量，平均压强
§4-2 对控制体的流体力学积分方程（续27z）
控制体所受质量力只有重力，沿流线方向分
Q2
Q0 2
1 cosθ
注意：同一个问题，控制体可以有不同的取法，
合理恰当的选取控制体可以简化解题过程。
§4-2 对控制体的流体力学积分方程（续23）
微元控制体的连续 方程和动量方程
从流场中取一段长度为l 的流管元，因
为流管侧面由流线组成，因此无流体穿过；流 体只能从流管一端流入，从另一端流出。
CS
定义在系统上 的变量N对时 间的变化率
定义在固定控制 体上的变量N对 时间的变化率
N变量流出控制 体的净流率
——雷诺输运定理的数学表达式，它提供了对
于系统的物质导数和定义在控制体上的物理量
变化之间的联系。
§4-2 对控制体的流体力学积分方程 一、连续方程
在流场内取一系统其体积为 ，则系统内
的流体质量为：
根据物质导数的定义，有：
工程流体水力学第四章习题答案
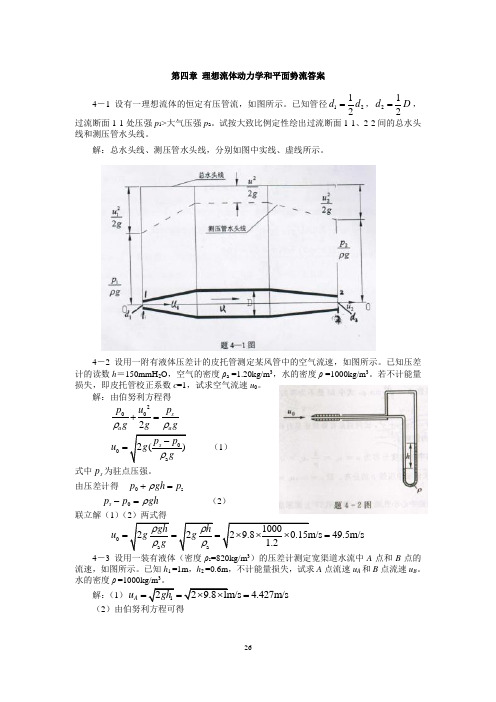
第四章 理想流体动力学和平面势流答案4－1 设有一理想流体的恒定有压管流，如图所示。
已知管径1212d d =，212d D =，过流断面1-1处压强p 1>大气压强p a 。
试按大致比例定性绘出过流断面1-1、2-2间的总水头线和测压管水头线。
解：总水头线、测压管水头线，分别如图中实线、虚线所示。
4－2 设用一附有液体压差计的皮托管测定某风管中的空气流速，如图所示。
已知压差计的读数h ＝150mmH 2O ，空气的密度ρa =1.20kg/m 3，水的密度ρ =1000kg/m 3。
若不计能量损失，即皮托管校正系数c =1，试求空气流速u 0。
解：由伯努利方程得2002s a a p u p g g gρρ+= 00a 2()s p p u g gρ-=（1） 式中s p 为驻点压强。
由压差计得 0s p gh p ρ+=0s p p gh ρ-= （2）联立解（1）（2）两式得0a a 10002229.80.15m/s 49.5m/s 1.2gh h u gg g ρρρρ===⨯⨯⨯= 4－3 设用一装有液体（密度ρs =820kg/m 3）的压差计测定宽渠道水流中A 点和B 点的流速，如图所示。
已知h 1 =1m ，h 2 =0.6m ，不计能量损失，试求A 点流速u A 和B 点流速u B 。
水的密度ρ =1000kg/m 3。
解：（1）1229.81m/s 4.427m/s A u gh ==⨯⨯= （2）由伯努利方程可得22A AA u p h g gρ+= （1）22B BB u p h g gρ+= （2）式中A h 、A p 和B h 、B p 分别为A 点和B 点处的水深和驻点压强。
由（1）、（2）式可得2222A B A BA B p p u u h h g g gρ-=+-- （3） 由压差计得，22ρρρρ--++=A A s B B p gh gh gh gh p ，所以220.82A BA B p p h h h h gρ-=+-- (4) 由（3）式、（4）式得2222 4.427(10.82)0.6(10.82)0.8922229.8B A u u h g g =--=--=⨯ 29.80.892m/s 4.18m/s B u =⨯⨯=。
北航水力学 第四章理想流体动力学和恒定平面势流解读
z1
p1
u12 2g
z2
p2
u22 2g
4.2.2 由动能定理推导理想流体的伯努利方程
推导过程同学们自学
z1
p1
u12 2g
z2
p2
u22 2g
本公式是由动能定理推导而得，它使伯努利方程有更加明确的 物理意义，说明伯努利方程是一能量方程。
第三节 元流伯努利方程的意义和应用
4.3.1 沿流线的伯努利方程的水力学意义
可见，在同一流线上各点的流函数为一常数，故等流函数线就是流线。
2、平面内任意两点流函数值的差等于通过这两点连线的流量。
y ABdrBnA x
d r dxi dy j
n cos i sin j dy i dx j
dr dr V ui v j
dq V
ndr
u
dy dr
v
dx dr
等 线和等Ψ线，这两族曲线互相垂直，构
成流网。
两族曲线所构成的正交网络，称为流网
流网的特征：
流网
等 线和速度矢量垂直，或者说， 等 线与等Ψ线（流线）垂直，
【例题】
已知90度角域内无粘流动，速度分布
ux kx uy ky
(k 0, x 0, y 0)
求：（1）判断该流场是否存在速度势函数， 若存在请给出并画出等势线；
流动。但粘滞性对流动 的影响很微小时，影响可以忽略。 --机械能守恒
引入势流的意义：使问题简化。
波浪运动，无分离的边界层外部的流动，多孔介质的流动（渗流） 等等可以看为势流。
4.4.1 流速势函数
以二维流动为例，根据流体运动学，它与无旋流动等价
由 ux 0 无旋流的条件→涡量 z 0
第4章流体动力学基础1
2、连续性微分方程有哪几种形式？不可压缩流体的连续性 、连续性微分方程有哪几种形式？ 微分方程说明了什么问题？ 微分方程说明了什么问题？ 质量守恒
第二节 元流的伯努利方程
欧拉运动微分方程组各式分别乘以 ， ， （ 欧拉运动微分方程组各式分别乘以dx，dy，dz（流场任意相邻两点间距 各式分别乘以 ds的坐标分量）： 的坐标分量）： 的坐标分量
1 ( Xdx +Ydy + Zdz) − ρ ( ∂p dx + ∂p dy + ∂p dz) = dux dx + ∂x ∂y ∂z dt duy dt
dy + duz dz dt
<I> 考虑条件 、 考虑条件 1、恒定流
<II>
<III>
一、在势流条件下的积分
∂p ∂p =0 ∂t
∂ux ∂uy ∂uz = = =0 ∂t ∂t ∂t
∂ux ∂y ∂uy ∂z ∂ux ∂z
= = =
∂uy ∂x ∂uz ∂y ∂uz ∂x
积分得：
z+γ +
p
u2 2g
=c
•
理想势流（无黏性） 理想势流（无黏性）伯努利方程
z+γ +
p
或
u2 2g
=c
p2 u22 2g
z1 + γ +
p1
u12 2g
= z2 + γ +
在同一恒定不可压缩流体重力势流 恒定不可压缩流体重力势流中 物理意义：在同一恒定不可压缩流体重力势流中 ，各点的总比能值相等 即在整个势流场中，伯努利常数 均相等。（应用条件 均相等。（应用条件： 即在整个势流场中，伯努利常数C均相等。（应用条件：“——”所示） ”所示）
流体力学ppt课件-流体动力学
g
g
2g
水头
，
z
p
g
v2
2g
总水头， hw 水头损失
第二节 热力学第一定律——能量方程
水头线的绘制
总水头线
hw
对于理想流体，总水
1
v12 2g
2
v22 2g
头线是沿程不变的，
测压管水头线
p2
为一水平直线，对于
g
实际流体，总水头沿 程降低，但测压管水
p1 g
头线沿程有可能降低、
z2
不变或者升高。
z1
v2 A2 e2
u22 2
gz2
p2
v1A1 e1
u12 2
gz1
p1
微元流管即为流线，如果不 可压缩理想流体与外界无热 交换，热力学能为常数，则
u2 gz p 常数
2
这个方程是伯努利于1738年首先提出来的，命名为伯努利 方程。伯努利方程的物理意义是沿流线机械能守恒。
第二节 热力学第一定律——能量方程
皮托在1773年用一根弯成直角的玻璃管，测量了法国塞纳河 的流速。原理如图所示，在液体管道某截面装一个测压管和 一个两端开口弯成直角的玻璃管（皮托管），皮托管一端正 对来流，一端垂直向上，此时皮托管内液柱比测压管内液柱 高h，这是因为流体流到皮托管入口A点受到阻滞，速度降为 零，流体的动能变化为压强势能，形成驻点A，A处的压强称 为总压，与A位于同一流线且在A上游的B点未受测压管的影 响，其压强与A点测压管测得的压强相等，称为静压。
第四章 流体动力学
基本内容
• 雷诺输运公式 • 能量方程 • 动量方程 • 流体力学方程应用
第一节 雷诺输运方程
• 前面解决了流体运动的表示方法,但要在流 体上应用物理定律还有困难.
流体力学第四章ppt课件
对于定常无旋运动，式（4－3）括弧内的函数
不随空间坐标ｘ，ｙ，ｚ和时间ｔ变化，因此
它在整个流场为常数。精选课件
10
U p V2 C
2
(通用常数)
对于理想、不可压缩流体、在重力作用下的 定常无、旋运动，因Ｕ＝－ｇｚ，上式可写成
p V2
z
C
(通用常数)
2g
上式为上述条件下的拉格朗日积分式，Ｃ在
整个流场都适用的通用常数，因此它在整个流场
建立了速度和压力之间精的选课件关系。
11
若能求出了流场的速度分布（理论或实验的 方法），就能用拉格朗日积分式求流场的压力分 布，再将压力分布沿固体表面积分，就可求出流 体与固体之间的相互作用力。
应用拉格朗日积分式，可解释许多重要的物
理现象：如机翼产生升力的原因；两艘并排行
U 2
2
g
近似代替 20
适用于有限大流束的伯努利方成为：
z p U2 const
2g
或
z1p1U 21g2 z2p2
U22 2g
方程适用条件：
（13） （14）
（１）理想流体，定常流动；
（２）只有重力的作用；
（３）流体是不可压缩的；
（4）１.２截面处流动须是渐变流。但1.2两断
面间不必要求为渐变流精动选课件。
驶而又靠得很近的船舶为什么会产生互相吸引
的“船吸现象”；以及在浅水航道行驶的船舶为
什么会产生“吸底现象”等等。
精选课件
12
讨论： 1. 如果理想、不可压缩流体作定常、无旋流
动且只有重力作用时，同一水平面上的两 点，其速度和压力的关系如何？ 2. 两艘并排行驶而又靠得很近的船舶为什么会产 生互相吸引的“船吸现象”。
理想流体动力学
2 r0 ln r 1 2 r 2
当 r = r0时 , =
2
ln r0 常 数 , 可见，圆柱表面为一流线。
2
2、速度分布 流场中任一点 p r ,
的速度分量为：
2 r0 v v 1 2 sin r r 2 r
J
A
d J 2 n d A
A
18
2、速度环量 流体质点的旋转角速度矢量无法直接测量，所以旋涡强 度不能直接计算。但是，旋涡强度与它周围的速度密切相关， 旋涡强度愈大，对周围流体速度的影响也就愈大。因此，这 里引入与旋涡周围速度场有关的速度环量的概念。 给定瞬时，在流场的任意封闭曲线上，流体速度矢量沿 封闭曲线的线积分，定义为速度环量，用符号 表示，即
2 r0 vr v 1 2 co s r r
当 r 时 , v r v cos , v v ห้องสมุดไป่ตู้ sin
表明流体在远离圆柱体处保持原来的均匀流，即满足无穷远 处的边界条件。
3
柱面上 r r0 速度分布：
2 r0 v v 1 2 sin r r 2 r
L
2 0
2 1 2 p v 2 v sin r0 sin d v 2 2 r0
12
L v
上式就是著名的库塔-儒可夫斯基（Kutta-Zhoukowski）升力 公式。上面的计算结果表明，理想流体对圆柱体作有环量绕 流时，流体作用在圆柱体上的阻力等于零，而作用在单位长 度圆柱体上的升力等于流体密度、来流速度和速度环量三者 的乘积。 升力的方向由前方来流速 度矢量 v 沿反环流的方 向旋转 9 0 0 来确定，如图 所示。
水力学 第四章 理想流体动力学和平面势流
§4-1 理想流体的运动微分方程—欧拉运动方程
6
3、欧拉运动微分方程和求解条件
运动微分方程组
u u u 1 p u x ux x u y x uz x x t x y z u y u y u y 1 p u y fy ux uy uz y t x y z 1 p u z u z u z u z fz ux uy uz z t x y z fx
§4-1 理想流体的运动微分方程—欧拉运动方程
14
4-1-2 葛罗米柯(又称兰姆)运动微分方程
矢量表示形式：
1 u2 u 2 2ω u f ρ p t
§4-1 理想流体的运动微分方程—欧拉运动方程
15
4-1-3 葛罗米柯运动微分方程的应用—伯努利方程 1、 伯努利方程的推导条件
2
对加速度在y及z的投影做同样处理，即可得到葛罗米柯运动 微分方程，如下：
1 p 1 u 2 u x fx 2ω y uz ωz u y ρ x 2 x t 1 p 1 u 2 u y fy 2ωz u x ωx uz ρ y 2 y t 1 p 1 u 2 uz fz 2ωx u y ω y u x ρ z 2 z t
1 上面三个式的矢量形式为 ： f p du dt
上式为理想流体的运动微分方程，反映了在任意流体微元上单 位质量力、惯性力与压强的平衡关系。 适用范围：恒定流或非恒定流，可压缩流体或不可压缩流体。
§4-1 理想流体的运动微分方程—欧拉运动方程
4
2、欧拉运动微分方程
加速度表示式按欧拉运动描述展开为 du u u u dt t
6
3、欧拉运动微分方程和求解条件
运动微分方程组
u u u 1 p u x ux x u y x uz x x t x y z u y u y u y 1 p u y fy ux uy uz y t x y z 1 p u z u z u z u z fz ux uy uz z t x y z fx
§4-1 理想流体的运动微分方程—欧拉运动方程
14
4-1-2 葛罗米柯(又称兰姆)运动微分方程
矢量表示形式：
1 u2 u 2 2ω u f ρ p t
§4-1 理想流体的运动微分方程—欧拉运动方程
15
4-1-3 葛罗米柯运动微分方程的应用—伯努利方程 1、 伯努利方程的推导条件
2
对加速度在y及z的投影做同样处理，即可得到葛罗米柯运动 微分方程，如下：
1 p 1 u 2 u x fx 2ω y uz ωz u y ρ x 2 x t 1 p 1 u 2 u y fy 2ωz u x ωx uz ρ y 2 y t 1 p 1 u 2 uz fz 2ωx u y ω y u x ρ z 2 z t
1 上面三个式的矢量形式为 ： f p du dt
上式为理想流体的运动微分方程，反映了在任意流体微元上单 位质量力、惯性力与压强的平衡关系。 适用范围：恒定流或非恒定流，可压缩流体或不可压缩流体。
§4-1 理想流体的运动微分方程—欧拉运动方程
4
2、欧拉运动微分方程
加速度表示式按欧拉运动描述展开为 du u u u dt t
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Q=0.036m3/s，水柱的来流速度V=30m/s，若被截取的流量
Q=0.012m3/s，试确定水柱作用在板上的合力R和水流的偏
转角
（略去水的重量及粘性）。 解：设水柱的周围均为大气压。由于不计重力，因此由伯努利方程可知
由连续方程
取封闭的控制面如图，并建立 坐标，设平板对射流柱的作用力为 （由于不考虑粘性，仅为压力）。由动量定理
<<
,
<<
以及与水箱A中流出的流量相比，从B中吸出的流量为小量。） 解：（1）在
及
的假定下，本题可看作小孔出流 由Torricelli定理
处为基准，对水箱 自由液面及最小截面
建立总流伯努利方程 其中
， 故 要使最小截面处压强
低于大气压即为负值必须使 由连续方程
得 故
得此时的条件应为 （2）若从水槽中吸出水时，需具备的条件为 或者 将 代入
时，
例如，当 则
【4.18】 如图,锅炉省煤气的进口处测得烟气负压 h1=10.5mmH2O，出口负压h2=20mmH2O。如炉外空气 ρ=1.2kg/m3，烟气的密度ρ'= 0.6 kg/m3，两测压断面高度 差H=5m，试求烟气通过省煤气的压强损失。 解：本题要应用非空气流以相对压强表示的伯努利方程形式。 由进口断面1至出口断面2列伯努利方程
即 或者 ，
由于 将上述不等式代入
得 【4.14】 如图，一消防水枪，向上倾角
水管直径D=150mm，压力表读数p=3m水柱高，喷嘴直径 d=75mm，求喷出流速，喷至最高点的高程及在最高点的 射流直径。 解：不计重力，对压力表截面1处至喷咀出口2处列伯努利方程
其中
得
式得
另外，由连续方程 得 上式代入
） 若
， 处的截面面积各为 及 ，由连续方程
得 将上式代入（ ）式
得
则文丘里管中的流量
倘若阀门C关闭，阀门D开启时，真空容器内的压强减至
水 则
银柱时，
即
此时流量
【4.11】
如图，一呈上大下小的圆锥形状的储水池，底部 有一泄流管，直径d=0.6m，流量因数μ＝0.8，容器内初始 水深h=3m，水面直径D=60m，当水位降落1.2m后，水面直 径为48m，求此过程所需时间。 解：本题按小孔出流，设某时刻
式中 其它同上 则
以此 代入上述动量定理式中解得
【.1】 【4.20】 下部水箱重224N，其中盛水重897N，如 果此箱放在秤台上，受如图所示的恒定流作用。问 秤的读数是多少。
解：水从上、下水箱底孔中出流速度由Torricelli定理得
流量 而流入下水箱时的流速，由伯努利方程
式中 ，
则 设封闭的控制面如图，设下水箱中水受到重力为 ,水箱对其作用力为 ,并建立坐标轴
当叶片喷咀均固定时，设流体受到叶片的作用力为
由动量定理
方向：
即
得
叶片受到射流对其作用力大小为
，方向与
方向相反。
(2)当控制体在作匀速运动时，由于固结于控制体上的坐
标系仍是惯性
系，在动量定理中只要将相对速度代替
绝对速度即可。
现当叶片以
速度后退，此时射流相对于固结于叶片上的控制面的
相
对速度为
，因此叶片受到的力大小为
由动量定理 即 即 因此秤的读数 水箱自重+流体对水箱的作用力
因此 设最高点位置为
，则根据质点的上抛运动有
射流至最高点时，仅有水平速度
，列喷咀出口处2至 （在大气中压强均为零）。
最高点处3的伯努利方程
得 或者水平速度始终是不变的 由连续方程，最高点射流直径 为
故
【4.15】
如图，水以V=10m/s的速度从内径为50mm的喷管
中喷出，喷管的一端则用螺栓固定在内径为100mm水管的
其中
，
， 则 管内体积流量
(2)以管口2处为基准，对自由液面1处及管内最高点 列1流
线伯努利方程。则 其中
, , , ,
即 9 807
即 点的真空压强
(3)当
不变，
点
增大时，当
点的压强
等于水的汽化压强时，
此时
点发生水的汽化，管内的流动即中止。查表，在常温下
（15
℃）水的汽化压强为1 697
（绝对压强）以管口2为基准，列
式中
【4.19】
故
得
如图,直径为d1=700mm的管道在支承水平面上分 支为d2=500mm的两支管，A—A断面的压强为70kN/m2，管 道流量Q=0.6m3/s，两支管流量相等。（1）不计水头损 失，求支墩受的水平推力；（2）若水头损失为支管流速水 头的5倍，求支墩受的水平推力。（不考虑螺栓连接的作 用） 解：(1)在总管上过流断面上平均流速为
解：以右箱出口处4为基准，对右箱自由液面3到出口处4列流 线伯努利方程
其中
，
则
以左箱出口处2为基准，对左箱自由液面1到出口处2列流线
伯
努利方程
其中
，
，
故
流入右 等，即
当流动处于恒定流动时，应有右箱出口处的流量和左水箱 水箱的流量及补充入左水量的流量均相
即
或者
且左水箱需补充的流量为
【4.8】
本题要注意的是左水箱的水仅是流入右水箱，而不能从1-4直 接列一条流线。
其中 ，
即
由连续性原理，由于 故
又 由于 故 由于
故
流经管路的体积流量
（2）以管口为基准，该处总水头等于
，由于不计粘性损失，因此各截面上总水头均等于
【4.9】
。 如图，在水箱侧壁同一铅垂线上开了上下两个小孔，若两股 射流在O点相交,试证明
。 解： 列容器自由液面0至小孔1及2流线的伯努利方程，可得到 小孔处出流速度
方向： 即
方向：
即
故
代入
式
即作用在板上合力大小为
，方向与
方向相反
【4.17】
一水射流对弯曲对称叶片的冲击如图所示，试就下
面两种情况求射流对叶片的作用力：（1）喷嘴和叶片都固
定；（2）喷嘴固定，叶片以速度
后退。 解：(1)射流四周均为大气压，且不计重力，由伯努利方程， 各断面上的流速均相同。取封闭控制面如图，并建立 坐标，
时，水面已降至
处， 则由托里拆利公式，泄流管处的出流速度为
储水池锥度为 ，因此当水面降至 处时，水面的直径为
由连续方程 在
时间内流出的水量等于液面下降的水量 故
由于 故
本题从总的过程是非恒定流，若应用非恒定流的伯努利方程很 复杂，为此将整个过程微分，每个微分时间内作为恒定流来处 理，然后应用积分的方法来求解。 【4.12】 如图，水箱通过宽B=0.9m，高H=1.2m的闸门往外泄 流，闸门开口的顶端距水面h=0.6m。试计算（1）闸门开 口的理论流量；（2）将开口作为小孔处理时所引起的百分 误差。 解：（1）由图
（
）
计算题
【4.6】
如图，设一虹吸管a=2m,h=6m,d=15cm。试求：
（1）管内的流量；（2）管内最高点S的压强；（3）若h不
变，点S继续升高（即a增大，而上端管口始终浸入水
内），问使吸虹管内的水不能连续流动的a值为多大。
解：(1)以水箱底面为基准，对自由液面上的点1和虹吸管下端 出口处2建立1-2流线伯努利方程，则
点的伯 努利方程，
， ， ， ，
【4.7】
其中
（大气绝对压强） 即
本题要注意的是伯努利方程中两边的压强计示方式要相同，由 于 为绝对压强，因此出口处也要绝对压强。 如图，两个紧靠的水箱逐级放水，放水孔的截面积分别为A1 与A2，试问h1与h2成什么关系时流动处于恒定状态，这时 需在左边水箱补充多大的流量。
由于
，故本题应按大孔出流来处理，将大孔口，沿水
平
方向分割成许多小孔，然后对于每一小孔
按Torricelli定理
出流速度
，小孔面积
理论出流量为
总出流量
（2）当按小孔出流处理时， 出流量
两者引起的相对误差为
【4.13】
今想利用水箱A中水的流动来吸出水槽B中的 水。水箱及管道各部分的截面积及速度如图所示。试求 （1）使最小截面处压强低于大气压的条件；（2）从水槽B 中把水吸出的条件。（在此假定
。此公式称托里拆利公式（Toricelli），它在形式上与初始速 度为零的自由落体运动一样，这是不考虑流体粘性的结果。
由
公式，分别算出流体下落
距离所需的时间，其中
经过
及
时间后，两孔射流在某处相交，它们的水平距离相
等，
即
， 其中
，
， 因此
即
【4.10】 如图，
Venturi管A处的直径d1=20cm，B处的直径
d2=2cm。当阀门D关闭，阀门C开启时测得U型压力计中水
银柱的差h=8mm，求此时Venturi管内的流量。又若将阀门
C关闭，阀门D开启，利用管中的射流将真空容器内的压强
减至100mm（水银柱）时，管内的流量应为多大。
解：由于本题流体是空气，因此忽略其重力。
从A至B两过流断面列总流伯努利方程
因此 （
第4章 理想流体动力学
选择题
【.1】 【4.1】 如图等直径水管，A—A为过流断面，B—B 为水平面，1、2、3、4为面上各点，各点的运
；（
）
。
解：对于恒定渐变流过流断面上的动压强按静压强的分布规 律，即 ，故在同一过流断面上满足
（ ） 【4.2】 伯努利方程中
表示（ ）单位重量流体具有的机械能；（
法兰上，如不计损失，试求作用在连接螺栓上的拉力。
解：由连续方程
故
对喷管的入口及出口列总流伯努利方程