三重积分 柱坐标与极坐标PPT
合集下载
微积分：利用柱坐标计算三重积分
a Dxy
r
,
cos
x
o
y
z x2 y2
I
4
a
2 4 cos
d d r 2 sin2 r 2 sin dr
x r sin cos
y
r
sin
sin
z r cos
00 0
dv r2 sin drdd
I ( x2 y2 )dxdydz
2
a
d 4 d cos r 2 sin2 r 2 sin dr
2
2
dz d
ze z2 rdr
1
0 0r
2 2 ez2 zdz (e4 e). 1
z
z2
z x2 y2
z1
O
y
x
y Dz
x
x2 y2 z2
计算(x y z)2dv,
其中是抛物面 z
x2
y2和 球 面x2
y2
z
z2
2
所围成的空间闭区域.
解 ( x y z)2 x2 y2 z2 2( xy yz zx)
且 当( x, y) Dxy时, x2 y2 z 2 x2 y2 ,
Dxy : x2 y2 1,
y Dxy
x
x2 y2 z 2 x2 y2,
x2 y2 1
2 x2 y2
V 1 dv dxdy
1 dz
x2 y2
Dxy
(2 2 x 2 2 y 2 )dxdy
Dxy
2
2
d
1 (1 r 2 )rdr
0
0
0
0
t (0, )
0 r t
所以,F (t)在(0, )内 单调增加.
计算三重积分详细方法
一般，先对 z 积分，再对 r ，最后对 积分。 6
例1 利用柱面坐标计算三重积分 zdxdyd, z 其中
是由z曲 x2面 y2与平 z面 4所围成的闭
解 (1) 画 图
z
(2) 确定 z，r， 的上下限
44
将 向 xoy 面投影，得
D :x2y24
或
02,
D:
0r2.
o•(r,)
yy
xx
就叫M 点 的柱面坐标． z
规定： 0r,
02 ,
•M (x,y,z)
z . 简单地说，柱面坐标就是
or
y
•
P(r,)
x
xoy 面上的极坐标 + z 坐标
4
如图，三坐标面分别为
r 为常数
为常数
z 为常数
圆柱面； 半平面； 平 面．
柱面坐标与直角坐标的 关系为
x r cos ,
y
r
sin
,
z
z.
z
z
or
y
x
z
M (x ,y,z)
•
o
x
r
y
• P(r,) 5
如图，柱面坐标系中的 体积元素为
d v rdd rd, z
z
rd
dr r dz
于是，
o
y
f(x,y,z)dxdydz
x d
f (r c o ,r ssi,z n )r d dr d . z
再根据 中 z，r， 的关系，化为三次积分。
z
R
任取一 [0,2],过 z
轴作半平面，得
04.
在半平面上，任取一
[0, 4],
x
柱坐标、球坐标下的三重积分
解：由图知：直角系：
D
y
x
2
4 x2
6x2 y2
I dx
dy
f (x, y, z)dz
2
4x2
x2 y2
柱标系： I
2
d
2
rdr
6r 2
f (r cos , r sin , z)dz
0
0
r
杂例
在三种坐标系下化三重积分 f (x, y, z)dv为三次积分，
z
其中：z 6 x2 y2, z x2 y2 z 6 x2 y2 6
四、柱坐标、球坐标下的三重积分
1. 柱坐标：(θ,r,z)
zz
变换为：x r cos , y r sin , z z
即：(x, y, z) (r cos , r sin , z),其中：
0 r ,0 2 ,| J || (x, y, z) | r ( , r, z)
x
注：柱坐标— 极坐标平面竖起一根Z轴。x
上顶： z 1 x2 y2
下底： z = 0
z
Dxy: x 2 y 2 1
x y
I dxdy
zdz
Dxy
用哪种坐标？ 柱面坐标 .
.
2π
1
1r 2
I = 0 dθ 0 rdr0 zdz
Dxy 0
1
4
x
z0
1y
注：用柱坐标求 fdv分成两个步骤：
第一步：先一后二，对z积分后将二重积分化为极坐 标下的二重积分；
元素区域由六个坐标面围成：
半平面及+d ;
半径为r及 r+dr的园柱面；
平面 z及 z+dz；
dz
极坐标与球面坐标计算三重积分
方向转到有向线段
的角．
OP
这样的三个数r、围为
x
0 r<，0 j <，0q 2．
r j
O
q x
M(x, y, z)
y
y
P
坐标面rr0，jj 0，q q 0的意义： z
j O
q
x
ry
点的直角坐标与球面坐标的关系：
x r sin j cosq ,
一、利用柱面坐标计算三重积分
设M(x, y, z)为空间内一点，则点M与数 r、q 、z相对应， 其中P(r, q )为点M在xOy面上的投影的极坐标．
三个数 r、q 、z 叫做点M 的柱面坐标．
这里规定r、q 、z的变化范围为： 0 r<， 0 q 2 ， < z<．
z z
M(x, y, z)
O
2
dq
a
dj
2a cosj r 2 sin jdr
0
0
0
jr
2
a
s in jdj
2a cosj r 2 dr
0
0
a
16a3 a cos3 j sinjdj 30
O
y
4a3 (1 cos4 a) ．
x
3
例3 求均匀半球体的重心．
z
解 取半球体的对称轴为 z 轴， 原点取在球心上，又设球半径为a．
坐标面rr0，q q 0，zz0的意义：
x
z
z0
rr0 O
r0 q0
zz0
q q 0 y
直角坐标与柱面坐标的关系：
z
x r cosq ,
y
r
sin
q
,
z z.
利用柱面坐标计算三重积分
`z
z
j r
zdv
dvΒιβλιοθήκη zdvO
dv
a 2 0 2
．
q
x
a y
dv 2 dj dq
2
0
0
2a 3 , r sin jdr 3
a
1 a4 , zdv 2 dj dq r cos j r 2 sin jdr 2 0 0 0 2 4 3a 3a 因此`z ．重心为(0，0， )． 8 8
§9．5 利用柱面坐标和球面坐标计算三重积分
一、利用柱面坐标计算三重积分
柱面坐标、 柱面坐标系的坐标面 直角坐标与柱面坐标的关系、柱面坐标系中的体积元素
柱面坐标系中的三重积分
二、利用球面坐标计算三重积分
球面坐标、球面坐标系的坐标面 直角坐标与球面坐标的关系、球面坐标系中的体积元素 球面坐标系中的三重积分
，r sin q ，z) rdrdqdz．
例1 例1 利用柱面坐标计算三重积分 zdxdydz，其中是由曲
面 zx2y2 与平面 z4 所围成的闭区域．
z 4 zx2y2 或 zr2
解 闭区域可表示为：
r 2z4，0r2，0q2． 于是
zdxdydz zrdrdqdz
2 r sin jdrdjdq dq sin j dj r 4 dr a 2 M , 0 0 0 5
4 3
2
3
a
4 3 其中 M a 为球体的质量． 3
一、利用柱面坐标计算三重积分
设M(x, y, z)为空间内一点，则点M与数 r、q 、z相对应， 其中P(r, q )为点M在xOy面上的投影的极坐标． 三个数 r、q 、z 叫做点M 的柱面坐标． z 这里规定r、q 、z的变化范围为： 0 r<， 0 q 2 ， < z<． O x r y P(r, q ) y z
z
j r
zdv
dvΒιβλιοθήκη zdvO
dv
a 2 0 2
．
q
x
a y
dv 2 dj dq
2
0
0
2a 3 , r sin jdr 3
a
1 a4 , zdv 2 dj dq r cos j r 2 sin jdr 2 0 0 0 2 4 3a 3a 因此`z ．重心为(0，0， )． 8 8
§9．5 利用柱面坐标和球面坐标计算三重积分
一、利用柱面坐标计算三重积分
柱面坐标、 柱面坐标系的坐标面 直角坐标与柱面坐标的关系、柱面坐标系中的体积元素
柱面坐标系中的三重积分
二、利用球面坐标计算三重积分
球面坐标、球面坐标系的坐标面 直角坐标与球面坐标的关系、球面坐标系中的体积元素 球面坐标系中的三重积分
，r sin q ，z) rdrdqdz．
例1 例1 利用柱面坐标计算三重积分 zdxdydz，其中是由曲
面 zx2y2 与平面 z4 所围成的闭区域．
z 4 zx2y2 或 zr2
解 闭区域可表示为：
r 2z4，0r2，0q2． 于是
zdxdydz zrdrdqdz
2 r sin jdrdjdq dq sin j dj r 4 dr a 2 M , 0 0 0 5
4 3
2
3
a
4 3 其中 M a 为球体的质量． 3
一、利用柱面坐标计算三重积分
设M(x, y, z)为空间内一点，则点M与数 r、q 、z相对应， 其中P(r, q )为点M在xOy面上的投影的极坐标． 三个数 r、q 、z 叫做点M 的柱面坐标． z 这里规定r、q 、z的变化范围为： 0 r<， 0 q 2 ， < z<． O x r y P(r, q ) y z
§9.5[1]利用柱面坐标和极坐标计算三重积分
![§9.5[1]利用柱面坐标和极坐标计算三重积分](https://img.taocdn.com/s3/m/548e0093daef5ef7ba0d3c78.png)
再根据 中 z,r,θ 的关系,化为三次积分. , , 的关系,化为三次积分. 积分. 一般, 积分, 一般,先对 z 积分,再对 r ,最后对 θ 积分.
例1 利用柱面坐标计算三重积分
∫∫∫ z dxdydz ,
其中 其中
所围成的闭区域. 是由曲面 z = x2 + y2 与平面 z = 4 所围成的闭区域.
2
A
过 (r, θ )∈D 做平行于 z 轴 ∈ 的直线, 的直线,得
4
z
r2 ≤ z ≤ 4
0 ≤ θ ≤ 2π , : 0 ≤ r ≤ 2, 2 r ≤ z ≤ 4
o (r,θ )
x
y
即
r =2
o
2
于是, 于是,
A
∫∫∫ z dxdydz = ∫∫∫ z r drdθ dz.
= ∫0 dθ ∫0 dr∫r2 r z dz
规定: 规定:
z
0 ≤ r < +∞,
0 ≤ ≤π,
o θ
x
r
M( x, y, z)
y
0 ≤ θ ≤ 2π .
P
z
如图, 如图,三坐标面分别为
r 为常数
球
面;
r
为常数
θ 为常数
圆锥面; 圆锥面; 半平 面.x来自zoθ
y
球面坐标与直角坐标的关系为
x = r sin cosθ , y = r sin sinθ , z = r cos.
= 2π ∫0 (Hr 3 r4 )dr
π H5 . =
10
二,利用球面坐标计算三重积分
设 M( x, y, z) 为空间内一点,则点M 可用三个有次 为空间内一点, 来确定, 序的数r,,θ 来确定,其中r 为原点O 与点 M 间 的距离, θ 轴正向所夹的角, 的距离, 为有向线段OM与z 轴正向所夹的角, 为从正z 轴来看自x 轴按逆时针方向转到有 向线段 OP 的角,这里P 为点 M 在 xoy 面上的投影,这 的角, 面上的投影, 的球面坐标. 样的三个数r,,θ 就叫做点M 的球面坐标.
8.3.1 三重积分-直角坐标系切片法,柱面坐标系
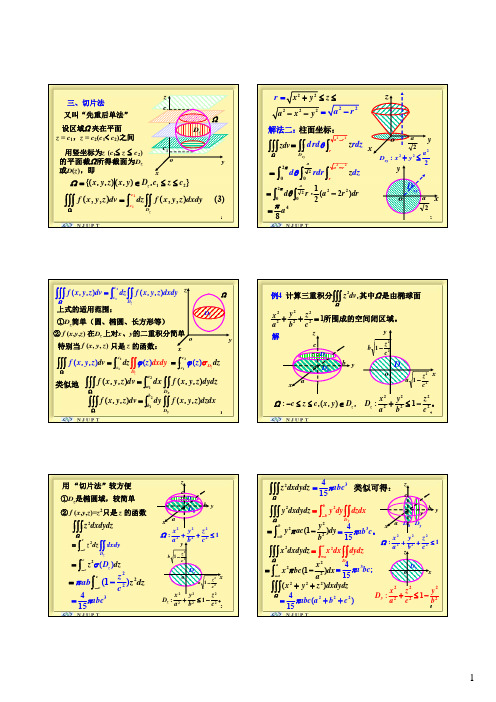
三、切片法又叫“先重后单法”设区域Ω夹在平面z =c 1，z =c 2(c 1<c 2)之间Ω1c 2c z用竖坐标为z c ≤z ≤c zD 1},),(),,{(21c z c D y x z y x z ≤≤∈=Ωyxo (12)的平面截Ω所得截面为D z 或D (z )，即21(,,)(,,) (3)zc c D f x y z dv dz f x y z dxdy Ω=⎰⎰⎰⎰⎰⎰柱解法二：面坐标：⎰⎰⎰zdv ∙yzxo2a 2a 22222x y z a x y +≤≤--22a r=-r =22r ra z d rd rdz θ-=⎰⎰⎰22a yxo⎰⎰-⋅=202220)2(21a dr r a r d πθΩ48a π=xyD 22:2xy D x y +≤xyD 22220a r ra z d rdr dzπθ-=⎰⎰⎰ΩzyozD ⎰⎰⎰⎰⎰⎰=zD c c dxdy z y x f dz dv z y x f ),,(),,(21Ω特别当f (x , y , z ) 只是z 的函数：②f (x ,y ,z ) 在D z 上对x 、y 的二重积分简单①D z 简单（圆、椭圆、长方形等）上式的适用范围：3x类似地⎰⎰⎰⎰⎰⎰=ΩxD a adydzz y x f dx dv z y x f ),,(),,(21⎰⎰⎰⎰⎰⎰=ΩyD b bdzdxz y x f dy dv z y x f ),,(),,(2121(,,)()zc c D dxd dv d f y z y x z z ϕΩ=⎰⎰⎰⎰⎰⎰21()z c c D z dzϕσ=⎰解2222222,14z dv y z x a b c ΩΩ++=⎰⎰⎰计算三重积分其中是由椭球面所围成的空间例闭区域。
zc y 21z b -4,),(,:z D y x c z c ∈≤≤-Ω。
2222221:c z b y a x D z -≤+D 0D z xyz ab o zD 221cz a -x o2c ⎰⎰⎰Ωdxdydzz 2D 0D z z x yz ab oc ①D z 是椭圆域，较简单②f (x ,y ,z )=z 2只是z 的函数用“切片法”较方便1:222222≤++cz b y a x Ω2cz 53154abcπ=zD 221c z a -yx o221c zb -。
D10_3三重积分 柱坐标与极坐标
利用柱坐标计算三重积分的步骤
考虑是否用柱坐标计算
化为柱坐标系下 三重积分
积分次序：
定限方法：
化为累次积分
计算累次积分
注意
对一个变量积分时，将其余变量视为常数
Ω的投影为圆或圆的一部分
f(x,y,z)中含有
或
三变、一勿忘
积分区域
Ω
积分区域
Ω
球坐标表示
被积函数
体积元素
一个勿忘
一般先r后φ再θ．
观察、想象．
三重积分的定义和计算
在直角坐标系下的体积元素
（计算时将三重积分化为三次积分）
小结
方法1. “先一后二”
方法2. “先二后一”
2. 确定上下曲面函数，得 z的积分限;
1. 把Ω往xoy平面上投影,得积分区域D;
4. 最后计算单积分
第三节
一、三重积分的概念
二、三重积分的计算
三重积分
第十章
回忆用投影法（先一后二）计算三重积分
如果积分区域 在坐标面上的投影区域 D 是圆域
则二重积分应当考虑用极坐标计算.
这就等于用柱面坐标计算三重积分.
2. 利用柱坐标计算三重积分
2. 利用柱坐标计算三重积分
于所求立体的体积为
此球面的方程为x2y2(za)2a2 即x2y2z22az
例6.
的立体的体积
由圆锥面和球面围成 ,
解:
采用球面坐标，
锥面方程为
在球面坐标下球面方程为r2acos ,
例7. 计算三重积分
解: 在球面坐标系下
所围立体.
其中
面
是由两个球
解:
例7. 计算三重积分
考虑是否用柱坐标计算
化为柱坐标系下 三重积分
积分次序：
定限方法：
化为累次积分
计算累次积分
注意
对一个变量积分时，将其余变量视为常数
Ω的投影为圆或圆的一部分
f(x,y,z)中含有
或
三变、一勿忘
积分区域
Ω
积分区域
Ω
球坐标表示
被积函数
体积元素
一个勿忘
一般先r后φ再θ．
观察、想象．
三重积分的定义和计算
在直角坐标系下的体积元素
（计算时将三重积分化为三次积分）
小结
方法1. “先一后二”
方法2. “先二后一”
2. 确定上下曲面函数，得 z的积分限;
1. 把Ω往xoy平面上投影,得积分区域D;
4. 最后计算单积分
第三节
一、三重积分的概念
二、三重积分的计算
三重积分
第十章
回忆用投影法（先一后二）计算三重积分
如果积分区域 在坐标面上的投影区域 D 是圆域
则二重积分应当考虑用极坐标计算.
这就等于用柱面坐标计算三重积分.
2. 利用柱坐标计算三重积分
2. 利用柱坐标计算三重积分
于所求立体的体积为
此球面的方程为x2y2(za)2a2 即x2y2z22az
例6.
的立体的体积
由圆锥面和球面围成 ,
解:
采用球面坐标，
锥面方程为
在球面坐标下球面方程为r2acos ,
例7. 计算三重积分
解: 在球面坐标系下
所围立体.
其中
面
是由两个球
解:
例7. 计算三重积分
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
4}
上边界曲面为z 4 下边界曲面为z .
(x2 y2)dv
2
d
2
d
2 2 dz
0
0
dv d ddz
2
2 3d
2
dz 2
2 3(2 )d 16
0
0
5
例3. 计算三重积分
其中 由球面
x2 y2 z2 2与抛物面
x2 y2 z 所围成 .
解:
由 2 z2 2 知交线为
0
0
2
2 π 1 2 (16 2 )d 20
xO y dv d ddz
64 .
3
例2. 计算
(x2 y2 )dv, 其中 由圆锥面
与平面 z 2所围成 .
z x2 y2
解：
由z z
2
x2
y2
得交线 上投影区域为
x2
y2 4, 故在xOy平面
Dxy {(x, y) | x2 y2
设 M (x, y, z) R3,将x, y用极坐标, 代替, 则（, , z)
就称为点M 的柱坐标.
直角坐标与柱面坐标的关系:
x cos y sin
zz
坐标面分别为
常数 常数
z 常数
00z2π
圆柱面 半平面 平面
z z
M (x, y, z)
O
y
x
(x,
y,0)
元素区域由六个坐标面围成
常见曲面的柱面坐标方程
用柱面坐标计算三重积分的一般步骤：
次序为：zr
1、将区域往xoy面上投影，确定平面区域D
2、利用公式
x r cos, y r sin, z z.
将的边界曲面、被积函数 f（x，y，z）、体积元素、三重积分化为柱面坐标 系下形式；
3、过D内任一点（x，y）做平行于z 轴的直线，穿区域确定z的上下限；
利用柱坐标计算三重积分的步骤
考虑是否用柱坐标计算
Ω的投影为圆或圆的一部分 f(x,y,z)中含有x2 y2或arctan y
x
f ( x, y, z)dxdydz
三
变
化为柱坐标系下 三重积分
、 一 勿
积分区域 Ω 被积函数f (x, y, z) 体积元素 dxdydz
忘 一个勿忘
柱坐标表示 f ( cos, sin, z) d d dz
2 z
z 1, 1,
z
上边界: z 2 2 , 下边界: z 2,
原式 =
2π
d
1
d
2 2
zdz
x
0
0
2
o
y
1 2
2
d
0
1(2 2 4)d
0
2
1 4
4
1 6
6
1 0
7 12
.
例4. 计算三重积分
其中 为
由柱面 x2 y2 2x 及平面 z 0, z a (a 0), y 0 所
柱面 与 d;
半平面与 d;
平面z与z dz
在柱面坐标系中体积元素为
d v d dd z
因此
f (x, y, z)dxdydz
z
o
x
dv z dz
z
y
d
d
d d dz
d d d
当积分域的投影域D为与圆域有关的区域时,
一般选用柱面坐标,此时曲面应表示为z z(r, ).
z Dz
2. 对z∈[a,b]用过点(0,0,z)且平行 xOy平面的平面去截Ω ，得截面Dz;
a y
3. 先求关于x,y的二重积分,得
x
F(z) f (x, y, z)dxdy
4. 最后计算单积分
b
a F (z)dz
Dz
第三节
第十章
三重积分
一、三重积分的概念 二、三重积分的计算
2. 利用柱坐标计算三重积分
定限方法：观察、想象．
计算累次积分 注意 对一个变量积分时，将其余变量 视为常数．
小结
三重积分的定义和计算
（计算时将三重积分化为三次积分）
在直角坐标系下的体积元素
dv dxdydz
方法1. “先一后二” 方法2. “先二后一”
dxdy z2 (x,y) f (x, y, z)d z
D
z1(x, y)
b
a d zDZ f (x, y, z)dxdy
先一后二”积分法的基本步骤:
z
1. 把Ω往xoy平面上投影,得积分区域D;
2. 确定上下曲面函数，得 z的积分限;
3. 先求关于z的定积分,得x,y的二元函数;
4. 再求关于x,y的二重积分. “先二后一”积分法的基本步骤:
z
O x
Dxy得z的积分限[a,b];
三
变
化为球坐标系下 三重积分
、 一 勿
积分区域 Ω 被积函数f (x, y, z) 体积元素 dxdydz
忘 一个勿忘 r2 sin
球坐标表示 F (r,, ) r2 sindrdd
化为累次积分
f (r sin sin , r sin cos , r cos )r2 sindrdd
积分次序：一般先r后φ再θ．
如图所示, 在柱面坐标系中体积元素为 z
d v d dd z
z
因此
f (x, y, z)dxdydz
d d dz
dz
O
y
其中
F(, , z) f ( cos , sin , z )
x d
d
d d d
适用范围:
1) 积分域表面用柱面坐标表示时方程简单 ;
2) 被积函数用柱面坐标表示时变量互相分离.
常见曲面的柱面坐标方程
曲面
半球面
圆锥面 旋转抛物面
直角坐标方程 z a2 x2 y2 z x2 y2 z x2 y2
柱面坐标方程 z a2 r2
zr z r2
圆柱面 圆柱面 圆柱面
x2 y2 a2 x2 y2 2ax x2 y2 2ay
ra
r 2a cos r 2asin
4、在 D上分别确定r、上下限（类同于平面极坐标）
柱面坐标常用于：
圆柱体和圆锥体上的三重积分。
例1. 计算三重积分
其中 由抛物面
z x2 y2 与平面 z 4 所围成 .
解: 在xOy面上的投影区域D:
z
上边界曲面为z 4 下边界曲面为z .
4
在柱面坐标系下
原式 =
2π
d
2
d
4
zd z
z
回忆用投影法（先一后二）计算三重积分
f (x, y, z)dV dxdy z2 (x,y) f (x, y, z)dz
D
z1 ( x, y )
O
Dxy
y
x
如果积分区域 在坐标面上的投影区域 D 是圆域
则二重积分应当考虑用极坐标计算.
这就等于用柱面坐标计算三重积分.
2. 利用柱坐标计算三重积分
化为累次积分
f ( cos , sin , z)dddz
积分次序：一般先z后ρ再θ
定限方法：投影、发射
计算累次积分 注意 对一个变量积分时，将其余变量 视为常数
利用球坐标计算三重积分的步骤
考虑是否用球坐标计算
Ω的球或球的一部分 f(x,y,z)中含有x2 y2 z2
f ( x, y, z)dxdydz