圆复习总结与经典题型
关于圆的题型归纳和解题技巧

关于圆的题型归纳和解题技巧
一、题型归纳
1、求圆的半径和面积:
有时会给出圆的弦或者其他部分的参数,通过这些参数可以求出圆的半径和面积;有时可以使用圆的性质,如圆的内接三角形、外接三角形等,来求出圆的半径和面积;有时候还可以使用极坐标系来求解;
2、求圆的直径和周长:
一般来说周长=直径×π,可以利用这个公式求圆的周长;有时可以利用圆的性质,如圆的内接三角形、外接三角形等,来求圆的直径;也可以利用极坐标系来求解;
3、求圆心角:
有时给出的是圆的扇形的面积或者弧长,可以通过求出这个面积或者弧长对应的角度来求出圆心角;有时也给出的是圆弧上一点与圆心的连线,可以利用此线段及其他线段的角度来求出圆心角;
4、求圆的外接矩形或者其他图形:
有时给出的是圆的面积和某种图形的面积,可以计算出圆外接图形的面积,从而求出圆的外接矩形;有时也可以使用圆的性质,如圆的内接三角形、外接三角形等,来求出圆的外接矩形或者其他图形。
二、解题技巧
1、多用圆的性质:
圆的性质是圆的重要组成部分,其中有很多性质都可以用来帮助
解答圆的问题,如圆的内接三角形、外接三角形等;
2、注意圆的关键参数:
在回答圆的问题时,要特别注意特殊参数,如半径、直径等,它们可以使用其他参数来求出;
3、利用极坐标系:
极坐标系是求解圆的一种重要方法,它可以帮助我们简化复杂的问题,使得计算更简单、更快捷;
4、利用其他图形的特殊参数:
有些圆的题目可以利用其他图形的特殊参数来求解,例如外接矩形的长和宽,或者外接三角形的边长等。
关于圆的题型归纳和解题技巧

关于圆的题型归纳和解题技巧
一、关于圆形的题型归纳
1. 圆的概念:一种特殊的平面图形,具有圆心、半径和圆周的性质,由起点和终点构成的曲线,其形状和位置完全由圆心和半径控制。
2. 圆的性质:圆的面积等于圆的半径的平方乘以π,即S=πr2;圆的周长等于圆的半径乘以2π,即C=2πr。
3. 圆的分类:根据圆的形状可分为完全圆形,半圆形,四分圆形,椭圆形等。
4. 关于圆的极角:圆的极角为起点和终点之间的夹角;对任意一点在圆上,该点到圆心的距离称为该点的弦长,而连接该点和圆心的射线称为该点的极角,极角单位为度(°)。
5. 关于圆的直径、弦、弧、圆心角:直径是圆的最长的一条线段,其中任意两点到圆心的距离相等;弦是圆的一部分,由圆的两个端点和圆心连接而成的线段;弧是圆的一部分,由圆的两个端点和圆周连接而成的曲线;圆心角是两个弦的夹角,其角度值等于圆周长除以圆的直径所得到的结果。
二、解题技巧
1. 关于圆的题目一般都是关于坐标图形的,因此,解题的步骤就应当是确定坐标,然后根据坐标去求圆的性质,比如求圆心、半径、圆周等。
2. 在求解圆的性质时,可以利用两点定理、勾股定理等几何知
识,先求出圆上的点与点之间的距离,然后求出圆的半径,再根据圆的性质求其他的信息。
3. 在处理相关问题时,要掌握好圆的各项性质,不要忘记极角、直径、弦以及圆心角的概念,以免出现误解圆的基本性质,从而出现差错。
4. 针对求圆面积或圆周长的题目,要熟悉圆的性质,圆面积为πr2,圆周长为2πr,因此,只要计算出圆的半径,就可以得出答案。
(完整版)圆知识点总结与例题讲解

一、圆的概念与周长1.圆的定义:平面上的一种曲线图形。
2.将一张圆形纸片对折两次,折痕相交于圆中心的一点,这一点叫做圆心。
圆心一般用字母O表示。
它到圆上任意一点的距离都相等.3.半径:连接圆心到圆上任意一点的线段叫做半径。
半径一般用字母r表示。
把圆规两脚分开,两脚之间的距离就是圆的半径。
∆4.圆心确定圆的位置,半径确定圆的大小。
5.直径:通过圆心并且两端都在圆上的线段叫做直径。
直径一般用字母d表示。
6.在同一个圆内,所有的半径都相等,所有的直径都相等。
7.在同一个圆内,有无数条半径,有无数条直径。
8.在同一个圆内,直径的长度是半径的2倍,半径的长度是直径的一半。
用字母表示为:d=2r r =12d用文字表示为:半径=直径÷2 直径=半径×29.圆的周长:围成圆的曲线的长度叫做圆的周长。
△10.圆的周长总是直径的3倍多一些,这个比值是一个固定的数。
我们把圆的周长和直径的比值叫做圆周率,用字母π表示。
圆周率是一个无限不循环小数。
在计算时,取π≈3.14。
世界上第一个把圆周率算出来的人是我国的数学家祖冲之。
☆11.圆的周长公式:C=πd 或C=2πr圆周长=π×直径圆周长=π×半径×212.轴对称图形:如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形。
折痕所在的这条直线叫做对称轴。
☆13.有一条对称轴的图形有:角、等腰三角形、等腰梯形、扇形、半圆。
有2条对称轴的图形是:长方形有3条对称轴的图形是:等边三角形有4条对称轴的图形是:正方形有无数条对称轴的图形是:圆、圆环。
△14.圆是轴对称图形,直径所在的直线是圆的对称轴。
例题讲解:一、填空题△1、圆是()图形,()所在的直线是圆的(),圆有()条对称轴。
2、圆的周长是它的直径的()倍多一些,这个倍数是一个固定的数,我们把它叫(),常用字母()表示。
它是一个()小数,取两位小数是()。
中考数学复习《圆》经典题型及测试题(含答案)
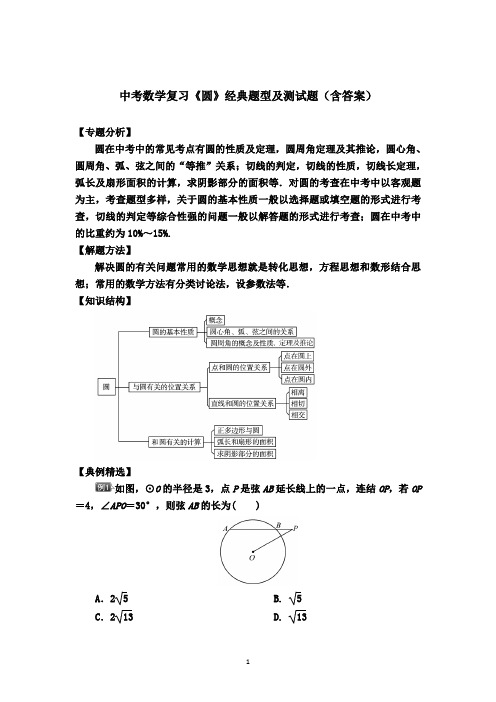
中考数学复习《圆》经典题型及测试题(含答案)【专题分析】圆在中考中的常见考点有圆的性质及定理,圆周角定理及其推论,圆心角、圆周角、弧、弦之间的“等推”关系;切线的判定,切线的性质,切线长定理,弧长及扇形面积的计算,求阴影部分的面积等.对圆的考查在中考中以客观题为主,考查题型多样,关于圆的基本性质一般以选择题或填空题的形式进行考查,切线的判定等综合性强的问题一般以解答题的形式进行考查;圆在中考中的比重约为10%~15%.【解题方法】解决圆的有关问题常用的数学思想就是转化思想,方程思想和数形结合思想;常用的数学方法有分类讨论法,设参数法等.【知识结构】【典例精选】如图,⊙O的半径是3,点P是弦AB延长线上的一点,连结OP,若OP =4,∠APO=30°,则弦AB的长为( )A.2 5 B. 5C.213 D. 13【思路点拨】先过点O作OC⊥AP,连结OB,根据OP=4,∠APO=30°,求出OC的值,在Rt△BCO中,根据勾股定理求出BC的值,进而得出AB的值.【解析】如图,过点O作OC⊥AP于点C,连结OB,∵OP=4,∠APO=30°,∴OC=4×sin 30°=2.∵OB=3,∴BC=OB2-OC2=32-22=5,∴AB=2 5.故选A.答案:A规律方法:利用垂径定理进行证明或计算,通常是在半径、圆心距和弦的一半所组成的直角三角形中,利用勾股定理构建方程求出未知线段的长.如图,从一块直径是8 m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )A.4 2 m B.5 m C. 30 m D.215 m【思路点拨】首先连结AO,求出AB,然后求出扇形的弧长BC,进而求出扇形围成的圆锥的底面半径,最后应用勾股定理求出圆锥的高即可.【解析】如图,连结AO,∵AB=AC,点O是BC的中点,∴AO⊥BC.又∵∠BAC=90°,∴∠ABO=∠ACO=45°,∴AB=2OB=2×(8÷2)=42(m).∴l BC=90π×42180=22π(m).∴将剪下的扇形围成的圆锥形的半径是22π÷2π=2(m).∴圆锥的高是422-22=30(m).故选C.答案:C规律方法:解决圆锥的相关问题,可以利用圆的周长等于扇形的弧长建立方程,利用方程解决问题.如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心、ED 为半径作半圆,交A,B所在的直线于M,N两点,分别以MD,ND为直径作半圆,则阴影部分的面积为( )A.9 5 B.18 5 C.36 5 D.72 5【思路点拨】根据图形可知阴影部分的面积=两个小的半圆的面积+△DMN 的面积-大半圆的面积,MN为半圆的直径,从而可知∠MDN=90°,在Rt△MDN 中,由勾股定理可知MN2=MD2+DN2,从而可得到两个小半圆的面积=大半圆的面积,故此阴影部分的面积=△DMN的面积,在Rt△AED中,ED=AD2+AE2=62+32=35,所以MN=65,然后利用三角形的面积公式求解即可.【解析】根据图形可知阴影部分的面积=两个小的半圆的面积+△DMN的面积-大半圆的面积.∵MN为大半圆的直径,∴∠MDN=90°.在Rt△MDN中,MN2=MD2+DN2,∴两个小半圆的面积和=大半圆的面积.∴阴影部分的面积=△DMN 的面积.在Rt△AED中,ED=AD2+AE2=62+32=35,∴阴影部分的面积=△DMN的面积=12MN·AD=12×65×6=18 5.故选B.答案:B规律方法:求阴影部分的面积,一般是将所求阴影部分进行分割组合,转化为规则图形的和或差.如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,连结CD.(1)求证:∠A=∠BCD.(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.【思路点拨】(1)根据圆周角定理可得∠ADC=90°,根据直角三角形的性质可得∠A+∠ACD=90°,再由∠DCB+∠ACD=90°,可得∠A=∠BCD;(2)当点M是BC的中点时,直线DM与⊙O相切.连结DO,证明∠ODM =90°,进而证得直线DM与⊙O相切.【自主解答】(1)证明:∵AC为直径,∴∠ADC=90°,∴∠A+∠ACD=90°.∵∠ACB=90°,∴∠BCD+∠ACD=90°,∴∠A=∠BCD.(2)解:当点M是BC的中点时,直线DM与⊙O相切.理由如下:如图,连结DO,∵DO=CO,∴∠1=∠2.∵∠BDC=90°,点M是BC的中点,∴DM=CM,∴∠4=∠3.∵∠2+∠4=90°,∴∠1+∠3=90°,∴直线DM与⊙O相切.规律方法:在判定一条直线是圆的切线时,如果这条直线和圆有公共点,常作出经过公共点的半径,证明这条直线与经过公共点的半径垂直,概括为“连半径,证垂直,得切线”.【能力评估检测】一、选择题1.如图,AB是⊙O的直径,点C在⊙O上,AE是⊙O的切线,A为切点,连结BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为( B )A.40° B.50° C.60° D.20°2.如图,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=2,则弦BC的长为( C )A. 3 B.3 C.2 3 D.43.如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为( A )A.25° B.50° C.60° D.30°4.如图,直线CD与以线段AB为直径的圆相切于点D并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD上移动.当∠APB的度数最大时,则∠ABP 的度数为( B )A.15° B.30° C.60° D.90°5.如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心、AB长为半径的扇形(忽略铁丝的粗细),则所得扇形DAB的面积为( D )A.6 B.7 C.8 D.96.如图,已知AB为⊙O的直径,AD切⊙O于点A,EC=CB.则下列结论中不一定正确的是( D )A.BA⊥DA B.OC∥AEC.∠COE=2∠CAE D.OD⊥AC7.如图,菱形ABCD的对角线BD,AC分别为2,23,以B为圆心的弧与AD,DC相切,则阴影部分的面积是( D )A.23-33π B.43-33πC.43-π D.23-π8.如图,正六边形ABCDEF是边长为2 cm的螺母,点P是FA延长线上的点,在A,P之间拉一条长为12 cm的无伸缩性细线,一端固定在点A,握住另一端点P拉直细线,把它全部紧紧缠绕在螺母上(缠绕时螺母不动),则点P运动的路径长为( B )A .13π cmB .14π cmC .15π cmD .16π cm9.如图,在矩形ABCD 中,AB =4,AD =5,AD ,AB ,BC 分别与⊙O 相切于E ,F ,G 三点,过点D 作⊙O 的切线交BC 于点M ,切点为N ,则DM 的长为( )A. 133B. 92C. 4313 D .2 5 解:如图,连接OE ,OF ,ON ,OG .∵AD ,AB ,BC 分别与⊙O 相切于E ,F ,G 三点,∴∠AEO =∠AFO =∠OFB =∠BGO =90°.∴四边形AFOE ,FBGO 都是正方形.∴AF =BF =AE =BG =2.∴DE =3.∵DM 是⊙O 的切线,∴DN =DE =3,MN =MG . ∴CM =5-2-MN =3-MN .在Rt △DMC 中,DM 2=CD 2+CM 2,∴(3+MN )2=(3-MN )2+42.∴NM =43.∴DM =3+43=133.故选A. 答案:A二、填空题10.在平面直角坐标系中,O 为坐标原点,则直线y =x +2与以O 点为圆心,1为半径的圆的位置关系为 相切.11.如图,圆内接四边形ABCD 两组对边的延长线分别相交于点E ,F ,且∠A =55°,∠E =30°,则∠F =40° .12.如图,正三角形ABC 的边长为2,点A ,B 在半径为2的圆上,点C 在圆内,将正三角形ABC 绕点A 逆时针旋转,当点C 第一次落在圆上时,点C 运动的路线长为 .【解析】设点C 落在圆上的点为C ′,连结OA ,OB ,OC ′,则OA =OB = 2.又∵AB =2,∴OA 2+OB 2=AB 2,∴∠AOB =90°,∴∠OAB =45°,同理∠OAC ′=45°,∴∠BAC ′=90°.∵△ABC 为等边三角形,∴∠CAB =60°,∴∠CAC ′=30°,∴点C 运动的路线长为30π×2180=π3.故答案为π3. 答案:π3 13.如图,在△ABC 中,∠BAC =90°,AB =5 cm ,AC =2 cm ,将△ABC 绕顶点C按顺时针方向旋转45°至△A 1B 1C 的位置,则线段AB 扫过区域(图中的阴影部分)的面积为 cm 2.【解析】在Rt△ABC 中,BC =AC 2+AB 2=29(cm),S 扇形BCB 1=45π×292360=29π8(cm 2),S △CB 1A 1=12×5×2=5(cm 2),S 扇形CAA 1=45π×22360=π2(cm 2),故S 阴影部分=S 扇形BCB 1+S △CB 1A 1-S △ABC -S 扇形CAA 1=29π8+5-5-π2=25π8(cm 2). 答案:25π8三、解答题14.如图,AB 是⊙O 的直径,BC 切⊙O于点B ,OC 平行于弦AD ,过点D 作DE ⊥AB 于点E ,连结AC ,与DE 交于点P .求证:(1)PE =PD ;(2)AC ·PD =AP ·BC .证明:(1)∵AB 是⊙O 的直径,BC 是切线,∴AB ⊥BC ,∵DE ⊥AB ,∴DE ∥BC ,∴△AEP ∽△ABC ,∴EP BC =AE AB .又∵AD ∥OC ,∴∠DAE =∠COB ,∴△AED ∽△OBC ,∴ED BC =AE OB =AE 12AB =2AE AB .∴ED =2EP ,∴PE =PD . (2)∵AB 是⊙O 的直径,BC 是切线,∴AB ⊥BC ,∵DE ⊥AB ,∴DE ∥BC ,∴△AEP ∽△ABC ,∴AP AC =PE BC .∵PE =PD ,∴AP AC =PD BC,∴AC ·PD =AP ·BC . 15.如图,在△OAB 中,OA =OB =10,∠AOB =80°,以点O 为圆心,6为半径的优弧MN 分别交OA ,OB 于点M ,N .(1)点P 在右半弧上(∠BOP 是锐角),将OP 绕点O 逆时针旋转80°得OP ′,求证:AP =BP ′;(2)点T 在左半弧上,若AT 与弧相切,求点T 到OA 的距离;(3)设点Q 在优弧MN 上,当△AOQ 的面积最大时,直接写出∠BOQ 的度数.(1)证明:如图,∵∠AOP=∠AOB+∠BOP=80°+∠BOP,∠BOP′=∠POP′+∠BOP=80°+∠BOP,∴∠AOP=∠BOP′.又∵OA=OB,OP=OP′,∴△AOP≌△BOP′.∴AP=BP′.(2)解:如图,连结OT,过点T作TH⊥OA于点H.∵AT与MN相切,∴∠ATO=90°.∴AT=OA2-OT2=102-62=8.∵12OA·TH=12AT·OT,即12×10×TH=12×8×6,∴TH=245,即点T到OA的距离为245.(3)10°,170°.16.如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.(1)判断直线BC与⊙O的位置关系,并说明理由;(2)若AC=3,∠B=30°.①求⊙O的半径;②设⊙O与AB边的另一个交点为E,求线段BD,BE与劣弧DE所围成的阴影部分的面积(结果保留根号和π).解:(1)直线BC与⊙O相切.理由如下:如图,连结OD,∵OA=OD,∴∠OAD=∠ODA,∵∠BAC的角平分线AD交BC边于点D,∴∠CAD=∠OAD,∴∠CAD=∠ODA,∴OD∥AC,∴∠ODB=∠C=90°,即OD⊥BC.∴直线BC与⊙O相切.(2)①设OA=OD=r,∵在Rt△BDO中,∠B=30°,∴OB=2r,∴在Rt△ACB中,∠B=30°,∴AB=2AC=6,∴3r=6,解得r=2.②∵在Rt△ODB中,∠B=30°,∴∠BOD=60°,∴S扇形ODE=60π×22360=23π,∴阴影部分面积为S△BOD-S扇形ODE=23-23π.11。
中考圆的复习资料(经典+全)

圆的知识点复习知识点1垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
题型1.在直径为1000mm的圆柱形油槽内装入一些油后,截面如图所示,若油面宽AB=800mm,则油的最大深度为 mm.2. 如图,在△ABC中,∠C是直角,AC=12,BC=16,以C为圆心,AC为半径的圆交斜边AB于D,求AD的长。
3. 如图,弦AB垂直于⊙O的直径CD,OA=5,AB=6,求BC长。
CBDA4. 如图所示,在⊙O中,CD是直径,AB是弦,AB⊥CD于M,CD=15cm,OM:OC=3:5,求弦AB的长。
知识点2 圆心角:顶点在圆心的角叫做圆心角。
弦心距:过圆心作弦的垂线,圆心与垂足之间的距离叫弦心距。
定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角度数相等,所对的弦相等。
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角度数相等,所对的弧相等。
题型1. 如果两条弦相等,那么()A.这两条弦所对的弧相等 B.这两条弦所对的圆心角相等C.这两条弦的弦心距相等 D.以上答案都不对2.下列说法正确的是()A.相等的圆心角所对的弧相等 B.在同圆中,等弧所对的圆心角相等C.相等的弦所对的圆心到弦的距离相等 D.圆心到弦的距离相等,则弦相等3.线段AB是弧AB 所对的弦,AB的垂直平分线CD分别交弧AB、AC于C、D,AD的垂直平分线EF分别交弧AB、AB于E、F,DB的垂直平分线GH分别交弧AB、AB于G、H,则下面结论不正确的是()A.弧AC=弧CB B.弧EC=弧CG C.EF=FH D.弧AE=弧EC4. 弦心距是弦的一半时,弦与直径的比是________,弦所对的圆心角是_____.5. 如图,AB 为⊙O 直径,E 是BC 中点,OE 交BC 于点D ,BD=3,AB=10,则AC=_____.6. 如图,AB 和DE 是⊙O 的直径,弦AC ∥DE ,若弦BE=3,则弦CE=________.7. 如图,已知AB 、CD 为⊙O 的两条弦,弧AD =弧BC , 求证:AB =CD 。
圆的知识点总结及典型例题

圆的知识点总结(一)圆的有关性质[知识归纳]1. 圆的有关概念:圆、圆心、半径、圆的内部、圆的外部、同心圆、等圆;弦、直径、弦心距、弧、半圆、优弧、劣弧、等弧、弓形、弓形的高;圆的内接三角形、三角形的外接圆、三角形的外心、圆内接多边形、多边形的外接圆;圆心角、圆周角、圆内接四边形的外角。
2. 圆的对称性圆是轴对称图形,经过圆心的每一条直线都是它的对称轴,圆有无数条对称轴;圆是以圆心为对称中心的中心对称图形;圆具有旋转不变性。
3. 圆的确定不在同一条直线上的三点确定一个圆。
4. 垂直于弦的直径垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧;推论1(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧。
垂径定理及推论1可理解为一个圆和一条直线具备下面五个条件中的任意两个,就可推出另外三个:①过圆心;②垂直于弦;③平分弦(不是直径);④平分弦所对的优弧;⑤平分弦所对的劣弧。
推论2圆的两条平行弦所夹的弧相等。
5. 圆心角、弧、弦、弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等;所对的弦的弦心距相等。
推论在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。
此定理和推论可以理解成:在同圆或等圆中,满足下面四个条件中的任何一个就能推出另外三个:①两个圆心角相等;②两个圆心角所对的弧相等;③两个圆心角或两条弧所对的弦相等;④两条弦的弦心距相等。
圆心角的度数等于它所对的弧的度数。
6. 圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半;推论1同弧或等弧所对的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧也相等;推论2半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径;推论3如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
九年级上册圆题型归纳
九年级上册圆题型归纳一、圆的基本概念相关(5题)题1:已知圆的半径为5cm,求圆的周长和面积。
解析:圆的周长公式为C = 2π r,面积公式为S=π r^2,其中r = 5cm。
周长C=2π×5 = 10π cm≈ 10×3.14=31.4cm面积S=π×5^2=25π cm^2≈25× 3.14 = 78.5cm^2题2:在圆O中,弦AB的长为8,圆心O到弦AB的距离为3,求圆O的半径。
解析:设圆O的半径为r,圆心O到弦AB的距离为d = 3,弦长AB=8。
根据垂径定理,半弦长、圆心到弦的距离与圆的半径构成直角三角形。
半弦长为(AB)/(2)=(8)/(2) = 4由勾股定理r^2=d^2+<=ft((AB)/(2))^2r=√(3^2)+4^{2}=√(9 + 16)=√(25)=5题3:已知圆O的直径为10,点A在圆O上,求∠ AOB的度数(其中O为圆心,B为圆上另一点且AB为圆的弦)。
解析:因为圆O的直径为10,则半径r = 5。
当AB为直径时,∠ AOB=180^∘;当AB为非直径的弦时,0^∘<∠AOB<180^∘。
由于题目没有更多关于AB弦的信息,所以仅能得出∠ AOB的取值范围是0^∘<∠ AOB≤slant180^∘题4:圆O中,弧AB所对的圆心角为60^∘,半径为6,求弧AB的长。
解析:弧长公式l=(nπ r)/(180)(n为圆心角度数,r为半径)已知n = 60^∘,r=6弧AB的长l=(60π×6)/(180)= 2π题5:判断:相等的圆心角所对的弧相等。
()解析:错误。
在同圆或等圆中,相等的圆心角所对的弧相等。
如果没有同圆或等圆这个前提条件,即使圆心角相等,所对的弧长也不一定相等。
二、与圆的切线相关(5题)题1:直线l与圆O相切于点A,圆O的半径为3,若OA与直线l的夹角为30^∘,求圆心O到直线l的距离。
关于圆的题型归纳和解题技巧
关于圆的题型归纳和解题技巧
一、关于圆的题型归纳
1、求圆的周长、面积;
2、求圆的弦长、切线长;
3、求圆的外接矩形面积;
4、求圆的内接正三角形面积;
5、求圆的内切正三角形面积;
6、求扇形的面积;
7、求弧长、圆心角;
8、求圆的关系题;
9、求圆的判断题;
10、求圆外一点与圆的关系;
11、求外切圆与内切圆;
12、求圆的标准方程;
13、求圆的对称性;
14、求圆的有关数据推导;
15、求圆的分析绘图;
16、求圆的位置关系;
17、求圆的等价关系;
18、求圆的数字抽象;
二、关于圆的解题技巧
1、对圆的判断题,可以用圆心、半径、圆周等参数来判断;
2、圆内外的点是成对称的,可利用对称性解题;
3、求外切圆与内切圆时,可以找到相同的弦长、半径最大值最小值;
4、求弧长时,可以用圆心角的正弦余弦公式,通过求出弧长和半径的比值来计算出弧长;
5、求扇形的面积,可以用圆心角的正弦余弦公式求出扇形的三角形面积,再乘上圆心角的度数;
6、求两圆之间的关系时,可以用其半径大小比较,进行判断;
7、圆的位置关系一般利用同心圆或相切圆的方式来进行求解;
8、求圆的数字抽象时,要根据题目中提到的圆的参数,抽取出通用的圆的方程;
9、求圆的等价关系,可以用圆的标准方程,结合圆的圆心和半径,进行求解;
10、求圆的参数关系时,可以根据圆的标准方程来求出圆的参数和面积等;
11、圆的分析绘图时,要把握好图形的特征,找出圆的圆心,半径,角度等关系;
12、求圆的有关数据的推导时,可以用圆的标准方程,结合圆的圆心和半径等求解。
圆知识梳理+题型归纳附答案-(详细知识点归纳+中考真题)
圆【知识点梳理】一、圆的概念集合形式的概念: 1、 圆可以看作是到定点的距离等于定长的点的集合; 2、圆的外部:可以看作是到定点的距离大于定长的点的集合; 3、圆的内部:可以看作是到定点的距离小于定长的点的集合 轨迹形式的概念:1、圆:到定点的距离等于定长的点的轨迹就是以定点为圆心,定长为半径的圆;(补充)2、垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线(也叫中垂线); 3、角的平分线:到角两边距离相等的点的轨迹是这个角的平分线;4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线;5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线。
二、点与圆的位置关系1、点在圆内 ⇒ d r < ⇒ 点C 在圆内;2、点在圆上 ⇒ d r = ⇒ 点B 在圆上;3、点在圆外 ⇒ d r > ⇒ 点A 在圆外; 三、直线与圆的位置关系1、直线与圆相离 ⇒ d r > ⇒ 无交点;2、直线与圆相切 ⇒ d r = ⇒ 有一个交点;3、直线与圆相交 ⇒ d r < ⇒ 有两个交点; 四、圆与圆的位置关系外离(图1)⇒ 无交点 ⇒ d R r >+; 外切(图2)⇒ 有一个交点 ⇒ d R r =+; 相交(图3)⇒ 有两个交点 ⇒ R r d R r -<<+; 内切(图4)⇒ 有一个交点 ⇒ d R r =-; 内含(图5)⇒ 无交点 ⇒ d R r <-; 五、垂径定理垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。
推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧; (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,rd d CBAO即:①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD 中任意2个条件推出其他3个结论。
关于圆的题型归纳和解题技巧
关于圆的题型归纳和解题技巧
一、圆的题型归纳
1. 直线与圆的位置关系:直线与圆可以相切、相交、外切、内切。
2. 圆的性质:取点到圆心的距离相等;圆两点到圆心的连线,长度相等,角度相等;圆周上的点,到圆心两条连线的比值相等。
3. 圆心角:圆心角及其扇形的面积,与圆上两点的距离有关。
4. 关于圆的全等:两个半径相等的圆,它们的圆心角两端的线段的角度也相等;重心相等的圆,它们的圆心角也是相等的。
5. 关于圆的切线:圆上的点到圆心连线,为切线;圆上两点连线为切线;任一点到圆心的连线与任一点到圆上另外一点的连线的夹角为切线。
二、解题技巧
1. 图形分析法:根据题意绘制出合理的几何图形,对圆形的部分应尽量详细地描绘出来,综合分析各个部分的相互关系,以此判断圆形的计算结果。
2. 数字分析法:根据数据来分析圆形的特性,比如圆的半径是给定的,那么可以根据圆的性质和圆心角来推算其他参数的值;又如圆心角的角度是已知的,则可以推算出其它参数的值。
3. 结论法:圆周上的点,所到圆心的连线的比值都是相同的;圆心角的扇形面积和它的的圆心角的角度有关。
这些基本性质可以在解题中灵活地运用,通过比较不同扇形的面积来判断其可行的解,从
而推断出解题的具体值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.关于圆的常见辅助线:《圆》题型分类资料一. 圆的有关概念:1.下列说法:①直径是弦 ②弦是直径 ③半圆是弧,但弧不一定是半圆 ④长度相等的两条弧是等弧,正确的命题有( )A . 1个B .2个C .3个D .4个 2.下列命题是假命题的是( )A .直径是圆最长的弦B .长度相等的弧是等弧C .在同圆或等圆中,相等的圆心角所对的弧也相等D .如果三角形一边的中线等于这条边的一半,那么这个三角形是直角三角形。
3.下列命题正确的是 ( )A .三点确定一个圆B .长度相等的两条弧是等弧C .一个三角形有且只有一个外接圆D .一个圆只有一个外接三角形 4.下列说法正确的是( )A .相等的圆周角所对的弧相等B .圆周角等于圆心角的一半 C.长度相等的弧所对的圆周角相等 D .直径所对的圆周角等于90° 5.下面四个图中的角,为圆心角的是( )A .B .C .D . 二.和圆有关的角:1. 如图1,点O是△ABC的内心,∠A=50 ,则∠BOC=_________A图1 图2 图3 图42.如图2,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD的度数为( )A.116°B.64°C. 58°D.32°3. 如图3,点O为优弧AB所在圆的圆心,∠AOC=108°,点D在AB的延长线上,BD=BC,则∠D的度数为4. 如图4,AB、AC是⊙O的两条切线,切点分别为B、C,D是优弧BC上的一点,已知∠BAC=80°,那么∠BDC=_________度.5. 如图5,在⊙O中,BC是直径,弦BA,CD的延长线相交于点P,若∠P=50°,则∠AOD =.A图5 图6 图7 图8 6. 如图6,A ,B ,C ,是⊙O 上的三个点,若∠AOC =110°,则∠ABC = °. 7.圆的内接四边形ABCD 中,∠A :∠B :∠C =2:3:7,则∠D 的度数为 。
8. 若⊙O 的弦AB 所对的劣弧是优弧的13,则∠AOB = .9.如图7,AB 是⊙O 的直径,C 、D 、E 都是⊙O 上的点,则∠1+∠2=________ 10.如图8,△ABC 是O 的内接三角形,点C 是优弧AB 上一点(点C 不与A ,B 重合),设OAB α∠=,C β∠= (1)当35α=时,求β的度数;(2)猜想α与β之间的关系为11.已知:如图1,四边形ABCD 内接于⊙O ,延长BC 至E ,求证:∠A +∠B C D=180°,∠DCE =∠A ;如图2,若点C 在⊙O 外,且A 、C 两点分别在直线BD 的两侧,试确定∠A +∠BCD 与180°的大小关系;如图3,若点C 在⊙O 内,且A 、C 两点分别在直线BD 的两侧,试确定∠A +∠BCD 与180°的大小关系。
图1 图2 图 312.如图,四边形ABCD 是O 的内接四边形,四边形ABCO 是菱形(1)求证:AB BC =; (2)求D ∠的度数13.(1)如图O 的直径,AC 是弦,直线EF和O 相切于点C ,AD FE ⊥,垂足为D ,求证CAD BAC ∠=∠;(2)如图(2),若把直线EF 向上移动,使得EF 与O 相交于G ,C 两点(点C 在G的右侧),连结AC ,AG ,若题中其他条件不变,这时图中是否存在与∠CAD 相等的角?若存在,找出一个这样的角,并证明;若不存在,说明理由。
三.和圆有关的位置关系: (一)点和圆的位置关系:1.已知⊙O 的半径为4,A 为线段PO 的中点,当OP =10时,点A 与⊙O 的位置关系为( )A .在圆上B .在圆外C .在圆内D .不确定2. 如图,在R t △ABC 中∠ACB =90°,AC =6,AB =10,CD 是斜边AB 上的中线,以AC 为直径作⊙O ,设线段CD 的中点为P ,则点P 与⊙O 的位置关系是点P ( )。
A . 在⊙O 内B . 在⊙O 上C . 在⊙O 外D . 无法确定 3.如图1,已知O 的半径为5,点O 到弦AB 的距离为3,则O 上到弦AB 所在直线的 图1 距离为2的点有( )备用图A .1个B .2个C .3个D .4个4.变式训练:如图1,已知⊙O 的半径为5,点O 到弦AB 的距离为3,则⊙O 上到弦AB 所在直线的距离为1的点有( )A .1个B .2个C .3个D .4个5. Rt △ABC 中,∠C =90°,AC =2,BC =4,如果以点A 为圆心,AC 为半径作⊙A ,那么斜边中点D 与⊙O 的位置关系是( )A .点D 在⊙A 外B .点D 在⊙A 上C .点D 在⊙A 内 D .无法确定(二)直线和圆的位置关系:1.如图,在RT △ABC 中,∠C =90°,∠B =30°,BC =34cm ,以点C 为圆心,以32cm 的长为半径,则⊙C 与AB 的位置关系是 ;2.如图,已知AB 是⊙O 的一条直径,延长AB 至C 点,使得AC =3BC ,CD 与⊙O 相切,切点为D .若CD =3,则线段BC 的长度等于__________.3.如图Rt △ABC 中∠C =90°,∠A =30°,在AC 边上取点O 画圆使⊙O 经过A 、B 两点,下列结论中:①AO =2CO ; ②AO =BC ; ③以O 为圆心,以OC 为半径的圆与AB 相切;④延长BC 交⊙O 于 点D ,则A 、B 、D 是⊙O 的三等分点,正确的序号是 4.如图,AB 是⊙O 的直径,⊙O 交BC 的中点于D ,DE ⊥AC 于E ,连接AD ,则下列结论:①AD ⊥BC ;②∠EDA =∠B ;③AD =AO ;④AB =AC ;⑤DE 是⊙O 切线.正确的是_______________.5. 如图,∠AOB =30°,M 为OB 边上一点,以M 为圆心、2为半径作⊙M . 若点M 在OB 边上运动,则当OM = 时,⊙M 与OA 相切;当OM 满足 时,⊙M 与OA 相交;当OM 满足 时,⊙M 与OA 相离.6. 在Rt △ABC 中,∠C =90°,AC =3cm ,BC =4cm ,以C 为圆心,r 为半径的圆与AB 有何位置关系?为什么?(1)r =2cm ;(2)r =2.4cm ;(3)r =3cm7. 已知:如图,在△ABC 中,D 是AB 边上一点,圆O 过D 、B 、C 三点, ∠DOC =2∠ACD =90︒。
(1) 求证:直线AC 是圆O 的切线;(2) 如果∠ACB =75︒,圆O 的半径为2,求BD 的长。
8. 如图,点A 、B 、C 分别是⊙O 上的点,⊙B =60°,AC =3,CD 是⊙O 的直径,P是CD 延长线上的一点,且AP =AC . (1)求证:AP 是⊙O 的切线;(2)求PD 的长.9.如图,四边形ABCD 是等腰梯形,AD ∥BC ,BC =2,以线段BC 的中点O 为圆心,以OB 为半径作圆,连结OA 交⊙O 于点M 。
若点E 是线段AD,OA =2,求证:直线AD的中点,AE =与⊙O 相切。
10. 如图,已知四边形OABC 是菱形,∠O 的60°,点M 是边OA 的中点.以点O 为圆心,r 为半径作⊙O 分别交OA ,OC 于点D ,E ,连接BM 。
若BM⌒DE. 求证:直线BC 与⊙O 相切.11. 如图,在正方形ABCD 中,E 是AB 边上任意一点,∠ECF =45°,CF 交AD 于点F ,将PE△CBE 绕点C 顺时针旋转到△CDP ,点P 恰好在AD 的延长线上. (1)求证:EF =PF ;(2)直线EF 与以C 为圆心,CD 为半径的圆相切吗?为什么? 12. 如图,已知AB 是O 的直径,点D 在O 上,C 是O 外一点.若AD//OC ,直线BC与O 相交,判断直线CD 与O 的位置关系,并说明理由.13. 如图,□ABCD 中,O 为AB 边上一点,连接OD ,OC ,以O 为圆心,OB 为半径画圆,分别交OD ,OC 于点P ,Q .若OB =4,OD =6,∠ADO=∠A ,⌒PQ =2π,判断直线DC 与⊙O 的位置关系,并说明理由.14. 如图,□ABCD 中,O 为BC 边上一点,OD 平分∠ADC ,以O 为圆心,OC 为半径画圆,交OD 于点E ,若AB =6.□ABCD 的面积是,弧EC =π,判断直线AB 与⊙O 的位置关系,并说明理由.15. 已知四边形ABCD 内接于⊙O ,∠ADC =90°,∠DCB <90°,对角线AC 平分∠DCB ,延长DA ,CB 相交于点E . (1)如图1,EB =AD ,求证:△ABE 是等腰直角三角形;16.已知直线PA 交⊙O 于A 、B ,AE 是⊙O 的直径,点C 为⊙O 上一点,且AC 平分∠PAE ,过点C 作CD ⊥PA ,垂足为D .(1)求证:CD 是⊙O 的切线;(2)若DC +DA =6,⊙O 的直径为10,求AB 的长度.17.如图,AB 为⊙O 的直径,C 为⊙O 上一点,AD 和过点C 点的切线互相垂直,垂足为D ,AD 交⊙O 于点E . (1)求证:AC 平分∠DAB ;A(2)若∠B =60°,CD=,求AE 的长。
18.如图,已知AB 是⊙O 的直径,点C 在⊙O 上,H 是AC 的中点,且OH =1,∠A =30º. (1)求劣弧AC ⌒的长;(2)若∠ABD =120º,BD =1,求证:CD 是⊙O 的切线.19.如图,⊙O 是△ABC 的外接圆,AC 是直径,过点O 作OD ⊥AB 于点D ,延长DO 交⊙O 于点P ,过点P 作PE⊥AC 于点E ,作射线DE 交BC 的延长线于F 点,连接PF 。
(1)若∠POC =60°,AC =12,求劣弧PC 的长;(结果保留π)(2)求证:OD =OE ;(3) PF 是⊙O 的切线。
四.和圆有关的计算:(一)有关弦长、半径、弦心距等的计算:1.半径为5的圆中有两条平行弦,长度分别为4和6,则这两条弦之间的距离是 .2.如图1,点P 是半径为5的⊙O 内的一点,且OP =3,设AB 是过点P 的⊙O 内的弦,且AB ⊥OP ,则弦AB 长是 ;图1 图23.在直角坐标系中,一条弧经过网格点A、B 、C ,其中点B 的坐标为(4,4),则该圆弧所在圆的圆心的坐标为 ;4.如图,⊙O 的直径为20 cm ,弦AB =16 cm ,AB OD ⊥,垂足为D .则AB 沿射线OD 方向平移 cm 时可与⊙O 相切.5.已知,如图,⊙O 是△ABC 的内切圆,切点分别为D 、E 、F ,若AB =7,AC =8,BC =9,求AD 、BE 、CF 的长。
