直线与平面垂直、平面与平面垂直的性质课件(优质课)
合集下载
直线与平面垂直的判定与性质(共26张PPT)

直线与平面垂直的判定与性 质(共26张ppt)
目 录
• 直线与平面垂直的判定 • 直线与平面垂直的性质 • 直线与平面垂直的证明 • 直线与平面垂直的应用 • 总结与展望 • 参考文献
01
直线与平面垂直的判定
直线与平面垂直的定义
01
直线与平面垂直是指直线与平面 内的任意一条直线都垂直。
02
如果一条直线与平面内的任意一 条直线都垂直,则这条直线与该 平面垂直。
建筑设计
在建筑设计中,直线与平面垂直的应用非常重要, 如确定建筑物的垂直度和水平面等。
机械制造
在机械制造中,直线与平面垂直的应用可以帮助 制造出精确的机械部件。
道路建设
在道路建设中,直线与平面垂直的应用可以帮助 确保道路的平直度和坡度等。
05
总结与展望
总结直线与平面垂直的判定与性质
判定方法 通过直线与平面内两条相交直线垂直来判定直线与平面垂直。
通过直线与平面内无数条直线垂直来判定直线与平面垂直。
总结直线与平面垂直的判定与性质
• 通过直线与平面垂直的性质定理来判定直线与平面垂直。
总结直线与平面垂直的判定与性质
01
性质定理
02
03
04
直线与平面垂直,则该直线与 平面内任意一条直线都垂直。
直线与平面垂直,则该直线所 在的所有直线都与该平面垂直
证明
假设有一条直线l与平面α垂直,那么直线l与平面α内的任意一条直线m都垂直。 由于直线l与平面α内的直线m都垂直,所以它们之间的夹角为90°,即直线l与平 面α内的任意一条直线都垂直。
直线与平面垂直的性质推论
推论1
证明
推论2
证明
如果一条直线与平面内的两 条相交直线都垂直,那么这
目 录
• 直线与平面垂直的判定 • 直线与平面垂直的性质 • 直线与平面垂直的证明 • 直线与平面垂直的应用 • 总结与展望 • 参考文献
01
直线与平面垂直的判定
直线与平面垂直的定义
01
直线与平面垂直是指直线与平面 内的任意一条直线都垂直。
02
如果一条直线与平面内的任意一 条直线都垂直,则这条直线与该 平面垂直。
建筑设计
在建筑设计中,直线与平面垂直的应用非常重要, 如确定建筑物的垂直度和水平面等。
机械制造
在机械制造中,直线与平面垂直的应用可以帮助 制造出精确的机械部件。
道路建设
在道路建设中,直线与平面垂直的应用可以帮助 确保道路的平直度和坡度等。
05
总结与展望
总结直线与平面垂直的判定与性质
判定方法 通过直线与平面内两条相交直线垂直来判定直线与平面垂直。
通过直线与平面内无数条直线垂直来判定直线与平面垂直。
总结直线与平面垂直的判定与性质
• 通过直线与平面垂直的性质定理来判定直线与平面垂直。
总结直线与平面垂直的判定与性质
01
性质定理
02
03
04
直线与平面垂直,则该直线与 平面内任意一条直线都垂直。
直线与平面垂直,则该直线所 在的所有直线都与该平面垂直
证明
假设有一条直线l与平面α垂直,那么直线l与平面α内的任意一条直线m都垂直。 由于直线l与平面α内的直线m都垂直,所以它们之间的夹角为90°,即直线l与平 面α内的任意一条直线都垂直。
直线与平面垂直的性质推论
推论1
证明
推论2
证明
如果一条直线与平面内的两 条相交直线都垂直,那么这
线面垂直、面面垂直的性质与判定定理ppt课件

a⊥β α
b
a
B
γ
证明:过a作平面γ交于b, 因为直线a//,所以a//b
β 又因为a⊥AB,所以b⊥AB
A
又⊥β,∩β=AB
辅助线(面):
所以b⊥β
发展条件的使解题过 程获得突破的
进而a⊥β
【课后自测】4、如图,已知SA⊥平面ABC,
平面SAB⊥平面SBC,求证:AB⊥BC
证明:过点A作AD⊥SB于D, ∵平面SAB⊥平面SBC,
直线l在平面α内,那么直线l与平面β
的位置关系有哪几种可能?
α l
β
平行
α
l
β
相交
α
l β
线在面内
知识探究:
思考2:黑板所在平面与地面所在平面垂 直,在黑板上是否存在直线与地面垂直? 若存在,怎样画线?
α
β
证明问题:
已知: , A , C B , 且 D C A . 求D 证:B CD
β
a
l
A α
a
l
a
a l
作用: 面面垂直线面垂直
垂直体系
判定
判定
线线垂直
线面垂直 面面垂直
定义
性质
问题2 , a , a , 判 断 a 与 位 置 关 系
α
a
a //
l
问题3: β
思考:已 , , 知直 平 a,且 线 面 ,A,B
a/ /,aA,B 试判断 a与直 平 的 线 面 位置关
符号语言:
ab
a ,b a //b
α
线面垂直关 系
最新版整理ppt
线线平行关 系
3
平面与平面垂直的性质
温故知新
直线与平面垂直的性质、平面与平面垂直的性质 课件

【训练2】 设平面α⊥平面β,点P在平面α内,过点P作平面β 的垂线a,试判断直线a与平面α的位置关系.
解 如图,设α∩β=c,过点P在平面α内作直线b⊥c.
根据平面与平面垂直的性质定理有b⊥β. 因为过一点有且只有一条直线与平面β垂直, 所以直线a与直线b重合,因此a⊂α.
类型三 线线、线面、面面垂直的综合应用(互动探究) 【例3】 如图所示,在四棱锥P-ABCD中,底面
线与另一个平面_垂__直___
α⊥β _αa_⊂_∩_α_β=l⇒a⊥β
_a_⊥__l_
图形语言
作用
①面面垂直⇒___线___面____垂直 ②作面的垂线
1.判断题 (1)两条平行直线中的一条垂直于一个平面,另一条也垂直于这 个平面.(√ ) (2)垂直于同一平面的两个平面平行.(× ) (3)如果两个平面垂直,那么经过第一个平面内一点且垂直于第 二 个 平 面 的 直 线 在 第 一 个 平 面 内 . 即 α⊥β , A ∈ α , A ∈ b , b⊥β⇒b⊂α.( √ ) (4)如果平面α⊥平面β,那么平面α内的所有直线都垂直于平面
在直角梯形ABCD中,易证△ABO ≌△BCD, ∠BAO=∠CBD,∠CBD+∠ABD=90°, ∴∠BAO+∠ABD=90°,∴AO⊥BD, 又PO∩AO=O,∴BD⊥平面PAO,∴BD⊥PA, 即PA与BD相互垂直.
[课堂小结] 1.线面垂直的性质定理揭示了空间中“平行”与“垂直”关
系的内在联系,提供了“垂直”与“平行”关系相互转化 的依据. 2.面面垂直的性质定理揭示了“面面垂直、线面垂直及线线 垂直”间的内在联系,体现了数学中的转化与化归思想, 其转化关系如下:
法二 如图,α∩γ=a,
β∩γ=b,在α内作m⊥a, 在β内作n⊥b. ∵α⊥γ,β⊥γ,∴m⊥γ,n⊥γ,∴m∥n. 又∵n⊂β,m⊄β,∴m∥β, 又α∩β=l,m⊂α,∴m∥l,∴l⊥γ.
直线与平面垂直的性质、平面与平面垂直的性质课件

直线与平面垂直的性质 平面与平面垂直的性质
1.直线与平面垂直的性质定理
文字语言 垂直于同一个平面的两条直线_____平__行_____
符号语言
a⊥α b⊥α ⇒___a_∥__b______
图形语言
作用
①线面垂直⇒线线平行 ②作平行线
2.平面与平面垂直的性质定理
文字语言
两个平面垂直,则_一__个__平___面__内__垂直于__交__线___的直 线与另一个平面___垂__直____
所以四边形 AMNO 为平行四边形. 所以 ON=AM. 因为 ON=12AB, 所以 AM=12DC=12AB. 所以 M 是 AB 的中点.
证明线线平行的常用方法 (1)利用线线平行定义:证共面且无公共点. (2)利用三线平行公理:证两线同时平行于第三条直线. (3)利用线面平行的性质定理:把证线线平行转化为证线面平 行. (4)利用线面垂直的性质定理:把证线线平行转化为证线面垂 直. (5)利用面面平行的性质定理:把证线线平行转化为证面面平 行.
(2)取 CA 的中点 N,连接 MN,BN, 则 MN∥EC,且 MN=12EC. 因为 EC∥BD,BD=12EC, 所以 MN∥═BD, 所以 N 点在平面 BDM 内. 因为 EC⊥平面 ABC, 所以 EC⊥BN.
又 CA⊥BN,所以 BN⊥平面 ECA. 因为 BN 在平面 MNBD 内, 所以平面 MNBD⊥平面 ECA, 即平面 BDM⊥平面 ECA. (3)由第二问易知 DM∥BN,BN⊥平面 CAE, 所以 DM⊥平面 ECA. 又 DM⊂平面 DEA, 所以平面 DEA⊥平面 ECA.
如图所示,在三棱柱 ABC-A1B1C1 中,∠BAC =90°,BC1⊥AC,则 C1 在平面 ABC 上的射影 H 必在直线____________上.
1.直线与平面垂直的性质定理
文字语言 垂直于同一个平面的两条直线_____平__行_____
符号语言
a⊥α b⊥α ⇒___a_∥__b______
图形语言
作用
①线面垂直⇒线线平行 ②作平行线
2.平面与平面垂直的性质定理
文字语言
两个平面垂直,则_一__个__平___面__内__垂直于__交__线___的直 线与另一个平面___垂__直____
所以四边形 AMNO 为平行四边形. 所以 ON=AM. 因为 ON=12AB, 所以 AM=12DC=12AB. 所以 M 是 AB 的中点.
证明线线平行的常用方法 (1)利用线线平行定义:证共面且无公共点. (2)利用三线平行公理:证两线同时平行于第三条直线. (3)利用线面平行的性质定理:把证线线平行转化为证线面平 行. (4)利用线面垂直的性质定理:把证线线平行转化为证线面垂 直. (5)利用面面平行的性质定理:把证线线平行转化为证面面平 行.
(2)取 CA 的中点 N,连接 MN,BN, 则 MN∥EC,且 MN=12EC. 因为 EC∥BD,BD=12EC, 所以 MN∥═BD, 所以 N 点在平面 BDM 内. 因为 EC⊥平面 ABC, 所以 EC⊥BN.
又 CA⊥BN,所以 BN⊥平面 ECA. 因为 BN 在平面 MNBD 内, 所以平面 MNBD⊥平面 ECA, 即平面 BDM⊥平面 ECA. (3)由第二问易知 DM∥BN,BN⊥平面 CAE, 所以 DM⊥平面 ECA. 又 DM⊂平面 DEA, 所以平面 DEA⊥平面 ECA.
如图所示,在三棱柱 ABC-A1B1C1 中,∠BAC =90°,BC1⊥AC,则 C1 在平面 ABC 上的射影 H 必在直线____________上.
高中数学人教A版必修第二册《空间直线、平面的垂直---直线与平面、平面与平面垂直的性质》名师课件

掌握平面与平面垂直的性质定理.
核心素养
逻辑推理
逻辑推理
学习目标
课程目标
1.理解直线和平面、平面和平面垂直的性质定理并能运用其解决相关问题.
2.通过对性质定理的理解和应用,培养学生的空间转化能力和逻辑推理能力.
数学学科素养
1.逻辑推理:探究归纳直线和平面、平面和平面垂直的性质定理,线线垂直、线面垂直、
变式训练
3.如图所示,在四棱锥PABCD中,底面ABCD是边长为a的菱形,且∠DAB=60°,G为AD边
的中点,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.
(1)求证:BG⊥平面PAD;(2)求证:AD⊥PB.
证明
(1)因为在菱形ABCD中,G为AD的中点, ∠DAB=60° ,所以BG⊥AD.
复习引入
直线与平面垂直的定义:
如果直线与平面内的任意一条直线都垂直,我们说直
线与平面互相垂直,记作 ⊥ .
直线与平面垂直的判定定理:
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平
面垂直.
复习引入
平面与平面垂直的定义
一般地,两个平面相交,如果它们所成的二面角是直二面角,就说
这两个平面互相垂直.
求证:(1)DE=DA;(2)平面BDM⊥平面ECA;(3)平面DEA⊥平面ECA.
证明
(1)如图,取EC的中点F,连接DF.
因为EC⊥平面ABC,BC⊂平面ABC,所以EC⊥BC.
易知DF//BC,所以DF⊥EC.
在Rt△EFD和Rt△DBA中
因为EF= EC,EC=2BD,所以EF=BD.
又FD=BC=AB所以Rt△EFD≌Rt△DBA ,故DE=DA.
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,所以BG⊥平面PAD.
核心素养
逻辑推理
逻辑推理
学习目标
课程目标
1.理解直线和平面、平面和平面垂直的性质定理并能运用其解决相关问题.
2.通过对性质定理的理解和应用,培养学生的空间转化能力和逻辑推理能力.
数学学科素养
1.逻辑推理:探究归纳直线和平面、平面和平面垂直的性质定理,线线垂直、线面垂直、
变式训练
3.如图所示,在四棱锥PABCD中,底面ABCD是边长为a的菱形,且∠DAB=60°,G为AD边
的中点,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.
(1)求证:BG⊥平面PAD;(2)求证:AD⊥PB.
证明
(1)因为在菱形ABCD中,G为AD的中点, ∠DAB=60° ,所以BG⊥AD.
复习引入
直线与平面垂直的定义:
如果直线与平面内的任意一条直线都垂直,我们说直
线与平面互相垂直,记作 ⊥ .
直线与平面垂直的判定定理:
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平
面垂直.
复习引入
平面与平面垂直的定义
一般地,两个平面相交,如果它们所成的二面角是直二面角,就说
这两个平面互相垂直.
求证:(1)DE=DA;(2)平面BDM⊥平面ECA;(3)平面DEA⊥平面ECA.
证明
(1)如图,取EC的中点F,连接DF.
因为EC⊥平面ABC,BC⊂平面ABC,所以EC⊥BC.
易知DF//BC,所以DF⊥EC.
在Rt△EFD和Rt△DBA中
因为EF= EC,EC=2BD,所以EF=BD.
又FD=BC=AB所以Rt△EFD≌Rt△DBA ,故DE=DA.
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,所以BG⊥平面PAD.
直线与平面垂直判定完整版课件

绘制图表,将实验数据 可视化展示,便于分析 和比较。
03
分析实验数据,总结直 线与平面垂直的判定方 法和规律。
04
根据实验结果,评估实 验方法的准确性和可靠 性,并提出改进意见。
06
课程总结与回顾
知识点梳理
01
直线与平面垂直的定义
如果直线$l$与平面$alpha$内的任意一条直线都垂直,那么我们就说
角的范围
异面直线所成角的取值范围是 (0, 90°]。
异面直线所成角求解方法
01
02
03
平移法
将两条异面直线平移到同 一个起点上,然后用余弦 定理或三角函数求解。
向量法
建立空间直角坐标系,将 异面直线的方向向量表示 出来,然后通过向量的夹 角公式求解。
投影法
将一条直线投影到另一条 直线上,通过投影长度和 原长度之间的关系,利用 三角函数求解。
易错点提示
忽略直线与平面内两条相交直线 都垂直的条件,只考虑与其中一
条直线垂直或平行的情况。
在证明直线与平面垂直时,未明 确说明平面内的两条相交直线, 或者错误地认为只要与平面内无
数条直线垂直即可。
符号使用不规范,如将直线与平 面垂直的符号误写为平行或相交
等。
下一讲预告
下一讲我们将继续深入学习空间几何中的直线与平面的位置关系,包括直线与平面 平行的判定和性质等内容。
确定未知量
根据题目要求,确定需要求解 的未知量。
建立方程
利用已知条件和几何性质,建 立关于未知量的方程。
求解方程
解方程得到未知量的值,注意 解的合理性。
解答题规范步骤和答案
画出图形
根据题意画出相应 的图形,标注已知 量和未知量。
人教版人教高中数学3直线、平面垂直的判定与性质 -三垂线定理 (共16张PPT)教育课件
《
《
我
是
算
命
先
生
》
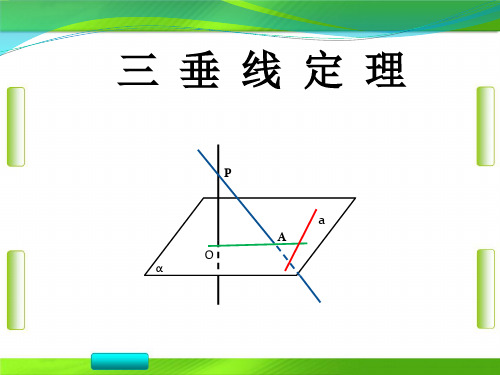
证明: PO⊥α
①
PO⊥a ②
aα
AO⊥a a⊥平面POA ③
PO AO O PA 平面POA a⊥PA
①
②
③
线面垂直
线线垂直
线面垂直
线线垂直
性质定理
判定定理
性质定理
新知探究 • 定理内容
三垂线定理:在平面内的一条直线,如果和这个
平面的一条斜线的正射影垂直,那么它也和这条 斜线垂直。
P 定理
人
的
一
生
说
白
了
,
也
就
是
三
万
余
天
,
贫
穷
与
富
贵
,
都
是
一
种
生
活
境
遇
。
懂
得
爱
自
己
的
人
,
对
生
活
从
来
就
没
有
过
高
的
奢
望
,
只
是
对
生
存
的
现
状
欣
然
接
受
。
漠
漠
红
尘
,
芸
芸
众
生
皆
是
客
,
时
光
深
处
,
流
年
似
水
,
转
瞬
间
,
光
阴
就
会
老
去
,
留
在
直线与平面垂直课件(共17张PPT)

线与平面垂直吗?
(2)如果一条直线与一个平面内的 无数条直线 都垂直,那么这条
直线与平面垂直吗?
l
任意一条直线
α P. …
线不在多, 所有直线 相交则灵
4.概念辨析,巩固新知
小结:证明线面垂直的方法:线线垂直 线面垂直
1.定义: 任意一条直线
所有直线 无限
2.判定定理: 两条相交直线
有限
线不在多, 相交则灵
3.操作确认,探究定理
当且仅当 折痕 AD 是 BC 边上的高时,AD 所在直线与桌面所在平面垂直.
二、直线与平面垂直的判定定理
文字语言:一条直线与一个平面内的 两条相交直线 都垂直,则该
直线与此平面垂直.
线线垂直 线面垂直
图形语言:
符号语言:
4.概念辨析,巩固新知
思考:
两条相交直线
(1)如果一条直线与一个平面内的 两条直线 垂直,那么这条直
又
m ∩ n=P,
∴ b⊥α .
5.推理论证,定理应用
练习 如图,在三棱锥 S-ABC 中,∠ACB = 90°, SA⊥平面ABC .
求证:BC⊥平面SAC .
S
证明:
线面垂直 线线垂直 A来自B C线线垂直 线面垂直
6.渗透文化,拓展延申
刘徽,是魏晋期间伟大的数学家,中国 古典数学理论的奠基人之一。
4.数学文化 的渗透
7.课堂小结,课后思考
1.如果要检验一根新旗杆与地面是否垂直, 你有什么好方法吗? 2.我们通过直观感知和操作确认,已经 从直观上得出了线面垂直的判定定理, 你能从理论上用所学的知识解释它吗?
谢谢观看,再见!
8.6.2 直线与平面垂直
1.复习引入,类比研究
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图,在长方体ABCD—A1B1C1D1中,
平面AC 平面D1C 平面AC 平面D1C DC
D1D 平面D1C
A1
D A B D1 B1 C1
D1D CD
D1D 平面AC
C
平面与平面垂直的性质定理
两个平面垂直,则一个平面内垂 文字语言 直于交线的直线与另一个平面垂直.
图形语言
交线的直线b 要证a // , 只需在平
b 面内作一直线b // a a a // b
b
a
即可。而题中条件有 又 a , b a , ,因此,
a // 必有b .
即直线a与平面平行
规律方法:
生活中的数学
直线和平面垂直的性质定理
文字语言 垂直于同一个平面的两条直线平行. 图形语言
a
b
符号语言
a , b a // b
线线平行
简记: 线面垂直
作用:证明空间直线的平行。
课堂练习(一):
判断下列命题是否正确:
(1)垂直于同一条直线的两个平面互相平行。(
)
(2)垂直于同一个平面的两条直线互相平行。(
AB
简记: 线面垂直 面面垂直
性质定理 判定定理
D A
C
B
定理的作用:证明线面垂直。
面面垂直
线面垂直
线面、面面之间的关系的转化是解决空间图 形问题的重要思想方法。
应用举例
例2:已知平面 , , , 直线a满足a , a ,判断直线a与平面的位置关系。 解:在内作垂直于与 分析:
)
(3)平行于同一个平面的两条直线互相平行。(
)
课堂练习(二):
小心陷阱
已知直线a, b和平面,且a b, b , 则a与的位置关系是 ( D )
A、a // C、a
B、a
D、a 或a //
应用举例
例1:在正方体ABCD A1 B1C1 D1中,M是AB上 一点,N是A1C上的一点,MN 平面A1 DC 求证:MN // AD1
线垂直于平面内两条 - CD 的平面角 相交直线,而题中条 件已有一条,故可过 该直线作辅助线 . AB BE
E
B
D
A
C
AB CD
CD , BE , BE CD B AB
平面与平面垂直的性质定理
CD, AB , AB CD ,
C B
AD1 平面A1DC
MN 平面A1DC MN // AD1
A
M
规律方法:
线面垂直的性质定理也是证明线线平行的一
个方法,在有线面垂直的条件下,要证平行
关系,就应考虑线面垂直的性质定理。
新知探究二:平面与平面垂直的性质
你能找到互相垂
直的两个平面吗?
新知探究二:平面与平面垂直的性质
大化高中欢迎您
大化高中
陆翠柏
钓鱼岛
a
b
a
b
旧知回顾
1、 直线和平面垂直的判定定理
l
m O n
l m, l n m, n l mnO
(1)定义法 (2)判定定理
2、平面和平面垂直的判定
α
l
l ,l
β
新知探究一:线面垂直Hale Waihona Puke 性质 AB 想方法?
联系?
3、思想方法:
类比思想 归纳猜想思想 转化思想
P73.习题2.3.A组. 作业:
第5题
D
C
B
A
符号语言
, AB , AB CD CD,
AB
平面与平面垂直的性质定理
已知: , CD,AB , AB CD 求证:AB 证明: 在内过点B作BE CD 分析:要证明直线垂 直于平面,须证明直 则ABE是二面角
要证 MN // AD1 , 只需证明 A1 ADD 分析: 证明: 1是正方形
AD A1 D AD A 1 平面 1 1 DC .只需证 平面A1 ADD 明CD AD1垂直于平面 A1 DC 1 内
A1
O N
D1 B1
D
C1
AD1 CD 的两条相交直线即可。
又CD A1D D
面面垂直的性质是作平面的垂线的重要的
方法,因此,在有面面垂直的条件下,若
需要平面的垂线,要首先考虑面面垂直的 性质。
课堂练习三
如图,四棱锥P-ABCD的底面是矩形,平面
PAB⊥平面ABCD.求证:平面PAB⊥平面PBC
P
A
D
B
C
小结反思
1、直线和平面垂直的性质定理 线线、线面、面面之 a , b 本节课我们学习了哪些性 a // b 间的关系的转化是解 本节课我们探究问题 决空间图形问题的重 2、两平面垂直的性质定理 质定理?其内容各是什么? 的时候用到了哪些思 要思想方法。 , CD , AB , AB CD 两个性质定理之间有什么
平面AC 平面D1C 平面AC 平面D1C DC
D1D 平面D1C
A1
D A B D1 B1 C1
D1D CD
D1D 平面AC
C
平面与平面垂直的性质定理
两个平面垂直,则一个平面内垂 文字语言 直于交线的直线与另一个平面垂直.
图形语言
交线的直线b 要证a // , 只需在平
b 面内作一直线b // a a a // b
b
a
即可。而题中条件有 又 a , b a , ,因此,
a // 必有b .
即直线a与平面平行
规律方法:
生活中的数学
直线和平面垂直的性质定理
文字语言 垂直于同一个平面的两条直线平行. 图形语言
a
b
符号语言
a , b a // b
线线平行
简记: 线面垂直
作用:证明空间直线的平行。
课堂练习(一):
判断下列命题是否正确:
(1)垂直于同一条直线的两个平面互相平行。(
)
(2)垂直于同一个平面的两条直线互相平行。(
AB
简记: 线面垂直 面面垂直
性质定理 判定定理
D A
C
B
定理的作用:证明线面垂直。
面面垂直
线面垂直
线面、面面之间的关系的转化是解决空间图 形问题的重要思想方法。
应用举例
例2:已知平面 , , , 直线a满足a , a ,判断直线a与平面的位置关系。 解:在内作垂直于与 分析:
)
(3)平行于同一个平面的两条直线互相平行。(
)
课堂练习(二):
小心陷阱
已知直线a, b和平面,且a b, b , 则a与的位置关系是 ( D )
A、a // C、a
B、a
D、a 或a //
应用举例
例1:在正方体ABCD A1 B1C1 D1中,M是AB上 一点,N是A1C上的一点,MN 平面A1 DC 求证:MN // AD1
线垂直于平面内两条 - CD 的平面角 相交直线,而题中条 件已有一条,故可过 该直线作辅助线 . AB BE
E
B
D
A
C
AB CD
CD , BE , BE CD B AB
平面与平面垂直的性质定理
CD, AB , AB CD ,
C B
AD1 平面A1DC
MN 平面A1DC MN // AD1
A
M
规律方法:
线面垂直的性质定理也是证明线线平行的一
个方法,在有线面垂直的条件下,要证平行
关系,就应考虑线面垂直的性质定理。
新知探究二:平面与平面垂直的性质
你能找到互相垂
直的两个平面吗?
新知探究二:平面与平面垂直的性质
大化高中欢迎您
大化高中
陆翠柏
钓鱼岛
a
b
a
b
旧知回顾
1、 直线和平面垂直的判定定理
l
m O n
l m, l n m, n l mnO
(1)定义法 (2)判定定理
2、平面和平面垂直的判定
α
l
l ,l
β
新知探究一:线面垂直Hale Waihona Puke 性质 AB 想方法?
联系?
3、思想方法:
类比思想 归纳猜想思想 转化思想
P73.习题2.3.A组. 作业:
第5题
D
C
B
A
符号语言
, AB , AB CD CD,
AB
平面与平面垂直的性质定理
已知: , CD,AB , AB CD 求证:AB 证明: 在内过点B作BE CD 分析:要证明直线垂 直于平面,须证明直 则ABE是二面角
要证 MN // AD1 , 只需证明 A1 ADD 分析: 证明: 1是正方形
AD A1 D AD A 1 平面 1 1 DC .只需证 平面A1 ADD 明CD AD1垂直于平面 A1 DC 1 内
A1
O N
D1 B1
D
C1
AD1 CD 的两条相交直线即可。
又CD A1D D
面面垂直的性质是作平面的垂线的重要的
方法,因此,在有面面垂直的条件下,若
需要平面的垂线,要首先考虑面面垂直的 性质。
课堂练习三
如图,四棱锥P-ABCD的底面是矩形,平面
PAB⊥平面ABCD.求证:平面PAB⊥平面PBC
P
A
D
B
C
小结反思
1、直线和平面垂直的性质定理 线线、线面、面面之 a , b 本节课我们学习了哪些性 a // b 间的关系的转化是解 本节课我们探究问题 决空间图形问题的重 2、两平面垂直的性质定理 质定理?其内容各是什么? 的时候用到了哪些思 要思想方法。 , CD , AB , AB CD 两个性质定理之间有什么
