正态分布的概率密度与分布函数(修)
(项目管理)正态分布原理PMP项目管理分享资料

正态分布(一)正态分布正态分布的概率密度如果连续型随机变量的概率密度为,(4.29)其中,,则称随机变量服从参数为,的正态分布,记作。
正态分布的数学期望和方差正态分布的图形有如下性质:1.它是一条以直线为对称轴的钟形曲线;2.它以横轴为渐近线,并且在处有拐点;3.它在处取得最大值,最大值为:由此可见,标准差越大,的图形就越平缓,标准差越小,的图形就越陡峭。
正态分布的分布函数,(4.30)(二)标准正态分布标准正态分布的概率密度参数,的正态分布,称为标准正态分布,记为。
标准正态分布的概率密度通常用表示,,(4.31)的图形如图4.12所示,它是一条以纵轴为对称轴的钟形曲线。
图4.12 标准正态分布概率密度函数标准正态分布的分布函数标准正态分布的分布函数通常用表示,,(4.32)图4.13 标准正态分布函数标准正态分布函数表对于非负的实数,可由标准正态分布函数表,直接查出的数值。
对于负的实数,根据标准正态分布的对称性,可由下式(4.33)计算出数值。
标准正态分布分位数设随机变量服从标准正态分布,对于给定的概率水平,满足等式(4.34)的正数,称为标准正态分布的水平的双侧分位数;满足等式(4.35)的正数,称为标准正态分布的水平的上侧分位数。
图4.14 正态分布双侧分位数例4.21假设,求下列概率:1.;2.;3.;4.。
解1.2.3.4.(三)正态分布与标准正态分布的关系如果,则于是,在正态分布与标准正态分布的概率密度和、分布函数和之间存在下列关系式:1.(4.36)2.(4.37)3.(4.38)这就是说,计算任一正态分布随机变量的概率都能通过标准正态分布来实现。
例4.22设,求下列概率:1.2.解因为,所以。
1.2.例4.23设,求下列概率:1.2.3.解1.2.3.从上面的结果可以看出,事件的概率很小,因此的取值几乎全部落在区间内,超出这个范围的可能性还不到。
这就是在产品质量控制中有重要应用的准则。
1.正态分布的概率密度与分布函数

1 P(2 X 100 2) 1[ (2) (2)]
0.6 1[0.9772 (1 0.9772)] 0.0456 4.56%.
概率论与数理统计
§4.1 正态分布的概率密度与分布函数
1
(
t) et2
2dt
2 π
e t2 2dt
t
e t 2
2dt.
2 π
2 π
因为 e t2 2dt 2 π , t et2 2dt 0 ,所以
E(X ) .
概率论与数理统计
§4.2 正态分布的数字特征
D(X ) 1
(x
)2
e(
x )2 2 2
dx
2 π
2 t 2 et2 2dt . 2 π
当 y 0 时,
FY ( y) 0 ;
概率论与数理统计
§4.1 正态分布的概率密度与分布函数
当 y 0 时,
y
FY ( y) P( y X y)
y
1
y x2
e 2 dx
2π y
所以,Y 的分布函数为
y o
yx
FY ( y)
2
y x2
e 2 dx ,
2π 0
0,
y 0; y 0.
e
(
x )2 2 2
,
x
.
2.标准正态分布N(0 ,1)的概率密度与分布函数:
(x) Φ(x)
1
x2
e 2,
2π
x
.
1
x t2
e 2 dt.
2 π
概率论与数理统计
概率分布正态化总结讲解

a
1 b
(
1
1)
b
0.5772
2
标准差
ab 23
x (e 2 1)e(2 2 )
1
ab
( 2 1) [( 1 1)]2
b
b
1 6
x
4 2
统计参数向分布参数的转化
第一章:为什么要研究随机变量的分布
目前概率论预测方法的应用已经遍及自然科学和社会科学 的各个领域。从电子、航空、宇航、核能等尖端工业部门扩展 到电机与电力系统、机械设备、动力、土木建筑、冶金、化工 等部门。可靠性的应用也从复杂航天器的设计推广普及到日常 生活中的机电产品设计之中,并贯穿于产品的开发研制、设计、 制造、试验、使用、运输、保管及维修保养等各个环节。
第二章:常见的随机变量的分布类型
正态分布 均匀分布 指数分布 对数正态分布 极值分布( Gumbel ) 瑞利分布(Rayleigh) 韦伯分布( Weibull )
正态分布概要
正态分布是在统计以及许多统计测试中最广泛应用的一 类分布。在概率论中, 正态分布是几种连续分布和离散分布 的极限分布。各种各样的心理学测试和物理现象都被发现近 似地服从正态分布。
正态分布概要
由上图可以看出约68%的数值分布在距离平均值有1个标准 差之内的范围,约95%数值分布在距离平均值有2个标准差之内 的范围,以及约99.7%数值分布在距离平均值有3个标准差之内 的范围。称为 "68-95-99.7法则"或"经验法则".
关于非正态分布需要转化的一些说明
由于正态分布具有上述一些优良的特性,而且工程界的大 多数参数都是服从正态分布的,因此在目前比较成熟的可靠 性分析方法中,很多方法(改进一次二阶矩方法,一次、二 次响应面法)往往都是针对正态分布展开的,因此我们对非 正态分布变量需要采用当量正态化。具体方法将在第三章中 详细介绍,为了能更好的理解各种分布类型的相关特性,对 实验数据的获得提供相应参考,本章将对一些常见的非正态 变量的分布类型分类进行简要阐述。
《正态分布》说课稿

《正态分布》说课稿正态分布是统计学中非常重要的一个概念,它描述了大量随机变量的分布规律,被广泛应用于各个领域的数据分析和预测中。
本文将介绍正态分布的基本概念、性质、应用以及如何利用正态分布进行统计推断。
一、正态分布的基本概念1.1 正态分布的定义:正态分布又称高斯分布,是一种连续概率分布,其概率密度函数呈钟形曲线,左右对称,中间最高。
1.2 正态分布的特点:正态分布具有唯一的均值和标准差,均值决定了曲线的中心位置,标准差决定了曲线的宽度。
1.3 正态分布的标准化:通过标准化可以将正态分布转化为标准正态分布,即均值为0,标准差为1的正态分布。
二、正态分布的性质2.1 正态分布的均值和中位数相等:正态分布的均值和中位数相等,即曲线对称中心位置处的值。
2.2 正态分布的68-95-99.7法则:约68%的数据落在均值附近的一个标准差范围内,约95%的数据落在两个标准差范围内,约99.7%的数据落在三个标准差范围内。
2.3 正态分布的线性组合仍然是正态分布:对于正态分布的线性组合,如两个正态分布的和或差,仍然是正态分布。
三、正态分布的应用3.1 在自然科学中的应用:正态分布常用于测量误差、实验数据分析等领域,如物理学、化学等。
3.2 在社会科学中的应用:正态分布被广泛应用于人口统计、心理学研究、经济学分析等领域。
3.3 在工程技术中的应用:正态分布在质量控制、可靠性分析、风险评估等方面有重要应用。
四、利用正态分布进行统计推断4.1 正态分布的参数估计:通过样本数据估计总体的均值和标准差,得到对总体的估计。
4.2 正态分布的假设检验:利用正态分布进行假设检验,判断总体参数是否符合某种假设。
4.3 正态分布的置信区间估计:通过正态分布的性质,构建总体参数的置信区间,对总体参数进行估计。
五、结语正态分布作为统计学中重要的概念,具有丰富的性质和广泛的应用。
通过深入理解正态分布的基本概念和性质,我们可以更好地应用正态分布进行数据分析和推断,为各个领域的研究和实践提供有力支持。
正态分布的概率密度与分布函数(修)
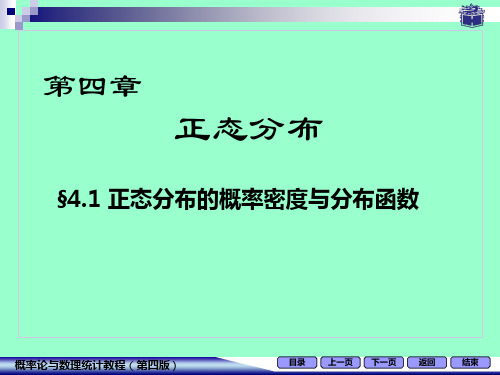
P ( X − µ < 2σ ) = 2Φ (2) − 1 = 0.9544,
第四章
正态分布
§4.1 正态分布的概率密度与分布函数
概率论与数理统计教程(第四版)
目录
上一页
下一页
返回
结束
§4.1 正态分布的概率密度与分布函数
正态分布是最常见因而也是最重要的分布: 正态分布是最常见因而也是最重要的分布: 1. 很多随机现象可以用正态分布描述或近似描述; 2. 在一定条件下,某些概率分布可以利用正态分布 近似计算; 3. 在非常一般的充分条件下, 大量独立随机变量的 和近似地服从正态分布; 4. 数理统计中:(1)某些常用分布是由正态分布推导 得到的.(2) 统计推断中常用正态分布的统计量.
σ = Φ (k ) − Φ (−k )
σ
= Φ (k ) − [1 − Φ (k )]
= 2Φ (k ) − 1, k = 1 ,2 ,3 ,L.
概率论与数理统计教程(第四版)
目录
上一页
下一页
返回
结束
§4.1 正态分布的概率密度与分布函数
查附表2得 P ( X − µ < σ ) = 2Φ (1) − 1 = 0.6826,
§4.1 正态分布的概率密度与分布函数
正态分布 N ( µ ,σ 2 ) 的分布函数为
1 F(x) = ∫e 2πσ
F (x )
1
( x−µ)2 x − 2σ 2 −∞
dx , − ∞ < x < +∞.
0.5
O
µ
x
概率论与数理统计教程(第四版)
目录
上一页
下一页
返回
结束
§4.1 正态分布的概率密度与分布函数
1.正态分布的概率密度与分布函数

解:(1) P( X 1.96) (1.96) 0.975;
(2) P(1.6 X 2.5)
(2.5) (1.6) (2.5) [1 (1.6)] (2.5) 1 (1.6) 0.9938 1 0.9452
0.9390.
概率论与数理统计
§4.1 正态分布的概率密度与分布函数
正态分布的概率计算
定理. 设 X ~ N ( , 2 ) , 则
P( x1
X
x2
)
(
x2
) ( x1
).
证: P(x1 X x2 )
t
xμ σ
1
2π
x2 t2
e 2 dt
x1
1
e dx x2
(
x )2 2 2
标准正态分布的概率密度:
(x)
1 2π
x2
e2
,
ห้องสมุดไป่ตู้
x
;
标准正态分布的分布函数:
Φ(x) 1
x t2
e 2 dt .
2 π
(x) 的性质:
(0) 0.5; () 1; (x) 1 (x).
概率论与数理统计
§4.1 正态分布的概率密度与分布函数
例1.设X服从标准正态分布N (0 ,1) , 求
概率论与数理统计
§4.1 正态分布的概率密度与分布函数
例4.设随机变量 X 服从标准正态分布 N (0 ,1) , 求随
机变量函数 Y X 2 的概率密度.
解:已知随机变量X 的概率密度
fX (x)
1
x2
e 2,
2π
x .
正态分布 课件

总之,正态分布广泛存在于自然界、生产及科学技术的许多领域中。
正态分布在概率和统计中占有重要地位。
4、正态曲线的性质
(1)曲线在x轴的上方,与x轴不相交.
(μ-σ,μ+σ]
0.6826
(μ-2σ,μ+2σ]
0.9544
(μ-3σ,μ+3σ]
0.9974
(2)曲线是单峰的,它关于直线x=μ对称.
(4)曲线与x轴之间的面积为1.
(3)曲线在x=μ处达到峰值(最高点)
(5)若 固定, 随 值的变化而沿x轴平移, 故 称为位置参数
(6)当μ一定时,曲线的形状由σ确定 .σ越大,曲线越“矮胖”,表示总体的分布越分散;σ越小,曲线越“瘦高”,表示总体的分布越集中.
5、特殊区间的概率:
m-a
m+a
x=μ
若X~N ,则对于任何实数a>0,概率 为如图中的阴影部分的面积,对于固定的 和 而言,该面积随着 的减少而变大。这说明 越小, 落在区间 的概率越大,即X集中在 周围概率越大。
4
0.04
[0.5,1)
8
0.08
[1,1.5)
15
0.15
[1.5,2)
22
0.22
[2,2.5)
25
0.25
[2.5,3)
14
0.14
[3,3.5)
6
0.06
[3.5,4)
4
0.04
[4,4.5)
2
0.02
11
高尔顿钉板实验的 频率分布直方图
这条曲线具有 “中间高,两头低” 的特征,像这种类型的曲线, 就是(或近似地是)以下函数的图像:
表示标准正态分布的概率密度函数,用Φ(x)

第三节 连续型随机变量的分布
2.3、连续型随机变量的分布
2.3.1、连续型随机变量的概率密度函数
由于连续型随机变量取值可以充满某个区间, 为了研究其概率分布,类似于质量分布的求法, 已知质量分布的线密度函数 μ(x) 时,在区间 [a,b]上分布的质量m可由质量密度函数积分求 得,即
m b(x)dx a
3
3
3
(2)P(2 X 10) P( 2 5 X 5 10 5) P(1 X 5 1.67)
3
3
3
3
(1.67) (1) 0.9525 (1 (1)) 0.7938
一般,设 X ~ N(, 2 ) , 则有
P(a
X
b)
( b
)
( a
)
案例分析见2.16~2.18
案例分析
【解答】(3). P{| X | 2} 1 P{| X | 2}
1 P{2 X 2}
1 [( 2 3 ) ( 2 3)]
2
2
1 [(2.5) (0.5)]
1 (0.9938 0.6915)
0.6977.
(4). P{ X 3} 1 P{ X 3}
1 (0)
x
1
x2
e2
2
x
x
( x) (t)dt
1 t2 e 2 dt
2
标准正态分布的概率密度函数和分布函数 的图形
图2-6 标准正态分布的重要性在于,一般的正态分布都 可以转化为标准正态分布进行研究.
定理 设 X ~ N(, 2 ), 则 Y X ~ N (0,1)
证明 P(a Y b) P(a X b)
1
xa a xb
xb
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(k) [1 (k)] 2 (k) 1, k 1 ,2 ,3 ,.
§4.1 正态分布的概率密度与分布函数
查附表2得
P( X ) 2 (1) 1 0.6826, P( X 2 ) 2 (2) 1 0.9544, P( X 3 ) 2 (3) 1 0.9973. 说明: 若 X ~ N ( , 2 ) , 则 P( X 3 ) 1 P( X 3 )
(x)
1 2
π
x2
e2
,
x
;
标准正态分布的分布函数:
Φ(x)
(x) 的性质:
1
x t2
e 2 dt .
2 π
(0) 0.5; () 1; (x) 1 (x).
§4.1 正态分布的概率密度与分布函数
[例1] 设 X 服从标准正态分布 N (0 ,1) , 求 (1) P(X 1.96); (2) P(1.6 X 2.5).
2(2) 1 0.9544
故产品的正品率为 0.9544
[例5]
公共汽车车门的高度是按男子与车门碰头的
机会在 0.01 以下来设计的。 设男子的身高
X ~ N (168, 72 ). 问车门的高度应如何确定?
解 设车门高度为 x(cm), 则 P( X x) 0.01
于是 P( X x) 0.99
[定理] 设 X ~ N( , 2) , 则
P(x1
X
x2
)
(
x2
)
( x1
).
证:
t
x
P(x1 X x2 )
1
x2 t2
e 2 dt
2 π x1
1
e dx x2
(
x )2 2 2
2 x1
1
x2 t 2
e 2 dt
2 π
1
x1 t 2
e 2 dt
2 π
( x2 ) ( x1 ).
[例4]
某机器生产的螺栓的长度(cm)服从正态分布
N (10.05, 0.062 ) ,规定长度在范围 10.05 0.12
内为正品, 求产品的正品率。
解 X ~ N (10.05, 0.062 ) P( x 10.05 0.12) P( x 10.05 2) 0.06 (2) (2)
第四章
正态分布
§4.1 正态分布的概率密度与分布函数
§4.1 正态分布的概率密度与分布函数
正态分布是最常见因而也是最重要的分布:
1. 很多随机现象可以用正态分布描述或近似描述;
2. 在一定条件下, 近似计算;
某些概率分布和近似地服从正态分布;
大量独立随机变量的
即 由于
P( X 168 x 168) 0.99, (
7
7
(2.33) 0.9901 0.99,
可取
x
x 168) 0.99, 7
168 2.33
x 184.31
7
故车门高度应设计为 184.31 厘米。
§4.1 正态分布的概率密度与分布函数
[例6] 设随机变量 X 服从标准正态分布 N (0 ,1) , 求随
§4.1 正态分布的概率密度与分布函数
[例3] 设随机变量 X 服从正态分布 N ( , 2 ) , 求 X 落 在区间 ( k , k ) 内的概率, 这里 k 1 ,2 ,3 ,.
解:
P( X k ) P( k X k )
( k ) ( k )
(k) (k)
正态分布(或高斯分布). 记作:
X ~ N ( , 2). 特别,当 0, 1 时称 X 服从标准正态分布. 记为:
X ~ N (0 ,1).
§4.1 正态分布的概率密度与分布函数
正态分布的概率密度与分布函数
正态分布 N ( , 2 ) 的概率密度 f (x) 的图形:
f (x)
分布曲线的特征:
4. 数理统计中:(1)某些常用分布是由正态分布推导
得到的.(2) 统计推断中常用正态分布的统计量.
§4.1 正态分布的概率密度与分布函数
正态分布的定义
[定义] 若随机变量 X 的概率密度为
f (x)
1
e ,
(
x )2 2 2
x ,
2 π
其中 及 都是常数, 0. 则称随机变量 X 服从
1
2
1.关于直线 x 对称;
2.在 x 处达到最大值;
3.在 x 处有拐点;
O
x
4. x 时曲线以 x 轴为渐近线.
§4.1 正态分布的概率密度与分布函数
5. 固定 , 改变 . 则图形沿 x 轴平移而不改变
其形状.
f (x)
6. 固定 , 改变 , 则当 很小时,
曲线的形状与一尖塔相似;
1 0.9973 0.0027 0.003.
§4.1 正态分布的概率密度与分布函数
由此可知 X 落在 ( 3 , 3 ) 之外的概率小于 3 ‰, 根据小概率事件的实际不可能性原理, 通常把区间 ( 3 , 3 ) 看作是随机变量 X 的实际 可能的取值 区间. 这一原理叫做 “三倍标准差原理” (或"3 法则").
当 值增大时,
曲线将趋于平坦.
O
1
1.5 3 7.5 x
§4.1 正态分布的概率密度与分布函数
正态分布 N ( , 2 ) 的分布函数为
F(x) 1
x
(
e
x )2 2 2
dx
,
x .
2 π
F (x)
1
0.5
O
x
§4.1 正态分布的概率密度与分布函数
标准正态分布的概率密度:
§4.1 正态分布的概率密度与分布函数
[例2] 设随机变量 X 服从正态分布 N (1 ,22 ) , 求概率 P(1.6 X 2.4).
解:P(1.6 X 2.4) (2.4 1) (1.6 1)
2
2
(0.7) (1.3)
(0.7) [1 (1.3)]
0.7580 (1 0.9032) 0.6612.
解:(1) P( X 1.96) (1.96) 0.975;
(2) P(1.6 X 2.5)
(2.5) (1.6) (2.5) [1 (1.6)] (2.5) 1 (1.6) 0.9938 1 0.9452
0.9390.
§4.1 正态分布的概率密度与分布函数
一般正态分布的概率计算
机变量函数 Y X 2 的概率密度.
解: 已知随机变量 X 的概率密度
fX (x)
1
x2
e 2,
2π
x .
先求随机变量 Y 的分布函数:
