第2章静力平衡

力矩的特性
1、力作用线过矩心，力矩为零；
2、力沿作用线移动，力矩不变。
合力矩定理
一个力对一点的力矩等于它的两个分力对
同一点之矩的代数和。
例 1 求图中荷载对A、B两点之矩
(a) 解： 图（a）： MA = - 8×2 = -16 kN ·m
(b)
MB = 8×2 = 16 kN ·m
图（b）： MA = - 4×2×1 = -8 kN ·m MB = 4×2×1 = 8 kN ·m
YA 4kN ( )
Y 0 :
YA RB 3q P 0 RB 3q P YA
【解】 1.研究对象：外伸梁。 2. 受力分析：如图示。 3. 列式求解：
m
X 0: X
9 ( F ) 3RB 5P q M 2 9 3 28 5 12 4 6 2 84 60 18 6 0 故计算正确无误。
A
A
0
讨论：若用二矩式，则情况如何？
【例4】一端为固定铰链，另一端为可动铰链的梁称之为简支梁，其上作用有 一均匀分布的荷载 q（简称均布荷载），试画出梁的受力图。
XA
YA 【解】1.研究对象：梁AB。 2.画受力图 —— 标力。 （1）主动力：均布荷载 q（照搬） （2）约束反力： （按约束类型来画）
YB
① 固定铰链 A：XA、YA （指向可设）；
4 20kN + 0 50kN 20kN 5
2.1.4 支座的约束与反力
（1）固定铰支座
YC XC
约束特点：只能限制物体上下、左右的平动，而不能限制物体的转动（双向约束）。 反力方向：方位是两分力正交（如
YA 等）；指向可以假设。 X C、 YC，或 X A、
（2）可动铰支座
NA
平面任意力系
X 0: XA 0 l m (F ) 0 : (ql ) 2 Y l 0 l 0 m (F ) 0 : Y l (ql ) 2
B
A
YA
A
B
1 ql 2 1 YB ql 2
校核： Y 0 : YA YB ql
ql ql ql 0 2 2
—— 正负号之规定：
① 若 a b ，与 x 轴同向， X 取正；反之取负；
② 若 a b，与 y 轴同向， Y 取正；反之取负。
（2）力的合成： 若已知 X 和 Y ，则力 F 的大小和方位角为：
F X 2 Y 2 tg Y X
（3）合力投影定理：合力在任一轴上的投影等于各分 力在该轴上之投影的代数和。
力偶系的平衡 显然，当物体平衡时，合力偶必须为零，
即：
M 0
上式称为力偶系的解析平衡条件。
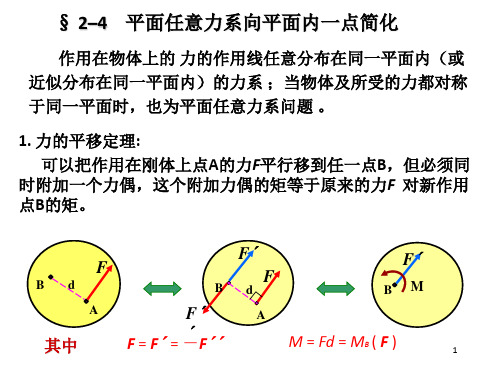
2.2.3 力之平移定理
作用在 A 点的力
F ，是否可以平行移动至 B 点变成 F ？
问题：力在刚体上可沿其作用线滑动，但能否平行搬动？
在B点加一平衡力
( F , F )为一力偶
力偶矩为 m
3 m ( F ) 0 : ( 3 q ) M P 2 YA 3 0 B 2 1 9 YA ( q M 2 P) 3 2 1 9 ( 4 6 2 12) 4kN ( 3 2
X 0: X
B
A
0
)
（ ）
m (F ) 0 : m (F ) 0 :
O
基 本 式
X 0 Y 0 mO ( F ) 0
独立的平衡方程数
＝
3
求解
三个未知量
2）平面汇交力系之平衡方程 设平面汇交力系 F1、F2、…Fn 交于 O 点，此时只能合成一个合力，不可能存在 合力偶。若取汇交点 O 为矩心，则
m
O
( F ) 0 自然满足。当该力系平衡时，有
基 本 式
X 0 Y 0
求解
独立的平衡方程数 ＝ 2
二个未知量
2.3.3 平衡方程的应用 【例1】试求简支梁 A、B 两处的约束反力。
【解】1.研究对象：AB 梁
2.受力分析： A 处（XA，YA ） ， B 处YB。 均布荷载 q ， （q、XA、YA、YB） 3.列式求解： （1）基本式
例2
求图中力对A点之矩
解：将力F沿X方向和Y方向 等效分解为两个分力，由 合力矩定理得：
M A Fx d x Fy d y
由于 dx = 0 ，所以：
2 M A Fy d y 20 2 28.28kN m 2
2.2.2 力偶和力偶矩 力偶 —— 大小相等的二个反向平行力称之为一
由合力投影定理有： Rx=X1+X2+…+Xn=X Ry=Y1+Y2+…+Yn=Y
合力：
R Rx Ry
2
2
X Y
2
2
tan
Ry Rx

Y X
表示合力R与 x轴所夹的锐角， 合力的指向由∑X、∑Y的符号判定。
【例1】 试分别求出图2-6中各力的合力在x轴和y轴上投影。已知
2.3.2 力系的平衡方程 1)平面任意力系之平衡方程 设平面任意力系 F1、F2、…Fn ，当该力系平衡时，则有
R0
（各分力在 x 轴上投影之代数和为零） X 0 Y 0 （各分力在 y 轴上投影之代数和为零）
M 0
m (F ) 0（各分力对任意点 O 之矩代数和为零）
即，合力为原两力的矢量和。 矢量表达式：R= F1+F2
A F1
F2
R
四、三力平衡汇交定理 一刚体受不平行的三力作用而平衡时，此三力 的作用线必共面且汇交于一点。
五、作用力和反作用力定律 两个物体间的相互作用的一对力，总是大小相等， 方向相反，作用线相同，并分别而且同时作用于这 两个物体上。
[例] 吊灯
X 0:
XA 0
l 2 YA 1 ql 2 1 ql 2
mB (F ) 0 : (ql ) YAl 0
Y 0 :
YA YB ql 0
YB
（2）二矩式
【例2】已知外伸梁的 M = 6KN·m，q = 4KN/m，P =12KN，求 A、B 支座反力。
力是一矢量，用数学上的矢量记号来表示，如图。
F
2.1.2 静力学基本公理 一、二力平衡公理
作用于刚体上的两个力平衡的充分与必要 条件是这两个力大小相等、方向相反、作用线 在一条直线上。
二力体：只在两个力作用下平衡的刚体叫二力体。
二力杆
二、加减平衡力系公理 在作用于刚体上的已知力系上，加上或减 去任意一个平衡力系，不会改变原力系对刚体 的作用效应。
F1 20N
F2 40N F3 50N ，各力方向如图所示。
【解】 可得出各力的合力在x、y轴上的投影为
FRx Fx F1 cos90 F2 cos 0 F3
， ，
3 32 42
4 32 42
3 0 40kN + 50kN 10kN 5
FRy Fy F1 sin 90 F2 sin 0 F3
约束特点：只能限制物体沿法线方向的平动（单向约束）。
反力方向：方位为沿其法线，指向可以假设。
3）固定端支座
构件的一端被牢固地嵌住而不能动
车刀
P
XA
mA
P
YA
约束特点：既限制物体的平动，又限制物体的转动。 反力方向：限制平动，用约束反力（ 如 XA 、YA ）表示，指向可以假设； 限制转动，用约束反力偶（如 mA ）表示，转向可以假设。
F F F
△
结论：
F F m 且 m mB ( F ) F d
力之平移定理
牛腿柱
2.3 力系的平衡
2.3.1 力系之平衡条件
刚体 平衡 （1）二力之平衡 两个力 刚体
必要且充分条件
不能平动
不能转动
R＝0（合力为零）
M＝0（合力矩为零）
刚体平衡之必 要且充分条件
个力偶。
力偶的作用效果是引起物体的转动，和力
矩一样，产生转动效应。
力偶的转动效应用力偶矩表示，它等于力偶 中任何一个力的大小与力偶臂d 的乘积，加上适
当的正负号，即
式中：F 是力的大小； d 是力偶臂，是力偶中两
个力的作用线之间的距离；
正负号规定与力矩统一。常
力偶的图例
用单位为 KN· m 。
力偶特性一：
2.1 力的基本概念
2.1.1 力和力系的概念 力是物体之间的相互作用，其效果使物体运动状态和形状 大小发生改变。 实践证明，力对物体的作用效应取决于以下三个要素： (1) 力的大小。指物体间相互作用的强弱程度。国际单位 制(SI)中，力的单位为牛[顿](N)或千牛[顿](KN)。 (2) 力的方向。通常包含力的方位和指向两个含义。例如 重力的方向是“铅垂向下”，“铅垂”是指力的方位；“向下” 是说力的指向。 (3) 力的作用点。力的作用点是指力在物体上作用的位置。 力系：物体所受的一群力总称为力系。
力偶的转动效应与转动中心的位置 无关，所以力偶在作用平面内可任意移 动。 力偶特性二： 力偶的合力为零，所以力偶的效应
只能与转动效应平衡，即只能与力偶或
力矩平衡，而不能与一个力平衡。
力偶系的合成 作用在一个物体上的一组力偶称为一个力偶
系。力偶系的合成结果为一个合力偶M。 即：
M M1 2 M n M
O
F3 c) 汇交力系
O
O
b) 力三角形
a) 平行四边形法则