§2.5闭环传递函数§2.6 梅逊公式
梅逊公式
2.4 控制系统的方块图、信号流图与梅逊公式控制系统的方块图是系统各元件特性、系统结构和信号流向的图解表示法。
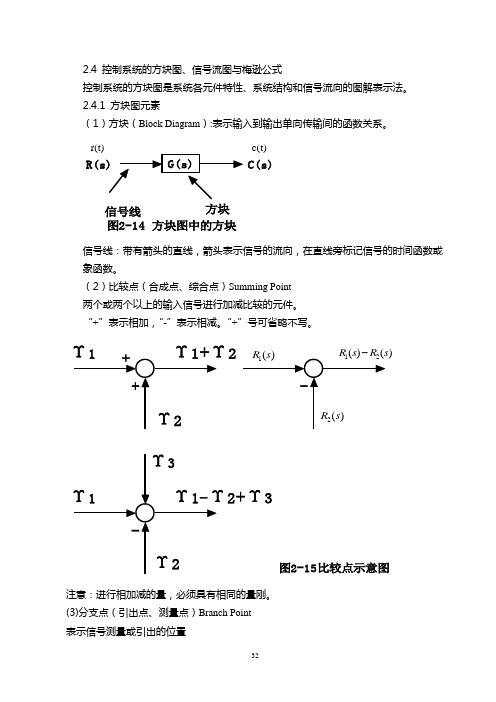
2.4.1 方块图元素(1)方块(Block Diagram ):表示输入到输出单向传输间的函数关系。
C(s)图2-14 方块图中的方块信号线方块r(t)c(t)信号线:带有箭头的直线,箭头表示信号的流向,在直线旁标记信号的时间函数或象函数。
(2)比较点(合成点、综合点)Summing Point 两个或两个以上的输入信号进行加减比较的元件。
“+”表示相加,“-”表示相减。
“+”号可省略不写。
2)2+Υ3图2-15比较点示意图注意:进行相加减的量,必须具有相同的量刚。
(3)分支点(引出点、测量点)Branch Point 表示信号测量或引出的位置图2-16分支点示意图注意:同一位置引出的信号大小和性质完全一样。
2.4.2 几个基本概念及术语R(s)N(s)打开反馈图2-17 反馈控制系统方块图(1) 前向通路传递函数 假设N(s)=0打开反馈后,输出C(s)与R(s)之比。
在图中等价于C(s)与误差E(s)之比。
)()()()()(21s G s G s G s E s C == (2) 反馈回路传递函数 Feedforward Transfer Function 假设N(s)=0 主反馈信号B(s)与输出信号C(s)之比。
)()()(s H s C s B = (3) 开环传递函数 Open-loop Transfer Function 假设N(s)=0 主反馈信号B(s)与误差信号E(s)之比。
)()()()()()()(21s H s G s H s G s G s E s B == (4) 闭环传递函数 Closed-loop Transfer Function 假设N(s)=0 输出信号C(s)与输入信号R(s)之比。
)()(1)()()(1)()()()(21s G s H s G s G s H s G s G s R s C +=+= 推导:因为)()]()()([)()()(s G s H s C s R s G s E s C -== 右边移过来整理得)()(1)()()(s G s H s G s R s C += 即开环传递函数前向通路传递函数+=+=1)()(1)()()(s G s H s G s R s C **(5) 误差传递函数 假设N(s)=0 误差信号E(s)与输入信号R(s)之比。
梅森公式求传递函数

梅森公式求传递函数梅森公式求传递函数在探讨开环传递函数和闭环传递函数之前,我们需要先了解一些基础知识。
传递函数通常是指线性系统的输出与输入之间的关系,其中输入通常是一个函数,输出也是一个函数。
当我们了解传递函数的性质时,我们可以更好地设计控制系统,调整输入,使输出达到我们所需的目标。
在这里,我们将重点介绍梅森公式是如何求解传递函数的,梅森公式是一种常见的、快速且可靠的方法,用于解决反馈控制系统的稳定性问题。
梅森公式是一种特殊的公式,它同时适用于电气和机械系统,尤其适用于系统的加减法运算芯片,用于测量和放大信号。
首先,我们需要了解梅森公式的组成部分——单位环,单位环是指输入信号沿着反馈路径回到输入的路径。
这通常是因为系统的输出通过反馈路径的增强或减弱,来调节系统的调制。
如果我们能够计算出反馈路径的增强和输入信号的比例,我们就可以确定系统的传递函数了。
那么,如何确定反馈路径的增强和输入信号的比例呢?这就需要用到梅森公式了。
梅森公式表明,任何一个带有反馈路径的系统都可以由输入的单位环来描述。
在这种情况下,反馈系数是最小的。
因此,我们可以通过计算单位环的增益和相位移,来确定系统的传递函数。
梅森公式的常见形式为:$H(s) = \frac{N(s)}{D(s)} =\frac{1}{\Delta}\sum_{i=1}^{n}(-1)^{i+1}\Delta_i(s)\frac{D_i(s)}{N_i(s)}$其中,$\Delta$为通分多项式,$D(s)$为系统的分母多项式,$N(s)$为系统的分子多项式,$D_i(s)$和$N_i(s)$为单位环考虑时的分母多项式和分子多项式,$\Delta_i(s)$为通分多项式的第$i$个因式。
这个梅森公式看起来很复杂,但它告诉我们的是,我们可以把系统的分子多项式和分母多项式分解成多个分式(即$\frac{D_i(s)}{N_i(s)}$),然后通过单位环考虑时,根据各个分式的反馈系数(即$(-1)^{i+1}$)和分式的分母和分子多项式得到系统的传递函数。
梅逊公式的应用

2.6
解: 前向通道(1条): 反馈回路(5个):每个均为
P1
系统信号流图及梅逊公式
1
R C s 1
RCs
3
3
3
1 1
则
a
La
5 RCs
两个互不接触回路(6个):①②、①③、③④、①⑤、②③、④⑤
每对传递函数之积为:
1 R C s
2 2 2
则
Lb Lc
6 R C s
3
2 2 2
系统信号流图及梅逊公式
②
-
1/G2(s) G2(s) H1(s)
①
H2(s) Y0 G4(s)
+
Xi(s)
+
G1(s)
+
X0(s)
-
-
-
G3(s)
③ ④
第二步、消去反馈回路①,另相加点(比较点)③前移
1/G2 H2
Xi(s)
+
G1
②
+
③
G3(1+G2H1)/G2G4
X0(s)
G2G4 /(1+G2 H1 )
2.6
系统信号流图及梅逊公式
二、梅逊公式的应用示例
例1:利用梅逊公式求如图所示系统的传递函数
R(s)
1/R 1/Cs
④
1/R 1/Cs
⑤
1/R 1/Cs
Y(s)
①
②
③
系统的信号流图为:
-1 -1
R(s) 1
④
1/R 1/Cs 1 1/R 1 1/Cs
⑤
1 1/R 1/Cs
Y(s)
①
-1
如何用梅逊公式求传递函数

二、分别用梅森公式求取输出节点及该节点对输入节点的传递 函数,然后把它们的结果相比,即可得到输出对该混合节点的 传递函数。
2/8/2022
21
第21页,本讲稿共29页
梅逊公式||例2-15
例2-15:数数有几个回路和前向通道。
G6
R
G5
1
G2 1
混合节点:既有输入支路又有输出支路的节点。如: X2,X3,X4,X5,X6,X7。混合节点相当于结构图中的信号相加点和分 支点。它上面的信号是所有输入支路引进信号的叠加。
通路:沿支路箭头方向穿过各个相连支路的路线,起始点和 终点都在节点上。若通路与任一节点相交不多于一次,且起点 和终点不是同一节点称为开通路。起点在源点,终点在阱点的 开通路叫前向通路。
11,21G 1H 1
P 1 k 2 1 P k k 1 G 1 H 1 G 1 G G 3 2 H G 3 2 G G 1 3 G G 2 4 G 3 G H 1 1 G H 3 G 2 4 H G 1 1 G 3 H 1 H 2
2/8/2022
19
第19页,本讲稿共29页
2/8/2022
16
第16页,本讲稿共29页
梅逊公式||例2-13
1
ui ue
1
1
R1
1
b 1
C1s
a
1
1
R2
I1 I u
1
C2s
I2 uo
1
1
讨论:信号流图中,a点和b点之间的传输为1,是否可以将该两
点合并。使得将两个不接触回路变为接触回路?如果可以的话,
总传输将不一样。
不能合并。因为a、b两点的信号值不一样。
§2.5 信号流图与梅森公式

e
g
a f
b
c
h
C(s)
前向通路两条
四个单独回路, 四个单独回路,两个回路互不接触 ab c d + e d (1 – b g) C(s) = – a – bg – c – R(s) 1 f h e h g f + af c h
— ∑L
a
Pk—从R(s)到C(s)的第 条前向通路传递函数 的第k条前向通路传递函数 从 到 的第
称为第k条前向通路的余子式 △k称为第 条前向通路的余子式
求法: 去掉第k条前向通路后所求的 △k求法 去掉第 条前向通路后所求的△ 条前向通路后所求的△
△k=1-∑LA+ ∑LBLC- ∑LDLELF+…
P2= G4G3
L4= – G4G3
P1=G1G2G3
L1= –G1 H1 L2= – G3 H3 L5 = – G1G2G3
L3= – G1G2G3H3H1
L1L2= (–G1H1) (–G3H3) = G1G3H1H3
L1L4=(–G1H1)(–G4G3)=G1G3G4H1
G3(s) R(s) R(s) R(s) R(s) G3 (s) E(S)G(s) G33(s) E(S) E(S) E(S) GG (s) 1 (s) G(s)
1 1
梅逊公式求E(s) 梅逊公式求
N(s) N(s) N(s)
G2(s) G2(s) G22(s) G (s) HH (s) 2 (s) H(s) 2 2 C(s) C(s) C(s) C(s)
P2= - G3G2H3 △ 2= 1 P2△2=?
HH (s) 1 (s) H(s) 1 1
H3(s) H3(s) H33(s) H (s)
控制系统的传递函数及信号流图和梅逊公式
1 Ln LrLsLt
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
例2-7 试用梅逊公式求系统的闭环传递函数 C(S)
R(S)
图2-45 例2-7图
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
解: P1 G1G2G3.
路 开通路—通路与任一节点相交不多于一次
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
闭通路—通路的终点也是通路的起点,并且与任何其它节 点相交不多于一次
6)前向通路—从输入节点到输出节点的通路上,通过任何节 点不多于一次,此通路自然保护区为前向通路
7)回路—就是闭环通路 8)不接触回路—如果一些回路间没有任何公共节点 9)前向通路增益—在前向通路中多支路增益的乘积。 10)回路增益—回路中多支路增益的乘积。
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
信号流图的性质 (1)信号流图只适用于线性系统。 (2)支路表示一个信号对另一个信号的函数关系;信 号只能沿着支路上的箭头指向传递 (3)在节点上可以把所有输入支路的信号叠加,并把 相加后的信号传送到所有的输出支路。
(4)具有输入和输出支路的混合节点,通过增加一个具 有单位增益的支路,可以把它作为输出节点来处理。 (5)对于一个给定的系统,其信号流图不是唯一的, 这是由于描述的方程可以表示为不同的形式。
参考输入误差的传递函数为
CR(s) ER(s)G1(s)G2(s)
CR(s)
G1( s )G 2( s )
R(s) 1 G1(s)G2(s)H (s)
ER(s)G1(s)G2(s)
如何用梅逊公式求传递函数
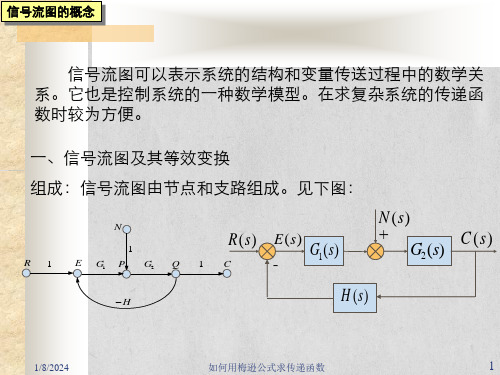
• 通路传输(增益):通路中各支路传输的乘积称为通路传输或通 路增益。前向通路中各支路传输的乘积称为前向通路传输或前 向通路增益。
• 回路传输(增益):回路上各支路传输的乘积称为回路传输或回
路增益。
1/8/2024
如何用梅逊公式求传递函数
4
信号流图的等效变换
• 串联支路合并:
ab x1 x2 x3
8
例2: 已知结构图如下,可在结构图上标出节点,如上图所示。 然后画出信号流图如下图所示。
k
R(S) b
m
d
V1
l
g V3 e
V2
h
C(S)
f f
m
h
R1
Ⅰ
b
l
Ⅱ
V3
k
Ⅲ
Ⅳ
C
V1 d Ⅴ e V2 1
g
1/8/2024
如何用梅逊公式求传递函数
9
信号流图的绘制
例2: 按微分方程拉氏变换后
的代数方程所表示的变量间
信号流图的概念
信号流图可以表示系统的结构和变量传送过程中的数学关 系。它也是控制系统的一种数学模型。在求复杂系统的传递函 数时较为方便。
一、信号流图及其等效变换
组成:信号流图由节点和支路组成。见下图:
R1
N
1
E G1 P
G2
Q
1
R(s)
C
E(s)
-
G1(s)
N (s)
+ G2(s) C (s)
H
H (s)
式中: La 流图中所有不同回路的回路传输之和;
LbLc 所有互不接触回路中,每次取其中两个回
路传输乘积之和;
LdLeLf 所有互不接触回路中,每次取其中三个
第二章 传递函数-梅逊公式
r(t) i1 R R1 A i2
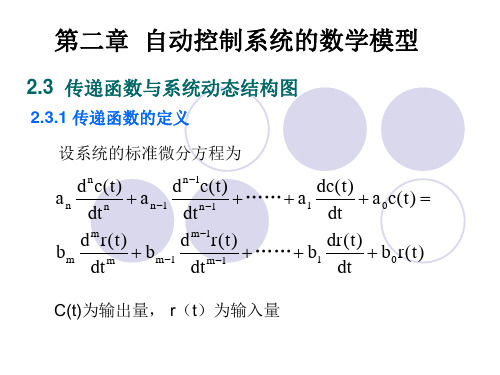
当 T=∞ 时,惯性 环节近似为积分 环节;当 T=0 时, 惯性环节近似为 比 例 环 节 。
2
R2 C
运算放大器:
若初值为0,上式的拉氏变换为:
(Td TmS2 + Tm S +1)N(S)= Ua(S)/Ce 1 Ce (Td TmS2 + TmS +1) 1
3)引出点 在信号线上的“•”,表示信号引出的位置。 4)方 框
方框中为元部件或系统的传递函数,方框的输 出量等于方框内的传递函数与输入量的乘积。
2.3 动态结构图与梅森公式
动态结构图建立步骤是
1
2
3
4
建立系统各元部件的微分 方程。要注意,必须先明确系 统的输入量和输出量,还要考 虑相邻元件间的负载效应。 按照各元部件的输 入、输出,对各方程进 行一定的变换,并据此 绘出各元部件的动态结 构图。
输入量取角度时的 传递函数即为微分 环节。
U (s) K t s(s)
U ( s) Kt s ( s )
那么该元件的传递函数为 G ( s )
微 分 环 节 的 传 递 函 数
一阶微分环节: c(t)= Tdr(t)/dt + r(t) 传递函数:G(S)=C(S)/R(S)= TS+1 方框图: R(S) C(S) TS+1
第二章 自动控制系统的数学模型
2.3 传递函数与系统动态结构图
2.3.1 传递函数的定义 设系统的标准微分方程为
d n c(t) d n 1c(t) dc(t) an a n 1 …… a1 a 0c(t) n n 1 dt dt dt d m r(t) d m 1r(t) dr(t) bm b m 1 …… b1 b0 r(t) m m 1 dt dt dt
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Mason 公式(3)
例 3 求传递函数 C(s)/R(s)
控制系统结构图
例 3 求C(s)/R(s)
1 [ 5
1 1 1 ] 6 3 RCs ( RCS ) 2 ( RCs)
自动控制原理
潍坊科技学院机械工程学院 李世琛
自动控制原理
第二章 控制系统的数学模型
§2.1 §2.2 §2.3 §2.4 §2.5 §2.6 引言 控制系统的时域数学模型 控制系统的复域数学模型 控制系统的结构图及其等效变换 控制系统的传递函数 控制系统的信号流图
课程回顾
2.3 复域数学模型 —— 传递函数 (1)传递函数的定义、性质和适用范围 (2)常用控制元件的传递函数 (3)典型环节 2.4 控制系统的结构图及其等效变换 (1)系统结构图的导出 (2)结构图等效化简
控制系统结构图
例 5 求C(s)/R(s)
1 [ G2 H 2 G1G2G3G4 H 1 G1G2G4 H 1 ] 1 G2 H 2 G1G2G3G4 H 1 G1G2G4 H1 P1 G1G2G3G4 1 1 P2 G1G2G4 2 1 P3 G2G3G4G5 3 1 P4 G2G4G5 4 1 P5 G3G4G6 5 1 P6 G6 H 2G2G4 6 1
§2.6 控制系统的信号流图
⑽回路增益:回路中各支路增益的乘积,称为回路增益 ⑾ 不接触回路:信号流图中没有任何共同节点的回路,称为不接触回路或互不 接触回路。
4、信号流图与结构图的对应关系
信号流图 源节点 阱节点 混合节点 支路 支路增益 前向通路 回路 互不接触回路 结构图 输入信号 输出信号 比较点,引出点 环节 环节传递函数
(1)结构图 信号流图
(2)结构图 信号流图
§2.6.2 梅逊(Mason)增益公式
1 n G(s) Pk Δ k Δ k 1
— 特征式
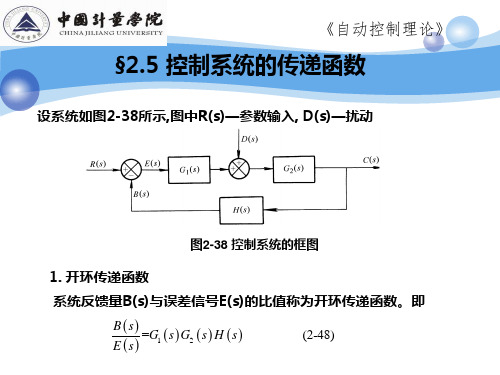
1 La Lb Lc Ld Le L f
— 第k条前向通路的余子式(把与第k条前向通路接触的回路去除, 剩余回路构成的子特征式
G1G2G3G4 G1G2G4 G2G3G4G5 G2G4G5 G3G4G6 G2G4G6 H 2 ( s ) 1 G2 H 2 G1G2G3G4 H 1 G1G2G4 H 1
Mason 公式(6)
例 6 求传递函数 C(s)/R(s), C(s)/N(s)
控制系统结构图
例6 求 C(s)/R(s), C(s)/N(s)
1 [ G2 H G1G2 G1G3 ] G1G2G3 H
1 G2 H G1G2 G1G3 G1G2G3 H
P1 G1G2
P2 G1G3
PN 1 1 PN 2 G4G1G2
1 1
§2.5 控制系统的传递函数
<2、扰动输入作用下的误差传递函数 令R(s) =0,可求出误差对扰动作用的闭环传递函数,简称扰动误差传递函数, 即 N(s)
<3、控制输入和扰动同时作用下系统的总误差 利用叠加原理可求出系统在控制输入和扰动输入同时作用下系统的总误差为
不难发现,四种闭环传递函数 Φ(s)、Φn(s)、 Φe(s)、Φen(s) 具有相同的分母即 =1+ G(s)H(s)。这正是闭环控制系统的本质特征。通常把这 个分母多项式称为闭环系统的特征多项式。1+ G(s)H(s) 称为闭环系统的特征方
§2.6 控制系统的信号流图
5、结构图与信号流图的关系:信号流图<=> 结构图
⑴由结构图向信号流图转化应尽量精简节点的数目。 ⑵两个相邻的节点支路增益为1时,一般可以合并为一个节点,但对于输入节点 和输出接点却不能合并掉 ⑶比较点之前无引出点或比较点之后有引出点只需在比较点处设置一个节点即可 ⑷比较点之前有引出点应在二者之处各设置一个节点,以表示两个不同的变量。 ⑸相邻的N个比较点可以用一个节点表示,相邻的N个引出点也可以用一个节点 表示 ⑹标完节点后应给每个节点标上序号,这样在计算前向通道条数、回路个数、看 回路与回路接触不接触、回路与前向通道接触不接触时不容易出错。
§2.6 控制系统的信号流图
3、信号流图的常用术语
⑴ 入支路:进入节点的支路 ⑵ 出支路:离开节点的支路 ⑶源节点:只有输出支路而无输入支路的节点称为源节点或输入节点,相当于输 入信号。 ⑷阱节点:只有输入支路而无输出支路的节点称为阱节点或输出节点,对应系统 的输出信号。 ⑸混合节点:既有输入支路又有输出支路的节点称为混合节点,相当于比较点或 引出点。 ⑹通路:沿支路的箭头方向顺序通过各相连支路的路径成为通路。 ⑺前向通路:从源节点开始并且终止于阱节点,与其他节点相交不多于一次的通 路称为前向通路。 ⑻回路:如果通路的起点和终点是同一节点,并且与其他任何节点相交不多于一 次的闭合路径称为回路。 ⑼前向通路增益:前向通路中各支路增益的乘积称为前向通路增益。
2 1 G2 H
N 1 1 G2 H N2 1
G1G2 G1G3 ( s ) 1 G2 H G1G2 G1G3 G1G2G3 H
N ( s)
( 1 G1G3G4 )(1 G2 H ) G1G2G4 1 G2 H G1G2 G1G3 G1G2G3 H
需要指出,这里的开环传递函数是针对闭环系统而言的,而不是指开环系统 的 传递函数。
§2.5 控制系统的传递函数
2、系统的闭环传递函数
<1.给定输入作用下的闭环传递函数 当只研究系统控制输入作用时,令 N(s)=0,可求出系统输出C(s)对输入R(s)的闭 环传递函数为
N(s)
<2 .扰动输入作用下的闭环传递函数 当只研究系统在扰动输入作用时,令R(s)=0,可求得输出C(s)对扰动作用N(s)的 传递函数
n Pk La L L L L L k
b c
d e
— 前向通路的条数 — 第k条前向通路的总增益 — 所有不同回路的回路增益之和 — 两两互不接触回路的回路增益乘积之和
f
— 互不接触回路中,每次取其中三个的回路增益乘积之和
Mason 公式(1)
例 1 求传递函数 C(s)/R(s)
控制系统结构图
§2.6 控制系统的信号流图
1、引言
信号流图是表示线性代数方程组的示图,采用信号流图可以直接对代数方程组求 解。在控制工程中,信号流图和结构图一样,可用以表示系统的结构及变量传递 过程中的数学关系。由于它的符号简单,便于绘制,而且可以通过梅逊公式(不 必经过图形简化)直接求得系统的传递函数,因此特别适合对于复杂结构系统的 分析。
§2.5 控制系统的传递函数
一、引言
前文所述的传递函数都是在输入信号作用下讨论的。实际的控制系统不仅会
受到控制输入信号的作用,还会受到干扰信号的作用。下图所示是具有扰动作用
的闭环系统,图中R(s)表示控制输入信号, N(s)表示干扰信号, 代表系统的输出, E(s)代表误差信号。若将R(s)和N(s)分别看作系统的外作用,C(s)和E(s)看做系统
P1 G1G2G3G4G5G6
1 1
G1G2G3G4G5G6 ( s ) 1 G2G3 H 2 G4G5 H 3 G3G4 H 4 G1G2G3G4G5G6 H 1 G2G3G4G5 H 2 H 3
Mason 公式(2)
例 2 求传递函数 C(s)/R(s)
控制系统结构图
第二章小结
例1
求C(s)/R(s)
1 [ G2G3 H 2 G4G5 H 3 G3G4 H 4 G1G2G3G4G5G6 H 1] (G2G3 H 2 )( G4G5 H 3 )
1 G2G3 H 2 G4G5 H 3 G3G4 H 4 G1G2G3G4G5G6 H1 G2G3G4G5 H 2 H 3
1 H1 G1 G2 G1G2 G3 H1
P1 G1G2 P2 G3
1 1
2 1 H1
G1G2 G3 (1 H 1 ) ( s ) 1 H 1 G1 G2 G1G2 G3 H 1
Mason 公式(5)
例 5 求传递函数 C(s)/R(s)
§2.5 控制系统的传递函数
<3、输入和扰动同时作用下系统的总输出 根据线性系统的叠加原理,系统在多个输入作用下,其总输出等于各输入单独作 用所引起的输出分量的代数和,可求得系统的总输出为
3、系统的误差传递函数
<1、控制输入作用下的误差传递函数 在N(s)=0的情况下,可求出系统的误差传递函数,即
§2.6 控制系统的信号流图
2、信号流图的组成要素
信号流图中的基本图形符号有三种:节点、支路和支路增益。 ⑴ 节点—用符号“○”表示。节点代表系统中的一个变量(信号)。 ⑵ 支路—用符号“→—”表示,支路是连接两个节点的有向线段,其中的箭头表 示信号的传递方向。 ⑶ 增益—用标在支路旁边的传递函数“G”表示支路增益。支路增益定量描述信 号从支路一端沿箭头方向传送到另一端的函数关系,相当于结构图中环节的传 递函数。
P1
1 ( RCs) 3
1 1
1 ( s ) ( RCs) 3 5( RCs) 2 6( RCs) 1
Mason 公式(4)
例 4 求传递函数 C(s)/R(s)
控制系统结构图
例 4 求C(s)/R(s)
1 [ H G1 G 2 G1G2 G 3 G3 ] G3 H 1 1
例 2 求C(s)/R(s)
1 [ G1G2 H1 G2G3 H 2 G1G2G3 G4 H 2 G1G4 ]
