大学物理第四讲动能定理功能原理
大学物理第四章--功和能

a
l
xdx
2l
前已得出:
Af
mg(l a)2
2l
mg(l 2 a2 ) mg(l a)2 1 mv2
2l
2l
2
得v
g l
1
(l 2 a 2 ) (l a)2 2
§3 保守力的功与势能 一、 保守力
rB
B
两个质点之间的引力
B
第四章 功和能
§4.1 功 §4.2 动能定理 §4.3 保守力功与势能 §4.4 功能原理机械能守恒定律
§1 功和功率
一、恒力做功 直线运动
A=Fcos S
记作A F S F r
F
F
M
M
S
位移无限小时:
dA
F
dr
dA称为元功
功等于质点受的力和它的位移的点积(标积)
例1一水平放置的弹簧,其一端固定,另一端系一小球,求小
球的位置由A到B的过程中弹力对它所做的功。(在O处弹簧无 形变)
解:根据胡克定律 F F kx
W F dr
xB Fdx
xA
xB xA
kxdx
O
1 2
A
k xB2
B
xA2
1 2
k xA2
作用在质点
上.在该质点从坐标原点运动到(0,2R)位
置过程中,力
F
对它所作的功为多少?
y
b
b
A a F.dr a (Fxdx Fydy)
R
x O
例4 如图,水平桌面上有质点 m ,桌面的摩 擦系数为μ 求:两种情况下摩擦力作的功
动能定理课件ppt

在足球、篮球等球类运动中,动能定理可以用来研究球的飞行轨迹,预测球的落 点,以及分析碰撞过程中的能量转换。此外,动能定理还可以帮助优化球的速度 和旋转,提高射门或投篮的准确性。
车辆行驶
总结词
运用动能定理可以研究车辆行驶过程中 的各种问题,包括车辆的加速、制动以 及行驶稳定性等。
VS
详细描述
实验器材
滑轮
速度传感器 质量块
细绳 弹簧测力计
实验步骤与数据记录
2. 使用弹簧测力计测量质量块受 到的拉力F。
4. 记录数据:拉力F、速度v和质 量块的质量m。
1. 将滑轮固定在一个支架上,通 过细绳连接质量块和滑轮。
3. 启动速度传感器,测量质量块 的速度v。
5. 在实验过程中,不断改变质量 块的速度,重复步骤2-4,获得多 组数据。
详细描述
力对物体做功会引起物体的动能变化。动能 定理是指合外力的功等于物体动能的增量, 即合外力对物体做的功等于物体动能的增量 。这个定理可以用来定量描述力与动能之间 的关系。
05
动能定理的拓展形式
势能与动能的关系
势能与动能是相互依存的两种能量形式,势能可以转化为动能,动能也可以转化为 势能。
在机械系统中,势能和动能的总和是恒定的,这种关系可以通过机械能守恒定律来 描述。
圆周运动的动能定理
总结词
简单描述圆周运动的动能定理的公式和含义。
详细描述
在圆周运动中,物体动能的增加量等于外力对物体所做的功。即外力做的功等 于物体动能的增加量。特别地,在物体做匀速圆周运动时,由于速度大小不变 ,所以物体的动能增量为零,合外力对物体不做功。
03
动能定理的应用场景
投掷比赛总Βιβλιοθήκη 词动能定理课件目录
大学物理功-动能定理-保守力的功

解: 抛体在重力场中运动,
m g 是一恒量,
y
但m 的轨迹是一抛物线, 取一元位移d r
dr b
a
m g 与位移的夹角θ时时在变 在这一元段内写出元功
mg
x
dA Fdrmgdr
m gdscosmgdy
b
b
b
A
Fdr
a
Fcosds mg
a
a
dy
m g(ybya) 9
解:(1)建坐标系如图
l-a O
fμ m(lg x)/l l l μmg
A f afdra l (lx)dx μm(g lx)2l μm(g la)2
a x
2l
a 2l
注意:摩擦力作负功! 21
(2)对链条应用动能定理:
l-x O
A= AP+ Af 1 2m2v 1 2m0 2v
x
v0
0AP+ Af
1m2v 2
x
A Pa lp d r a lm l x gd m x(l2 2 g l a 2 )
前已得出: Af
μm (gl a)2
2l
m(lg 2a2)μ m(lg a)21m2v
2l
2l
2
得 v
g l
1
(l2 a 2)μ (l a )22
13
3) A为合外力作功的代数和,不是合外力中某 一个力的功。动能定理中的速度必须相对同一 个惯性系。
4)通过作功,质点与外界进行能量交换。 如果 外力对物体做正功,质点动能增加; 如果 外力对物体做负功,质点的动能减少,
即物体克服外力作功,是以减少自身的动能为 代价。
所以,动能是物体因运动而具有的作功的本领。
2.5 动能定理和功能原理

结论:
成对 保守内力功 特点:只取决于相互作
用质点的始末相对位置,是始末位置的函数。
§2.5 动能定理和功能原理 第二章 质点动力学
4. 成对保守内力 作功特点
《大学物理》教程
讨论
一对
m' m m' m W1 W2 ( G ) ( G ) 万有引力作功 rA rB
ACB
A
D
C
B
Fc dr Fc dr
BDA
Fc dr Fc dr
ACB
ADB
0
§2.5 动能定理和功能原理
始末位置 相同
第二章 质点动力学
3. 成对力作功
《大学物理》教程
有人问:
力是一种 相互作用 力总是成对 出现,满足 牛三律 这对力作功 有特点吗?
§2.5 动能定理和功能原理 第二章 质点动力学
1. 质点 的动能定理
《大学物理》教程
b
a
1 1 2 2 F dr mvb mva 2 2
定义功(过程量):力对空间的累积量
W
① 元功:
b
a
F dr
dW F dr ② 功率:单位时间内作的功 P F v dt dt
xb
xa
1 2 1 2 kxdx kxa kxb 2 2
小结: 弹簧力做功与路径无关,只与运动 起点和终点的位置有关。
§2.5 动能定理和功能原理 第二章 质点动力学
《大学物理》教程
讨论
定义式法 求功的计算举例
例3 万有引力做功 以 m 2 为参考系
a m
r (t ) F
2013 动能定理 功能原理
引力势能:
Aab ( L )
b
a
f dr ( L )
rb
Gm1m2
3
r dr
Gm1m2
Gm1m2 rb
ra
Aab E p E pa E pb
m1,m2 两质点引力势能 重力势能:
Ep GmM R GmM ( R h)
ra r 选 rb= 为零势点,Epb=0
m1m2 r
dy dx f i j k E p x y z
fy
fds cos dE p dE p fs ds dE
p
f
fz
dE p dz
令
i j k y z x
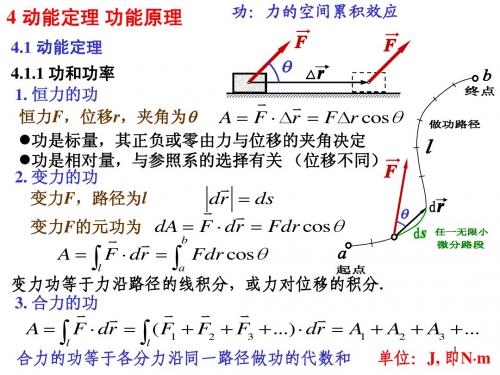
4 动能定理 功能原理
4.1 动能定理
功:力的空间累积效应
4.1.1 功和功率 1. 恒力的功 恒力F,位移r,夹角为 A F r Fr cos 功是标量,其正负或零由力与位移的夹角决定 功是相对量,与参照系的选择有关 (位移不同) 2. 变力的功 变力F,路径为l dr ds 变力F的元功为 dA F dr Fdr cos b A F dr Fdr cos
( L) ( L)
b
f dr
m1
ra
a
rb
Gm1m2 r dr ra r 3 r dr rb Gm1m2 Gm1m2 Gm1m2 ra r 3 r dr r r a b
r dr r dr cos
12
弹性力做功 f
f x kx
大学物理课件第4章-功和能
如图,求船从离岸 x1处移到 x2 处的 过程中,力 F 对船所作的功.
F
解:判别F 是否为变力作功(大小不变,方
向变元),功属于dW变力作F功.建dx立坐F标,取dx元过co程sa
h
o x2
a
dx x x1 x
cosa x
x2 h2 x
dW F dx
x2 h2
功在数值上等于示功图
F
曲线下的面积。
3. 功率
0 x1
x2 x
dx
平均功率: P =ΔΔWt
瞬时功率:
P
= lim
Δt 0
Δ Δ
Wt =
dW dt
=
F
. dr
dt
= F .v
[ 例1 ] 有一单摆,用一水平力作用于m
使其极其缓慢上升。当θ 由 0 增大到 0 时,
求: 此力的功。
{
F T sinθ T cosθ mg
两边平方
v 2 v12
由动量守恒
2v1
v2
v 22
v
v1
v2
由机械能守 恒( 势能无变化)
v2
v12
v
2 2
v1 v2 0 两球速度总互相垂直
例8:已知半圆柱形光滑木凹槽,放在光滑桌面上,
如图,求质点下滑至最低点时给木块的压力.
解:
mv MV 0
•2.碰撞分类
正碰 斜碰
(从碰撞前后两球中心连线角度分类 )
弹性碰撞 非弹性碰撞 完全非弹性碰撞
一般非弹性碰撞
(从碰撞能量损失角度分类)
例7:在平面上两相同的球做完全弹性碰撞,其中一球开始时处于
功能原理(大学物理)

va a
4R E
RE
2R E
∵G
m Em R2
E
=m
g
设:卫星在a 点的速率为va
所受的向心力是由万有引力
提供,由牛顿第二定律可得:
b vb
F向心力= m a =m
v2 R
G (m2RE mE)2 =m
v2 a
2R E
∴
Gm R2
E
E
=g
代入上式得:
∴ va=
gR E 2
va a
≥
5 2
R
C
(2)小球在 A 点受重力mg 及
A
轨道对小球的正压力N 作用。
H
B
·R
N0
(3)如果小球由H =2R 的高处滑下
mg 小球将不能到达A点就掉下来了。
本题结束
例题: 如图所示,子弹水平地射入一端固定在弹簧上
的木块内,已知:子弹质量是0.02kg ,木块质量是 8.98kg。弹簧的劲度系数是100N/m,子弹射人木块 后,弹簧被压缩10cm。设木块与平面间的滑动摩擦系 数为0.2,求:子弹的速度。
和轨道对小 球的正压力
N
+mg
=
m
v2 A
R
(1 )
不脱轨的条件为: N = mRvA2-m g ≥ 0
m
v2 A
R
≥
mg
(2)
N
+mg
=
m
v2 A
R
(1)
m
v2 A
R
≥
mg
(2)
0+mg( H
-
2R
)=
1 2
m
v
(完整版)动能定理

动能定理知识梳理 一、动能(一)动能的表达式1.定义:物体由于运动而具有的能叫做动能。
2。
公式:E k =12mv 2,动能的单位是焦耳。
说明:(1)动能是状态量,物体的运动状态一定,其动能就有确定的值,与物体是否受力无关.(2)动能是标量,且动能恒为正值,动能与物体的速度方向无关.一个物体,不论其速度的方向如何,只要速度的大小相等,该物体具有的动能就相等。
(3)像所有的能量一样,动能也是相对的,同一物体,对不同的参考系会有不同的动能.没有特别指明时,都是以地面为参考系相对地面的动能。
(二)动能定理1。
内容:力在一个过程中对物体所做的功,等于物体在这个过程中动能的变化.2。
表达式:W=E 2k -E 1k ,W 是外力所做的总功,E 1k 、E 1k 分别为初末状态的动能.若初、末速度分别为v 1、v 2,则E 1k =12mv 21,E 2k =12mv 22. 3。
物理意义:动能定理揭示了外力对物体所做的总功与物体动能变化之间的关系,即外力对物体做的总功,对应着物体动能的变化,变化的大小由做功的多少来度量.动能定理的实质说明了功和能之间的密切关系,即做功的过程是能量转化的过程。
利用动能定理来求解变力所做的功通常有以下两种情况: ①如果物体只受到一个变力的作用,那么:W=E k2-E k1.只要求出做功过程中物体的动能变化量ΔE k ,也就等于知道了这个过程中变力所做的功.②如果物体同时受到几个力作用,但是其中只有一个力F 1是变力,其他的力都是恒力,则可以先用恒力做功的公式求出这几个恒力所做的功,然后再运用动能定理来间接求变力做的功:W 1+W 其他=ΔE k .可见应把变力所做的功包括在上述动能定理的方程中. ③注意以下两点:a.变力的功只能用表示功的符号W来表示,一般不能用力和位移的乘积来表示.b.变力做功,可借助动能定理求解,动能中的速度有时也可以用分速度来表示.4.理解动能定理(1)力(合力)在一个过程中对物体所做的功,等于物体在这个过程中动能的变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b
b
a
r
F
b
× b F
(L)
d r 称为“力沿路径 L 的线积分” L m
(1)功是过程量; (2)功是标量(有正负);
× a
Aab d A F d r
a a
b
b
直角坐标系: A 合力的功:
xb
xa
Fx dx Fy dy Fz dz
ya za
初位形(A): m1----A1,m2----A2 末位形(B): m1----B1,m2----B2
(B)
说明:
AAB 对
(A)
(B)
f 2 d r21
(或
(A)
f1 d r12 )
1.一对力的功等于其中一个质点受的力沿着它相对 于另一质点移动的路径所作的功。 2.由于一对力的功只与“相对路径”有关,所以与 参考系的选取无关。
“合力对质点作的功等于质点动能的增量”
说明:
1.一个过程量=始末两个状态量之差。 2.动能定理只适用于惯性系。
二 . 质点系的动能定理:
对第 i个质点:合外力的功 ── 合内力的功 ──
A外i A内i
A外i A内 i EK 2i EK1i
对质点系:
简记为
A
i
外i
A内i EK 2i EK1i
yb
zb
A (Fi ) dr
a i i
b
(瞬时)功率: 若在 t t + dt 内,力 F 的元功为 dA,
则 t 时刻的功率
F dr A
b a i i
i
d A F d r P F v dt dt
由动力机械驱动时,马达的输出功率是一定的,速度 小、力大,速度大、力小。 ---------“牛马关系”
例1. 重力的功 地面附近质量为 m 的物体从 a 到 b,求重力的功。
y
dr
b
Ap mg d r (mgj ).(d xi d yj )
mg d y mg ( ya yb )
ya
b
b
a o
mg
x
a y b
a
例2. 一人从10m深的井中提水,起始 时桶和水共重10kg,由于水桶漏水, 每升高1m要漏去0.2kg的水。求将水 桶匀速地从井中提到井口,人所作的 功。
f1 f 2 , r21 r2 r1
一对力的元功
r1
m1
d r1
A1
f1
r21
f2
d r2
m2
A2
r2
x
0
y
d A对 f1 d r1 f2 d r2 f2 (d r2 d r1 ) f 2 d(r2 r1 ) f 2 d r21
1 1 1 2 2 2 f r l MV mv mv0 2 2 2
将V代入, 可得
m V (v 0 v ) M
2 1 1 1 m 2 2 2 v0 v f r m v0 v l 2 2 M
讨论:1. 量纲对 2. 特例对(当 M 0时)
m V ( v 0 v ) (>0) M
由动能定理: A外 + A内 = Ek2 - Ek1 现在外力的功为零; 内力的功 就是一对阻力的功, 我们以砂箱为参照系来计算这一对阻力的功:
设子弹受的平均阻力为 f r (即看作常数) ,
而子弹相对砂箱的位移即为l ,
1 1 1 2 2 2 所以, f r l MV mv mv0 2 2 2
爆炸力
4.2.2 势能和势能曲线
一对保守力的功只与系统的始末相对位形 有关, 说明系统存在一种只与相对位形有关的能 量。 一对保守力的功(过程量)都可以写成两 个状态量之差,这两个状态量称为系统的势能, 表示 E p A12 Ep1 Ep 2 Ep 2 Ep1 Δ Ep
ˆ ˆ ˆ y z (梯度算符) 算符 x x y z
则
d 1 2 fx kx kx dx2
蚂蚁在作功
附1. 一质量为2kg的物体,在变力 F 6ti 的作用下作直线运动,如果物体从静止开始运动, 求前两秒此力所作的功。
4.1.2 动能定理
一. 质点的动能定理 设合力为 F ,由牛II, 2 2 A12 F d r Ft d r
1 1
2 2
2
m
1 dv m at d r m vdt 1 1 dt v2 1 1 2 2 m vd v mv 2 mv1 E K 2 E K 1 2 2 v1
N
v1
一对正压力的功恒为零!
一对滑动摩擦力之功恒小于零!
ff
vv
讨论 一个物体在地面上滑行, 受摩擦 f 作用,经过距离 s 停了下来。
在地面系看:摩擦力 f 作负功,A = -f s 物体动能减少,动能转化为热能,温度升高。 在物体参考系看:摩擦力 f 不作功,A=0.
(矛盾?) f 到底作不作功? 若 f 不作功,热能从何而来?
GmM Ep 万 dr 2 r r GmM GmM R r
R地
r R
h
Ep 万
GmM GmM GmM dr 2 r R r r GmM (r R) 令 r Rh 若 h<<R, Rr GmMh Ep 万 mgh 2 R
GM g 2 9.8x
(直接用冲量定理?) 【解】 由题给的条件,根据动量的规律, 可先求出子弹射出时砂箱的速度。 再根据能量的规律,由计算一对力的功 的办法,求出子弹受的平均阻力。
系统:砂箱和子弹 水平外力为零, 水平动量守恒, 设子弹射出时砂箱的速度为V,如图, 设V
v0 m
则有
M l
v x
MV mv mv0
3. 搞清它们与参考系的关系。 例如: 功的计算是否依赖参考系? 如何理解重力势能属于“物体与地球”系统? 某一惯性系中机械能守恒,是否在 其它惯性系也守恒?
4.1 动能定理
4.1.1 功和功率
功: 力和它所作用的质元(质点)的位移的点积。 对微小过程,可当成恒力、直线运动
Aab d A F d r
4.2 保守力与非保守力 势能
一对万有引力的功: 以 M为参考系的原点, 计算起来就非常方便, 只要算一个力的功 即可。 2 r2 GMm ˆ f r 2 r M
r1
r
1
ˆdr dr r
f m
dr
ˆ r
A12对 f d r
1
2
2
1
GMm ˆdr r 2 r
这个问题从一对摩擦力之功来分析就无矛盾:
v
f f
A
s s
B
地面系: A对 f s fs
物体系: A '对 f s f s
fs f s
A对 A '对
两者相等,而且都是负值。(动能转化为热能!)
例3. 在光滑水平面上停放一个砂箱,长度为 l, 质量为M。一质量为 m的子弹以水平初速 v0 穿透砂箱,射出时速度减为 v,方向仍为水平。 试求砂箱对子弹的平均阻力。
则
f保 x
Ep
x y z Ep Ep Ep ˆ ˆ ˆ) f保 ( x y z x y z
, f保 y
Ep
, f保 z
Ep
记作
grad E p E p
例 . 由弹性势能求弹性力。 1 2 E p弹 kx 已知 2
一对力的功,可认为一个质点静止,例如,重力做功
3.
AAB对 f 2 d r21 , d r21 0 (相对位置不变),
A
B
例、一对静摩擦力的功是多大?
或 d r21 f2 时,A对 0
一对静摩擦力的功恒为零!
无论大物体怎么运动,这一对力 的功总是零,没有相对运动。
v
例、小物体下滑大物体后退,一对正压力的 功是多大? N 不垂直于 v1 , AN 0 N 1 v2 2 N 不垂直于 v2,AN 0 v12
1 2
1
x2 kxi d xi k xd x x1
(1)
(2)
注意
1 1 2 2 kx1 kx2 2 2
(<0)
功的数值依赖于参考系的选择。
例如,上题中,在桌面参照系 f 作负功; 在小球参照系弹性力对小球 f 并不作功!
保守力的另一定义(重要性质):一质点相对 于另一质点沿闭合路径运动一周时,它们之间 2 的保守力做的功必然是零。 L1 若 f 是保守力,必有 f dr f dr 0 L2 m L M 1 2 1 f dr f dr f dr
1 L1
2 L 2
1 L1
2
f dr
1 L2
2
f dr 0
常见的保守力: 万有引力 弹力
f kx(或位置的单值函数)
f mg(或恒力)
ˆ ( 或有心力) f f (r )r
重力
常见的非保守力(耗散力): 摩擦力
4. 动能定理 功能原理
• • • • • • 4.1 动能定理 4.2 保守力和非保守力 势能 4.3 功能原理和机械能守恒 4.4 三种宇宙速度 4.5 能量守恒定律 4.6 质心 质心运动定理
