第三章 傅里叶变换 知识要点
傅里叶变换的基本概念及基本定理
g ( x) sin( 2πnf 0 x)dx = 0
采用指数傅里叶级数展开，可以使展开系数的表达式统一而简洁。 采用指数傅里叶级数展开，可以使展开系数的表达式统一而简洁。
二维傅里叶变换
——指数傅里叶级数 可以在(-∞ 可以在 展为 满足狄氏条件的函数 g(x) 具有有限周期τ,可以在 ∞,+ ∞)展为 Байду номын сангаас数傅里叶级数: 指数傅里叶级数
第三讲 二维傅里叶变换的基本概念及基本定理
• 恩格斯(Engels) 把傅里叶 傅里叶的数学成 傅里叶 就与他所推崇的哲学家黑格尔 (Hegel) 的辩证法相提并论.
他写道：傅里叶 傅里叶是一首数学的诗， 傅里叶 黑格尔是一首辩证法的诗.
1、三角傅里叶级数展开 、
满足狄氏条件的函数 g(x) 具有有限周期τ,可以在(-∞,+ ∞)展 为三角傅里叶级数:
+∞
f (x, y) = ∫∫ F( fx , f y ) exp[ j2π ( fx x + f y y)df xdf y
−∞
记作:
f(x,y)=
-1{F(f
x,fy)}.
显然
-1
{f(x,y)}= f(x,y)
综合可写:
f(x,y)
F.T. F.T.-1
F(fx,fy)
f(x,y)和F(fx,fy)称为傅里叶变换对 x (y) 和 fx (fy )称为一对共轭变量, 它们在不同 的范畴(时空域或频域) 描述同一个物理对象.
图1-5-1 函数 ei2π(fxx+fyy) 的零位相直线族
二维傅里叶变换 2-D Fourier Transform 广义 F.T.
对于某些不符合狄氏条件的函数, 求F.T.的方法. 对某个可变换函数组成的系列取极限→不符合狄氏条件的函数, 函数系列变换式的极限→原来函数的广义F. T.
傅立叶变换知识点总结
傅立叶变换知识点总结一、傅立叶级数傅立叶变换的基础是傅立叶级数，它是一种将周期性信号表示为一组基本正弦和余弦函数的方法。
傅立叶级数的表达式为：其中，a和b分别为信号的系数，n为频率。
傅立叶级数的这种表示方法是非常有用的，因为它可以将任意周期性函数分解为无穷多个基本正弦和余弦函数的叠加。
二、傅立叶变换的定义傅立叶变换是将一个时间域或空间域中的信号经过傅立叶变换得到其频率域表示的过程。
傅立叶变换的定义为：其中，F(ω)为信号在频率域的表示，f(t)为信号在时间域的表示。
傅立叶变换将信号从时间域转换到频率域，这样可以更容易地对信号进行分析和处理。
三、傅立叶变换的性质傅立叶变换具有许多重要的性质，这些性质对于理解和应用傅立叶变换非常重要。
以下是傅立叶变换的一些主要性质：1. 线性性质：傅立叶变换是线性的，即对于两个信号f1(t)和f2(t)，它们的傅立叶变换分别为F1(ω)和F2(ω)，那么它们的和的傅立叶变换为F1(ω) + F2(ω)。
2. 积分性质：傅立叶变换可以表示为一种积分形式，即：3. 时移性质：如果信号f(t)的傅立叶变换为F(ω)，那么延迟τ秒的信号f(t-τ)的傅立叶变换为F(ω)exp(-jωτ)。
4. 频移性质：如果信号f(t)的傅立叶变换为F(ω)，那么频率为ω0的信号f(t)exp(jω0t)的傅立叶变换为F(ω-ω0)。
5. 对称性质：如果信号f(t)是实值函数，那么它的傅立叶变换的实部和虚部是奇函数和偶函数。
以上是傅立叶变换的一些主要性质，它们对于理解和应用傅立叶变换非常重要。
四、傅立叶变换的应用傅立叶变换在信号处理、图像处理和其他领域中有着广泛的应用，下面我们将从几个方面来介绍傅立叶变换的应用：1. 信号分析：傅立叶变换可以将一个信号从时间域转换到频率域，从而可以更容易地对信号进行分析，比如分析信号的频谱、功率谱等。
这对于理解和处理信号非常有用，比如在通信、音频处理等领域中广泛应用。
第三章 傅里叶变换
2 T
t0 T t0
f
(t) sin(nw1t)dt
令 An
an2 bn2
，n
arctan
bn an
，则：
An ：称为n次谐波分量的振幅，是n的偶函数。
n ：称为n次谐波分量的相位，是n的奇函数。
一、三角形式
3.1 周期信号的傅里叶级数
f
(t)
a0 2
n1
An
cos(nw1t
n )
A0 2
1.5
1.5
1
1
1
1
1
1
0.4
0.4
0.4
0.2
0.2
0.4
0.2
0.2
－ 6－ 5 － 4－ 3－ 2 － o 2 3 4 5 6
－ 6－ 5 － 4－ 3－ 2 － o 2 3 4 5 6
(a)
相位谱：
(a) n 45° n
45°
45° 45°
30°
30°
30°
20°
30°
20°
15° 10°
（2）时域非周期信号，造成频域连续的谱。
连续 非周期
3.2 非周期信号的傅里叶变换
二、典型非周期信号的频谱函数
（1） g (t)
Sa( w )
2
解： F(w)
g
(t
)e
jwt
dt
2
1
e
jwt
dt
2
e jwt 2
2
jw
jw
jw
e 2 e 2
jw
2sin( w )
2
w
sin( w )
性质中所对应的原函数都是乘以 (-jt)。
第三章离散傅里叶变换及其快速计算方法(DFT、FFT)
X (e jw )
（2）Z 变换 -- 提供任意序列的 z 域表示。
n
x( n)e jnw
X (z)
n
x ( n) z n
这两种变换有两个共同特征：
（1）变换适合于无限长序列 （2）它们是连续变量 ω 或 z 的函数
华北电力大学自动化系
3
3.1 问题的提出：可计算性
X (z)
而对于
n
x ( n) z n
n
x ( n) z n
找不到衰减因子使它绝对可和（收敛）。为此，定义新函 数，其 Z 变换：
华北电力大学自动化系
15
DFS 定义：正变换
X ( z)
n
x ( n) z n ~ ( n ) z n x
华北电力大学自动化系
6
3.1 问题的提出：傅里叶变换的四种形式 （3）
2. 周期连续时间信号：傅里叶级数 FS
~ (t ) x X (n 0 )
t T
时域周期频域离散
0
2 T
x(t)
~
n -
X(n 0 )e jn0t
时域连续函数造成频域是非周期的谱。 频域的离散对应时域是周期函数。
X (e jT )
T T
X (e jT )e jnT d
取样定理
n
x(nT )e jnT
1 X ( 0 ) T n
时域的离散化造成频域的周期延拓 时域的非周期对应于频域的连续
华北电力大学自动化系
8
基础知识积累—傅里叶变换
三、傅里叶变换
傅里叶变换能将满足一定条件的某个函数表示成三角函数 （正弦函数或余弦 函数）或者它们的积分的线性组合。在不同的研究领域，傅里叶变换具有多种不 同的变体形式， 如连续傅里叶变换和离散傅里叶变换。最初傅里叶分析是作为热 过程的解析分析的工具被提出的。
变换提出
傅里叶是一位法国数学家和物理学家的名字，英语原名是 Jean Baptiste Joseph Fourier(1768-1830), Fourier 对热传递很感兴趣，于 1807 年在法国科学 学会上发表了一篇论文，运用正弦曲线来描述温度分布，论文里有个在当时具有 争议性的决断： 任何连续周期信号可以由一组适当的正弦曲线组合而成。当时审 查这个论文的人，其中有两位是历史上著名的数学家拉格朗日(Joseph Louis Lagrange, 1736-1813)和拉普拉斯(Pierre Simon de Laplace, 1749-1827)，当拉 普拉斯和其它审查者投票通过并要发表这个论文时，拉格朗日坚决反对，在他此 后生命的六年中，拉格朗日坚持认为傅里叶的方法无法表示带有棱角的信号， 如 在方波中出现非连续变化斜率。 法国科学学会屈服于拉格朗日的威望，拒绝了傅 里叶的工作，幸运的是，傅里叶还有其它事情可忙，他参加了政治运动，随拿破
的傅里叶变换为
，且其导函数
的傅里叶变换存在，则
即导函数的傅里叶变换等于原函数的傅里叶变换乘以因子 。更一般地，若 的 阶导数 的傅里叶变换存在，则
即 阶导数的傅里叶变换等于原函数的傅里叶变换乘以因子
。
卷积特性
若函数 以及 都在 上绝对可积，则卷积函数为：
即傅里叶变换存在，且 Parseval 定理以及 Plancherel 定理 若函数 有： 以及 平方可积，二者的傅里叶变换分别为 与 ，则
傅里叶变换的基础知识
傅里叶变换的基础知识傅里叶变换是一项基础的数学工具，广泛应用于物理学、工程学、计算机科学、信号处理等领域。
本文将介绍傅里叶变换的基本概念，其中包括连续傅里叶变换和离散傅里叶变换。
1. 连续傅里叶变换在介绍傅里叶变换之前，我们需要先了解两个概念：周期函数和Fourier 级数。
周期函数是指在一定区间内具有重复特征的函数，而 Fourier 级数是将一个周期函数表示为正弦和余弦函数的和。
傅里叶变换是将一个函数表示为一系列不同频率的正弦和余弦函数的和，可以理解为是将 Fourier 级数推广到了一般的非周期函数上。
具体来说，若一个函数 f(x) 满足某些条件，那么它可以被表示为如下形式：F(ω) = ∫ f(x) e^(-iωx) dx其中，F(ω) 是函数 f(x) 的傅里叶变换，ω 表示角频率，即单位时间内变化的弧度数。
从公式可以看出，傅里叶变换将函数 f(x) 转化成一个复数F(ω)，表示了该函数在不同频率下的振幅和相位信息。
特别地，若函数f(x) 是实函数且满足对称性条件，那么它的傅里叶变换F(ω) 是一个实函数。
2. 离散傅里叶变换连续傅里叶变换适用于连续信号的处理，但在实际应用中，我们往往处理的是数字信号，即离散信号。
为了将连续傅里叶变换推广到离散信号上，人们发明了离散傅里叶变换。
离散傅里叶变换的定义如下：F_k = ∑_{n=0}^{N-1} f_n e^{(-i2πkn)/N}其中，f_n 表示离散信号在第 n 个采样点处的取值，N 表示采样点数量，k 表示在 K 点处的频率。
离散傅里叶变换是计算机领域中常用的算法，广泛应用于音频、图像等信号处理领域。
它可以将复杂的信号分解成一组频率，从而实现信号的压缩、降噪等处理操作。
需要注意的是，离散傅里叶变换对于周期信号是有局限性的，因为在离散信号中，我们无法表示无穷长的周期函数，因此在处理周期信号时，我们需要采用其他方法。
3. 傅里叶变换的应用傅里叶变换广泛应用于多个领域，下面简要介绍几个应用场景：(1) 信号处理：傅里叶变换可以将一个信号分解成它的频率成分，从而实现信号降噪、信号压缩等处理操作。
傅里叶变换需要具备的知识
傅里叶变换需要具备的知识傅里叶变换是一种数学工具，用于将一个函数或信号分解成多个不同频率的正弦和余弦函数的和。
它是由法国数学家傅里叶在19世纪提出的，被广泛应用于信号处理、图像处理、物理学、工程学等领域。
要理解傅里叶变换，首先需要具备以下几个基本知识点。
1. 函数的周期性：傅里叶变换是基于函数的周期性进行分解的，因此需要了解函数的周期性概念。
周期函数指在一定区间内具有重复性的函数。
2. 傅里叶级数展开：傅里叶级数展开是傅里叶变换的基础。
它表示任何周期函数都可以用一组正弦和余弦函数的线性组合来表示。
这个展开系数就是函数在不同频率上的振幅。
3. 正弦函数和余弦函数：正弦函数和余弦函数是傅里叶变换中的基础函数。
正弦函数表示周期性振动，而余弦函数则表示平稳的振动。
4. 频谱：频谱是指信号在不同频率上的能量分布情况。
傅里叶变换可以将信号从时域转换到频域，得到信号的频谱表示。
5. 快速傅里叶变换（FFT）：FFT是一种高效的计算傅里叶变换的算法，可以大大提高计算速度。
它通过将傅里叶变换的计算复杂度从O(n^2)降低到O(nlogn)，在实际应用中得到广泛使用。
在应用傅里叶变换时，需要注意以下几个方面。
1. 信号采样：傅里叶变换要求信号是连续的，而实际上我们处理的信号是离散的。
因此需要对信号进行采样，将其离散化。
2. 采样定理：为了避免信号采样引入失真，需要满足一定的采样定理。
最著名的是奈奎斯特采样定理，它要求采样频率至少是信号最高频率的两倍。
3. 频域滤波：傅里叶变换可以将信号从时域转换到频域，因此可以通过在频域对信号进行滤波来实现去噪、降噪等操作。
4. 逆傅里叶变换：傅里叶变换可以将信号从时域转换到频域，而逆傅里叶变换则可以将信号从频域转换回时域。
逆傅里叶变换的公式与傅里叶变换的公式互为逆运算。
傅里叶变换是一种非常强大的数学工具，可以用于解决各种信号处理和频谱分析的问题。
掌握傅里叶变换的基本知识，能够更好地理解和应用相关领域的理论和技术。
常用傅里叶变换+定理+各种变换规律(推荐)
√
√
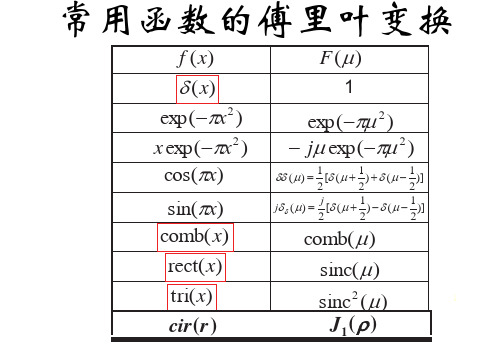
f
(t )
=
⎪⎧1 ⎨
−
t
⎪⎩
τ, t 0, t
<τ >τ
τSa 2
ωτ (
)
2
W Sa2 (Wt )
2π
2
F
(ω
)
=
⎪⎧1 ⎨
−
ω
⎪⎩
W,ω <W 0, ω > W
√ e−atu(t), Re{a} > 0
e −a t , Re{a} > 0 √
e−at cosω0tu(t), Re{a} > 0 √
)
√
时域微 分性质 时域积 分性质
√ 时域卷
积性质
√ 对称性
d f (t) dt
∫t f (τ )dτ −∞
f (t) * h(t)
f (−t) f * (t)
f * (−t)
jωF (ω)
F(ω) + πF (0)δ (ω) jω F (ω)H (ω)
F (−ω) F * (−ω ) F * (ω )
−∞ 1/ 2
= ∫ exp(− j2πux)dx
rect
x a
=
1, 0,
−1/ 2
=1
1/2
exp(− j2πux)
− j2πu
-1/2
= sin(πu) πu
结论：
x ≤a 2
其它
= sinc(u) rect（x） F.T. sinc（u）
5
普遍型
F
rect
x a
= a sin(πau) πau
2
2
2
+∞
2π ∑ Fkδ (ω − kω0 ) k =−∞
傅里叶变换知识点总结
傅里叶变换知识点总结本文将从傅里叶级数、傅里叶变换和离散傅里叶变换三个方面来介绍傅里叶变换的知识点，并且着重介绍它们的原理、性质和应用。
一、傅里叶级数1. 傅里叶级数的定义傅里叶级数是一种将周期函数表示为正弦和余弦函数的线性组合的方法。
它可以将任意周期为T的函数f(x)分解为如下形式的级数：f(x)=a0/2+Σ(an*cos(2πnfx / T) + bn*sin(2πnfx / T))其中an和bn是傅里叶系数，f为频率。
2. 傅里叶级数的性质（1）奇偶性：偶函数的傅里叶级数只包含余弦项，奇函数的傅里叶级数只包含正弦项。
（2）傅里叶系数：通过欧拉公式和傅里叶系数的计算公式可以得到an和bn。
（3）傅里叶级数的收敛性: 傅里叶级数在满足柯西收敛条件的情况下可以收敛到原函数。
二、傅里叶变换1. 傅里叶变换的定义傅里叶变换是将信号从时间域转换到频率域的一种数学工具。
对于非周期函数f(t)，它的傅里叶变换F(ω)定义如下：F(ω)=∫f(t)e^(-jwt)dt其中ω为频率，j为虚数单位。
2. 傅里叶变换的性质（1）线性性质：傅里叶变换具有线性性质，即对于任意常数a和b，有F(at+bs)=aF(t)+bF(s)。
（2）时移性质和频移性质：时域的时移对应频域的频移，频域的频移对应时域的时移。
（3）卷积定理：傅里叶变换后的两个函数的乘积等于它们的傅里叶变换之卷积。
3. 傅里叶逆变换傅里叶逆变换是将频域的信号反变换回时域的一种操作，其定义如下：f(t)=∫F(ω)e^(jwt)dω / 2π其中F(ω)为频域信号，f(t)为时域信号。
三、离散傅里叶变换1. 离散傅里叶变换的定义对于离散序列x[n]，其离散傅里叶变换X[k]的定义如下：X[k]=Σx[n]e^(-j2πnk / N)其中N为序列长度。
2. 快速傅里叶变换（FFT）FFT是一种高效计算离散傅里叶变换的算法，它能够在O(NlogN)的时间复杂度内完成计算，广泛应用于数字信号处理和通信系统中。
章傅里叶变换精品文档
情况1： T 4,F nT S a (n T )1 4S a (n 4 )
第一个过零点为n =4 。 F n 在2π/有4值1（谱线）
T
f (t)
1
2
o
2
谱线间隔 2 π T
1 Fn
4
2
O
T
t
第一个过零点：
Sa(2 ) 0
π 2π
t2
t1
cos(n1t)cos(m1t)dt 0
sin(n1t)sin(m1t)dt
0
,
mn
（2）“单位”常数性，即当 n 0 时，有
t1 t2 c o s 2 (n1 t)d tt1 t2 s in 2 (n1 t)d t T 2 t2 2 t1
t2t1
t2 t1
f(t)cos(n1t)dt,
t2 f(t)dt, n0
t1
n0
数
bnt1 t2t1 tf2s(tin )s2i(n n(n1t)1td)tdtt22 t1
t2 t1
f(t)sin(n1t)dt
或 f(t)a 2 0n 1(a nc o sn1 t b nsinn1 t)
t21dt t1
T
t2
t1
可以将“任意”周期函数 f ( t ) 在这个正交函数集中展开为
f(t)a0 (ancosn1tbnsinn1t) n1
称为傅里叶级数
系
an
t2 t1
f(t)cos(n1t)dt
t1 t2cos2(n1t)dt
2 t21 t1
n1
傅里叶变换算法详细介绍要点
从头到尾彻底理解傅里叶变换算法、上前言第一部分、DFT第一章、傅立叶变换的由来第二章、实数形式离散傅立叶变换（Real DFT）从头到尾彻底理解傅里叶变换算法、下第三章、复数第四章、复数形式离散傅立叶变换/***************************************************************************************************/这一片的傅里叶变换算法，讲解透彻，希望对大家会有所帮助。
感谢原作者们（July、dznlong）的精心编写。
/**************************************************************************************************/前言：“关于傅立叶变换，无论是书本还是在网上可以很容易找到关于傅立叶变换的描述，但是大都是些故弄玄虚的文章，太过抽象，尽是一些让人看了就望而生畏的公式的罗列，让人很难能够从感性上得到理解”---dznlong，那么，到底什么是傅里叶变换算法列?傅里叶变换所涉及到的公式具体有多复杂列?傅里叶变换（Fourier transform）是一种线性的积分变换。
因其基本思想首先由法国学者傅里叶系统地提出，所以以其名字来命名以示纪念。
哦，傅里叶变换原来就是一种变换而已，只是这种变换是从时间转换为频率的变化。
这下，你就知道了，傅里叶就是一种变换，一种什么变换列?就是一种从时间到频率的变化或其相互转化。
ok，咱们再来总体了解下傅里叶变换，让各位对其有个总体大概的印象，也顺便看看傅里叶变换所涉及到的公式，究竟有多复杂：以下就是傅里叶变换的4种变体（摘自，维基百科）连续傅里叶变换一般情况下，若“傅里叶变换”一词不加任何限定语，则指的是“连续傅里叶变换”。
连续傅里叶变换将平方可积的函数f（t）表示成复指数函数的积分或级数形式。
傅里叶变换知识点
傅里叶变换知识点傅里叶变换是一种利用正弦函数和余弦函数来描述复杂周期信号的重要数学工具。
这个知识点在数学、物理、工程和计算机科学等领域有着广泛的应用和深厚的理论基础。
本文将从数学和应用两方面来介绍傅里叶变换的基本概念、公式和实际应用。
一、傅里叶级数和傅里叶变换的基本概念傅里叶级数是傅里叶变换的基础，它描述了周期信号可以分解成一系列正弦、余弦函数的和的形式。
具体地，设一个周期为T的连续信号x(t)，则它可以表示为如下级数的形式：$$x(t)=\displaystyle\sum_{k=-\infty}^{\infty}c_ke^{j2\pi kt/T}$$其中，$c_k$是信号的傅里叶系数，它表示了信号中各个频率分量的振幅和相位信息。
这个级数给出了信号在频域的分布特征，即展开了信号的频谱。
傅里叶级数是离散信号傅里叶变换的前身，它在许多工程和科学领域中有重要应用，比如音频处理、图像处理和自然界中的周期性现象等。
傅里叶变换是将连续信号的傅里叶级数推广到非周期信号的情形，它通过对一个信号进行积分，得到了信号在连续频域上的表示。
具体地，设一个连续信号x(t)的傅里叶变换为X(f)，则有如下的变换公式：$$X(f)=\int_{-\infty}^{\infty}x(t)e^{-j2\pi ft}dt$$其中，$e^{-j2\pi ft}$是频率为f的复指数，表示了不同频率分量的相位和振幅信息。
傅里叶变换的实质是将时域信号转换为频域信号，这个变换过程对信号的分析和处理具有非常重要的意义。
二、傅里叶变换的重要性和应用傅里叶变换的重要性体现在它广泛地应用于信号处理、通信、图像处理、光学等领域。
下面主要介绍一下其中的一些应用。
1. 频谱分析傅里叶变换的主要作用是将时域信号转换为频域信号，从而方便对信号的各种频率成分进行分析。
以音频处理为例，一个音频信号可以用复杂的波形描述，但是通过傅里叶变换，我们可以将其分解成一些简单的正弦信号，从而分析和处理这些分量。
傅里叶变换基础知识
（3）正、余弦信号
（4）一般周期信号
（5）周期单位脉冲序列
傅里叶变换基础知识
1.
最简单有最常用的信号是谐波信号，一般周期信号利用傅里叶级数展开成多个乃至无穷多个不同频率的谐波信号，即一般周期信号是由多个乃至无穷多个不同频率的谐波信号线性叠加而成。
1.1
在有限区间上，任何周期信号 只要满足狄利克雷（dirichlet）条件，都可以展开成傅里叶级数。
1.1.1
2.2
一个信号可以进行时域描述和频域描述。两种描述通过傅里叶变换来确立彼此一一对应的关系，因此，熟悉傅里叶变换的一些主要性质十分必要。
性质
时域
频域
函数的奇偶虚实性
实偶函数
实偶函数
实奇函数
虚奇函数
虚偶函数
实偶函数
虚奇函数
实奇函数
线性叠加
对称
续尺度改变
时移
频移
时域卷积
频域卷积
时域微分
频域微分
积分
2.3
（1）举行窗函数
式中： 为信号的常值分量； 为信号的余弦信号幅值； 为信： 为信号的周期； 为信号的基频，即角频率， ， 。
合并同频项也可表示为
式中：信号的幅值 和初相位 分别为
1.1.4
（1）信号的频谱（三角频谱）：构成信号的各频率分量的集合，表征信号的幅值和相位随频率的变化关系，即信号的结构，是 （或 ）和 （或 ）的统称；
（1）第一类间断点（有限型间断点）：
a.可去间断点：函数在该点左极限、右极限存在且相等，但不等于该点函数值或函数在该点无定义（ 令分母为零时等情况）；
b.跳跃间断点：函数在该点左极限、右极限存在，但不相等（ 在点 处等情况）。
傅里叶变换
第三章 傅里叶变换一.周期信号的傅里叶级数知 识 要 点1、 周期信号的傅里叶级数任一满足狄利克雷条件的周期信号()f t （1T 为其周期）可展开为傅里叶级数。
(1)三角函数形式的傅里叶级数 0111()[cos()sin()]nn n f t a an t b n t ωω∞==++∑式中112T πω=，n 为正整数。
直流分量010011()t T t a f t dt T +=⎰ 余弦分量的幅度010112()cos()t T t a f t n t dt T ω+=⎰正弦分量的幅度01112()sin()t T n t b f t n t dt T ω+=⎰ 三角函数形式的傅里叶级数的另一种形式为011()cos()nn n f t c cn t ωϕ∞==++∑频谱：离散性、谐波性、收敛性或011()sin()nn n f t d dn t ωϑ∞==++∑以上几种表示形式中各个量之间的关系为000a c d ==n n c d ==cos sin n n n n n a c d ϕϑ== sin cos n n n n n b c d ϕϑ=-=tan nn n a b ϑ=tan nn na b ϕ=-(1,2,)n =,,n n n a c d 为1n ω的偶函数，,,n n n b ϕϑ为1n ω的奇函数。
（2）指数形式的傅里叶级数11()()jn tn f t F n eωω∞=-∞=∑式中，n 为从-∞到+∞的整数。
复数频谱0110111()()t T jn tn t F F n f t e dt T ωω+-==⎰n F 与其他系数之间的关系为 0000F c d a ===1()2n j n n n n F F c a jb ϕ==-1()2n j n n n n F F c a jb ϕ---==+1122n n n n F F c d -====n n n F F a -+=n n n F F c -+=()n n n b j F F -=-n F 是1n ω的偶函数。
傅里叶变换详细讲述
第三章傅里叶变换3-1 概述对于一件复杂的事情，人们总是从简单的一步开始做起，富丽堂皇的高楼大厦，是人们一块砖一块砖垒起来的。
为了简化问题的求解，人们往往也使用“变换分析”这种技巧，所起“变换”大家可能会感到陌生，其实我们在中学时已经运用了“变换分析”技巧，大家一定还记得对数运算，它实际上也是一种数学变换，我们知道两个数的乘积的对数等于两个数的对数和，两个数的商的对数等于这两个数的对数差，利用对数这个运算规则我们可以将数的乘积运算转换（准确地说变换）为数的加法运算，可以将数的除法运算转换（变换）为数的减法运算，可见“变换分析”给我们解决问题带来了方便，傅里叶变换就是给我们分析问题和解决问题极为方便的数学工具。
线性非时变系统的卷积分析实际上是基于将输入信号分解为一组加权延时的单位冲激（或样值）激励的线性组合。
本章将讨论信号和系统的另一种表示，其基本观点还是将信号分解为一组简单函数的线性组合，但是这里用的简单函数不是单位冲激（或样值）而是三角函数（或复指数函数）。
用“三角函数和”表示信号的想法至少可以追溯到古代巴比伦时代，当时他们利用这一想法来预测天体运动。
这一问题的近代研究始于1748年，欧拉在振动弦的研究中发现：如果在某一时刻振动弦的形状是标准振动（谐波）模的线性组合，那么在其后任何时刻，振动弦的形状也是这些振动模的线性组合。
另外，欧拉还证明了在该线性组合中，其后的加权系数可以直接从前面时间的加权系数中导出。
欧拉的研究成果表明了：如果一个线性非时变系统输入可以表示为周期复指数或正弦信号的线性组合，则输出也一定能表示成这种形式。
现在大家已经认识到，很多有用的信号都能用复指数函数的线性组合来表示，但是在18世纪中期，这一观点还进行着激烈的争论。
1753年D.伯努利（D.Bernoulli）曾声称：一根弦的实际运动都可以用标准（谐波）振荡模的线性组合来表示。
而以J.L.拉格朗日(grange)为代表的学者强烈反对使用三角级数来研究振动弦运动的主张，他反对的论据就是基于他自己的信念，即不可能用三角级数来表示一个具有间断点的函数。
傅里叶变换超详细总结
“周期信号都可表示为谐波关系的正弦信号的加权”——傅里叶的第一个主要论点——“非周期信号都可用正弦信号的加权积分表示”——傅里叶的第二个主要论点——频域分析：傅里叶变换，自变量为 j Ω复频域分析：拉氏变换，自变量为 S = σ +j ΩZ域分析：Z 变换，自变量为z傅立叶级数是一种三角级数，它的一般形式是)sin cos (10t n b t n a A n n n ωω++∑∞=将周期性的(非正弦的)波,用一系列的正弦波的迭加来表示,然后对每一项正弦波进行分析,因此提出了把周期函数 f(x) 展开成三角级数01()sin()n n n f t A A n t ωϕ∞==++∑01(cos sin )n n n A a n t b n t ωω∞==++∑为了讨论如何把周期函数展开成三角级数，首先考虑三角函数系的正交性。
{}1,cos ,sin ,cos 2,sin 2,,cos ,sin ,t t t t n t n t ωωωωωω⋯⋯正交性:不同的基本单位向量的点积(内积)等于零,而相同的基本单位向量不等于零傅里叶变换•周期信号的傅里叶级数分析(FS)•非周期信号的傅里叶变换(FT)•周期序列的傅里叶级数（DFS）•非周期的离散时间信号的傅里叶变换（DTFT）•离散傅里叶变换（DFT）1 周期信号的傅里叶级数分析(FS)三角函数集是最重要的基本正交函数集，正、余弦函数都属是三角函数集。
优点：(1)三角函数是基本函数；(2)用三角函数表示信号，建立了时间与频率两个基本物理量之目的联系；(3)单频三角函数是简谐信号，简谐信号容易产生、传输、处理；(4)三角函数信号通过线性时不变系统后，仍为同频三角函数信号，仅幅度和相位有变化，计算方便。
由于三角函数的上述优点，周期信号通常被表示(分解)为无穷多个正弦信号之和。
利用欧拉公式还可以将三角函数表示为复指数函数，所以周期函数还可以展开成无穷多个复指数函数的之和，其优点是与三角函数级数相同。
第三章 傅里叶变换 知识要点
可能存在任何具有频率为基波频率非整数倍的分量。 （3）收敛性 各条谱线的高度，也即各次谐波的振幅，总的趋势是随着谐波次数的增高而
逐渐减小的；当谐波次数无限增高时，谐波分量的振幅亦就无限趋小。
∞
但是，冲激函数序列δT (t) = ∑δ (t − nT1 ) 的频谱不满足收敛性。 n = −∞
(ω )⎤⎦
=
1 2π
∞ F (ω )e jωt dω
−∞
可简记为： f (t ) ←⎯FT→ F (ω )
（二）典型信号的傅里叶变换
1、δ (t ) ←⎯→1
2、δ ' (t ) ←⎯→ jω δ (n) (t ) ←⎯→ ( jω )n
3、1←⎯→ 2πδ (ω)
4、 u (t ) ←⎯→πδ (ω ) + 1
3、周期三角脉冲信号
∑ f
(t)
=
E 2
+
4E π2
∞ n=1
1 n2
sin 2
⎛ ⎜⎝
nπ 2
⎞ ⎟⎠
cos
(
nω1t
)
周期三角脉冲的频谱只包含直流、基波及奇次谐波频率分量，谐波的幅度以
1 的规律收敛。 n2
4、周期半波余弦信号
6
( ) ∑ f
(t
)
=
E π
−
2E π
∞ n=1
1 n2 −1
cos⎜⎛ ⎝
=
2π T1
这是因为它在区间 (t0 ,t0 + T1 )内满足：
⎧0
∫t0 +T1
t0
cos(mω1t
)cos(nω1t )dt
概述傅里叶变化的主要内容
概述傅里叶变化的主要内容傅里叶变换是一种在数学、物理和工程领域广泛应用的工具，主要用于分析周期性或非周期性信号的频谱特征。
其主要内容包括傅里叶级数、傅里叶积分、傅里叶变换及其逆变换，以及傅里叶变换的性质和应用。
1. 傅里叶级数傅里叶级数是一种将周期性函数表示为无穷级数的方法。
该级数由正弦函数和余弦函数之和组成，每个函数都以某个频率振动。
通过傅里叶级数，我们可以将任何周期性函数表示为一系列不同频率的正弦和余弦函数的线性组合。
2. 傅里叶积分傅里叶积分是用于将非周期函数展开为无穷积分的方法。
与傅里叶级数类似，它也是基于正弦和余弦函数的，但适用于非周期性函数。
通过傅里叶积分，我们可以将任何非周期性函数表示为一系列不同频率的正弦和余弦函数的积分组合。
3. 傅里叶变换及其逆变换傅里叶变换和逆变换是傅里叶理论的核心内容。
傅里叶变换可以将一个函数从时域转换到频域，而逆变换则可以将一个频域函数转换回时域。
通过傅里叶变换，我们可以分析信号的频谱特征，而通过逆变换，我们可以恢复原始信号。
4. 傅里叶变换的性质傅里叶变换具有一些重要性质，包括线性、可移位性、对称性和卷积定理等。
这些性质在信号处理中非常重要，例如在滤波、调制和解调等方面。
5. 傅里叶变换的应用傅里叶变换在许多领域都有广泛的应用，包括信号处理、图像处理、通信系统、控制系统等。
例如，在信号处理中，我们可以使用傅里叶变换来分析信号的频率成分，进行频谱分析和滤波等操作；在图像处理中，我们可以使用傅里叶变换来分析图像的频域特征，进行图像增强和去噪等操作。
此外，傅里叶变换在通信系统中也起着关键作用，如调制和解调等操作都离不开傅里叶变换的支持。
总之，傅里叶变换是一种强大的数学工具，可以用于分析信号和系统的频率特性，广泛应用于各种领域。
通过对傅里叶变换的学习和实践掌握其基本原理和方法，可以更好地解决实际问题并提高我们的专业素养。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2
周期信号的平均功率等于直流、基波及各次谐波分量有效值的平方和。也就
是说，时域和频域的能量是守恒的。
这是帕塞瓦尔定理在傅里叶级数情况下的具体体现。
6、有限项傅里叶级数的方均误差
∑( ) EN
=
ε
2 N
(t
)
=
f
2
(t)
−
⎡⎢⎣a02
+
1 2
N n=1
an2 + bn2
⎤ ⎥⎦
∫ f 2 (t ) = 1 t0 f 2 (t ) dt T1 t0 （二）傅里叶级数的主要性质
率分量。但其主要能量集中在第一个零点以内。在允许一定失真的条件下，可以
要求一个通信系统只把 ω ≤ 2π 频率范围内的各个频谱分量传送过去，而舍弃 τ
ω
>
2π τ
的分量。这样，常常把 ω
=0
~
2π τ
这段频率范围称为矩形信号的频带宽
度，记作 B ，于是
Bω
=
2π τ
或 Bf
=1 τ
显然，频带宽度 B 只与脉宽τ 有关，而且成反比关系。
（四）典型周期信号的傅里叶级数 1、周期矩形脉冲信号 矩形信号的三角形式傅里叶级数为
∑ f (t) =
Eτ T1
+ 2Eτ T1
∞ ⎛ nπτ
Sa ⎜ n=1 ⎝
T1
⎞ ⎟
cos
(
nω1t
)
⎠
或
∑ f
(t)
=
Eτ T1
+
Eτω1 π
∞ n=1
Sa
⎛ ⎜⎝
nω1τ 2
⎞ ⎟⎠
cos
(
nω1t
)
矩形信号的指数形式傅里叶级数为
（4）若信号脉冲宽度τ 相同，周期 T1 不同，谱线包络线的零点所在位置不
变。当周期增长时，相邻谱线的间隔减小，频谱变密。如果周期无限增长（这时 就成为非周期信号），相邻谱线的间隔将趋于零，周期信号的离散谱线就过渡到 非周期信号的连续频谱。
（5）若信号周期 T1 相同，脉冲宽度τ 不同。由于周期相同，因而相邻谱线
∑ f
(t)
=
Eτ T1
∞ n=−∞
Sa
⎛ ⎜⎝
nω1τ 2
⎞ ⎟⎠
e
jnω1t
周期矩形信号频谱特点：
（1）周期矩形脉冲信号的频谱具有一般周期信号频谱的共同特点。它们的
频谱是离散的。它仅含有 ω
=
nω1 的各分量，其相邻两谱线的间隔是ω1（ =
2π T1
），
5
周期T1 愈大，谱线间隔愈小，频谱愈稠密；反之，则愈稀疏。
4
即 cn ~ ω （或 Fn ~ ω ）的关系，称为信号的幅度谱。
以各次谐波的相位ϕn 为纵坐标，以频率（或角频率）为横坐标，按频率高 低依次排列起来的线图，称为信号的相位频谱，简称相位谱。
即ϕn ~ ω 的关系，称为信号的相位谱。
3、周期信号频谱特点 周期信号频谱具有离散性、谐波性、收敛性。 （1）离散性 周期信号频谱由不连续的线条组成，每一条线代表一个正弦分量。这样的频 谱称为离散频谱或不联系频谱。 （2）谐波性
jπδ
'
(ω )
−
1 ω2
tn
←⎯→ 2π
(
j )n
dn dωn
δ
(ω )
8
（三）傅里叶变换的性质 1、对称性
若 f (t ) ←⎯→ F (ω)
则 F (t ) ←⎯→2π f (−ω )
例 2.1 试求抽样函数 Sa(t ) = sin t 的频谱函数。
t
若 f (t ) ←⎯FS→ Fn
( ) 则 f ∗ t ←⎯FS→ F−∗n
f (−t ) ←⎯FS→ F−n
f
(t ) cos (ω1t ) ←⎯FS→
1 2
( Fn−1
+
) Fn+1
f
(t )s in (ω1t ) ←⎯FS→
1 2j
( Fn−1
−
Fn+1
)
f (k) (t ) ←⎯FS→ ( jnω1 )k Fn
( ) f t − t0 ←⎯FS → Fne− jnω1t0
（三）周期信号的频谱 1、周期信号可分解为直流、基波（ω1 ）和各次谐波（ nω1 ：基波角频率的
整数倍）的线性组合。 2、信号的频谱
为了直观地表示出信号所含各频率分量振幅的大小，以频率 f（或角频率ω ）
为横坐标，以各次谐波的振幅 cn 或虚指数函数的幅度 Fn 为纵坐标，按频率高低 依次排列起来的线图，称为信号的幅度频谱，简称幅度谱。图中每条竖线代表该 频率分量的幅度，称为谱线。
（ ω1
=
2π T1
）
16、
fΔ
(t)
=
⎜⎝⎛1
−
2 τ
t
⎞ ⎟⎠
⎡ ⎢⎣u
⎛ ⎜⎝
t
&
u
⎛ ⎜⎝
t
−τ 2
⎞⎤ ⎟⎠⎥⎦
←⎯→ τ 2
Sa2
⎛ ⎜⎝
ωτ 4
⎞ ⎟⎠
17、 t ←⎯→ j2πδ ' (ω )
t
←⎯→ −
2 ω2
1 ←⎯→ − jπ Sgn (ω )
t
tu
(t ) ←⎯→
∗
dt
⎧0 = ⎩⎨T1
2、三角函数形式的傅里叶级数
m≠n m=n
任何周期信号 f (t) 可以分解为
∞
∑ （1） f (t) = a0 + ⎡⎣an cos (nω1t ) + bn sin (nω1t )⎤⎦ n=1 傅里叶系数：
1
⎧ ⎪ ⎪
∫ ( ) a0
=
1 T1
f t0 +T1
t0
t
dt
jω
5、 sgn (t ) ←⎯→ 2
jω
7
6、 Gτ
(t ) ←⎯→τ
Sa
⎛ ⎜⎝
ωτ 2
⎞ ⎟⎠
7、
Sa(ω 0 t )
↔
π ω0
G2ω0
(ω )
Sa (t ) ←⎯→πG2 (ω)
8、 e−atu (t ) ←⎯→ 1
a + jω
（ a 为正实数）
9、 e−a t
←⎯→
2a a2 +ω2
10、 e jω0t ←⎯→ 2πδ (ω − ω0 )
(ω
−
ω0
)⎤⎦
+
ω02
jω − ω2
14、
s
in
(ω0t
)u
(t
) ←⎯→
π 2j
⎡⎣δ
(ω
+
ω0
)
−
δ
(ω
−
ω0
)⎤⎦
+
ω0 ω02 − ω 2
∞
∞
∞
∑ ∑ ∑ 15、δT (t ) = δ (t − nT1 ) ←⎯→ω1 δ (ω − nω1 ) = e− jnωT1
n=−∞
n=−∞
n = −∞
arctan
an bn
n = 1, 2,3,L n = 1, 2,3,L
3、虚指数形式的傅里叶级数
∞
∑ f (t) =
Fne jnω1t
n=−∞
傅里叶系数：
∫ ( ) Fn
=
1 T1
f t0 +T1
t0
t e− jnω1t dt
n = 0, ±1, ±2,L
Fn 与其它系数有如下关系：
F0 = c0 = d0 = a0
∫ ⎪
⎨an ⎪
=
2 T1
t0 +T1 t0
f
(t ) cos (nω1t ) dt
∫ ⎪
⎪ bn ⎩
=
2 T1
t0 +T1 t0
f
(t )sin (nω1t ) dt
n = 1, 2,3,L n = 1, 2,3,L
其中 ω1
=
2π T1
∞
∑ （2） f (t) = c0 + cn cos (nω1t + ϕn ) n=1
(ω )⎤⎦
=
1 2π
∞ F (ω )e jωt dω
−∞
可简记为： f (t ) ←⎯FT→ F (ω )
（二）典型信号的傅里叶变换
1、δ (t ) ←⎯→1
2、δ ' (t ) ←⎯→ jω δ (n) (t ) ←⎯→ ( jω )n
3、1←⎯→ 2πδ (ω)
4、 u (t ) ←⎯→πδ (ω ) + 1
（ n 为奇数）
在奇谐函数的傅里叶级数中，只会含有基波和奇次谐波的正弦、余弦项。而
不会包含偶次谐波项。
3
5、周期信号的平均功率
( ) ∫ ( ) ∑( ) ∑ ∑ P = f 2 t
=1 T1
T1 0
f
2
t
dt
=
a
2 0
+1 2
∞ n=1
an2
+ bn2
=
c02
+
1 2
∞
c
2 n
n=1
=
∞
Fn
n=−∞
3、周期三角脉冲信号
∑ f
(t)
=
E 2
+
4E π2
∞ n=1
1 n2
sin 2
⎛ ⎜⎝
nπ 2
⎞ ⎟⎠
cos
(
nω1t
)