第三章真值表的判断作用
真值表及其作用

6.与“并非做坏事而不受惩罚”这个判断等值的充
分条件假言判断是(
)。
7.“只有通过考试,才能录取”转换为等值的充分
条件的假言判断是(
);转换为等值的联言
判断的负判断是(
)。
8.“并非小王既是大学生又是运动员”等值于选言
判断( );也等值于充分条件假言判断( )。
答案:6.如果做坏事,那么要受惩罚。
.
P:甲第一, q:丙第二。
小刘预测 小林预测
④由真值表第2行可得,当p、q均真时, 判断┓q与(p← q)不同真。
⑤由此可得:甲第一、丙第二、乙第三。
.
例3:用真值表判定下列推理是否有效。 或者逻辑难学,或者没有多少学生喜欢
它。如果数学容易学,那么逻辑不难学。因 此,如果许多学生喜欢逻辑,那么学数学并 不太容易。
相容选言判断的负判断; (p∨q)
4.如果事故不是机械故障,那么就一定有人破坏, 这种说法不对。
充分条件假言判断的负判断; (p→q)
5.除非ቤተ መጻሕፍቲ ባይዱ效地治理污染,否则不能保护环境。
必要条件假言判断;p←q
.
三、指出下列判断中哪些具有等值关系,并写出它 们的等值式。
1.如果甲公司不中标,则乙公司一定中标。 2.并非甲公司中标并且乙公司中标。 3.或者甲公司不能中标,或者乙公司不能中标。 4.或者甲公司中标,或者乙公司中标。
解:①令p表示“小金当选班长”, q表示 “小赵当选学习委员” ②把ABC符号化为: A: (┓p∨q) B: q C: (p∨q) ③列真值表如下:
.
P: q:
B
小委 小
金员 赵
当当
选选
班学 长习
A
C
真值表名词解释

真值表名词解释真值表是计算机科学中的一个重要概念,它可以用来设计计算机中的程序。
真值表是用来确定真假的表格,它的功能就是将输入的真假的数据转换成指定的输出。
一个真值表可以通过将真假的条件成对地列出来,然后按照相应的规则来确定真假,从而实现一个程序的功能。
一个真值表可以由一到多个变量组成,每一个变量都有相应的取值,比如0或1。
一般而言,在一个普通的真值表中,0表示假,1表示真,但也可以使用其他的取值来表示真和假,比如Yes和No。
对于一个真值表,输入的真假的数据可以通过真假的规则确定输出的结果,每一组输入数据可以按照特定的规则确定一个输出,从而实现真假的判断。
一个真值表可以用来控制一个计算机程序的运行,可以用来解决多种问题,比如数学、科学和工程等。
真值表中的参数可以按照不同的模式来执行,比如逻辑模式、数学模式和统计模式等。
每一种模式都有自己的输入和输出。
比如逻辑模式可以以如下规则输入:如果A 等于B,那么结果就是真;如果A不等于B,那么结果就是假。
统计模式的输入可以是:如果X大于Y,那么结果就是真;如果X不大于Y,那么结果就是假。
真值表在计算机系统中起着重要作用,它可以帮助我们控制不同的计算机程序,实现复杂的功能。
真值表可以提供更多精度,可以更好地处理不同的数据,而这也是程序设计和计算机编程中非常重要的一点。
在程序设计中,真值表是一种非常常用的工具,它可以提高程序的运行效率和准确性。
真值表的使用方法很简单,只需要将真假的参数输入,然后按照指定的规则确定真假,然后输出指定的结果。
真值表可以很容易地理解,同时也可以用来解决很多复杂的问题。
总之,真值表是计算机科学中一个非常重要的概念,它可以帮助我们更好地控制计算机程序,实现复杂的功能。
真值表的使用方法简单易懂,只需要按照规则输入数据,然后输出指定的结果,从而提高了程序的准确性和运行效率。
3.1.3第三章命题逻辑6+2练习

2.1.3命题推理的真值形式: 先分别写出各前提和结论的真值形式; 用“∧”号将各前提的真值形式联结起来; 用“→”号将前提的合取式和结论联结起来。 所得的蕴涵式即为所要判定的命题推理的真值
形式。
(前提1∧前提2) →结论
如果地球围绕太阳公转,但并不围绕自己的轴线自 转,那么,地球上就不会有白天和黑夜 。事实上, 地球上有白天和黑夜。所以,或者地球并不公转, 或者地球既公转又自转。
为了证明一个蕴涵式是重言式,必须证明它不可能前 件真且后件假。先假设所要判定的蕴涵式前件真且后 件假,并根据这个假设’给每个命题变项赋值,使其 满足前件真且后件假。在这样的赋值过程中,如果出 现矛盾赋值,即必须同时给同一命题变项既赋真,又 赋假,那么,这说明原假设不能成立,因而它是重言 式;反之,如果不出现矛盾赋值,则说明存在一组赋 值满足前件真且后件假,因而不是重言式。
前提1:如果地球围绕太阳公转,但是并不围绕自己的轴 线自转,那么,地球上就没有白天和黑夜。 前提2:因为事实是地球上有白天和黑夜, 结论:所以,或者地球并不公转,或者地球既公转又自转。
设:地球围绕太阳公转(p) 围绕自己的轴线自转(q), 地球上有白天和黑夜(r) 。 前提1:(p q) r; 前提2: r 结论: p (p q) 真值形式: (((p q) r) r) (p (p q))
2.2寻求判定方法
真值表方法、归谬赋值法、范式方法和自然 推理方法
2.2.1真值表方法
▪ 真值表,就是指能显示一个真值形式在它的 命题变项的各种真值组合下所取真值的图表。
真值表可以判定任一真值形式是否为重言式, 或矛盾式,或可真式,因此,自然也可以判 定任一命题推理的蕴涵式是否为重言式。
数字电子技术基础(第四版)课后习题答案_第三章
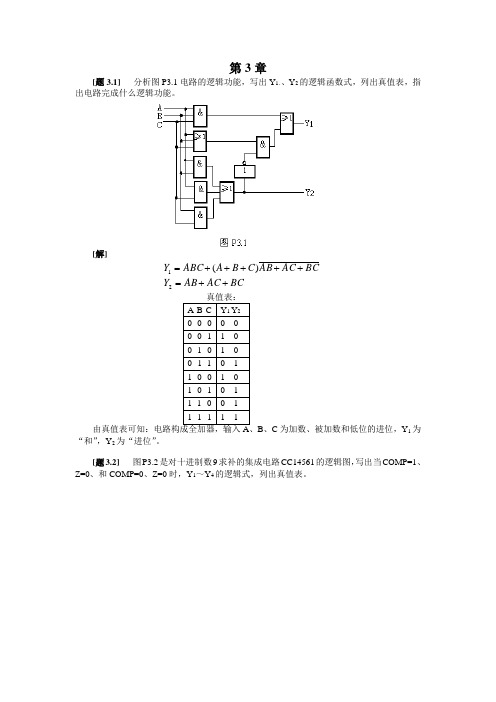
第3章[题3.1] 分析图P3.1电路的逻辑功能,写出Y 1、、Y 2的逻辑函数式,列出真值表,指出电路完成什么逻辑功能。
[解]BCAC AB Y BCAC AB C B A ABC Y ++=+++++=21)(B 、C 为加数、被加数和低位的进位,Y 1为“和”,Y 2为“进位”。
[题3.2] 图P3.2是对十进制数9求补的集成电路CC14561的逻辑图,写出当COMP=1、Z=0、和COMP=0、Z=0时,Y 1~Y 4的逻辑式,列出真值表。
[解](1)COMP=1、Z=0时,TG 1、TG 3、TG 5导通,TG 2、TG 4、TG 6关断。
3232211 , ,A A Y A Y A Y ⊕===, 4324A A A Y ++=(2)COMP=0、Z=0时,Y 1=A 1, Y 2=A 2, Y 3=A 3, Y 4=A 4。
COMP =0、Z=0的真值表从略。
[题3.3] 用与非门设计四变量的多数表决电路。
当输入变量A 、B 、C 、D 有3个或3个以上为1时输出为1,输入为其他状态时输出为0。
[解] 题3.3的真值表如表A3.3所示,逻辑图如图A3.3所示。
ABCD D ABC D C AB CD B A BCD A Y ++++= BCD ACD ABC ABC +++=B C D A C D A B D A B C ⋅⋅⋅=[题3.4] 有一水箱由大、小两台泵M L 和M S 供水,如图P3.4所示。
水箱中设置了3个水位检测元件A 、B 、C 。
水面低于检测元件时,检测元件给出高电平;水面高于检测元件时,检测元件给出低电平。
现要求当水位超过C 点时水泵停止工作;水位低于C 点而高于B 点时M S 单独工作;水位低于B 点而高于A 点时M L 单独工作;水位低于A 点时M L 和M S 同时工作。
试用门电路设计一个控制两台水泵的逻辑电路,要求电路尽量简单。
[解] 题3.4的真值表如表A3.4所示。
逻辑学真值表

➢(p:美国绕开联合国向伊拉克改动战争; q:联合国的权威就会受到破坏)
➢推理形式:(p→q)→(﹁q → ﹁p)
2021/8/5
5
p q ﹁p ﹁q p→q ﹁q→﹁p (p→q)→(﹁q → ﹁p)
TTFF T
T
T
TFFT F
F
T
FTTF T
T
T
FFTT T
T
T
2021/8/5
6
部分资料从网络收集整 理而来,供大家参考,
➢(p:乔丹是美国总统;q:乔丹是美国 领导人)
➢推理形式:((p→q)∧﹁p)→ ﹁q
2021/8/5
3
p q ﹁p ﹁q p→q (p→q)∧﹁p ((p→q)∧﹁p)→﹁q
TTFF T
F
T
TFFT F
F
T
FTTF T
T
F
FFTT T
T
T
2021/8/5
4
➢2.如果美国绕开联合国向伊拉克改动战 争,联合国的权威就会受到破坏。所 以,要想联合国的权威不会受到破坏, 美国就不绕开联合国向伊拉克改动战 争。
p q ﹁p ﹁q ﹁p∨q p→q q←p ﹁q→﹁p ﹁p←﹁q
TTFF T
T
T
T
T
TFFT F
F
F
F
F
FTTF T
T
T
T
T
FFTT T
T
T
T
T
1/8/5
1
➢ 真值表方法: ➢ 1.用符号表达出命题形式。 ➢ 2.列出命题形式中的命题变元。 ➢ 3.根据括号和联结词的用法确定命题形式内部的次序。 ➢ 4.画出真值表。 ➢ 5.依照确定的表达式次序检验真值。 ➢ 6.根据最后一步即主联结词一栏的真值情况对该表达式做
逻辑学真值表法

逻辑学真值表法
逻辑学真值表法是一种常用的推理方法,它可以帮助我们研究、解释和理解复杂的或超越思维能力的问题。
它是一种基于逻辑规则的知识表示法,为给定的条件和结果构建一种以真值表的形式运算的推导系统,从而完成推理和判断工作。
绘制真值表是实现此类推理的基本步骤。
真值表一般由有终止性的几个命题组成,每个命题都有两个可能的真假值,即真和假。
通过将这些真假值进行组合,可以确定输入命题和输出命题者之间的关系。
结果,关于给定条件或结论的结论可以提出。
在使用逻辑学真值表法之前,必须先弄清楚问题当中的信息,以及我们要得到的结果。
通常,我们需要将问题表达成操作,接着写出信息和推测,再将命题连接起来,用Negation,Disjunction,Conjunction和implication来构建命题,从而明确解决问题的思路。
接着,就可以使用真值表来回答问题了。
简而言之,要使用逻辑学真值表法来解决问题,必须首先明确问题的描述,然后将问题表达为的操作和命题,最后通过真值表法得出答案。
真值表法是一种有效的推理方法,掌握了它,就可以有效地解决复杂的问题,从而提高求解能力和解决问题的速度。
因此,它是一种有效的学习工具,是非常重要的数学和逻辑学知识。
真值表判定方法
TT F F T
F
F
TF F T F
T
T
FT T F F
T
T
FF T T F
T
T
二、真值表的判定作用
1、真值表可以判定一个复合判断推理形式是 否有效(这是真值表的主要作用)
任何一个推理都可以表达成一个蕴含式,前 件是前提,后件是结论。如果这个蕴含式 的真值全部为真(重言式),那么这个推 理形式就是有效的。否则是无效的。
即((p ∨ q )∧ ﹃ p) → q这个推理是有效的。
2、真值表方法可以用来判定两个真值形 式是否等值
如果两个真值形式的真值完全相同,那 么它们就是等值的。否则是不等值的。 例如:
﹃ (p∧q) 就是与﹃ p ∨ ﹃ q等值的。
pq ﹃p﹃q p∧q ﹃p∧q ﹃p∨﹃q
TT F F T
F
F
真值形式的构成,可以利用真值表来判定它们 的真值。原则上我们可以用真值表来判定 任何真值形式的真值。
一、构造真值表的步骤
1、列出变项及其取值(暂假定只有pq两个变 项);
2、由简而繁地列出该真值形式的各个组成部 分,最后为该真值形式本身;
3、根据基本真值表,逐步计算出各组成部分 的真q (p ∧ q) →(﹁ p ∨ ﹁ q)
如我们要判定“p或者q,非p,那么q”是否为 有效式,也就是要判定“((p∨q)∧ ﹃ p) → q”的真值是否全部为真。
p q ﹃ p p ∨ q (p ∨ q)∧ ﹃ p ((p ∨ q )∧ ﹃ p) → q
TT F T
F
T
TF F T
F
T
FT T T
T
T
FF T F
F
T
该蕴含式的真值全部为真,因此这个蕴含式是重言式,
命题逻辑的真值表和范式
命题逻辑的真值表和范式命题逻辑是研究命题(陈述句)之间的逻辑关系的一种逻辑学分支。
在命题逻辑中,我们使用真值表和范式来表示和分析命题的逻辑结构。
本文将介绍真值表和范式在命题逻辑中的重要性和应用。
一、真值表真值表是用来表示和计算命题的真假值情况的一种工具。
它列举了命题中每个命题变量的可能取值情况,并根据命题之间的逻辑运算规则计算出整个命题的真假值。
真值表通常由命题变量和逻辑运算符组成。
例如,对于两个命题变量P和Q,我们可以构建如下的真值表:P | Q | P∧Q | P∨Q | P→Q | P↔Q----------------------T | T | T | T | T | T----------------------T | F | F | T | F | F----------------------F | T | F | T | T | F----------------------F | F | F | F | T | T在真值表中,"T"代表命题的真值为真,"F"代表命题的真值为假。
通过观察真值表,并根据命题之间的逻辑运算规则,我们可以推断出命题之间的逻辑关系。
例如,P∧Q表示P与Q的合取,只有当P和Q 都为真时,合取才为真。
类似地,P∨Q表示P与Q的析取,只要P和Q中至少有一个为真,析取就为真。
真值表为我们提供了一种清晰的逻辑分析工具,能够帮助我们理解和推理命题之间的逻辑关系。
二、范式范式是用来简化和表示复杂命题的一种方法。
它将命题表示为若干个简单命题之间的逻辑连接,并以逻辑运算符为界限构成。
在命题逻辑中,最常见的范式有析取范式(DNF)和合取范式(CNF)。
析取范式将命题表示为若干个合取式之间的析取,而合取范式将命题表示为若干个析取式之间的合取。
例如,对于命题P、Q和R,我们可以将它们表示为析取范式和合取范式。
析取范式(DNF):(P∧Q∧¬R)∨(¬P∧Q∧R)∨(¬P∧¬Q∧R)合取范式(CNF):(P∨¬Q∨¬R)∧(¬P∨Q∨¬R)∧(¬P∨Q∨R)范式的使用可以帮助我们简化和理解复杂的逻辑表达式。
负判断和其推理以及真值表的作用 PPT
全称肯定判断的负判断的逻辑形式是:¬SAP。 由于SAP的矛盾判断是SOP,所以,¬SAP ←→SOP。就是说,全称肯定判断 的负判断的等值判断是一个同素材的特称否定判断。例如,判断“并非所有的科 学家都是天生聪明的”等值于判断“有的科学家不是天生聪明的”。 全称否定判断的负判断的逻辑形式是: ¬SEP。 由于SEP的矛盾判断是SIP,所以,¬SEP←→SIP。就是说,全称否定判断的负 判断的等值判断是一个同素材的特称肯定判断。例如,判断“并非所有作品都不 是杰作”等值于判断“有的作品是杰作”。 特称肯定判断的负判断的逻辑形式是:¬SIP。 由于SIP的矛盾判断是SEP,所以¬SIP←→SEP。就是说,特称肯定判断的负 判断的等值判断是一个同素材的全称否定判断。例如,判断“并非有的人是长生 不老的”等值于判断“所有的人都不是长生不老的”。 特称否定判断的负判断的逻辑形式是: ¬SOP。 由于SOP的矛盾判断是SAP,所以,¬SOP←→SAP。就是说,特称否定判断 的负判断的等值判断是一个同素材的全称肯定判断。例如,判断“并非有的结果 不是有原因的”等值于判断“所有的结果都是有原因的”。 单称肯定判断的负判断的逻辑形式是: ¬SaP。 由于SaP的矛盾判断是SeP,所以¬SaP←→SeP。就是说,单称肯定判断的负判 断的等值判断是一个同素材的单称否定判断。例如,判断“并非小李是北京人” 等值于判断“小李不是北京人”。 单称否定判断的负判断的逻辑形式是: ¬SeP。 由于SeP的矛盾判断是SaP,所以¬SeP←→SaP。就是说,单称否定判断的 负判断的等值判断是一个同素材的单称肯定判断。例如,判断“并非克林顿总统 不是受到弹劾的”等值于判断“克林顿总统是受到弹劾的”。
大学教材《逻辑学教程》经典教案第三章真值表的判定作用
第三章真值表的判定作用第一节重言式矛盾式可满足式一、真值联结词比较下面两个例子1、如果天下雨,那么地上湿。
2、如果2+2=4,那么北京是个大城市。
第一例我们听起来就觉得顺耳,符合我们的语言习惯。
第二句我们听起来觉得有点别扭,不符合我们的语言习惯。
这就说明我们平时说“如果……那么……”时除了考虑前后件的真假以外,还考虑了前后件之间意义上的联系。
但是从现代逻辑的观点看,这两个命题都是正确的。
因为现代逻辑撇开了命题间意义上的联系,仅研究命题间的真假关系。
由于现代命题逻辑和传统逻辑一样都属二值逻辑,真和假是命题仅有的两个值,统称“真值”,因此,复合命题与肢命题之间在真假方面的联系,就是真值联系。
所谓真值联结词是指仅仅表示复合命题与肢命题之间真假关系的联结词。
基本的真值联结词有五个1、否定(并非)┒2、合取(并且)∧3、析取(或者)∨4、蕴涵(如果……那么……)→5、等值(当且仅当……才)←二、真值形式定义:真值形式是指由真值联结词和命题变项所构成的形式结构。
第二章所讲的所有的复合命题的形式结构和复合命题推理的形式结构都是真值形式。
但是第五章中的讲的性质命题和第六章所讲的关系的命题不是真值形式。
例:P∧q (P∧q)→P 是真值形式但 SAP aRb 不是真值形式真值形式是命题形式的一部分。
最基本的真值形式有五种1、否定式:┒P2、合取式:P∧q3、析取式:P∨q4、蕴涵式:P→q5、等值式:P←q其他的真值形式都是由这五种基本真值形式构成的。
三、重言式、矛盾式、可满足式(一)重言式的定义如果一真值形式不论其中的变项赋什么值,这个真值形式的值总是真的,这样的真值形式叫做重言式。
(重言式)如P∨ ┑q,P→P等等(二)矛盾式的定义如果一真值形式不论其中的变项赋什么值,这个真值形式的值总是假的,这样的真值形式就叫矛盾式。
(永假式)如P∧ ┑q(三)可满足式的定义如果一真值形式当其中的变项赋不同的值后,这个真值形式的值在有些情况下是真的,在有些情况下是假的,那么这样的真值形式就是可满足式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
T F T T
F F T T
T T T F
由真值表可知这个真值形式不是重言式
3、((P∨q)∧ ¬q)→P
p q ¬q p∨q TT F TF T T T (p∨q)∧ ¬q F T ((p∨q)∧ ¬q ) → p T T
F T F
F F T
T
F
F
F
T
T
由真值表可知这个真值形式是重言式
• 二、请用真值表判定下列各组命题形式 之间是否具有等值关系。
• 1、 ¬(P→q) • • P∧¬q • 2、 ¬(P∧¬q)
¬P∨q
¬(P→q)
p T T q T F
P∧¬q
P∧¬q F T
¬q (P→q) ¬ (P→q)
F T T F F T
F
F
T
F
F
T
T
T
F
F
F
F
由真值表可知这两个命题之间具有等值 关系。
¬(P∧¬q)
p
T
¬P∨q
P∧¬q ¬(P∧¬q)
• 解 设p表示“王军考上了大学”;q表 示“李伟 考上大学”。
• A:p→ ¬ q • B:¬p
p T T
q T F
¬q
F T
¬p
F F
p→ ¬ q F T
F
F
T
F
F
T
T
T
T
T
• 答:由真值表可以看出,当A、B两个命 题恰有一个为假时,王军考上了大学。
四、列出A、B、C三命题的真值表,并回答当A、 B、C三命题恰有一真时,是否甲村所有人家都 有彩电? • A、甲村所有人家都有彩电,并且乙村所有人 家都有彩电。 • B、或者甲村所有人家都有彩电,或者乙村所 有人家都有彩电。 • C、如果乙村所有人家都有彩电,那么甲村有 些人家没有彩电。
p q ¬p ¬q (p T T F F T F F T F T T F F F T T
∨ q) ¬(p ∨ q) ¬p∨¬q T F F T F T T F T F T T
由真值表可知这两个命题之间不具有等 值关系。
¬(p → q)←→p T T F T
∧ ¬q
F F
p q ¬q (p → q) ¬(p → q) p ∧ ¬ q T F T F T F
F F T
F T
T
T F
F
T F
F
所以原等值式成立
三、真值表还可以帮助解 决一些推理问题
• 当A、B、C三命题恰有一个为真时,甲是 否是木工? • A、如果甲不是木工,则乙是泥工。 • B、如果乙不是泥工,则甲不是木工。 • C、甲不是木工,且乙不是泥工 。
• 解 设p表示“甲是木工”;q表示“乙 是泥 工”。
• 2、矛盾式(又叫永假式)是指在一个命 题形式中不论其中的变项取什么值,该 命题形式的值总是假的。
• 如: p∧ ¬p
p
T F
¬p
T
p∧ ¬p
F
F
F
• 3、可满足式是指在一个命题形式中不 论其中的变项取什么值,该命题形式 的值至少在一种情况下是真的。 • 如:p ∧ q
p
T T F F T F T F
• 1、 P ∨ ¬p
• 2、((P→q)∧ ¬p)→q
• 3、((P∨q)∧ ¬q)→P
1、 P ∨ ¬p
p T
¬p
F
P ∨ ¬p T
F
T
T
由真值表可知这个真值形式是 重言式
2、((P→q)∧ ¬p)→q
p q ¬p T T F T F F F T T F F T
(P→q) (P→q) ∧ ¬p ((P→q) ∧ ¬p)→q
F T
q
T
¬P ¬q
F F
¬P∨q
T
T
F F
F
T F
F
T T
T
F T
T
F F
F
T T
F
T T
由真值表可知这两个命题之间具有等值 关系。
• 三、列出A、B两命题的真值表,并回答A、 B恰有一个为假时,王军是否考上了大学? • A:如果王军考上了大学,那么李伟就没 有考上大学。 • B:王军没有考上大学。
• 解 设p表示“甲村所有人家都有彩电”;q表 示“乙村所有人家都有彩电”。
• 甲村有些人家没有彩电,即并非甲村所有人家 都有彩电。 • A:p ∧ q • B: p ∨ q • C: q → ¬ p
p q ¬p p ∧ q
p∨ q
q→ ¬p
T T F
T F F F T T F F T
T
F F F
T
T T F
F
T T T
• 答:由真值表可以看出,当A、B、C三 命题恰有一个为真时,并非甲村所有人 家都有彩电。
• 1、假定被判定的真值形式(蕴涵式)是假的。 • 2、第二步,从这一假定出发,根据真值表,依 次对公式中的各部分公式赋以相应的真值,直 到所有的变项都被赋以确定的真值为止。 • 3、第三步,检查所有变项的直值,如果其中至 少有一个变项既真又假,即出现了逻辑矛盾 (注:如果有多于一种真值指派,则需每种指 派时都出现矛盾),那么可以证明被判定的公 式不可能为假,只能为真,因而它是一个重言 式;如果并未导致逻辑矛盾,这就证明原假定 成立,因而被判定的公式不是重言式。
一、真值联结词
• 定义:真值联结词是指仅仅表示复合命题 与肢命题之间真假关系的联结词。 • 真值联结词主要有五个: • ¬(否定)、∧(合取)、 • ∨(析取)、→(蕴涵)、 • ←→(等值)
二、真值形式
• 定义:真值形式是指由真值联结词和命
题变项所构成的形式结构。
五种基本的真值形式 否定式: ¬p 合取式:p∧q 析取式:p∨q
F T T
F F T
T
F
T
F
T
T
由真值表可知((p∨q)∧¬p)→q 是重言式。
• 例2、((p∨q)∧p)→ ¬ q
((p∨q)∧p)→ p q ¬q p∨q (p∨q)∧ p ¬ q TT F TF T T T T T F T
F T F
F F T
T
F
F
F
T
T
• 由真值表可知((p∨q)∧p)→ ¬ q 不是重言式。
• A:¬p→q • B:¬q→¬p • C:¬p∧¬q
p q ¬p ¬q
¬p→q ¬q→¬p
T
T T F
¬p∧¬q
F
F F T
T T F
T F F F T T F F T
F
T F T
T
F T T
• 答:由真值表可以看出,当A、B、C三 命题恰有一个为真时,甲是木工。
练习题
• 一、用真值表判定下列真值形式是否是重 言式
• • • •
• 蕴涵式:p→q • 等值式:p←→q
三、五种基本真值形式的真值表
• T 表示“真”、F 表示“假”
• 1、¬p
T
p F
¬p
T
F
2、 p∧q
p T T T F q p∧q T F
F
F
T
F
F
F
p T
T F F
3、p∨q
q T
F T F
p∨q T
T T F
p T
T F F
4、p→q
二、真值表可以判定任意两个复 合命题之间是否具有等值关系
• 例1、¬(p ∧ q) •
¬p ∨ ¬q
p
T T
q
T F
¬p ¬q (p∧q) ¬(p∧q)
F F F T T F F T
¬p∨¬q
F T
F
F
T
F
T
T
F
T
F
F
T
TTBiblioteka T由真值表可知这两个命题之间具有等值 关系。
例2、 ¬(p∨ q) ¬p ∨ ¬q
q
p∧q
T F F F
• 真值表判定方法的三个步骤: 1、找出给定的真值形式里的所有变项,列 举出这些变项的各种真值组合(2n)。
p∧q
p T
T F F
q T
F T F
2、根据真值形式的构成过程,由简而繁 地列举出一个真值形式的各个组成部分, 最后一栏为该形式本身。 3、根据真值形式的真值表,计算出每栏 中各组成部分的真值,最后得出该形式 的真值。
q T
F T F
p →q T
F T T
p T
T F F
5、p←→q
q T
F T F
p ←→ q T
F F T
四、重言式、矛盾式、可满足 式
• 1、重言式(又叫永真式)是指在一个命题形 式中不论其中的变项取什么值,该命题形式 的值总是真的。 • 如: p∨ ¬p
p T F F T
¬p
p∨ ¬p T T
• ((P→q)∧ ¬ q )→ ¬ p是否为重 言式? •
• 判定((p→q)∧ ( q →r))→( p →r) • 是否为重言式
p∧q
p T
T F F
q T
F T F
p∧q T
F F F
¬(p ∧ ¬p)
p T F
¬p
F T
(p ∧ ¬p)
F F
¬(p ∧ ¬p)
T T
真值表的判定作用
一、真值表可以判定任一命题形式是否是 重言式。 例1、((p∨q)∧¬p)→q
((p∨q)∧¬p) p q ¬p p∨q (p∨q)∧¬p →q T T F T F F T T F F T T
