压杆稳定小结
压杆稳定 实验报告

压杆稳定实验报告压杆稳定实验报告一、引言在物理学中,稳定性是一个重要的概念。
对于一个物体或系统来说,稳定性意味着它能够保持在一个平衡状态,不会因外界干扰而倾倒或崩溃。
压杆稳定是一个经典的物理实验,通过改变杆的长度和重心位置,我们可以探索压杆在不同条件下的稳定性。
二、实验目的本实验的目的是通过改变压杆的长度和重心位置,观察和分析压杆在不同条件下的稳定性。
通过实验,我们可以进一步了解压杆稳定的物理原理,并探讨压杆稳定性与杆长、重心位置之间的关系。
三、实验装置和方法1. 实验装置:压杆、支架、重物、测量工具(如尺子和天平)等。
2. 实验方法:a. 将支架放置在水平的桌面上,并固定好。
b. 将压杆放在支架上,调整杆的位置和角度,使其保持平衡。
c. 在压杆的一端悬挂一个重物,称为A端。
d. 在压杆的另一端悬挂一个重物,称为B端。
e. 记录下A端和B端的质量,以及压杆的长度和角度。
f. 通过改变A端和B端的质量、压杆的长度和角度等条件,重复实验,记录数据。
四、实验结果与分析在实验中,我们通过改变A端和B端的质量、压杆的长度和角度等条件,观察压杆在不同条件下的稳定性。
下面是我们的实验结果和分析:1. 改变质量:我们分别改变A端和B端的质量,观察压杆的稳定性。
实验结果表明,当A端和B端的质量相等时,压杆更容易保持平衡。
这是因为在这种情况下,压杆的重心位置更接近中间,稳定性更高。
当A端或B端的质量增加时,压杆的稳定性减弱,容易发生倾倒。
2. 改变长度:我们改变压杆的长度,观察压杆的稳定性。
实验结果显示,当压杆的长度较短时,压杆更容易保持平衡。
这是因为较短的压杆有更小的杆长,重心位置更接近中间,稳定性更高。
当压杆的长度增加时,压杆的稳定性减弱,容易发生倾倒。
3. 改变角度:我们改变压杆的角度,观察压杆的稳定性。
实验结果表明,当压杆的角度接近水平时,压杆更容易保持平衡。
这是因为在这种情况下,压杆的重心位置更接近支点,稳定性更高。
压杆稳定实验报告结论_压杆稳定实验报告

压杆稳定实验报告结论_压杆稳定实验报告压杆稳定实验姓名:学号:班级:同组者:一.实验目的观察压杆失稳现象;通过实验确定临界载荷Fcr,并与理论结果比较;自主设计实验步骤,进行实验结果处理和撰写实验报告。
实验设备和仪器压杆失稳试验装置;电阻应变仪;实验试件板条材料65Mn弹簧钢,调质热处理,达到δs=780MPa, δ电桥图:四.实验步骤1.测板条长L,宽B,厚H;2.拧螺母加压力,为防粘片开胶,压头下移最大1mm,对3中安装状态,各实验两遍,用百分表测压头的位移,用应变仪测压力P=εpEBH 五.数据处理压条尺寸:,1、两端固支压条长度:L=430mm. (1)数据列表:1932107796112114481709188921122284-105-259-427-471-474-475-478-480-481856208834223784380838163840385638643872(2)P-ε由图线可得失稳压力. (3)误差分析:理论失稳压力为:P相对误差:η=2、一端铰支,另一端固定压条长度:L=464mm.:(1)数据列表:149523 662 772 865 961 1050 1140 1350 -99 -148 -171 -180 -178 -189 -193 -196 -199 -200 808 1200 138444015281560158416081616(2)P-ε由图线可得失稳压力P=1614N. (3)误差分析:理论失稳压力为:P相对误差:η=3、两端铰支压条长度:L=498mm.(1)数据列表:132248351435527667 752 839 921 -48 -72 -83 -90 -96 -98 -98 -99 -99 -100 400 592 680 732 786 800 800808816(2)P-ε由图线可得失稳压力P=814N.(3)误差分析:理论失稳压力为:P相对误差:η=六.思考题1.失稳现象和压缩屈服现象本质上有何不同?答:失稳和压缩屈服,都是失效。
压杆稳定小结
压杆稳定小结1、 压杆稳定的概念稳定平衡是指干扰撤去后可恢复的原有平衡;反之则为不稳定平衡。
压杆稳定性是指压杆保持或恢复原有平衡状态的能力。
压杆的临界压力是指压杆由稳定平衡转变为不稳定平衡时所受轴向压力的界限值,用cr F 来表示。
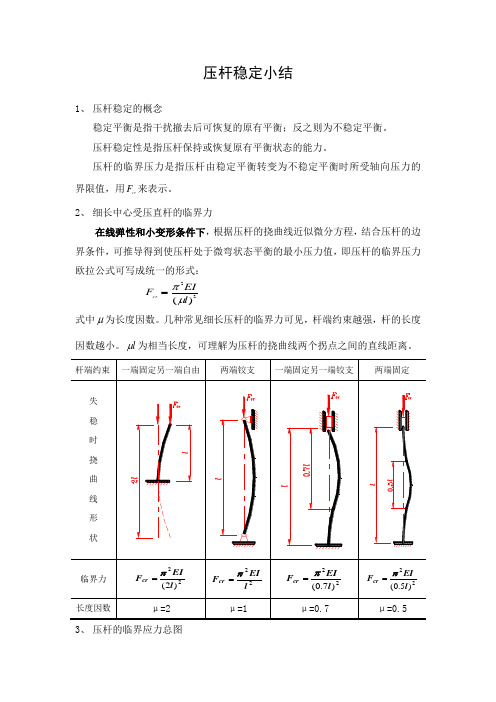
2、 细长中心受压直杆的临界力在线弹性和小变形条件下,根据压杆的挠曲线近似微分方程,结合压杆的边界条件,可推导得到使压杆处于微弯状态平衡的最小压力值,即压杆的临界压力欧拉公式可写成统一的形式:22)(l EIF crμπ=式中μ为长度因数。
几种常见细长压杆的临界力可见,杆端约束越强,杆的长度因数越小。
l μ为相当长度,可理解为压杆的挠曲线两个拐点之间的直线距离。
(d)(d)(d)3、 压杆的临界应力总图(1) 压杆的临界应力压杆在临界力作用下,其横截面上的平均应力称为压杆的临界应力, crcr F Aσ=(2) 欧拉公式的适用范围线弹性范围,()22cr cr p 22F EI E A l A ππσσλμ===≤ 即p λλ≥= 时,欧拉公式才能适用。
通常称p λλ≥的压杆为大柔度压杆或细长压杆。
(3) 压杆的柔度(或长细比)i l μλ=是一无量纲的量。
一般情况下,由于杆端约束(μ)或惯性半径(i )的不同,压杆在不同的纵向平面内具有不同的柔度值,压杆失稳首先发生在柔度最大的纵向平面内。
(4) 临界应力总图压杆的临界应力随柔度λ变化的λσ-cr 图称为临界应力总图。
大柔度杆p λλ≥,临界应力低于比例极限,可按欧拉公式计算,22λπσEcr= ;中柔度杆p s λλλ≤≤,临界应力超过比例极限,可按经验公式计算,如直线公式: λσb a cr -=,其中a 、b 为与材料有关的常数。
或钢结构设计中采用的抛物线公式,以及折减弹性模量理论进行计算;图13-12小柔度杆s λλ≤(或b λ),临界应力达极限应力:塑性材料s cr σσ=,脆性材料cr b σσ=,属于强度问题。
材料力学之压杆稳定

材料力学之压杆稳定引言材料力学是研究物体内部受力和变形的学科,压杆稳定是其中的一个重要内容。
压杆稳定是指在受到压力作用时,压杆能够保持稳定,不发生失稳或破坏的现象。
本文将介绍压杆稳定的基本原理、稳定条件以及一些常见的失稳形式。
压杆的受力分析在进行压杆稳定分析前,我们首先需要对压杆受力进行分析。
压杆通常是一根长条形材料,两端固定或铰接。
在受到外部压力作用时,压杆会受到内部的压力,这些压力会导致杆件产生变形和应力。
在分析压杆稳定性时,我们主要关注压杆的弯曲和侧向稳定性。
压杆的基本原理压杆的稳定性是由杆件的弯曲和侧向刚度共同决定的。
当压杆弯曲和侧向刚度足够大时,压杆能够保持稳定。
所以,为了提高压杆的稳定性,我们可以采取以下几种措施:1.增加杆件的截面面积,增加抗弯能力;2.增加杆件的高度或长度,增加抗弯刚度;3.增加杆件的横向剛性,增加抗侧向位移能力;4.添加支撑或加固结构,增加整体稳定性。
压杆的稳定条件压杆稳定的基本条件是在承受外部压力时,内部应力不超过材料的极限强度。
当内部应力超过材料的极限强度时,压杆将会发生失稳或破坏。
在实际工程中,我们一般采用压杆的临界压力比来判断压杆的稳定性。
临界压力比是指杆件在失稳前的临界弯曲载荷与临界弯曲载荷之比。
当临界压力比大于1时,压杆是稳定的;当临界压力比小于1时,压杆是不稳定的。
临界压力比的计算可以采用欧拉公式或者Vlasov公式等方法。
这些方法能够给出压杆在不同边界条件下的临界压力比。
在工程实践中,我们可以根据具体问题选择合适的方法来计算临界压力比。
压杆的失稳形式压杆失稳通常有两种形式:弯曲失稳和侧向失稳。
弯曲失稳压杆的弯曲失稳是指杆件在受到外部压力作用时,发生弯曲变形并导致失稳。
在弯曲失稳中,压杆的弯曲形态可以分为四种:1.局部弯曲失稳:杆件出现弯曲局部失稳,形成凸起或凹陷;2.局部弯扭失稳:杆件出现弯曲和扭曲共同失稳;3.全截面失稳:整个杆件截面均发生失稳;4.全体失稳:整个杆件完全失稳并失去稳定性。
第五章 压杆稳定

由已知条件,钢压杆在xy平面内的杆端约束为两 端铰支,μ=1;在xz平面内杆端约束为一端铰支、一端 固定,μ=0.7。故失稳将发生在xy平面内,应取μ=1进行 计算。 临界力为
π 2 EI π 2 200109 0.049104 Fcr N 2 2 ( l ) 1 4 0.6 106 N 600kN
cr
cr
p
cr
p
c
图中抛物线和欧拉曲线在C处光滑连接,C点对应 的柔度λc=123,临界应力为134MPa。由于经验公式更 符合压杆的实际情况,故在实用中,对Q235钢制成的 压杆: 当λλc=123时,用欧拉公式计算临界应力 当λ<123时,用抛物线公式计算临界应力
5.3 压杆的稳定计算
5.3.1 安全因数法 1. 稳定条件
由于在桁架平面内AB杆两端为铰支,故μ=l。 AB杆的柔度为
1 3.6 103 113.4 i 31.75
l
利用公式算得折减因数为
2800
2
0.218
AB杆的工作应力为
F 25 10 N A 1102 106 m 2 2.066MPa 2.18MPa
p p
●Q235钢材制成的压杆,λp≈100。 ●木压杆,λp≈110。
5.2.3 抛物线公式
1. 公式
λ<λp的压杆称为中、小柔度压杆。 这类压杆的临界应力通常采用经验公式进行计算。 经验公式是根据大量试验结果建立起来的,目前常用的 有直线公式和抛物线公式两种。这里仅介绍抛物线公式 ,其表达式为
以三种情况来说明
F<Fcr F=Fcr F>Fcr
(1)压力F不大时 给杆一微小的横向干扰,使杆发
压杆稳定实验报告

压杆稳定实验一、实验目的:1、观察压杆的失稳现象2、测定两端铰支压杆的临界压力二、实验原理和方法:1、理论计算:理想压杆,当压力P 小临界压力cr P 时,压杆的直线平衡是稳定的。
当压力到达临界压力cr P 时,压杆的直线平衡变为不稳定,它可能转为曲线平衡。
两端铰支细长杆的临界压力由欧拉公式计算 ,其中I 为横截面对z 轴的惯性矩。
2、实测时:实际压杆难免有初弯曲,材料不均匀和压力偏心等缺陷,由于这些缺陷,在P 远小于cr P 时,压杆已经出现弯曲。
开始,δ很不明显,且增长缓慢。
随着P 逐步接近cr P ,δ将急剧增大。
只有弹性很好的细长杆才可以承受大挠度,压力才可能略微超过cr P ,实测时,在压杆两侧各贴一应变片,测定P-ε曲线,当施加压力增量很小而变形突增时即可得出临界压力。
三、实验结果: 1、理论计算参数记录:b=15.30mm, h=1.80mm, l=391mm, E=210GPa 由欧拉公式计算得出临界压力的理论值为:100.81N 2、实验数据记录:力-应变曲线图四、实验结果分析:数据处理得到以下“力-应变曲线图”。
通过曲线可以发现临界压应力为81N左右。
其结果小于根据公式计算得出的理论值。
分析实测值小于理论值的原因有:1、该试件已被使用多次,由于疲劳效应,更容易产生变形。
2、两端V形支座的底线不在压杆的同一纵向对称平面内,则有一扭矩产生,会使得压杆更容易失稳,故实测临界压力降低。
3、有可能是V形支座的底线不在压杆的同一纵向对称平面内,也有可能是材料的不均匀程度较大,压力偏心现象严重,导致临界压力实测值远低于理论值。
简明材料力学作业-压杆稳定

未来发展趋势
跨学科应用
01
压杆稳定分析将与计算机科学、人工智能等跨学科领域结合,
实现更加精准和高效的分析。
数值模拟与实验验证
02
压杆稳定分析将更多地采用数值模拟方法,并结合实验验证,
以提高分析的可靠性和精度。
智能化与自动化
03
压杆稳定分析将借助智能化和自动化技术,实现快速、自动的
分析和优化设计。
Part
实验结果分析
1. 根据实验数据,绘制出压杆的 载荷-位移曲线,分析曲线的变化 趋势。
4. 根据实验结果,总结出提高压 杆稳定性的方法与措施。
2. 比较不同直径和长度的压杆的 临界载荷,分析影响压杆稳定性 的因素。
3. 通过实验结果与理论计算结果 的比较,验证理论模型的正确性。
Part
04
压杆稳定的实际应用
5. 重复实验,对不同直径 和长度的压杆进行测试, 以获得更全面的数据。
2. 在压杆的末端逐个增加 砝码,观察压杆的变形情 况,记录下砝码质量和对 应的位移数据。
4. 继续增加砝码,直至压 杆发生失稳,记录下失稳 时的临界载荷。
3. 在实验过程中,注意观 察压杆的弯曲程度,判断 其是否出现失稳现象。
工程实例介绍
桥梁结构
桥梁的桥墩、桥拱等关键部位, 需要承受较大的压力和弯矩,压 杆稳定的分析对于确保桥梁安全
至关重要。
建筑结构
高层建筑的柱、梁等承重结构,需 要承受建筑物自重和风载等外部载 荷,压杆稳定的分析有助于提高建 筑的稳定性。
机械装备
机械设备中的轴、杆等部件,在受 到外力作用时,需要进行压杆稳定 分析,以确保设备的正常运行。
临界载荷分析
临界载荷分析是研究压杆在达到临界 状态时所承受的载荷,即屈曲载荷。
压杆稳定 实验报告

压杆稳定实验报告实验目的本实验的目的是研究压杆稳定性,了解不同因素对压杆稳定性的影响,并通过实验结果验证压杆稳定的理论原理。
实验设备和材料•一根长而细的杆子•一块平整的地面•一个测量尺•一个水平仪实验步骤1. 实验前准备首先,将地面清理干净,确保表面平整。
然后,将杆子竖直插入地面,确保杆子能够自由旋转。
2. 测量杆子的长度和质量使用测量尺准确测量杆子的长度,并记录下来。
然后使用天平等工具测量杆子的质量,并记录下来。
3. 确定杆子的重心将杆子固定在一个支点上,使其能够平衡。
使用水平仪测量杆子的水平位置,并标记出杆子的重心。
4. 施加压力在杆子的一端施加一个向下的压力,使杆子开始倾斜。
记录下施加的压力大小。
5. 观察杆子的稳定性观察杆子的倾斜角度,以及是否能够保持稳定。
如果杆子能够保持稳定,记录下杆子的最大倾斜角度。
6. 改变实验条件重复步骤4和步骤5,但是每次都改变一个实验条件。
例如,可以改变杆子的长度、质量、地面的摩擦力等。
实验结果与分析实验结果根据实验步骤所得数据,可以得出不同实验条件下杆子的倾斜角度与稳定性的关系。
条件倾斜角度稳定性杆子长度增加角度变小更稳定杆子质量增加角度变小更稳定地面摩擦力增大角度变小更稳定结果分析从实验结果可以看出,杆子的长度、质量以及地面的摩擦力都会影响杆子的稳定性。
当杆子的长度增加、质量增加或地面的摩擦力增大时,杆子的倾斜角度减小,稳定性增加。
这是因为杆子的稳定性取决于重心的位置。
当杆子倾斜时,重心会发生变化。
如果重心位置在支点上方,则杆子会保持稳定;如果重心位置在支点下方,则杆子会失去稳定性。
通过增加杆子的长度或质量,或者增加地面的摩擦力,可以将重心位置向支点上方移动,从而增加杆子的稳定性。
结论通过本实验,我们验证了压杆稳定的理论原理,并得出以下结论: 1. 增加杆子的长度、质量或地面的摩擦力可以提高杆子的稳定性。
2. 杆子的稳定性与重心位置密切相关,重心位置在支点上方时杆子更加稳定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
压杆稳定小结
1、 压杆稳定的概念
稳定平衡是指干扰撤去后可恢复的原有平衡;反之则为不稳定平衡。
压杆稳定性是指压杆保持或恢复原有平衡状态的能力。
压杆的临界压力是指压杆由稳定平衡转变为不稳定平衡时所受轴向压力的界限值,用cr F 来表示。
2、 细长中心受压直杆的临界力
在线弹性和小变形条件下,根据压杆的挠曲线近似微分方程,结合压杆的边界条件,可推导得到使压杆处于微弯状态平衡的最小压力值,即压杆的临界压力欧拉公式可写成统一的形式:
2
2
)
(l EI
F cr
μπ=
式中μ为长度因数。
几种常见细长压杆的临界力可见,杆端约束越强,杆的长度因数越小。
l μ为相当长度,可理解为压杆的挠曲线两个拐点之间的直线距离。
(d)
(d)表13-1
(d)
表13-1
3、 压杆的临界应力总图
(1) 压杆的临界应力
压杆在临界力作用下,其横截面上的平均应力称为压杆的临界应力, cr
cr F A
σ=
(2) 欧拉公式的适用范围
线弹性范围,()22cr cr p 22
F EI E
A l A ππσσλμ===≤ 即 p λλ≥
= 时,欧拉公式才能适用。
通常称p λλ≥的压杆为大柔度压杆或细长压杆。
(3) 压杆的柔度(或长细比)
i l μλ=
是一无量纲的量。
一般情况下,由于杆端约束(μ)或惯性半径(i )的不同,压杆在不同的纵向平面内具有不同的柔度值,压杆失稳首先发生在柔度最大的纵向平面内。
(4) 临界应力总图
压杆的临界应力随柔度λ变化的λσ-cr 图称为临界应力总图。
大柔度杆p λλ≥,临界应力低于比例极限,可按欧拉公式计算,2
2
λπσE
cr
= ;
中柔度杆p s λλλ≤≤,临界应力超过比例极限,可按经验公式计算,如直线公式: λσb a cr -=,其中a 、b 为与材料有关的常数。
或钢结构设计中采用的抛物线公式,以及折减弹性模量理论进行计算;
小柔度杆s λλ≤(或b λ),临界应力达极限应力:塑性材料s cr σσ=,脆性材料
cr b σσ=,属于强度问题。
其中,p p E
σπλ2=,s s a b
σλ-=为材料常数,仅与压杆的材料有关。
4、 压杆的稳定计算 (1) 压杆的稳定条件
采用稳定安全因数法,压杆的稳定条件为: []st st n n ≥ 或 []st st
cr
F n F F =≤
][ 或 []st st cr n σσσ=≤][ 式中,[]st n 为规定的稳定安全因素。
st n 为工作安全因数,由下式确定:
图13-12
σ
σcr
cr st F F n ==
其中[]st F 为稳定许用压力,[]st σ为稳定许用应力。
采用稳定因数法,则压杆的稳定条件为:
[][]st σσϕσ≤=
式中,ϕ为稳定因数,[]σ为强度许用应力。
在我国的钢结构设计规范和木结构设计规范中,给出了常用材料不同截面类型及不同柔度下的稳定因数值。
(2) 压杆稳定计算的步骤:
① 计算压杆的最大柔度;
② 判断压杆类型,计算临界应力(临界力);
③ 根据稳定条件进行稳定计算。
主要进行稳定校核和许可载荷的计算。
5、 提高压杆稳定性的措施
(1) 选择合理的截面形状 (2) 减小压杆支承间的长度 (3) 改变压杆杆端的约束条件 (4) 合理选择材料。
