导线三角高程计算表(表内自带计算公式)
精密三角高程计算表
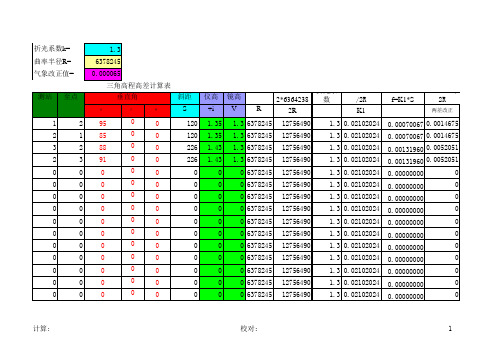
折光系数k=曲率半径R=气象改正值=三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表
三角高程高差计算表。
导线测量常用计算公式

导线测量常用计算公式导线测量是土木工程或电气工程中的一项重要工作,主要用于确定建筑物的位置、土地边界以及计算地形的变化等。
在导线测量中,有很多常用的计算公式可以帮助工程师或测量师进行精确的测量和计算。
以下是一些常用的导线测量计算公式:1.距离计算公式:-垂直平距(垂距):D=SQRT((ΔN)^2+(ΔE)^2)-水平平距:H=SQRT((ΔN)^2+(ΔE)^2+(ΔH)^2)-斜距:L=SQRT((ΔN)^2+(ΔE)^2+(ΔH)^2)- 仰角:A = arctan(ΔH / H)-前视高差:h1=H1-H0-反视高差:h2=H0-H22.坐标计算公式:- 相对平差量:ΔX = (ΔN * cosα) + (ΔE * sinα)- 相对平差量:ΔY = (ΔN * sinα) - (ΔE * cosα)-新坐标X=X0+∑(ΔX)-新坐标Y=Y0+∑(ΔY)3.角度计算公式:- 方位角:I = arctan((ΔE2 - ΔE1) / (ΔN2 - ΔN1))-转角:θ=I2-I1-内角和:∑θ=∑(Ii)-外角和:∑θ=n*180°-∑(Ii)4.高程计算公式:-平均高程:H=(H0+H1+H2)/3-高程改正:ΔHi=Hi-H-净高差:Nh=h1+ΔH5.线性状况计算公式:-输沙率:Q=W/(T*B)其中,Q为输沙率,W为沙子的质量,T为时间,B为河道截面积。
6.面积计算公式:-梯形法计算面积:A={0.5*(a+b)*h}- 辛普森法计算面积:A = {h / 3 * (y0 + 4y1 + 2y2 + 4y3 + ... + yn)}7.建筑斜率计算公式:-百分比斜率:P=(ΔH/L)*100- 度数斜率:s = tan^-1(ΔH / L)这些计算公式是导线测量中常用的工具,可以帮助工程师或测量师在实际工作中准确地计算测量结果。
需要根据具体的测量需求和情况选择合适的公式进行计算,并注意测量文档中的单位和精度要求,以确保测量结果的准确性。
三角高程测量的计算公式

三角高程测量的计算公式三角高程测量是地理测量中常用的一种方法,用于测量地面上的点的高程。
本文将介绍三角高程测量的计算公式,并解释其原理和应用。
三角高程测量是基于三角法原理的一种测量方法。
它利用三角形的一些特性和测量数据,通过计算可以得到被测点的高程。
三角高程测量适用于各种地形条件,无论是平原、山地还是高原,都可以通过三角高程测量来确定各个点的高程。
三角高程测量的计算公式如下:h = H + d * tan(a)其中,h表示被测点的高程,H表示参考点的高程,d表示两个测点之间的水平距离,a表示两个测点之间的夹角。
根据这个公式,我们可以通过测量参考点和被测点之间的距离和夹角,再加上参考点的高程,就可以计算出被测点的高程。
这个公式的原理是基于三角形的相似性原理,即两个三角形的对应边的比例相等。
在实际测量中,我们首先需要选择一个参考点,可以是已知高程的点或者固定测量设备的位置。
然后,利用测量仪器测量参考点和被测点之间的水平距离和夹角。
最后,根据测量数据和计算公式,我们可以计算出被测点的高程。
三角高程测量在地理测量中具有广泛的应用。
它可以用于绘制地形图、制作地图、建筑工程设计等。
通过三角高程测量,我们可以快速准确地确定地面上各个点的高程,为地理信息系统的建设和规划提供重要的数据支持。
在实际应用中,三角高程测量需要考虑一些误差因素。
例如,测量仪器的精度、天气条件、地形复杂度等都会对测量结果产生影响。
因此,在测量过程中要注意选择合适的测量仪器、控制测量误差,并进行合理的数据处理和分析。
三角高程测量是一种常用的地理测量方法,通过测量参考点和被测点之间的距离和夹角,再结合计算公式,可以准确地确定被测点的高程。
它在地理信息系统、地形图制作、建筑工程设计等领域具有重要的应用价值。
在实际应用中,我们需要注意测量误差的控制和数据处理,以提高测量结果的精度和可靠性。
通过三角高程测量,我们可以更好地了解地球表面的地形特征,为人类的生活和发展提供有益的信息。
三角高程计算样表

置镜点号前视点号度分秒度分秒度CPII46-2CPII46-18949 3.501056.50.182361112701059.301059.30.18313889仪器高棱镜高2701058.901058.90.183027781.3541.5548949 1.901058.10.18280556平均值8949 2.301057.70.182694442701056.301056.30.182305562701056.101056.10.182250008949 2.301057.70.18269444平均值8949 1.201058.80.183000002701057.301057.30.182583332701057.101057.10.182527788949 1.401058.60.18294444平均值8949 1.301058.70.182972222701058.701058.70.182972222701058.701058.70.182972228949 2.701057.30.18258333平均值平均值置镜点号前视点号度分秒度分秒度CPII46-1CPII46-290929.50929.5-0.158194442695033.30926.7-0.15741667仪器高棱镜高2695032.50927.5-0.157638891.5331.47190928.50931.5-0.15875000平均值90929.40929.4-0.158166672695032.80927.2-0.157555562695031.40928.6-0.1579444490930.60930.6-0.15850000平均值90930.80930.8-0.158555562695032.50927.5-0.157638892695032.30927.7-0.1576944490929.20930.8-0.15855556平均值90929.90929.9-0.158305562695032.10927.9-0.157750002695031.30928.7-0.1579722290928.80928.8-0.15800000平均值平均值竖直角竖直角置镜点号前视点号度分秒度分秒度CPII46-2CPII45-29008.3008.3-0.002305562695952.2007.8-0.00216667仪器高棱镜高2695951.1008.9-0.002472221.3541.457900 6.500 6.5-0.00180556平均值900 6.900 6.9-0.001916672695954.100 5.9-0.001638892695954.200 5.8-0.001611119008.7008.7-0.00241667平均值9009.4009.4-0.002611112695952.6007.4-0.002055562695952.2007.8-0.002166679007.1007.1-0.00197222平均值9007.8007.8-0.002166672695951.8008.2-0.002277782695952.9007.1-0.001972229008.1008.1-0.00225000平均值平均值置镜点号前视点号度分秒度分秒度CPII45-2CPII46-2895731.20228.80.04133333270230.20230.20.04172222仪器高棱镜高270230.50230.50.041805561.3511.47189572902310.04194444平均值895729.20230.80.04188889270231.70231.70.0421388927023202320.04222222895729.50230.50.04180556平均值895729.70230.30.04175000270227.10227.10.04086111270227.50227.50.04097222895732.10227.90.04108333平均值895729.10230.90.04191667270230.90230.90.04191667270230.80230.80.0418888989572702330.04250000平均值平均值竖直角竖直角置镜点号前视点号度分秒度分秒度CPII45-2CPII45-1894023.901936.10.326694442701936.601936.60.32683333仪器高棱镜高2701936.701936.70.326861111.3511.505894022.701937.30.32702778平均值894023.401936.60.326833332701939.501939.50.327638892701939019390.32750000894023.701936.30.32675000平均值894023.701936.30.326750002701935.801935.80.326611112701935.301935.30.32647222894025.501934.50.32625000平均值894024.101935.90.326638892701936.201936.20.326722222701935019350.32638889894025.301934.70.32630556平均值平均值置镜点号前视点号度分秒度分秒度CPII45-1CPII45-2901837.101837.1-0.310305562694122.601837.4-0.31038889仪器高棱镜高2694122.501837.5-0.310416671.491.399901838.501838.5-0.31069444平均值901837.901837.9-0.310527782694120.601839.4-0.310944442694121.301838.7-0.31075000901839.601839.6-0.31100000平均值901837.301837.3-0.310361112694122.601837.4-0.31038889269412301837-0.31027778901837.801837.8-0.31050000平均值901838.801838.8-0.310777782694122.601837.4-0.310388892694122.601837.4-0.31038889901837.701837.7-0.31047222平均值平均值置镜点号前视点号竖直角竖直角竖直角度分秒度分秒度CPII46-1CPII45-1895210.30749.70.13047222270750.30750.30.13063889仪器高棱镜高270750.10750.10.13058333 1.533 1.505895211.90748.10.13002778平均值895211.50748.80.13022222270748.40748.40.13011111270749.10749.10.13030556895213.60746.40.12955556平均值895212.60747.40.12983333270749.50749.50.13041667270749.40749.40.13038889895212.90747.10.12975000平均值89521107490.13027778270748.80748.80.13022222270748.50748.50.13013889895212.80747.20.12977778平均值平均值竖直角置镜点号前视点号度分秒度分秒度CPII45-1CPII46-190743.60743.6-0.128777782695217.40742.6-0.12850000仪器高棱镜高2695217.70742.3-0.128416671.49 1.52390743.50743.5-0.12875000平均值90742.50742.5-0.128472222695216.90743.1-0.128638892695216.10743.9-0.1288611190741.70741.7-0.12825000平均值90742.10742.1-0.128361112695218.10741.9-0.128305562695216.90743.1-0.1286388990740.40740.9-0.12802778平均值90742.60742.6-0.128500002695217.90742.1-0.128361112695218.40741.6-0.1282222290742.10742.1-0.12836111平均值平均值斜距高差弧度0.00318280310.087710.794492240.00319638310.087910.798702240.00319444310.087710.798100250.00319056310.087710.796897580.00319104310.087760.797048080.00318862310.087710.796296250.00318183310.087810.794191890.00318086310.087810.793891230.00318862310.087710.796296250.00318498310.087760.795168900.00319395310.087810.797950240.00318668310.087710.795694910.00318571310.087710.795394240.00319298310.087810.797649580.00318983310.087760.796672240.00319347310.087810.797799910.00319347310.087910.797800230.00319347310.087610.797799260.00318668310.087710.795694910.00319177310.087760.79727358310.087760000.79654070斜距弧度-0.00276101310.08530-0.78660266-0.00274744310.08540-0.78239360-0.00275132310.08530-0.78359600-0.00277071310.08550-0.78960986-0.00275762310.08538-0.78555053-0.00276053310.08530-0.78645233-0.00274986310.08600-0.78314689-0.00275665310.08540-0.78524993-0.00276635310.08560-0.78825714-0.00275835310.08558-0.78577657-0.00276732310.08550-0.78855753-0.00275132310.08520-0.78359573-0.00275229310.08530-0.78389666-0.00276732310.08550-0.78855753-0.00275956310.08538-0.78615186-0.00276295310.08530-0.78720399-0.00275326310.08550-0.78419787-0.00275714310.08560-0.78540081-0.00275762310.08540-0.78555060-0.00275774310.08545-0.78558832310.08544375-0.78576682斜距弧度-0.00004024287.19203-0.10808345-0.00003782287.19213-0.10738728-0.00004315287.19193-0.10891886-0.00003151287.19173-0.10557723-0.00003818287.19196-0.10749170-0.00003345287.19183-0.10613417-0.00002860287.19193-0.10474182-0.00002812287.19183-0.10460259-0.00004218287.19193-0.10864039-0.00003309287.19188-0.10602974-0.00004557287.19193-0.10961503-0.00003588287.19193-0.10683034-0.00003782287.19193-0.10738728-0.00003442287.19193-0.10641264-0.00003842287.19193-0.10756132-0.00003782287.19163-0.10738728-0.00003975287.19153-0.10794422-0.00003442287.19143-0.10641264-0.00003927287.19163-0.10780498-0.00003782287.19156-0.10738728287.19183000-0.10711751斜距弧度0.00072140287.190430.093652900.00072819287.190430.095602170.00072964287.190730.096020100.00073207287.190630.096716200.00072783287.190560.095497840.00073110287.190630.096437730.00073546287.190230.097690520.00073692287.190230.098108220.00072964287.190430.096019870.00073328287.190380.097064090.00072867287.190530.095741480.00071316287.190730.091286150.00071510287.190530.091842930.00071704287.190430.092399790.00071849287.190560.092817590.00073158287.190600.096576940.00073158287.190600.096576940.00073110287.190400.096437550.00074176287.190300.099500620.00073401287.190480.09727301287.190491250.09566313斜距弧度0.00570189236.93720 1.201389110.00570432236.93710 1.201962870.00570480236.93690 1.202076590.00570771236.93680 1.202765230.00570468236.93700 1.202048450.00570432236.93700 1.201962300.00571838236.93720 1.205294630.00571595236.93680 1.204717990.00570286236.93700 1.201617690.00571038236.93700 1.203398150.00570286236.93690 1.201617120.00570044236.93710 1.201043930.00569802236.93700 1.200469010.00569414236.93690 1.199549490.00569886236.93698 1.200669890.00570092236.93710 1.201158790.00570238236.93710 1.201503400.00569656236.93700 1.200124410.00569511236.93680 1.199778650.00569874236.93700 1.20064131236.93699375 1.20168945斜距弧度-0.00541585236.93550-1.18779606-0.00541731236.93560-1.18814121-0.00541779236.93570-1.18825661-0.00542264236.93590-1.18940637-0.00541840236.93568-1.18840006-0.00541973236.93560-1.18871555-0.00542700236.93560-1.19043857-0.00542361236.93540-1.18963341-0.00542797236.93540-1.19066722-0.00542458236.93550-1.18986369-0.00541682236.93580-1.18802741-0.00541731236.93550-1.18814067-0.00541537236.93550-1.18768120-0.00541925236.93570-1.18860122-0.00541719236.93563-1.18811262-0.00542410236.93540-1.18974828-0.00541731236.93540-1.18814013-0.00541731236.93550-1.18814067-0.00541876236.93550-1.18848527-0.00541937236.93545-1.18862859236.93556250-1.18875124斜距弧度0.00227717124.645700.313058500.00228008124.645700.313421080.00227911124.645900.313300680.00226941124.645800.312091850.00227644124.645780.312968020.00227281124.645800.312514860.00227087124.645800.312273140.00227426124.645700.312695920.00226117124.645800.311064540.00226978124.645780.312137110.00226602124.645800.311668840.00227620124.645500.312937180.00227572124.645800.312877440.00226456124.645800.311487550.00227062124.645730.312242750.00227378124.645600.312635260.00227281124.645700.312514630.00227135124.645600.312333110.00226505124.645900.311548210.00227075124.645700.31225780124.645743750.31240142斜距弧度-0.00224760124.64470-0.31193143-0.00224275124.64490-0.31132758-0.00224129124.64470-0.31114585-0.00224711124.64520-0.31187211-0.00224469124.64488-0.31156924-0.00224226124.64480-0.31126693-0.00224517124.64480-0.31162950-0.00224905124.64470-0.31211272-0.00223838124.64480-0.31078349-0.00224372124.64478-0.31144816-0.00224032124.64480-0.31102521-0.00223935124.64470-0.31090413-0.00224517124.64470-0.31162928-0.00223451124.64480-0.31030006-0.00223984124.64475-0.31096467-0.00224275124.64490-0.31132758-0.00224032124.64490-0.31102543-0.00223790124.64480-0.31072306-0.00224032124.64460-0.31102477-0.00224032124.64480-0.31102521124.64480000-0.31125182。
三角高程测量计算表格

高差 (m)
1
A
B
50.00
30.00
20.00
2
A
C
60.00
20.00
18.00
3
A
D
40.00
15.00
15.00
4
B
A
50.00
-30.00
-20.00
5
B
C
60.00
-20.00
-18.00
6
B
D
40.00
-15.00
-15.00
在上述表格中,每一行代表一次测量操作,其中点号表示测量的顺序,测站点表示测量时站立的位置,目标点表示要测量的目标点。水平距离表示测站点和目标点之间的水平距离,垂直距离表示测站点和目标点之间的垂直距离,高差表示测站点和目标点之间的高差。
根据需要,您可以在表格中添加其他列,例如角度、仪器型号、观测员等,以便更好地记录和整理测量数据。
三角高程测量的计算公式

三角高程测量的计算公式三角高程测量是一种常用的地理测量方法,随着测量技术的发展和应用领域的拓宽,其计算公式也越来越重要。
本文将从计算公式的基本原理、计算过程和误差控制三方面进行阐述,以期让读者更深入地了解三角高程测量的计算方法。
一、基本原理三角高程测量,顾名思义,是以三角形理论为基础进行测量的一种方法。
通常情况下,我们选取三个站点进行测量,这三个站点构成一个三角形,我们可以测量得到三个角的角度和三边的长度。
在此基础上,我们可以运用三角函数,求得这个三角形的高程。
具体来说,我们可以通过以下公式进行计算:H = L(a sin B + b sin A)/ sin C其中,H为目标点的高程,L为相邻两个点的距离,A 和B为相邻两点到目标点的水平角,C为相邻两点之间的斜线距离。
在实际操作中,我们一般采用三边测量和两边一角测量两种方法来进行三角高程测量。
无论采用哪种方法,都需要进行角度和距离的测量,然后通过计算公式求得目标点的高程。
二、计算过程在进行三角高程测量之前,我们需要对测量区域进行勘验,确定三个测量点的位置,并在每个站点上架设三角测量仪器。
在具体的测量过程中,我们首先测量站点之间的距离和角度。
这一步骤可以采用三边测量或两边一角测量方式。
如果采用三边测量方式,则需要同时测量两个角度。
如果采用两边一角测量方式,则需要测量三个角度。
在完成角度和距离的测量之后,我们可以将数据输入到计算公式中,求解目标点的高程。
需要注意的是,三角高程测量的计算精度受到多种因素的影响,例如测量仪器的精度、环境因素以及人为操作错误等。
因此,在进行计算之前,我们需要对数据进行校核,以确保计算结果的准确性。
三、误差控制三角高程测量存在着测量误差,这不可避免。
为了尽可能地减小误差对测量结果的干扰,我们可以采取一些措施。
具体来说,我们可以从以下几方面入手:(1)选择合适的测量仪器。
测量仪器的精度和稳定性对测量结果的影响很大。
因此,我们需要选用精度高、稳定性好的测量仪器来进行测量。
三角高程测量高差计算表
竖直角α -2°44′33.17″ 2°45′41.33″ -4°06′18.5″ 4°08′51.7″ -2°15′50.17″ 2°16′03″ -2°09′53.83″ 2°09′56.17″ 3°57′24″ -3°57′53.33″ -6°25′56.17″ 6°31′38.17″
测站仪器高i 1.4670
11.497 12.27311
测站点
GP11
GP12
目标点
GP12
GP11
水平距离D 202.5528 202.55148
竖直角α
0°50′54″ -0°46′16.67″
测站仪器高i 1.4373
1.4303
目标棱镜高v 1.347
1.797
球气差改正f 0.00277
0.00277
单向高差h 3.09233 -3.09078
高差较差△h
-2.30889
-0.35639
0.04924
2.57790
1.81133
1.10113
限差值△h限
20.977
平均高 -
差
h
-25.49189
注:△h限=±40√D
记录:
13.775 14.11044
14.726 9.18379 计算:
15.172 -16.47160
13.077 10.12723 复核:
0.00139
0.00139
0.00084
0.00084
0.00395
0.00395
0.00207
0.00207
0.00046
0.00046
单向高差h -0.44887 0.45135 12.91050 -12.90432 -10.81016 10.81087 -6.86823 6.85952 -6.17095 6.16955 12.27352 -12.27271
三角高程测量记录及计算表
三角高程测量记录及计算表
三角高程测量记录及计算表是用于记录三角高程测量中的观测数据和计算结果的表格。
它通常包括以下内容:
1. 观测点的编号:记录测量点的编号,用于标识不同测点。
2. 观测角度:记录三角形的各个角度的观测值,包括水平角和垂直角。
3. 距离测量:记录测量点之间的距离,通常使用测距仪或测量杆进行测量。
4. 视线高差:记录测量点之间的视线高差,即测量点的垂直距离。
5. 平差高差:通过对观测角度和距离进行平差计算得到的高程差。
6. 高程值:通过测量点的已知高程和高差计算得到的绝对高程值。
7. 备注:记录测量过程中的特殊情况或其他需要备注的信息。
根据测量的具体要求,还可以在表格中添加其他需要记录的信息。
测量完成后,根据观测数据和计算结果,可以进行表格中的数据处理和检查,对测量结果进行校核和审查。
精密三角高程计算表
#DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0!
计算:李九玲
校对: 姜荣柱
1/5
三角高程高差计算表 测站 至点 仪高(i) 镜高(v) 斜距 垂直角 高差 #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! 计算:李九玲 校对: 姜荣柱 0.000 #DIV/0! 2/5 0.000 #DIV/0! 0.000 #DIV/0! 0.000 #DIV/0 0.000 #DIV/0! 0.000 #DIV/0! 0.000 #DIV/0! 0.000 #DIV/0! 高差互差 允许差 高差平均值
计算:李九玲
校对: 姜荣柱
3/5
三角高程高差计算表 测站 至点 仪高(i) 镜高(v) 斜距 垂直角 高差 #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! 计算:李九玲 校对: 姜荣柱 0.000 #DIV/0! 4/5 0.000 #DIV/0! 0.000 #DIV/0! 0.000 #DIV/0! 0.000 #DIV/0! 0.000 #DIV/0! 0.000 #DIV/0! 0.000 #DIV/0! 0.000 #DIV/0! 0.000 #DIV/0! 高差互差 允许差 高差平均值
三角高程计算公式及其含义
三角高程计算公式及其含义在地理测量和地理信息系统中,三角高程计算是一种常用的方法,用于确定地表上各点的高程。
三角高程计算公式是一种基于三角测量原理的数学公式,通过测量三角形的边长和角度,来计算出三角形的高程。
这种方法可以用来确定地表上任意点的高程,对于地形测量和地图制图非常有用。
三角高程计算公式的一般形式如下:h = (a sin(B)) / sin(A)。
其中,h表示目标点的高程,a表示已知边长,B表示已知角度,A表示未知角度。
这个公式基于正弦定理,通过已知的边长和角度来计算出目标点的高程。
这种方法可以用来测量地表上任意点的高程,无论是平原还是山地,都可以通过三角高程计算公式来确定其高程。
三角高程计算公式的含义非常重要,它可以帮助测量员确定地表上各点的高程,从而绘制出精确的地形图。
地形图是地理信息系统中非常重要的一部分,它可以用来确定地表的起伏和坡度,对于农业、建筑和城市规划等领域都非常有用。
通过三角高程计算公式,可以确定地表上各点的高程,从而绘制出准确的地形图,为各种应用提供重要的参考数据。
三角高程计算公式的应用非常广泛,不仅可以用于地形测量和地图制图,还可以用于工程测量和建筑规划。
在工程测量中,三角高程计算可以帮助工程师确定工程场地的高程,从而进行设计和施工。
在建筑规划中,三角高程计算可以帮助规划师确定建筑场地的高程,从而进行布局和设计。
通过三角高程计算公式,可以为各种工程和建筑提供准确的高程数据,为实际施工和规划提供重要的参考。
总之,三角高程计算公式是地理测量和地理信息系统中非常重要的一种方法,它可以帮助确定地表上各点的高程,为地形测量、地图制图、工程测量和建筑规划提供重要的参考数据。
通过三角高程计算公式,可以为各种应用提供准确的高程数据,为实际工作提供重要的支持。
因此,掌握和应用三角高程计算公式是地理测量和地理信息系统工作者的基本技能,也是各种应用领域的重要工具。
