高斯定理与环路定理在万有引力场中的推广
类比法在万有引力场教学中的应用

类比法在万有引力场教学中的应用孙红霞【期刊名称】《网友世界·云教育》【年(卷),期】2014(000)013【摘要】用类比的方法将静电场的高斯定理和环路定理推广到万有引力场的“高斯定理”和“环路定理”,定义了万有引力场强和万有引力势。
通过引力场的“高斯定理”得出了两种特殊对称性引力场分布及物体所受引力规律,简化了积分运算;通过引力场的“环路定理”得出地球周围物体的万有引力势能。
%By way of analogy,the Gauss theorem of electrostatic field and loop theorem to the Gauss theorem of gravitational field "and"loop theorem ",defined the gravitational field and the gravitational potential.The gravitational field of the"Gauss theorem"of the two kinds of special symmetric gravitationalfield and the force law of gravity, simplifies the integral operation;by the gravitational field of the earth"loop theorem"objects around the gravitational potential energy.【总页数】2页(P242-243)【作者】孙红霞【作者单位】铁岭师范高等专科学校【正文语种】中文【相关文献】1.以类比为刀刃,行庖丁解牛之术——类比法在高中物理教学中的应用研究 [J], 何志锋2.范例法在《医学物理学》教学中的应用(二)--引力场与静电场 [J], 吴静;张鹏程3.类比法与万有引力场的描述 [J], 王敏4.类比法研究万有引力场的高斯定理 [J], 周国全; 黄华玲5.关联法和类比法在生物化学教学中的应用研究 [J], 易杨因版权原因,仅展示原文概要,查看原文内容请购买。
大学物理 高斯定理环路定理
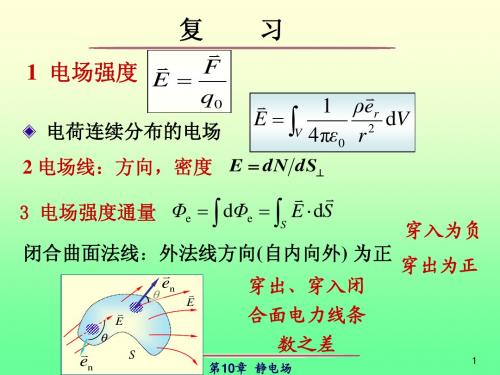
1 E dS ε0
第10章 静电场
n
Φe
S
qi
in
i 1
6
轴对称性电场
例10.8 P17 “无限长” 均匀带电直线,电荷线密度为 + 求 电场强度分布。
解 电场分布具有轴对称性
第10章 静电场
7
解
电场分布具有轴对称性 ,以高为l 的同轴圆柱面为高斯面,电通量 e E dS
ADC
B
D
C
E
q0 ( E dl
ABC
E dl ) 0
CDA
A
结论:沿闭合路径一周, 静电场是保守场! 电场力作功为零.
E dl 0
l
在静电场中电场强度的 环流为零。
第10章 静电场
20
练习 试用静电场的环路定理证明,电场线 为一系列不均匀分布 的平行直线的静电场 不存在.
第10章 静电场
q0
q
rA
A
18
任意带电体的电场(点电荷的组合)
E
i
Ei
A q0 E dl
l
q
0 i
l
Ei dl
结论:静电场力做功,与路径无关.
第10章 静电场
19
二
q0
静电场的环路定理
E dl q0
ABC
E dl
dA qq 0 4 πε0r
2
电势能
B
dr
dl
rB
r
er
E
高斯定理在万有引力场中的应用

与静电场相似 , 任何物体的周围空间都存在引力场 , 万有引力是通过引力场来传递的 。在静电场中 , 我
们用电场强度来描述电场中某点性质 , 同样 , 在引力场中 , 我们可以把场中每点的 F / m 定义为该点的引力
※
场强度 , 用Eg 表示 , 即
※
Eg
=
F m
(1)
※
其中 m 为试探质点质量 , F 为试探质点在某点受到的引力 , Eg 即为该点的引力场强度 , 简称引力场强 。
16
(湖南人文科技学院 物理与信息工程系 , 湖南 娄底 417000)
摘 要 :通过类比万有引力场和静电场 , 给出了引力场强度的概念 , 在此基础上 , 将静电 场中的高斯 定理推广 到万有引 力场中 , 并利用它分析了两个具体问题 , 说明了利用高斯定理可以简化具有对称性的引力场的相关 计算 。
场中任一闭合面的引力场通量等于该曲面内所有物体的质量和乘以 4πG 的负值 , 即 :
可以看出 ,(6)式同静电场的高斯定理
∑ ※
※
Eg·d S =-4πG mi
S
i =1
(6)
∑ S
※
E·dቤተ መጻሕፍቲ ባይዱ
※
S
=
1 ε0
qi
i
(7)
非常相似 ,(6)式中的常数 4πG 相当于(7)式中的常数 ε10 ,(6)式中的 mi 相当于(7)式中的 qi 。 下面举例说明 :当质量分布具有某些特殊的对称性 , 从而使相应的引力场分布也具有一定的对称性
过 P 点作一半径为 r , 高为 l 的同轴闭合圆柱面 , 则通过此闭合面的引力场通量
= 侧 + 上底 + 下底 =-Eg2πrl +0 +0 =-Eg2πrl 上式不论 P 点在柱面外(r > R)或在柱面内(r < R)都适用 。
高斯定理和环路定理

高斯定理和环路定理高斯定理和环路定理是电磁学中两个重要的基本定律。
它们描述了电场和磁场的分布和变化规律,是理解电磁现象的基础。
本文将对高斯定理和环路定理进行详细介绍。
一、高斯定理高斯定理又称为高斯电场定理,它是描述电场分布的基本原理之一。
高斯定理表明,电场通过一个闭合曲面的通量等于该曲面内部电荷的代数和与真空介电常数的乘积。
具体来说,如果一个闭合曲面内部有正电荷和负电荷,那么通过这个曲面的电场通量将等于正电荷和负电荷的代数和除以真空介电常数。
高斯定理的数学表达式为:∮E·dA = Q/ε0其中,∮E·dA表示曲面上的电场通量,Q表示曲面内部的电荷总量,ε0为真空介电常数。
高斯定理的应用非常广泛。
例如,在计算电场分布时,可以通过选择适当的高斯曲面来简化计算。
通过高斯定理,可以快速得到电场在各个位置的大小和方向。
高斯定理也被用于推导其他电场分布的公式,如电偶极子和球壳电场的公式。
二、环路定理环路定理又称为安培环路定理,它是描述磁场分布的基本原理之一。
环路定理表明,磁场沿着一个闭合回路的线积分等于该回路内部电流的代数和乘以真空磁导率。
具体来说,如果一个闭合回路内部有电流通过,那么沿着这个回路的磁场线积分将等于电流的代数和除以真空磁导率。
环路定理的数学表达式为:∮B·dl = μ0I其中,∮B·dl表示回路上的磁场线积分,μ0为真空磁导率,I表示回路内部的电流。
环路定理的应用也非常广泛。
例如,在计算磁场分布时,可以通过选择适当的环路来简化计算。
通过环路定理,可以快速得到磁场在各个位置的大小和方向。
环路定理也被用于推导其他磁场分布的公式,如长直导线和环形线圈的磁场公式。
三、高斯定理与环路定理的关系高斯定理和环路定理是电磁学中两个基本定理,它们描述了电场和磁场的分布与变化规律。
虽然它们描述的是不同的物理量,但在某些情况下,它们是相互关联的。
例如,在静电场中,高斯定理可以推导出库仑定律,即电荷间的相互作用力与它们之间的距离成反比。
《高斯定理环路定理》课件

环路定理的应用
总结词:广泛适用
VS
详细描述:环路定理在电磁学、电动 力学、麦克斯韦方程组等多个领域都 有广泛应用。它可以用来计算磁场穿 过任意封闭曲线的线积分,从而解决 一系列实际问题,如电磁感应、磁场 分布、电磁波传播等。
03 高斯定理与环路定理的比较
定理表述的比较
总结词
高斯定理和环路定理的表述形式各有特点,高斯定理强调空间区域内的电荷分布 ,而环路定理则关注磁场的变化。
应用。
02 环路定理
环路定理的表述
总结词:简洁明了
详细描述:环路定理表述为“磁场穿过一个封闭曲线的线积分等于零”,即磁场在封闭曲线上的线积分与路径无关,只与起 点和终点的磁通量有关。
环路定理的证明
总结词:严谨推导
详细描述:通过引入矢量场和微分同胚等概念,利用矢量场的散度和旋度的性质,经过严谨的数学推 导,证明了环路定理的正确性。
复杂模型应用
在此添加您的文本16字
分析一个通电螺线管的磁场分布,通过环路定理确定磁 场方向和大小,展示环路定理在实际问题中的应用。
在此添加您的文本16字
对比验证
在此添加您的文本16字
通过对比环路定理和传统积分方法的计算结果,验证环 路定理的正确性和高效性,强调环路定理在电磁学中的重 要地位。
05ቤተ መጻሕፍቲ ባይዱ总结与展望
环路定理是电磁学中的基本定理之一 ,它表述了磁场沿闭合路径的线积分 等于穿过该闭合路径所围成的面积的 磁通量。环路定理反映了磁场沿闭合 路径的线积分与磁通量之间的关系, 是计算磁场分布、磁通量、磁感应线 和磁力等方面的重要工具。
比较与联系
高斯定理和环路定理都是电磁学中的 基本定理,它们之间有着密切的联系 。通过高斯定理可以推导出环路定理 ,反之亦然。它们在描述电场和磁场 分布方面具有不同的侧重点,但都是 描述电磁场性质和行为的重要工具。
《高斯定理与环路定理在万有引力场中的推广》

《高斯定理与环路定理在万有引力场中的推广》读了这篇文章, 我觉得这俩个定理的应用于推广最大的特点是应用类比的方法。
通过在万有引力场中定义引力场强矢量和万有引力势,将静电场中的高斯定理和静电环路定理推广到了经典万有引力场中,然后举例说明了这两个定理分别在某些质量对称分布的问题和天文上的应用。
用类比的方法从静电场的高斯定理和环路定理导出了万有引力场中的“高斯定理”和“环路定理”并定义了引力场强度矢量。
说实话,做出这个结论并不是很难,就是简单套用公式逐一对比并定义新的常量,但是把高斯定理和环路定理推广到另一个完全不同的力学领域的思维方式确实很难得。
我个人认为物理科学不仅仅要的是知识渊博,更为重要的是一种全新的思维方式,一种不同于传统敢于创新的理念。
比如说这个推广,我们学生往往把高斯和环路定理局限在电学知识领域,哪里会认为这两个定理还可以继续向广度方向进一步推广,然而这篇文章的作者却独具慧眼发现并很好地总结了这个规律。
首先,文章讲了高斯定理的推广。
由库伦定律和万有引力定律得出质量对应于电荷量,并进一步深入,和电场强度类似,在万有引力场中定义了一个引力场强度矢量,也就是引力常数g,就这样依葫芦画瓢的出一个引力场“高斯定理”。
这种“高斯定理”在某些具有对称性的问题中可以大大简化原本复杂的积分运算过程。
其次,文章讲到环路定理的推广。
它在万有引力场中引入了引力势和引力势能。
如此根据电势能和电势公式就能相应得出引力势能和引力公式。
作者还将这个公式代入到卫星环绕问题中去进行进一步检验。
万有引力场中的高斯定理说明了穿过闭合曲面的引力场强通量只和它包围的质量有关。
万有引力场中的环路定理说明了万有引力沿闭合路径的环流为0。
静电场和万有引力场,最大的共同之处就是都是力的作用形式相似。
两个物体相互作用,形成相互作用力。
力的表达形式也极为相似。
这应该是促使作者做出将高斯定理与环路定理向万有引力场推广的一个重要表象。
我想很多人读到这篇文章,肯定会不以为意,因为高斯定理和环流定理在万有引力中的推广很好理解,如果让我们自己推导的话应该也不会有太大的问题。
《高斯定理环路定理》课件
本课件将深入浅出地讲解高斯定理和环路定理,为您揭开物理学的神秘面纱。 通过实例和推导,让您轻松理解这两大重要定理。
高斯定理
定义
应用
推导过程
高斯定理是描述电场、磁场与它 们的源之间关系的基本定理之一。
高斯面积定理可用于计算电场的 强度;高斯电场定理可用于计算 电场在任意分布情况下的总电通 量;高斯磁场定理可用于计算磁 场在任意分布情况下的总磁通量。
高斯定理与环路定理的联系
1
电场情况下的关系
高斯面积定理和环路定理可以在描述电场问题时相互转化,即可以利用高斯面积定理 来得出它们的应用环路定理,也可以利用安培环路定理来得出它们的应用高斯电场定 理。
2
磁场情况下的关系
对于静态磁场问题,磁场的旋度为0,因此环路定理不适用,但它可以通过高斯定理类 推出高斯磁场定理;当磁场有变化时,环路定理可以应用于计算磁场的涡旋,高斯定 理则无法使用。
3 可能存在的问题和研究方向
在使用高斯定理和环路定理进行研究的过程中,也可能会面临一些问题,例如精度不够、 误差较大等。为此,我们需要不断开展相关的研究,以求对问题有更好的解决。考文献1 23
Wang, S. Z., &Liang, Z. W. (2017). 高等物理学教程 第二卷 珍珠岩版. 高等教育出版社.
我们将通过详实的推导过程,让 您逐步理解高斯定理的计算原理。
环路定理
定义
环路定理是描述电流与磁场 之间关系的基本定理之一, 它也被称为安培环路定理或 法拉第电磁感应定律。
应用
我们可以利用安培环路定理 来计算磁场的强度,利用法 拉第电磁感应定律来分析发 电机的工作原理等。
推导过程
环路定理的推导过程相对简 单,通过本节内容,您将轻 松地掌握环路定理的应用。
引力场中高斯定理的应用
引力场中高斯定理的应用
王宁;孙彩霞;齐玉红
【期刊名称】《山东轻工业学院学报(自然科学版)》
【年(卷),期】2010(024)004
【摘要】本文用类比的方法将静电场中的高斯定理的形式推广到万有引力场中,从而引出万有引力场中的"高斯定理".通过万有引力场中的"高斯定理",将某些质量分布具有对称性的物体引起的引力场强的计算得到简化.
【总页数】3页(P78-80)
【作者】王宁;孙彩霞;齐玉红
【作者单位】黄河科技学院实验中心,河南,郑州,450006;黄河科技学院数理部,河南,郑州,450006;郑州大学,河南,郑州,450006
【正文语种】中文
【中图分类】O314
【相关文献】
1.高斯定理与环路定理在万有引力场中的推广 [J], 陈国云;骆成洪;辛勇;黄国庆;文小庆;赵书毅
2.高斯定理在万有引力场中的应用 [J], 唐淑红
3.引力场的高斯定理及应用 [J], 魏益焕
4.引力场中的高斯定理在计算煤矸石重量方面的应用 [J], 李颢
5.高斯定理在万有引力场中的推广及应用 [J], 谢谦;唐卫斌;刘俊
因版权原因,仅展示原文概要,查看原文内容请购买。
引力场中的高斯定理
引力场中的高斯定理引力和静电力都是有势力,相应的引力势和静电势都满足三维空间里最简单的二阶(偏微分)方程——拉普拉斯方程.用ψ代表引力势或者静电势场,它在三维空间里所满足的拉普拉斯方程采取如下的形式:(∂2/∂x2+∂2/∂y2+∂2/∂z2)ψ(x,y,z)=0.由于相应的静电力和引力等于势的微分(的负值),它的大小便与半径r成反比了,即ψ(r)∝1/r,F(r)=- dψ/dr∝1/r2由于万有引力定律与Coulomb,s law本质是一样的,因此引力场中也存在高斯定理,并且与万有引力定律等价.Ⅰ、预备知识引力场场强:引力场场强是一个向量,其大小等于1千克的质点在该处所受引力的大小,方向与该质点在该处所受引力的方向一致.引力线:如果在引力场中出一些曲线,使这些曲线上每一点的切线方向和该点的引力场强方向一致,那么所有这样可以作出的曲线叫做引力线.引力线数密度:在引力场中任一点取一小面元ΔS与该点的场强方向垂直,设穿过ΔS 的引力线有ΔN根,则比值ΔN/ΔS叫做该点的引力线数密度,它的意义是通过该点单位垂直截面的引力线根数,规定引力场场强E∝ΔN/ΔS.引力线性质:引力线其自无穷远点,止与该质点,引力线在宇宙中处处存在.一个质点的任何两条引力线不会相交,不形成闭合线.引力通量:通过一面元ΔS的引力通量为该点场强的大小E与ΔS在垂直于场强方向的投影面积ΔS′=ΔScosθ的乘积.Ⅱ、通过一个任意闭合曲面S的引力通量φ=4πG∑m,与闭合曲面外的引力质量无关.证明:(1)通过包括质点m的同心球面的引力通量都等于4πGm.以质点m所在处为中心以任意半径r作一球面.根据万有引力定律,在球面上各点场强大小一样E=G m /r2,场强的方向沿半径向外呈辐射状.在球面上任意取一面元dS,其外法线向量n也是沿着半径方向向外的,即n和E间夹角θ=0,所以通过dS的引力通量为dφ=EcosθdS=EdS= G m /r2dS,通过整个闭合球面的引力通量为φ=dS= G m /r2×4πr2=4πGm.(2)通过包围质点的任意闭合曲面S的引力通量都等于4πGm在闭合面S内以质点m所在处O为中心作一任意半径的球面S′,根据(1)通过此球面的事情感兴趣,要勤奋地工作!”。
高斯定理在万有引力场中的应用
高斯定理在万有引力场中的应用
高斯定理是物理学界以及数学界较为重要的定理之一,它可以被广泛地用于万有引力场的研究中。
首先,我们需要了解高斯定理的核心部分——高斯梯度定理:它指出了引力场的数学表示和图像的梯度的空间表示之间的联系,即:万有引力场的空间表示有一个正定的悬赏函数,和任意点的梯度之间存在明确的联系,此外,这个悬赏函数的倒数是一个完全定义的单值函数,接下来,我们就可以用这个悬赏函数来求出万有引力场的强度以及各种有关物理量。
另一方面,万有引力场对空间上某点上发生的结构变化也有着重要的影响,它可以通过高斯梯度定理来计算这种变化。
高斯梯度定理中,梯度是一个十分重要的概念,它是三维空间中某点处的万有引力场变化速率。
对此,高斯定理可以让我们通过知道梯度 at 点 P 的方向和大小来推断出空间上某个点处的引力场的强度和变化情况,也就是我们可以根据某点的梯度来计算出空间上的点的引力场的强度以及计算出不同空间上的点之间的引力场是否在变化。
至此,我们可以看出,高斯定理在万有引力场的有效应用中发挥了重要作用,它提供了万有引力场变化情况的推断,可以让我们很快的分析出物体之间的引力场变化情况,这样使我们可以进一步研究万有引力场,更好的理解它。
此外,高斯定理也有许多其它的应用,例如他可以用于空气动力学,静电学以及地学等领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《高斯定理与环路定理在万有引力场中的推广》读
后感
课本中从电场到磁场,我们学习或是解题过程中总是免不了要运用到高斯定理和静电环路定理作为解题的第一步骤。
因此我们知道了电磁学中的高斯定理和静电环路定理是反应静电场基本性质的两个定理,利用这两个定理可以解决很多电荷具有对称分布的静电学问。
本篇文章则利用了类比的科学研究方法,将静电场中的高斯定理和静电环路定理推广到了经典万有引力场中。
进一步引入引力场强度,引力势能,引力场强通量,说明了万有引力场是一种有源场,并引入引力环流的概念,说明了,万有引力场也是一种无旋场。
文章中通过大量的计算,公式的推导,结合利用牛顿万有引力定律和微积分,万有引力势能导出第一、第二字宙速度,用万有引力场中的高斯定理等求解相关的问题来证明了其类比假设的正确性。
最值得注意的就是其中的类比方法,有时在学习或是生活中适当地掺入类比的思想,不仅可以全面提高分析问题和解决问题的能力,或许还会受到其他更多的意想不到的效果。
电磁学中的高斯定理和静电环路定理是反应静电场基本性质的两个定理,利用这两个定理可以解决很多电荷具有对称分布的静电学问题。
高斯定理的定义:通过任意闭合曲面的电通量等于该闭合曲面所包围的所有电荷量的代数和与电常数之比。
高斯定理的说明:高斯定理反映了静电场是有源场这一特性,它表示,电场强度对任意封闭曲面的通量只取决于该封闭曲面内电荷的代数和,与曲面内电荷的分布情况无关,与封闭曲面外的电荷亦无关。
环路定理
静电场环路定理:在静电场中,场强沿任意闭合路径的线积分等于0. 与静电场力作功和路径无关是一致的.这种力场也叫保守力场或势场.
安培环路定理:在稳恒磁场中,磁感强度H沿任何闭合路径的线积分,等于这闭合路径所包围的各个电流之代数和。
万有引力定律:自然界中任何两个物体都是相互吸引的,引力的大小跟这两个物体的质量乘积成正比,跟它们的距离的二次方成反比。
引力场:引力场中的某点的是该点位置的矢量函数,对于多个质点产生的引力场,引力场强满足叠加原理
万有引力场中高斯定理:万有引力场中的高斯定理,与静电场中的高斯定理具有相似的形式
万有引力场中的环路定理:即引力场强在闭合回路上的积分为零,称为万有引力场中的环路定理
引力势能:在量值上等于将物体。
从0点移动到
零势能点万有引力所做的功。
万有引力场中的高斯定理说明了穿过闭合曲面的引力场强通量只和它包围的质量有关。
万有引力
场中的环路定理说明了万有引力沿闭合路径的环流为0,在万有引力场中可以定义引力势的概念。
万有引力场也是一种有源无旋场,它的源就是质量分布。
