§12-6麦克斯韦速率分布
合集下载
麦克斯韦速率分布
M1W1 M 2W2 M nWn
真实值
N足够大：平均值
----统计平均值 涨落：统计规律总伴随有涨落 N越大，涨落越小；N越小，涨落越大。 热学系统，N足够大，涨落很小。
二、麦克斯韦速率分布律
1、速率分布函数
按统计假设，各种速率下的分子都存在， 用某一速率区间内分子数占总分子数的百分比， 表示分子按速率的分布规律。 N: 总分子数 dN: 速率区间 v v dv 内的分子数
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3 8.31 300 v 508m / s 3 29 10
2
3kT v m
§6. 麦克斯韦速率分布律/三.麦克斯韦速率分布律应用
【讨论题】： 1.如图所示，SA= SB，v0代表什么？
S A f (v ) dv
0
v0
f (v )
S B f ( v ) dv
总分子数的百分比; 也表示在速率 v 附近单位 速率间隔内分子出现的概率，即概率密度。
2) 速率分布曲线： 即 f(v)~v 曲线
dN f (v ) Ndv dN f (vdv
v
dN N
§6. 麦克斯韦速率分布律/ 二、麦克斯韦速率分布规律
3) 在 f(v)~v 曲线下的面积为该速率区间 内分子出现的概率。
dN 表示速率区间 v v dv 内的分子 ： N 数占总分子数的百分比，也表示在速率 区间 v dv 内分子出现的概率。 v
大学物理第十二章气体动理论第6节 麦克斯韦气体分子速率分布律
解
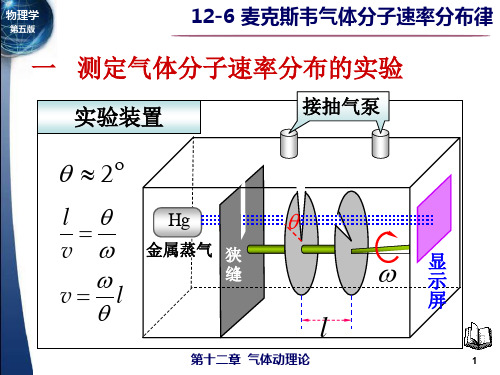
m(H 2 ) m(O2 ) v p ( H 2 ) v p (O 2 )
vp (H2 ) 2 000m.s-1
2kT vp m
o
2 000
v/ ms
1
vp ( H 2 )
m( O 2 ) 32 4 v p (O 2 ) m( H 2 ) 2
vp (O2 ) 500m.s
f ( v)
dS
dN f ( v)dv dS N
v
第十二章 气体动理论
o
v v dv
概率密度
3
物理学
第五版
12-6 麦克斯韦气体分子速率分布律
f (v)dv物理意义
表示在温度为 T 的平衡状态下，速 率在 v 附近单位速率区间 的分子数占总 数的百分比 .
f (v)dv 的物理意义：
表示速率在 v v dv 区间的分 子数占总分子数的百分比.
第十二章 气体动理论
4
物理学
第五版
12-6 麦克斯韦气体分子速率分布律 麦克斯韦气体分子速率分布律 12-6
dN Nf ( v)dv 速率在 v v dv 内分子数： 速率位于 v1 v2区间的分子数： v2 N v N f (v)dv 1 速率位于 v1 v2 区间的分 f ( v)
-1
第十二章 气体动理论
17
f (v )
vp v v
2
第十二章 气体动理论
vp v 2 v
v
15
物理学
第五版
12-6 麦克斯韦气体分子速率分布律 麦克斯韦气体分子速率分布律 12-6
讨论 1 已知分子数 N ，分子质量 m ，分布函 数 f ( v) . 求 （1） 速率在 vp ~ v 间的分子 数；（2）速率在 vp ~ 间所有分子动能 之和 . 解 （ 1）
麦克斯韦速率分布
2. 朗缪尔实验装置 v L
N
(总分子数 )
3. 实验原理
N
(v ~vv的分子数)
由于凹槽有一定宽度，因而速度选择器选择的不是某一个
速率大小，而是某一个速率范围：v ~ v+∆v
令N表示单位时间内穿过第一个凹槽进入速度选择器的总分子数 ，
∆N表示速率在v ~ v+∆v 范围的分子数，
⑵ 曲线下的细窄条面积
f (v)dv dN N
表示了分子出现在v ~ v+dv 区间段的概率
⑶ 曲线下v1 ~ v2 区间的阴影面积为：
vv12
f
(v)dv
vv12 4
(
m
)
3 2
exp(
mv
2
)
v
2dv
2 kT
2kT
表示分子速率处于v1 ~ v2 区间的概率
⑷ 对全部分子可出现的速率求和，即f(v)曲线下总面积：
这是一本划时代巨著，它与牛顿时代的
19世纪伟大的英国 物理学家、数学家。 经典电磁理论的奠 基人，气体动理论 的创始人之一。
《自然哲学的数学原理》并驾齐驱，它 是人类探索电磁规律的一个里程碑。 •在气体动理论方面，他还提出气体分子
按速率分布的统计规律。
§2.3.1 分子射线束实验
用实验方法测定麦氏速率分布的实验有很多。 最早是德国物理 学家斯特恩于1920年做的银蒸气分子射线束实验。 后来不断改进， 包括1934年葛正权测定铋蒸汽分子速率分布，1955年精确验证麦氏 分布率的密勒·库士的铊蒸汽原子束实验。
dN dv N dv
例如，取 v 10m/s
ΔN /( NΔv) o
麦克斯韦速率分布
目录摘要 (1)Abstract (1)1.引言 (1)2.麦克斯韦速率分布 (2)2.1麦克斯韦速率分布函数 (2)2.2三种速率 (3)2.3理想气体平均自由程 (4)3.麦克斯韦速度分布律 (5)3.1根据概率理论导出麦克斯韦速度分布律 (5)4.由麦克斯韦速度分布导出气体分子碰壁数 (8)5.结论 (10)参考文献 (10)附录 (12)麦克斯韦速率和速度分布的初步研究摘要：麦克斯韦速率和速度分布函数是气体动力学理论中的一个重点和难点。
本文首先介绍了麦克斯韦速率分布函数的意义及其应用，然后讨论了麦克斯韦速度分布函数的推导建立过程，并根据速度分布率研究了气体分子碰壁数。
关键字：麦克斯韦速度分布函数；麦克斯韦速率分布函数；最概然速率；平均速率；平均自由程；气体分子碰壁数。
Preliminary study of the distribution of Maxwell speed andspeedAbstract: Maxwell speed and velocity distribution function is a key and difficult point in the theory of gas dynamics. This paper firstly introduces the meaning and application of Maxwell speed distribution function, then discusses the derivational process of Maxwell velocity distribution function, and studies the collision frequency of gas molecules according to the velocity distribution rate.Keywords:Maxwell velocity distribution function, Maxwell speed distribution function, most probable speed, average speed, mean free path, collision frequency of gas molecules.1.引言1859年，J.C.麦克斯韦首先推导出气体分子速度的分布规律，之后，该规律又被L.玻耳兹曼由碰撞理论严格导出。
12-6麦克斯韦气体分子速率分布律
12.6 麦克斯韦速率分布定律
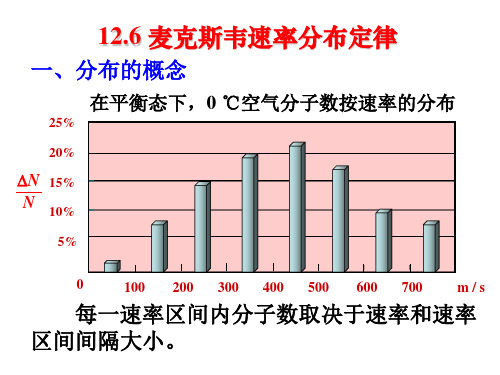
一、分布的概念
在平衡态下，0 ℃空气分子数按速率的分布
25% 20%
N 15% N 10%
5%
0
100
200
300
400
500
600
700
m/s
每一速率区间内分子数取决于速率和速率 区间间隔大小。
二、气体速率分布的实验测定 L
蒸气源 检测器
R
抽 气
抽 气
l v
理想气体在平衡态下，气体中速率在 v~v + dv 区间内的分子数与总分子数的比率为
dN f ( v)dv N 2 2 kT 4 π v e dv 2 πkT 2. v1~v2 区间内的分子数N占总分子数N的比率
v2 32
v2
v1
N f ( v)dv N
3. 曲线下面的总面积等于1
0
N f ( v)dv 1 N
O
f (v )
v2
v1
f ( v)dv
(归一化条件) 4. 最概然速率vp f (v ) 极大值对应的速率。
2kT f ( v) 0 vp dv
v1 vp f (v ) v2 v
O
vp
v
对一定量的理想气体
T 和 对速率分布的影响
dN 2 4 π ve N 2πkT
32
v 2
2 kT
dv
例3 已试用速率分布函数推出气体分子热运动算 术平均速率。 解：根据平均速率的定义，有
v
vdN
N
0
vNf ( v)dv N
一、分布的概念
在平衡态下，0 ℃空气分子数按速率的分布
25% 20%
N 15% N 10%
5%
0
100
200
300
400
500
600
700
m/s
每一速率区间内分子数取决于速率和速率 区间间隔大小。
二、气体速率分布的实验测定 L
蒸气源 检测器
R
抽 气
抽 气
l v
理想气体在平衡态下，气体中速率在 v~v + dv 区间内的分子数与总分子数的比率为
dN f ( v)dv N 2 2 kT 4 π v e dv 2 πkT 2. v1~v2 区间内的分子数N占总分子数N的比率
v2 32
v2
v1
N f ( v)dv N
3. 曲线下面的总面积等于1
0
N f ( v)dv 1 N
O
f (v )
v2
v1
f ( v)dv
(归一化条件) 4. 最概然速率vp f (v ) 极大值对应的速率。
2kT f ( v) 0 vp dv
v1 vp f (v ) v2 v
O
vp
v
对一定量的理想气体
T 和 对速率分布的影响
dN 2 4 π ve N 2πkT
32
v 2
2 kT
dv
例3 已试用速率分布函数推出气体分子热运动算 术平均速率。 解：根据平均速率的定义，有
v
vdN
N
0
vNf ( v)dv N
麦克斯韦速率分布定律
(4) 平均速率和方均根速率.
f ( )
解：（1）求 C :
C (0 ) (0 0 ) 0 ( 0 )
0
f ( )d 1 C
6
3 0
（2） N 0 ~ 0 / 4 N
0 / 4
0
5 f ( ) d N 32
0 df ( ) （3）最可几速率 0 p d p 2
6.5 麦克斯韦速率分布定律
气体中个别分子的速度大小和方向完全是偶然的 , 但 平衡态下，气体分子的速度分布遵从一定的统计规律 — — 麦克斯韦速度分布定律. 若不考虑分子速度的方向， 这个规律就成为麦克斯韦速率分布定律.
1859年, 麦克斯韦用概率论导出了气体分子速率分布 定律，后由玻尔兹曼使用经典统计力学理论导出. 1920年史特恩用分子束实验, 获得分子有着确定的速 度分布的信息, 但未能给出定量的结果. 1934年我国留学 生葛正权在伯克利首次获得此定律的精确实验验证. 此 成功经报界报道, 当时闻名欧美, 在很大程度上改变了外 国人眼中“中国留学生只会读书不能动手, 我们不欢迎” 的形象, 对当时欧美中国留学生有极大的影响和鼓舞.
f (v )
av ， (0 v v 0 ) 0 ， (v v 0 )
2
f (v )
v0 v 求： （1）常量 a 和υ0 的关系 0 （2）平均速率 v v0 （3）速率在 0 之间分子的平均速率 v 2
解： （1）由归一化条件
0
2 0
0
f ( )d 1
3 得 a 3 v0
f ( v)
T1 300K T2 1200K
f ( v)
麦克斯韦气体分子速率分布律
7
5. 分子运动的自由度
自由度 分子能量中独立的速度和坐标 的二次方项数目叫做分子能量自由度的数目, 简称自由度，用符号 i 表示. 自由度数目
i t r v
平 动 转 动 振 动
单原子分子的能量自 由度 i=3 ;
刚性双原子分子的能量自由 度 i=5 ;
8
非刚性双原子分子的能量自由度 i=7 .
f( v ) 4 π ( 2 π kT
k 玻耳兹曼常数，若m、T
给定， 函数的形式可概括为
曲线
2 m v m 32 2 2 kT ) e v
速率分布曲线 有单峰，不对称
快减
快增
两者相乘
曲线
速率
恒取正
对分子质量为m 、热力学温度为T 、处于平衡态的气体 速率在 到 区间内的分子数 与总 分子数 之比
刚性分子能量自由度 自由度 分子 单原子分子 双原子分子 多原子分子
t 平动
3 3 3
r转动
0 2 3
i总
3 5 6
9
二
能量均分定理
理想气体，平衡态，分子平均平动动能 因 故
每个平动自由度的平均平动动能均为
将等概率假设推广到转动动能，每个转动自由度的转 动能量相等，而且亦均等于
（能量按自由度均分定理）
理想气体的内能
m 'i i m ' E RT RT ( 为气体的摩 ) M 2 2 M
理想气体内能变化
i dE RdT 2
12
第一节
麦克斯韦气体分子速率分布律 处于平衡态的气体，其分子沿各向运动的机会均 等，这并非意味着每个分子的运动速率完全相同， 而是大量不同运动速度（大小和方向）的分子，在 一定条件下所形成的一种热动平衡状态。 麦克斯韦速率分布律，是表示气体处于热平衡时， 气体的分子数按速度大小（速率）分布的规律。
5. 分子运动的自由度
自由度 分子能量中独立的速度和坐标 的二次方项数目叫做分子能量自由度的数目, 简称自由度，用符号 i 表示. 自由度数目
i t r v
平 动 转 动 振 动
单原子分子的能量自 由度 i=3 ;
刚性双原子分子的能量自由 度 i=5 ;
8
非刚性双原子分子的能量自由度 i=7 .
f( v ) 4 π ( 2 π kT
k 玻耳兹曼常数，若m、T
给定， 函数的形式可概括为
曲线
2 m v m 32 2 2 kT ) e v
速率分布曲线 有单峰，不对称
快减
快增
两者相乘
曲线
速率
恒取正
对分子质量为m 、热力学温度为T 、处于平衡态的气体 速率在 到 区间内的分子数 与总 分子数 之比
刚性分子能量自由度 自由度 分子 单原子分子 双原子分子 多原子分子
t 平动
3 3 3
r转动
0 2 3
i总
3 5 6
9
二
能量均分定理
理想气体，平衡态，分子平均平动动能 因 故
每个平动自由度的平均平动动能均为
将等概率假设推广到转动动能，每个转动自由度的转 动能量相等，而且亦均等于
（能量按自由度均分定理）
理想气体的内能
m 'i i m ' E RT RT ( 为气体的摩 ) M 2 2 M
理想气体内能变化
i dE RdT 2
12
第一节
麦克斯韦气体分子速率分布律 处于平衡态的气体，其分子沿各向运动的机会均 等，这并非意味着每个分子的运动速率完全相同， 而是大量不同运动速度（大小和方向）的分子，在 一定条件下所形成的一种热动平衡状态。 麦克斯韦速率分布律，是表示气体处于热平衡时， 气体的分子数按速度大小（速率）分布的规律。
麦克斯韦速率分布律.pptx
第3页/共20页
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度，
说明下式的物理意义：
(1)nf (v)dv
f (v) dN , n N
Ndv
V
nf (v)dv
dN V
表示单位体积内分布在速率区间 v 内v的 dv
分子数。
第4页/共20页
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度， 说明下式的物理意义：
(2)Nf (v)dv
f (v) dN Ndv
Nf (v)dv dN
表示分布在速率区间 v v 内的dv分子数。
第5页/共20页
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度，
说明下式的物理意义：
(3)n v2 f (v)dv
v1
f (v)
dN
,n
N
Ndv
V
n v2 f (v)dv N N N
把这些量值代入，即得
W v＝ 1 v p 50
N＝
N
4
99 100
2
e
99 100
2
1 50
1.66%
第19页/共20页
f (v ) p3
T1
T2
T1 T2 T3
温度越高，速率 大的分子数越多
T3
v v v O
p1 p 2 p3
v
第15页/共20页
气体的三种统计速率
同一温度下不同种气体速率分布比较
f (v)
m1
m1 m2 m3
m2
分子质量越小，速
率大的分子数越多
。
m3
O
v
第16页/共20页
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度，
说明下式的物理意义：
(1)nf (v)dv
f (v) dN , n N
Ndv
V
nf (v)dv
dN V
表示单位体积内分布在速率区间 v 内v的 dv
分子数。
第4页/共20页
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度， 说明下式的物理意义：
(2)Nf (v)dv
f (v) dN Ndv
Nf (v)dv dN
表示分布在速率区间 v v 内的dv分子数。
第5页/共20页
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度，
说明下式的物理意义：
(3)n v2 f (v)dv
v1
f (v)
dN
,n
N
Ndv
V
n v2 f (v)dv N N N
把这些量值代入，即得
W v＝ 1 v p 50
N＝
N
4
99 100
2
e
99 100
2
1 50
1.66%
第19页/共20页
f (v ) p3
T1
T2
T1 T2 T3
温度越高，速率 大的分子数越多
T3
v v v O
p1 p 2 p3
v
第15页/共20页
气体的三种统计速率
同一温度下不同种气体速率分布比较
f (v)
m1
m1 m2 m3
m2
分子质量越小，速
率大的分子数越多
。
m3
O
v
第16页/共20页
麦克斯韦速率分布
麦克斯韦速率分布
麦克斯韦速率分布是描述气体分子速度分布的概率分布函数之一。
它由麦克斯韦速度分布定律提出，该定律认为在一定温度下，分子速度的分布服从麦克斯韦速率分布。
麦克斯韦速率分布的表达式为：
f(v) = (m / (2 * π * k * T))^(3/2) * 4 * π * v^2 * exp(-(m * v^2) / (2 * k * T))
其中，f(v)是速度为v的气体分子出现的概率密度，m是分子的质量，k是玻尔兹曼常数，T是温度。
麦克斯韦速率分布描述了速率在不同范围内的分子数的相对比例。
麦克斯韦速率分布具有以下特点：
1. 最概然速率：在麦克斯韦速率分布曲线上，存在一个速度值，使得该速度值对应的气体分子出现的概率最高，这个速度就是最概然速率。
2. 平均速率：麦克斯韦速率分布曲线的面积下的整数倍等于总分子数，因此可以通过平均积分得到平均速率。
3. 方均根速率：方均根速率是指速率的平方取平均后开根号的值，它与麦克斯韦速率分布曲线的宽度有关。
麦克斯韦速率分布在解释气体的物理性质和进行气体动力学研究中起着重要的作用，尤其在理解气体温度、分子碰撞等方面具有较高的应用价值。
麦克斯韦速率分布定律
υ 附近单位速率区
间的分子数
(5) nf ()d N dN dN
VN V
单位体积中速率在υ ~ υ+dυ区间的分子数
(6) 2 f ()d 1
dN N
N1 2 N
速率在υ1 ~ υ2区间的分
子数占总分子数的百分比
(7) 2 Nf ()d 1
1920年史特恩用分子束实验, 获得分子有着确定的速 度分布的信息, 但未能给出定量的结果. 1934年我国留学 生葛正权在伯克利首次获得此定律的精确实验验证. 此 成功经报界报道, 当时闻名欧美, 在很大程度上改变了外 国人眼中“中国留学生只会读书不能动手, 我们不欢迎” 的形象, 对当时欧美中国留学生有极大的影响和鼓舞.
p (O2 ) 500 m/s
例4. 设某气体的速率分布函数为
f (v )
av 2，(0 v v0 )
0 ， (v v 0 )
f (v )
求：（1）常量 a 和υ0 的关系 0 v0
v
（2）平均速率 v
（3）速率在 0 v 0 之间分子的平均速率v
2
解：（1）由归一化条件
(1) f () dN Nd
(2) f ( )d dN
N
υ附近单位速率区间的分子
数占总分子数的百分比
速率在υ ~ υ+dυ区间的分
子数占总分子数的百分比
(3) N f ()d N dN dN
N
速率在υ ~ υ+dυ
区间的分子数
(4) N f () N dN dN Nd d
f ()
T1
T2 T1
T2
p
2kT m
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
N v3 p
415
(2)在v=10vp附近，v=1m·s-1内的分子数占分子总数的比率为
N4
N
1vv3 p 0 p 2e1v0 p2
v2 p v410e 010 0 1 415
2.01-4 04 2.01-4 0% 2
8/23/2019
理学院 物理系
(2)dx段的质量百分比
dW dMMxfdxfxdx d M M x d f x
M
M
(3)f(x)的物理意义
fx
①f(x)表示在位置 x 附近单
位长度上的质量占总质量的
百分比; ②f(x)dx表示在x→x+dx区间
fxdxdM
M
x
内的质量占总质量的百分比; O x xdx
8/23/2019
理学院 物理系
大学物理
§12-6 麦克斯韦速率分布
vp
2kT1.41 RT
m
M
物理意义
气体在一定温度下分布在最概然速
率 v p 附近单位速率间隔内的相对分子数
最多.
8/23/2019
理学院 物理系
大学物理
§12-6 麦克斯韦速率分布
f v
O
vp v
v2
v
某一温度下分子速率的三个统计值
解： 麦克斯韦速率分布定律
d W d N N 4 2 m k 3 T 2 e 2 m kv T 2 v 2 d v fv d v
N N42m kT 32e2m kT v2v2v
N N
4
v2 v3p
ev2
v2pv
8/23/2019
f v
m1
m1 m2 m2
O
500
v/ms
1000
1500
2000
相同温度下，不同质量气体分子的麦克斯韦速率分布曲线
8/23/2019
理学院 物理系
大学物理
§12-6 麦克斯韦速率分布
3.分子速率的三种统计平均值
(1)气体分子的平均速率（average speed）
vv(fv)dv
在该间隔内的分子数占总分子数的百分数。
(4)麦克斯韦速率分布和温度的关系
f v
73K
O2
273K
127K 3
O
500
1000
1500
不同温度下O2的麦克斯韦速率分布曲线
v/ms
2000
8/23/2019
理学院 物理系
大学物理
§12-6 麦克斯韦速率分布
(5)麦克斯韦速率分布和气体分子质量 m 的关系
大学物理
§12-6 麦克斯韦速率分布
§12-6 麦克斯韦速率分布
一、分布的概念
1.不均匀细杆的密度函数
x
d M x d x
d M x d x
O
x xdx
x
L
M0Lxdx
8/23/2019
理学院 物理系
大学物理
§12-6 麦克斯韦速率分布
2. 质量分布函数
(1)质量分布函数
0
fvdv1
v0 Cdv 1 0
C 1 v0
8/23/2019
理学院 物理系
大学物理
§1ห้องสมุดไป่ตู้-6 麦克斯韦速率分布
(2)粒子的平均速率
v v0vf(v)dv v0vCdv
0
0
1 v0 vdv v0 0
v0 2
v2 v0v2f(v)dv v0v2Cdv 1
v0 v2 dv
v
2 0
0
0
v0 0
3
粒子的方均根速率
v2 v0 3v0 33
8/23/2019
理学院 物理系
大学物理
§12-6 麦克斯韦速率分布
例题3 在300K时，空气中速率在(1)vp附近； (2)10vp附 近，速率区间v=1m·s-1内的分子数占分子总数的比率
各是多少？空气的摩尔质量为29。
v2 vvp
8/23/2019
理学院 物理系
大学物理
§12-6 麦克斯韦速率分布
例题1 H2在00C时方均根速率、平均速率和最概然速率
v2 3R T 3 28 .3 1 2 0 3 73 18m 4s3
v 8RT169m 8 /s
vp
2RT150m 2 /s
8/23/2019
理学院 物理系
大学物理
§12-6 麦克斯韦速率分布
f (v)dv dN N
代表气体中速率v 在v—v+dv间的分子 数的比率
Nf(v)d vdN代表分布在速率v 附近 v—v + dv 间隔 内的分子数
v2
v2
Nf(v)dvdN 代表速率分布在 v1—v2 之间的分子数
8/23/2019
理学院 物理系
大学物理
§12-6 麦克斯韦速率分布
例题2 大量粒子的速率分布曲线如图所示，求：(1)C;
(2)平均速率、方均根速率。
f (v)
解： (1)由速率分布曲线可得：
C
f(v)C 0vv0 f(v)0 vv0
0
根据速率分布的归一化条件，可得：
v0 v
二、麦克斯韦速率分布
1.麦克斯韦速率分布 (1)分子按速率分布
气体分子的速率服从确定的分布规律。
(2)气体速率分布函数
dWdNfvdv
f(v) 称为气体速率分布函数。 速率 v 附近单位速率区间内分
N
子数占总分子数的百分比。
(3)麦克斯韦速率分布定律
d W d N 4 m 3 2 e 2 m kv T 2 v 2 d v fv d v N 2kT
0
8km T
8RT
(2)气体分子的方均根速率（root-mean-square speed）
v2 v2f(v)dv3kT
0
m
v2 3kT 3RT
m
(3)气体分子的最概然速率（most probable speed）
d f 0 d v vvp
vp
2kT m
2R T 141R T
f v 42m kT32e-2m kTv2v2
(2)麦克斯韦速率分布曲线
f v
8/23/2019
dN fvdv
N
O
v vdv
某一温度下麦克斯韦速率分布曲线
v
理学院 物理系
大学物理
§12-6 麦克斯韦速率分布
(3)f(v)dv的物理意义
既表示某分子速率在间隔v→v+dv内的概率，又表示
L
③ f (x) 满足归一化条件。
质量分布函数曲线
8/23/2019
理学院 物理系
物理学
12-6 麦克斯韦气体分子速率分布律
第五版
测定气体分子速率分布的实验
实验装置
接抽气泵
2
l v v l
Hg
金属蒸气 狭 缝
l
第十二章 气体动理
显 示
屏
大学物理
§12-6 麦克斯韦速率分布
v1
v1
v 2 f (v )dv
v 2 dN
1
v2 dN
vp
vp
N
N vp
代表速率处在 v p ~ 区域中 所有分子速率的
平方的总和被 总分子数除。
8/23/2019
理学院 物理系
大学物理
§12-6 麦克斯韦速率分布
2.麦克斯韦速率分布函数的物理意义 (1)麦克斯韦速率分布函数
理学院 物理系
vp
2kT m
大学物理
§12-6 麦克斯韦速率分布
300K时，空气的最概然速率为：
vp2 m kT 2 R T2 2 8 .3 9 1 1 -3 300 4 01 m s5 -1
(1)在v=vp附近，Δv=1m·s-1内的分子数占分子总数的比率为
N 4v2e v2v2 p v41e 1 1 0 .00 0 .2 2 %
令ρ(x)=Mf(x), 称 f(x)为杆的质量分布函数。
fx 1 x
x
M
d M x d x M x d x f
L
0
fxdx1
归一化条件
d M x d x
O
x xdx
x
L
8/23/2019
理学院 物理系
大学物理
§12-6 麦克斯韦速率分布