沪教版高中二年级数学第一学期二阶行列式
沪教版高中二年级数学第一学期二阶行列式

的
条件。
(B)构造一个二元一次方程组,使它的解的情况分别是
“有唯一解”、“无解”、“有无穷多解”.
选做题:用行列式解方程组
5 x
7 y
3
7
x
9 y
4
9
4
(3) D 2
5
8
5 0, Dx 4
2
5
4
5 0, 2
Dy 2
8 0
4
∴方程组有无穷多解。
2.
解关于x、y的二元一次方程组
mx
y
1
3mx my 2m 3
并对解的情况进行讨论。
解:D m 1 m2 3m m(m 3)
3m m
当D=0,而Dx=0且Dy=0时,方程组有无数多组解。
问题三:解关于x,y的二元一次方程组
mx
x
4 my
ym m
2
,
并对解的情况进行讨论。
解:D= m 4 m2 4
1m
Dx=
m m
2
4 m2 2m
m
m Dy= 1
m2 m
m2 m 2
(1)当D0即m2时,方程组有唯一解
1 1
Dx 2m 3
m 2m 3 (m 3) m
m Dy 3m
1 2m2 3m 3m 2m(m 2m 3
当m0且m-3时,方程组有唯一解
3)
x
Hale Waihona Puke yDx D Dy D
高二数学沪教版9.3.2_二阶行列式 (共11张PPT)

当 D Dx Dy 0 时,方程组有无穷多解
例1.利用行列式判断下列方程组解的情形:
2 3 2 x 3 y 7 D 0 有唯一解 (1) 5 2 5 x 2 y 1 3 2 4 x 2 y 3 D 0, Dx 0 无解 (2) 5 9 18 x 9 y 5
则
Dy Dx ,y 当 D 0 时,解为 x D D
一、二元线性方程组解的其它情形
a1 x b1 y c1 当 a1b2 a2b1 0 时, 没有唯一解 a2 x b2 y c2 a1 b1 c1 b1 a1 c1 若记 D , Dx , Dy a2 b2 c2 b2 a2 c2
8 6 4 x 6 y 8 D 0 , Dx 0 (3) 4 3 2 x 3 y 4 4 8 Dy 0 无穷多解 2 4
mx 2 y m 4 例2.解关于 x, y 的方程 2 x my m
解: D (m 2)(m 2) , Dx m(m 2) , Dy (m 4)(m 2) ①当 m 2 即 D 0 时,方程组有唯一解:
x1 二阶行列式 y1
y
x2 表示平面上 OA, OB 所张成的 y2
推论2: O, A, B 构成 AOB
平行四边形的有向面积. (证明利用第八章知识,这里略)
B( x2 , y2 )
SOAB
A( x1 , y1 )
O
1 x1 2 y1
x2 y2
x
课外阅读材料——二阶行列式几何意义证明
证: SOACB | OA || OB | sin
(选讲)二、二阶行列式的几何意义
二阶行列式PPT优秀课件1 沪教版

128.医生知道的事如此的少,他们的收费却是如此的高。――[马克吐温] 129.问题不在于:一个人能够轻蔑、藐视或批评什么,而是在于:他能够喜爱、看重以及欣赏什么。――[约翰·鲁斯金]
9.3二阶行列式(2)
上海八中许颖龙春朝 2009年12月15日
一、要点回
顾
1、a1 a2
b1 b2
a1b2 a2b1
2、用行列式解二元一次方程组
4x 8x
3 6
y y
5 22
解:D 4
8
3 6
48
0,Dx
5 22
3
4
6 96, Dy 8
5 48
22
方程组的解为x
方程组
Dx Dy
Dx Dy
有无数组解。
二元一次方程组解的判别
一般地,通过消元法可将二元一次方程组
a1 x a2 x
b1 y b2 y
c1 c2
,其中
D
a1 a2
b1 b2
, Dx
c1 c2
b1 , b2
D当yD0aa时12 ,cc12方,程组有D唯叫一做解方程xy 组 DD解DD xy 的;判别式
91.要及时把握梦想,因为梦想一死,生命就如一只羽翼受创的小鸟,无法飞翔。――[兰斯顿·休斯] 92.生活的艺术较像角力的艺术,而较不像跳舞的艺术;最重要的是:站稳脚步,为无法预见的攻击做准备。――[玛科斯·奥雷利阿斯] 93.在安详静谧的大自然里,确实还有些使人烦恼.怀疑.感到压迫的事。请你看看蔚蓝的天空和闪烁的星星吧!你的心将会平静下来。[约翰·纳森·爱德瓦兹]
沪教版高二上册数学二阶行列式教案二级第一学期(1)
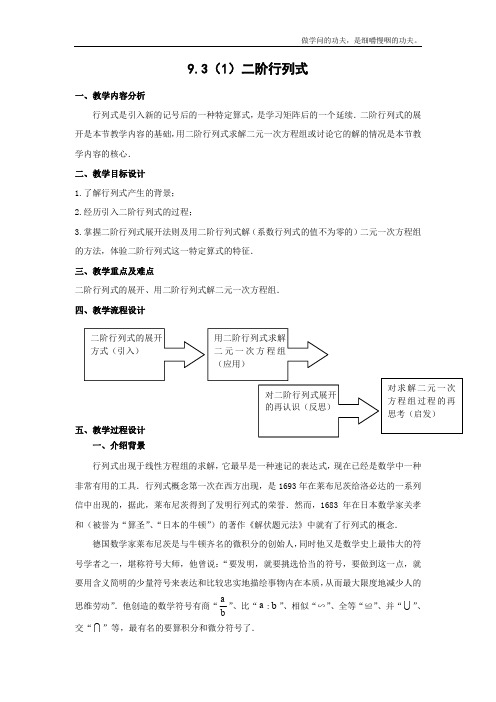
9.3(1)二阶行列式一、教学内容分析行列式是引入新的记号后的一种特定算式,是学习矩阵后的一个延续.二阶行列式的展开是本节教学内容的基础,用二阶行列式求解二元一次方程组或讨论它的解的情况是本节教学内容的核心. 二、教学目标设计 1.了解行列式产生的背景; 2.经历引入二阶行列式的过程;3.掌握二阶行列式展开法则及用二阶行列式解(系数行列式的值不为零的)二元一次方程组的方法,体验二阶行列式这一特定算式的特征. 三、教学重点及难点二阶行列式的展开、用二阶行列式解二元一次方程组. 四、教学流程设计五、教学过程设计一、介绍背景行列式出现于线性方程组的求解,它最早是一种速记的表达式,现在已经是数学中一种非常有用的工具.行列式概念第一次在西方出现,是1693年在莱布尼茨给洛必达的一系列信中出现的,据此,莱布尼茨得到了发明行列式的荣誉.然而,1683年在日本数学家关孝和(被誉为“算圣”、“日本的牛顿”)的著作《解伏题元法》中就有了行列式的概念.德国数学家莱布尼茨是与牛顿齐名的微积分的创始人,同时他又是数学史上最伟大的符号学者之一,堪称符号大师,他曾说:“要发明,就要挑选恰当的符号,要做到这一点,就要用含义简明的少量符号来表达和比较忠实地描绘事物内在本质,从而最大限度地减少人的思维劳动”.他创造的数学符号有商“ba”、比“a :b ”、相似“∽”、全等“≌”、并“ ”、交“ ”等,最有名的要算积分和微分符号了.[说明]教师、学生课前收集有关资料,在授新课前(由学生或老师)作简单介绍,这是数学文化的一种渗透.二、学习新课 1.二阶行列式的引入 设二元一次方程组(*)⎩⎨⎧=+=+222111c y b x a c y b x a(其中y x ,是未知数,2121,,,b b a a 是未知数的系数且不全为零,21,c c 是常数项.)用加减消元法解方程组(*).当01221≠-b a b a 时,方程组(*)有唯一解:⎪⎪⎩⎪⎪⎨⎧--=--=1221122112211221b a b a c a c a y b a b a b c b c x ,引入记号21a a 21b b 表示算式1221b a b a -,即 21a a 21b b 1221b a b a -=. 从而引出行列式的相关概念,包括行列式、二阶行列式、行列式的展开式、行列式的值、行列式的元素、对角线法则等.记=D 21a a21b b ,=x D 21c c21b b ,=y D 21a a21c c ,则当=D21a a21b b =01221≠-b a b a 时,方程组(*)有唯一解,可用二阶行列式表示为⎪⎪⎩⎪⎪⎨⎧==DD y D D x y x. 2.例题分析分析讲解教材例题1、例2; 例1.展开并化简下列行列式: (1)8521 (2)8125(3)θθsin cos θθcos sin -(4)11-a 112++-a a点评:①正确运用对角线法则展开;②由(1)(2)可知,行列式中元素的位置是不能随意改变的.例2.用行列式解下列二元一次方程组:(1)⎩⎨⎧-=+=+61548115y x y x(2)⎩⎨⎧=-+=--012053y x y x[说明] ①当所给方程组的形式不是方程组(*)的形式时,应先化为方程组(*)的形式,才能得到正确的x D 和y D ;②注意到这两个方程组的系数行列式的值均不为零.3.问题拓展①二阶行列式展开的逆向使用的问题;如:算式ac b 42-可用怎样的二阶行列式来表示等. ②二阶行列式的值为零时,行列式中的元素有何特征?③举例说明,当二元一次方程组的系数行列式的值为零时,方程组的解会有怎样的可能?[说明]问题拓展围绕教学内容(知识点)的基础上进行;同时为下一教学课时作准备. 三、巩固练习数学课本第91页,练习9.3(1). 四、课堂小结①二阶行列式的展开法则;②用二阶行列式解二元一次方程组的方法及过程表达(书写). 五、作业布置数学练习部分第51页,习题9.3 A 组,第1、2、3题.。
沪教版(上海)高二第一学期新高考辅导与训练第9章矩阵和行列式初步9.3二阶行列式
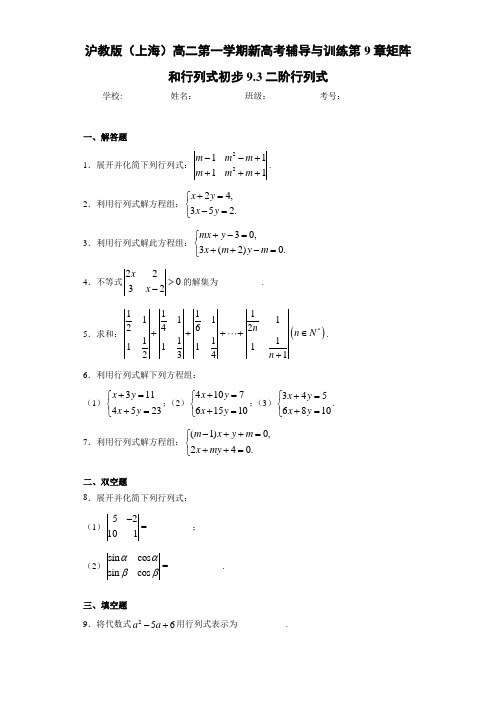
沪教版(上海)高二第一学期新高考辅导与训练第9章矩阵和行列式初步9.3二阶行列式学校:___________姓名:___________班级:___________考号:___________一、解答题1.展开并化简下列行列式:221111m m m m m m --++++.2.利用行列式解方程组:24,35 2.x y x y +=⎧⎨-=⎩3.利用行列式解此方程组:30,3(2)0.mx y x m y m +-=⎧⎨++-=⎩4.不等式22032x x >-的解集为__________.5.求和:()*111111112462111111113214n n N n ++++∈+.6.利用行列式解下列方程组: (1)3114523x y x y +=⎧⎨+=⎩;(2)410761510x y x y +=⎧⎨+=⎩;(3)3456810x y x y +=⎧⎨+=⎩. 7.利用行列式解方程组:(1)0,240.m x y m x my -++=⎧⎨++=⎩二、双空题8.展开并化简下列行列式: (1)52101-=__________;(2)sin cos sin cos ααββ=____________.三、填空题9.将代数式256a a -+用行列式表示为___________.10.计算12121211221212a a a a a ab c b c b b c c =+++是否正确?______________.11.已知2075x=-,则x =________.12.已知关于,x y 的方程组()222(1)1,(1)1a x a y a a x a y a ⎧--+=+⎪⎨-+=-⎪⎩有唯一解,则实数a 的取值范围是__________.四、单选题13.设二元一次方程组为1112220,0.a xb yc a x b y c ++=⎧⎨++=⎩若x Dx D =,则x D 为( ).A .1212b bc c -B .1122b c b c -C .1122c b c b -- D .1122b c b c --14.已知互不相同的三个实数,,{1,2,3}x y z ∈,则行列式0x y z可能的值有( ). A .3个 B .4个C .5个D .6个参考答案1.2- 【分析】直接利用行列式的运算求解. 【详解】()()222211(1)1(1)111m m m m m m m m m m m m --+=-⋅++-+⋅-++++,()()33112m m =--+=-.【点睛】本题主要考查行列式的化简,还考查了运算求解的能力,属于基础题.2.24111011x y ⎧=⎪⎪⎨⎪=⎪⎩【分析】分别取得,,x y D D D 的值,进而得到方程组的解,得到答案. 【详解】由方程组24352x y x y +=⎧⎨-=⎩,可得121135D ==--,422425x D ==--,141032y D ==-,所以原方程组的解是24111011x y D x D D y D ⎧==⎪⎪⎨⎪==⎪⎩. 【点睛】本题主要考查了用行列式解方程组问题,其中解答中熟记行列式的运算法则,以及求解方程组的解法是解答的关键,着重考查推理与运算能力. 3.答案不唯一,具体见解析 【分析】利用行行列式求出D ,Dx ,Dy ,然后讨论m 的取值即可求解. 【详解】原方程组化为3,3(2).mx y x m y m +=⎧⎨++=⎩则2123(3)(1)32m D m m m m m ==+-=+-+,31262(3)2x D m m m m ==+=++,239(3)(3)3y mD m m m m==-=+-.①当3m ≠-且1m ≠时,0D ≠,原方程组有唯一解;2,13.1x y D x D m D m y D m ⎧==⎪⎪-⎨-⎪==⎪-⎩②当1m =时,0,0x D D =≠,原方程组无解;③当3m =-时,0x y D D D ===,原方程组有无穷多解.此时方程组为33,3 3.x y x y -=-⎧⎨-=-⎩令()x t t R =∈,则方程组的解为,()33x t t R y t =⎧∈⎨=+⎩.【点睛】本题考查行列式计算、利用行列式求解方程组,考查基本分析求解能力,属基础题. 4.()(),13,-∞-+∞【分析】利用二阶行列式可得出关于x 的二次不等式,解出该不等式即可. 【详解】()22226032x x x x =-->-,整理得2230x x -->,解得1x <-或3x >.因此,原不等式的解集为()(),13,-∞-+∞.故答案为:()(),13,-∞-+∞.本题考查二阶行列式的计算,同时也考查了一元二次不等式的求解,考查计算能力,属于基础题. 5.(21)2(1)n n n -++【分析】根据行列式的运算,求得111112112111n n n n ⎛⎫=-- ⎪+⎝⎭+,再结合裂项法求和,即可求解. 【详解】由行列式的运算,可得11111121112(1)2111n n n n n n ⎛⎫=-=-- ⎪++⎝⎭+,所以原式111111122231n n n ⎛⎫=-+-+⋯+-- ⎪+⎝⎭11(21)1212(1)n n n n n -+⎛⎫=--= ⎪++⎝⎭. 【点睛】本题主要考查了行列式的运算,以及数列的裂项求和的应用,着重考查了推理与运算能力,属于基础题.6.(1)23x y =⎧⎨=⎩;(2)原方程组无解;(3)()534x t t R t y =⎧⎪∈⎨-=⎪⎩.【分析】(1)计算出0D ≠、x D 、y D ,由此可得出原方程组的解为xy D x D D y D⎧=⎪⎪⎨⎪=⎪⎩; (2)计算出系数行列式0D =,且0x D ≠,0y D ≠,据此可判断出原方程组无解; (3)计算出0x y D D D ===,据此可判断出原方程组有无穷多解,令x t =,求得y ,由此可得原方程组的解.(1)13745D ==-,11314235x D ==-,11121423y D ==-,故14272137x y D x D D y D -⎧===⎪⎪-⎨-⎪===⎪-⎩;(2)4100615D ==,710501015x D ==≠,4720610y D ==-≠,故原方程组无解;(3)34068D ==,540108x D ==,350610y D ==,故原方程组有无穷多解.令x t =,则原方程组的解为()534x t t R t y =⎧⎪∈⎨-=⎪⎩.【点睛】本题考查利用行列式求解二元一次方程组的解,考查计算能力,属于基础题. 7.答案不唯一,具体见解析 【分析】利用行行列式求出D ,x D ,y D ,然后讨论m 的取值即可求解. 【详解】2112(2)(1)2m D m m m m m-==--=-+,214(2)(2)4x m D m m m m-==-+=-+--,1242(2)24y m m D m m --==-+=---,(1)当1m ≠-且2m ≠时,0D ≠,原方程组有唯一解2,121m x m y m +⎧=-⎪⎪+⎨⎪=-⎪+⎩,(2)当1m =-时,0,60y D D ==≠,原方程组无解, (3)当2m =时,0x y D D D ===,原方程组有无穷多解.此时方程组为2020x y x y ++=⎧⎨++=⎩,令()x t t R =∈,则方程组的解为,()2.x t t R y t =⎧∈⎨=--⎩【点睛】本题考查了利用行列式求二元一次方程组,考查了计算能力,属于基础题. 8.25 sin()αβ- 【分析】利用二阶行列式的计算公式以及两角差的正弦公式即可求解. 【详解】 (1)()525121052025101-=⨯--⨯=+=.(2)()sin cos sin cos cos sin sin sin cos αααβαβαβββ=-=-.故答案为:25;sin()αβ- 【点睛】本题考查了行列式的化简、二倍角的正弦公式,属于基础题. 9.235a a --【分析】先化简256(5)3(2)a a a a -+=--⨯-,再写出所求行列式. 【详解】 因为a b a d b c c d=⨯-⨯,256(5)(2)3a a a a -+=---⨯,所以代数式256a a -+用行列式表示为235a a --.故答案为:235a a --.【点睛】本题主要考查行列式,意在考查学生对该知识的理解掌握水平. 10.正确 【分析】直接利用行列式的运算求解. 【详解】因为()()121222111122=++++-a a a b c a b c b c b c , 12122121-=+-a b a c a b a c ,而1212122112211212-=++-a a a a a b a b a c a c b b c c , 所以12121211221212a a a a a abc b c b b c c =+++. 故答案为:正确 【点睛】本题主要考查行列式的计算,还考查了运算求解的能力,属于基础题. 11.107-【分析】根据二阶行列式可得出关于x 的等式,解方程即可. 【详解】2107075xx =--=-,解得107x =-. 故答案为:107-. 【点睛】本题考查二阶行列式的计算,同时也考查了一次方程的求解,考查计算能力,属于基础题. 12.1()a a R ≠-∈把方程组()222(1)1(1)1a x a y a a x a y a ⎧--+=+⎪⎨-+=-⎪⎩中的两个方程对应两条直线,结合两直线的位置关系,即可求解. 【详解】由方程组()222(1)1(1)1a x a y a a x a y a ⎧--+=+⎪⎨-+=-⎪⎩中的两个方程对应两条直线,则方程组的解就是两直线的交点,要使得两直线只有一个交点,则满足22(2)(1)(1)0a a a a -+-+≠, 即2(1)0a -+≠,解得1()a a R ≠-∈. 故答案为:1()a a R ≠-∈. 【点睛】本题主要考查了二元一次方程的解法,以及两直线位置关系的应用,其中解答中把方程组的解转化为两直线的位置关系是解答的关键,注重考查转化思想,以及计算能力. 13.C 【分析】直接解方程组得到x 的值,再将其解转化为行列式可得x D 的值. 【详解】解:给方程组中第1式、第2式分别乘以21,b b 得12121221212100a b x b b y c b a b x b b y c b ++=⎧⎨++=⎩, 两式相减得,12211221()()0a b a b x c b c b -+-=,当12210a b a b -≠时,1122211211122122c b c b c b c b x a b a b a b a b ---==-, 所以1122x c b D c b -=-【点睛】此题考查的是利用二阶行列式表示二元一次方程组的解,属于基础题. 14.A 【分析】 先计算行列式0x y z,再根据互不相同的三个实数,,{1,2,3}x y z ∈确定可能取值.【详解】x xz y z=,而互不相同的三个实数,,{1,2,3}x y z ∈ 所以2,3,6,xz =,即可能的值有3个 故选:A. 【点睛】本题考查行列式计算,考查基本分析求解能力,属基础题.。
2019-2020年高二数学 《二阶行列式》教案 沪教版

教学目的:理解二阶行列式的定义;掌握用二阶行列式解二元一次方程组;用行列式判断二元一次方程组解的情况。
教学过程:一、设问:什么叫二阶行列式?(一)定义:1、我们用记号表示算式即 =其中记号叫做行列式,因为它只有两行、两列,所以把它叫做二阶行列式。
叫做行列式的展开式,其计算结果叫做行列式的值。
2、 叫做行列式的元素。
(二)二阶行列式的展开满足:对角线法则1122a b a b 实线表示的对角线叫主对角线,虚线表示的对角线叫副对角线。
二阶行列式是这样两项的代数和:一个是从左上角到右下角的对角线(又叫行列式的主对角线)上两个元素的乘积,取正号;另一个是从右上角到左下角的对角线(又叫次对角线)上两个元素的乘积,取负号.(三)例和练习:例1、判断以下几项中哪些是二阶行列式?是的,求出值。
(1)(2)(3)123456(4)(5)1212343412242363--例2:将下列各式用行列式表示:——解唯一吗?(1)2214;(2)5;(3)422b ac x y x x ---+ 二、用二阶行列式解二元一次方程组 (四)设有二元一次方程组111222,(1)().(2)a x b y c A a x b y c +=⎧⎨+=⎩ 用加减消元法得 122112212211221();().a b a b xc b c b a b a b y a c a c -=--=- (1)当 时,有(A )有唯一解,(B) 122112211221122c b c b x a b a b a c a c y a b a b -⎧=⎪-⎪⎨-⎪=⎪-⎩求根公式。
(2)当 时,122112210c b c b a c a c -=-=无穷组解;(3)当 时122112210,0c b c b or a c a c -≠-≠无解。
(五)记,系数行列式 ,——类比,对照则(1)当D ≠0时,方程组(A) 的解(B)可以表示成X yD x D D y D⎧=⎪⎪⎨⎪=⎪⎩; (2)当D =0时, 无穷组解;(3) 当D =0时, 无解。
沪教版(上海) 高二第一学期 新高考辅导与训练 第9章 矩阵和行列式初步 9.3二阶行列式
沪教版(上海) 高二第一学期新高考辅导与训练第9章矩阵和行
列式初步 9.3二阶行列式
一、解答题
(★★) 1. 展开并化简下列行列式:.
(★★) 2. 利用行列式解方程组:
(★★) 3. 利用行列式解此方程组:
(★★) 4. 不等式的解集为__________.
(★★★) 5. 求和:.
(★★) 6. 利用行列式解下列方程组:
(1);(2);(3).
(★★) 7. 利用行列式解方程组:
二、双空题
(★★) 8. 展开并化简下列行列式:
(1)__________;
(2)____________.
三、填空题
(★) 9. 将代数式用行列式表示为___________.
(★★) 10. 计算是否正确?______________.
(★) 11. 已知,则________.
(★★★) 12. 已知关于的方程组有唯一解,则实数 a的取值范围是 __________ .
四、单选题
(★) 13. 设二元一次方程组为若,则为(). A.B.C.D.(★) 14. 已知互不相同的三个实数,则行列式可能的值有(). A.3个B.4个C.5个D.6个。
2019-2020年高二数学上册 9.3《二阶行列式》教案(2) 沪教版
2019-2020年高二数学上册 9.3《二阶行列式》教案(2) 沪教版 教学目的:理解二阶行列式的定义;掌握用二阶行列式解二元一次方程组;用行列式判断二元一次方程组解的情况。
教学过程:一、 设问:什么叫二阶行列式?(一)定义:1、 我们用记号表示算式即 =其中记号叫做行列式,因为它只有两行、两列,所以把它叫做二阶行列式。
2、 叫做行列式的展开式,其计算结果叫做行列式的值。
3、 叫做行列式的元素。
(二)二阶行列式的展开满足:对角线法则1122a b a b 实线表示的对角线叫主对角线,虚线表示的对角线叫副对角线。
二阶行列式是这样两项的代数和:一个是从左上角到右下角的对角线(又叫行列式的主对角线)上两个元素的乘积,取正号;另一个是从右上角到左下角的对角线(又叫次对角线)上两个元素的乘积,取负号.(三)例和练习:例1、判断以下几项中哪些是二阶行列式?是的,求出值。
(1)(2)(3)123456(4)(5)1212343412242363--例2:将下列各式用行列式表示:——解唯一吗?(1)2214;(2)5;(3)422b ac x y x x ---+二、 用二阶行列式解二元一次方程组(四)设有二元一次方程组111222,(1)().(2)a xb yc A a x b y c +=⎧⎨+=⎩ 用加减消元法 得 1221122112211221();().a b a b x c b c b a b a b y a c a c -=--=- (1)当 时,有(A )有唯一解, (B) 122112211221122c b c b x a b a b a c a c y a b a b -⎧=⎪-⎪⎨-⎪=⎪-⎩求根公式。
(2)当 时,122112210c b c b a c a c -=-=无穷组解;(3)当 时122112210,0c b c b or a c a c -≠-≠无解。
(五)记,系数行列式 ,——类比,对照则(1)当D ≠0时,方程组(A) 的解(B)可以表示成X yD x D D y D⎧=⎪⎪⎨⎪=⎪⎩; (2)当D =0时, 无穷组解;(3) 当D =0时, 无解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当m=0时,D=0,Dx0,∴方程组无解。
1、二元一次线性方程组解的判别: 当D0时,方程组有唯一解; 当D=0,Dx0或Dy0时,方程组无解; 当D=0,Dx=Dy=0时,方程组有无穷多组解。
2、二元一次方程组的系数行列式D0是 方程组有唯一解的的充要条件。
思考题:
(A)“二元一次方程组系数行列式D=0”是“方程组有唯一解”
问题一:方程组84
x x
3 6
y y
5 的解的情况如何?
22
解: 原方程组可化 为44
x x
3 3
y y
5, 11
∴方程组无解。
此时 D= 4 3 =0
86
而Dx 5
3 36 0
22 6
方程Dx=Dx无解 即方程组无解。
问题二:方程组84
x x
3 6
y y
11的解的情况如何?
22
解:
原方程组可化为44
x x
3y 3y
11, 11
∴有无穷多组解。
此时 D= 4 3 =0
86
而Dx 11 3 0
22 6
而Dy 3
11
0
6 22
方程组
Dx
Dy
Dx Dy
有无数组解。
二元一次方程组解的判别
(2)当D=0即m=2或-2,
x
Dx D
y
Dy D
m m2
m1 m2
(i)若m=2,D=Dx=Dy=0, 方程组有无数多组解; (ii)若m=-2,D=0, Dx0, 方程组无解。
1. 不解方程组,判别下列方程组解的情况:
(1)52
x x
3 2
y y
的
条件。
(B)构造一个二元一次方程组,使它的解的情况分别是
“有唯一解”、“无解”、“有无穷多解”.
选做题:用行列式解方程组
5 x
7 y
3
7
x
9 y
4
1 1
Dx 2m 3
m 2m 3 (m 3) m
m Dy 3m
1 2m2 3m 3m 2m(m 2m 3
当m0且m-3时,方程组有唯一解
3)
x
y
Dx D Dy D
1 m
2
当m=-3时,D=Dx=Dy=0,∴方程组有无穷多解;
1、 a1 a2
b1 b2
a1b2 a2b1
2、用行列式解二元一次方程组
4 x 8 x
3 6
y y
5 22
解:D 4
8
3 6
48
0,Dx
5 22
3
4
6 96, Dy 8
5 48
22
方程组
的 解 为
x
y
Dx D Dy D
2 1
当D=0,而Dx=0且Dy=0时,方程组有无数多组解。
问题三:解关于x,y的二元一次方程组
mx
x
4Байду номын сангаасmy
ym m
2
,
并对解的情况进行讨论。
解:D= m 4 m2 4
1m
Dx=
m m
2
4 m2 2m
m
m Dy= 1
m2 m
m2 m 2
(1)当D0即m2时,方程组有唯一解
7 1
4x 2 y 3 (2)18x 9 y 5
4x 5 y 8
(3) 2 x
5 2
y
4
解:(1) D 2 3 415 0, ∴方程组有唯一解。
5 2
(2) D 4
18
2
3
9 0, Dx 5
2 17 0, ∴方程组无解。
一般地,通过消元法可将二元一次方程组
a1 x a2 x
b1 y b2 y
c1 c2
,其中 D
a1 a2
b1 b2
, Dx
c1 c2
b1 , b2
D当yD0aa时12 ,cc12方,程组有D唯叫一做解方程xy 组 DD解DDxy 的;判别式
当D=0,而Dx0或Dy0时,方程组无解;
9
4
(3) D 2
5
8
5 0, Dx 4
2
5
4
5 0, 2
Dy 2
8 0
4
∴方程组有无穷多解。
2.
解关于x、y的二元一次方程组
mx
y
1
3mx my 2m 3
并对解的情况进行讨论。
解:D m 1 m2 3m m(m 3)
3m m
