信号与系统分析(张华清)第二章PPT课件
合集下载
信号与系统 第二章ppt剖析

网络拓扑约束:由网络结构决定的电压电流约束关系, KCL,KVL。
第
例1 求并联电路的端电压 vt 与激励 is t 间的关系。
7 页
电阻
iR t
1 R
vt
电感
iLt
1 L
t v d
ist
电容
iC
t
C
dv d
t
t
iR iL R LC
a ic
vt
b
根据KCL iRt iLt iC t iS t
系统的完全响应
第 17
页
求出齐次解rh t 和特解rp t 相加即得方程的完全解:
n
rt Aieit rp t i 1
利用初始条件求待定系数Ai 我们一般将激励信号加入的时刻定义为t=0,响应
的求解区间定为 t ,如0 果响应在0时刻没有跳变,通常
取t=0,这样对应的一组条件称为初始条件。
1
2
10
B1
, 3
B2
, 9
B3 27
所以,特解为
rp t
1 3
2 9
t
10 27
第 15
页
(2)
(原方程:
d2 rt
dt2
2
d rt
dt
3r t
d et
dt
et
)
当et et时, 很明显, 可选rt Bet。这里,B是待定系数。
代入方程后有:
Bet 2Bet 3Bet et et
于是,特解为 1 et。 3
B 1 3
几种典型激励函数相应的特解
第 16
页
激励函数e(t)
E(常数)
响应函数r(t)的特解
第
例1 求并联电路的端电压 vt 与激励 is t 间的关系。
7 页
电阻
iR t
1 R
vt
电感
iLt
1 L
t v d
ist
电容
iC
t
C
dv d
t
t
iR iL R LC
a ic
vt
b
根据KCL iRt iLt iC t iS t
系统的完全响应
第 17
页
求出齐次解rh t 和特解rp t 相加即得方程的完全解:
n
rt Aieit rp t i 1
利用初始条件求待定系数Ai 我们一般将激励信号加入的时刻定义为t=0,响应
的求解区间定为 t ,如0 果响应在0时刻没有跳变,通常
取t=0,这样对应的一组条件称为初始条件。
1
2
10
B1
, 3
B2
, 9
B3 27
所以,特解为
rp t
1 3
2 9
t
10 27
第 15
页
(2)
(原方程:
d2 rt
dt2
2
d rt
dt
3r t
d et
dt
et
)
当et et时, 很明显, 可选rt Bet。这里,B是待定系数。
代入方程后有:
Bet 2Bet 3Bet et et
于是,特解为 1 et。 3
B 1 3
几种典型激励函数相应的特解
第 16
页
激励函数e(t)
E(常数)
响应函数r(t)的特解
信号与系统课件第二章解读

8.1 Z变换的定义
fs (t) f (t) T (t) f (t) (t kT)
k
Fs (s)
f (t ) (t kT )estdt
k
f (kT )eskT
k
引入一个新的复变量z,令z esT或s 1 ln z T
则上式变为F (z) f (k )zk k
当 1时,级数收敛, 1时,级数发散, 1不定
8.1 Z变换的定义
3、有限长序列的收敛域
f (k) f (k) 0
k1 k k2 其它
k2
F (z) f (k )zk k k1
为有限项之和,最小收敛域为0 z
若k1 0, k2 0则存在负幂项,z 0 若k1 0, k2 0则只有正幂项,z 0,不含z , 0 z
Z[u(k)]
1 1 z1
z
z 1
即u(k) z z 1 z1
z 1
8.2 常用序列的Z变换
例3、求指数序列a k u(k )的z变换
解:Z[aku(k )] ak zk ( a )k
k0
k0 z
当 a 1即 z | a | 时,有 z
Z[aku(k)] 1 z 1 a za z
因为 a 1 ,所以 a z a1,则 f k 的双边Z变换存在
F z
z za
z z a1
z2
a a1 a a1
z z1
a z a1
若 a 1 ,则由于左边序列与右边序列的Z变换没有公共的收 敛域,此时该序列不存在双边Z变换。
8.3 Z变换的性质
1、线性性质
if
f1(k) F1(z) f2 (k) F2 (z)
| z || a |,
信号与系统第2章ppt课件

,这种频谱搬移技术在通信系统中
得到广泛的应用。调幅,调频都是
在该基础上进行的。
精选ppt
由此可见,将时间信号f(t)
乘以Cos(ω0t) 或Sin(ω0t)
,等效于将f(t)的频谱一分
为二,即幅度减小一半,沿
频率轴向左和向右各平移ω0.
第二章 傅立叶变换
例2 求如下矩形调幅信号的频谱函数
f(t) G (t)c o s 0 t
例7 如图a所示系统,已知乘法器的输入为
f (t) sin(2t) s(t)co3st)(
t
系统的频率响应为:
求输出y(t).
精选ppt
第二章 傅立叶变换
f (t) sin(2t) s(t)co3st)(
t
乘法器的输出信号为: x(t)f(t)s(t)
依频域卷积定理可知:X(j)21F(j)*S(j) 这里 f(t)F(j) s(t)S(j)
当 0 时 当 0 时
A () li m 0 A e () lim A e ( 0) lim 2 0 2 0
所以
A () li m 0A e()()
B()li m0Be()j
精选ppt
第二章 傅立叶变换
(6)符号函数 符号函数sgn(t)如图所示
由于sgn(t)不符合绝对可积条件, 故使用间接方法计算。
利用傅里叶反变换公式计算
第二章 傅立叶变换
例4 试求图示周期信号的频谱函数,图(b)中冲激函数的强度均为1.
(b)
[提示:(a)F()F[1]1F[cos(t)]
22
)
(b
Cn
1 T
T
2 T
fT(t)ejntdt
2
fT(t)(t)(tT2)
得到广泛的应用。调幅,调频都是
在该基础上进行的。
精选ppt
由此可见,将时间信号f(t)
乘以Cos(ω0t) 或Sin(ω0t)
,等效于将f(t)的频谱一分
为二,即幅度减小一半,沿
频率轴向左和向右各平移ω0.
第二章 傅立叶变换
例2 求如下矩形调幅信号的频谱函数
f(t) G (t)c o s 0 t
例7 如图a所示系统,已知乘法器的输入为
f (t) sin(2t) s(t)co3st)(
t
系统的频率响应为:
求输出y(t).
精选ppt
第二章 傅立叶变换
f (t) sin(2t) s(t)co3st)(
t
乘法器的输出信号为: x(t)f(t)s(t)
依频域卷积定理可知:X(j)21F(j)*S(j) 这里 f(t)F(j) s(t)S(j)
当 0 时 当 0 时
A () li m 0 A e () lim A e ( 0) lim 2 0 2 0
所以
A () li m 0A e()()
B()li m0Be()j
精选ppt
第二章 傅立叶变换
(6)符号函数 符号函数sgn(t)如图所示
由于sgn(t)不符合绝对可积条件, 故使用间接方法计算。
利用傅里叶反变换公式计算
第二章 傅立叶变换
例4 试求图示周期信号的频谱函数,图(b)中冲激函数的强度均为1.
(b)
[提示:(a)F()F[1]1F[cos(t)]
22
)
(b
Cn
1 T
T
2 T
fT(t)ejntdt
2
fT(t)(t)(tT2)
信号与系统 第二章ppt_part2
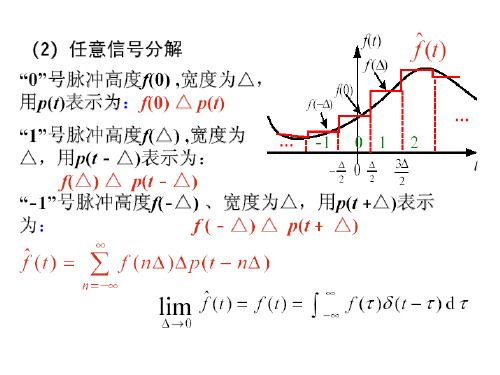
1
0 t 1
[1 e(t 1) ]
演示
[1 e(t 1) ]u(t 1) f1 (t ) f2 (t )
f1 (t )* f2 (t )
1
0
1
t
解法二:f 2 ( ) 不变,反褶 f1 ( ), f 2 ( ) f1 ( )
1 1 1
f1 (t ) f2 (t ) f 2 ( ) f1 (t )d
f
( 1) 2
t e d u ( ) e t u (t ) (1 e t )u (t ) (t ) e u ( )d 0
t
f1(t)*f2(t)=(1-e-t) u(t)- [(1-e-(t-2)] u(t-2)
n
即
y zs (t ) lim x(kt )h(t kt )t
t 0 k 0
y zs (t ) lim x(kt )h(t kt )t
t 0 k 0
n
当 t 0 时,t d , kt ,
t 0
t 0
lim
t k 0 0
s(t )
1 e
T
(t T )
e ]u(t T )
t
t
(t T )
]u(t T )
1
0
t
T
演示
例2-13 已知信号x(t)与h(t)如下图所示,求 h(t) x(t) 1 1
y(t ) x(t ) h(t )
-1/2 0 解:
1
t
0
2
t
y (t ) x( )h(t )d
h(t )
1
0 t 1
[1 e(t 1) ]
演示
[1 e(t 1) ]u(t 1) f1 (t ) f2 (t )
f1 (t )* f2 (t )
1
0
1
t
解法二:f 2 ( ) 不变,反褶 f1 ( ), f 2 ( ) f1 ( )
1 1 1
f1 (t ) f2 (t ) f 2 ( ) f1 (t )d
f
( 1) 2
t e d u ( ) e t u (t ) (1 e t )u (t ) (t ) e u ( )d 0
t
f1(t)*f2(t)=(1-e-t) u(t)- [(1-e-(t-2)] u(t-2)
n
即
y zs (t ) lim x(kt )h(t kt )t
t 0 k 0
y zs (t ) lim x(kt )h(t kt )t
t 0 k 0
n
当 t 0 时,t d , kt ,
t 0
t 0
lim
t k 0 0
s(t )
1 e
T
(t T )
e ]u(t T )
t
t
(t T )
]u(t T )
1
0
t
T
演示
例2-13 已知信号x(t)与h(t)如下图所示,求 h(t) x(t) 1 1
y(t ) x(t ) h(t )
-1/2 0 解:
1
t
0
2
t
y (t ) x( )h(t )d
h(t )
1
信号与系统课件 L02_CH2 更多课件可进我文库查看

:初始相位
周期信号
t
0
0
T0
2π
0
A
4
2.1 连续时间信号的时域描述
——典型普通信号
3. 指数类信号 — 实指数信号
f (t ) Aet
f (t ) Ae
t
0
0
A
0
t
5
2.1 连续时间信号的时域描述
——典型普通信号
3. 指数类信号 — 虚指数信号
周期性:
f (t ) ' (t t0 )dt f ' (t0 )
(取样特性) (展缩特性)
' (t )
1
' (t )
( 0)
' (t ) ' (t )
' (t )dt 0
29
d (t ) ' (t ) dt
(t ) ' ( )d
t
du(t ) (t ) dt dr (t ) u(t ) dt
u (t ) ( )d
t
r (t ) u ( )d
30
t
f (t ) e
j0t
f (t ) f (t T ) e j0t e j0 (t T )
0T 2πm, m 1, 2
虚指数信号的基本周期:
Euler公式: 1 j t cos( t ) (e e jt ) 2
T 2π
0
1 jt sin(t ) (e e jt ) 2j
1 t 0 u(t ) ( )d 0 t 0
信号与系统第二章ppt课件

解 先画出f1(t-τ)|t=0, 即f1(-τ)和f2(τ)波形如题解图2.6(a)所 示。再令t从-∞ 开始增长,随f1(t-τ)波形右移,分区间计算卷 积积分:
30
第2章 连续信号与系统的时域分析 31
最后整理得
第2章 连续信号与系统的时域分析
波形如题解图2.6(b)所示。
32
第2章 连续信号与系统的时域分析
3
(2) 因为
第2章 连续信号与系统的时域分析
所以
4
第2章 连续信号与系统的时域分析
2.2 写出下列复频率s所表示的指数信号est的表达式,并画 出其波形。
(1) 2; (2) -2; (3) -j5; (4) -1+j2。
5
第2章 连续信号与系统的时域分析
解 (1) f1(t)=e2t,波形如题解图2.2(a)所示。 (2) f2(t)=e-2t, 波形如题解图2.2(b)所示。显然, f1(t)和f2(t)都 是实指数信号。 (3) f3(t)=e-j5t=cos5t-j sin5t。f3(t)是虚指数信号,其实部、 虚部分别是等幅余弦、正弦信号。实部信号波形如题解图2.2(c) 所示。 (4) f4(t)=e(-1+j2)t=e-t·ej2t=e-t(cos2t+j sin2t)。f4(t)是复指数信 号,其实部和虚部分别是幅度按指数规律衰减的余弦和正弦信 号。实部信号波形如题解图2.2(d)所示。
(4) 由于tε(t)|t=-∞=0,有 所以
38
第2章 连续信号与系统的时域分析
2.8 已知f1(t)和f2(t)如题图2.4所示。设f(t)=f1(t)*f2(t),试求 f(-1)、f(0)和f(1)的值。
题图 2.4
30
第2章 连续信号与系统的时域分析 31
最后整理得
第2章 连续信号与系统的时域分析
波形如题解图2.6(b)所示。
32
第2章 连续信号与系统的时域分析
3
(2) 因为
第2章 连续信号与系统的时域分析
所以
4
第2章 连续信号与系统的时域分析
2.2 写出下列复频率s所表示的指数信号est的表达式,并画 出其波形。
(1) 2; (2) -2; (3) -j5; (4) -1+j2。
5
第2章 连续信号与系统的时域分析
解 (1) f1(t)=e2t,波形如题解图2.2(a)所示。 (2) f2(t)=e-2t, 波形如题解图2.2(b)所示。显然, f1(t)和f2(t)都 是实指数信号。 (3) f3(t)=e-j5t=cos5t-j sin5t。f3(t)是虚指数信号,其实部、 虚部分别是等幅余弦、正弦信号。实部信号波形如题解图2.2(c) 所示。 (4) f4(t)=e(-1+j2)t=e-t·ej2t=e-t(cos2t+j sin2t)。f4(t)是复指数信 号,其实部和虚部分别是幅度按指数规律衰减的余弦和正弦信 号。实部信号波形如题解图2.2(d)所示。
(4) 由于tε(t)|t=-∞=0,有 所以
38
第2章 连续信号与系统的时域分析
2.8 已知f1(t)和f2(t)如题图2.4所示。设f(t)=f1(t)*f2(t),试求 f(-1)、f(0)和f(1)的值。
题图 2.4
信号与系统PPT课件(共9章)第2章连续时间信号的时域分析可修改全文

17
2.3 奇异信号
在信号与系统分析中,经常要遇到函数本身有不连续 点或其导数与积分有不连续点的情况,这类函数统称为奇 异函数或奇异信号。
1. 单位斜变信号
斜变信号指的是从某一时刻开始随时间正比例增长的 信号。其表达式为
R(t)
t 0
t0 t0
(2.2 1)
R(t)
R(t
t0
)
t 0
t0
t t0 t t0
0 cos
e jt cos t j sin t -1 12
2.2 常用连续时间信号
3. Sa(t)函数(抽样函数)
所谓抽样函数是指sin t与 t 之比构成的函数,以符号
Sa(t)表示 Sa(t) sin t t
波形如图:
(2.2 5)
13
2.2 常用连续时间信号
Sat 的性质:
(1) Sat Sa(t) 偶信号
6
2.2 常用连续时间信号
1. 实指数信号 2. 正弦信号 3. 抽样函数 4. 复指数信号 重点:典型确定性信号的描述 难点:复指数信号,抽样信号
7
2.2 常用连续时间信号
下面,我们将给出一些典型信号的表达式和波形。
1. 指数信号 指数信号的表达式为
f (t) Aet
(2.2 1)
f (t) Aet ( 0)
34
2.4 信号的运算
1. 信号的加减 2. 信号的乘法和数乘 3. 信号的反褶、时移、尺度变换 4. 信号的微分与积分运算 5. 信号的卷积
重点:信号的尺度变换,信号的卷积积分 难点:信号时移、反褶、尺度变换同时都有的情况
35
2.4 信号的运算
1. 信号的加减
两个信号的和(或差)仍然是一个信号,它在任意 时刻的值等于两信号在该时刻的值之和(或差),即
2.3 奇异信号
在信号与系统分析中,经常要遇到函数本身有不连续 点或其导数与积分有不连续点的情况,这类函数统称为奇 异函数或奇异信号。
1. 单位斜变信号
斜变信号指的是从某一时刻开始随时间正比例增长的 信号。其表达式为
R(t)
t 0
t0 t0
(2.2 1)
R(t)
R(t
t0
)
t 0
t0
t t0 t t0
0 cos
e jt cos t j sin t -1 12
2.2 常用连续时间信号
3. Sa(t)函数(抽样函数)
所谓抽样函数是指sin t与 t 之比构成的函数,以符号
Sa(t)表示 Sa(t) sin t t
波形如图:
(2.2 5)
13
2.2 常用连续时间信号
Sat 的性质:
(1) Sat Sa(t) 偶信号
6
2.2 常用连续时间信号
1. 实指数信号 2. 正弦信号 3. 抽样函数 4. 复指数信号 重点:典型确定性信号的描述 难点:复指数信号,抽样信号
7
2.2 常用连续时间信号
下面,我们将给出一些典型信号的表达式和波形。
1. 指数信号 指数信号的表达式为
f (t) Aet
(2.2 1)
f (t) Aet ( 0)
34
2.4 信号的运算
1. 信号的加减 2. 信号的乘法和数乘 3. 信号的反褶、时移、尺度变换 4. 信号的微分与积分运算 5. 信号的卷积
重点:信号的尺度变换,信号的卷积积分 难点:信号时移、反褶、尺度变换同时都有的情况
35
2.4 信号的运算
1. 信号的加减
两个信号的和(或差)仍然是一个信号,它在任意 时刻的值等于两信号在该时刻的值之和(或差),即
《信号与系统分析》课件第2章

p 1 y(t) 1 py(t)
p
p
(2.12)
p 1 y(t) d t y( )d y(t)
p
dt
1 py(t) t [ d y( )] d y(t) y() y(t)
p
d
(对应先微分后积分)的算子运算不 能相消, 而对“先除后乘”(对应先积分后微分)的算子运算 可以相消。
u(t)与i(t)之间的关系。 解 画出图2.3(a)所示电路对应的算子模型如图
2.3(b)
图 2.3 例2.3的图
由节点电压法列出u(t)
( p 1 1 )u(t) i(t) 2 2 22p
(p2+2p+2)u(t)=2(p+1)i(t)
d 2u (t ) d2t
2
du(t) dt
2 y(t )
图 2.2 例2.2的电路图
解 设两回路中的电流分别为i1(t)和i2(t), 由基尔霍
LCR2e(t)
L di1(t) 1 dt C
t
i2 ( )d R2i2 (t) e(t)
LR1e(t)
1 1 d2u(t)
L
du(t) 1
de(t)
L( ) R1 R2
d2t
(
1)
R1R2C
dt
y(t)=yzi (t)+yzs(t) 式中, yzi (t)为零输入响应, yzs (t)为零状态响应。
(2.24)
2.2.2
1. 系统的零输入响应是指没有外加激励信号的作用, 仅由 系统初始状态所产生的响应。 为求系统的零输入响应就要
7
d
2 y(t d2t
)
16 dy(t) dt
12 y(t )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1 描述某LTI系统的数学模型为y''(t)5y'(t)6y(t)e(t) 已 知 e ( t) 1 0 c o s t( t) ,y ( 0 ) 2 ,y '( 0 ) 0 求系统响应 y(t) (t)
l l 解 : 特 征 方 程 2 + 5+ 6 = 0
l l 特 征 根 1 = - 2 , 2 = - 3
5P5P5Q5Q100
P 1
Q
1
ypt= co st+ sint2co s(t- 4)
全 解yt= ypt+ yht
代人初始条= 件c1e- 2t+ c2e- 3t+2cost- 4
yy00 = = c- 1+2 cc21 + - 3c 22- cos24sin = 24= 0
c1= 2 c2= - 1
其各阶导数在t=0处的跳变量
y
( f
j)
(0
)
,在此(t)仅
用来表示在t=0处有一个单位的跳变量。
例3: y''(t)4y'(t)3y(t)d'(t)2d(t)
已知 y(0)1, y'(0)0
求 y'(0+), y(0)
总结:用d函数平衡法求响应及其各阶导数在激励加人 时刻的跳变量时,应注意以下几点:
齐 次 解 y ht= c 1 e - 2 t+ c 2 e - 3 t 查 表 2 - 2 , 可 设 特 解 为 y p t = P c o s t + Q s i n t
求 yp、 yp, 将 yp、 yp、 yp代 人 原 方 程 , 整 理 后 有
5P5Q cost+ - 5P + 5Q sint= 10cost
(2) e(t) d (t)时 y(0 )
(3) e(t) d (t)时 y(0 )
注意:匹配应从微分方程的最高阶项开始
发生跳变的条件:微分方程右端含d(t)及其各阶导数
例2:y''(t)3y'(t)2y(t)2d(t)6(t)
已知 y(0)2, y'(0)0 求 y'(0+), y(0)
注意:d匹配法不是求方程的解, 而仅仅求响应y(t)及
t=0
uC1
uC2
C1=1F
C2=1/2F
b. d匹配法( d函数平衡法)
对任意系统的数学模型普遍适用的方法 基本思路:
n
m
(1 ) Q a iy(i)(t) b je(j)(t) 0 t
i 0
j 0
n
m
a iy(i)(t) bje(j)(t) 0t0
i 0
j 0
(2)引入d(t)后函数在跳变点的导数存在
解 得y(t)= yht+ ypt
2e2t e3t 2cos(t4)(t)
y(t)= 2 e 2 t e 3 t2c o s(t) t 0
4
齐次解 自由响应
暂态响应
特解 强迫响应 稳态响应
当输入信号是阶跃函数或有始的周期 函数时,系统的全响应也可分解为瞬态响 应和稳态响应。
2.1.2 关于系统在t=0-与0+状态的讨论(难点)
求解微分方程时,一般限于0+t范围, 应当利用y(j)(0)作为初始条件,求齐次解的系数。 因此,需要从已知的初始状态y(j)(0-)设法求得 y(j)(0)。
2. 初始条件(即跳变量) 的确定方法
a. 对电路模型利用物理概念进行判断
已 知 u 1 ( 0 ) 1 V u 2 ( 0 ) 0 求 u 1 ( 0 ) u 2 ( 0 ) u ( 0 )
讨论的前提
n
m
1 ) a iy(i)(t) bje(j)(t) 0t
i 0
j 0
2) t <0时 e(t)=0
3)求 t 0时系统的响应y(t)
1. 初始状态与初始条件
e (t)加入
y ( j ) (0 ) 初始状态(第二类初始条件)
j0,1,2,L,n1
e (t) 加入 e(t) 加入
初始状态反映历史信息而与激励无关
第二章 连续时间系统的时域分析
时域分析:对系统的分析与计算均以时间t 为变量 优点:直观、物理概念清楚 缺点:对高阶系统或复杂激励计算复杂
2.1 系统微分方程的经典解
一、微分方程(数学模型)的建立
为建立线性系统的数学模型,需找出描述其工作
特性的微分方程式。
图所示电路写出以uL为响应的数学模型
is
iL
如果由于激励信号的加入,在方程右端出现d(t)及其 各阶导数,则方程左端也相应产生与之对应的d(t)及其 各阶导数项使之方程两端平衡 ,而左端冲激函数的产 生意味着左端y ( i )(t)中的某些项在t=0处有跳变。
例1: y' (t) 3y(t) 3e(t) y(0 ) 0
求 (1)e(t) (t)时 y(0 )
iR
ic
L
i
'' L
R
i
' L
1 C
iL
L uL
R uR C
uC
R
1 C
i
s
写出图所示系统的数学模型
e (t)
x ''' ( t )
1
y (t)
2
x '' ( t 5
x (t)
e (t)
y (t)
LTI
对于任意一个单输入—单输出的LTI系统,其数学模 型的一般形式为
a n y ( n ) (t ) an1y(n1)(t)L a1y'(t) a 0 y (t ) bme(m) (t) bm1e(m1)(t) L b1e' (t) b0 e ( t )
简记为
n
m
aiy(i)(t) bje(j)(t)
i0
j0
二、微分方程的经典解法
用时域法求解连续系统的流程图
建立系统的微分方程
求特征根li , 确定齐次解
yh(t)的形式(查表2–1)
由e(t)确定特解yp(t)
的形式(查表2–2)
y(t)yh(t)yp(t)(含待定系数)
由初始条件确定系数
系统响应y(t)
(1)此方法只匹配d(t)及其各阶导数,使方程两边 d(t)及其各阶导数平衡。 (2)此方法先使方程右边d(t)最高次导数项与方程 左边y ( i )(t)的最高阶次项得到平衡。 (3)当平衡低阶次d(t)项时,若方程左边同阶次d(t)函 数项的系数之和不能与右边平衡时,则由方程左边y ( i )(t) 的最高阶次项来补偿。
前瞬间 后瞬间
0– 0+ 0
y ( j ) (0 ) 初始条件(第一类初始条件)
t
由 y(j)(0 )和 e(t)共 同 决 定
y (j)(t)从 0 :0 可 能 发 生 跳 变 即 y(j)(0)y(j)(0)
令 V y ( j ) ( 0 ) y ( j ) ( 0 + ) - y ( j ) ( 0 - ) 跳 变 量
