偏置直动滚子推杆盘形凸轮Matlab编程(附录程序)
matlab解析法画凸轮轮廓线
班级：：学号：基于matlab的凸轮轮廓设计一、设计凸轮机构的意义在工业生产中，经常要求机器的某些部件按照规定的准确路线运动，仅应用连杆机构已难以满足这个要求，所以需要利用工作外表具有一定形状的凸轮。
凸轮在所有基本运动链中，具有易于设计和能准确预测所产生的运动的优点。
如果设计其他机构来产生给定的运功、速度、和加速度，其设计工作是很复杂的，但是设计凸轮机构则比较容易，而且运动准确、有效。
所以在许多机器中，如纺织机、包装机、自动机床、自动化专用机床、数控机床、印刷机、内燃机、建筑机械、矿山机械、电脑的辅助装备及农业机具等，都可以找到凸轮机构。
在进行研究时，先设计一个简单的凸轮，在给定的旋转角度内有一定的总升距。
设计凸轮轮廓的基本方法是把凸轮固定，使从动件以其与凸轮的相关位置绕凸轮回转而形成凸轮轮廓。
因此设计凸轮时，必须画出足够多的点，使凸轮轮廓平滑可靠。
Matlab软件提供了强大的矩阵处理和绘图功能，具有核心函数工具箱。
其编程代码接近数学推导公式，简洁直观，操作简易，人机交互性能好。
因此，基于matlab软件进行凸轮机构的设计可以解决设计工作量大的问题。
运用解析法进行设计，matlab可以精确的计算出轮廓上每一点的坐标，然后更为精确的绘制出凸轮轮廓曲线。
二、设计凸轮机构的已知条件凸轮做逆时针方向转动，从动件偏置在凸轮轴心右边。
从动件在推程做等加/减速运动，在回程做余弦加速运动。
基圆半径rb=50mm，滚子半径rt=10mm，推杆偏距e=10mm，推程升程h=50mm，推程运动角ft=100º，远休止角fs=60º，回程运动角fh=90º。
三、分析计算1、建立坐标系以凸轮轴心为坐标原点建立平面直角坐标系XOY，取杆件上升方向为Y轴正方向。
2、推杆运动规律计算凸轮运动一周可分为5个阶段：推程加速阶段、推程减速阶段、远休止阶段、回程阶段、进休止阶段。
根据已知条件，推程阶段为等加/减速，故推程阶段的运动方程为：推程加速阶段〔0~f t/2〕{s(f)=2∗ℎ∗f2ft2v(f)=ds(f)=4∗ℎ∗fft2推程减速阶段〔f t/2~f t〕{s(f)=ℎ−2∗ℎ∗(f t−f)2ft2v(f)=ds(f)=4∗ℎ∗(f t−f)ft2远休止阶段〔f t~(f t+f s)〕推杆运动方程为{s(f)=0v(f)=ds(f)=0根据已知条件，在回程做余弦加速运动，因此回程阶段〔(f t+f s)~(f t+f s+fℎ)〕的运动方程为{s(f)=ℎ∗[1+cos(π∗(f−f t−f s)fℎ)]2v(f)=ds(f)=−π∗ℎ∗sin(π∗(f−f t−f s)fℎ)2∗fℎ近休止阶段（(f t+f s+fℎ)~360°〕的运动方程为{s(f)=0v(f)=ds(f)=0 3、凸轮理论轮廓线计算{x(f)=[s e+s(f)]∗sin(f)+e∗cos(f) y(f)=[s e+s(f)]∗cos(f)−e∗sin(f)式中s e=√r b2−e2，为推杆滚子中心到X轴的垂直距离。
基于Matlab和Pro_E的凸轮轮廓曲线精确设计_陈韵
Ｐｒｅｃｉｓｅ Ｄｅｓｉｇｎ ｏｆ ｔｈｅ Ｃａｍ Ｐｒｏｆｉｌｅ Ｃｕｒｖｅ ｂａｓｅｄ ｏｎ ＭＡＴＬＡＢ ａｎｄ Ｐｒｏ ／Ｅ
ＣＨＥＮ Ｙｕｎ （Ｈｅｎａｎ Ｍｅｃｈａｎｉｃａｌ ａｎｄ Ｅｌｅｃｔｒｉｃａｌ Ｅｎｇｉｎｅｅｒｉｎｇ Ｃｏｌｌｅｇｅ， Ｘｉｎｘｉａｎｇ Ｈｅｎａｎ ４５３００２，Ｃｈｉｎａ）
７π ６ ≤ δ４ ≤ ３π。 推杆的位移方程为
S＝０ 。
２ ＭＡＴＬＡＢ 程序的编制和三维建模
根据凸轮理论轮廓曲线的数学模型，在 ＭＡＴ－
收稿日期：２０１１－０１－０１ 作者简介：陈 韵（１９７８—），女，河南淮阳人，助教，硕士，研究方向为先进制造技术。
77
Equipment Manufactring Technology No.4，2011
中图分类号：ＴＨ１２２
文献标识码：Ｂ
文章编号：１６７２－５４５Ｘ（２０１１）０４－００７７－０２
凸轮机构在各种机械，特别是自动机械和自动 控制装置中被广泛应用。凸轮机构的最大优点，就是 只要适当设计出凸轮的轮廓曲线，就可以使推杆得 到各种预期的运动规律。因此凸轮机构的设计，关键 是获得精确的凸轮轮廓曲线。如果用作图法和解析 法来设计凸轮轮廓，一种方法是精确度低，一种方法 是工作量大。随着计算机的快速发展，凸轮机构的设 计效率也得到了快速提高。
所示。
图 １ ＭａｔＬａｂ 凸轮理论轮廓曲线 Ｍ 文件程序
图 ４ Ｐｒｏ／Ｅ 凸轮轮廓曲线
图 ５ 凸轮的三维模型
３ 结束语
图 ２ ＭａｔＬａｂ 凸轮理论轮廓曲线
运 行 程 序 生 成 凸 轮 理 论 轮 廓 曲 线 坐 标 的 ．ＩＢＬ 文件，但这还不完全符合 Ｐｒｏ／Ｅ 的文件格式，需要修 改一下。用记事本打开 ｔｕｌｕｎ．Ｉｂｌ，在文件前加入命 令，如图 ３ 所示。
偏置直动滚子推杆盘形凸轮Matlab编程(附录程序)
机械原理大作业学院：机械与电子信息学院授课老师：曾小慧姓名：张京学号：20131004547日期：2015-5-23目录1.求轮廓曲线○1推程阶段○2远休止阶段○3回程阶段○4近休止阶段○5Matlab程序设计○6轮廓图形2.求工作廓线○1推程阶段○2远休止阶段○3回程阶段○4近休止阶段○5Matlab程序设计○6轮廓图形３．求解最大压力角○1压力角公式○2MATLAB程序设计○3根据MATLAB程序作图可得出其压力角与角度的关系并分析○4失真情况分析４．附录 Matlab程序凸轮轮廓9-14试设计偏置直动滚子推杆盘形凸轮机构的理论轮廓曲线和工作廓线。
已知凸轮轴置于推杆轴线右侧，偏距e=20mm ，基圆半径ｒ。
=50mm ，滚子半径rr=10mm 。
凸轮以等角速度沿顺时针方向回转，在凸轮转过角d 1=120º的过程中，推杆按正弦加速度运动规律上升h=50mm ；凸轮继续转过d 2=30º时，推杆保持不动；其后，凸轮再回转角度d 3=60º时，推杆又按余弦加速度运动规律下降至起始位置；凸轮转过一周的其余角度时，推杆又静止不动。
解：1.求理论廓线对于偏置直动滚子推杆盘形凸轮机构，凸轮理论廓线上B 点（即滚子中心）的直角坐标为]cos sin )[(0δδe s s x ++-=δδsin cos )(0e s s y -+= （a ） 式中mm mm e r s 826.452050222200=-=-=① 推程阶段3212001πδ=︒=)]2/()3sin()2/3[()]2/()/2sin()/[(110110111πδπδπδπδδδ-=-=h h s （⎥⎦⎤⎢⎣⎡=32,01πδ） ② 远休止阶段 63002πδ=︒=502=s ⎥⎦⎤⎢⎣⎡=6,02πδ③ 回程阶段36003πδ=︒=2/)]3cos(1[2/)]/cos(1[30333δδπδ+=+=h h s ⎥⎦⎤⎢⎣⎡=3,03πδ ④ 近休止阶段6515004πδ=︒= 04=s ⎥⎦⎤⎢⎣⎡=65,04πδ○5Matlab 程序设计： a1=linspace(0,2*pi/3); %推程阶段的自变量s1=h*(3*a1/2/pi-sin(3*a1)/2/pi); %推杆产生的相应位移x1=-((s0+s1).*sin(a1)+e*cos(a1)); %x 函数y1=(s0+s1).*cos(a1)-e*sin(a1); %y 函数a2=linspace(0,pi/6); %远休止阶段的自变量s2=50; %推杆位移x2=-((s0+s2).*sin(a2+2*pi/3)+e*cos(a2+2*pi/3)); %x 函数y2=(s0+s2).*cos(a2+2*pi/3)-e*sin(a2+2*pi/3); %y 函数a3=linspace(0,pi/3); %回程阶段的自变量s3=h*(1+cos(3*a3))/2; %推杆位移x3=-((s0+s3).*sin(a3+5*pi/6)+e*cos(a3+5*pi/6)); %x 函数y3=(s0+s3).*cos(a3+5*pi/6)-e*sin(a3+5*pi/6); %y 函数a4=linspace(0,5*pi/6); %近休止阶段的自变量s4=0; %推杆位移x4=-((s0+s4).*sin(a4+7*pi/6)+e*cos(a4+7*pi/6)); %x 函数y4=(s0+s4).*cos(a4+7*pi/6)-e*sin(a4+7*pi/6); %y 函数a0=linspace(0,2*pi); %基圆自变量x5=r0*cos(a0); %x 函数y5=r0*sin(a0); %y 函数○6轮廓图形 通过Matlab 软件，编写程序,将以上各相应值代入式(a)计算理论轮廓线上各点的坐标值。
偏置直动滚子从动件盘形凸轮机构
河北工程大学机电学院机械原理课程设计说明书设计题目：偏置直动滚子从动杆盘型凸轮机构班级：姓名：学号：目录（一）设计题目及设计思路 (1)（二）凸轮基圆半径及滚子尺寸的确定 (1)（三）原始数据分析…………（四）从动杆的运动规律及凸轮轮廓线方程 (3)（五）凸轮机构的廓线设计原理 (4)（六）图解法设计盘型凸轮机构……………（七）检验压力角是否满足许用压力角的要求 (7)（八）机构示意简图 (8)（九）计算机源程序………（十）计算机程序结果及分析 (12)（一）机械原理课程设计的目的和任务一、机械原理课程设计的目的：1、机械原理课程设计是一个重要实践性教学环节。
其目的在于：进一步巩固和加深所学知识；2、培养学生运用理论知识独立分析问题、解决问题的能力；3、使学生在机械的运动学和动力分析方面初步建立一个完整的概念；4、进一步提高学生计算和制图能力，及运用电子计算机的运算能力。
二、机械原理课程设计的任务：1、偏置直动滚子从动杆盘型凸轮机构2、采用图解法设计：凸轮中心到摆杆中心A的距离为20mm，凸轮以逆时针方向等速回转，摆杆的运动规律如表：3、设计要求：①升程过程中，限制最大压力角αmax≤30º,确定凸轮基园半径r0②合理选择滚子半径rr③选择适当比例尺，用几何作图法绘制从动件位移曲线，并画于图纸上；④用反转法绘制凸轮理论廓线和实际廓线，并标注全部尺寸（用A2图纸）⑤将机构简图、原始数据、尺寸综合方法写入说明书4、用解析法设计该凸轮轮廓，原始数据条件不变，要写出数学模型，编制程序并打印出结果备注：凸轮轮廓曲率半径与曲率中心理论轮廓方程()()x xy yϕϕ=⎧⎨=⎩，其中2222////x dx d x d x dy dy d x d y dϕϕϕϕ⎧==⎪⎨==⎪⎩其曲率半径为：3 222 () x y xy xyρ+=--；曲率中心位于：2222()()y x yx xxy xyx x yy xxy xyρρ⎧+=-⎪-⎪⎨+⎪=-⎪-⎩三、课程设计采用方法：对于此次任务，要用图解法和解析法两种方法。
4-9偏置直动滚子从从动件盘形凸轮设计(精)
作者：韦志钢 单位：浙江工贸职业技术学院
所属学科：工科 课程：激光设备机械设计基础
专业：光机电应用技术 适用对象：光机电应用技术专业的学生
偏置直动滚子从动件盘形凸轮设计
教学目标：
了解偏置直动滚子从动件盘形凸轮设 计方法。
偏置直动滚子从动件盘形凸轮设计
问题引入：
已知凸轮的基圆半径为r0,滚子半径rr,,偏心 距e,已知运动规律，凸轮沿顺时针方向等速回转。 当尖顶从动件变成滚子从动件时如何设计凸轮轮 廓？
偏置直动滚子从动件盘形凸轮设计
已知偏置直动滚子从动件盘形凸轮，基圆 半径为rb,偏心距e,凸轮沿逆时针方向等速回 转，滚子半径rr。运动规律如右下图。试设计 此凸轮。Leabharlann 偏置直动滚子从动件盘形凸轮设计
-
S
h 1 2 s1
3
s2
1
1
2
2
rb
O
1'
1
s1
s2
1
h
3
e
作图方法： 2 ）以 O为圆心， rb 为 1) 先将滚子中心看作 4) 3) 将 在其切线与基圆 1 ， 2 ，3…. 连成 5) 以理论廓线上各点 6) 再作此圆族的包 半径作基圆，以 e 尖顶，然后按尖顶 光滑曲线，便是所要 的交点上量取 S1 、 为圆心，以滚子半径 络线，即为凸轮工 为半径作偏距圆， 偏置从动件凸轮廓 求的凸轮理论廓线； S2 、…得反转后尖 r 作廓线（实际廓 线的设计方法确定 r为半径，作一系列 在偏距圆上1’点 顶所占据的一系列 圆； 滚子中心的轨迹， 作其切线与基圆的 线）。 称其为凸轮的理论 位置，即 1、2、 交点为从动件尖顶 廓线； 3… ； 的初始位置；
凸轮的matlab绘制
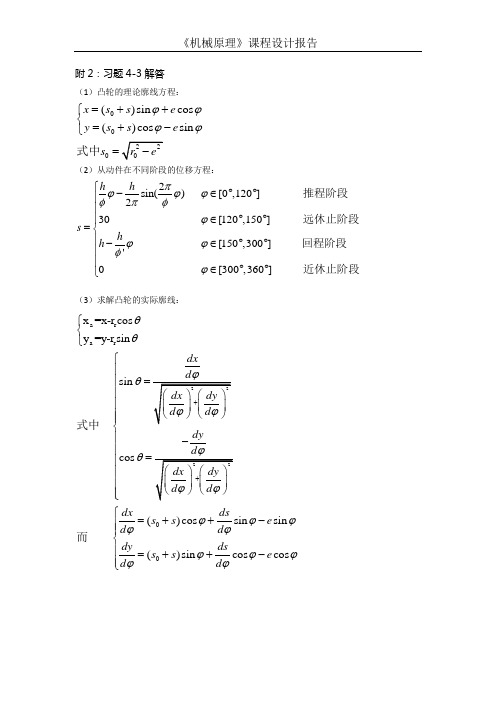
附2：习题4-3解答（1）凸轮的理论廓线方程：000()sin cos ()cos sin x s s e y s s e s ϕϕϕϕ=++⎧⎨=+-⎩=式中 （2）从动件在不同阶段的位移方程：2sin()[0,120]230[120,150][150,300]'0[300,360]h h s h h πϕϕϕφπφϕϕϕφϕ⎧-∈︒︒⎪⎪∈︒︒⎪=⎨⎪-∈︒︒⎪⎪∈︒︒⎩推程阶段远休止阶段回程阶段近休止阶段（3）求解凸轮的实际廓线：a r a r 00x =x-r cos y =y-r sin sin cos ()cos sin sin ()sin cos cos dx dy dxds s s e d d dy ds s s e d d θθθθϕϕϕϕϕϕϕϕϕϕ⎧⎨⎩⎧⎪=⎪⎪⎪⎪⎪⎨⎪-⎪=⎪⎪⎪⎪⎩⎧=++-⎪⎪⎨⎪=++-⎪⎩式中而同样，由于位移s 与从动件所处的运动阶段有关，所以有：2cos()[0,120]0[120,150]s [150,300]'0[300,360]h hd hd πϕϕφφφϕϕϕφϕ⎧-∈︒︒⎪⎪∈︒︒⎪=⎨⎪∈︒︒⎪⎪∈︒︒⎩推程阶段远休止阶段回程阶段近休止阶段（4）代入已知条件，并用Matlab 语言编程求解，编程代码如下： disp ' ******** 偏置直动滚子从动件盘形凸轮设计 ********' disp '已知条件:'disp ' 凸轮作逆时针方向转动,从动件偏置在凸轮轴心的右边'disp ' 从动件在推程作摆线运动规律运动,在回程作等速运动规律运动' ro = 50;rr = 10;e = 12;h = 30;ft = 120;fs = 30;fh = 150;fprintf (1,' 基圆半径 ro = %3.4f mm \n',ro) fprintf (1,' 滚子半径 rr = %3.4f mm \n',rr) fprintf (1,' 推杆偏距 e = %3.4f mm \n',e) fprintf (1,' 推程行程 h = %3.4f mm \n',h) fprintf (1,' 推程运动角 ft = %3.4f 度 \n',ft) fprintf (1,' 远休止角 fs = %3.4f 度 \n',fs) fprintf (1,' 回程运动角 fh = %3.4f 度 \n',fh) hd = pi / 180;du = 180 / pi; so = sqrt( ro^2 - e^2 ); d1 = ft + fs;d2 = ft + fs + fh; disp ' 'disp '计算过程和输出结果:'disp ' 1-1 推程(摆线运动规律运动)' s = zeros(ft);ds = zeros(ft);d2s = zeros(ft); for f = 1 : fts(f) = h * f / ft - h * sin(2 * pi * f / ft) / (2 * pi);s = s(f);ds(f) = h / (ft * hd) - h / (ft * hd) * cos(2 * pi * f / ft);ds = ds(f); d2s(f) = 2 * pi * h / (ft * hd) ^ 2 * sin(2 * pi * f / ft);d2s = d2s(f); enddisp ' 1-2 回程(等速运动规律运动)' s = zeros(fh);ds = zeros(fh);d2s = zeros(fh); for f = d1 : d2s(f) = h - h * (f-150) / fh; s = s(f); ds(f) = - h / (fh * hd);ds = ds(f); d2s(f) = 0;d2s = d2s(f); enddisp ' 2- 计算凸轮理论廓线与实际廓线的直角坐标'n = 360;s = zeros(n);ds = zeros(n);r = zeros(n);rp = zeros(n);x = zeros(n);y = zeros(n);dx = zeros(n);dy = zeros(n);xx = zeros(n);yy = zeros(n);xa = zeros(n);ya = zeros(n);xxa = zeros(n);yya = zeros(n);for f = 1 : nif f <= fts(f) = h * f / ft - h * sin(2 * pi * f / ft) / (2 * pi);s = s(f);ds(f) = h /(ft * hd) - h / (ft * hd) * cos(2 * pi * f / ft); ds = ds(f);elseif f > ft & f <= d1s = h;ds = 0;elseif f > d1 & f <= d2s(f) = h - h * (f-150) / fh; s = s(f);ds(f) = - h / (fh * hd);ds = ds(f);elseif f > d2 & f <= ns = 0;ds = 0;endxx(f) = (so + s) * sin(f * hd) + e * cos(f * hd); x = xx(f);yy(f) = (so + s) * cos(f * hd) - e * sin(f * hd); y = yy(f);dx(f) = (ds - e) * sin(f * hd) + (so + s) * cos(f * hd); dx = dx(f);dy(f) = (ds - e) * cos(f * hd) - (so + s) * sin(f * hd); dy = dy(f);xxa(f) = x + rr * dy / sqrt(dx ^ 2 + dy ^ 2);xa = xxa(f);yya(f) = y - rr * dx / sqrt(dx ^ 2 + dy ^ 2);ya = yya(f);r(f) = sqrt (x ^2 + y ^2 );rp(f) = sqrt (xa ^2 + ya ^2 );enddisp ' 2-1 推程(摆线运动规律运动)'disp ' 凸轮转角理论x 理论y 实际x 实际y' for f = 10 : 10 :ftnu = [f xx(f) yy(f) xxa(f) yya(f)];disp(nu)enddisp ' 2-2 回程(等速运动规律运动)'disp ' 凸轮转角理论x 理论y 实际x 实际y' for f = d1 : 10 : d2nu = [f xx(f) yy(f) xxa(f) yya(f)];disp(nu)enddisp ' 2-3 凸轮轮廓向径'disp ' 凸轮转角理论r 实际r'for f = 10 : 10 : nnu = [f r(f) rp(f)];disp(nu)enddisp '绘制凸轮的理论轮廓和实际轮廓:'plot(xx,yy,'r-.') % 理论轮廓(红色,点划线)axis ([-(ro+h-10) (ro+h+10) -(ro+h+10) (ro+rr+10)]) % 横轴和纵轴的下限和上限axis equal % 横轴和纵轴的尺度比例相同text(ro+h+3,0,'X') % 标注横轴text(0,ro+rr+3,'Y') % 标注纵轴text(-5,5,'O') % 标注直角坐标系原点title('偏置直动滚子从动件盘形凸轮设计') % 标注图形标题hold on; % 保持图形plot([-(ro+h) (ro+h)],[0 0],'k') % 横轴(黑色)plot([0 0],[-(ro+h) (ro+rr)],'k') % 纵轴(黑色)plot([e e],[0 (ro+rr)],'k--') % 初始偏置位置(黑色,虚线) ct = linspace(0,2*pi); % 画圆的极角变化范围plot(ro*cos(ct),ro*sin(ct),'g') % 基圆(绿色)plot(e*cos(ct),e*sin(ct),'c--') % 偏距圆(蓝绿色,虚线)plot(e + rr*cos(ct),so + rr*sin(ct),'y') % 滚子圆(黄色)plot(xxa,yya,'b') % 实际轮廓(蓝色)（5）求解凸轮理论廓线和实际廓线坐标值如下：******** 偏置直动滚子从动件盘形凸轮设计********已知条件:凸轮作逆时针方向转动,从动件偏置在凸轮轴心的右边从动件在推程作摆线运动规律运动,在回程作等速运动规律运动基圆半径ro = 50.0000 mm滚子半径rr = 10.0000 mm推杆偏距 e = 12.0000 mm推程行程h = 30.0000 mm推程运动角ft = 120.0000 度远休止角fs = 30.0000 度回程运动角fh = 150.0000 度计算过程和输出结果:1-1 推程(摆线运动规律运动)1-2 回程(等速运动规律运动)计算凸轮理论廓线与实际廓线的直角坐标2-1 推程(摆线运动规律运动)凸轮转角理论x 理论y 实际x 实际y10.0000 20.2659 45.8284 16.5674 36.537520.0000 28.1734 42.3200 23.8536 33.301230.0000 36.0243 38.3959 31.4216 29.518140.0000 44.1625 33.9622 39.1460 25.311550.0000 52.6430 28.5078 46.7788 20.407760.0000 61.0261 21.3770 53.9159 14.345370.0000 68.4036 12.1267 59.9368 6.8057 80.0000 73.6533 0.8019 64.1128 -2.1946 90.0000 75.8133 -12.0000 65.8180 -12.3064 100.0000 74.4098 -25.3056 64.6887 -22.9602 110.0000 69.5921 -38.0996 60.7079 -33.5092 120.0000 62.0165 -49.6616 54.2107 -43.41102-2 回程(等速运动规律运动)凸轮转角理论x 理论y 实际x 实际y 150.0000 28.8770 -74.0165 25.2424 -64.7004 160.0000 14.9014 -76.0270 14.3851 -66.0404 170.0000 1.1258 -75.4900 2.4259 -65.5749 180.0000 -12.0000 -72.5386 -8.9229 -63.0238 190.0000 -24.0666 -67.3832 -19.3110 -58.5864 200.0000 -34.7179 -60.3010 -28.4390 -52.5180 210.0000 -43.6616 -51.6242 -36.0665 -45.1192 220.0000 -50.6772 -41.7260 -42.0190 -36.7223 230.0000 -55.6208 -31.0065 -46.1908 -27.6786 240.0000 -58.4280 -19.8770 -48.5462 -18.3440 250.0000 -59.1126 -8.7451 -49.1177 -9.0659 260.0000 -57.7635 1.9999 -48.0018 -0.1704 270.0000 -54.5386 12.0000 -45.3524 8.0487 280.0000 -49.6567 20.9409 -41.3723 15.3401 290.0000 -43.3865 28.5615 -36.3031 21.5028 300.0000 -36.0357 34.6616 -30.4141 26.39132-3 凸轮轮廓向径凸轮转角理论r 实际r10.0000 50.1094 40.118220.0000 50.8402 40.962930.0000 52.6498 43.111940.0000 55.7114 46.616350.0000 59.8663 51.036660.0000 64.6619 55.791770.0000 69.4702 60.322080.0000 73.6577 64.150490.0000 76.7571 66.9586100.0000 78.5951 68.6426110.0000 79.3387 69.3420120.0000 79.4501 69.4501130.0000 79.4501 69.4501140.0000 79.4501 69.4501150.0000 79.4501 69.4501160.0000 77.4736 67.5889170.0000 75.4984 65.6197180.0000 73.5245 63.6524190.0000 71.5521 61.6869200.0000 69.5812 59.7237210.0000 67.6121 57.7628220.0000 65.6448 55.8044230.0000 63.6795 53.8489240.0000 61.7165 51.8964250.0000 59.7559 49.9474260.0000 57.7981 48.0021270.0000 55.8432 46.0611280.0000 53.8916 44.1247290.0000 51.9438 42.1935300.0000 50.0000 40.2681310.0000 50.0000 40.0000320 50 40330.0000 50.0000 40.0000340 50 40350.0000 50.0000 40.0000360.0000 50.0000 40.0000（6）由Matlab绘制的实际图轮廓线和理论图轮廓线如下：图例：绿色——基圆；红色点划线——理论廓线；蓝色——实际廓线；黄色——滚子圆；蓝绿色，虚线——偏距圆；黑色，虚线——初始偏置位置；。
matlab凸轮摇杆机构设计动画代码
matlab凸轮摇杆机构设计动画代码一、引言凸轮摇杆机构是机械工程中常见的一种机构，其运动特性决定了它在很多领域都有广泛的应用，例如发动机、汽车、船舶等。
而在设计凸轮摇杆机构时，需要进行大量的计算和试验，这对于工程师来说是一个非常繁琐的过程。
但是，通过使用MATLAB软件可以大大简化这个过程，并且可以生成动画效果来更直观地展示凸轮摇杆机构的运动特性。
二、MATLAB凸轮摇杆机构设计代码以下是MATLAB代码实现凸轮摇杆机构的动画效果：1. 定义凸轮形状首先需要定义凸轮的形状，可以采用圆弧、正弦曲线等方式进行定义。
例如，在此我们采用正弦曲线进行定义：```matlabtheta = linspace(0,2*pi,100);r = 1+sin(theta);```2. 定义摇杆长度和连杆长度根据具体情况定义摇杆长度和连杆长度：```matlabL1 = 3;L2 = 6;```3. 计算连杆末端位置坐标根据凸轮形状和连杆长度，可以计算出连杆末端的位置坐标：```matlabx1 = r.*cos(theta);y1 = r.*sin(theta);x2 = x1 + L1*cos(theta);y2 = y1 + L1*sin(theta);```4. 计算摇杆末端位置坐标根据连杆长度和摇杆长度，可以计算出摇杆末端的位置坐标：```matlabtheta2 = asin((y2-L2)./L1);x3 = x2 - L2*cos(theta-theta2);y3 = y2 - L2*sin(theta-theta2);```5. 绘制动画效果最后，使用MATLAB的plot函数绘制凸轮摇杆机构的动画效果：```matlabfor i=1:length(x3)plot([0,x2(i),x3(i)],[0,y2(i),y3(i)],'k-o','linewidth',4,'MarkerFaceColor','r','MarkerSize',10)axis equalpause(0.01)end```三、MATLAB凸轮摇杆机构设计代码详解1. 步骤一：定义凸轮形状在此我们采用正弦曲线进行定义。
凸轮机构matlab程序
凸轮轮廓程序：>> e=20;s0=77.46;a1=0:pi/36:pi/3;s1=50*[3*a1/pi-sin(6*a1)/(2*pi)];x1=(s0+s1).*sin(a1)+e*cos(a1);y1=(s0+s1).*cos(a1)-e*sin(a1);k1=150/pi*[1-cos(6*a1)];>> i1=[(k1-e).*sin(a1)+(s0+s1).*cos(a1)].*[(k1-e).*(k1-e)+(s0+s1).*(s0+s1)].^(-1/2);>> j1=[-(k1-e).*cos(a1)+(s0+s1).*sin(a1)].*[(k1-e).*(k1-e)+(s0+s1).*(s0+s1)].^(-1/2);>> x10=x1-10*j1;>> y10=y1-10*i1;a2=pi/3:pi/36:pi;s2=50;x2=(s0+s2).*sin(a2)+e*cos(a2);y2=(s0+s2).*cos(a2)-e*sin(a2);k2=0;>> i2=[(k2-e).*sin(a2)+(s0+s2).*cos(a2)].*[(k2-e).*(k2-e)+(s0+s2).*(s0+s2)].^(-1/2);j2=[-(k2-e).*cos(a2)+(s0+s2).*sin(a2)].*[(k2-e).*(k2-e)+(s0+s2).*(s0+s2)].^(-1/2);x20=x2-10*j2;y20=y2-10*i2;>> a3=pi:pi/36:4*pi/3;>> s3=50*[1-3*(a3-pi)/pi+sin(6*(a3-pi))/(2*pi)];>> x3=(s0+s3).*sin(a3)+e*cos(a3);>> y3=(s0+s3).*cos(a3)-e*sin(a3);>> k3=50*[-3/pi+3/pi*cos(6*(a3-pi))];>> i3=[(k3-e).*sin(a3)+(s0+s3).*cos(a3)].*[(k3-e).*(k3-e)+(s0+s3).*(s0+s3)].^(-1/2);>> j3=[-(k3-e).*cos(a3)+(s0+s3).*sin(a3)].*[(k3-e).*(k3-e)+(s0+s3).*(s0+s3)].^(-1/2);>> x30=x3-10*j3;>> y30=y3-10*i3;>> a4=4*pi/3:pi/36:2*pi;>> s4=0;>> x4=(s0+s4).*sin(a4)+e*cos(a4);>> y4=(s0+s4).*cos(a4)-e*sin(a4);>> k4=0;>> i4=[(k4-e).*sin(a4)+(s0+s4).*cos(a4)].*[(k4-e).*(k4-e)+(s0+s4).*(s0+s4)].^(-1/2);>> j4=[-(k4-e).*cos(a4)+(s0+s4).*sin(a4)].*[(k4-e).*(k4-e)+(s0+s4).*(s0+s4)].^(-1/2);>> x40=x4-10*j4;>> y40=y4-10*i4;>> plot(x10,y10,'-g*',x20,y20,'-r*',x30,y30,'-b*',x40,y40,'-k*')>>plot(x10,y10,'-g*',x20,y20,'-r*',x30,y30,'-b*',x40,y40,'-k*',x1,y1,'-g*',x2,y2,'-r*',x3,y3,'-b*',x4,y4,'-k*')>>凸轮压力角：>> x=0:0.01:pi/3;>> t=5.76*sin(6*x)+6*x.*sin(6*x)+(2-2*pi/15)*cos(6*x)-2+2*pi/15; >> xx =Columns 1 through 60 0.0100 0.0200 0.0300 0.0400 0.0500Columns 7 through 120.0600 0.0700 0.0800 0.0900 0.1000 0.1100Columns 13 through 180.1200 0.1300 0.1400 0.1500 0.1600 0.1700 Columns 19 through 240.1800 0.1900 0.2000 0.2100 0.2200 0.2300 Columns 25 through 300.2400 0.2500 0.2600 0.2700 0.2800 0.2900 Columns 31 through 360.3000 0.3100 0.3200 0.3300 0.3400 0.3500 Columns 37 through 420.3600 0.3700 0.3800 0.3900 0.4000 0.4100 Columns 43 through 480.4200 0.4300 0.4400 0.4500 0.4600 0.4700 Columns 49 through 540.4800 0.4900 0.5000 0.5100 0.5200 0.5300 Columns 55 through 600.5400 0.5500 0.5600 0.5700 0.5800 0.5900 Columns 61 through 660.6000 0.6100 0.6200 0.6300 0.6400 0.6500 Columns 67 through 720.6600 0.6700 0.6800 0.6900 0.7000 0.7100 Columns 73 through 780.7200 0.7300 0.7400 0.7500 0.7600 0.7700 Columns 79 through 840.7800 0.7900 0.8000 0.8100 0.8200 0.8300 Columns 85 through 900.8400 0.8500 0.8600 0.8700 0.8800 0.8900 Columns 91 through 960.9000 0.9100 0.9200 0.9300 0.9400 0.9500 Columns 97 through 1020.9600 0.9700 0.9800 0.9900 1.0000 1.0100 Columns 103 through 1051.0200 1.0300 1.0400>> tt =Columns 1 through 60.0000 0.3461 0.6925 1.0379 1.3809 1.7202 Columns 7 through 122.0546 2.3825 2.70283.0141 3.3150 3.6042 Columns 13 through 183.88044.1424 4.3889 4.6187 4.83075.0237 Columns 19 through 245.1967 5.3487 5.4788 5.5861 5.6698 5.7292 Columns 25 through 305.7636 5.7725 5.7555 5.7122 5.6422 5.5455 Columns 31 through 365.4219 5.2715 5.0944 4.8908 4.6610 4.4055 Columns 37 through 424.1248 3.8196 3.4906 3.1387 2.7647 2.3699 Columns 43 through 481.9552 1.5219 1.0714 0.6051 0.1243 -0.3692 Columns 49 through 54-0.8740 -1.3882 -1.9102 -2.4381 -2.9701 -3.5044 Columns 55 through 60-4.0388 -4.5716 -5.1008 -5.6243 -6.1401 -6.6464 Columns 61 through 66-7.1410 -7.6221 -8.0877 -8.5359 -8.9648 -9.3727 Columns 67 through 72-9.7578 -10.1184 -10.4528 -10.7596 -11.0372 -11.2843 Columns 73 through 78-11.4996 -11.6820 -11.8304 -11.9439 -12.0215 -12.0627 Columns 79 through 84-12.0668 -12.0335 -11.9623 -11.8531 -11.7059 -11.5207 Columns 85 through 90-11.2979 -11.0378 -10.7410 -10.4081 -10.0399 -9.6374 Columns 91 through 96-9.2016 -8.7339 -8.2356 -7.7081 -7.1530 -6.5722 Columns 97 through 102-5.9674 -5.3405 -4.6937 -4.0291 -3.3489 -2.6554Columns 103 through 105-1.9511 -1.2383 -0.5195>> x=0.46:0.001:0.47;>> t=5.76*sin(6*x)+6*x.*sin(6*x)+(2-2*pi/15)*cos(6*x)-2+2*pi/15; >> xx =Columns 1 through 60.4600 0.4610 0.4620 0.4630 0.4640 0.4650Columns 7 through 110.4660 0.4670 0.4680 0.4690 0.4700>> tt =Columns 1 through 60.1243 0.0755 0.0266 -0.0225 -0.0717 -0.1210Columns 7 through 11-0.1704 -0.2199 -0.2696 -0.3193 -0.3692>> x=0.462:0.0001:0.463;>> t=5.76*sin(6*x)+6*x.*sin(6*x)+(2-2*pi/15)*cos(6*x)-2+2*pi/15; >> xx =Columns 1 through 60.4620 0.4621 0.4622 0.4623 0.4624 0.4625Columns 7 through 110.4626 0.4627 0.4628 0.4629 0.4630>> tt =Columns 1 through 60.0266 0.0217 0.0168 0.0119 0.0070 0.0021Columns 7 through 11-0.0028 -0.0077 -0.0126 -0.0176 -0.0225>> z=[0 0.4625];>> y=[150/pi*(1-cos(6*z))-20].*[45.8+50*(3*z/pi-sin(6*z)/(2*pi))];>> y=[150/pi*(1-cos(6*z))-20]./[45.8+50*(3*z/pi-sin(6*z)/(2*pi))];>> yy =-0.4367 1.1121>> a=atan(y)a =-0.4117 0.8384>> a*180/pians =-23.5900 48.0382>>以上是计算推程压力角的临界值。
MATLAB大作业
偏置直动滚子推杆盘形凸轮机构设计推程运动规律：余弦加速度运动回程运动规律：正弦加速度运动凸轮机构的推杆在近休，推程，远休及回程段的凸轮转角偏置直动滚子推杆盘形凸轮机构已知参数推杆运动规律1）推程运动规律：余弦加速度运动推程运动方程式：s=h［1-cos(πδ/δ)］/2,v=πhωsin(πδ/δ0)/(2δ),a=π2hω2cos(πδ/δ0)/(2δ2)2）回程运动规律：正弦加速度运动回程运动方程式：s=h[1-(δ/δ0’)+sin(2πδ/δ0’)/(2π)v=hω[cos(2πδ/δ0’-1)]/δ0’a=-2πhω2sin(2πδ/δ0’)/(δ0’2)滚子中心坐标：x=(s+s0)sinδ+ecosδy=(s+s0)cosδ-ecosδ其中实际轮廓曲线坐标：其中计算压力角：计算曲率半径：计算程序符号的表示含义：r0初选基圆半径x理论轮廓曲线的x坐标y理论轮廓曲线的y坐标X实际轮廓曲线的x坐标Y实际轮廓曲线的x坐标p曲率半径s推杆位移rr滚子半径a压力角paamin许用最小曲率半径pamin实际曲率半径的最小值a1max回程前压力角的最大值a2max回程后压力角的最大值e偏距h推杆行程a1推程许用压力角a2回程程许用压力角dar0每次修正r0所加的长度N计算点数k1近休角k2推程角k3远休角k4回程角kamin实际曲率半径最小值所对应的角度k1max回程前压力角的最大值所对应的角度k2max回程后压力角的最大值所对应的角度子程序1计算最大压力角：function[amax,kmax]=yalijiao1(a,N1,b)amax=0;kmax=0;amax=max(a);for i=1:N1if a(i)==amaxkmax=i*b;endendend子程序2计算最小曲率半径：function[pamin,kamin]=qulv(p,b,N)pamin=0;kamin=0;for i=1:N-1p(i)=abs(p(i));endpamin=min(p);for i=1:N-1pamin=min(p)if p(i)==paminkamin=i*b;endendend子程序3计算回程前的压力角及修正r0：function[A,r0]=haha(r0,rr,e,h,a1,dar0,N,k1,k2,k3,k4)N1=(k1+k2)/360*N;eta=pi/180;%化为弧度while(1)s0=(r0^2-e^2)^(1/2);syms k s dk ds d2k d2sn1=k1/360*N;k11=linspace(0,k1,n1);s1=k11./k11.*0;x1=e.*cos(k11.*pi/180)+(s0+s1).*sin(k11.*pi/180);y1=(s0+s1).*cos(k11.*pi/180)-e.*sin(k11.*pi/180);n2=k2/360*N;k22=linspace(k1,k1+k2,n2);s2=(h/2).*(1-cos(pi.*(k22-k1)/k2));x2=e.*cos(k22.*pi/180)+(s0+s2).*sin(k22.*pi/180);y2=(s0+s2).*cos(k22.*pi/180)-e.*sin(k22.*pi/180);x=[x1,x2];y=[y1,y2];k=[k11,k22];s=[s1,s2];dx=diff(x)./diff(k);dk=k(1:end-1);dy=diff(y)./diff(k);dk=k(1:end-1);ds=diff(s)./diff(k);dk=k(1:end-1);ds(N1)=0;for i=1:N1f(i)=(ds(i)-e)/(sqrt(r0^2-e^2)+s(i));a(i)=atan(f(i));%计算a压力角A(i)=abs(a(i))/eta;if A(i)>a1r0=r0+dar0;break;endendif i==N1break;endendend子程序4计算回程后的压力角及修正r0：function[A,r0]=hahaha(r0,rr,e,h,a2,dar0,N,k1,k2,k3,k4)N2=(k3+k4)/360*N;b=360/N;eta=pi/180;%化为弧度while(1)s0=(r0^2-e^2)^(1/2);syms k s dk ds d2k d2sn3=k3/360*N;k33=linspace(k1+k2,k1+k2+k3,n3);s3=k33./k33.*h;x3=e*cos(k33*pi/180)+(s0+h).*sin(k33*pi/180);y3=(s0+h).*cos(k33*pi/180)-e*sin(k33*pi/180);n4=k4/360*N;k44=linspace(k1+k2+k3,k1+k2+k3+k4,n4+1);s4=h.*(1-(k44-k1-k2-k3)./k4+sin(2*pi.*(k44-k1-k2-k3)./k4)/(2*pi));x4=e.*cos(k44*pi/180)+(s0+s4).*sin(k44*pi/180);y4=(s0+s4).*cos(k44*pi/180)-e*sin(k44*pi/180);x=[x3,x4];y=[y3,y4];k=[k33,k44];s=[s3,s4];dx=diff(x)./diff(k);dk=k(1:end-1);dy=diff(y)./diff(k);dk=k(1:end-1);ds=diff(s)./diff(k);dk=k(1:end-1);ds(N2)=0;for i=1:N2f(i)=(ds(i)-e)/(sqrt(r0^2-e^2)+s(i));a(i)=atan(f(i));%计算a压力角A(i)=abs(a(i))/eta;if A(i)>a2r0=r0+dar0;break;endendif i==N2break;endendend子程序5计算曲率半径，并修正r0，计算理论轮廓曲线坐标和实际轮廓曲线的坐标及曲率半径，拖杆位移：function[x,y,X,Y,p,s,r0]=qulvvv(r0,rr,e,h,paamin,dar0,N,k1,k2,k3,k4)eta=pi/180;%化为弧度i=1;while(1)s0=(r0^2-e^2)^(1/2);syms k s dk ds d2k d2sn1=k1/360*N;k11=linspace(0,k1,n1);s1=k11./k11.*0;x1=e.*cos(k11.*pi/180)+(s0+s1).*sin(k11.*pi/180);y1=(s0+s1).*cos(k11.*pi/180)-e.*sin(k11.*pi/180);n2=k2/360*N;k22=linspace(k1,k1+k2,n2);s2=(h/2).*(1-cos(pi.*(k22-k1)/k2));x2=e.*cos(k22.*pi/180)+(s0+s2).*sin(k22.*pi/180);y2=(s0+s2).*cos(k22.*pi/180)-e.*sin(k22.*pi/180);n3=k3/360*N;k33=linspace(k1+k2,k1+k2+k3,n3);s3=k33./k33.*h;x3=e*cos(k33*pi/180)+(s0+h).*sin(k33*pi/180);y3=(s0+h).*cos(k33*pi/180)-e*sin(k33*pi/180);n4=k4/360*N;k44=linspace(k1+k2+k3,k1+k2+k3+k4,n4);s4=h.*(1-(k44-k1-k2-k3)./k4+sin(2*pi.*(k44-k1-k2-k3)./k4)/(2*pi));x4=e.*cos(k44*pi/180)+(s0+s4).*sin(k44*pi/180);y4=(s0+s4).*cos(k44*pi/180)-e*sin(k44*pi/180);x=[x1,x2,x3,x4];y=[y1,y2,y3,y4];k=[k11,k22,k33,k44];s=[s1,s2,s3,s4];dx=diff(x)./diff(k);dk=k(1:end-1);dy=diff(y)./diff(k);dk=k(1:end-1);ds=diff(s)./diff(k);dk=k(1:end-1);d2x=diff(dx)./diff(dk);d2y=diff(dy)./diff(dk);d2y(N)=0;dy(N)=0;dx(N)=0;d2x(N)=0;while(1)p(i)=(dx(i)^2+dy(i)^2)^(3/2)/(dx(i)*d2y(i)-dy(i)*d2x(i));%计算曲率半径pp(i)=abs(p(i))if pp(i)-rr<paaminr0=r0+dar0;i=1;break;elsefor ii=1:Nsino(ii)=dx(ii)/(dx(ii)^2+dy(ii)^2)^0.5;coso(ii)=(-1)*dy(ii)/(dx(ii)^2+dy(ii)^2)^0.5;X(ii)=x(ii)-rr*coso(ii);%定义实际轮廓线的X座标Y(ii)=y(ii)-rr*sino(ii);%定义实际轮廓线的Y座endendi=i+1;if i==Nbreak;endendif i==Nbreak;endendend主程序function[r0,x,y,X,Y,p,s,a,pamin,kamin,a1max,k1max,a2max,k2max]=zuizhong(r0,rr,e,h,a1,a2,paamin,dar0, N,k1,k2,k3,k4)N1=(k1+k2)/360*N;N2=(k3+k4)/360*N;b=360/N;eta=pi/180;%化为弧度a11=0;a22=0;s=0;pamin=0;kamin=0;a1max=0;k1max=0;a2max=0;k2max=0;while(1)while(1)[a11,r0]=haha(r0,rr,e,h,a1,dar0,N,k1,k2,k3,k4);%计算符合推程许可压力角的修正的r0r1=r0;[a22,r0]=hahaha(r0,rr,e,h,a2,dar0,N,k1,k2,k3,k4);%计算符合回程许可压力角的修正的r0r2=r0;if r0~=r1break;else[x,y,X,Y,p,s,r0]=qulvvv(r0,rr,e,h,paamin,dar0,N,k1,k2,k3,k4);%计算满足最小许可曲率半径条件的修正的r0，计算实际轮廓曲线坐标和理论轮廓曲线坐标，及曲率半径r3=r0;if r0~=r2break;endendif r0==r3break;endendif r0==r3break;endend[pamin kamin]=qulv(p,b,N);[a1max k1max]=yalijiao1(a11,N1,b);[a2max k2max]=yalijiao1(a22,N2,b);a=[a11a22];figure(1);plot(x,y);hold on;t=linspace(0,2*pi,N);x=r0*cos(t);y=r0*sin(t);plot(0,0,'*',x,y,X,Y);title('凸轮的理论轮廓曲线');axis([-70,70,-70,70]);axis square;end只需输入[r0,x,y,X,Y,p,s,a,pamin,kamin,a1max,k1max,a2max,k2max]=zuizhong(20,14,10,30,40,70,4.2,1,72, 45,165,50,100)即可得到所需图形和数据。
机械原理课程设计 偏置直动滚子推杆盘形凸轮
凸轮大作业选题：凸轮5-C一：题目及原始数据：利用计算机辅助设计完成偏置直动滚子推杆盘形凸轮机构的设计，已知数据如下所示，凸轮沿逆时针方向做匀速运动。
具体要求如下：1.推程运动规律为等加速等减速运动，回程运动规律为五次多项式运动；2.近休凸轮转角为0°-30°；推程凸轮转角30°-210°；远休凸轮转角210°-280°；回程凸轮转角280°-360。
°3.初选基圆半径为22mm；4.偏距为+14mm5.滚子半径为18mm6.推杆行程为35mm7.许用压力角为α1=35°，α2=65°。
8.最小曲率半径为0.35r r9.计算点数取120.二：推杆运动规律及凸轮轮廓线方程1.推程加速阶段：s1=70.*a1.*a1/pi/pi;x1=(s0+s1).*sin(a1)+e*cos(a1);y1=(s0+s1).*cos(a1)-e*sin(a1);k1=140*a1/pi^2;i1=[(k1-e).*sin(a1)+(s0+s1).*cos(a1)].*[(k1-e).*(k1-e)+(s0+ s1).*(s0+s1)].^(-1/2);j1=[-(k1-e).*cos(a1)+(s0+s1).*sin(a1)].*[(k1-e).*(k1-e)+(s0 +s1).*(s0+s1)].^(-1/2);x10=x1-18*j1;y10=y1-18*i1;2.推程减速阶段：s11=35-70.*(pi-a11).*(pi-a11)/pi/pi;x11=(s0+s11).*sin(a11)+e*cos(a11);y11=(s0+s11).*cos(a11)-e*sin(a11);k11=140.*(pi-a1)/pi^2;i11=[(k11-e).*sin(a11)+(s0+s11).*cos(a11)].*[(k11-e).*(k11-e)+(s0+s11).*(s0+s11)].^(-1/2);j11=[-(k11-e).*cos(a11)+(s0+s11).*sin(a11)].*[(k11-e).*(k11 -e)+(s0+s11).*(s0+s11)].^(-1/2);x101=x11-18*j11;y101=y11-18*i11;3.远休阶段：x2=(s0+s2).*sin(a2)+e*cos(a2);y2=(s0+s2).*cos(a2)-e*sin(a2);k2=0;i2=[(k2-e).*sin(a2)+(s0+s2).*cos(a2)].*[(k2-e).*(k2-e)+(s0+ s2).*(s0+s2)].^(-1/2);j2=[-(k2-e).*cos(a2)+(s0+s2).*sin(a2)].*[(k2-e).*(k2-e)+(s0 +s2).*(s0+s2)].^(-1/2);x20=x2-18*j2;y20=y2-18*i2;4.回程阶段：a30=33*pi/18-a3;s3=(350.*a30.*a30.*a30/(4*pi/9)^3-525.*a30.*a30.*a30.*a30/( 4*pi/9)^4+210.*a30.*a30.*a30.*a30.*a30/(4*pi/9)^5);x3=(s0+s3).*sin(a3)+e*cos(a3);y3=(s0+s3).*cos(a3)-e*sin(a3);k3=-1050.*a30.*a30/(4*pi/9)^3+2100.*a30.*a30.*a30/(4*pi/9)^ 4-1050.*a30.*a30.*a30.*a30/(4*pi/9)^5;i3=[(k3-e).*sin(a3)+(s0+s3).*cos(a3)].*[(k3-e).*(k3-e)+(s0+ s3).*(s0+s3)].^(-1/2);j3=[-(k3-e).*cos(a3)+(s0+s3).*sin(a3)].*[(k3-e).*(k3-e)+(s0 +s3).*(s0+s3)].^(-1/2);x30=x3-18*j3;y30=y3-18*i3;5.近休阶段：s4=0;x4=(s0+s4).*sin(a4)+e*cos(a4);y4=(s0+s4).*cos(a4)-e*sin(a4);k4=0;i4=[(k4-e).*sin(a4)+(s0+s4).*cos(a4)].*[(k4-e).*(k4-e)+(s0+ s4).*(s0+s4)].^(-1/2);j4=[-(k4-e).*cos(a4)+(s0+s4).*sin(a4)].*[(k4-e).*(k4-e)+(s0 +s4).*(s0+s4)].^(-1/2);x40=x4-18*j4;y40=y4-18*i4;三：matlab计算程序e=14;r0=22s0=sqrt(r0^2-e^2);c111=1;c3=1;for(i=1:0.1:200) %由压力角条件循环求合适基圆半径if (c111<35/180)&&(c3<65/180) %判断条件else a1=0:pi/60:pi/2; % 推程加速阶段 s1=70.*a1.*a1/pi/pi;x1=(s0+s1).*sin(a1)+e*cos(a1);y1=(s0+s1).*cos(a1)-e*sin(a1);k1=140*a1/pi^2; % 对s1求导i1=[(k1-e).*sin(a1)+(s0+s1).*cos(a1)].*[(k1-e).*(k1-e)+(s0+ s1).*(s0+s1)].^(-1/2);j1=[-(k1-e).*cos(a1)+(s0+s1).*sin(a1)].*[(k1-e).*(k1-e)+(s0 +s1).*(s0+s1)].^(-1/2);x10=x1-18*j1;y10=y1-18*i1;a11=pi/2:pi/60:pi; % 推程减速阶段s11=35-70.*(pi-a11).*(pi-a11)/pi/pi;x11=(s0+s11).*sin(a11)+e*cos(a11);y11=(s0+s11).*cos(a11)-e*sin(a11);k11=140.*(pi-a1)/pi^2;i11=[(k11-e).*sin(a11)+(s0+s11).*cos(a11)].*[(k11-e).*(k11-e)+(s0+s11).*(s0+s11)].^(-1/2);j11=[-(k11-e).*cos(a11)+(s0+s11).*sin(a11)].*[(k11-e).*(k11 -e)+(s0+s11).*(s0+s11)].^(-1/2);x101=x11-18*j11;y101=y11-18*i11;a2=pi:pi/60:25*pi/18; %凸轮远休阶段s2=35;%推杆行程x2=(s0+s2).*sin(a2)+e*cos(a2);y2=(s0+s2).*cos(a2)-e*sin(a2);k2=0;i2=[(k2-e).*sin(a2)+(s0+s2).*cos(a2)].*[(k2-e).*(k2-e)+(s0+ s2).*(s0+s2)].^(-1/2);j2=[-(k2-e).*cos(a2)+(s0+s2).*sin(a2)].*[(k2-e).*(k2-e)+(s0 +s2).*(s0+s2)].^(-1/2);x20=x2-18*j2;y20=y2-18*i2;a3=25*pi/18:pi/60:33*pi/18;%推杆回程阶段a30=33*pi/18-a3;s3=(350.*a30.*a30.*a30/(4*pi/9)^3-525.*a30.*a30.*a30.*a30/( 4*pi/9)^4+210.*a30.*a30.*a30.*a30.*a30/(4*pi/9)^5);x3=(s0+s3).*sin(a3)+e*cos(a3);y3=(s0+s3).*cos(a3)-e*sin(a3);k3=-1050.*a30.*a30/(4*pi/9)^3+2100.*a30.*a30.*a30/(4*pi/9)^ 4-1050.*a30.*a30.*a30.*a30/(4*pi/9)^5;i3=[(k3-e).*sin(a3)+(s0+s3).*cos(a3)].*[(k3-e).*(k3-e)+(s0+ s3).*(s0+s3)].^(-1/2);j3=[-(k3-e).*cos(a3)+(s0+s3).*sin(a3)].*[(k3-e).*(k3-e)+(s0 +s3).*(s0+s3)].^(-1/2);x30=x3-18*j3;y30=y3-18*i3;a4=33*pi/18:pi/60:2*pi;%推杆近休阶段s4=0;x4=(s0+s4).*sin(a4)+e*cos(a4);y4=(s0+s4).*cos(a4)-e*sin(a4);k4=0;i4=[(k4-e).*sin(a4)+(s0+s4).*cos(a4)].*[(k4-e).*(k4-e)+(s0+ s4).*(s0+s4)].^(-1/2);j4=[-(k4-e).*cos(a4)+(s0+s4).*sin(a4)].*[(k4-e).*(k4-e)+(s0 +s4).*(s0+s4)].^(-1/2);x40=x4-18*j4;y40=y4-18*i4;plot(x10,y10,'-g*',x101,y101,'-g+',x20,y20,'-r*',x30,y30,'-b*',x40,y40,'-k*',x1,y1,'-g*',x11,y11,'-g+',x2,y2,'-r*',x3,y3,'-b*',x4,y4,'-k*')%凸轮轮廓曲线绘制title(‘凸轮轮廓曲线绘制');xlabel('Variable X'); %X轴ylabel('Variable Y'); %Y轴text(-250,-200,'工作廓线') %文字标注text(100,-100,'理论廓线');grid on %加网格axis equal%坐标相等a1=0:pi/60:pi/2;%压力角计算force1=abs(atan((k1).*(s0+s1).^-1)); c1=max(force1);a11=pi/2:pi/60:pi;force11=abs(atan((k11).*(s0+s11).^-1));c11=max(force11);c111=max(c1,c11);a2=pi:pi/60:25*pi/18;force2=abs(atan((k2).*(s0+s2).^-1));c2=max(force2);a3=25*pi/18:pi/60:33*pi/18;force3=abs(atan((k3).*(s0+s3).^-1));c3=max(force3);a4=33*pi/18:pi/60:2*pi;force4=abs(atan((k4).*(s0+s4).^-1));c4=max(force4);r0=r0+1; %每循环一次基圆半径+1s0=sqrt(r0^2-e^2);endend%求最大压力角位置c111c3[m1,n1]=sort(force1);bend1=n1(end-1+1:end)jiaodu1=(bend1(end)-1)*3[m11,n11]=sort(force11);bend11=n11(end-1+1:end)jiaodu11=(bend11(end)-1)*3+90 [m3,n3]=sort(force3);bend3=n3(end-1+1:end)jiaodu=(bend3(end)-1)*3+250vv=i1./j1;vv1=diff(vv);vv2=diff(vv,2);vv22=[0,vv2];p=(1+vv1.^2).^(3/2)./vv22;g=min(p)vv1=i11./j11;vv11=diff(vv1);vv21=diff(vv1,2);vv221=[0,vv21];p1=(1+vv11.^2).^(3/2)./vv221;g1=min(p1)vv2=i2./j2;vv222=diff(vv2);vv223=diff(vv2,2);vv2211=[0,vv223];p2=(1+vv222.^2).^(3/2)./vv2211;g2=min(p2)vv=i3./j3;vv1=diff(vv);vv2=diff(vv,2);vv22=[0,vv2];p=(1+vv1.^2).^(3/2)./vv22;g3=min(p)vv=i4./j4;vv1=diff(vv);vv2=diff(vv,2);vv22=[0,vv2];p=(1+vv1.^2).^(3/2)./vv22;g4=min(p))ro=sqrt(s0^2+e^2) %求合适基圆半径x1y1x11y11x2y2x3y3x4y4x10y10x101y101x20y20x30y30x40y40force1force11force2force3force4c111c3jiaodu11jiaodu3四：计算结果及分析：（1）工作廓线坐标：1;推程加速阶段X坐标14 24.9479312972938 35.8335795427018 46.6331664128873 57.323071617132667.8798591305935 78.2803034241300 88.5014157831108 98.5204708048515108.315033160764 117.862984704875 127.142552005136 136.132334367976144.811332419744 153.158977301315 161.155160523920 168.780264525614176.015193958402 182.841407726263 189.240951783976 195.196492695966200.691351943287 205.709540955551 210.235796832989 214.255618712129 217.755304716715 220.721989423648 223.143681761924 225.009303250807226.308726472013 227.0328136593412推程加速阶段Y坐标209.532813659341 208.532370629552 206.998924199561 204.935879972465202.347567871334 199.239236813805 195.617049448531 191.488076931747186.860293712014 181.742572281261 176.144677840557 170.0772******** 163.551861181761 156.580882432274 149.177605251176 141.356170650697133.131574562033 124.519659744732 115.537106908501 106.20142493273596.5309400655771 86.5447839816669 76.2628805759777 65.705931370278654.8953994088027 43.8534915206956 32.6031388287473 21.16797538678679.57231483194954 -2.15887505719948 -14.00000000000003推程减速阶段X坐标227.032813659341 227.134619685286 226.568905051752 225.331644205755 223.421214513810 220.838411540547 217.586454974950 213.670985176905209.100050353069 203.884084407342 198.0358******** 191.570525763878184.505401336072 176.860074548737 168.656256843411 159.917723656843150.670231233150 140.941425726738 130.760744942876 120.159313091203109.169828954466 97.8264479001947 86.1646581868564 74.221152038085562.0336919788640 49.6409729459048 37.0824807009210 24.398347089867511.6292027035831 -1.18397249451846 -14.00000000000004推程减速阶段Y坐标-14.0000000000000 -25.9228338599749 -37.8904674143353 -49.8635381159681 -61.8024134893063 -73.6673405558026 -85.4185959941913 -97.0166364509177 -108.422248415730 -119.596697079292 -130.501873593764 -141.100440163605 -151.355972402351 -161.233098401750 -170.697633972432 -179.716713530067 -188.258916117849 -196.294386074865 -203.794947880574 -210.734214728044 -217.0876******** -222.832864069368 -227.949297596606 -232.418705078147 -236.225024238547 -239.354479443456 -241.795636066125 -243.539445995213 -244.579284102998 -244.910975527746 -244.5328136593415远休阶段X坐标-14.0000000000000 -26.7786721222032 -39.4839457654822 -52.0809966579133 -64.5352971586108 -76.8127108955902 -88.8795863311907 -100.702848998602 -112.250092156677 -123.489665614559 -134.390762482652 -144.923503612169 -155.059019491793 -164.769529377011 -174.028********* -182.810305697758 -191.0911******** -198.848174053764 -206.060195464824 -212.707420203182 -218.771628687875 -224.236199344965 -229.086154166116 -233.308199762282 6远休阶段Y坐标-244.532813659341 -243.464986549453 -241.729838834477 -239.332126433691 -236.278421310122 -232.577093457254 -228.238287957455 -223.273897175014 -217.697528159994 -211.524465352257 -204.771628687875 -197.457527222762 -189.602208400634 -181.227203104369 -172.355466641343 -163.011315824535 -153.220362321829 -143.009442456216 -132.406543649295 -121.440727709697 -110.142051176688 -98.5414829372844 -86.6708193426842 -74.5625970566802 7减速阶段X坐标-234.573962542258 -237.924423961410 -240.528414701632 -242.301034179885 -243.179109387654 -243.122053300159 -242.111828793401 -240.152099129043 -237.266657296952 -233.497236106624 -228.900808808014 -223.546496133102 -217.512199933386 -210.881086014932 -203.738039329490 -196.166213373622 -188.243792502170 -180.0410******** -171.618025436311 -163.022********* -154.287835944964 -145.434490148429 -136.467891333878 -127.380539946257 -118.153582814159 -108.759487623767 -99.16559150875688减速阶段Y坐标-70.4794512845940 -58.1011116825609 -45.5418784536957 -32.8365161989020 -20.0390090002643 -7.21694579130250 5.55380225566372 18.194003075560030.6254874984057 42.7749931638176 54.5773610652433 65.978032703814576.9348117792082 87.4188705720677 97.4149974868349 106.921098432862115.946980634777 124.512462892978 132.644871079527 140.375991577690147.738568287212 154.762440563530 161.470429890068 167.874092062809173.969459073374 179.732900602872 185.1172389914419近休X坐标-92.6420511766881 -82.6518154464002 -72.4350368350310 -62.0197188225945 -51.4344090718031 -40.7081211809080 -29.8702551594429 -18.9505168448415 -7.97883648080264 3.01471331942776 13.999999999999910近休Y坐标1 188.460739555420 193.050970998372 197.112063148625 200.632884834880203.603785729623 206.016622800007 207.864782627336 209.143199533988209.848369468082 209.978359607845 209.532813659341（2）理论廓线坐标;推程加速阶段X坐标12.8000000000000 22.8728273179084 32.8885297342726 42.825360681316652.6617133932777 62.3761432336542 71.9473900632018 81.354400741436490.5763518517692 99.5926727370081 108.383068927807 116.927546041764125.206434225271 133.200413203958 140.890538000620 148.258265371979155.285481007489 161.954527524708 168.248233286539 174.149942056033179.643543494319 184.713504496809 189.344901352090 193.523452696839197.235553228942 200.468308129584 203.209568133643 205.447965176251 207.172948531918 208.374821351328 209.044777489697推程加速阶段Y坐标191.572858202826 190.652383395923 189.241484022951 187.343250393275 184.961604006512 182.101293199539 178.767888983898 174.967781050798170.708173911217 165.997083129187 160.843331597179 155.256545793692149.247151954669 142.826372082411 136.006219708068 128.799495316842121.219781338553 113.281436600464 104.999590134052 96.390134222989187.4697165758390 78.2557315040260 68.7663099834431 59.020308476717649.0372963926355 38.8375420595755 28.4419970910307 17.87227902341457.15065210936054 -3.69999384635310 -14.6561667163081推程减速阶段X坐标209.193734991700 209.188778273809 208.573036193737 207.342473187261 205.495287697520 203.0319******** 199.955103403567 196.269775760348191.983156349172 187.104683111356 181.645993349332 175.620886984768169.0452******** 161.937156885096 154.316496362355 146.205213858842137.627077770212 128.607625755855 119.174072750844 109.35521228870799.1813115200797 88.6840003369476 77.8961550352902 66.851776970326355.5858666782191 44.1342939559169 32.5336644067296 20.82118297320159.03451499079487 -2.78835469420737 -14.6092639913715推程减速阶段Y坐标-16.4015145824514 -27.3181030218633 -38.2760890490105 -49.2392576762938 -60.1711110106104 -71.0350090000076 -81.7943109934888 -92.4125175513741 -102.853********* -113.0812******** -123.060653160544 -132.757237971647 -142.137258475553 -151.167983975963 -159.817777845352 -168.0562******** -175.854233625249 -183.184184769079 -190.020********* -196.337291242469 -202.113395111709 -207.327521359409 -211.960806247121 -215.996393696655 -219.419502857395 -222.217487685822 -224.379888298036 -225.898473888143 -226.767277038293 -226.982619279687 -226.543127798025远休阶段X坐标-12.9711482618274 -24.8107233108544 -36.5822938918588 -48.2535949481094 -59.7926362546736 -71.1677901013991 -82.3478779822689 -93.3022560535201 -104.000899126289 -114.414482963567 -124.514464655894 -134.273160855494 -143.663823654403 -152.660713898624 -161.239171737366 -169.375684213972 -177.0479******** -184.234939088932 -190.916953302526 -197.0756******** -202.694230799421 -207.757213383730 -212.250747887182 -216.162517844044远休阶段Y坐标-226.562241489795 -225.572888364055 -223.965255630689 -221.743749699274 -218.914459563151 -215.485140109924 -211.465190865844 -206.865630232365 -201.699065285474 -195.979657220565 -189.723082537593 -182.946490072876 -175.668453995324 -167.908922895934 -159.689165110094 -151.0317******** -141.960288314811 -132.499762924347 -122.676064893652 -112.516120296192 -102.0477******** -91.2997275085610 -80.3014319762869 -69.0830358006497回程阶段X坐标-217.335260464284 -220.421346316413 -222.795183195622 -224.398577389943 -225.188547506355 -225.137585355545 -224.233655449440 -222.479896624979 -219.893983296304 -216.507098988589 -212.362488116223 -207.513585489574 -202.021********* -195.953825087341 -189.379262026933 -182.367612804067 -174.985894648424 -167.296364561343 -159.354690783951 -151.208619312605 -142.897173644983 -134.450395994491 -125.889635960919 -117.228428433346 -108.474068637267 -99.6300563428237 -90.6995930141100回程阶段Y坐标-65.2999580017652 -53.9008411016096 -42.4544037000726 -30.9651421357433 -19.4561855319938 -7.96455046569805 3.46312822959339 14.774462367317425.9148401896814 36.8306478920168 47.4721553190688 57.795992842225267.7671217377121 77.3601986319145 86.5602513186570 95.3626114072227103.772082503801 111.801357318003 119.468732676936 126.795209558515133.801107529679 140.502367786106 146.906758880859 153.010*********158.793589895652 164.219890434419 169.232439040273近休阶段X坐标-84.7013039329720 -75.5673741224230 -66.2263193920283 -56.7037429235150 -47.0257454370771 -37.2188536511159 -27.3099475743478 -17.3261868295693 -7.29493621101956 2.75630932061967 12.8000000000000近休阶段Y坐标172.306961879241 176.503744912797 180.216743450172 183.435780420462 186.152032667084 188.358055131435 190.0478******** 191.216639573932191.861366370818 191.980214498602 191.572858202826凸轮压力角0 0.00354431855997765 0.00708657544025155 0.0106247131274339 0.01415668242241860.0176804465517903 0.0211939852247537 0.0246952986180828 0.02818241127214470.0316533758817331 0.0351062769662460 0.0385392344046481 0.04195040682166590.0453379948127508 0.0487002439965149 0.0520354478845675 0.05534195055995420.0586181491567104 0.0618624961343669 0.0650735013425822 0.06824973387240840.0713898236920071 0.0744924630659183 0.0775564077582259 0.08058047802116060.0835635593718112 0.0865046031606886 0.0894026269368794 0.09225671461544470.0950660164535557 0.09782974884260520.193821958696751 0.189734216357270 0.185711813762507 0.1817521166416040.177852583825628 0.174010762147141 0.170224281603430 0.1664908507660410.162808252420337 0.159174339419789 0.155587030740642 0.1520443077234660.148544210488885 0.145084834515539 0.141664327368999 0.1382808855710030.134932751598957 0.131618********* 0.128335589653967 0.1250832510466050.121859593761707 0.118663048967569 0.115492078020447 0.1123451701345160.109220840117705 0.106117626166793 0.103034087715421 0.09996880332880770.0969203686391774 0.0938873943159862 0.09086850406519340 0.00400661352098117 0.0148078747736643 0.0306996316187834 0.05014161972168330.0717513439654380 0.0942968396397606 0.116689817584795 0.1379787986736630.157341636795524 0.174077401612658 0.187598363402544 0.1974234691999150.203175079625608 0.204580805091460 0.201482016062883 0.1938499534402010.181809249049959 0.165667032050483 0.145943761057100 0.1233999352907570.0990517714422343 0.0741698891884142 0.0502587840423935 0.02902100443043590.0123165659206908 0.00213229641216247推程最大压力角：0.193821958696751*180出现位置：90回程最大压力角：0.204580805091460*180出现位置292最小曲率半径：g2=4.2145<0.35*18故满足要求最后确定基圆半径：ro = 211五：凸轮机构图六：体会和建议在本次设计中，对凸轮结构的各项参数对最终凸轮形状的影响有了更深刻的认识。
凸轮运动Matlab仿真-Matlab课程设计
Matlab 课程设计李俊机自091设计题目一：凸轮机构设计已知轮廓为圆形的凸轮（圆的半径为100mm、偏心距为20mm），推杆与凸轮运动中心的距离20mm，滚子半径为10mm，请利用matlab仿真出凸轮推杆的运动轨迹和运动特性（速度，加速度），并利用动画演示出相关轨迹和运动特性。
%总程序代码clc;clf;clear;p=figure('position',[100 100 1200 600]);for i=1:360%画圆形凸轮R=100; %圆形凸轮半径A=0:0.006:2*pi;B=i*pi/180;e=20; %偏心距a=e*cos(B);b=e*sin(B);x=R*cos(A)+a;y=R*sin(A)+b;subplot(1,2,1)plot(x,y,'b','LineWidth',3);%填充fill(x,y,'y')axis([-R-e,R+e,-R-e,R+e+100]);set(gca,'Xlim',[-R-e,R+e])set(gca,'Ylim',[-R-e,R+e+100])axis equal;axis manual;axis off;hold on;plot(a,b,'og')plot(e,0,'or')plot(0,0,'or','LineWidth',3)%画滚子gcx=0; %滚子中心X坐标r=10; %滚子半径gcy=sqrt((R+r)^2-a^2)+b; %滚子中心Y坐标gx=r*cos(A)+gcx; %滚子X坐标gy=r*sin(A)+gcy; %滚子Y坐标plot(gx,gy,'b','LineWidth',2);%画其它部分plot([0 a],[0 b],'k','LineWidth',4)plot([3 3],[170 190],'m','LineWidth',4)plot([-3 -3],[170 190],'m','LineWidth',4)%画顶杆gc=120;dgx=[0 0];dgy=[gcy gcy+gc];plot(dgx,dgy,'LineWidth',4);hold off%画位移图sx(i)=B;sy(i)=gcy;subplot(3,2,2)plot(sx,sy,'b','LineWidth',3)title('位移线图')grid onhold off;%画速度图vx(i)=B;vy(i)=20*cos(B) + (40*cos(B).*sin(B))./(121 - 4*cos(B).^2).^(1/2);subplot(3,2,4)plot(vx,vy,'g','LineWidth',3)title('速度线图')grid onhold off;%画加速度图ax(i)=B;ay(i)=(40*cos(B).^2)./(121 - 4*cos(B).^2).^(1/2) - 20*sin(B) - (40*sin(B).^2)/(121 -4*cos(B).^2).^(1/2) - (160*cos(B).^2.*sin(B).^2)/(121 - 4*cos(B).^2).^(3/2); subplot(3,2,6)plot(ax,ay,'r','LineWidth',3),xlabel('B')title('加速度线图')grid onhold off;M=getframe;end截图附：通过求导求速度和加速度%求速度syms B;a=e*cos(B);b=e*sin(B);s=sqrt((R+r).^2-a.^2)+b;v=diff(s)结果：v =20*cos(B) + (40*cos(B)*sin(B))/(121 - 4*cos(B)^2)^(1/2)%求加速度syms B;v =20*cos(B) + (40*cos(B)*sin(B))/(121 - 4*cos(B)^2)^(1/2);a=diff(v)结果：a =(40*cos(B)^2)/(121 - 4*cos(B)^2)^(1/2) - 20*sin(B) - (40*sin(B)^2)/(121 - 4*cos(B)^2)^(1/2) - (160*cos(B)^2*sin(B)^2)/(121 - 4*cos(B)^2)^(3/2)。
matlab凸轮设计
偏置直动尖端推杆盘型凸轮机构一、凸轮参数二、推杆运动规律进程段 余弦加速度运动进程段 S= H-H*(1-cos(pi*i/J1))/2 （00～900） 回程段 余弦加速度运动回程段 S= H*(1-cos(pi*i/J3))/2 (1800~2700) 凸轮廓线方程：)sin(*)()cos(*22J S E R J E X +-+= )sin(*)cos(*)(22J E J S E R Y -+-= 三、程序设计%凸轮机构参数E=10; %偏距H=50; %升程b=0:pi/10:2*pi;R=40; %基圆半径x2=R*cos(b); %基圆轮廓y2=R*sin(b);x1=10*sin(b);%偏心圆轮廓y1=10*cos(b);J1=90; %推程J3=90; %回程s0=sqrt(R^2-E^2);s1=(H/2)*(1-cos(pi*i/J1)); %推程，余弦加速度运动 s2=H*eig(eye(360))'; %停歇，s=Hs3=H-(H/2)*(1-cos(pi*i/J3));%回程，余弦加速度运动 s4(1,360)=0; %停歇，s=0 x(1,360)=0;y(1,360)=0;%凸轮机构循环代码for i=1:360if i>=270s(i)=0;elseif i>=180s(i)=H-H*(1-cos(pi*i/J1))/2;elseif i>=90s(i)=H;elses(i)=H*(1-cos(pi*i/J3))/2;endx(i)=E*cos(pi*i/180)+(s0+s(i))*sin(pi*i/180);y(i)=(s0+s(i))*cos(pi*i/180)-E*sin(pi*i/180); end%凸轮轮廓曲线figure(1)plot(x,y,'-r',x1,y1,'-b',x2,y2,'-g','linewidth',2); title('凸轮轮廓曲线');xlabel('x'),ylabel('y');axis([-80,120,-100,60]);grid on;%位移曲线figure(2)plot(s,'-r','linewidth',2);title('位移曲线');xlabel('转角'),ylabel('位移')axis([0,400,-10,60]);grid on;四、运行结果。
偏置直动滚子从动件盘形凸轮机构的设计
广东工业大学华立学院课程设计（论文）课程名称机械原理课程设计题目名称偏置直动滚子从动件盘形凸轮机构的设计学生学部（系）机电工程学部专业班级机械班学号学生姓名 lilili指导教师2012 年6月28日目录目录......................................... 错误！未定义书签。
课程设计（论文）任务书. (3)摘要....................................... 错误！未定义书签。
一、根据已知基尺寸做出圆..................... 错误！未定义书签。
二、绘制推杆的位移图线....................... 错误！未定义书签。
三、用反转法设计图轮廓线..................... 错误！未定义书签。
四、压力角是否满足许用压力角的要求.......... .错误！未定义书签。
五、参考文献...............................................- 11 -广东工业大学华立学院课程设计（论文）任务书题目名称偏置直动滚子从动件盘形凸轮机构的设计学生学部（系）机电工程学部专业班级机械班姓名学号设计一个偏置直动滚子从动件盘形凸轮机构。
设计参数如表中所示，凸轮回转方向为顺时针（或逆时针），从动件推程以正弦加速度运动规律上升，回程以等加速等减速运动规律下降，其中，e、r r、r b、h分别代表偏距、滚子半径、基圆半径及从动件最大升程，ф、фs、ф‘、фs’分别代表凸轮的推程角、远休止角、回程角及近休止角。
1、设计数据：设计内容偏置直动滚子从动件盘形凸轮轮廓设计符号 e r r r b h ффsф‘фs’单位mm (º)数据10 55 40 180 30 120 302、设计要求1）、用图解法设计此盘形凸轮机构，正确确定偏距e的方向；2）、用图解法设计此盘形凸轮机构，将计算过程写在说明书中。
Matlab编程五次凸轮
附录１１、用解析法设计凸轮２的实际轮廓曲线。
1、建立凸轮轮廓的数学模型。
图l 为往复式偏心从动件盘形凸轮的机构运动简图，B 为理论轮廓线上的任意一点，在图示的直角坐标系中，B 的坐标，即凸轮理论廓线上的直角坐标参数方程为：X=OE+EF=（S0+S ）*Sin （J ）＋e*Cos （J ）Y=BD – FD=（S0+S ）*Cos （J ） – e*Sin （J ）式中：X ，Y ：凸轮理论廓线上的某一点坐标 (mm)e ：从动件的偏心距(mm)，OCR ：凸轮的基圆半径(mm)，OAS 0：220E R S -=(mm)，CKJ ：凸轮的转角 S ：S ＝f(J)从动件运动方程，KBBC ＝CK 十KB ＝S 0十S因为工作廓线在法线方向的距离处处相等，且等于滚子半径r ’,故当已知理论廓线上的任意一点B(X,Y)时，只要沿理论廓线在该点的法线的方向取距离为r ’，即得到工作廓线上的相应点B ’(X ’,Y ’).由高等数学可知，理论廓线B 点处的法线n-n 的斜率（与切线斜率互为负倒数）应为 Tan a=-dx/dy=(dx/dJ)/(dx/dJ)/(-dy/dJ)=sina/cosa注： a 为理论廓线B 点处的法线和X 轴的夹角。
根据（1）（2）两式有dx/dJ=(ds/dJ-e)sin(J)+(s0+s)cos(J) (3)dy/dJ=(ds/dJ-e)cos(J)-(s0+s)sin(J) (4)可得Sin a=(dx/dJ)/((dx/dJ)^2+(dy/dJ)^2)^0.5 (5)Cos a=-(dy/dJ)/((dx/dJ)^2+(dy/dJ)^2)^0.5 (6)工作廓线上对应的点B ’(x ’,y ’)坐标为：x ’=x-r ’cos ay ’=y- r ’sin a2、 从动件运行规律：五次多项式运行规律从动件运动形式为：升—停—降—停型推程（升）δ1 远休止（停）δ2回程（降）δ3近休止（停）δ4 等加速等减速 S 1=10h(δ/δ1)^3-15h S 2=h等减速等加速 S 1=h-h(10(δ/δ3)^3-15(δ/δ3)^4+6(δ/δ3)^5) S 4=0图13、绘制凸轮曲线的程序框图（１）升回程运动函数的子程序框图(3)绘制凸轮轮廓的主程序框图定义升程的运行规律定义远休的运行规律定义回程的运行规律定义近休的运行规律绘制S－δ曲线（4）绘制S－δ曲线的程序框图4、程序编写（以下程序在Matlab7.0上运行通过）（１）升回程运动函数的子程序function y = s(x) %申明从动件运行规律函数deg=pi/180; ％转化为弧度制的参数h=10; %从动件行程if (x<0)|(x>2*pi)error('Input Range error(0~2*pi)');elseif x<(60*deg)&(x>=0)y=h*(10*(x/(60*deg))^3-15*(x/(60*deg))^4+6*(x/(60*deg))^5);％升程运动规律elseif(x>=60*deg)&(x<70*deg)y=h;％远休运动规律elseif(x>=70*deg)&(x<130*deg)y=h-h*(10*((x-70*deg)/(60*deg))^3-15*((x-70*deg)/(60*deg))^4+6*((x-70*deg)/(60*deg))^5);％回程运动规律elsey=0;％近休运动规律endendendend（２）绘制ds/dδ运动函数的子程序function d=ds(x) %申明ds/dδ运行规律函数h=10; %凸轮2行程deg=pi/180;if (x<0)|(x>2*pi)error('Input Range error(0~2*pi)');elseif x<(60*deg)&(x>=0)d=h/(60*deg)*((30*(x/(60*deg))^2-60*(x/(60*deg))^3+30*(x/(60*deg))^4));％对S求导elseif(x>=60*deg)&(x<70*deg)d=0; ％对S求导elseif(x>=70*deg)&(x<130*deg)d=-h/(60*deg)*((30*((x-70*deg)/(60*deg))^2-60*((x-70*deg)/(60*deg))^3+30*((x-70*deg)/(60* deg))^4));％对S求导elsed=0; ％对S求导endendendend（3）绘制凸轮轮廓的主程序clear;i=1;r0=60; %基圆半径rr=4;%滚子圆半径e=0; %偏距eta=1; %凸轮顺时钉转向s0=(r0^2-e^2)^0.5;deg=pi/180;st=0.05*deg;%步长a=0;if a<2*pix(i)=(s(a)+s0)*sin(eta*a)-e*cos(eta*a);％定义理论轮廓线的X座标y(i)=(s(a)+s0)*cos(eta*a)+e*sin(eta*a); ％定义理论轮廓线的Y座标dx=ds(a)*sin(eta*a)-eta*(s(a)+s0)*cos(eta*a)-e*eta*sin(eta*a);dy=ds(a)*cos(eta*a)+eta*(s(a)+s0)*sin(eta*a)-e*eta*cos(eta*a);sino=dx/(dx^2+dy^2)^0.5;coso=dy/(dx^2+dy^2)^0.5;X(i)=x(i)-rr*coso;％定义实际轮廓线的X座标Y(i)=y(i)+rr*sino;％定义实际轮廓线的Y座标i=i+1;a=a+st;endplot(x,y,X,Y);％绘制理论和实际轮廓线axis('square','equal');grid on主程序运行的结果为凸轮轮廓曲线：（4）绘制S－δ曲线的程序为：h=10;t1=linspace(0,60*pi/180); %定义升程角范围y1=h*(10*(t1/(60*deg)).^3-15*(t1/(60*deg)).^4+6*(t1/(60*deg)).^5); ％升程运动规律t2=linspace(60*pi/180,70*pi/180); %定义远休角范围y2=h;％远休运动规律t3=linspace(70*pi/180,130*pi/180); %定义回程角范围y3=h-h*(10*((t3-70*deg)/(60*deg)).^3-15*((t3-70*deg)/(60*deg)).^4+6*((t3-70*deg)/(60*deg)). ^5); ％回程运动规律t4=linspace(130*pi/180,360*pi/180); %定义近休角范围y4=0;％近休运动规律plot(t1,y1,t2,y2,t3,y3,t4,y4)％绘制S－δ曲线程序运行的结果为：。
凸轮廓线设计MATLAB程序
凸轮轮廓及其综合1. 凸轮机构从动件的位移凸轮是把一种运动转化为另一种运动的装置。
凸轮的廓线和从动件一起实现运动形式的转换。
凸轮通常是为定轴转动，凸轮旋转运动可被转化成摆动、直线运动或是两者的结合。
凸轮机构设计的内容之一是凸轮廓线的设计。
定义一个凸轮基圆r b 作为最小的圆周半径。
从动件的运动方程如下：L(ϕ)=r b +s(ϕ)设凸轮的推程运动角和回程运动角均为β，从动件的运动规律均为正弦加速度运动规律，则有：s(ϕ)＝h(βϕ-π21sin(2πϕ/β)) ０≤ϕ≤βs(ϕ)＝h －h(ββϕ--π21sin(2π(ϕ-β/β)) β≤ϕ≤2βs(ϕ)＝0 2β≤ϕ≤2π上式是从动件的位移，h 是从动件的最大位移，并且0≤β≤π。
如果假设凸轮的旋转速度ω＝d ϕ／dt 是个常量，则速度υ、加速度a 和瞬时加速度j （加速度对时间求异）分别如下：速度：υ(ϕ)＝βωh（1-cos(2πϕ/β)） 0≤ϕ≤β υ(ϕ)＝－βωh（1-cos(2π(ϕ-β)/β) β≤ϕ≤2β υ(ϕ)＝0 2β≤ϕ≤2π加速度：a(ϕ)＝222βπωhsin(2πϕ/β)） 0≤ϕ≤βa(ϕ)＝-222βπωhsin(2π(ϕ-β)/β) β≤ϕ≤2βa(ϕ)＝0 2β≤ϕ≤2π瞬时加速度：j(ϕ)＝3324βωπhcos(2πϕ/β)） 0≤ϕ≤βj(ϕ)＝-3324βωπhcos(2π(ϕ-β)/β) β≤ϕ≤2βj(ϕ)＝0 2β≤ϕ≤2π定义无量纲位移S=s/h 、无量纲速度V=υ/ωh 、无量纲加速度A=a/h ω3和无量纲瞬时加速度J=j/h ω3。
若β＝60°，则如下程序可以对以上各个量进行计算。
beta=60*pi/180;phi=linspace(0,beta,40); phi2=[beta+phi]; ph=[phi phi2]*180/pi; arg=2*pi*phi/beta;arg2=2*pi*(phi2-beta)/beta;s=[phi/beta-sin(arg)/2/pi 1-(arg2-sin(arg2))/2/pi]; v=[(1-cos(arg))/beta-(1-cos(arg2))/beta]; a=[2*pi/beta^2*sin(arg)2*pi/beta^2*sin(arg2)];j=[4*pi^2/beta^3*cos(arg)4*pi^2/beta^3*cos(arg2)]:subplot(2,2,1) plot(ph,s,ˊK ˊ)xlabel(ˊCam angle(degrees)ˊ) ylabel(ˊDisplacement(S)ˊ) g=axis; g(2)=120; axis(g) subplot(2,2,2)plot(ph,v,ˊk ˊ,[0 120],[0 0],ˊk--ˊ) xlabel(ˊCam angle(degrees)ˊ) ylabel(ˊVelocity(V)ˊ) g=axis; g(2)=120; axis(g) subplot(2,2,3)plot(ph,a,ˊk ˊ,[0 120],[0 0],ˊk--ˊ) xlabel(ˊCam angle(degrees)ˊ)ylabel(ˊAcceleration(A)ˊ)g=axis;g(2)=120;axis(g)subplot(2,2,4)plot(ph,j,ˊkˊ,[0 120],[0 0],ˊk--ˊ)xlabel(ˊCam angle(degrees)ˊ)ylabel(ˊJerk(J)ˊ)g=axis;g(2)=120;axis(g)2 平底盘形从动作参考下图得到如下关系：在（x,y）坐标系中，凸轮轮廓的坐标为Ｒx和Ｒy,刀具的坐标为Ｃx和Ｃy：Ｒx＝Ｒcos( θ+ϕ) Ｒy＝Ｒsin( θ+ϕ)C x＝Ccos( γ+ϕ) C y＝Ccos( γ+ϕ)其中，R=θcos Lθ=arctan ⎪⎪⎭⎫ ⎝⎛ϕd dL L 1 c=γγcos cL + γ=arctan ⎪⎪⎭⎫ ⎝⎛+c L d dL γϕ/ r c 是刀具的半径，且dL/d ϕ＝Ｖ（ϕ）/ω。
基于MATLAB软件的凸轮轮廓曲线设计-
基于ＭＡＴＬＡＢ软件的凸轮轮廓曲线设计摘要：以偏置移动从动件盘形凸轮为例，基于ＭＡＴＬＡＢ软件对凸轮轮廓曲线进行了解析法设计．绘制出轮廓曲线。
运行结果表明：在从动件运动规律确定的情况下，利用ＭＡＴＬＡＢ软件以很方便、快捷地得到凸轮的轮廓曲线。
关键词：凸轮机构；凸轮轮廓曲线；ＭＡＴＬＡＢ；解析法前言凸轮轮廓曲线的设计，一般可分为图解法和解析法．利用图解法能比较方便地绘制出各种平面凸轮的轮廓曲线．但这种方法仅适用于比较简单的结构，用它对复杂结构进行设计则比较困难，而且利用图解法进行结构设计，作图误差较大，对一些精度要求高的结构不能满足设计要求。
解析法可以根据设计要求，通过推导机构中各部分之间的几何关系，建立相应的方程，精确地计算出轮廓线上各点的坐标，然后把凸轮的轮廓曲线精确地绘制出来．但是，当从动件运动规律比较复杂时，利用解析法获得凸轮的轮廓曲线的工作量比较大．而ＭＡＴＬＡＢ软件提供了强大的矩阵处理和绘图功能，具有核心函数和工具箱．其编程代码接近数学推导公式，简洁直观，操作简易，人机交互性能好，且可以方便迅速地用三维图形、图像、声音、动画等表达计算结果、拓展思路［１］。
因此，基于ＭＡＴＬＡＢ软件进行凸轮机构的解析法设计，可以解决设计工作量大的问题。
本文基于ＭＡＴＬＡＢ软件进行凸轮轮廓曲线的解析法设计，利用《机械原理》课程的计算机辅助教学，及常用机构的计算机辅助设计．其具体方法为首先精确地计算出轮廓线上各点的坐标，然后运用ＭＡＴＬＡＢ绘制比较精确的凸轮轮廓曲线。
1 设计的意义与已知条件1.1意义凸轮机构是由具有曲线轮廓或凹槽的构件，通过高副接触带动从动件实现预期运动规律的一种高副机构，它广泛地应用于各种机械，特别是自动机械、自动控制装置和装配生产线中，是工程实际中用于实现机械化和自动化的一种常用机构。
所以，在凸轮的加工中，精确的确定凸轮的轮廓，这对于保证凸轮所带动从动件的运动规律是尤为重要的。
1.2已知条件偏置移动从动件盘形凸轮设计已知条件（图1）:凸轮作逆时针方向转动,从动件偏置在凸轮轴心的右边从动件在推程作等加速/等减速运动,在回程作余弦加速度运动基圆半径rb = 40 mm，滚子半径rt = 10mm，推杆偏距e = 15 mm，推程升程h = 50 mm，推程运动角ft = 100度，远休止角fs = 60度回程运动角fh = 90度，推程许用压力角alp = 35度。
基于MATLAB的凸轮设计
中国地质大学〔武汉〕1. 凸轮要求设计一对心直动滚子推杆盘形凸轮机构,滚子半径r r =10mm,凸轮以等角速度逆时针回转.凸轮转角δ=0~120 时,推杆等速上升20mm ；δ=120~180 时,推杆远休止；δ=180~270时,推杆等加速等减速下降20mm ；δ=270~360时,推杆近休止.要求推程的最大压力角α<=30,试选取合适的基圆半径,并绘制凸轮的廓线.问此凸轮是否有缺陷,应如何补救.2．列出凸轮运动方程 {S =30π∗δV =30πa =00<δ<2/3π{S =20V =0a =02/3π<δ<π {S =−140+320π∗δ−160π∗δ^2V =320π−320π2∗δa =−320/π^2π<δ<54π{S =360−480π∗δ+160π2∗δ^2V =−480π−320π2∗δa =−320/π^25/4π<δ<32π {S =0V =0a =02/3π<δ<2π3.由方程写MATLAB 源程序%1.已知参数 clear;r0=50; %基圆半径 rr=10; %滚子半径 h=20; %行程delta01=120;%推程运动角 delta02=60; % 远休角 delta03=90;%回程运动角 hd=pi/180; du=180/pi;n1=delta01+delta02; n2=delta01+delta02+delta03;%2凸轮曲线设计n=360;for i=1:360%计算推杆运动规律if i<=delta01s<i>=30/pi*<i*hd>;ds<i>=30/pi;ds=ds<i>;elseif i>delta01 && i<=n1;s<i>=h;ds<i>=0;ds=ds<i>;elseif i>n1 && i<=<n1+delta03/2>s<i>=-140+320/pi*<i*hd>-160/pi^2*<i*hd>^2;ds<i>=320/pi-320/pi^2*<i*hd>;ds=ds<i>;elseif i><n1+delta03/2> && i<=n2s<i>=360-480/pi*<i*hd>+160/pi^2*<i*hd>^2;ds<i>=-480/pi+320/pi^2*<i*hd>;ds=ds<i>;elseif i>n2 && i<=ns<i>=0;ds=0;end%计算凸轮轨迹曲线xx<i>=<r0+s<i>>*sin<i*hd>;%计算理论轮廓曲线yy<i>=<r0+s<i>>*cos<i*hd>;dx<i>=ds*sin<i*hd>+<r0+s<i>>*cos<i*hd>;%计算导数dy<i>=ds*cos<i*hd>-<r0+s<i>>*sin<i*hd>;xp<i>=xx<i>+rr*dy<i>/sqrt<dx<i>^2+dy<i>^2>;yp<i>=yy<i>-rr*dx<i>/sqrt<dx<i>^2+dy<i>^2>;end%3.输出凸轮轮廓曲线figure<1>;hold on;grid on;axis equal;axis<[-<r0+h-30> <r0+h+10> -<r0+h+10> <r0+rr+10>]>; text<r0+h+3,4,'X'>;text<3,r0+rr+3,'Y'>;text<-6,4,'O'>;title<'对心直动滚子推杆盘形凸轮设计'>;xlabel<'x/mm'>;ylabel<'y/mm'>;plot<[-<r0+h-40> <r0+h>],[0 0],'k'>;plot<[0 0],[-<r0+h> <r0+rr>],'k'>;plot<xx,yy,'r--'>;%»绘凸轮实际轮廓曲线ct=linspace<0,2*pi>;plot<r0*cos<ct>,r0*sin<ct>,'g'>;%绘凸轮基圆plot<rr*cos<ct>,r0+rr*sin<ct>,'k'>;%绘滚子圆plot<0,r0,'o'>;%滚子圆中心plot<[0 0],[r0 r0+30],'k'>;plot<xp,yp,'b'>; %绘凸轮实际轮廓曲线%4. 凸轮机构运动仿真%计算凸轮滚子转角xp0=0;yp0=r0-rr;dss=sqrt<diff<xp>.^2+diff<yp>.^2>;%对轮廓曲线进行差分计算ss<1>=sqrt<<xp<1>-xp0>^2+<xp<1>-yp0>^2>;%轮廓曲线第一点长度for i=1:359ss<i+1>=ss<i>+dss<i>;%计算实际廓曲线长度endphi=ss/rr;%计算滚子转角%运动仿真开始figure<2>;m=moviein<20>;j=0;for i=1:360j=j+1;delta<i>=i*hd;%凸轮转角xy=[xp',yp'];%凸轮实际轮廓曲线坐标A1=[cos<delta<i>>,sin<delta<i>>;%凸轮坐标旋转矩阵-sin<delta<i>>,cos<delta<i>>];xy=xy*A1;%旋转后实际凸轮曲线坐标clf;%绘凸轮plot<xy<:,1>,xy<:,2>>;hold on;axis equal;axis<[-<120> <470> -<100> <140>]>;plot<[-<r0+h-40> <r0+h>],[0],'k'>;%绘凸轮水平轴plot<[0 0],[-<r0+h> <r0+rr>],'k'>;%绘凸轮垂直轴plot<r0*cos<ct>,r0*sin<ct>,'g'>;%绘基圆plot<rr*cos<ct>,r0+s<i>+rr*sin<ct>,'k'>;绘滚子圆plot<[0 rr*cos<-phi<i>>],[r0+s<i> r0+s<i>+rr*sin<-phi<i>>],'k'>; % 绘滚子圆标线plot<[0 0],[r0+s<i> r0+s<i>+40],'k'>;%绘推杆%绘推杆曲线plot<[1:360]+r0+h,s+r0>;plot<[<r0+h> <r0+h+360>],[r0 r0],'k'>;plot<[<r0+h> <r0+h>],[r0 r0+h],'k'>;plot<i+r0+h,s<i>+r0,'*'>;title<'对心直动滚子推杆盘形凸轮设计'>;xlabel<'x/mm'>;ylable<'y/mm'>;m<j>=getframe;endmovie<m>;4.运动仿真结果在MATLAB中可以看出轮廓曲线有一处缺口.应用圆弧连接起来. 5.计算结果由于数据太多,只等间隔取了三十六组数据Xx8.9718 18.2411 27.5000 36.4246 44.6859 51.9615 57.9477 62.3712 65.0000 65.6539 64.2123 60.6218 53.6231 44.9951 35.0000 23.9414 12.1554 0.0000 -12.0696 -23.2658 -32.7778 -39.9163 -44.3549 -47.1503 -48.8408 -49.7267 -50.0000 -49.2404 -46.9846 -43.3013 -38.3022 -32.1394 -25.0000 -17.1010 -8.6824 -0.0000Yy50.8817 50.1169 47.6314 43.4092 37.4959 30.0000 21.0912 10.9977 0.0000 -11.5765 -23.3714 -35.0000 -44.9951 -53.6231 -60.6218 -65.7785 -68.9365-70.0000 -68.4502 -63.9223 -56.7728 -47.5704 -37.2182 -27.2222 -17.7766 -8.7682 -0.0000 8.6824 17.1010 25.0000 32.1394 38.3022 43.3013 46.984649.2404 50.0000Dx52.5400 53.3830 52.4060 49.5474 44.8111 38.2699 30.0646 20.4019 9.5493 -2.1723 -14.3980 -26.7301 -44.9951 -53.6231 -60.6218 -65.7785 -68.9365-70.0000 -67.4676 -60.0514 -48.2845 -33.0207 -19.8785 -12.5201 -7.1415 -3.1953 0.0000 8.6824 17.1010 25.0000 32.1394 38.3022 43.3013 46.984649.2404 50.0000Dy0.4324 -9.2677 -19.2301 -29.1094 -38.5478 -47.1869 -54.6817 -60.7129 -65.0000 -67.3121 -67.4784 -65.3964 -53.6231 -44.9951 -35.0000 -23.9414 -12.1554-0.0000 17.6425 33.9010 47.4799 57.2560 58.9047 55.6385 52.7117 50.7094 50.0000 49.2404 46.9846 43.3013 38.3022 32.1394 25.0000 17.10108.6824 0.0000。
凸轮设计Matlab代码
plot(x1,y1,'b-',x2,y2,'g-',x3,y3,'m-',x4,y4,'c-',...
x6,y6,'b-',x7,y7,'g-',x8,y8,'m-',x9,y9,'c-',...
y6=y1-r*p1; %y' 函数
m2=-(s0+s2).*cos(a2+2*pi/3)+e*sin(a2+2*pi/3); % 中间变量 dx/d$
n2=-(s0+s2).*sin(a2+2*pi/3)-e*cos(a2+2*pi/3); % 中间变量 dy/d$
p2=-m2./sqrt(m2.^2+n2.^2); %sin&
y4=(s0+s4).*cos(a4+7*pi/6)-e*sin(a4+7*pi/6); %y 函数
a0=linspace(0,2*pi); % 基圆自变量
x5=r0*cos(a0); %x 函数
y5=r0*sin(a0); %y 函数
%工作廓线
m1=-(h*3/2/pi*(1-cos(3*a1))-e).*sin(a1)-(s0+s1).*cos(a1); % 中间变量 dx/d$
%凸轮理论廓线与工作廓线的画法
clear %清除变量
r0=50; %定义基圆半径
e=20; %定义偏距
h=50; %推杆上升高度
s0=sqrt(r0^2-e^2);
r=10; %滚子半径
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
机械原理大作业学院：机械与电子信息学院授课老师：曾小慧：京学号：20131004547日期：2015-5-23目录1.求轮廓曲线○1推程阶段○2远休止阶段○3回程阶段○4近休止阶段○5Matlab程序设计○6轮廓图形2.求工作廓线○1推程阶段○2远休止阶段○3回程阶段○4近休止阶段○5Matlab程序设计○6轮廓图形３．求解最大压力角○1压力角公式○2MATLAB程序设计○3根据MATLAB程序作图可得出其压力角与角度的关系并分析○4失真情况分析４．附录 Matlab程序凸轮轮廓9-14试设计偏置直动滚子推杆盘形凸轮机构的理论轮廓曲线和工作廓线。
已知凸轮轴置于推杆轴线右侧，偏距e=20mm ，基圆半径ｒ。
=50mm ，滚子半径rr=10mm 。
凸轮以等角速度沿顺时针方向回转，在凸轮转过角d 1=120º的过程中，推杆按正弦加速度运动规律上升h=50mm ；凸轮继续转过d 2=30º时，推杆保持不动；其后，凸轮再回转角度d 3=60º时，推杆又按余弦加速度运动规律下降至起始位置；凸轮转过一周的其余角度时，推杆又静止不动。
解：1.求理论廓线对于偏置直动滚子推杆盘形凸轮机构，凸轮理论廓线上B 点（即滚子中心）的直角坐标为]cos sin )[(0δδe s s x ++-=δδsin cos )(0e s s y -+= （a ） 式中mm mm e r s 826.452050222200=-=-=① 推程阶段3212001πδ=︒=)]2/()3sin()2/3[()]2/()/2sin()/[(110110111πδπδπδπδδδ-=-=h h s （⎥⎦⎤⎢⎣⎡=32,01πδ） ② 远休止阶段 63002πδ=︒=502=s ⎥⎦⎤⎢⎣⎡=6,02πδ③ 回程阶段36003πδ=︒=2/)]3cos(1[2/)]/cos(1[30333δδπδ+=+=h h s ⎥⎦⎤⎢⎣⎡=3,03πδ ④ 近休止阶段6515004πδ=︒= 04=s ⎥⎦⎤⎢⎣⎡=65,04πδ○5Matlab 程序设计： a1=linspace(0,2*pi/3); %推程阶段的自变量s1=h*(3*a1/2/pi-sin(3*a1)/2/pi); %推杆产生的相应位移x1=-((s0+s1).*sin(a1)+e*cos(a1)); %x 函数y1=(s0+s1).*cos(a1)-e*sin(a1); %y 函数a2=linspace(0,pi/6); %远休止阶段的自变量s2=50; %推杆位移x2=-((s0+s2).*sin(a2+2*pi/3)+e*cos(a2+2*pi/3)); %x 函数y2=(s0+s2).*cos(a2+2*pi/3)-e*sin(a2+2*pi/3); %y 函数a3=linspace(0,pi/3); %回程阶段的自变量s3=h*(1+cos(3*a3))/2; %推杆位移x3=-((s0+s3).*sin(a3+5*pi/6)+e*cos(a3+5*pi/6)); %x 函数y3=(s0+s3).*cos(a3+5*pi/6)-e*sin(a3+5*pi/6); %y 函数a4=linspace(0,5*pi/6); %近休止阶段的自变量s4=0; %推杆位移x4=-((s0+s4).*sin(a4+7*pi/6)+e*cos(a4+7*pi/6)); %x 函数y4=(s0+s4).*cos(a4+7*pi/6)-e*sin(a4+7*pi/6); %y 函数a0=linspace(0,2*pi); %基圆自变量x5=r0*cos(a0); %x 函数y5=r0*sin(a0); %y 函数○6轮廓图形 通过Matlab 软件，编写程序,将以上各相应值代入式(a)计算理论轮廓线上各点的坐标值。
在计算时应注意：在推程阶段取1δδ=，在远休止阶段取201δδδ+=，在回程阶段取30201δδδδ++=，在近休止阶段取4030201δδδδδ+++=。
画出的图形如下图所示2.求工作廓线θcos 'r r x x -= θsin 'r r y y -= （b ）其中 22)/()/(/)/(sin δδδθd dy d dx d dx +-= 22)/()/(/)/(cos δδδθd dy d dx d dy +=① 推程阶段⎥⎦⎤⎢⎣⎡=32,01πδ 1011cos )(sin })2/()]3cos(1[3{/δδπδδs s e h d dx +----=1011sin )(cos })2/()]3cos(1[3{/δδπδδs s e h d dy +---=② 远休止阶段⎥⎦⎤⎢⎣⎡=6,02πδ )3/2cos()()3/2sin(/202δπδπδ++-+=s s e d dx)3/2sin()()3/2cos(/202δπδπδ++-+-=s s e d dy③ 回程阶段⎥⎦⎤⎢⎣⎡=3,03πδ )6/5cos()()6/5sin(]2/)3sin(3[/3033δπδπδδ++-++=s s e h d dx)6/5sin()()6/5cos(]2/)3sin(3[/3033δπδπδδ++-++-=s s e h d dy④ 近休止阶段⎥⎦⎤⎢⎣⎡=65,04πδ )6/7cos()()6/7sin(/404δπδπδ++-+=s s e d dx)6/7sin()()6/7cos(/404δπδπδ++-+-=s s e d dy○5Matlab 程序设计： %工作廓线m1=-(h*3/2/pi*(1-cos(3*a1))-e).*sin(a1)-(s0+s1).*cos(a1); %中间变量dx/d$ n1=(h*3/2/pi*(1-cos(3*a1))-e).*cos(a1)-(s0+s1).*sin(a1); %中间变量dy/d$ p1=-m1./sqrt(m1.^2+n1.^2); %sin&q1=n1./sqrt(m1.^2+n1.^2); %cos&x6=x1-r*q1; %x'函数y6=y1-r*p1; %y'函数m2=-(s0+s2).*cos(a2+2*pi/3)+e*sin(a2+2*pi/3); %中间变量dx/d$ n2=-(s0+s2).*sin(a2+2*pi/3)-e*cos(a2+2*pi/3); %中间变量dy/d$ p2=-m2./sqrt(m2.^2+n2.^2); %sin&q2=n2./sqrt(m2.^2+n2.^2); %cos&x7=x2-r*q2; %x'函数y7=y2-r*p2; %y'函数m3=(h*3/2*sin(3*a3)+e).*sin(a3+5*pi/6)-(s0+s3).*cos(a3+5*pi/6); %中间变量dx/d$ n3=-(h*3/2*sin(3*a3)+e).*cos(a3+5*pi/6)-(s0+s3).*sin(a3+5*pi/6);%中间变量dy/d$ p3=-m3./sqrt(m3.^2+n3.^2); %sin&q3=n3./sqrt(m3.^2+n3.^2); %cos&x8=x3-r*q3; %x'函数y8=y3-r*p3; %y'函数m4=-(s0+s4).*cos(a4+7*pi/6)+e*sin(a4+7*pi/6); %中间变量dx/d$ n4=-(s0+s4).*sin(a4+7*pi/6)-e*cos(a4+7*pi/6); %中间变量dy/d$p4=-m4./sqrt(m4.^2+n4.^2); %sin&q4=n4./sqrt(m4.^2+n4.^2); %cos&x9=x4-r*q4; %x'函数y9=y4-r*p4; %y'函数○6轮廓图形同理，通过Matlab软件，编写程序,将以上各相应值代入式(a)计算理论轮廓线上各点的坐标值。
获得凸轮的工作廓线如下图所示。
将滚子画在上图中，可得最终的图形。
将Matlab中编程获得的凸轮轮廓曲线点的坐标保存为后缀名为dat文件，导入到UG中，完成凸轮的三维建模，如下图所示。
3.求解最大压力角○1压力角公式 压力角|)0/()e -/(|arctan s s d ds +=σα○2MATLAB 程序设计 clearr0=50;e=20;h=50;s0=sqrt(r0^2-e^2);r=10;a1=0:0.01:2*pi/3;s1=h*(3*a1/2/pi-sin(3*a1)/2/pi);c1=h*(3/2/pi- 3*cos(3*a1)/2/pi); %中间变量ds/d бt1=atan( abs((c1-e)/(s0+s1))); %压力角的计算plot(a1,t1)grid onhold ona2=2*pi/3:0.01:5*pi/6;s2=50;c2=0;t2=atan( abs((c2-e)/(s0+s2)));plot(a2,t2)grid onhold ona3=5*pi/6:0.01:7*pi/6;s3=h*(1+cos(3*(a3-5*pi/6)))/2;c3=-h*3*sin(3*(a3-5*pi/6))/2;t3=atan( abs((c3-e)/(s0+s3)));plot(a3,t3)grid onhold ona4=7*pi/6:0.01:2*pi;s4=0;c4=0;t4=atan( abs((c4-e)/(s0+s4)));plot(a4,t4)grid on○3根据MATLAB 程序作图可得出其压力角与角度的关系并分析当在推程段时，0=δ度时，得最大压力角度即为5.2341.0=α； 当在远休止段时，其压力角为定值，度即为7.1121.0=α；当其在回程段时，度时189=δ，得最大压力角度；即为8.5597.0=α 当在近休止段时，其压力角为定值，度即为5.2341.0=α○4失真情况分析由实际轮廓线可知其并未出现尖端，故其没有发生失真情况。
４.附录 Matlab程序%凸轮理论廓线与工作廓线的画法clear %清除变量r0=50; %定义基圆半径e=20; %定义偏距h=50; %推杆上升高度s0=sqrt(r0^2-e^2);r=10; %滚子半径%理论廓线a1=linspace(0,2*pi/3); %推程阶段的自变量s1=h*(3*a1/2/pi-sin(3*a1)/2/pi); %推杆产生的相应位移x1=-((s0+s1).*sin(a1)+e*cos(a1)); %x函数y1=(s0+s1).*cos(a1)-e*sin(a1); %y函数a2=linspace(0,pi/6); %远休止阶段的自变量s2=50; %推杆位移x2=-((s0+s2).*sin(a2+2*pi/3)+e*cos(a2+2*pi/3)); %x函数y2=(s0+s2).*cos(a2+2*pi/3)-e*sin(a2+2*pi/3); %y函数a3=linspace(0,pi/3); %回程阶段的自变量s3=h*(1+cos(3*a3))/2; %推杆位移x3=-((s0+s3).*sin(a3+5*pi/6)+e*cos(a3+5*pi/6)); %x函数y3=(s0+s3).*cos(a3+5*pi/6)-e*sin(a3+5*pi/6); %y函数a4=linspace(0,5*pi/6); %近休止阶段的自变量s4=0; %推杆位移x4=-((s0+s4).*sin(a4+7*pi/6)+e*cos(a4+7*pi/6)); %x函数y4=(s0+s4).*cos(a4+7*pi/6)-e*sin(a4+7*pi/6); %y函数a0=linspace(0,2*pi); %基圆自变量x5=r0*cos(a0); %x函数y5=r0*sin(a0); %y函数%工作廓线m1=-(h*3/2/pi*(1-cos(3*a1))-e).*sin(a1)-(s0+s1).*cos(a1); %中间变量dx/d$ n1=(h*3/2/pi*(1-cos(3*a1))-e).*cos(a1)-(s0+s1).*sin(a1); %中间变量dy/d$ p1=-m1./sqrt(m1.^2+n1.^2); %sin&q1=n1./sqrt(m1.^2+n1.^2); %cos&x6=x1-r*q1; %x'函数y6=y1-r*p1; %y'函数m2=-(s0+s2).*cos(a2+2*pi/3)+e*sin(a2+2*pi/3); %中间变量dx/d$n2=-(s0+s2).*sin(a2+2*pi/3)-e*cos(a2+2*pi/3); %中间变量dy/d$p2=-m2./sqrt(m2.^2+n2.^2); %sin&q2=n2./sqrt(m2.^2+n2.^2); %cos&x7=x2-r*q2; %x'函数y7=y2-r*p2; %y'函数m3=(h*3/2*sin(3*a3)+e).*sin(a3+5*pi/6)-(s0+s3).*cos(a3+5*pi/6); %中间变量dx/d$ n3=-(h*3/2*sin(3*a3)+e).*cos(a3+5*pi/6)-(s0+s3).*sin(a3+5*pi/6);%中间变量dy/d$ p3=-m3./sqrt(m3.^2+n3.^2); %sin&q3=n3./sqrt(m3.^2+n3.^2); %cos&x8=x3-r*q3; %x'函数y8=y3-r*p3; %y'函数m4=-(s0+s4).*cos(a4+7*pi/6)+e*sin(a4+7*pi/6); %中间变量dx/d$n4=-(s0+s4).*sin(a4+7*pi/6)-e*cos(a4+7*pi/6); %中间变量dy/d$p4=-m4./sqrt(m4.^2+n4.^2); %sin&q4=n4./sqrt(m4.^2+n4.^2); %cos&x9=x4-r*q4; %x'函数y9=y4-r*p4; %y'函数%画滚子g1=x1(1)+r*cos(a0);j1=y1(1)+r*sin(a0);g2=x1(25)+r*cos(a0);j2=y1(25)+r*sin(a0);g3=x1(50)+r*cos(a0);j3=y1(50)+r*sin(a0);g4=x1(60)+r*cos(a0);j4=y1(60)+r*sin(a0);g5=x1(75)+r*cos(a0);j5=y1(75)+r*sin(a0);g6=x1(90)+r*cos(a0);j6=y1(90)+r*sin(a0);g7=x2(1)+r*cos(a0);j7=y2(1)+r*sin(a0);g8=x2(50)+r*cos(a0);j8=y2(50)+r*sin(a0);g9=x3(1)+r*cos(a0);j9=y3(1)+r*sin(a0);g10=x3(25)+r*cos(a0);j10=y3(25)+r*sin(a0);g11=x3(40)+r*cos(a0);j11=y3(40)+r*sin(a0);g12=x3(50)+r*cos(a0);j12=y3(50)+r*sin(a0);g13=x3(75)+r*cos(a0);j13=y3(75)+r*sin(a0);g14=x4(1)+r*cos(a0);j14=y4(1)+r*sin(a0);g15=x4(50)+r*cos(a0);j15=y4(50)+r*sin(a0);figure %创建图形窗口plot(x1,y1,'b-',x2,y2,'g-',x3,y3,'m-',x4,y4,'c-',...x6,y6,'b-',x7,y7,'g-',x8,y8,'m-',x9,y9,'c-',...'LineWidth',2) %画函数曲线grid on %加网格hold on %保持图像plot(x5,y5,'r--',g1,j1,'k-',g2,j2,'k-',g3,j3,'k-',...g4,j4,'k-',g5,j5,'k-',g6,j6,'k-',g7,j7,'k-',...g8,j8,'k-',g9,j9,'k-',g10,j10,'k-',g11,j11,'k-',...g12,j12,'k-',g13,j13,'k-',g14,j14,'k-',g15,j15,'k-','LineWidth',2) %画基圆title('凸轮理论廓线与工作廓线','FontSize',16) %标题axis ([-100,80,-120,60])axis('equal')points=[x6',y6',zeros(100,1);x7',y7',zeros(100,1);...x8',y8',zeros(100,1);x9',y9',zeros(100,1)]％最大压力角clearr0=50;e=20;h=50;s0=sqrt(r0^2-e^2);r=10;a1=0:0.01:2*pi/3;s1=h*(3*a1/2/pi-sin(3*a1)/2/pi);c1=h*(3/2/pi- 3*cos(3*a1)/2/pi); %中间变量ds/dбt1=atan( abs((c1-e)/(s0+s1))); %压力角的计算plot(a1,t1)grid onhold ona2=2*pi/3:0.01:5*pi/6;s2=50;c2=0;t2=atan( abs((c2-e)/(s0+s2))); plot(a2,t2)grid onhold ona3=5*pi/6:0.01:7*pi/6;s3=h*(1+cos(3*(a3-5*pi/6)))/2; c3=-h*3*sin(3*(a3-5*pi/6))/2; t3=atan( abs((c3-e)/(s0+s3))); plot(a3,t3)grid onhold ona4=7*pi/6:0.01:2*pi;s4=0;c4=0;t4=atan( abs((c4-e)/(s0+s4))); plot(a4,t4)grid on。