信号分析与处理-杨西侠版-第3章习题答案
信号与系统课后习题与解答第三章
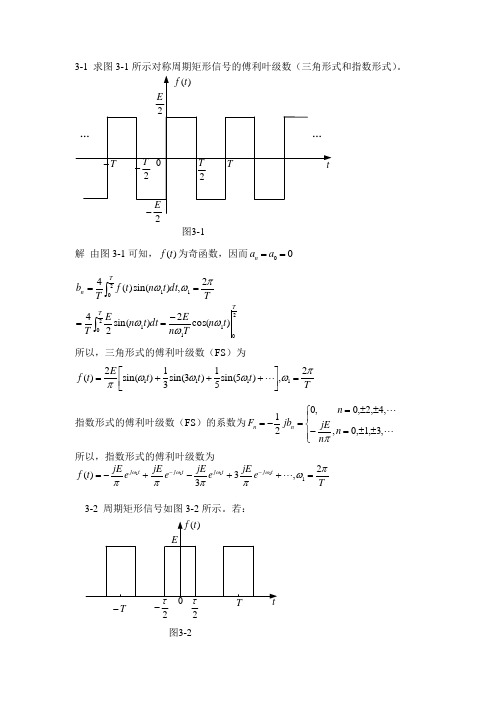
3-1 求图3-1所示对称周期矩形信号的傅利叶级数(三角形式和指数形式)。
图3-1解 由图3-1可知,)(t f 为奇函数,因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以,三角形式的傅利叶级数(FS )为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数(FS )的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以,指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。
若:图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。
解 对于图3-2所示的周期矩形信号,其指数形式的傅利叶级数(FS )的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n则的指数形式的傅利叶级数(FS )为∑∑∞-∞=∞-∞=⎪⎭⎫ ⎝⎛==n tjn n tjn n e n Sa TE eF t f 112)(1ωωτωτ其直流分量为TE n Sa T EF n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω将各参数的值代入,可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示,)(1t f 的参数为s μτ5.0=,s T μ1= ,V E 1=; )(2t f 的参数为s μτ5.1=,s T μ3= ,V E 3=,分别求:(1))(1t f 的谱线间隔和带宽(第一零点位置),频率单位以kHz 表示; (2))(2t f 的谱线间隔和带宽; (3))(1t f 与)(2t f 的基波幅度之比; (4))(1t f 基波与)(2t f 三次谐波幅度之比。
《信号与系统分析基础》第3章部分习题解答
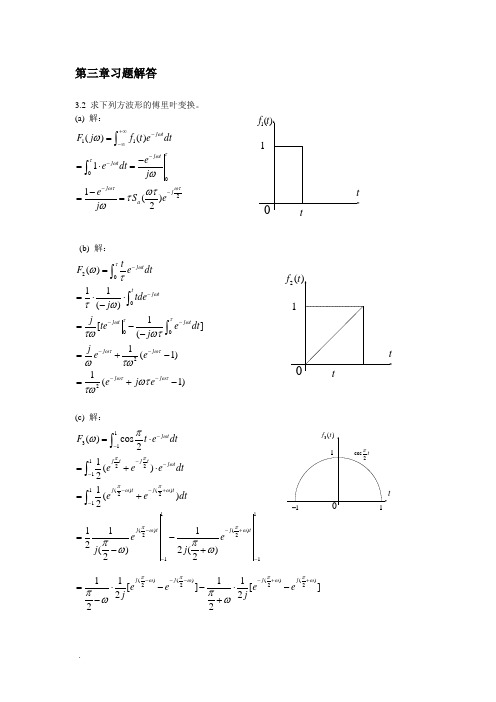
第三章习题解答3.2 求下列方波形的傅里叶变换。
(a) 解:1102()()11()2j t j t j t j j a F j f t e dt e e dt j e S e j ωτωτωωτωτωωωττω+∞--∞----=-=⋅=-==⎰⎰(b) 解:200022()11()1[](1(1)1(1)j t t j t j t j t j j j j tF e dttde j j te e dt j j e e ej eτωωττωωωτωτωτωτωττωτωωτωτωωττω--------==⋅⋅-=--=+-=+-⎰⎰⎰(c) 解:13112211()()22111()()2211()cos21()21()21112()2()22j t j t j t j t j t j t j t j tF t e dte e e dt e e dt e ej j ωππωππωωππωωπωππωω-------+---+--=⋅=+⋅=+=--+⎰⎰⎰()()()()22221111[][]2222j j j j e e e e j j ππππωωωωππωω----++=⋅--⋅--+2222sin()sin()cos ()cos ()cos 2222()()2222ππππωωωωωωπωππππωωωω-+⋅++⋅-⋅=+==-+--3.3依据上题中a,b 的结果,利用傅里叶变换的性质,求题图3.3所示各信号的傅里叶变换. (b) 解:262()()()f t g t g t =+,而()()2g t Sa τωττ↔2()6(3)2()F Sa Sa ωωω∴=+如利用3.2中(a)的结论来解,有:211'()(3)(1)f t f t f t ττ=+++,其中6,'2ττ==.3211'()()()6(3)2()j j F e F e F Sa Sa ωωττωωωωω∴=⋅+⋅=+(如()()f t F ω↔,则00()()j t f t t eF ωω±↔)(c) 解:32222()2()2(),1f t f t f t τττ=++-+= 由3.2(b)知,2221()(1)j j F e j e ωτωτωωττω--=+-32222222222222()2()2(),1112(1)2(1)222222444cos (1cos )j j j j j j j j j j F e F e F e e j e e e j e je je ωτωτωωωωωωωωωωωτωωωωωωωωωωωωωωω-----∴=+-==⋅⋅+-+⋅⋅--=+-+--=-=-3.4利用对称性求下列各函数的傅里叶变换.(2) 222(),.f t t tαα=-∞<<+∞+ 解:222t e αααω-↔+ ,由对称性,2222et αωαπα-↔+(3)2()f t444444444244()(2)(2)1(2)()21111()(2)(2)[()]*[()][()()]22282,()()0.22,()()2;26,()()f t Sa t Sa t Sa t g f t Sa t Sa t g g g g g g g g d g g d πππππππωππππππππωππωωωωππωπωωπωπωωυωππωπωωυ-=⋅↔=⋅↔=*<-*=-<<*==+<<*=⎰解:而,利用频域卷积特性,得:积分:2444246.6,()()0g g πωππππωππωωπωω-=-+=->*=⎰3.8(3) ()(2)()2()dF t f t j F d ωωω-↔-(6) (25)f t -;由1[()]()j b a F f at b e F a a ωω--=⋅,2,5,a b == 2.51(25)()22j f t e F ωω-∴-↔⋅3.9 计算下列各信号的傅里叶变换.(2) 3()2(32)()2[2()],2u t t u t t δδδ+-=+-是偶函数332232()1,1[()]().2, 3.112(32)21,()().21()2(32)()j b aj j j t F f at b e F a aa b t e e u t j u t t e j ωωωωδωδπδωωδπδωω----↔-===∴-↔⋅⋅⋅=↔+∴+-↔++ 由(7) 33(2)63(3)9[(2)(3)](2)(3)tt t e u t u t eu t e e u t e --+---+--=⋅+-⋅-33(2)23(3)31().11();(2)331(3)3t t t j t j e u t j e u t e u t e j j e u t e j αωωαωωωω---+---↔+∴↔+↔++-↔+ 同理:32(3)3(3)1[(2)(3)]()3t j j e u t u t e e j ωωω-+-+∴+--↔-+3.13 已知阶跃函数和正弦、余弦函数的傅里叶变换如下:0000001[()]()[c o s ][()()][s i n ][()()]F u t j F t F t j πδωωωπδωωδωωωπδωωδωω=+=++-=+-- 求单边正弦函数和单边余弦函数的傅里叶变换。
信号分析与处理作者杨西侠柯晶1信号概述共24页文档

24、勇气很有理由被当作人类德性之 首,因 为这种 德性保 证了所 有其余 的德性 。--温 斯顿. 丘吉尔 。 25、梯子的梯阶从来不是用来搁脚的 ,它只 是让人 们的脚 放上一 段时间 ,以便 让别一 只脚能 够再往 上登。
1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事,无字句处读书。——周恩来 5、阅读使人充实,会谈使人敏捷,写作使人精确。——培根
随机信号分析(第3版)第三章 习题答案

Z (t )的均值: E[ Z (t )] = E[ A ⋅ X (t ) ⋅ Y (t )] = E[ A] ⋅ E[ X (t )] ⋅ E[Y (t )] = 2 E[ X (t )] ⋅ E[Y (t )]
2 mX = RX (∞) = lim
2 cos ω0τ = 0 → mX = 0 τ →∞ eτ
⎡ 2 1.3 0.4 __ ⎤ ⎢ __ 2 1.2 0.8⎥ ⎢ ⎥ ⎢ 0.4 1.2 __ 1.1 ⎥ ⎢ ⎥ ⎣ 0.9 __ __ 2 ⎦ 3.12 解:根据广义平稳随机信号过程的自相关函数矩阵的对称性,得到: ⎛ 2 1.3 0.4 0.9 ⎞ ⎜ 1.3 2 1.2 0.8 ⎟ ⎟ C= ⎜ ⎜ 0.4 1.2 2 1.1 ⎟ ⎜ ⎟ ⎝ 0.9 0.8 1.1 2 ⎠ 3.13
= E[100 sin 2 (ω 0 t + θ ) ×100 sin 2 (ω 0 t + ω 0τ + θ ) ] = 2500 E[1 − cos(2ω 0τ ) − cos(4ω 0 t + 2ω 0τ + 4θ )] = 2500 E[1 − cos(2ω 0τ ) ] ∴ R Z (τ ) 仅与 τ 有关,且均值为常数,故 Y(t ) 是平稳过程。
3.6 给定随机过程 X ( t ) = A cos (ω 0t ) + B sin (ω 0t ) ,其中 ω 0 是常数, A 和 B 是 两个任意的不相关随机变量,它们均值为零,方差同为 σ 2 。证明 X ( t ) 是广义平 稳而不是严格平稳的。 3.6 证明:Q m X (t ) = E[X(t )] = E[ A cos(ω 0 t ) + B sin(ω 0 t) ] = 0
信号分析与处理课后习题答案

信号分析与处理课后习题答案第五章 快速傅里叶变换1.如果一台通用计算机的速度为平均每次复乘需要50us ,每次复加需要10us ,用来就散N=1024点的DFT ,问:(1)直接计算需要多少时间?用FFT 计算呢?(2)照这样计算,用FFT 计算快速卷积对信号进行处理是,估计可实现实时处理的信号最高频率? 解:分析:直接利用DFT 计算:复乘次数为N 2,复加次数为N(N-1);利用FFT 计算:复乘次数为20.5log N N ,复加次数为2log N N ;(1) 直接DFT 计算:复乘所需时间2215010245052.4288T N us us s =⨯=⨯=复加所需时间2(1)101024(10241)1010.47552T N N us us s =-⨯=-⨯= 所以总时间1262.90432DFT T T T s =+=FFT 计算:复乘所需时间3220.5log 500.51024log 1024500.256T N N us us s =⨯=⨯⨯⨯= 复加所需时间422log 101024log 1024100.1024T N N us us s =⨯=⨯⨯= 所以总时间为340.3584FFT T T T s =+= (2) 假设计算两个N 长序列1()x n 和2()x n 的卷积计算过程为如下:第一步:求1()X k ,2()X k ;所需时间为2FFT T ⨯第二步:计算12()()()X k X k X k =•,共需要N 次复乘运算所需时间为501024500.0512To N us us s =⨯=⨯=第三步:计算(())IFFT X k ,所需时间为FFT T所以总时间为230.35840.0512 1.1264FFT T T To s s s =⨯+=⨯+= 容许计算信号频率为N/T=911.3Hz2.设x(n)是长度为2N 的有限长实序列,()X k 为x(n)的2N 点得DFT 。
信号分析与处理杨西侠版第3章习题答案

3-1 求以下序列的频谱)X(e j ω(1)δ(n) (2)δ(n-3)(3) δ(n+1)+δ(n)+ δ(n-1) (4) a n u(n), 0<a<1 (5) 矩形序列R N (n) 解:序列频谱的定义为)X(e j ω= ∑+∞∞=--n )(ωjn e n x(1) )X(e j ω=∑+∞∞=--n )(ωδjn e n = 1(2) )X(e j ω= ∑+∞∞=---n )3(ωδjn e n = ω-j3e(3) )X(e j ω=ωδδδjn e n n n -+∞∞=∑-+++-n )]1(5.0)()1(5.0[= ωj 0.5e + 1 +ω-j 0.5e= 1 +2ωωj j e e -+= 1 +ω cos (4) )X(e j ω=∑+∞∞=--n )(ωjn nen u a= ∑+∞=-0n ωjn n e a= n j ae )(0n ∑+∞=-ω (∵0 < a < 1, ∴收敛)= 11ωj ae-- (5) )X(e j ω=∑+∞∞=--n )(ωjn N e n R= ∑-=-1n N jn e ω= 11ωωj jN ee ----=22ωωj N jee--·2222ωωωωj j N jN je e ee ----= ω21-N j-e2sin 2sinωωN 3-2 设)X(e j ω和)Y(e j ω分别是x(n)和y(n)的傅里叶变换,试求下面序列的傅里叶变换 (1) x(n-n 0)(2) x *(n)(3) x(-n)(4) x(n)* y(n) (5) x(n) y(n) (6) nx(n) (7) x(2n)(8) x 2(n)x ( 2n), n 为偶数(9) x a (n) =0,n 为奇数(1) DTFT[x(n-n 0)] = ∑+∞∞=---n 0)(ωjn e n n xωω0-m 0)(jn jm e e m x n n m -+∞∞=-∑-== ωω0)X(e j jn e -(2) DTFT[x *(n)] = ∑+∞∞=--n *)(x ωjn e n= *-n ])(x [∑+∞∞=ωjn e n = *-n )(])(x [∑+∞∞=--ωjn e n= )(e X -j *ω(3) DTFT[x(-n)] = ∑+∞∞=--n x (-n)ωjn e∑-∞+∞=---=m )(x (m)ωjm enm= )X(e -j ω(4) DTFT[x(n)* y(n)] = ∑+∞∞=--n y(n)] * [x (n)ωjn e=∑∑+∞∞=-+∞∞=--n -m )()(ωjn e m n y m x= ∑∑+∞-∞=-+∞-∞=-n jn m e m n y m x ω)()( = ωωjm j m e e Y m x -+∞-∞=∑)()( = ωωjm m j e m x e Y -+∞-∞=∑)()(= )()(ωωj j e Y e X(5) DTFT[x(n) y(n)] = ωjn n e n y n x -+∞-∞=∑)()(= ωππθθθπjn n jn j e n y d e e X -+∞-∞=-∑⎰)(])(21[=θπθωππθd e n y e X n jn j ])()[(21)(∑⎰+∞-∞=---=θπππθωθd e Y e X j j ⎰--)()(21)(= )(*)(21ωωπj j e Y e X (6) DTFT[nx(n)] = ωjn n e n nx -+∞-∞=∑)(=)]([ωωj e X d d j (7) DTFT[x(2n)] = ωjn n e n x -+∞-∞=∑)2(2)(2ωjmm em x n m -+∞-∞=∑=∑+∞-∞=---+m jm m jm e m x e m x m ])()1()([2122ωω取整数 = 2)(21ωjmm em x -+∞-∞=∑+mj m e m x )()(212ω-+∞-∞=-∑ = )(212ωj e X +)(212ωj e X - (8) DTFT[x 2(n)] = )(*)(21ωωπj j e X e X (9) DTFT[x a (n)] = ωjn n a e n x -+∞-∞=∑)(= ωn j n a e n x 2)2(-+∞-∞=∑= ωn j n e n x 2)(-+∞-∞=∑= )(2ωj e X1 | ω | < ω03-3 已知)X(e j ω=0 ω0≤ | ω | ≤π求)X(e j ω的傅里叶反变换解:x(n) =ωπωππωd e e X jn j ⎰-)(21=⎰-21ωωωωπd e jn=0|21ωωωπ-jn e jn = je e n jn jn 2100ωωπ--⋅= πωn n 0sin = 000sin ωωπωn n ⋅ = )(00ωπωn Sa 3-4 周期序列x p (n), 如图3-44所示,周期N=4,求DFS[x p (n)] = X p (k)解: 由DFS 的定义 X p (k) = nk N N n pW n x∑-=10)(∴ X p (0) = 0210)(⨯--=∑πjn N n pen x=∑=3)(n pn x= 4X p (1) =n j n pen x23)(π-=∑= 2 + (–j ) + 0 + j = 2n-141图3-442-23512X p (2) = πjn n p e n x -=∑3)(= 2 + (–1 ) + 0 + (–1 ) = 0X p (3) =233)(πjnn pen x-=∑= 2 + j + 0 + (–j ) = 2∵ X p (k)是周期函数,其周期长度N=4∴ X p (k) = Z[1+cos( 2πk )]或 X p (0) = 4, X p (1) = 2, X p (2) = 0, X p (3) = 23-5 如果x p (n)是一个周期为N 的序列,也是周期为2N 的序列,令X p1(k)表示当周期为N 时的DFS 系数,X p2(k)是当周期为2N 时的DFS 系数。
随机信号分析(第3版)第三章习题及答案

3.1 随机电压信号()U t 在各不同时刻上是统计独立的,而且,一阶概率密度函数是高斯的、均值为0,方差为2,试求:(1)密度函数();f u t 、()1212,;,f u u t t 和()1212,,...,;,,...,k k f u u u t t t ,k 为任意整数;(2)()U t 的平稳性。
3.1解:(1)2(;)}4x f u t =-22121,2121,12,21(;,)()()exp{}44u u f u u t t f u t f u t π+==-211,212,1(,,;,,)()}4kiki k k i i i uf u u u t t t f u t ====-∑∏(2)由于任意k 阶概率密度函数与t 无关,因此它是严平稳的。
3.23.33.4 已知随机信号()X t 和()Y t 相互独立且各自平稳,证明新的随机信号()()()Z t X t Y t =也是平稳的。
3.4解:()X t 与()Y t 各自平稳,设X m =[()]E X t ,Y m =[()]E Y t ,()[X()X()]X R E t t ττ=+,()[Y()Y()]Y R E t t ττ=+Z ()[Z()][()Y()][()][()]X Y m t E t E X t t E X t E Y t m m ===⨯=,为常数(,)[Z()Z()][()Y()()Y()][X()()][Y()()]()()()Z X Y Z R t t E t t E X t t X t t E t X t E t Y t R R R τττττττττ+=+=++=+⨯+=⨯=∴()Z R τ仅与τ有关,故Z()t =()Y()X t t 也是平稳过程。
3.5 随机信号()()010sin X t t ω=+Θ,0ω为确定常数,Θ在[],ππ-上均匀分布的随机变量。
若()X t 通过平方律器件,得到2()()Y t X t =,试求:(1)()Y t 的均值; (2)()Y t 的相关函数;(3)()Y t 的广义平稳性。
信号分析与处理习题答案(P155)

信号分析与处理习题答案(P155)3、绘图程序:%sinusoidal sequence n=0:29;x=sin(16*pi/5*n+pi/4); stem(n,x);xlabel('n');ylabel('x(n)');title('Sinusoidal sequence'); grid;55825162=∴===N N m序列为周期序列为有理数πππω4、绘图程序:%delta sequencen=[-5 -4 -3 -2 -1 0 1 2 3 4 5]; x=[0 5 0 0 2 0 -4 0 3 0 0]; stem(n,x);xlabel('n');ylabel('x(n)');title('delta sequence'); grid;8、根据DTFT 性质, (1)时域尺度变换特性:连续时间傅里叶变换的尺度变换表示为:⎪⎭⎫ ⎝⎛↔a X a at x ω1)( 然而,在离散时间的情况下,若a 不是整数,x[an]就不是一个序列。
另一方面,如果a 是一个整数,例如a=2,那么x[2n]仅包含x[n]的偶数样点。
因此,离散时间中的时域尺度变换与上式有些不同。
令m 为一正整数,则序列的傅里叶变换为⎩⎨⎧≠===km n kmn k x m n x n x m 0][]/[][)(()a b{})(][][][][)()()()(Ω====∑∑∑∞-∞=Ω-∞-∞=Ω-∞-∞=Ω-m X ek x ekm xen xn x F n km j n kmj m n nj m m所以)(0]/[][)(Ω↔⎩⎨⎧≠==m X km n km n m n x n x m⎪⎭⎫⎝⎛Ω↔a X an x )( (3)时域位移:)(][00Ω↔-Ω-X en n x n j)()1()()()2()(22Ω-=Ω-Ω↔--Ω-Ω-X e X eX n x n x j j10.(2)根据P109式3-26)())(()(1)()()(00101000Ω=Ω+=ΩΩ=∑∑-=Ω--=Ωk X qN k X en x Nk X e k X n x N k njk N k njk根据题意,序列x(n)的基本周期为N=8,Ω0=2π/N=π/4 根据欧拉公式,nj nj njnjee een 002121214cos 44Ω-Ω-+=⎪⎪⎭⎫ ⎝⎛+=πππ则x(n)的傅里叶系数为X(1)=1/2,X(-1)= X(-1+8)= X(7)=1/2,其他系数等于0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明:频移定理为
由IDFT的定义可知,
3-13
(1) ;
(2) 。
解:频移定理
(1)∵
∴
由频移特性:
(2)∵
∴
由频移特性:
3-14
求DFT[ y(n)]与X (k)的关系。
解:由DFT的定义可知,
3-15
证明:频域圆卷积定理,
若 则
同理可证
3-16
(1)x(n)(n) = x(n);
(2)x(n)(nn0) = x(nn0);
=
=
=
= = =
解:由DFS的定义
Xp(k)=
∴Xp(0)=
= = 4
Xp(1)= = 2 + (–j ) + 0 + j = 2
Xp(2)= = 2 + (–1 ) + 0 + (–1 ) = 0
Xp(3)= = 2 + j + 0 + (–j ) = 2
∵Xp(k)是周期函数,其周期长度N=4
证明:由卷积的定义可知来自(1)(2)3-17
解:
∴
∴
(3)
∴
3-9
解:
(1)
∴
. . .
. . .
∴
(2)
(3)
(4)
(5)
3-10
解:(1)
(2)
(3)
当 时,
当 时,
3-11
(1)x(n)与x(n)的线卷积;
(2)x(n)与x(n)的4点圆卷积;
(3)x(n)与x(n)的10点圆卷积;
(4)若要使x(n)与x(n)的线卷积等于圆卷积的结果,求序列长度的最小值。
0
0
0.5
相乘
0
0
0
0.25
取和
0.25
(2)
1) 反褶
2) 移位、相乘、求和
x(m)
0.5
1
1
0.5
xp(0-m)
0.5
0.5
1
1
相乘
0.25
0.5
1
0.5
取和
2.25
x(m)
0.5
1
1
0.5
xp(1-m)
1
0.5
0.5
1
相乘
0.5
0.5
0.5
0.5
取和
2
x(m)
0.5
1
1
0.5
xp(2-m)
1
1
∴Xp(k)= Z[1+cos( k)]
或Xp(0)= 4,Xp(1)= 2,Xp(2)= 0,Xp(3)= 2
3-5
解:由DFS的定义
Xp1(k)=
Xp2(k)=
= +
+
=Xp1( )+
=
=
=
3-6
解:与3-4答案相同,可由定义求出。只不过此时的x(k)非周期的。
Xp(k)= Z[1+cos( k)]R4(k)
解:图解法求卷积的步骤为:
1)反褶
2)移位(线移或圆移)
3)相乘
4)求和
(1)
1)反褶
2)移位、相乘、求和
x(m)
0.5
1
1
0.5
x(0-m)
0.5
0
0
0
相乘
0.25
0
0
0
取和
0.25
x(m)
0.5
1
1
0.5
x(1-m)
1
0.5
0
0
相乘
0.5
0.5
0
0
取和
1
x(m)
0.5
1
1
0.5
x(2-m)
1
1
0.5
3-1
(1)δ(n)(2)δ(n-3)
(3)0.5δ(n+1)+δ(n)+0.5δ(n-1)
(4)anu(n), 0<a<1
(5)矩形序列RN(n)
解:序列频谱的定义为
=
(1) = = 1
(2) = =
(3) =
= + 1 +
= 1 + = 1 +
(4) =
=
= (∵0 < a < 1,∴收敛)
=
(5) =
或Xp1(0)= 4,Xp1(1)= 2,Xp1(2)= 0,Xp1(3)= 2
3-7
解:先将有限长序列进行周期延拓,然后右移2位。再截取0~3点即得x1(n),如下左图所示。
先将有限长序列后褶,然后再进行周期延拓。再截取0~3点即得x2(n),如下右图所示。
3-8
解:(1)由定义得,
∴
(2)∵
∴只要 ,N就取整数
0
相乘
0.5
1
0.5
0
取和
2
x(m)
0.5
1
1
0.5
x(3-m)
0.5
1
1
0.5
相乘
0.25
1
1
0.25
取和
2.5
x(m)
0.5
1
1
0.5
x(4-m)
0
0.5
1
1
相乘
0
0.5
1
0.5
取和
2
x(m)
0.5
1
1
0.5
x(5-m)
0
0
0.5
1
相乘
0
0
0.5
0.5
取和
1
x(m)
0.5
1
1
0.5
x(6-m)
0
0.5
0.5
相乘
0.5
1
0.5
0.25
取和
2.25
x(m)
0.5
1
1
0.5
xp(3-m)
0.5
1
1
0.5
相乘
0.25
1
1
0.25
取和
2.5
(3)
反褶:
移位、相乘、求和:
(4)由(3)可得,当x(n)由4点通过补零扩为10点时,此时的圆卷积和线卷积的结果相同。由于线卷积的长度为4+4-1=7
∴可知x(n)由4点通过补零扩为最少7点时,圆卷积和线卷积相等。
=
=
= ·
=
3-2
(1)x(n-n0)(2)x*(n)(3)x(-n)
(4)x(n)*y(n)(5)x(n)y(n)(6)nx(n)
(7)x(2n)(8)x2(n)
x( ),n为偶数
(9)xa(n) =
0,n为奇数
(1)DTFT[x(n-n0)] =
=
(2)DTFT[x*(n)] =
=
=
=
(3)DTFT[x(-n)] =
=
(4)DTFT[x(n)*y(n)] =
=
=
=
=
=
(5)DTFT[x(n)y(n)] =
=
=
=
=
(6)DTFT[nx(n)]=
=
(7)DTFT[x(2n)]=
= +
= +
(8)DTFT[x2(n)]=
(9)DTFT[xa(n)]=
=
=
=
1|ω| <ω0
3-3
0ω0≤|ω|≤π
求 的傅里叶反变换
解:x(n)=
