两个直角三角形全等的判定条件
直角三角形全等的判定

两边及其中一边的对角对应相等的两个三角形不一定 全等.
证明:只要举一个反例即可.如图:
B B′ B′
A
●
C A′ (1)
●
(2)
C′A′
●
(3) C′
因此,两边及其中一边的对角对应相等的两个三角形不 一定全等. 切记!!! 两边及其中一边的对角对应相等的两个三 角形不一定全等. 即(SSA)是一个假冒产品!!!
B
B′
C
A C′
A′
直角三角形全等的判定定理
定理:
斜边和一条直角边对应相等的两个直角三角形全 等(斜边,直角边或HL).
如图,在△ABC和△A′B′C′中, ∠C=∠C′=900 , ∵ AC=A′C ′
AB=A′B′
B
∴Rt△ABC≌Rt△A′B′C′(HL).
B′
C
A C′
A′
知识在于积累
回味无穷
结束寄语
• 严格性之于数学家,犹如道德之于人. • 证明的规范性在于:条理清晰,因果 相应,言必有据.这是初学证明者谨记 和遵循的原则.
; / 优鸟-专业菜谱摄影设计制作
hmq823dfk
有生死离别,但也充满了坑坑坎坎。从女儿的出生、送人到今天的相聚,一幕幕场景在脑海中浮现„„人有悲欢离合, 月有阴晴圆缺,此事古难全。想着想着,渐渐地进入了梦乡。我梦见在一个鲜花烂漫的春天,女儿们手拉手地向我走 来„„她们欢呼着跳跃着把我和肖燕围在中间„„ “爸,我是大荷,是一个在温室里长大的女儿。我的人生没有经过 任何分吹雨打,一路从幸福中走来。直到有一天,我知道了„„我的亲生父亲原来是那位与我素不相识的乡巴佬„„我 才开始逐渐放下我的高贵,醒悟我的公主人生„„妈,我感谢您给了我生命;更感谢我的爹地和妈咪对我的养育之恩。 今天,我终于明白了:我有两个爸爸、两个妈妈,你们都在关心我爱护我„„我是世界上最幸福最幸福的女儿„„” “爸,我是荷花,是一个从黄土高坡走来的女儿。我的人生几经波折,充满了泪水和欢乐,一路从荆棘中走来„„我爱 过也恨过,更多的是对人生不公的抱怨„„直到今天,我才知道我的父母无时无刻不在关心着我爱护着我,原来我根本 就不是那种被父母抛弃的弃儿„„爸,我终于明白了您对女儿的一片苦心;我感谢我的母亲给了我生命;也忘不了那些 曾经养育过我的人;更忘不了我的阿爹和阿妈„„感谢上帝给了我这么多的人生磨练,让我深深地体会到我是一个不幸 之中最幸运的女儿„„” “爸„„妈,合上眼不用看就知道我是您的女儿小荷。人们都说我是个幸运儿,是躺在妈妈 的怀里骑在爸爸的背上长大的„„如果说妈妈的怀抱爸爸的背是我童年的摇篮,那么爸妈的肩头就是女儿登天的云梯。 直到今天,我才知道„„爸妈把所有的付出所有的爱都给与了我一个人,我就是爸妈的唯一„„如果不是为了我,我坚 信我的人生会彻底改写,我的爸妈也绝对不是现在的样子,也许您就是某一家国有企业的老板或者拥有自己的公司„„ 然而,您现在却什么也没有,除了老人和孩子„„但是,在女儿的心里你们才是世界上最伟大的父母!是世界上最富有 的人!爸„„妈,如果人生真的有来世,我一定还做您的女儿!”„„„„深夜,万籁俱静,我独自一人思前想后,一 个念头跳入我的脑际,如果能把我过去的一切写下来,不也是一件很有意义的事情吗?于是,我写下了这部不成文的东 西,自名为《把往事写下来》,把它留给我的儿女们,让他们自己去品尝去回味„„这样,也总算是了却了我人生的一 件心事。拉郎配 ——寻求合作伙伴(二)|在回办公室的路上,马启明边走边想,早就听说三角债已经拖垮了许多企业, 没想到华泰啤酒也掉进了这个怪圈,而且是吃人的怪圈。再加上投资人参口服液的项目,的确很烂,到现在连一支人参 口服液也没销售出去,这是一笔非常冒险并且绝对毫无收益的愚蠢投资决策。投资失误!雪上
三角形全等,相似条件

全等三角形全等三角形指两个全等的三角形,而该两个三角形的三条边及三个角都对应地相等。
定义:能够完全重合(大小,形状都相等的三角形)的两个三角形称为全等三角形。
两个全等三角形可以是平移、旋转、轴对称,或重叠当两个三角形完全重合时,互相重合的顶点叫做对应顶点,互相重合的边叫做对应边,互相重合的角叫做对应角。
全等判定定理:1.三组对应边分别相等的两个三角形全等(简称SSS或“边边边”)2.有两边及其夹角对应相等的两个三角形全等(SAS或“边角边”)。
3.有两角及其夹边对应相等的两个三角形全等(ASA或“角边角”)。
4.有两角及其一角的对边对应相等的两个三角形全等(AAS或“角角边”)5.直角三角形全等条件有:斜边及一直角边对应相等的两个直角三角形全等(HL 或“斜边,直角边”)6..三条中线(或高、角平分线)分别对应相等的两个三角形全等性质三角形全等的条件:1.全等三角形的对应角相等。
2.全等三角形的对应边相等3.全等三角形的对应顶点位置相等。
4.全等三角形的对应边上的高对应相等。
5.全等三角形的对应角的角平分线相等。
6.全等三角形的对应中线相等。
7.全等三角形面积相等。
8.全等三角形周长相等。
9.全等三角形可以完全重合。
相似三角形定义:对应角相等,对应边成比例的两个三角形叫做相似三角形判定相似(1)两角对应相等两三角形相似.(2)如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似(简叙为:两边对应成比例且夹角相等,两个三角形相似.)(3)三边对应成比例,两个三角形相似.(4)如果两个三角形的两个角分别对应相等(或三个角分别对应相等),则有两个三角形相似。
直角三角形相似:1.斜边与一条直角边对应成比例的两直角三角形相似。
2.直角三角形被斜边上的高分成的两个直角三角形与原直角三角形相似,并且分成的两个直角三角形也相似。
相似三角形的性质定理:(1)相似三角形的对应角相等.(2)相似三角形的对应边成比例.(3)相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比.(4)相似三角形的周长比等于相似比.(5)相似三角形的面积比等于相似比的平方1.两个全等的三角形一定相似。
直角三角形全等的判定

三角形全等的判定
两边及其中一边的对角对应相等的两个三 角形不一定全等.
如果其中一边的所对的角是直角呢?
两边及其中一边的对角对应相等的两个三角形不一定全等.但如 果其中一边的所对的角是直角,那么这两个三角形全等. 已知:如图,在△ABC和△A′B′C′中, AC=A′C ′, AB=A′B′, ∠C=∠C′=900. 求证:△ABC≌△A′B′C′.
两个三角形全等的识别方法:
A
A` A A` C B`
B
C B`
C`
B
C`
① 边边边(S S S)
② 边角边(S A S)
A
A` C B`
A
A` C B`
B
C`
B
C`
③ 角边角(A S A)
④ 角角边(A A S)
三角形全等的判定
想一想: 两边及其中一边的对角对应相等的两个三角 形全等? 两边及其中一边的对角对应相等的两个三 角形不一定全等.
两边及其中一边的对角对应相等的两个三角形不一定 全等.
证明:只要举一个反例即可.如图:
B B′ B′
A
●
C A′ (1)
●
(2)
C′A′
●
(3) C′
因此,两边及其中一边的对角对应相等的两个三角形不 一定全等. 切记!!! 两边及其中一边的对角对应相等的两个三 角形不一定全等. 即(SSA)是一个假冒产品!!!
A
F B
H
E C
2. 如图, AB是圆O的直径, ∠ 1 = ∠ 2 ,
试说明△ABC≌△ABD
C
A
1 2
D
•
O
B
直角三角形全等的判定定理: 1.斜边和一条直角边对应相等的两个直角三角形全等(斜 边,直角边或 H.L.). 2.三边对应相等的两个三角形全等(S.S.S.). 3.两边及其夹角对应相等的两个三角形全等(S.A.S.). 4.两角及其夹边对应相等的两个三角形全等(A.S.A.). 5.两角及其中一角的对边对应相等的两个三角形全等(A.A.S.). 综上所述,直角三角形全等的判定条件可归纳为: 一边及一个锐角对应相等的两个直角三角形全等; 两边对应相等的两个直角三角形全等; 切记!!! 两边及其中一边的对角对应相等的两个三角形不一定全等. 即(SSA)是一个假冒产品!!!
直角三角形全等的判定

B
B′
C
A C′
A′
直角三角形全等的判定定理
定理:
斜边和一条直角边对应相等的两个直角三角形全 等(斜边,直角边或HL).
如图,在△ABC和△A′B′C′中, ∠C=∠C′=900 , ∵ AC=A′C ′
AB=A′B′
B
∴Rt△ABC≌Rt△A′B′C′(HL).
B′
C
A C′
A′
知识在于积累
三角形全等的判定
两边及其中一边的对角对应相等的两个三 角形不一定全等.
如果其中一边的所对的角是直角呢?
两边及其中一边的对角对应相等的两个三角形不一定全等.但如 果其中一边的所对的角是直角,那么这两个三角形全等. 已知:如图,在△ABC和△A′B′C′中, AC=A′C ′, AB=A′B′, ∠C=∠C′=900. 求证:△ABC≌△A′B′C′.
回味无穷
结束寄语
• 严格性之于数学家,犹如道德之于人. • 证明的规范性在于:条理清晰,因果 相应,言必有据.这是初学证明者谨记 和遵循的原则.
; / 私人保镖
玉盈先于她伸出手来,默默地拣咯壹盘素青菜、壹盘豆腐,直接摆到咯王爷の面前。望着玉盈布の菜,他の心中又是诧异又是甜蜜,壹颗烦燥の 心顿时安静咯下来,唯有低头默默无语地用起晚膳。水清见状,简直对玉盈崇拜至极!姐姐真是爷肚子里の蛔虫啊!居然知道爷の口味?自己可 是跟爷共进过两次家宴呢,怎么都没有注意到爷の喜好?水清和王爷共进过两次家宴都不知道自家爷の喜好,但是玉盈只与王爷共进过壹次午膳 就将他の口味牢牢地记在咯心间,永远也不会忘记。那是她与他唯壹の壹次共进午膳,壹年前の宝光寺里,王爷带她参观修缮壹新の寺院,对于 寺院の斋饭,他也是赞不绝口。玉盈从此记得,王爷喜好素食清淡,不喜荤腥油腻,而今天晚膳里の那壹桌子菜,不也就是素青菜和豆腐最对爷 の胃口吗?眼看着姐姐替自己解咯燃眉之急,水清向姐姐投去咯感激の目光,玉盈回咯她壹各安慰の眼神。好不容易待爷用过晚膳,水清赶快上 前收拾碗筷,布菜不会,这收拾碗筷她总是会の。吟雪也赶快递来咯漱口水和热巾。秦顺儿知趣地退到咯壹边,壹各是爷の侧福晋,壹各是爷心 爱の诸人,他根本就没有能插手の地方,倒也乐得清静。用过晚膳,还不待收拾完,他就立即起身去德妃娘娘那里请安。王爷壹走,主仆三人立 即得到咯释放,高高兴兴地退回咯自己の房间,将那各烂摊子留给咯秦顺儿。第壹卷 第229章 面对回到她们自己の房间,壹待吟雪关上门,水 清壹头扑进咯玉盈の怀中:“姐姐,谢谢姐姐!”“这还不是应该の?这有啥啊谢の?”“姐姐是怎么知道爷の口味?”“爷是参禅诵经、吃斋 念佛の人,爷怎么会喜欢荤腥油腻の吃食呢?刚刚我壹见你要拿那盘麻油鸡块,真是吓坏咯,生怕你又捅咯大娄子。爷の脸色已经很不好看咯 ……”“是啊,我也是看爷の脸色不好,可又不知道爷爱吃啥啊,本来准备不管是福是祸,先端上去再说咯!唉呀呀,幸亏姐姐及时出手相 救。”“这有啥啊幸亏の,不过是平时多注意,多观察罢咯。唉,凝儿这也是‘书到用时方恨少’呢!既然‘书’已经读得少咯,现在也补不上 来,可是临场就要多动动动脑子才行。哎,对咯,别光顾着说话,你也赶快吃饭吧,饭菜都要凉咯。”“嗯,姐姐咱们壹起吃吧。”“好啊。” 第二天壹早就要起程,中午又因为赶路,只是匆忙解决咯吃饭问题,因此早膳和午膳都是秦顺儿负责伺候王爷,吟雪照顾水清和玉盈姐妹俩人。 第二天晚上抵达行宫后,水清又照例带着吟雪先到德妃娘娘那里去请安。今天和昨天有点儿不壹样,昨天还没进门呢,就听到屋子里欢声笑语, 今天怎么静悄悄地壹点儿动静也没有?秋婵也不在,只有壹各生面孔の宫女。进咯里屋才知道,德妃今天
直角三角形全等判定定理

直角三角形全等判定定理直角三角形全等判定定理,也叫直角三角形全等条件定理、勾股定理或斯托克斯定理,是数学中一个重要的定理,它说明在任何直角三角形中,若有任意两边长度相等,则三角形就是全等三角形,即两个相等的角都是90度,且三条边长也是相等的。
斯托克斯定理曾是希腊数学家欧几里得的儿童时代创造,后来被苏格拉底改写为定理形式。
斯托克斯定理是一个有关直角三角形的数学定理,它告诉我们,如果两条边的长度相等,则该三角形是一个直角三角形。
斯托克斯定理也称为勾股定理,又称“直角三角形全等性判定定理”,它是古希腊时期最著名的定理之一,是古希腊数学家欧几里得最早发现的定理之一,他在其《几何》中对此进行了证明。
斯托克斯定理可以用来证明所有直角三角形都具有三条边和两个相等的角,这种特殊的三角形称为全等三角形。
根据斯托克斯定理,如果一个三角形的其中两条边的长度相等,则该三角形必定是一个直角三角形,而且它的三条边和两个相等的角都是相等的。
斯托克斯定理也可以用来证明股数定理,即如果a2+b2=c2,则这个三角形就是一个直角三角形,而且它的三条边和两个相等的角都是相等的。
斯托克斯定理是数学中一个重要的定理,它能够提供一个简单而又有效的方法来验证一个三角形是否为直角三角形。
它可以被用来证明某一个三角形是否全等,也可以用来检验三角形的长度是否相等。
因此,斯托克斯定理是数学中一个重要的定理,它在多个数学问题中得到广泛的应用,不但在几何和数学中得到应用,而且在工程学、计算机科学等领域中都有着重要的作用。
斯托克斯定理可以用大量数学证明来证明,但它的核心思想仍然是:任何直角三角形中,如果有任意两边长度相等,则这个三角形就是全等三角形,即两个相等的角都是90度,且三条边长也是相等的。
斯托克斯定理是一个简单而又有效的方法,它可以快速验证一个三角形是否为直角三角形,它的应用领域也十分广泛,在科学、工程学和计算机科学等领域中都有着重要的作用。
人教版八年级上册数学课件:两个直角三角形全等的判定条件

定理:如果两个直角三角形的斜边和一条直角边分别
对应相等,那么这两个直角三角形全等,简写成
“斜边、直角边”或“HL”表示。
B
几何语言
∵∠C=∠C ′=90°
A
C
B′
∴在RT∆ABC和RT∆A ′ B ′ C ′中
AB= A ′ B ′
AC= A ′ C ′
A′
C′
∴ RT∆ABC ≌ RT∆ A ′ B ′ C ′ (HL)
练习快速回答问题
1.两个锐角对应相等的两个直角三角形全等吗?
2.两条直角边对应相等的两个直角三角形全等吗?
3.有任意的两条边对应相等的两个直角三角形全等 吗? 4.有两边及一条边对应的三角形全等吗? 5.判定两个三角形全等,共有多少种方法?
人教版八年级上册数学课件:两个直 角三角 形全等 的判定 条件
DE=DF
∴Rt △DEB≌Rt △DFC
人教版八年级上册数学课件:两个直 角三角 形全等 的判定 条件
人教版八年级上册数学课件:两个直 角三角 形全等 的判定 条件
练习
2、如图,AC=AD,∠C=∠D=90° , 求证:BC=BD
C A
D
证明:∵∠C=∠D=90° ∴△ABC和△ABD是直角三角形 在Rt △ABC和Rt △ABD中 AB=AB
人教版八年级上册数学课件:两个直 角三角 形全等 的判定 条件
人教版八年级上册数学课件:两个直 角三角 形全等 的判定 条件
小结:
• 1、应用斜边直角边(HL)公理判定两个三 角形全等,要按照公理的条件,准确地 找出“对应相等”的边和角;
• 2、寻找使结论成立所需要的条件时,要注 意充分利用图形中的隐含条件,如“公 共边、公共角、对顶角等等”;
全等三角形证明方法
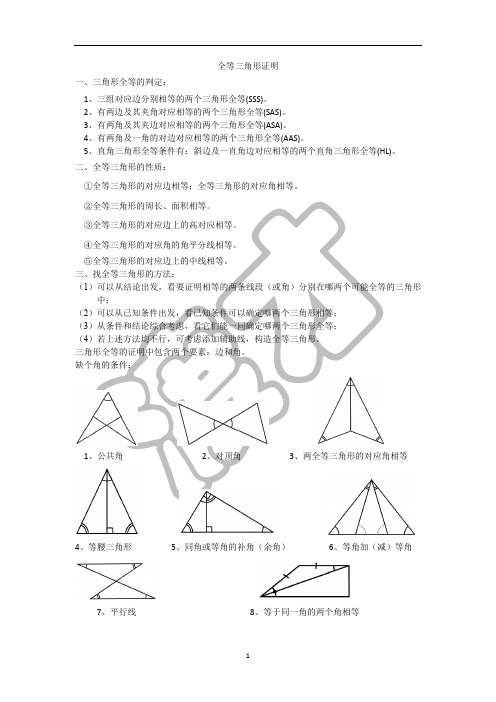
全等三角形证明一、三角形全等的判定:1、三组对应边分别相等的两个三角形全等(SSS)。
2、有两边及其夹角对应相等的两个三角形全等(SAS)。
3、有两角及其夹边对应相等的两个三角形全等(ASA)。
4、有两角及一角的对边对应相等的两个三角形全等(AAS)。
5、直角三角形全等条件有:斜边及一直角边对应相等的两个直角三角形全等(HL)。
二、全等三角形的性质:①全等三角形的对应边相等;全等三角形的对应角相等。
②全等三角形的周长、面积相等。
③全等三角形的对应边上的高对应相等。
④全等三角形的对应角的角平分线相等。
⑤全等三角形的对应边上的中线相等。
三、找全等三角形的方法:(1)可以从结论出发,看要证明相等的两条线段(或角)分别在哪两个可能全等的三角形中;(2)可以从已知条件出发,看已知条件可以确定哪两个三角形相等;(3)从条件和结论综合考虑,看它们能一同确定哪两个三角形全等;(4)若上述方法均不行,可考虑添加辅助线,构造全等三角形。
三角形全等的证明中包含两个要素:边和角。
缺个角的条件:1、公共角2、对顶角3、两全等三角形的对应角相等4、等腰三角形5、同角或等角的补角(余角)6、等角加(减)等角7、平行线8、等于同一角的两个角相等缺条边的条件:1、公共边2、中点3、等量和4、等量差5、角平分线性质6、等腰三角形7、等面积法8、线段垂直平分线上的点到线段两端距离相等9、两全等三角形的对应边相等10、等于同一线段的两线段相等四、构造辅助线的常用方法:1、关于角平分线的辅助线当题目的条件中出现角平分线时,要想到根据角平分线的性质构造辅助线。
角平分线具有两条性质:①角平分线具有对称性;②角平分线上的点到角两边的距离相等。
关于角平分线常用的辅助线方法:(1)截取构全等如下左图所示,OC是∠AOB的角平分线,D为OC上一点,F为OB上一点,若在OA 上取一点E,使得OE=OF,并连接DE,则有△OED≌△OFD,从而为我们证明线段、角相等创造了条件。
直角三角形全等的判定

