考点综合提升练(一)
高考语文大一轮复习第一章第二节小说阅读考点综合提升练(一)散文化小说

考点综合提升练(一) 散文化小说一、阅读下面的文字,完成文后题目。
桑吉奈尔的灯塔[法]都德三年前的许多美妙的不眠之夜,我住在桑吉奈尔的灯塔上。
在那里,在科西嘉的海岸边,阿雅克修海湾的入口处。
你们可以想象一下:一座荒野的红色岛屿,灯塔位于岛的一个尖角上,另一个尖角上有热那亚式古塔,古塔里住着一只鹰。
海水边有一座杂草丛生的荒弃的检疫站;然后便是沟壑,丛林,高大的岩石,几只野山羊,鬃毛在风中摇曳的科西嘉小马;在岛的高处,是灯塔房,海鸟在它四周盘旋,塔上的多面体大灯光芒四射……这便是桑吉奈尔岛。
三个守塔人,都是矮个子,胡子满腮,面孔棕褐色,皮肤皲裂,都穿着厚羊毛上衣,但神态和性情却不同。
他们都是善良、朴实、天真的人,对我这个客人殷勤备至!对他们来说,日子是那么漫长,回陆地时是那么快乐,在灯塔上三十天就可回陆地十天,这是规定;但到了冬天或气候恶劣时,就没规章可循了。
刮风起浪了,桑吉奈尔白浪滔天,守塔人两三个月被困在灯塔上,有时还会陷入更可怕的境况。
“先生,我曾遇到这样一件事,”吃晚饭时,老巴托利对我说道,“五年前,就在我们现在坐的桌子上……那个冬天的晚上,灯塔上只有我和谢戈……我们吃着晚餐,非常平静。
突然,我的伙伴停止吃东西,用奇怪的目光看了看我,然后‘扑通’一声倒在桌子上,手臂向前伸直,我摇着他:‘喂!谢戈,谢戈!’他死了!我是多么震惊啊。
我愣愣地,对着尸体发抖。
过了一阵,我突然想到‘灯塔!’我登上灯塔,把灯点亮。
夜幕降临……先生,那是怎样的夜晚啊!大海的声音跟平常不一样。
我每时每刻都好像听见有人在楼梯上喊我的名字。
天刚蒙蒙亮,我将死去的伙伴抱到他的床上,在他身上盖了一床被单,做完祈祷后,立即发出报警信号。
”可怜的老巴托利讲着,前额涌出冷汗。
以后,我们常一边晚餐,一边交谈,灯塔,大海,海滩,科西嘉海盗……之后,太阳平西,第一个值夜班人点亮小灯,带上烟斗,水壶,一部厚厚的红边的普鲁塔克写的《列传》,前往塔的高处。
中考数学 综合能力提升练习一(含解析)-人教版初中九年级全册数学试题
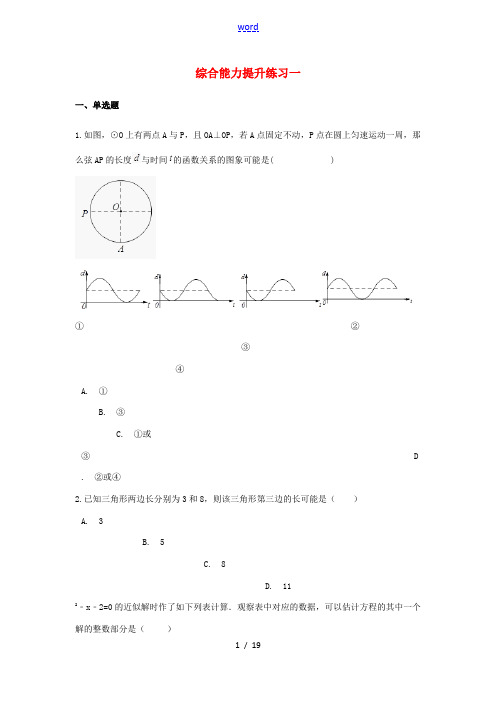
综合能力提升练习一一、单选题1.如图,⊙O上有两点A与P,且OA⊥OP,若A点固定不动,P点在圆上匀速运动一周,那么弦AP的长度与时间的函数关系的图象可能是( )①②③④A. ①B. ③C. ①或③D . ②或④2.已知三角形两边长分别为3和8,则该三角形第三边的长可能是()A. 3B. 5C. 8D. 112﹣x﹣2=0的近似解时作了如下列表计算.观察表中对应的数据,可以估计方程的其中一个解的整数部分是()x 1 2 3 42x2﹣x﹣2 ﹣14 13 26A. 4B. 3C. 2D. 14.三棱柱的顶点个数是()A. 3B. 4C. 5D. 62+3x+1=0的根的情况是()A. 有两个不相等的实数根B. 有两个相等的实数根 C. 没有实数根 D. 只有一个实数根6.有理数a、b在数轴上的位置如图所示,则下列各式符号的判断正确的是()A. a2﹣b>0B. a+|b|>0 C. a+b2>0 D. 2a+b>07.满足x-5>3x+1的x的最大整数是()A. 0B. -2C. -3D. -48.如图,Rt△APC的顶点A,P在反比例函数y=的图象上,已知P的坐标为(1,1),tanA=(n≥2的自然数);当n=2,3,4…2010时,A的横坐标相应为a2, a3, a4,…,a2010,则+++…+=()A. B. 2021 054 C. 2022060D.二、填空题9.已知△ABC的三个内角分别是∠A、∠B、∠C,若∠A=30°,∠C=2∠B,则∠B=________ °.10.如图,等腰直角三角形 ABC 中,∠BAC=90°,AB=AC,点 M,N 在边 BC 上,且∠MAN=45°.若 BM=1, =3,则 MN 的长为________ .11.计算:( +1)(3﹣)=________.12.一个多边形的每一个内角为108°,则这个多边形是________ 边形,它的内角和是________m________时,不等式mx<7的解集为x>-5℃,冷库乙的温度是-15℃,则温度高的是冷库________.三、计算题15.计算:16.计算:()2+(π﹣2016)0﹣4cos60°+()﹣3.17.先化简,再求值:÷(a﹣),其中a=2+ ,b=2﹣.18.计算(1)计算:+()﹣1﹣2cos60°+(2﹣π)0;(2)化简:.19.已知x﹣y=5,xy=4,求x2+y2的值.20.解方程:﹣= .四、解答题21.如图,△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AC于E,AE=2,求CE的长.22.如图,在四边形ABCD中,AD、BD相交于点F,点E在BD上,且.(1)∠1与∠2相等吗?为什么?(2)判断△ABE与△AC D是否相似?并说明理由.23.计算:|﹣3|﹣2.24.解方程组:.五、综合题25.甲、乙两人周末从同一地点出发去某景点,因乙临时有事,甲坐地铁先出发,甲出发0.2小时后乙开汽车前往.设甲行驶的时间为x(h),甲、乙两人行驶的路程分别为y1(km)与y2(km).如图①是y1与y2关于x的函数图象.(1)分别求线段OA与线段BC所表示的y1与y2关于x的函数表达式;(2)当x为多少时,两人相距6km?(3)设两人相距S千米,在图②所给的直角坐标系中画出S关于x的函数图象.答案解析部分一、单选题1.如图,⊙O上有两点A与P,且OA⊥OP,若A点固定不动,P点在圆上匀速运动一周,那么弦AP的长度与时间的函数关系的图象可能是( )①②③④A. ①B. ③C. ①或③D . ②或④【答案】C【考点】二次函数的图象【解析】【分析】由图中可知:长度d是一开始就存在的,如果点P向上运动,那么d的距离将逐渐变大;当点P运动到和0,A在同一直线上时,d最大,随后开始变小;当运动到点A时,距离d为0,然后继续运动,d开始变大;到点P时,回到原来高度相同的位置.①对,②没有回到原来的位置,应排除.④回到原来的位置后又继续运动了,应排除.如果点P向下运动,那么d的距离将逐渐变小,到点A的位置时,距离d为0;继续运动,d的距离将逐渐变大;当点P运动到和0,A在同一直线上时,d最大,随后开始变小,到点P时,回到原来高度相同的位置.③对.故选C.2.已知三角形两边长分别为3和8,则该三角形第三边的长可能是()A. 3B. 5C. 8D. 11【答案】C【考点】三角形三边关系【解析】【解答】解:根据三角形的三边关系,得第三边大于:8﹣3=5,小于:3+8=11.则此三角形的第三边可能是:8.故选:C.【分析】根据三角形的第三边大于两边之差,而小于两边之和求得第三边的取值X围,再进一步选择.2﹣x﹣2=0的近似解时作了如下列表计算.观察表中对应的数据,可以估计方程的其中一个解的整数部分是()x 1 2 3 42x2﹣x﹣2 ﹣14 13 26A. 4B. 3C. 2D. 1【答案】D【考点】估算一元二次方程的近似解【解析】【解答】解:根据表格中的数据,知:方程的一个解x的X围是:1<x<2,所以方程的其中一个解的整数部分是1.故选D.【分析】根据表格中的数据,可以发现:x=1时,2x2﹣x﹣2=﹣1;x=2时,2x2﹣x﹣2=4,故一元二次方程2x2﹣x﹣2=0的其中一个解x的X围是1<x<2,进而求解.4.三棱柱的顶点个数是()A. 3B. 4C. 5D. 6【答案】D【考点】认识立体图形【解析】【解答】解:一个直三棱柱由两个三边形的底面和3个长方形的侧面组成,根据其特征及欧拉公式V+F﹣E=2可知,它有6个顶点,故选:D.【分析】一个直三棱柱是由两个三边形的底面和3个长方形的侧面组成,根据其特征及欧拉公式V+F﹣E=2进行填空即可.2+3x+1=0的根的情况是()A. 有两个不相等的实数根B. 有两个相等的实数根 C. 没有实数根 D. 只有一个实数根【答案】A【考点】根的判别式【解析】【解答】解:∵a=1,b=3,c=1,∴△=b2﹣4ac=32﹣4×1×1=5>0,∴有两个不相等的实数根.故选A.【分析】首先求得△=b2﹣4ac的值,然后即可判定一元二次方程x2+3x+1=0的根的情况.6.有理数a、b在数轴上的位置如图所示,则下列各式符号的判断正确的是()A. a2﹣b>0B. a+|b|>0 C. a+b2>0 D. 2a+b>0【答案】A【考点】数轴【解析】【解答】解:根据数轴得a<﹣1,0<b<1,∴a2>1,b2<1,∴a2﹣b>0,故A正确;∴a+|b|<0,故B错误;∴a+b2<0,故C错误;∴2a+b<0,故D错误,故选A.【分析】根据数轴可得出a<﹣1,0<b<1,再判断a2, b2的X围,进行选择即可.7.满足x-5>3x+1的x的最大整数是()A. 0B. -2C. -3D. -4【答案】D【考点】解一元一次不等式,一元一次不等式的整数解【解析】【分析】先移项,再合并同类项,最后化系数为1,即可求得结果.x-5>3x+1-2x>6x<-3所以满足条件的x的最大整数是-4故选D.【点评】计算题是中考必考题,一般难度不大,学生要特别慎重,尽量不在计算上失分.8.如图,Rt△APC的顶点A,P在反比例函数y=的图象上,已知P的坐标为(1,1),tanA=(n≥2的自然数);当n=2,3,4…2010时,A的横坐标相应为a2, a3, a4,…,a2010,则+++…+=()A. B. 2021 054 C. 2022060D.【答案】B【考点】反比例函数的图象,反比例函数的性质,探索数与式的规律【解析】【分析】设CP=m,由tanA==得AC=mn,则A(1-m,1+mn),将A点坐标代入y=中,得出a n=1-m的表达式,寻找运算规律.【解答】依题意设CP=m,∵P点横坐标为1,则C点横坐标为1-m,即a n=1-m,又∵tanA==,∴AC=mn,则A(1-m,1+mn),将A点坐标代入y=中,得(1-m)(1+mn)=1,1-m+mn-m2n=1,m(n-1-mn)=0,则n-1-mn=0,1-m=,则a n=1-m=,即=n,∴+++…+=2+3+4+…+2010==2021054.故选B.【点评】本题主要考查反比例函数的图象和性质,关键是根据三角函数值设直角三角形的边长,表示A点坐标,根据A点在双曲线上,满足反比例函数解析式,从而得出一般规律.二、填空题9.已知△ABC的三个内角分别是∠A、∠B、∠C,若∠A=30°,∠C=2∠B,则∠B=________ °.【答案】50【考点】三角形内角和定理【解析】【解答】解:∵在△ABC中,∠A=30°,∠C=2∠B,∠A+∠B+∠C=180°,∴30°+3∠B=180°,∴∠B=50°.故答案是:50.【分析】根据三角形内角和是180°列出等式∠A+∠B+∠C=180°,据此易求∠B的度数.10.如图,等腰直角三角形 ABC 中,∠BAC=90°,AB=AC,点 M,N 在边 BC 上,且∠MAN=45°.若 BM=1, =3,则 MN 的长为________ .【答案】【考点】全等三角形的判定与性质,勾股定理的应用【解析】【解答】将逆时针旋转得到,连接,是等腰直角三角形,在和中,由勾股定理得,【分析】根据旋转的性质得到对应边、对应角相等;由△ABC是等腰直角三角形,得到△MAN≌△FAN,得到对应角、对应边相等,再根据勾股定理求出MN 的长.11.计算:( +1)(3﹣)=________.【答案】2【考点】二次根式的混合运算【解析】【解答】解:原式= ( +1)(﹣1)= ×(3﹣1)=2 .故答案为2 .【分析】先把后面括号内提,然后利用平方差公式计算.12.一个多边形的每一个内角为108°,则这个多边形是________ 边形,它的内角和是________【答案】五;540°【考点】多边形内角与外角【解析】【解答】解:∵多边形的每一个内角都等于108°,∴多边形的每一个外角都等于180°﹣108°=72°,∴边数n=360°÷72°=5,内角和为(5﹣2)×180°=540°.故答案为:五;540°.【分析】先求出这个多边形的每一个外角的度数,再用360°除以一个外角的度数即可得到边数.m________时,不等式mx<7的解集为x>【答案】<0【考点】不等式的性质【解析】【解答】根据不等式mx<7的解集为x>,可以发现不等号的方向发生了改变,根据不等式的性质,所以m<0.【分析】可根据不等式的性质,两边同时除以负数,不等号发生改变.-5℃,冷库乙的温度是-15℃,则温度高的是冷库________.【答案】甲【考点】有理数大小比较【解析】【解答】解:∵-5>-15∴温度高的是冷库甲故答案为:甲【分析】比较-5和-15的大小,可解答。
备战2021年九年级中考数学考点提升训练——专题:《三角形综合:全等与相似》(一)

备战2021年九年级中考数学考点提升训练——专题:《三角形综合:全等与相似》(一)1.已知:等边△ABC中.(1)如图1,点M是BC的中点,点N在AB边上,满足∠AMN=60°,求的值;(2)如图2,点M在AB边上(M为非中点,不与A、B重合),点N在CB的延长线上且∠MNB=∠MCB,求证:AM=BN.(3)如图3,点P为AC边的中点,点E在AB的延长线上,点F在BC的延长线上,满足∠AEP=∠PFC,求的值.2.(1)发现如图1,△ABC和△ADE均为等边三角形,点D在BC边上,连接CE.填空:①∠DCE的度数是;②线段CA、CE、CD之间的数量关系是.(2)探究如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在BC 边上,连接CE.请判断∠DCE的度数及线段CA、CE、CD之间的数量关系,并说明理由.(3)应用如图3,在Rt△ABC中,∠A=90°,AC=4,AB=6.若点D满足DB=DC,且∠BDC=90°,请直接写出DA的长.3.(1)问题发现:如图1,△ABC和△ADE均为等边三角形,点D在BC的延长线上,连接CE,求证:△ABD≌△ACE.(2)类比探究:如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,D点在边BC的延长线上,连接CE.请判断:①∠ACE的度数为.②线段BC,CD,CE之间的数量关系是.(3)问题解决:在(2)中,如果AB=AC=,CD=1,求线段DE的长.4.直角三角形ABC中,∠ACB=90°,直线l过点C.(1)当AC=BC时,如图①,分别过点A、B作AD⊥l于点D,BE⊥l于点E.求证:△ACD≌△CBE.(2)当AC=8,BC=6时,如图②,点B与点F关于直线l对称,连接BF,CF,动点M从点A出发,以每秒1个单位长度的速度沿AC边向终点C运动,同时动点N从点F出发,以每秒3个单位的速度沿F→C→B→C→F向终点F运动,点M、N到达相应的终点时停止运动,过点M作MD⊥l于点D,过点N作NE⊥l于点E,设运动时间为t秒.①CM=,当N在F→C路径上时,CN=.(用含t的代数式表示)②直接写出当△MDC与△CEN全等时t的值.5.已知在△ABC中,AB=AC,过点B引一条射线BM,D是BM上一点.(1)如图1,∠ABC=60°,射线BM在∠ABC内,∠ADB=60°,求证:∠BDC =60°.请根据以下思维框图,写出证明过程.(2)如图2,已知∠ABC=∠ADB=30°.①当射线BM在∠ABC内,求∠BDC的度数.②当射线BM在BC下方,请问∠BDC的度数会变吗?若不变,请说明理由;若改变,请直接写出∠BDC的度数.(3)在第(2)题的条件下,作AF⊥BD于点F,连结CF,已知BD=6,CD=2,求△CDF的面积.6.(1)问题发现如图1,在Rt△ABC和Rt△DBE中,∠ABC=∠DBE=90°,∠ACB=∠BED=45°,点E是线段AC上一动点,连接DE.填空:①则的值为;②∠EAD的度数为.(2)类比探究如图2,在Rt△ABC和Rt△DBE中,∠ABC=∠DBE=90°,∠ACB=∠BED=60°,点E是线段AC上一动点,连接DE.请求出的值及∠EAD的度数;(3)拓展延伸如图3,在(2)的条件下,取线段DE的中点M,连接AM、BM,若BC=4,则当△ABM是直角三角形时,求线段AD的长.7.如图,在△ABC中,AB=AC,点D在△ABC内,BD=BC,∠DBC=60°,点E 在△ABC外,∠CBE=150°,∠ACE=60°.(1)求∠ADC的度数.(2)判断△ACE的形状并加以证明.(3)连接DE,若DE⊥CD,AD=3,求DE的长.8.在等腰直角△ABC中,AB=AC,∠BAC=90°,以CA为边在∠ACB的另一侧作∠ACM=∠ACB,点D为射线BC上任意一点,在射线CM上截取CE=BD,连接AD、DE、AE.(1)如图1,当点D落在线段BC的延长线上时,直接写出∠ADE的度数;(2)如图2,当点D落在线段BC(不含边界)上时,AC与DE交于点F,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;(3)如图2,作AH⊥BC,垂足为H,作AG⊥EC,垂足为G,连接HG,判断△GHC 的形状,并说明理由.9.如图,已知在ABC中,AB=AC=5,BC=6,点M在△ABC内,AM平分∠BAC.点E与点M在AC所在直线的两侧,AE⊥AB,AE=BC,点N在AC边上,CN=AM,连接ME、BN;(1)根据题意,补全图形;(2)ME与BN有何数量关系,判断并说明理由;(3)点M在何处时BM+BN取得最小值?请确定此时点M的位置,并求出此时BM+BN 的最小值.10.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,以AB为一边向上作等边三角形ABD,点E在BC垂直平分线上,且EB⊥AB,连接CE,AE,CD.(1)判断△CBE的形状,并说明理由;(2)求证:AE=DC;(3)填空:①若AE,CD相交于点F,则∠AFD的度数为.②在射线AB上有一动点P,若△PBC为等腰三角形,则∠ACP的度数为.参考答案1.解:(1)∵△ABC为等边三角形,∴∠B=∠BAC=60°,AB=AC,∵点M是BC的中点,∴∠MAN=30°,∠AMB=90°,∵∠AMN=60°,∴∠BMN=30°,∴BM=2BN,AB=2BM,设BN=x,则BM=2x,AB=4x,∴AN=3x,∴;(2)证明:如图2,过点M作MG∥NC交AC于点G,∴∠A=∠AMG=∠AGM=60°,∴△AMG为等边三角形,∴AM=AG,∴BM=CG,∵∠AGM=∠ABC=60°,∴∠MGC=∠NBM=120°,∵MG∥BC,∴∠GMC=∠MCB,∵∠MNB=∠MCB,∴∠GMC=∠MNB,∴△MGC≌△NBM(AAS),∴MG=BN,∵△AMG为等边三角形,∴AM=MG,∴AM=BN;(3)如图3,过点P作PM∥BC交AB于点M,∴△AMP为等边三角形,∴AP=MP,∠AMP=60°,∵P为AC的中点,∴AP=PC,∴MP=PC,∵∠ACB=60°,∴∠EMP=∠PCF=120°,∵∠AEP=∠PFC,∴△PCF≌△PME(AAS),∴CF=ME,∴BF﹣BE=BC+CF﹣ME+MB,又∵P为AC的中点,MP∥BC,∴MB=,∴BF﹣BE=BC+BC=,∴.2.(1)发现解:①∵在△ABC中,AB=AC,∠BAC=60°,∴∠BAC=∠DAE=60°,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,在△BAD和△CAE中,,∴△BAD≌△CAE(SAS),∴∠ACE=∠B=60°,∴∠DCE=∠ACE+∠ACB=60°+60°=120°;故答案为:120°,②∵△BAD≌△CAE,∴BD=CE,∴BC=BD+CD=EC+CD,∴CA=BC=CE+CD;故答案为:CA=CE+CD.(2)探究∠DCE=90°;CA=CD+CE.理由:∵△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,∴AB=AC,AD=AE,∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE.∴△BAD≌△CAE(SAS).∴BD=CE,∠B=∠ACE=45°.∴∠DCE=∠ACB+∠ACE=90°.在等腰直角三角形ABC中,CB=CA,∵CB=CD+DB=CD+CE,∴CA=CD+CE.(3)应用DA=5或.作DE⊥AB于E,连接AD,∵在Rt△ABC中,AB=6,AC=4,∠BAC=90°,∴BC===2,∵∠BDC=90°,DB=DC,∴DB=DC=,∠BCD=∠CBD=45°,∵∠BDC=∠BAC=90°,∴点B,C,A,D四点共圆,∴∠DAE=45°,∴△ADE是等腰直角三角形,∴AE=DE,∴BE=6﹣DE,∵BE2+DE2=BD2,∴DE2+(6﹣DE)2=26,∴DE=1,DE=5,∴AD=或AD=5.3.(1)问题发现:证明:∵△ABC和△ADE是等边三角形∴AB=AC,AD=AE,且∠BAC=∠DAE=60°∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,在△ABD和△ACE中AB=AC,∠BAD=∠CAE,AD=AE,∴△ABD≌△ACE(SAS);(2)类比探究:①∵△ABC和△ADE均为等腰直角三角形,∴AB=AC,∠BAD=∠CAE,AD=AE,在△ACE与△ABD中,,∴△ACE≌△ABD(SAS),∴∠ACE=∠B=45°,故答案为:45°;②∵△ACE≌△ABD,∴BD=CE,∴BC+CD=CE,故答案为:BC+CD=CE;(3)问题解决:解:在(2)中,同(1)的方法可证:△ABD≌△ACE,∴∠ACE=∠ABD=45°,又∵∠ACB=45°,∴∠BCE=∠ACB+∠ACE=90°,在Rt△BAC中,,∴,又∵CD=1,由(2)得CE=BC+CD=3,在Rt△BAC中,,则线段DE的长是.4.解:(1)△ACD与△CBE全等.理由如下:∵AD⊥直线l,∴∠DAC+∠ACD=90°,∵∠ACB=90°,∴∠BCE+∠ACD=90°,∴∠DAC=∠ECB,在△ACD和△CBE中,,∴△ACD≌△CBE(AAS);(2)①由题意得,AM=t,FN=3t,则CM=8﹣t,由折叠的性质可知,CF=CB=6,∴CN=6﹣3t.故答案为:8﹣t;6﹣3t.②由折叠的性质可知,∠BCE=∠FCE,∵∠MCD+∠CMD=90°,∠MCD+∠BCE=90°,∴∠NCE=∠CMD,∴当CM=CN时,△MDC与△CEN全等,当点N沿F→C路径运动时,8﹣t=6﹣3t,解得,t=﹣1(不合题意),当点N沿C→B路径运动时,8﹣t═3t﹣6,解得,t=3.5,当点N沿B→C路径运动时,由题意得,8﹣t=18﹣3t,解得,t=5,当点N沿C→F路径运动时,由题意得,8﹣t=3t﹣18,解得,t=6.5,综上所述,当t=3.5秒或5秒或6.5秒时,△MDC与△CEN全等.5.(1)证明:在BM上取一点E,使AE=AD.∵∠ADB=60°,∴△ADE是等边三角形.∵AB=AC,∠ABC=60°,∴△ABC是正三角形,∴∠BAE=60°﹣∠EAC=∠CAD,∴△BAE≌△CAD(SAS),∴∠ADC=∠AEB=120°,∴∠BDC=120°﹣60°=60°.(2)①在BD上取一点E,AE=AD,如图2,∵∠ABC=∠ADB=30°,且AB=AC,∴∠ABC=∠ACB=30°,∠AED=∠ADE=30°,∴∠BAC=∠EAD=120°,∴∠BAE=∠CAD,∴△BAE≌△CAD(SAS),∴∠ADC=∠AEB=180°﹣30°=150°,∴∠BDC=150°﹣30°=120°.②会变.如图3.在DB延长线上取一点E,使得AE=AD,同理可得:△BAE≌△CAD,∴∠ADC=∠E=30°,∴∠BDC=∠ADE+∠ADC=30°+30°=60°.(3)如图,∵△BAE≌△CAD,∴BE=CD,且AE=AD,AF⊥DE,∴,作CH⊥BM,如图4,∵∠BDC=120°,∴∠CDH=60°,∴∠DCH=30°,∴,∴,∴如图5,∵△BAE≌△CAD,∴BE=CD,且AE=AD,AF⊥DE,∴,,∴.6.解:(1)∵∠ABC=∠DBE=90°,∴∠ABC﹣∠ABE=∠DBE﹣∠ABE即∠CBE=∠ABD,∵∠ACB=∠BED=45°,∴∠ACB=∠CAB=45°,∠BED=∠BDE=45°,∴AB=BC,DB=BE,∴△ABD≌△CBE(SAS),∴AD=CE,∠DAB=∠ECB=45°,∴=1,∠EAD=45°+45°=90°.故答案为:1,90°.(2),∠EAD=90°.理由如下:∵∠ABC=∠DBE=90°,∠ACB=∠BED=60°,∴∠ABD=∠EBC,∠BAC=∠BDE=30°,∴在Rt△ABC中,tan∠ACB==tan60°=,在Rt△DBE中,tan∠BED==tan60°=,∴=,又∵∠ABD=∠EBC,∴△ABD∽△∠CBE,∴==,∠BAD=∠ACB=60°.∵∠BAC=30°,∴∠EAD=∠BAD+∠BAC=60°+30°=90°.(3)如图,由(2)知:==,∠EAD=90°,∴AD=CE,在Rt△ABC中,∠BAC=30°,BC=4,∴AC=8,AB=4,∵∠EAD=∠EBD=90°,且点M是DE的中点,∴AM=BM=DE,∵△ABM为直角三角形,∴AM2+BM2=AB2=(4)2=48,∴AM=BM=2,∴DE=4,设EC=x,则AD=x,AE=8﹣x,Rt△ADE中,AE2+AD2=DE2,∴(8﹣x)2+(x)2=(4)2,解之得:x=2+2(负值舍去).∴EC=2+2.∴AD=CE=2+6.∴线段AD的长为(2+6).7.(1)解:∵BD=BC,∠DBC=60°,∴△DBC是等边三角形.∴DB=DC,∠BDC=∠DBC=∠DCB=60°.在△ADB和△ADC中,∵,∴△ADC≌△ADB(SSS).∴∠ADC=∠ADB.∴∠ADC=(360°﹣60°)=150°.(2)解:△ACE是等边三角形.理由如下:∵∠ACE=∠DCB=60°,∴∠ACD=∠ECB.∵∠CBE=150°,∠ADC═150°,∴∠ADC=∠EBC.在△ACD和△ECB中,∵,∴△ACD≌△ECB(ASA).∴AC=CE.∵∠ACE=60°,∴△ACE是等边三角形.(3)解:连接DE.∵DE⊥CD,∴∠EDC=90°.∵∠BDC=60°,∴∠EDB=30°.∵∠CBE=150°,∠DBC=60°,∴∠DBE=90°.∴EB=DE.∵△ACD≌△ECB,AD=3,∴EB=AD=3.∴DE=2EB=6.8.(1)解:∠ADE=45°.∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,∵∠ACM=∠ACB,∴∠ACM=∠ABC,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴AD=AE,∠CAE=∠BAD,∴∠DAE=∠BAC=90°,∴∠ADE=45°;(2)(1)中的结论成立证明:∵∠BAC=90°,AB=AC,∴∠B=∠ACB=45°.∵∠ACM=∠ACB,∴∠B=∠ACM=45°.在△ABD和△ACE中,,∴△ABD≌△ACE(SAS).∴AD=AE,∠BAD=∠CAE.∴∠CAE+∠DAC=∠BAD+∠DAC=∠BAC=90°.即∠DAE=90°.∵AD=AE,∴∠ADE=∠AED=45°.(3)△CGH为等腰直角三角形.理由如下:∵∠BCA=∠ACE=45°,∴∠GCH=90°,又∵AH⊥BC,AG⊥CE,∴AG=AH,∵∠ACG=∠AGC=45°,∴AG=CG,∵AB=AC,AH⊥BC,∴∠HCA=∠HAC=45°,∴AH=HC,∴CH=CG,∴△CGH为等腰直角三角形.9.解:(1)如图1所示:(2)ME=BN.证明:延长AM交BC于点F,如图.∵AM平分∠BAC,∴∠BAM=∠CAM.∵AE⊥AB,∴∠MAE+∠BAM=90°.∴∠MAE+∠CAM=90°∵AB=AC,AM平分∠BAC,∴AF⊥BC.∴∠C+∠CAM=90°.∴∠MAE=∠C.又∵AM=CN,AE=BC,∴△AME≌△CNB(SAS).∴ME=BN.(3)由(2)知ME=BN,则当B,M,E三点共线时,此时BM+BN取得最小值,点M的位置如图2,∵AB=5,BC=6,∴AE=BC=6,∴BE===.∴BM+BN的最小值是.10.解:(1)△CBE是等边三角形.理由如下:∵点E在BC垂直平分线上,∴EC=EB,∵EB⊥AB,∴∠ABE=90°,∵∠ABC=30°,∴∠CBE=60°,∴△CBE是等边三角形.(2)∵△ABD是等边三角形,∴AB=DB,∠ABD=60°,∵∠ABC=30°,∴∠DBC=90°,∵EB⊥AB,∴∠ABE=90°,∴∠ABE=∠DBC,由(1)可知:△CBE是等边三角形,∴EB=CB,∴△ABE≌△DBC(SAS).∴AE=DC;(3)①设AB与CD交于点G,∴∠EAB=∠CDB,又∵∠AGC=∠BGD,∴∠AFD=∠ABD=60°.故答案为:60°.②∵△BCP为等腰三角形,当BC=BP时,如图2,∠ABC=∠BCP+∠BPC=30°,∴∠BCP=15°,∴∠ACP=90°+15°=105°;当PC=PB时,如图3,∴∠PCB=30°,∵∠ACB=90°,∴∠ACP=60°;当BP=BC时,如图4,∵∠ABC=30°,∴∠PCB=∠CPB=(180°﹣30°)=75°,∴∠ACP=90°﹣75°=15°.综合上述可得∠ACP的度数为15°或60°或105°.故答案为:15°或60°或105°.。
2023年中考九年级数学高频考点提升练习--圆的综合题(含答案)
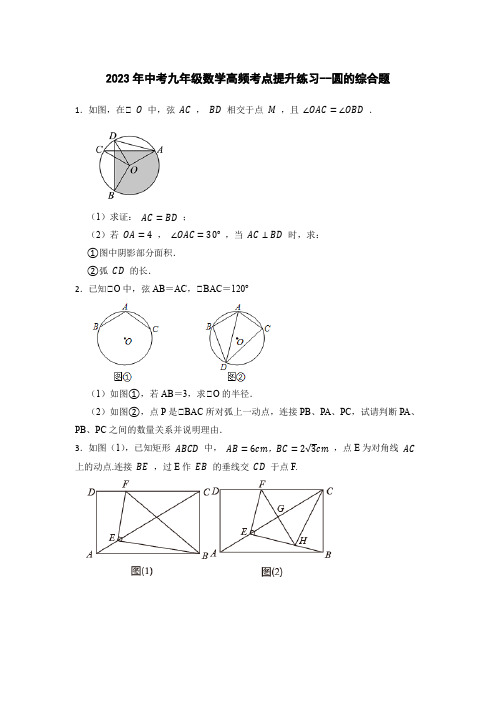
2023年中考九年级数学高频考点提升练习--圆的综合题1.如图,在⊙ O中,弦AC,BD相交于点M,且∠OAC=∠OBD.(1)求证:AC=BD;(2)若OA=4,∠OAC=30°,当AC⊥BD时,求:①图中阴影部分面积.②弧CD的长.2.已知⊙O中,弦AB=AC,⊙BAC=120°(1)如图①,若AB=3,求⊙O的半径.(2)如图②,点P是⊙BAC所对弧上一动点,连接PB、PA、PC,试请判断PA、PB、PC之间的数量关系并说明理由.3.如图(1),已知矩形ABCD中,AB=6cm,BC=2√3cm,点E为对角线AC 上的动点.连接BE,过E作EB的垂线交CD于点F.(1)探索BE与EF的数量关系,并说明理由.(2)如图(2),过F作AC垂线交AC于点G,交EB于点H,连接CH.若点E从A出发沿AC方向以2√3cm/s的速度向终点C运动,设E的运动时间为ts.①是否存在t,使得H与B重合?若存在,求出t的值;若不存在,说明理由;②t为何值时,△CFH是等腰三角形;③当CG=GH时,求△CGH的面积.4.如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.(1)求证:CD是⊙O的切线;(2)求证:⊙C=2⊙DBE.(3)若EA=AO=2,求图中阴影部分的面积.(结果保留π)5.定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到该边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,⊙ABC中,点D 是BC边上一点,连结AD,若AD2=BD⋅CD,则称点D是⊙ABC中BC边上的“好点”.(1)如图2,⊙ABC的顶点是4×3网格图的格点,请仅用直尺画出AB边上的一个“好点”.(2)⊙ABC中,BC=9,tanB=43,tanC=23,点D是BC边上的“好点”,求线段BD的长.(3)如图3,⊙ABC是⊙O的内接三角形,OH⊙AB于点H,连结CH并延长交⊙O于点D.①求证:点H是⊙BCD中CD边上的“好点”.②若⊙O的半径为9,⊙ABD=90°,OH=6,请直接写出CHDH的值.6.如图,⊙O为等边⊙ABC的外接圆,半径为2,点D在劣弧上运动(不与点A,B 重合),连接DA,DB,DC.(1)求证:DC是⊙ADB的平分线;(2)设四边形ADBC的面积为S,线段DC的长为x,试用含x的代数式表示S;(3)若点M,N分别在线段CA,CB上运动(不含端点),经过探究发现,点D 运动到每一个确定的位置,⊙DMN的周长有最小值t,随着点D的运动,t的值会发生变化,求所有t值中的最大值.7.在⊙ABC中,D,E分别是⊙ABC两边的中点,如果弧DE(可以是劣弧、优弧或半圆)上的所有点都在⊙ABC的内部或边上,则称弧DE为⊙ABC的中内弧.例如,图1中弧DE是⊙ABC其中的某一条中内弧.(1)如图2,在边长为4 √3的等边⊙ABC中,D,E分别是AB,AC的中点.画出⊙ABC的最长的中内弧DE,并直接写出此时弧DE的长;(2)在平面直角坐标系中,已知点A(2 √3,6),B(0,0),C(t,0),在⊙ABC中,D,E分别是AB,AC的中点.①若t=2 √3,求⊙ABC的中内弧DE所在圆的圆心P的纵坐标的取值范围;②请写出一个t的值,使得⊙ABC的中内弧DE所在圆的圆心P的纵坐标可以取全体实数值.8.如图,⊙O是⊙ABC的外接圆,AC是直径,过点O作OD⊙AB于点D,延长DO 交⊙O于点P,过点P作PE⊙AC于点E,作射线DE交BC的延长线于F点,连接PF.(1)若⊙POC=60°,AC=12,求劣弧PC的长;(结果保留π)(2)求证:OD=OE;(3)求证:PF是⊙O的切线.9.如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=32CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.(1)用关于x的代数式表示BQ=,DF=.(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长.(3)当点P在点A右侧时,作直线BG交⊙O于点N,若BN的弦心距为1,求AP的长.10.如图,⊙ABC中,⊙ACB=90°,D是边AB上一点,且⊙A=2⊙DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.(1)求证:AB是⊙O的切线;(2)若CD的弦心距为1,BE=EO,求BD的长.11.已知:A、B两点在直线l的同一侧,线段AO,BM均是直线l的垂线段,且BM 在AO的右边,AO=2BM,将BM沿直线l向右平移,在平移过程中,始终保持⊙ABP=90°不变,BP边与直线l相交于点P.(1)当P与O重合时(如图2所示),设点C是AO的中点,连接BC.求证:四边形OCBM是正方形;(2)请利用如图1所示的情形,求证:ABPB=OMBM;(3)若AO=2 √6,且当MO=2PO时,请直接写出AB和PB的长.12.(问题情境)如图①,小区A、B位于一条笔直的道路l的同侧,为了方便A,B两个小区居民投放垃圾,现在l上建一个垃圾分类站C,使得C与A,B的距离之比为2:1.(1)(初步研究)在线段AB上作出点C,使CACB=2.如图,做法如下:第一步:过点A作射线AM,以A为圆心,任意长为半径画弧,交AM于点P1;以P1为圆心,AP1长为半径画弧,交AM于点P2;以P2为圆心,AP1长为半径画弧,交AM于点P3.第二步:连接BP3,作∠AP2C=∠AP3B,交AB于点C.则点C即为所求.请证明所作的点C满足CACB=2.(2)(深入思考)如图,点C在线段AB上,点D在直线AB外,且DADB=CACB=2.求证:DC是∠ADB的平分线.(3)(问题解决)如图,已知点A,B和直线l,点C在线段AB上,且CACB=2.用直尺和圆规完成下列作图.(保留作图痕迹,不写作法)(⊙)在直线AB上作出点E(异于点C),使EAEB=2;(⊙)在直线l上作出点F,使FAFB=2.13.在矩形ABCD中,BC=2AB,点E是对角线AC上任意一点,过点E作AD的垂线分别交AD,BC于点F,G,作FH平行AC交CD于点H.(1)证明:EF=CH.(2)连结GH交AC于点K,若AE:CK=3,求AE:EK的值.(3)作⊙FGH的外接圆⊙O,且AB=1.①若⊙O与矩形的边相切时,求CH的长.②作点E关于GH的对称点E',当E'落在⊙O上时,直接写出⊙FGH的面积。
语言表达考点综合提升练(一)

考点综合提升练(一)1.阅读下面的文字,按要求回答问题。
宝玉摔玉宝玉听了,登时发作起痴狂病来,摘下那玉,就狠命摔去,骂道:“什么罕物,连人之高低不择,还说‘通灵’不‘通灵’呢!我也不要这劳什子了!”……宝玉满面泪痕泣道:“家里姐姐妹妹都没有,单我有,我说没趣,如今来了这么一个神仙似的妹妹也没有,可知这不是个好东西!”贾母忙哄他道:“你这妹妹原有这个来的,因你姑妈去世时,舍不得你妹妹,无法可处,遂将他的玉带了去了:一则全殉葬之礼,尽你妹妹之孝心;二则你姑妈之灵,亦可权作见了女儿之意。
因此他只说没有这个,不便自己夸张之意。
你如今怎比得他?还不好生慎重带上,仔细你娘知道了!”……宝玉听如此说,想一想,竟大有情理,也就不生别论了。
脂砚斋批注奇极!怪极!痴极!愚极!焉得怪人目为痴哉?所谓小儿易哄,余则谓“君子可欺以其方”云。
请用对偶句的形式概括以上文字塑造出来的贾宝玉形象。
不超过30个字。
答:________________________________________________________________________ 答案似傻如狂摔宝玉性乖张,平等叛逆抗天命真君子。
解析审题应注意三点:一是要概括出人物形象,二是要运用对偶的修辞手法,三是字数限制。
要细读材料抓住描写人物的语句,并结合点评文字,简明准确地作答。
2.品读下面一段文字,任选角度,写一段点评,50字左右。
莫春者,春服既成,冠者五六人,童子六七人,浴乎沂,风乎舞雩,咏而归。
(《论语·子路、曾皙、冉有、公西华侍坐》)答:________________________________________________________________________ 答案写几个成年人和一群少年沐浴春光郊游的情景。
行文运用白描手法,写他们快乐嬉游的画面,反映出天下太平、百姓和乐的状况。
3.高老头在病入膏肓、奄奄一息的时候,非常想见自己的女儿,可是两个女儿觉得自己的父亲已是一块榨干的橘子皮,谁也不去理他,高老头带着遗恨死去了。
散文阅读考点综合提升练(一)

考点综合提升练(一)一、阅读下面的文字,完成1~4题。
春的声音沉樱①如果说花是春的颜色,那么鸟应该是春的声音了。
但是幼年生长在枯燥的北方,住的又是城市,就是春天,也过得异常寂寞。
所谓春来了的时候,除了满城风沙,气候干燥之外再没有别的感受。
花草不是随地可见的,鸟声更是完全隔绝。
当时在幼稚的心目中,总以为所谓鸟,不过是那“喳喳”的喜鹊,“哑哑”的乌鸦,和终日在院中成群觅食的麻雀罢了。
②不知是哪一次战争,那时我好像有八九岁,为了避乱,全家搬到了乡下,恰好是三四月的光景,我这才第一次认识了并且享受了春天。
③初次离开了到处拥挤着房屋和街道的城市,到了一望无际的旷野,那愉快是难以形容的。
整天奔走在绿油油的田野里,编柳枝采野花之外,还有一桩乐事,便是听“播谷”叫。
这鸟的鸣声,无论是什么时候听去,总是远远的,仿佛要同人保持一种距离,故意躲在什么地方;却又一声声地清楚地叫着,像是对人说话那么富于亲切活泼的意味。
听了它的鸣声而不动心的人,恐怕是没有的。
难怪农人听了,觉得它是在提醒着“播谷!播谷!”而受折磨的儿媳妇听了,说它是大声疾呼着“姑恶!姑恶!”对于小孩子,虽然听不出什么意义,却也觉得趣味无穷。
不知是谁把它的鸣声似通非通地谐作“光棍托锄”,并把这作为它的名字,每逢这鸟一叫,我们便仰望着那声音所来的远方,模仿着它的调子做一种唱和。
我们对唱的开场是听它自报姓名似的先叫一声:“光棍托锄!”我们便紧跟着问:“你在哪里?”刚问完,它又叫第二声,像是回答:“我在山后。
”又问:“你吃什么?”“我吃石头。
”“你喝什么?”“我喝香油。
”大概小孩子简单的头脑再也想不出别的可问的了,便就此为止,只反复地问一遍又一遍,它也总不厌其烦地回答了又回答。
④“播谷”以外,还有一种为我所深爱的鸣鸟,便是鹧鸪。
前者可说是儿时的游伴,后者则是成年后才交结的朋友。
一切鸟声似乎都有婉转清脆的特点,唯有鹧鸪的叫是低沉的、缓慢的。
在我的心中,“播谷”好像一个活泼快乐的小孩,它叫的时候也仿佛是在蹦蹦跳跳的;而鹧鸪则像是一位沉思默想的老人,动也不动地缩在什么地方慢腾腾地自言自语,它也是远远地离开了人,可是它“咕咕咕”地一叫起来,就立刻把那繁华蓬勃的春天笼上一片宁静、和平与悠闲,使人不知不觉流入遐思,同时像对“播谷”似的悠然神往于飘渺的远方——一座人迹罕至的深山,或一片无边无际的幽林。
1.3运动图象 追及相遇问题 练习(知识构建、考点突破、通法指导、综合提升)

考点突破
考点一 运动图象的理解及应用 1、x-t 图象 【典例 1】(多选)(2021·武汉市洪山高级中学高三)甲、乙两车在同一平直公路上同向运动,甲做匀加 速直线运动,乙做匀速直线运动。甲、乙两车的位置 x 随时间 t 的变化如图所示。下列说法正确的是( )
-3-
A.在 t1 时刻两车速度相等 B.从 0 到 t1 时间内,两车走过的路程相等 C.从 0 到 t2 时间内,两车的平均速度相等 D.在 t1 到 t2 时间内的某时刻,两车速度相等
-2-
【答案】二、追及相遇问题 同一 相等 等于 3. 图例:常见情景:物体 A 追物体 B,开始两者相距 x0
(1)A 追上 B 时,必有 xA=x0+xB,且 vA≥vB (2)恰好不相撞,必有 xA=x0+xB 时 vA=vB,之后 vA≤vB (3)A 追不上 B 时,必有 vA=vB 时,xA<x0+xB,之后 vA≤vB 4、几个常见追及相遇问题解法
A.t=3s 时,两车具有共同的加速度 B.a 车做匀速运动,b 车做加速运动 C.在运动过程中,b 车始终没有超过 a 车 D.在 0~3s 的时间内,a 车的平均速度比 b 车的大
-4-
【答案】C 【详解】 A.t=3s 时,两图线斜率相等,所以两车的速度相等,a 的加速度为零,而 b 的加速度不为零,所以加速 度不同,故 A 错误;B.x﹣t 图象的斜率表示速度,由图可知,a 车做匀速直线运动,b 车做减速直线运动, 故 B 错误;C.由图象可知,b 车的位置坐标小于等于 a 的坐标,所以 b 车始终没有超过 a 车,故 C 正确;
D.在 0﹣3s 的时间内,a 车的位移为 6m,b 车的位移为 8m,由公式 v x 可知,a 车的平均速度小于 b 车 t
2015高考语文一轮文档:现代文阅读 第2章 专题2 考点综合提升练1

考点综合提升练(一)一、阅读下面的文字,完成文后题目。
文学与人生(节选)朱光潜从前中国人有“文以载道”的说法,后来有人嫌这看法的道学气太重,把“诗言志”一句老话抬出来,以为文学的功用只在言志;释志为“心之所之”,因此言志包含表现一切心灵活动在内。
文学理论家于是分文学为“载道”“言志”两派,仿佛以为这两派是极端,绝不相容——“载道”是“为道德教训而文艺”,“言志”是“为文艺而文艺”。
其实这问题的关键全在“道”字如何解释。
如果释“道”为狭义的道德教训,载道就显然小看了文学。
文学没有义务要变成劝世文或是修身科的高头讲章。
如果释“道”为人生世相的道理,文学就决不能离开“道”,“道”就是文学的真实性。
志为心之所之,也就要合乎“道”,情感思想的真实本身就是“道”,所以“言志”即“载道”,根本不是两回事。
哲学科学所谈的是“道”,文艺所谈的仍然是“道”,所不同者哲学科学的道是抽象的,是从人生世相中抽绎出来的,好比从盐水中所提出来的盐;文艺的道是具体的,是含蕴在人生世相中的,好比盐溶于水,饮者知咸,却不辨何者为盐,何者为水。
用另一个比喻来说,哲学科学的道是客观的、冷的、有精气而无血肉的;文艺的道是主观的、热的,通过作者的情感与人格的渗沥,精气与血肉凝成完整生命的。
换句话说,文艺的“道”与作者的“志”融为一体。
我常感觉到,与其说“文以载道”,不如说“因文证道”。
《楞严经》记载佛有一次问他的门徒从何种方便之门,发菩提心,证圆通道。
几十个菩萨罗汉轮次回答,有人说从声音,有人说从颜色,有人说从香味,大家总共说出二十五个法门。
读到这段文章,我心里起了一个幻想,假如我当时在座,轮到我起立作答时,我一定说我的方便之门是文艺。
我不敢说我证了道,可是从文艺的玩索,我窥见了道的一斑。
文艺到了最高的境界,从理智方面说,对于人生世相必有深广的观照与彻底的了解,如阿波罗凭高远眺,华严世界尽成明镜里的光影,大有佛家所谓万法皆空,空而不空的景象;从情感方面说,对于人世悲欢好丑必有平等的真挚的同情,冲突化除后的谐和,不沾小我利害的超脱,高等的幽默与高度的严肃,成为相反者之同一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考点综合提升练(一)
一、阅读下面的文言文,完成文后题目。
端木赐,卫人,字子贡。
子贡利口巧辞,孔子常黜其辩。
问曰:“汝与回也孰愈.?”对曰:“赐也何敢望回!回也闻一以知十,赐也闻一以知二。
”
陈子禽问子贡曰:“仲尼焉学?”子贡曰:“文武之道未坠于地在人贤者识其大者不贤者识其小者莫不有文武之道夫子焉不学而亦何常师之有!”又问曰:“孔子适是国必闻其政。
求之与?抑与之与?”子贡曰:“夫子温良恭俭让以得之。
夫子之求之也,其诸异乎人之求之也。
”
田常欲作乱于齐,惮高、国、鲍、晏[注],故移其兵欲以伐鲁。
孔子闻之,谓门弟子曰:“夫鲁,坟墓所处,父母之国。
国危如此,二三子何为莫出?”子路请出,孔子止之。
子张、子石请行,孔子弗许。
子贡请行,孔子许之,遂行。
至齐,说田常曰:“君之伐鲁过矣。
夫鲁,难伐之国,其城薄以卑.,其地狭以泄,其君愚而不仁,大臣伪而无用,其士民又恶甲兵之事,此不可与战。
君不如伐吴。
夫吴,城高以厚,地广以深,甲坚以新,士选以饱,重器精兵尽在其中,又使明大夫守之,此易伐也。
”田常忿然作色曰:“子之所难,人之所易;子之所易,人之所难。
而以.教常,何也?”子贡曰:“臣闻之,忧在内者攻强,忧在外者攻弱。
今君忧在内。
吾闻君三封.而三不成者,大臣有不听者也。
今君破鲁以广齐,战胜以骄主,破国以尊臣,而.君之功不与焉,则交日疏于主。
是君上骄主心,下恣.群臣,求以成大事,难矣。
夫上骄则恣,臣骄则争,是君上与主有隙,下与大臣交争也。
如此,则君之.立于齐危矣。
故曰不如伐吴。
伐吴不胜,民人外死,大臣内空,是君上无强臣之敌,下无民人之过,孤主制齐者唯君也。
”田常曰:“善。
虽然,吾兵业已加鲁矣,去而之吴,大臣疑我,奈何?”子贡曰:“君按兵无伐,臣请往使吴王,令之救鲁而伐齐,君因.以兵迎之。
”田常许之,使子贡南见吴王。
故子贡一出,存鲁,乱齐,破吴,强晋而霸越。
子贡一使,使势相破,十年之中,五国各有变。
子贡好废举,与时转货赀。
喜扬人之美,不能匿人之过。
常相鲁卫,家累千金,卒终于齐。
(节选自《史记·仲尼弟子列传第七》)
注高、国、鲍、晏:人名,高昭子、国惠子、鲍牧、晏圉。
1.对下列句子中加点词的解释,不正确的一项是()
A.汝与回也孰愈.愈:胜过
B.其城薄以卑.卑:低矮
C.吾闻君三封.而三不成者封:被封爵
D.是君上骄主心,下恣.群臣 恣:肆意
2.下列各组句子中,加点词的意义和用法都相同的一组是
( )
A.⎩⎪⎨⎪⎧
而以.教常,何也而秦武阳奉地图匣,以.次进 B.⎩⎪⎨⎪⎧
破国以尊臣,而.君之功不与焉人非生而.
知之者,孰能无惑? C.⎩⎪⎨⎪⎧
如此,则君之.立于齐危矣所以遣将守关者,备他盗之.出入与非常也 D.⎩⎪⎨⎪⎧
令之救鲁而伐齐,君因.以兵迎之君因.
我降,与君为兄弟
3.把文言文阅读材料中画横线的句子翻译成现代汉语。
(1)孔子适是国必闻其政。
求之与?抑与之与?
译文:________________________________________________________________________ (2)虽然,吾兵业已加鲁矣,去而之吴,大臣疑我,奈何?
译文:________________________________________________________________________
4.从第四段看,子贡给田常的建议是什么?田常接受子贡的建议是出于什么考虑的?请简要概括。
答:________________________________________________________________________
5.请用斜线(/)给下面文言短文中画线的部分断句。
(断句不超过6处)
古之君子,如伊尹、太公、管仲、乐毅之流,其王霸之略,皆定于畎亩中,非仕而后学者也。
淮阴侯见高帝于汉中,论刘、项短长,画取三秦如指诸掌,及佐帝定天下,汉中之言,无一不酬者。
诸葛孔明卧草庐中与先主策曹操孙权规取刘璋因蜀之资以争天下终身
二、阅读下面的文言文,完成文后题目。
马公,名燧,字洵美,汝州郏城人也。
天宝末安禄山拥幽陵之师南向以光禄卿贾循为留后燧以书干循劝诛逆将向润容等循疑留不决竟及于祸。
宝应中,陈郑节度李凉公移镇上党,雅知公才,表为晋州赵城尉。
时王师既破史朝议,乃复河洛,有回鹘可汗之助,因肆暴而归,以.
功自负,其强难屈,李凉公使上介致饩①
,皆惧不敢行。
公官方解巾②
,急病不让,径诣其垒。
申明要约,气盛词直,虏皆优从。
可汗乃授以旗帜,委之供办,且曰:“有犯禁者,公其董.
之。
”于是藩部肃然,莫不畏服。
河北副元帅仆固怀恩,居将相之重,侍父子之勇,可汗又其子婿也,借之为援,将有异图。
公密觇其情,请为.之备。
初,伪范阳节度使李怀仙,与相、卫、恒、定等四帅相继来降,怀恩结为党助,奏复其职。
至是拥.众据汾上,子玚围太原,相、卫馈运,以相掎角。
公至安阳,说其帅曰:“怀恩僭刻以逞欲,其子轻佻而好胜,人人自为计,坐待帐下之变耳?”深陈利病,劝喻激切,由是感公言,至涕泣改图。
因.约怀仙等三人,奉章献款。
既回鹡北归,怀恩与玚继死。
公之明识远略,皆此类也。
大历十年,夏五月,汴宋兵马使李灵耀以濮阳叛,俄据浚郊,国家始务靖叛,特屈常宪,因以节度留后授之,而又结魏师以略.东郡,不利。
六月,诏公与淮西节度李忠臣夹攻之。
时寇锋盛,忠臣每战皆北,将弃师以免者数矣,公激以壮志,或绐之吉梦。
忠臣既惭且.愤,引师复还。
先是忠臣军汴南,公军汴北,每与虏角.,所向无前,初败之于荥泽,又破之于西梁固。
至是灵耀以其勇悍者八千人,号为“饿狼营”,尽锐来拒,公引部决战,遂胜入郛。
翌日,馀党以城内八千人降于公,公悉让忠臣,退于坂桥,其士吏掳获,悉以家财购而复之,大梁之人,至今知感。
履险则忠以尽敌,成功则让以保身,此又将帅之明哲也。
(节选自唐代权德舆《司徒兼侍中上柱国北平郡王赠太傅马公行状》,有删改)
注 ①上介:古代官名。
致饩:馈赠礼物。
②解巾:巾,古代隐士常戴的一种头巾,后用解巾代指出任官职。
6.对下列句子中加点词的解释,不正确的一项是 ( )
A.有犯禁者,公其董.之 董:关注
B.至是拥.
众据汾上
拥:聚集 C.而又结魏师以略.东郡 略:劫掠 D.每与虏角.,所向无前
角:作战
7.下列各组句子中,加点词的意义和用法都相同的一组是
( )
A.⎩⎪⎨⎪⎧
以.功自负焉用亡郑以.
陪邻
B.⎩⎪⎨⎪⎧
请为.之备秦王不怿,为.一击缶 C.⎩⎪⎨⎪⎧
因.约怀仙等三人不如因.善遇之 D.⎩⎪⎨⎪⎧
忠臣既惭且.愤不出,火且.
尽
8.用斜线(/)给文言文阅读材料中画波浪线的部分断句。
天 宝 末 安 禄 山 拥 幽 陵 之 师 南 向 以 光 禄 卿 贾 循 为 留 后 燧 以 书 干 循 劝 诛 逆 将 向 润 容 等 循 疑 留 不 决 竟 及 于 祸
9.文言文阅读材料中有三个故事体现了马燧的“明识远略”,请简要概括。
答:________________________________________________________________________
10.把文言文阅读材料中画横线的句子翻译成现代汉语。
(1)时寇锋盛,忠臣每战皆北,将弃师以免者数矣,公激以壮志,或绐之吉梦。
译文:________________________________________________________________________ (2)履险则忠以尽敌,成功则让以保身,此又将帅之明哲也。
译文:________________________________________________________________________。
