37584_《集合之间的关系》教案1(新人教B版必修1)
集合之间的关系人教B版必修一优秀教学教案说课稿
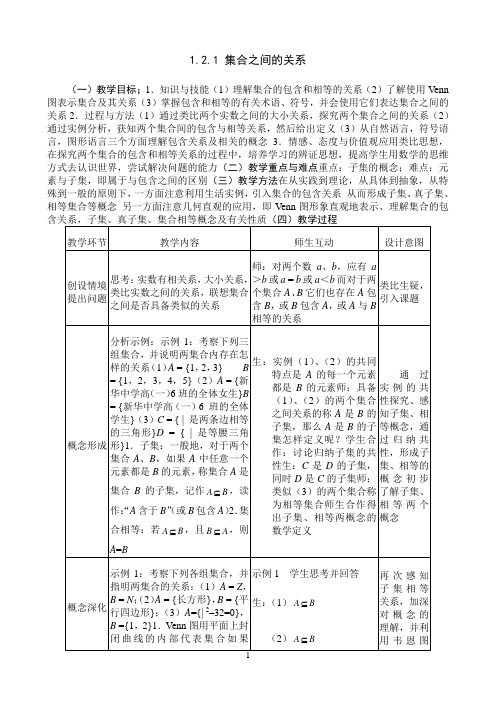
1.2.1 集合之间的关系(一)教学目标;1.知识与技能(1)理解集合的包含和相等的关系(2)了解使用Venn 图表示集合及其关系(3)掌握包含和相等的有关术语、符号,并会使用它们表达集合之间的关系2.过程与方法(1)通过类比两个实数之间的大小关系,探究两个集合之间的关系(2)通过实例分析,获知两个集合间的包含与相等关系,然后给出定义(3)从自然语言,符号语言,图形语言三个方面理解包含关系及相关的概念3.情感、态度与价值观应用类比思想,在探究两个集合的包含和相等关系的过程中,培养学习的辨证思想,提高学生用数学的思维方式去认识世界,尝试解决问题的能力(二)教学重点与难点重点:子集的概念;难点:元素与子集,即属于与包含之间的区别(三)教学方法在从实践到理论,从具体到抽象,从特殊到一般的原则下,一方面注意利用生活实例,引入集合的包含关系从而形成子集、真子集、相等集合等概念另一方面注意几何直观的应用,即Venn图形象直观地表示、理解集合的包备选训练题例1 能满足关系{a,b}{a,b,c,d,e}的集合的数目是( A )A.8个B.6个C.4个D.3个【解析】由关系式知集合A中必须含有元素a,b,且为{a,b,c,d,e}的子集,所以A 中元素就是在a,b元素基础上,把{c,d,e}的子集中元素加上即可,故A = {a,b},A = {a,b,c},A = {a,b,d},A = {a,b,e},A = {a,b,c,d},A = {a,b,c,e},A = {a,b,d,e},A = {a,b,c,d,e},共8个,故应选A例2 已知A = {0,1}且B = { |},求B【解析】集合A的子集共有4个,它们分别是:,{0},{1},{0,1}由题意可知B = {,{0},{1},{0,1}}例3 设集合A = { – , ,},B = {2 2,2 – 2,0},且A = B ,求实数和的值及集合A 、B【解析】∵A = B ,0∈B ,∴0∈A若 = 0或 – = 0,则2 – 2 = 0,这样集合B = {2 2,0,0},根据集合元素的互异性知: ≠0, – ≠0∴22220xy x y x y x y x y=⎧⎪-=-⎨⎪+=+⎩ (I ) 或22220xy x y x y x y x y=⎧⎪-=+⎨⎪+=-⎩ (II )由(I )得:00x y =⎧⎨=⎩或01x y =⎧⎨=⎩或10x y =⎧⎨=⎩ 由(II )得:00x y =⎧⎨=⎩或01x y =⎧⎨=-⎩或1x y =⎧⎨=⎩ ∴当 = 0, = 0时, – = 0,故舍去 当 = 1, = 0时, – = = 1,故也舍去 ∴01x y =⎧⎨=⎩或01x y =⎧⎨=-⎩, ∴A = B = {0,1,–1}例4 设A = { | 2 – 8 15 = 0},B = { | a – 1 = 0},若B A ⊆,求实数a 组成的集合,并写出它的所有非空真子集【解析】A = {3,5},∵B A ⊆,所以 (1)若B =,则a = 0;(2)若B ≠,则a ≠0,这时有或,即a =或a = 综上所述,由实数a 组成的集合为11{0,,}53其所有的非空真子集为:{0},111111{},{},{0,},{0,},{,}535353共6个。
人教新课标版数学高一- 人教B版必修1 《集合之间的关系》教案

1.2.1集合之间的关系教学目的:1、使学生掌握子集、真子集、空集、两个集合相等等概念,会写出一个集合的所有子集。
2、能过与不等式类比学习集合间的基本关系,掌握类比思想的应用。
教学重难点:重点是掌握集合间的关系,难点是子集与真子集的区别。
教学过程:一、复习提问1、元素与集合之间有什么关系?a与{a}有什么区别?2、集合的表示方法有几种?分别是什么?二、新课5<7 例1、A={1,2,3},B={1,2,3,4,5}或7>5 特点:A有的元素,B都有,即集合A的任何一个元素都是集合B的元素。
称为:集合A是集合B的子集。
记作:A⊆B,或B⊇A。
例2、A为高一(2)班女生的全体组成的集合,B为这个班学生的全体组成的集合。
特点:A有的元素,B都有,即集合A的任何一个元素都是集合B的元素。
定义:一般地,对于两个集合A、B,如果集合A中任意一个元素都是集合B中的元素,我们就说这两个集合有包含关系,称集合A是集合B的子集(subset)。
记作:A⊆B,或B⊇A。
用Venn图表示(右上图)。
5=5 例3、设C={x|x是两条边相等的三角形},D={x|x是等腰三角形}a ≤b 特点:集合C 中的任何一个元素都是集合D 中的元素,集合D 中的任何一 且b ≥a 个元素都是集合C 中的元素,即C ⊆D ,或D ⊇C 。
则a=b 所以,C=D 。
定义:如果集合A 是集合B 的子集(A ⊆B),且集合B 是集合A 的子集(B ⊆A),此时 集合A 与集合B 的元素是一样的,因此,集合A 与集合B 相等,记作:A=B 定义:若集合A ⊆B ,但在在元素x ∈B ,且x ∉A ,我们称集合A 是集合B 的真子集B ,或B A记作:A 例1中,集合A 是集合B 的真子集。
例2呢?方程x 2+1=0没有实数根,所以方程x 2+1=0的实数根组成的集合中没有元素。
定义:我们把不含任何元素的集合叫做空集,记为Ø,并规定:空集是任何集合的子 集。
高一数学上册《集合之间的关系》教案、教学设计

1.通过实际问题引入集合的概念,引导学生从具体实例中抽象出集合的定义,培养其从特殊到一般的归纳能力。
2.利用图形、表格等直观手段,帮助学生形象地理解集合之间的关系,提高其空间想象能力和直观感知能力。
3.通过小组讨论、合作探究的方式,引导学生自主发现集合运算的规律,培养其合作意识和团队精神。
-引导学生探索集合的其他性质,如幂集、无穷集合等,提高学生的数学素养。
-介绍集合论在数学及相关领域中的应用,增强学生的学习兴趣。
3.教学评价:
-采用多元化的评价方式,如课堂提问、课后作业、小组讨论、小测验等,全面了解学生的学习情况。
-关注学生的个体差异,鼓励学生积极参与,及时给予表扬和鼓励,提高学生的自信心。
-数学日记:要求学生以日记的形式记录自己在解决集合问题时的心得体会,促进学生对知识的内化。
4.预习作业:
-预习下一节课的内容:提前让学生预习下一节课关于集合的拓展知识,如幂集、无穷集合等,为课堂学习做好准备。
-提出疑问:鼓励学生在预习过程中提出自己的疑问,以便在课堂上进行讨论和解答。
在作业布置过程中,关注以下几点:
1.作业量适中,难度适宜,避免过度的作业压力,让学生有足够的时间消化和吸收所学知识。
2.鼓励学生主动思考和探究,培养其独立解决问题的能力。
3.注重作业反馈,及时批改和讲评,帮助学生发现并纠正错误,提高学习效果。
4.关注学生的个体差异,针对不同学生的学习情况,给予个性化的作业指导。
2.互动交流:
-各小组汇报讨论成果,分享解题方法。
-教师点评各小组的表现,给予鼓励和指导。
(四)课堂练习
在这一环节,我将设计一些具有针对性的练习题,让学生巩固所学知识。
1.练习题设计:
《集合之间的关系》教案

集合之间的关系(一)
【教学目标】
1. 理解子集、真子集概念;掌握子集、真子集的符号及表示方法;会用它们表示集合间的关系.
2. 了解空集的意义;会求已知集合的子集、真子集并会用符号及Venn图表示.
3. 培养学生使用符号的能力;建立数形结合的数学思想;培养学生用集合的观点分析问题、解决问题的能力.
【教学重点】
子集、真子集的概念.
【教学难点】
集合间包含关系的正确表示.
【教学方法】
本节课采用讲练结合、问题解决式教学方法,并运用现代化教学手段辅助教学.设计典型题目,并提出问题,层层引导学生探究知识,让学生在完成题目的同时,思维得以深化;切实体现以人为本的思想,充分发挥学生的主观能动性,培养其探索精神和运用数学知识的意识.。
高中数学集合之间的关系学案新人教B版必修1

高中数学 集合之间的关系学案 新人教B 版必修1一、三维目标: 知识与技能:(1)了解集合之间的包含、相等关系的含义;(2)理解子集、真子集的概念;(3)能利用Venn 图表达集合间的关系;(4)了解空集的含义。
过程与方法:理解集合之间包含与相等的含义,能识别给定集合的子集,能判断给定集合间的关系,掌握并能使用Venn 图表达集合间的关系。
情感态度与价值观:通过学习,提高利用类比发现新结论的能力,加强从具体到抽象的思维能力,树立数形结合的思想。
二、学习重、难点:重点:子集与空集的概念;能利用Venn 图表达集合间的关系。
难点:弄清属于与包含的关系。
三、学法指导:研读学习目标,了解本章重难点,精读教材,独立完成学案,通过小组学习解决部分疑难问题,再通过课堂各小组展示及质疑对抗,共同提高,完成学习任务。
【小组活动一】想一想:比较下面几个例子,试发现两个集合之间的关系: (1){1,2,3}A =,{1,2,3,4,5}B =; (2)}167|{班的同学级为国际学校x x C =;}67|{D 级的同学为国际学校x x =(3){|}Ex x =是两条边相等的三角形,{}F x x =是等腰三角形【小组活动二】1.阅读教材10---12页,完成下列表格:(1) 空集是任何集合的子集;(2) 空集是任何非空集合的真子集; (3) 任何一个集合是它本身的子集;例1、写出集合A={1,2,3}的所有子集和真子集。
例2 、说出下列每对集合之间的关系 (1) A={1,2,3,4,5} B={1,3,5} (2) P={1|2=xx }Q={1|||=x x }(3) C={1|>x x } D={2|≥x x } 跟踪练习:用适当的符号填空⑴ ___{0}∅ ⑵ 2___{(1,2)}⑶ ∅___2{R |20}x x ∈+=⑸ {3,5}___N⑹ {(2,3)}___{(3,2)} ⑺ {(1,2)}___2{|320}x x x -+=⑻{1,2}___2{|320}x x x -+=例3、设{|13},{|}A x xB x x a =-<<=>,若AB,则a 的取值范围是______跟踪练习:1.已知集合A=},52|{≤<-x x }121|{-≤≤+=m x m x B 且B A ⊆,求实数m 的取值范围1、 下列关系(1)}2,1{1∈(2)}2,1{∈φ(3)}1,2{}2,1{=(4)}2,1{)}2,1{(=(5)}0{⊆φ中正确的是____________2、 已知A={2,3},集合B ⊆A 则这样的集合B 一共有______个3、 判断题(1)空集没有子集。
高中高一数学上册《集合之间的关系》教案、教学设计

一、教学目标
(一)知识与技能
1.理解集合的包含关系,能够判断两个集合之间的包含与被包含关系。
2.掌握集合的交集、并集和补集的定义,能够运用这些概念进行集合运算。
3.学会使用集合的符号表示法,如大括号、小括号等,正确表示集合之间的关系和运算。
4.能够解决实际问题时运用集合之间的关系,如解决线性方程组、不等式组等问题。
2.培养严谨性:强调数学语言的严谨性和逻辑性,使学生养成认真、细致的学习习惯。
3.情感教育:通过数学史的了解,让学生感受数学家们为人类文明进步所做出的贡献,培养他们的爱国主义情怀。
4.价值观引导:引导学生认识到数学知识在实际生活中的重要作用,培养他们运用数学知识为人类服务的价值观。
二、学情分析
针对高中高一学生,他们在学习集合之间的关系这一章节时,已经具备了初步的数学逻辑思维能力和基本的代数运算技能。然而,由于集合概念较为抽象,学生在理解集合之间的包含关系、交集、并集和补集等概念时,可能会存在一定的困难。此外,学生在运用集合知识解决实际问题时,可能缺乏将问题转化为集合运算的能力。因此,在教学过程中,应注重以下几点:
9.教学反思:在课后对自己的教学进行反思,分析教学过程中的优点和不足,不断调整和优化教学方法,以提高教学效果。
四、教学内容与过程
(一)导入新课
在导入新课环节,我将采用生活实例和问题驱动的教学方法,激发学生的兴趣和求知欲。
1.生活实例引入:向学生展示一组照片,包括家庭成员、学习用品等,引导学生观察并说出这些照片的共同点和不同点。通过这个实例,让学生感受到集合的概念。
(四)课堂练习
课堂练习环节旨在巩固所学知识,提高学生的解题能力。
1.设计练习题:针对集合之间的关系和运算,设计不同难度的练习题,让学生在练习中掌握知识。
1.2.集合之间的关系-人教B版必修一教案
1.2. 集合之间的关系-人教B版必修一教案一、教学目标1.理解集合之间的含义和关系;2.掌握集合的表示方法;3.掌握集合的运算法则;4.能够解决集合的交、并、差、补等问题;5.能够用集合的运算法则进行实际问题的模型建立和解决。
二、教学重点1.集合的表示方法;2.集合的运算法则。
三、教学难点1.集合的交、并、差、补等问题的解决。
四、教学内容与步骤第一步:引入1.提问:“什么是集合?”2.对学生回答进行适当引导,深化对集合概念的理解。
第二步:集合的表示方法1.定义集合的表示方法;2.给出集合表示方法的例子;3.教师板书集合的表示方法。
第三步:集合的运算1.介绍集合的运算法则;2.给出运算法则的例子;3.教师板书集合的运算法则。
第四步:集合的关系1.介绍集合之间的关系;2.给出集合关系的例子;3.教师板书集合之间的关系。
第五步:集合的交、并、差、补等问题1.介绍集合的交、并、差、补等问题;2.给出集合交、并、差、补等问题的例子;3.讲解如何解决集合交、并、差、补等问题。
第六步:模型建立和解决1.给出实际问题;2.指导学生建立数学模型;3.讲解如何用集合的运算法则解决实际问题。
第七步:练习1.给出练习题目;2.让学生自主完成练习;3.讲解练习题目的解答方法。
五、教学反思本节课主要教授集合之间的关系和集合的运算法则等内容。
在教学过程中,我注重充分发挥学生的主动性和实践能力,通过不同的教学方式,激发学生的兴趣,使他们对这一知识点有更加深入的理解和掌握。
同时,我还注重与学生的互动交流,让他们更好地理解相关的知识点。
在实际教学中,我发现有些学生对集合的概念和运算法则掌握不够牢固,需要反复强化。
因此,我会在下一次课上继续巩固相关知识点,提高学生的学习效果。
最终目的是让每个学生都能够顺利掌握这一知识点,为以后的学习打下基础。
集合之间的关系的教案
集合之间的关系的教案
教案标题:集合之间的关系
一、教学目标
1. 知识与技能
- 了解集合的概念和基本符号表示
- 掌握集合之间的关系,包括并集、交集、差集和补集
- 能够用集合的概念解决实际问题
2. 过程与方法
- 通过实例和练习,培养学生分析问题和解决问题的能力
- 引导学生探索集合之间的关系,培养逻辑思维和抽象思维能力3. 情感态度价值观
- 培养学生对数学的兴趣和自信心
- 培养学生合作学习和团队合作的意识
二、教学重点与难点
1. 教学重点
- 集合的基本概念和符号表示
- 集合之间的并集、交集、差集和补集的概念和运算
- 实际问题中集合之间关系的应用
2. 教学难点
- 集合之间关系的抽象概念理解
- 集合运算符号的运用
三、教学过程
1. 导入新课
- 通过引入一个实际问题,引出集合的概念和集合之间的关系,激发学生的学习兴趣
2. 概念讲解
- 介绍集合的基本概念和符号表示
- 讲解集合之间的并集、交集、差集和补集的概念和运算方法
3. 练习与训练
- 给学生提供一些具体的例子,让学生通过练习来加深对集合之间关系的理解- 组织学生进行小组讨论,共同解决一些实际问题,培养学生的合作学习和团队合作意识
4. 拓展应用
- 引导学生运用集合的概念解决一些实际问题,如排列组合、概率等
四、教学反思
通过本节课的教学,学生对集合的概念和集合之间的关系有了初步的了解和掌握,但在实际问题的应用中还存在一定的困难,需要在后续的教学中加强练习和拓展应用的训练。
同时,要注重培养学生的逻辑思维和抽象思维能力,引导学生主动参与学习,提高学生的学习兴趣和自信心。
高中数学 1.2.1集合之间的关系教学设计 新人教B版必修1-新人教B版高一必修1数学教案
1.2.1 集合之间的关系整体设计教学分析课本从学生熟悉的集合出发,引入集合间的关系,同时,结合相关内容介绍子集等概念.在安排这部分内容时,课本注重体现逻辑思考的方法,如归纳等.值得注意的问题:在集合间的关系教学中,建议重视使用Venn图,这有助于学生通过体会直观图示来理解抽象概念;随着学习的深入,集合符号越来越多,建议教学时引导学生区分一些容易混淆的关系和符号,例如∈与 的区别.三维目标1.理解集合之间包含与相等的含义,能识别给定集合的子集,能判断给定集合间的关系,提高利用类比发现新结论的能力.2.在具体情境中,了解空集的含义,掌握并能使用Venn图表达集合的关系,加强学生从具体到抽象的思维能力,树立数形结合的思想.重点难点教学重点:理解集合间包含与相等的含义.教学难点:属于与包含之间的区别.课时安排1课时教学过程导入新课思路1.实数有相等、大小关系,如5=5,5<7,5>3等等,类比实数之间的关系,你会想到集合之间有什么关系呢?(让学生自由发言,教师不要急于作出判断,而是继续引导学生)欲知谁正确,让我们一起来观察、研探.思路 2.复习元素与集合的关系——属于与不属于的关系,填空:(1)0____N;(2)2____QR.类比实数的大小关系,如5<7,2≤2,试想集合间是否有类似的“大小”关系呢?(答案:(1)∈;(2);(3)∈)推进新课新知探究提出问题1观察下面几个例子:①A={1,2,3},B={1,2,3,4,5};②设A为国兴中学高一3班男生的全体组成的集合,B为这个班学生的全体组成的集合;③设C={x|x是两条边相等的三角形},D={x|x是等腰三角形};④E={2,4,6},F={6,4,2}.,你能发现两个集合间有什么共同特点吗?(2)例子①中集合A是集合B的子集,例子④中集合E是集合F的子集,同样是子集,有什么区别?(3)结合例子④,类比实数中的结论:“若a≤b,且b≤a,则a=b”,在集合中,你发现了什么结论?(4)按升国旗时,每个班的同学都聚集在一起站在旗杆附近指定的区域内,从楼顶向下看,每位同学是哪个班的,一目了然.试想一下,根据从楼顶向下看的,要想直观表示集合,联想集合还能用什么表示?(5)试用Venn图表示例子①中集合A和集合B.(6)已知A⊆B,试用Venn图表示集合A和B的关系.(7)与实数中的结论“若a≥b,且b≥c,则a≥c”相类比,在集合中,你能得出什么结论?活动:教师从以下方面引导学生:(1)观察两个集合间元素的特点.教师给出定义:一般地,如果集合A中的任意一个元素都是集合B的元素,那么集合A叫做集合B的子集,记作A⊆B或B⊇A.规定:空集是任何一个集合的子集.(2)从它们含有的元素间的关系来考虑.规定:如果A⊆B,但存在x∈B,且x A,我们称集合A是集合B的真子集,记作A B(或B A).(3)实数中的“≤”类比集合中的⊆.(4)把指定位置看成是由封闭曲线围成的,学生看成集合中的元素,从楼顶看到的就是把集合中的元素放在封闭曲线内.教师指出:为了直观地表示集合间的关系,我们常用平面内一条封闭曲线的内部代表集合,这种图称为维恩(Venn)图.(5)封闭曲线可以是矩形也可以是椭圆等等,没有限制.(6)分类讨论:当A⊆B时,A B或A=B.(7)类比子集.讨论结果:(1)①集合A中的元素都在集合B中;②集合A中的元素都在集合B中;③集合C中的元素都在集合D中;④集合E中的元素都在集合F中.可以发现:对于任意两个集合A、B有下列关系:集合A中的元素都在集合B中,或集合B中的元素都在集合A中.(2)例子①中A⊆B,但有一个元素4∈B,且4A,而例子②中集合E和集合F中的元素完全相同.(3)若A⊆B,且B⊆A,则A=B.(4)可以把集合中元素写在一个封闭曲线的内部来表示集合.(5)如图甲所示表示集合A,如图乙所示表示集合B.(6)如下图所示.(7)若A⊆B,B⊆C,则A⊆C;若A B,B C,则A C.应用示例思路1例1写出集合A={1,2,3}的所有子集和真子集.分析:如何一个不漏地写出集合{1,2,3}的所有子集呢?我们采用下面的步骤:(1)因为空集∅是所有集合的子集,所以首先写出∅;(2)写出所有由一个元素构成的子集:{1},{2},{3};(3)写出所有由两个元素构成的子集:{1,2},{1,3},{2,3};(4)写出所有由三个元素构成的子集:{1,2,3}.解:集合A的所有子集是:∅,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}.在上述子集中,除去集合A本身,即{1,2,3},剩下的都是A的真子集.点评:本题主要考查子集和真子集的概念,以及分类讨论的思想.通常按子集中所含元素的个数来写出一个集合的所有子集,这样可以避免重复和遗漏.思考:集合A中含有n个元素,那么集合A有多少个子集?多少个真子集?解:当n=0时,即空集的子集为∅,即子集的个数是1=20;当n=1时,即含有一个元素的集合如{a}的子集为∅,{a},即子集的个数是2=21;当n=2时,即含有两个元素的集合如{a,b}的子集为∅,{a},{b},{a,b},即子集的个数是4=22……集合A中含有n个元素,那么集合A有2n个子集,由于一个集合不是其本身的真子集,所以集合A有(2n-1)个真子集.变式训练已知集合P={1,2},那么满足Q⊆P的集合Q的个数是( )A.4 B.3 C.2 D.1解析:集合P={1,2}含有2个元素,其子集有22=4个,又集合Q⊆P,所以集合Q有4个.答案:A例2说出下列每对集合之间的关系:(1)A={1,2,3,4,5},B={1,3,5};(2)P={x|x2=1},Q={x||x|=1};(3)C={x|x是奇数},D={x|x是整数}.解:(1)B A;(2)P=Q;(3)C D.点评:本题主要考查集合间的包含关系.其关键是首先明确两集合中的元素具体是什么.判断两个集合A、B之间是否有包含关系的步骤是:先明确集合A、B中的元素,再分析集合A、B中的元素之间的关系,得:当集合A中的元素都属于集合B时,有A⊆B;当集合A中的元素都属于集合B,当集合B中至少有一个元素不属于集合A时,有A B;当集合A 中的元素都属于集合B,并且集合B中的元素也都属于集合A时,有A=B;当集合A中至少有一个元素不属于集合B,并且集合B中至少有一个元素也不属于集合A时,有A B,且B A,即集合A、B互不包含.变式训练某工厂生产的产品在重量和长度上都合格时,该产品才合格.若用A表示合格产品的集合,B表示重量合格的产品的集合,C表示长度合格的产品的集合.已知集合A、B、C均不是空集.(1)则下列包含关系哪些成立?A⊆B,B⊆A,A⊆C,C⊆A.(2)试用Venn图表示集合A、B、C间的关系.活动:学生思考集合间的关系以及Venn图的表示形式.当集合A中的元素都属于集合B时,则A⊆B成立,否则A⊆B不成立.用相同的方法判断其他包含关系是否成立.教师提示学生以下两点:(1)重量合格的产品不一定是合格产品,但合格的产品一定重量合格;长度合格的产品不一定是合格产品,但合格的产品一定长度合格.(2)根据集合A、B、C间的关系来画出Venn图.解:(1)包含关系成立的有:A⊆B,A⊆C.(2)集合A、B、C间的关系用Venn图表示,如下图所示.例3判定下列集合A与B的关系:(1)A={x|x是12的约数},B={x|x是36的约数};(2)A={x|x>3},B={x|x>5};(3)A={x|x是矩形},B={x|x是有一个角为直角的平行四边形}.解:(1)因为x是12的约数⇒x是36的约数,所以A⊆B;(2)因为x>5⇒x>3,所以B⊆A;(3)因为x是矩形⇔x是有一个角为直角的平行四边形,所以A=B.点评:A={x|p(x)},B={x|q(x)},则如果p(x) ⇔q(x),则A=B;反之,如果A=B,则p(x) ⇔q(x).变式训练本节练习A 4思路2例1已知集合A={-1,3,2m-1},集合B={3,m2}.若B A,则实数m=________.活动:先让学生思考B⊆A的含义,根据B⊆A,知集合B中的元素都属于集合A,集合元素的互异性,列出方程某某数m的值.因为B⊆A,所以3∈A,m22的值分类讨论.解析:∵B⊆A,∴3∈A,m2∈A.∴m2=-1(舍去)或m2=2m-1.解得m=1.∴m=1.答案:1点评:本题主要考查集合和子集的概念,以及集合元素的互异性.本题容易出现m2=3,其原因是忽视了集合元素的互异性.避免此类错误的方法是解得m的值后,再代入验证.讨论两集合之间关系时,通常依据相关的定义,观察这两个集合元素的关系,转化为解变式训练已知集合M={x|2-x<0},集合N={x|ax=1},若N M,某某数a的取值X围.分析:集合N是关于x的方程ax=1的解集,集合M={x|x>2}≠∅,由于N M,则N=或N≠∅,要对集合N是否为空集分类讨论.解:由题意得M={x|x>2}≠∅,则N=∅或N≠∅.当N=∅时,关于x的方程ax=1中无解,则有a=0;当N≠∅时,关于x 的方程ax =1中有解,则a≠0,此时x =1a. 又∵N M ,∴1a ∈M.∴1a >2.∴0<a <12. 综上所得,实数a 的取值X 围是a =0或0<a <12, 即实数a 的取值X 围是{a|0≤a<12}.例2 (1)分别写出下列集合的子集及其个数:∅,{a},{a ,b},{a ,b ,c}.(2)由(1)你发现集合M 中含有n 个元素,则集合M 有多少个子集?活动:学生思考子集的含义,并试着写出子集.(1)按子集中所含元素的个数分类写出子集;(2)由(1)总结当n =0,n =1,n =2,n =3时子集的个数规律,归纳猜想出结论.解:(1)∅的子集有:∅,即∅有1个子集;{a}的子集有:∅、{a},即{a}有2个子集;{a ,b}的子集有:∅、{a}、{b}、{a ,b},即{a ,b}有4个子集;{a ,b ,c}的子集有:∅、{a}、{b}、{c}、{a ,b}、{a ,c}、{b ,c}、{a ,b ,c},即{a ,b ,c}有8个子集.(2)由(1)可得:当n =0时,有1=20个子集;当n =1时,集合M 有2=21个子集;当n =2时,集合M 有4=22个子集;当n =3时,集合M 有8=23个子集.因此,含有n 个元素的集合M 有2n 个子集.点评:本题主要考查子集的概念以及分类讨论和归纳推理的能力.集合M 中含有n 个元素,则集合M 有2n 个子集,有2n -1个真子集,记住这个结论,可以提高解题速度.写一个变式训练已知集合A {2,3,7},且A 中至多有一个奇数,则这样的集合A 有… ( )A .3个B .4个C .5个D .6个解析:对集合A 所含元素的个数分类讨论.A =∅或{2}或{3}或{7}或{2,3}或{2,7}共有6个.答案:D知能训练1.判断正误:(1)空集没有子集.( )(2)空集是任何一个集合的真子集.( )(3)任一集合必有两个或两个以上子集.( )(4)若B ⊆A ,那么凡不属于集合A 的元素,则必不属于B.( )分析:关于判断题应确实把握好概念的实质.解:该题的4个命题,只有(4)是正确的,其余全错.对于(1)、(2)来讲,由规定:空集是任何一个集合的子集,且是任一非空集合的真子集.对于(3)来讲,可举反例,空集这一个集合就只有自身一个子集.对于(4)来讲,当x∈B时必有x∈A,则x A时也必有x B.2.集合A={x|-1<x<3,x∈Z},写出A的真子集.分析:区分子集与真子集的概念,空集是任一非空集合的真子集,一个含有n个元素的集合的子集有2n个,真子集有2n-1个,则该题先找该集合元素,后找真子集.解:因-1<x<3,x∈Z,故x=0,1,2,即A={x|-1<x<3,x∈Z}={0,1,2}.真子集有∅、{1}、{2}、{0}、{0,1}、{0,2}、{1,2},共7个.3.(1)下列命题正确的是( )A.无限集的真子集是有限集B.任何一个集合必定有两个子集C.自然数集是整数集的真子集D.{1}是质数集的真子集(2)以下五个式子中,错误的个数为( )①{1}∈{0,1,2}②{1,-3}={-3,1} ③{0,1,2}⊆{1,0,2}④∅∈{0,1,2}⑤∅∈{0}A.5 B.2 C.3 D.4(3)M={x|3<x<4},a=π,则下列关系正确的是( )A.a M B.a M C.{a}∈M D.{a}M解析:(1)该题要在四个选项中找到符合条件的选项,必须对概念把握准确,无限集的真子集有可能是无限集,如N是R的真子集,排除A;由于∅只有一个子集,即它本身,排除B;由于1不是质数,排除D.(2)该题涉及到的是元素与集合,集合与集合的关系.①应是{1}⊆{0,1,2},④应是∅⊆{0,1,2},⑤应是∅⊆{0}.故错误的有①④⑤.(3)M={x|3<x<4},a=π.因3<a<4,故a是M的一个元素.{a}是{x|3<x<4}的子集,那么{a}M.答案:(1)C (2)C (3)D4.判断如下集合A与B之间有怎样的包含或相等关系.(1)A={x|x=2k-1,k∈Z},B={x|x=2m+1,m∈Z};(2)A={x|x=2m,m∈Z},B={x|x=4n,n∈Z}.解:(1)因A={x|x=2k-1,k∈Z},B={x|x=2m+1,m∈Z},故A、B都是由奇数构成的,即A=B.(2)因A={x|x=2m,m∈Z},B={x|x=4n,n∈Z},又x=4n=2·2n,在x=2m中,m可以取奇数,也可以取偶数;而在x=4n中,2n只能是偶数.故集合A、B的元素都是偶数,但B中元素是由A中部分元素构成,则有B A.5.已知集合P={x|x2+x-6=0},Q={x|ax+1=0}满足Q P,求a所取的一切值.解:因P ={x|x 2+x -6=0}={2,-3},当a =0时,Q ={x|ax +1=0}=∅,Q P 成立. 又当a≠0时,Q ={x|ax +1=0}={-1a}, 要Q P 成立,则有-1a =2或-1a =-3,a =-12或a =13. 综上所述,a =0或a =-12或a =13. 点评:这类题目给的条件中含有字母,一般需分类讨论.本题易漏掉a =0,ax +1=0无解,即Q 为空集的情况,而当Q =∅时,满足Q P.6.已知集合A ={x∈R |x 2-3x +4=0},B ={x∈R |(x +1)(x 2+3x -4)=0},要使A P ⊆B ,求满足条件的集合P.解:由A ={x∈R |x 2-3x +4=0}=∅,B ={x∈R |(x +1)(x 2+3x -4)=0}={-1,1,-4}, 由A P ⊆B 知集合P 非空,且其元素全属于B ,即P 是B 的非空子集,则满足条件的集合P 为{1}或{-1}或{-4}或{-1,1}或{-1,-4}或{1,-4}或{-1,1,-4}.点评:要解决该题,必须确定满足条件的集合P 的元素,而做到这点,必须明确A 、B ,充分把握子集、真子集的概念,准确化简集合是解决问题的首要条件.7.集合A ={x|-2≤x≤5},B ={x|m +1≤x≤2m-1},(1)若B ⊆A ,某某数m 的取值X 围;(2)当x∈Z 时,求A 的非空真子集个数;(3)当x∈R 时,没有元素x 使x∈A 与x∈B 同时成立,某某数m 的取值X 围.解:(1)当m +1>2m -1即m <2时,B =∅满足B ⊆A.当m +1≤2m-1即m≥2时,要使B ⊆A 成立,需⎩⎪⎨⎪⎧ m +1≥-2,2m -1≤5,可得2≤m≤3.综上所得实数m 的取值X 围为m≤3.(2)当x∈Z 时,A ={-2,-1,0,1,2,3,4,5},∴A 的非空真子集个数为28-2=254.(3)∵x∈R ,且A ={x|-2≤x≤5},B ={x|m +1≤x≤2m-1},又没有元素x 使x∈A 与x∈B 同时成立.则①若B =∅即m +1>2m -1,得m <2时满足条件;②若B≠∅,则要满足条件有:⎩⎪⎨⎪⎧ m +1≤2m-1,m +1>5或⎩⎪⎨⎪⎧ m +1≤2m-1,2m -1<-2,解之,得m >4.综上,有m <2或m >4.点评:此问题解决要注意:不应忽略∅;找A 中的元素;分类讨论思想的运用. 拓展提升问题:已知A ⊆B ,且A ⊆C ,B ={0,1,2,3,4},C ={0,2,4,8},则满足上述条件的集合A共有多少个?活动:学生思考A⊆B,且A⊆C所表达的含义.A⊆B说明集合A是集合B的子集,即集合A中元素属于集合B,同理有集合A中元素属于集合C.因此集合A中的元素是集合B 和集合C的公共元素.思路1:写出由集合B和集合C的公共元素所组成的集合,得满足条件的集合A;思路2:分析题意,仅求满足条件的集合A的个数,转化为求集合B和集合C的公共元素所组成的集合的子集个数.解法一:因A⊆B,A⊆C,B={0,1,2,3,4},C={0,2,4,8},由此,满足A⊆B,有:∅,{0},{1},{2},{3},{4},{0,1},{0,2},{2,3},{2,4},{0,3},{0,4},{1,2},{1,3},{1,4},{3,4},{0,2,4},{0,1,2},{0,1,3},{0,1,4},{1,2,3},{1,2,4},{2,3,4},{0,3,4},{0,1,2,3},{1,2,3,4},{0,1,3,4},{0,2,3},{1,3,4},{0,1,2,4},{0,2,3,4},{0,1,2,3,4},共25=32(个).又满足A⊆C的集合A有∅,{0},{2},{4},{8},{0,2},{0,4},{0,8},{2,4},{2,8},{4,8},{0,2,4},{0,2,8},{0,4,8},{2,4,8},{0,2,4,8},共24=16(个).其中同时满足A⊆B,A⊆C的有8个,即∅,{0},{2},{4},{0,2},{0,4},{2,4},{0,2,4},实际上到此就可看出,上述解法太繁.解法二:题目只求集合A的个数,而未让说明A的具体元素,故可将问题等价转化为B、C的公共元素组成集合的子集数是多少.显然公共元素有0、2、4,组成集合的子集有23=8(个).点评:有关集合间关系的问题,常用分类讨论的思想来解决;关于集合的子集个数的结论要熟练掌握,其应用非常广泛.课堂小结本节课学习了:①子集、真子集、Venn图等概念;②能判断存在子集关系的两个集合谁是谁的子集,进一步确定其是否是真子集;③清楚两个集合包含关系的确定,主要靠其元素与集合关系来说明.作业课本本节练习B 2、3、4.设计感想本节教学设计注重引导学生通过归纳来获得新知,在实际教学中,要留给学生适当的思考时间,使学生自己通过归纳得到正确结论.丰富学生的学习方式、改进学生的学习方法是高中数学课程追求的基本理念,学生的数学学习活动不能仅限于对概念、结论和技能的记忆、模仿和接受,独立思考、自主探索、合作交流、阅读自学等都应成为学生学习数学的重要方式.备课资料[备选例题]例1下面的Venn图中反映的是四边形、梯形、平行四边形、菱形、正方形这五种几何图形之间的关系,问集合A、B、C、D、E分别是哪种图形的集合?分析:结合Venn图,利用平面几何中梯形、平行四边形、菱形、正方形的定义来确定.解:梯形、平行四边形、菱形、正方形都是四边形,故A={四边形};梯形不是平行四边形、菱形、正方形,而菱形、正方形是平行四边形,故B ={梯形},C ={平行四边形};正方形是菱形,故E ={正方形},即A ={四边形},B ={梯形},C ={平行四边形},D ={菱形},E ={正方形}.例2 设集合A ={x||x|2-3|x|+2=0},B ={x|(a -2)x =2},则满足B A 的a 的值共有( )A .2个B .3个C .4个D .5个解析:由已知得A ={x||x|=1或|x|=2}={-2,-1,1,2},集合B 是关于x 的方程(a -2)x =2的解集,∵B A ,∴B=∅或B≠∅.当B =∅时,关于x 的方程(a -2)x =2无解,∴a-2=0.∴a=2.当B≠∅时,关于x 的方程(a -2)x =2的解为x =2a -2∈A, ∴2a -2=-2或2a -2=-1或2a -2=1或2a -2=2. 解得a =1或0或4或3,综上所得,a 的值共有5个.答案:D例3 集合A ={x|0≤x<3且x∈N }的真子集...的个数是( ) A .16 B .8 C .7 D .4解析:A ={x|0≤x<3且x∈N }={0,1,2},则A 的真子集有23-1=7个.答案:C例4 已知集合A ={x|1≤x≤3},B ={x|(x -1)(x -a)=0},试判断集合B 是不是集合A 的子集?是否存在实数a 使A =B 成立?分析:先在数轴上表示集合A ,然后化简集合B ,由集合元素的互异性,可知此时应考虑a 的取值是否为1,要使集合B 成为集合A 的子集,集合B 的元素在数轴上的对应点必须在集合A 对应的线段上,从而确定字母a 的分类标准.解:当a =1时,B ={1},所以B 是A 的子集;当1<a≤3时,B 也是A 的子集;当a <1或a >3时,B 不是A 的子集.综上可知,当1≤a≤3时,B 是A 的子集.由于集合B 最多只有两个元素,而集合A 有无数个元素,故不存在实数a ,使B =A. 点评:分类讨论思想,就是科学合理地划分类别,通过“各个击破”,再求整体解决(即先化整为零,再聚零为整)的策略思想.类别的划分必须满足互斥、无漏、最简的要求,探索划分的数量界限是分类讨论的关键.[思考](1)空集中没有元素,怎么还是集合?(2)符号“∈”和“⊆”有什么区别?剖析:(1)疑点是总是对空集这个概念迷惑不解,并产生怀疑的想法.产生这种想法的原因是没有了解建立空集这个概念的背景,其突破方法是通过实例来体会.例如,根据集合元素的性质,方程的解能够组成集合,这个集合叫做方程的解集.对于1x=0,x 2+4=0等方程来说,它们的解集中没有元素.也就是说确实存在没有任何元素的集合,那么如何用数学符号来刻画没有元素的集合呢?为此引进了空集的概念,把不含任何元素的集合叫做空集.这就是建立空集这个概念的背景.由此看出,空集的概念是一个规定.又例如,不等式|x|<0的解集也是不含任何元素,就称不等式|x|<0的解集是空集.(2)难点是经常把这两个符号混淆,其突破方法是准确把握这两个符号的含义及其应用X 围,并加以对比.符号∈只能适用于元素与集合之间,其左边只能写元素,其右边只能写集合,说明左边的元素属于右边的集合,表示元素与集合之间的关系,如-1∈Z ,12Z ;符号⊆只能适用于集合与集合之间,其左右两边都必须写集合,说明左边的集合是右边集合的子集,表示集合与集合之间的关系,如{1}⊆{1,0},∅⊆{x|x <0}.。
高中数学 1.1.2 集合间的基本关系教案 新人教B版必修1
课题:§1.2集合间的基本关系教材分析:类比实数的大小关系引入集合的包含与相等关系了解空集的含义课 型:新授课教学目的:〔1〕了解集合之间的包含、相等关系的含义;〔2〕理解子集、真子集的概念;〔3〕能利用Venn 图表达集合间的关系;〔4〕了解与空集的含义。
教学重点:子集与空集的概念;用Venn 图表达集合间的关系。
教学难点:弄清元素与子集 、属于与包含之间的区别;教学过程:一、引入课题1、复习元素与集合的关系——属于与不属于的关系,填以下空白:〔1〕0N ;〔2〕2Q ;〔3〕-1.5R2、类比实数的大小关系,如5<7,2≤2,试想集合间是否有类似的“大小〞关系呢?〔宣布课题〕二、新课教学(一) 集合与集合之间的“包含〞关系;A={1,2,3},B={1,2,3,4}集合A 是集合B 的部分元素构成的集合,我们说集合B 包含集合A ;如果集合A 的任何一个元素都是集合B 的元素,我们说这两个集合有包含关系,称集合A 是集合B 的子集〔subset 〕。
记作:)(A B B A ⊇⊆或读作:A 包含于〔is contained in 〕B ,或B 包含〔contains 〕A当集合A 不包含于集合B 时,记作A B 用Venn图表示两个集合间的“包含〞关系(B B A ⊇⊆或(二)A B B A ⊆⊆且,那么B A =中的元素是一样的,因此B A =即 ⎩⎨⎧⊆⊆⇔=A B B A B A 练习结论:任何一个集合是它本身的子集(三) 真子集的概念假设集合B A ⊆,存在元素A x B x ∉∈且,那么称集合A 是集合B 的真子集〔proper⊆subset 〕。
记作:A B 〔或B A 〕读作:A 真包含于B 〔或B 真包含A 〕举例〔由学生举例,共同辨析〕(四) 空集的概念〔实例引入空集概念〕不含有任何元素的集合称为空集〔empty set 〕,记作:∅规定:空集是任何集合的子集,是任何非空集合的真子集。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.2.1集合之间的关系教学目的:1、使学生掌握子集、真子集、空集、两个集合相等等概念,会写出一个集合的所有子集。
2、能过与不等式类比学习集合间的基本关系,掌握类比思想的应用。
教学重难点:重点是掌握集合间的关系,难点是子集与真子集的区别。
教学过程:
一、复习提问
1、元素与集合之间有什么关系?a与{a}有什么区别?
2、集合的表示方法有几种?分别是什么?
二、新课
5<7 例1、A={1,2,3},B={1,2,3,4,5}
或7>5 特点:A有的元素,B都有,即集合A的任何一个元素都是集合B的元素。
称为:集合A是集合B的子集。
记作:A⊆B,或B⊇A。
例2、A为高一(2)班女生的全体组成的集合,B为这个班学生的全体组成的集合。
特点:A有的元素,B都有,即集合A的任何一个元素都是集合B的元素。
定义:一般地,对于两个集合A、B,如果集合A中任意一个元素都是集合B中的元素,我们就说这两个集合有包含关系,称集合A是集合B的子集(subset)。
记作:A⊆B,或B⊇A。
用Venn图表示(右上图)。
5=5 例3、设C={x|x是两条边相等的三角形},D={x|x是等腰三角形}
a≤b特点:集合C中的任何一个元素都是集合D中的元素,集合D中的任何一
且b≥a个元素都是集合C中的元素,即C⊆D,或D⊇C。
则a=b 所以,C=D。
定义:如果集合A是集合B的子集(A⊆B),且集合B是集合A的子集(B⊆A),此时集合A与集合B的元素是一样的,因此,集合A与集合B相等,记作:A=B
定义:若集合A⊆B,但在在元素x∈B,且x∉A,我们称集合A是集合B的真子集
记作:AB,
或B A
例1中,集合A是集合B的真子集。
例2呢?
方程x2+1=0没有实数根,所以方程x2+1=0的实数根组成的集合中没有元素。
定义:我们把不含任何元素的集合叫做空集,记为?,并规定:空集是任何集合的子集。
两个结论:(1)任何一个集合是它本身的子集,即A⊆A。
(2)对于集合A、B、C,如果A⊆B,且B⊆C,那么A⊆C
类比:a<b,b<c,则a<c
例3、写出集合{a,b}的所有子集,并指出哪些是它的真子集?
解:子集有:?,{a},{b},{a,b};真子集有:?,{a},{b}
练习:P131、2
作业:P133、4
(2008年江西高考理).定义集合运算:{}
A B z z xy x A y B
*==∈∈设
,,.
{}
B=,则集合A B
0,2
1,2
A=,{}
*的所有元素之和为()
A.0B.2 C.3D.6
答案:(C)。
