陕西省西安市第一中学2013-2014学年高一下学期第一次月考数学试题 Word版含答案
陕西省西安市长安区第一中学高一数学下学期第一次月考试题(实验班)
长安一中2015---2016学年度第二学期第一次月考 高一数学试题（实验班）一 、选择题（本大题共15小题，每小题5分，共75分，在每小题给出的四个选项中，只有一项是符合题目要求的）1.已知cos tan 0θθ⋅<，那么角θ是 （ ）Ａ．第一或第二象限角 Ｂ．第二或第三象限角Ｃ．第三或第四象限角 Ｄ．第一或第四象限角2.已知角α的终边过点()34，-P ，则ααcos sin 2+的值是（ ） A ．1或－1 B ．52或52- C ．1或52- D ． 52 3.某扇形的面积为12cm ，它的周长为4cm ，那么该扇形圆心角的度数为 （ ）A ．2°B ．2C ．4°D ．44．若角α和角β的终边关于x 轴对称，则角α可以用角β表示为 ( )A ．2k π＋β (k ∈Z )B ．2k π－β (k ∈Z )C ．k π＋β (k ∈Z )D ．k π－β (k ∈Z ) 5.若4cos 5α=-，α是第三象限的角，则1tan 21tan 2αα+=-（ ） A. 12- B. 12 C. 2 D. -2 6．对任意向量,a b r r ，下列关系式中不恒成立的是（ ）A ．||||||a b a b ⋅≤r r r rB ．||||||||a b a b -≤-r r r rC ．22()||a b a b +=+r r r rD ．22()()a b a b a b +-=-r r r r r r 7.已知1,,AB AC AB AC t t ⊥==u u u r u u u r u u u r u u u r ，若P 点是ABC ∆ 所在平面内一点，且4AB AC AP AB AC=+u u u r u u u r u u u r u u u r u u u r ，则PB PC ⋅u u u r u u u r 的最大值等于（ ）A ．13B ．15C ．19D ．218．A 、B 、C 是平面上不共线的三点，O 为△ABC 的中心，D 是AB 的中点，动点P 满足1[(22)(12)]()3OP OD OC R λλλ=-++∈u u u r u u u r u u u r ，则点P 的轨迹一定过△ABC 的（ ） A ．内心 B ．外心 C ．垂心 D ．重心9．设(2,3),(3,3),A B -若直线20ax y ++=与线段AB 有交点，则实数a 的取值范围是（ ）.A 55,32⎡⎤-⎢⎥⎣⎦ .B 55,,32⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭ .C 55,,23⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭ .D 55,23⎡⎤-⎢⎥⎣⎦10.设三棱柱的侧棱垂直于底面，所有棱长都为a ，顶点都在一个球面上，则该球的表面积为（ ）A. 2a πB. 273a π C ． 2113a π D ． 25a π 11. 已知函数()sin 3cos (0)f x x x ωωω=->的图象与x 轴的两个相邻交点的距离等于2π，若将函数()y f x =的图象向左平移6π个单位长度得到函数()y g x =的图象，则()y g x =的解析式是（ ）A ．2sin(2)6y x π=-B ．2sin 2y x =C ．2sin(4)6y x π=- D ．2sin 4y x = 12．若0<α<π2，－π2<β<0，cos ⎝ ⎛⎭⎪⎫π4＋α＝13，cos ⎝ ⎛⎭⎪⎫π4－β2＝33，则cos ⎝⎛⎭⎪⎫α＋β2等于( ) A ．33 B ．－33 C ．539 D ．－6913． 若函数y ＝A sin(ωx ＋φ) (A >0，ω>0，|φ|<π2)在一个周期内的图像如图所示，M ，N 分别是这段图像的最高点和最低点，且OM →·ON→＝0，则A ·ω等于 ( )A ．π6B ．712πC ．76πD ．73π 14.已知符号函数1,0,sgn 0,0,1,0.x x x x >⎧⎪==⎨⎪-<⎩()f x 是R 上的增函数，()()()(1)g x f x f ax a =->，则（ ）A ．sgn[()]sgn g x x =B ．sgn[()]sgn g x x =-C ．sgn[()]sgn[()]g x f x =D ．sgn[()]sgn[()]g x f x =-15．已知函数()()22,2,2,2,x x f x x x ⎧-≤⎪=⎨->⎪⎩ 函数()()2g x b f x =-- ，其中b R ∈，若函数()()y f x g x =- 恰有4个零点，则b 的取值范围是( )（A ）7,4⎛⎫+∞ ⎪⎝⎭ （B ）7,4⎛⎫-∞ ⎪⎝⎭ （C ）70,4⎛⎫ ⎪⎝⎭ （D ）7,24⎛⎫ ⎪⎝⎭ 二、填空题（本大题共5小题，每题5分，共25分，把答案填在题中横线上）16.若32)sin(-=-απ, 且)0,2(πα-∈, 则αtan 的值是____________ 17.已知1sin sin 3x y +=，则2sin cos y x -的最大值是____________ 18.函数y ＝2cos x －1的定义域为________．19.已知cos ⎝ ⎛⎭⎪⎫π6＋α＝33，则cos ⎝ ⎛⎭⎪⎫5π6－α的值是____________ 20.在等腰梯形ABCD 中，已知//,2,1,60AB DC AB BC ABC ==∠=o，动点E 和F 分别在线段BC 和DC 上，且，1,,9BE BC DF DC λλ==u u u r u u u r u u u r u u u r 则AE AF ⋅u u u r u u u r 的最小值为 ． 三、解答题（本大题共4小题，共50分，解答应写出文字说明、证明过程或演算步骤．）21.（本小题满分12分） 已知向量()2sin ,3cos a x x =r ，()sin ,2sin b x x =r ，函数()f x a b =⋅r r （Ⅰ）求)(x f 的单调递增区间；（Ⅱ）若不等式]2,0[)(π∈≥x m x f 对都成立，求实数m 的最大值. 22.（本小题满分12分）设f (x )是定义在R 上的奇函数，且对任意实数x ，恒有f (x ＋2)＝－f (x )．当x ∈[0,2]时，f (x )＝2x －x 2.(1)求证：f (x )是周期函数；(2)计算f (0)＋f (1)＋f (2)＋…＋f (2 016)．23.（本小题满分13分）已知在锐角△ABC 中，向量p ＝(2－2sin A ，c os A ＋sin A )，q ＝(sin A －cos A,1＋sin A )， 且p 与q 是共线向量．(1)求A 的大小；(2)求函数y ＝2sin 2B ＋23B C COS -取最大值时，B 的大小． 24．（本小题满分13分）已知圆M 过两点A (1，－1)，B (－1，1)，且圆心M 在直线x ＋y －2＝0上．(1)求圆M 的方程；(2)设P 是直线3x ＋4y ＋8＝0上的动点，PA 、PB 是圆M 的两条切线，A 、B 为切点，求四边形PAMB 面积的最小值．长安一中2015---2016学年度第二学期第一次月考高一数学答题纸（实验班）二、填空题（本大题共5小题，每题5分，共25分，把答案填在题中横线上）16. ． 17. ． 18. ．19.． 20. ．三、解答题（本大题共4小题，共50分，解答应写出文字说明、证明过程或演算步骤．）21.（本小题满分12分）22.（本小题满分12分）23.（本小题满分13分）24.（本小题满分13分）。
陕西省西安市高一下学期第一次月考数学试题(解析版)
高一数学试题说明：1．本试卷共4页，考试时间100分钟，满分100分. 2．请将所有答案都涂写在答题卡上，答在试卷上无效.第I 卷（选择题）一、单项选择题：（本题共8小题，每小题3分，共24分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1. 在平行四边形中，为上任一点，则等于（） ABCD M ABAM DM DB -+ A.B.C.D.BC AB AC AD【答案】B 【解析】【分析】根据相反向量的意义及向量加法的三角形法则，化简可得答案． AM DM DB -+【详解】 AM DM DB -+ AM MD DB =++ AD DB AB =+=故选：．B 2. 对于任意的平面向量，下列说法正确的是（ ） ,,a b cA. 若且，则B. 若，且，则//a b //b c //a c a b a c ⋅=⋅0a ≠b c =C. 若且，则D.a b = b c = a c = ()()a b c a b c ⋅=⋅【答案】C 【解析】【分析】平面向量共线的传递性可得A 错误，由向量数量积的定义可判断B ，根据向量相等的概念可判断C ，根据数量积及共线向量的概念可判断D.【详解】对A ，若且，则当为零向量时，与不一定共线，即A 错误；//a b //b c b a c 对B ，若，则，a b a c ⋅=⋅ cos ,cos ,a b a b a c a c ⋅=⋅ 又，所以，0a ≠ cos ,cos ,b a b c a c = 因为与的夹角不一定相等，所以不一定成立，即B 错误；,b c a b c =对C ，若且，则，即C 正确；a b =b c =a c =对D ，因为与共线，与共线，()c a b ⋅ c ()a b c ⋅a 所以不一定成立，即D 错误.()()a b c a b c ⋅=⋅故选：C ．3. 内角的对边分别为，已知，则（ ） ABC A ,,A B C ,,a b c 222b c a bc +-=A =A.B.C.D.6π56π3π23π【答案】C 【解析】【分析】利用余弦定理求出，再求出即可.cos A A 【详解】,，，.222b c a bc +-= 2221cos 222b c a bc A bc bc +-∴===0A π<< 3A π∴=故选：C4. 已知边长为3的正，则（ ） 2ABC BD DC= A ，AB AD ⋅=A. 3B. 9C.D. 6152【答案】D 【解析】【分析】由数量积的运算律化简后求解【详解】由题意得，2212()3333AD AB BD AB BC AB AC AB AB AC =+=+=+-=+故，AB AD ⋅= 1233AB AB AB AC ⋅+⋅221233cos60633=⨯+⨯⨯︒=故选：D5. 在中，已知，且，则是（ ）ABC A ||||AB AC AB AC +=-sin 2sin cos A B C =ABC A A. 等腰三角形 B. 直角三角形 C. 等腰直角三角形 D. 等腰或直角三角形【答案】C 【解析】【分析】由两边平方得，由化简得，得||||AB AC AB AC +=- AB AC ⊥sin 2sin cos A B C =B C =为等腰直角三角形.ABC A 【详解】由得，所以，所以||||AB AC AB AC +=-()()22AB ACAB AC +=- 0AB AC ⋅= AB AC⊥，所以为直角三角形；ABC A 由得，sin 2sin cos A B C =()()sin πsin 2sin cos B C B C B C --=+=所以 ，所以， sin cos cos sin 2sin cos +=B C B C B C sin cos cos sin 0B C B C -=即，因为，所以，所以为等腰三角形； ()sin 0B C -=π<πB C --<0B C -=ABC A 综上，为等腰直角三角形. ABC A 故选：C6. 在中，已知，D 为BC 中点，则（ ） ABC A π2,3,3AB AC A ==∠=AD =A. 2B.C.D.【答案】D 【解析】【分析】根据边长和角先求出，根据D 为BC 中点，可知，两边同时平方，将AB AC ⋅u u u r u u u r()12AD AB AC =+ 数带入计算结果即可.【详解】解：因为，所以， π2,3,3AB AC A ==∠=1cos 2332AB AC AB AC A ⋅=⋅⋅=⋅⋅= 因为D 为BC 中点，所以,两边同时平方可得：()12AD AB AC =+，(()2211192469444AD AB AB =+⋅⋅=++=所以AD = 故选:D7. 己知向量均为单位向量，且．向量与向量的夹角为，则的最大值为,a b12a b ⋅= - a c b c - π6a c - （ ）A.B. 1C.D. 2【答案】D 【解析】【分析】设，，.从而得到等边三角形,进一步可得的轨迹是两段圆弧,画出OA a = OB b =OC c = OAB A C 示意图可知当AC 是所在圆(上述圆弧)的直径时,取得最大值|AC|，从而可解.A AB ||a c -【详解】向量,向量均为单位向量， 12a b⋅=,a b,.111cos ,2a b ∴⨯⨯<>= π,3a b ∴<>=如图，设.则是等边三角形. ,,OA a OB b OC c ===OAB A 向量满足与的夹角为, .c -a cbc -π6π6ACB ∠=∴因为点在外且为定值,C AB ACB ∠所以的轨迹是两段圆弧,是弦AB 所对的圆周角.C ACB ∠因此：当AC 是所在圆(上述圆弧)的直径时,取得最大值|AC|, A AB ||a c -在中,由正弦定理可得:ABC A . 2sin 30ABAC ︒==取得最大值2.|a c ∴- ∣故选：D【点睛】关键点睛：设，关键能够根据已知条件确定的轨迹是弦AB 所对的两段圆弧,从而确定当AC ,,OA a OB b OC c ===C 是所在圆(上述圆弧)的直径时,取得最大值|AC|，即可求解.A AB ||a c -8. 已知a ，b ，c 分别为三个内角A ，B ，C 的对边，若且，则ABC A (cos )a C C b c =+5a =的周长的最大值为（ ）ABC A A. 15 B. 16C. 17D. 18【答案】A 【解析】【分析】利用正弦定理，两角和公式及辅助角公式可得，然后根据余弦定理及基本不等式可得60A =︒，即得.10b c +≤【详解】由已知及正弦定理得，sin cos sin sin sin A C A C B C +=+∴， ()sin cos sin sin sin sin cos cos sin sin A C A C A C C A C A C C +=++=++，因为， sin cos sin sin A C A C C =+sin 0C ≠，即，因为， cos 1A A -=()1sin 302A -︒=3030150A -︒<-︒<︒所以，从而，3030A -︒=︒60A =︒由余弦定理得，即，2222cos a b c bc A =+-()222253b c bc b c bc =+-=+-又，2332b c bc +⎛⎫≤ ⎪⎝⎭∴，即， ()()22134b c bc b c +-≥+()21254b c ≥+∴，当且仅当时等号成立，从而， 10b c +≤5b c ==15a b c ++≤∴的周长的最大值为15. ABC A 故选：A.二、多项选择题：（本题共4小题，每小题3分，共12分，在每小题给出的选项中，有多项符合题目要求.全部选对的得3分，部分选对的得1分，有选错的符0分.）9. 在中，，则角B 的值可以是（ ） ABC A π10,6a c A ===A.B.C.D.π12π47π123π4【答案】AC 【解析】【分析】由已知结合正弦定理可求C ，然后结合三角形的内角和定理可求.【详解】∵， π10,6a c A ===由正弦定理可得 ，得 ， sin sin a c A C =10sin C =sin C =∵，∴， a c <A C <则或，由，则角或． π4C =3π4C =πB A C =--7π12=B π12B =故选：AC.10. 若向量满足，则（ ）,a b||||2,||a b a b ==+=A.B. 与的夹角为2a b ⋅=- a bπ3C. D. 在上的投影向量为(2)a a b ⊥-a b - b 12b r 【答案】BC 【解析】【分析】由模与数量积的关系求得，再根据数量积的性质确定与的夹角，判断向量垂直，求2a b ×=a b 解投影向量即可得结论.【详解】因为，所以||||2==r r a b a b +====则，故A 不正确；2a b ×=又，，所以，即与的夹角为，故B 正21cos ,222a b a b a b ⋅===⨯⋅0,πa b ≤≤ π,3a b = a b π3确；又，所以，故C 正确；2(2)24220a a b a a b ⋅-=-⋅=-⨯=(2)a a b ⊥- 又在上的投影向量为，故a b - b ()221cos ,2a b b b b a b b a b a b b a bb b ba b bb b-⋅⋅---⋅=-⋅=⋅=--⋅D 不正确. 故选：BC.11. 中，为上一点且满足，若为线段上一点，且（ABC A D AB 3AD DB =P CD AP AB AC λμ=+λ，为正实数），则下列结论正确的是（ ）μA.B.1344CD CA CB =+432λμ+=C. 的最大值为 D.的最小值为3 λμ112113λμ+【答案】AD 【解析】【分析】由题设结合三点共线可得，再应用基本不等式求、43AP AD AC λμ=+433λμ+=λμ的最值，利用向量加减、数乘的几何意义求的线性关系. 113λμ+,,CD CA CB【详解】由题设，可得，又三点共线， 43AP AD AC λμ=+,,D P C ∴，即，B 错误； 413λμ+=433λμ+=由，为正实数，，则，当且仅当时等号成立，故C 错λμ433λμ+=≥316λμ≤31,82λμ==误；，当且仅当时等号成1111111(3)(5)(5333333343λμλμλμλμμλ+=++=++≥+=32μλ=立，故D 正确；，又，14CD CB BD CB BA =+=+ BA BC CA =+ ∴，故A 正确.131()444CD CB BC CA CB CA =++=+故选：AD.12. 在中，若，下列结论中正确的有（ ） ABC A ::4:5:6a b c =A. B. 是钝角三角形sin :sin :sin 4:5:6A B C =ABC AC. 的最大内角是最小内角的2倍D. 若，则 ABC A 6c =ABC A 【答案】ACD 【解析】【分析】根据正弦定理，余弦定理逐一判断即可.【详解】根据正弦定理由，因此选项A 正确； ::4:5:6sin :sin :sin 4:5:6a b c A B C =⇒=设，所以为最大角，4,5,6a k b k c k ===C ，所以为锐角，因此是锐角三角形，2222221625361cos 022458a b c k k k C ab k k +-+-===>⋅⋅C ABC A 因此选项B 不正确；，显然为锐角，2222222536163cos 22564b c a k k k A bc k k +-+-===⋅⋅A，23cos 2cos 1cos cos 224C C C A =-⇒====因此有，因此选项C 正确； 22CA C A =⇒=由1cos sin 8C C =⇒===外接圆的半径为：D 正确，ABC A 112sin 2c C ⋅==故选：ACD【点睛】关键点睛：根据正弦定理、余弦定理是解题的关键.第II 卷（非选择题）三、填空题：（本题共6小题，每小题4分，共24分.）13. 已知向量，，当时，__________.(1,2)a =- (sin ,cos )b αα= a bA tan α=【答案】## 12-0.5-【解析】【分析】由向量平行可得，进而可求出结果.2sin cos -=αα【详解】由可得，，得，//a b 2sin cos -=αα1tan 2α=-故答案为：. 12-14. 向量的夹角为，且，则等于__________．a b ，π3||1,||2a b == ||a b - 【解析】【分析】由向量的数量积的定义可得，再由向量的平方即为模的平方，计算化简即可得到所求·1a b =值．【详解】向量，的夹角是，，，a bπ3||1a = ||2b = 则， π1||||cos 12132a b a b ==⨯⨯=AA 则22||()a b a b -=-，22212143a a b b =-+=-⨯+= A即有||a b -=15. 已知中，，若满足上述条件的三角形有两个，则的范围是__________． ABC A π,23A AB ==BC【答案】)2【解析】【分析】由已知可得,从而得解. sin A AB BC AB ⋅<<【详解】解：如图所示，作，交于点为，垂足为，若要满足题π3A ∠=,BC AB '=AD 'C BC AC '''⊥C ''意，则有， sin BC A AB BC AB BC '''=⋅<<=易知∴的范围是.2,BC BC '''==BC )2故答案为：)216. 在中，，，，则的面积为__________．ABC A 1AB =3BC =1AB BC ⋅=-ABC A【解析】【分析】根据平面向量的夹角公式可求得，从而可得到，再根据三角形的面积公式即可求解．cos B sin B 【详解】依题意可得，解得，()()=cos π=13cos =1AB BC AB BC B B ⋅⋅⋅-⨯⨯-- 1cos =3B又，所以， ()0,πB ∈sin B所以的面积为 ABC A 11sin 1322ABC S AB BC B =⋅⋅⋅=⨯⨯=A．17. 如图，某林场为了及时发现火情，设立了两个观测点B 和C ，在B 点处观测到C 的方位角为，B155︒点和C 点相距25千米．某日两个观测站都观测到了A 处出现火情，在B 点处观测到A 的方位角为125︒．在C 点处，观测到A 的方位角为，则观测站C 与火情A 之间的距离为________．80︒【解析】【分析】由正弦定理求解即可【详解】在中，，，ABC A 15512530ABC ∠=-=︒︒︒180********BCA ∠=︒-︒+︒=︒，，1803010545BAC ∠=︒-︒-︒=︒25BC =由正弦定理可得，即，sin sin AC BCABC BAC =∠∠25sin 30sin 45AC =︒︒所以， 25sin 30sin 45AC ⨯︒==︒所以观测站与火情之间的距离为千米 C A故答案为18. 如图，在平面四边形中，，，，若点ABCD AB BC ⊥AD CD ⊥60BCD ∠=︒CB CD ==为边上的动点，则的最小值为_______.M BC AM DM ⋅【答案】 214【解析】【分析】如图所示，以为原点，以所在的直线为轴，以所在的直线为轴，求出， ，B BA x BC y A D C 的坐标，根据向量的数量积和二次函数的性质即可求出．【详解】如图所示：以为原点，以所在的直线为轴，以所在的直线为轴，B BA x BC y 过点作轴，过点作轴，D DP x ⊥D DQ y ⊥∵，，，AB BC ⊥AD CD ⊥120BAD ∠=︒CB CD ==∴，，，，()00B ，()20A ，(0,C (D 设，则，，()0,M a ()2,AM a =- (3,DM a =-故，故答案为． (22121644AM DM a a a ⎛⋅=+=+≥ ⎝ 214【点睛】本题考查了向量在几何中的应用，考查了运算能力和数形结合的能力，属于中档题．四、解答题：（本题共4小题，共40分.解答应写出文字说明、证明过程或演算步骤.）19. 已知(2,4),(3,1)a b ==- （1）设的夹角为，求的值；,a b θcos θ（2）若向量与互相垂直，求k 的值．k + a b - a kb 【答案】（1） （2）【解析】【分析】（1）根据平面向量的夹角公式即可解出；（2）根据垂直的数量积表示及模长即可解出．【小问1详解】 ，()23412a b ⋅=⨯-+⨯=- ，a ==b ==因为，所以cos a b a b θ⋅=⋅⋅ cos a b a b θ⋅===⋅ 【小问2详解】因为向量与互相垂直，所以， a kb +r r a kb - ()()2220a kb a kb a k b +⋅-=-= 所以，即，解得：.222a k b= 22010k =k =20. 已知在△ABC 中，D 为边BC 上一点，，，． 3CD =23AC AD ==1cos 3CAD ∠=（1）求AD 的长；（2）求sinB ．【答案】（1）2；（2【解析】 【分析】(1)在中，利用余弦定理建立方程求解即可；ACD A (2)利用(1)的结论求出，再在中由正弦定理计算可求．cos C ABC A sin B 【小问1详解】依题意，在中，由余弦定理得，ACD A 2222cos CD AC AD AC AD CAD =+-⋅⋅∠即，解得； 2223313()2223AD AD AD AD =+-⋅⋅⋅2AD =【小问2详解】在中，由(1)知，由余弦定理可得， ACD A 3AC =2222223327cos 22339AC CD AD C AC CD +-+-===⋅⨯⨯则有，sin C ==在中，由正弦定理得． ABC A sin sin AC B C AB ===． sin B ∴=21. 在中，角A ，B ，C 的对边分别为a ，b ，c ，且__________．在ABC A①；tan tan tan tan A C A C +=②； 2ABCS BC =⋅A③. πcos cos 2b C B ⎛⎫-= ⎪⎝⎭这三个条件中任选一个填在横线上，补充完整上面的问题，并进行解答．（1）求角B 的大小；（2）若角B 的内角平分线交AC 于D ，且，求的最小值．1BD =4a c +【答案】（1） 2π3B =（2）9【解析】【分析】（1）若选①：根据两角和差正切公式化简已知等式可求得，由()tan A C +()tan tan B A C =-+可求得，进而得到；若选②：根据三角形面积公式和平面向量数量积定义可构造方程求得tan B B tan B ，进而得到；若选③：利用正弦定理边化角，结合诱导公式可求得，进而得到；B tan B B （2）根据，利用三角形面积公式化简可得，由ABC ABD BCD S S S =+△△△111a c+=，利用基本不等式可求得最小值. ()1144a c a c a c ⎛⎫+=++ ⎪⎝⎭【小问1详解】若选条件①，由得：， tan tan tan A C A C +-=)tan tan 1tan tan A C A C +=-， tan tan 1tan tan A C A C+∴=-()tan A C +=则，. ()()tan tan πtan B A C A C ⎡⎤=-+=-+=⎣⎦()0,πB ∈2π3B ∴=若选条件②，由得：，2ABC S BC =⋅△ sin cos ac B B =，则，. sin ∴=B B tan B =()0,πB ∈2π3B ∴=若选条件③，，则， πcos cos 2b C B ⎛⎫-= ⎪⎝⎭sin cos b C B =由正弦定理得：，sin sin cos B C C B =，，，则，()0,πC ∈ sin 0C ∴≠sin ∴=B B tan B =又，. ()0,πB ∈2π3B ∴=【小问2详解】，， ABC ABD BCD S S S =+A A A 12π1π1πsinsin sin 232323ac c BD a BD ∴=⋅+⋅，，， =+a c ac ∴+=111a c ac a c +∴=+=（当且仅当，即时取等()11444559a c a c a c a c c a ⎛⎫∴+=++=++≥+= ⎪⎝⎭4a c c a =23a c ==号），的最小值为.4a c ∴+922. 在中，内角A ，B ，C 的对边分别为a ，b ，c ，已知． ABC A 2cos (cos cos )A c B b C a +=（1）求A ；（2）若为锐角三角形，且的取值范围． ABC A a =223b c bc ++【答案】（1）π3（2）(]11,15【解析】【分析】（1）先利用正弦定理化边为角，再结合和差公式整理即可得的值，进而即可求解； cos A A （2）结合（1），先根据正弦定理得，，再根据余弦定理得，从而2sin b B =2sin c C =223b c bc +=+可得到，结合题意可得到的取值范围，从而确定的取值范22π378sin 26b c bc B ⎛⎫++=+- ⎪⎝⎭B π26B -围，再结合正弦型函数的性质即可求解．【小问1详解】根据题意，由正弦定理得()2cos (sin cos sin cos )2cos sin 2cos sin sin A C B B C A B C A A A+=+==，又在中，有，所以，ABC A ()0,πA ∈sin 0A ≠所以，所以． 1cos 2A =π3A =【小问2详解】结合（1）可得，， sin A =2ππ3B C A +=-=由，得，， a =2sin sin sin a b c A B C ===2sin b B =2sin c C =根据余弦定理有，得，2222cos a b c bc A =+-223b c bc +=+所以 222π334316sin sin 316sin sin 3b c bc bc B C B B ⎛⎫++=+=+=+- ⎪⎝⎭， 2π3cos 8sin 724cos 278sin 26B B B B B B ⎛⎫=++=+-=+- ⎪⎝⎭又为锐角三角形，则有，，得， ABC A π0,2B ⎛⎫∈ ⎪⎝⎭2ππ0,32B ⎛⎫-∈ ⎪⎝⎭ππ,62B ⎛⎫∈ ⎪⎝⎭所以，所以， ππ5π2,666B ⎛⎫-∈ ⎪⎝⎭π1sin 2,162B ⎛⎫⎛⎤-∈ ⎪ ⎥⎝⎭⎝⎦故． (]22π378sin 211,156b c bc B ⎛⎫++=+-∈ ⎪⎝⎭【点睛】关键点点睛：根据正弦定理，余弦定理将求的范围转化为求正弦型函数223b c bc ++的值域，结合题意得到的取值范围，再结合正弦型函数的性质是解答小问()π78sin 26f B B ⎛⎫=+- ⎪⎝⎭B （2）的关键．。
陕西西安一中13-14学年高二上第一次(10月)月考-数学.
西安市第一中学2013-2014学年度第一学期高二年级第一次月考数学试题一、选择题（共10小题，每小题4分，共40分．在每小题给出的四个选项中, 只有一项是符合题目要求的）1、若R c b a ∈,,，且b a >，则下列不等式一定成立的是（ ）A.．c b c a -≥+ B ．bc ac > C ．02>-ba c D ．0)(2≥-cb a2、 若240x -≤，则( )A. 02x ≤≤B. 20x -≤≤C. 22x -≤≤D. 2x ≤-或2x ≥3、若01,0<<-<b a ，则有( )A. 2ab ab a >>B. a ab ab >>2C. 2ab a ab >>D. a ab ab >>24、设21a x x =--，1b x =-，则a 与b 的大小关系为( )A. a b >B. a b =C. a b <D. 与x 的取值有关5、下列函数中，最小值为2的为 ( ) A. 1y x x =+ B. 1lg (110)lg y x x x=+<< C.x x y -+=33 D. )20(sin 1sin π<<+=x x x y 6、已知关于x 的不等式20(0)ax bx c a ++≥≠的解集是∅，则( )A. 20,40a b ac <-≥B. 20,40a b ac <-<C. 20,40a b ac >-≥D. 20,40a b ac >-<7、若实数x ，y 满足不等式组1,2,0,y x y x y +≤⎧⎪-≤⎨⎪≥⎩则y x z 2-=的最小值为（ ） （A ）27- （B ） 2- （C ） （D ） 258．设R y x ∈,，且x+y=5,则y x 33+的最小值为（ ）A ． 0B ． 36C ． 64D ．3189.已知,x y 满足422+4x y x y -≤-≤-⎧⎨≤≤⎩，则2x y -的取值范围是 ( ) A. []6,0- B. []6,1-- C. []5,1-- D. []5,0- 10、若不等式04)2(2)2(2<--+-x a x a 对任意实数x 均成立，则实数a 的取值范围是 （ ）A ．]2,2(-B ．]2,2[-C ．),2(+∞D ．]2,(-∞二、填空题（共6小题，每小题4分，共24分．）11、不等式3115<++x x 的解集是____________12、不等式0)9)(43(22<---x x x 的解集为____________13、不等式248>---x x 的解集为____________14、已知,,,236,a b c a b c ∈++=则22249a b c ++的最小值_____________ 15、某企业生产甲、乙两种产品，已知生产每吨甲产品要用A 原料3吨、B 原料2吨；生产每吨乙产品要用A 原料1吨、B 原料3吨。
陕西省西安市高一下学期第一次月考数学试卷
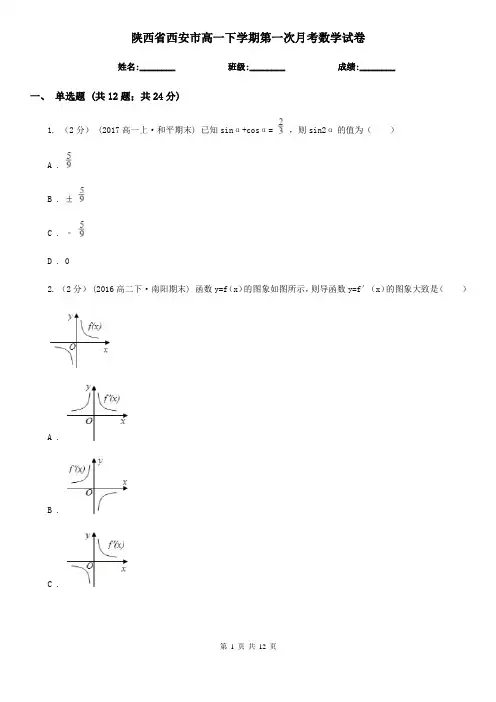
陕西省西安市高一下学期第一次月考数学试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分） (2017高一上·和平期末) 已知sinα+cosα= ，则sin2α的值为（）A .B . ±C . ﹣D . 02. （2分） (2016高二下·南阳期末) 函数y=f（x）的图象如图所示，则导函数y=f′（x）的图象大致是（）A .B .C .D .3. （2分） (2016高三上·黑龙江期中) 已知0＜x＜，sinx﹣cosx= ，存在a，b，c（a，b，c∈N*），使得（a﹣πb）tan2x﹣ctanx+（a﹣πb）=0，则2a+3b+c=（）A . 50B . 70C . 110D . 1204. （2分） (2016高二上·郴州期中) 已知变量x，y满足约束条件，则的取值范围是（）A .B .C . （﹣∞，3]∪[6，+∞）D . [3，6]5. （2分）(2016·青海) 已知函数在点（1，2）处的切线与的图像有三个公共点，则a的取值范围是（）A .B .C .D .6. （2分）已知两条不同直线l1和l2及平面，则直线的一个充分条件是（）A . 且B . 且C . 且D . 且7. （2分）直线与圆切于点，则的值为（）A . 1B . -1C . 3D . -38. （2分）已知一扇形的弧所对的圆心角为54°，半径r=20cm，则扇形的周长为（）A . 6π cmB . 60 cmC . （40+6π） cmD . 1 080 cm9. （2分）已知角的终边过点P(-4,3),则的值为（）A .B .C .D . 210. （2分） (2017高一上·定州期末) 函数的部分图象如图所示，若将图象上所有的点的横坐标缩短为原来的倍（纵坐标不变），得到函数的图象，则的解析式为（）A .B .C .D .11. （2分）(2017·武邑模拟) 设函数f（x）= ，若方程f（f（x））=a（a＞0）恰有两个不相等的实根x1 ， x2 ，则e •e 的最大值为（）A .B . 2（ln2﹣1）C .D . ln2﹣112. （2分）已知函数，若f（2）=f（﹣2），则k=（）A . 1B . -1C . 2D . -2二、填空题 (共4题；共6分)13. （1分） (2017高一上·吉林期末) 已知tanα=2，则sin2α+sinαcosα=________．14. （2分）已知函数，则f（x）的最小正周期为________；单调减区间为________．15. （1分） (2016高一上·徐州期末) 将函数f（x）=sinωx（ω＞0）的图象向右平移个单位后得到函数g（x）的图象，若对于满足|f（x1）﹣g（x2）|=2的x1 ， x2 ，有|x1﹣x2|min= ，则f（）的值为________．16. （2分） (2017高三上·石景山期末) 已知函数，①方程f（x）=﹣x有________个根；②若方程f（x）=ax恰有两个不同实数根，则实数a的取值范围是________．三、解答题 (共6题；共50分)17. （10分） (2016高一下·淄川期中) 已知向量，向量，函数f（x）= ．（1）求函数f（x）的单调递增区间；（2）将函数y=f（x）的图象上所有点向右平行移动个单位长度，得函数y=g（x）的图象，求函数y=g （x）在区间[0，π]上的值域．18. （10分） (2017高三上·邯郸模拟) 如图，在底面为矩形的四棱椎P﹣ABCD中，PB⊥AB．（1）证明：平面PBC⊥平面PCD；（2）若异面直线PC与BD所成角为60°，PB=AB，PB⊥BC，求二面角B﹣PD﹣C的大小．19. （5分）在直角坐标系xOy中，曲线C1的参数方程为（其中θ为参数），点M是曲线C1上的动点，点P在曲线C2上，且满足 =2 ．（Ⅰ）求曲线C2的普通方程；（Ⅱ）以原点O为极点，x轴的正半轴为极轴建立极坐标系，射线θ= 与曲线C1、C2分别交于A、B两点，求|AB|．20. （10分） (2016高一下·南市期末) 已知函数f（x）=（sinx+ cosx）2﹣2．（1）当x∈[0， ]时，求函数f（x）的单调递增区间；（2）若x∈[﹣， ]，求函数g（x）= f2（x）﹣f（x+ ）﹣1的值域．21. （5分）已知函数（1）求函数的单调区间；（2）求函数的值域．22. （10分） (2019高一上·郏县期中) 知函数（1）判断的奇偶性并给予证明；（2）求关于x的不等式的解集．参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共6分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共50分) 17-1、17-2、18-1、18-2、19-1、20-1、20-2、21-1、22-1、22-2、。
陕西省西安市第一中学2013-2014学年高一下学期第一次月考英语试题 Word版含答案
西安市第一中学2013-2014年度第二学期第一次月考高一年级英语试题一、语音知识（共5小题，每小题1分，满分5分）从每小题的A、B、C、D 四个选项中，找出其划线部分与所给单词的划线部分读音相同的选项。
1. origin A. design B. forgive C. gain D. digest2. steak A. scream B. bean C. break D. ahead3. award A. reward B. harvest C. starve D. barber4. birthday A. together B. gather C. breathe D. author5. sadness A. debt B. pineapple C. hostess D. penniless二、单选选择（共15小题，每小题1分，满分15分）6. Some festival are held to honour _____dead and also let people forget their work for ______while.A. / ; /B. the ; aC. a ; aD. a ; the7. “According to my research, neither your restaurants nor min e a healthy diet.” He said.A. offersB. offeringC. offerD. were offering8. No matter where she is, she makes _____a rule to go for a walk after lunch.A. him B this C. that D. it9. In the USA, Columbus Day is ______ of the arrival of Christopher Columbus in the new world.A. in memory ofB. in need ofC. in face ofD. in charge of10. The old pictures remind me of the happy times _____we spent together last year.A. whenB. 不填C. whereD. in which11. Wang Peng sat in his empty restaurant _____ very frustrated.A. feltB. to feelC. feelingD. feel12. ---Is Jack on duty today?---It ______be him. It’s his turn tomorrow.A. mustn’tB. won’tC. can’tD. needn’t13. A notice was _____in order to remind the students of the changed lecture time. A．looked up B．turned up C．brought up D．put up14. His first novel good reviews ever since it came out last month.A. receivesB. is receivingC. will receiveD. has received15. ---Henry, thank you so much for giving me a hand in time. ---______. A．That’s not Ok B. That’s right C. It doesn’t matter D. Don’t mention it16. You must come whenever you want and have_____ you like.A. whatB. whateverC. whichD. whichever17. As Li Fang _____ for home, he threw flowers and chocolates away.A. set offB. set upC. set aboutD. set aside18. Tom has grown up, so he is ___ enough to carry the heavy box .A. strongB. strongerC. much strongerD. the strongest19. The country, covered with cherry tree flowers, looks______ it is covered with pink snow.A. even ifB. likeC. as ifD. as20. The weather turned out to be sunny yesterday. I ______the trouble to carry my umbrella with me.A. should have takenB. could have takenC. needn’t have takenD. mustn’t have tak en三、完形填空：（共20小题，每小题1分，满分20分）Mark was walking home from school one day when he noticed the boy ahead of him had dropped all of the books. He was carrying, along with a baseball bat and several other things. Mark knelt down and helped the boy ___21___ these articles. 22 they were going the same way, he helped to carry some of them for him. As they walked, Mark 23 the boy’s name was Bill, that he 24 computer games, baseball and history, that he was having a lot of 25 with his other subjects and that he had just broken 26 with his girlfriend.They arrived at Bill’s home first and Mark was 27 in for a Coke and to watch some television. The afternoon passed 28 with a few laughs and some shared small talk, and then Mark went home. They 29 to see each other around school, had lunch together once or twice, and then both ended up from the same high school, Just three weeks before 30 ,Bill asked Mark if they 31 talk.Bill 32 him of the day years ago when t hey had first met. “Do you 33 wonder why I was carrying so many things home that day?” asked Bill. “You see, I 34 out my locker because I didn’t want to leave a mess(脏乱) 35 anyone else. I had planned to run away and I was going home to 36 my things. But after we spent some time together 37 and laughing, I realized that 38 I had done that, I would have 39 a new friend and missed allthe fun we would have together. So you see, Mark, when you picked up my books that day, you did a lot more. You 40 my life.”21．A．bring up B．set up C．turn up D．pick up 22．A．Although B．Since C．After D．Until 23．A．discovered B．realized C．said D．decided 24．A．played B．loved C．tried D．made 25．A．questions B．ideas C．doubt D.trouble26．A．up B．out C．off D．away 27．A．called B．helped C．invited D．allowed 28．A．peacefully B．willingly C．freely D．pleasantly 29．A．continued B．agreed C．forced D．offered 30．A．separation B．movement C．graduation D．vacation 31．A．would B．should C．could D．must 32．A．demanded B．reminded C．removed D．asked 33．A．ever B．usually C．even D．never 34．A．checked B．took C．cleaned D．put 35．A．over B．into C．for D．with36．A．find B．pick C．pack D．hold 37．A．talking B．playing C．reading D．watching 38．A．before B．if C．while D．as 39．A．forgotten B．passed C．left D．lost 40．A．helped B．recovered C．improved D．changed四、阅读理解（共4篇15个小题，每小题2分，满分30分）：第一节：阅读下列短文，根据短文内容，从各题的四个选项中选择一个最佳答案。
陕西省西安市第一中学2013-2014学年高一下学期第一次月考语文试题_Word版含答案
西安市第一中学2013-2014学年度第二学期3月份月考语文（必修三1—2单元）试题（本试卷共四个部分，满分100分，时间90分钟。
）一、基础知识和基本能力（共20分，其中1-5题，每小题2分，共10分；6题10分。
）1、下列一组句子选词填空完全正确的是：①“刚才，四老爷和谁生气呢？”我问。
“还不是和祥林嫂？”那短工（a.简洁b.直捷c.直接d.简捷）的说。
②但随后也就自笑，觉得（a.偶尔b.偶然c.间或d.随便）的事，本没有什么深意义，而我偏要细细推敲……③“我正要问你一件事”她那没有（a.精神b.神采c.光采d.精采）的眼睛忽然发光了。
④脸上瘦削不堪，黄中带黑，而且消尽了前（a.悲凉b.悲苦c.悲郁d.悲哀）的神色。
A、①a②a③b④aB、①d②a③d④dC、①c②b③d④bD、①d②a③a④d2、下列各组词语中，没有错别字的一组是（）A、潦倒侯爵峥嵘委曲求全B、寒喧砯崖马嵬放诞无礼C、桌帷放诞谪亲遍体鳞伤D、踌躇缪种杜撰雕梁画栋3、下列各句中加线的成语使用正确的一项是（）A、王熙凤一出场就与众不同：未见其人先闻其声，见其人时衣着美轮美奂，恍若神仙妃子。
从她的出场描写上，我们可以看出这个人的性格和爱好。
B、你自己荐她来，又合伙劫她去，闹得纷纷扬扬的，大家看了成个什么样子？C、这些人个个皆敛声屏气，恭肃严整得如此，这来者系谁，这样放诞无礼？D、直到指手画脚的将她和男人关在新房里，还是骂，阿呀呀，这真是……4、下列有关文学常识的表述，不正确的一项是( )A、我国唐代是诗歌发展的黄金时代，诗人众多，流派纷呈，除了李白、杜甫、白居易三位大诗人外，还有边塞派的王昌龄、岑参，山水田园诗派的孟浩然、高适、王维等。
B、李白，字太白，号青莲居士，盛唐诗坛的代表作家之一，是我国文学史上继屈原之后又一伟大的浪漫主义诗人，存诗九百九十余首。
其诗风格飘逸、豪放。
C、厄纳斯特•海明威，美国现代作家。
1954年获诺贝尔文学奖。
陕西省西安市第一中学2013-2014学年高一数学下学期期中(含解析)
某某市第一中学2013-2014学年度第二学期期中高一数学试题一．选择题：共10个小题，每小题4分，每题只有一个正确选项，共40分。
1.将-885°化为360(0360,αα+⋅≤<∈k k )Z 的形式是（ ） A.165(2)360-+-⨯ B.195(3)360+-⨯ C.195(2)360+-⨯ D.165(3)360+-⨯ 【答案】B【解析】将-885°化为360(0360,αα+⋅≤<∈k k )Z 的形式是195(3)360+-⨯。
2.若5-=θ,则角θ的终边在第（ ）象限 A.四 B. 三 C .二 D.一 【答案】D【解析】因为0157.3rad ≈,所以若5-=θ,则角θ的终边在第一象限。
3．下列函数中，周期为π，且在[π4，π2]上为减函数的是( )A ．y ＝sin(2x ＋π2)B ．y ＝cos(2x ＋π2)C.y ＝sin(x ＋π2) D ．y ＝cos(x ＋π2)【答案】A【解析】选项CD 的周期为2π，所以排除；又函数 y ＝cos(2x ＋π2)在[π4，π2]上为增函数，所以选A 。
4．sin 4π3＋tan 7π6的值为( )A.36 B ．－33 C ．－36 D.33【答案】C【解析】 sin 4π3＋tan 7π6=－sin 3π＋tan 6π=－36。
5.要得到函数x y cos 2=的图像，只要将函数)4sin(2π+=x y 的图像( )A.向左平移4π个长度单位，B. 向右平移4π个长度单位，C.向左平移8π个长度单位，D. 向右平移8π个长度单位【答案】A【解析】因为)2y x x π==+，所以要得到函数x y cos 2=的图像，只要将函数)4sin(2π+=x y 的图像向左平移4π个长度单位。
6.函数)32sin(π+=x y 的图像( )A.关于点)0,3(π对称，B.关于直线4π=x 对称， C.关于点)0,4(π对称，D.关于直线3π=x 对称【答案】A 【解析】由2,362k x k x k Z ππππ+==-+∈得，所以函数)32sin(π+=x y 的图像关于点)0,3(π对称。
陕西省西安市第一中学2014届高三下学期第二次模拟考试数学(文)试卷Word版含答案
西安市第一中学2013-2014学年度高三第二学期第二次模拟考试试题高三数学（文科）一、选择题：（本题共10小题，每小题5分，共计50分。
每小题只有一个选项符合题意）1、设集合若，则的范围是( )（A）（B）（C）（D）2、已知向量=(2，t), =(1，2)，若t=t1时，∥；t=t2时，⊥,则（）（A）t1=-4，t2=-1 （B）t1=-4，t2=1（C）t1=4，t2=-1（D）t1=4， t2=13、已知＜＜0，则（）(A)n＜m＜1 (B)m＜n＜1 (C)1＜m＜n (D)1＜n＜m4、.对某商店一个月内每天的顾客人数进行了统计，得到样本的茎叶图（如图所示），则该样本的中位数、众数、极差分别是（）A．46，45，56 B．46，45，53C．47，45，56 D．45，47，535、下面四个条件中，使a>b成立的充分而不必要的条件是（）(A) (B) (C) (D)6、复数,则（）.（A）（B）（C）（D）7、一个四面体ABCD的所有棱长都为，四个顶点在同一球面上，则此球的表面积为（）（A）（B）（C）（D）8、直线与圆没有公共点，则的取值范围是（）A． B． C． D．9、某三棱锥的三视图如图所示，该三棱锥的体积是（）A. B. 4C. 2D.10、对a，b∈R，记max{a，b}=函数f(x)=max{|x+1|，|x-2|}(x∈R)的最小值是（）(A)0 (B) (C) (D)3二、填空题：（本题共5小题，每小题5分，共计25分）11、双曲线的离心率为12、已知中，点的坐标分别为则的面积为13、若方程有实根，则实数的取值范围为14、设实数满足不等式组，则的最大值是15、（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）A ．（不等式选做题）若存在实数使成立，则实数的取值范围是B.（几何证明选做题）如图，在圆O 中，直径AB与弦CD 垂直，垂足为E ，，垂足为F ，若，，则C ．（坐标系与参数方程）直线与圆相交的弦长为三、解答题：（本题共6小题，要求写出必要的文字说明或推理过程）16、（本题12分）在中，角的对边分别为，已知，（1）求证：；（2）若，求的值.17、（本题12分）已知数列的前项和满足（1） 写出数列的前3项；（2） 求数列的通项公式.18、（本题12分）如图，四棱锥P －ABCD 的底面是正方形，PA ⊥底面ABCD ，PA ＝2，∠PDA=45，点E、F分别为棱AB、PD的中点．（1）求证：AF∥平面PCE；（2）求三棱锥C－BEP的体积．19、（本题12分）现有7道题，其中5道甲类题，2道乙类题，张同学从中任取2道题解答.试求：（1）所取的两道题都是甲类题的概率；（2）所取的两道题不是同一类题的概率.20、（本题13分）已知椭圆的离心率为,短轴一个端点到右焦点的距离为.(1)求椭圆的方程；(2)设不与坐标轴平行的直线与椭圆交于两点，坐标原点到直线的距离为，求面积的最大值.21、（本题14分）设函数.（Ⅰ）求函数的图像在点处的切线方程；（Ⅱ）求的单调区间；（III）若，为整数，且当时，，求的最大值．西安市第一中学2013-2014学年度高三第二学期第二次模拟考试试题高三数学（文科）一、选择题：（本题共10小题，每小题5分，共计50分。
陕西省西安市长安区第一中学高一数学下学期第一次月考试题(普通班,答案不全)
长安一中高一第二学期第一次月考数学试题一，选择题（每小题5分，共15小题75分） 1.函数x x y 21+-=的定义域为（ ）A.(]1,∞-B.[)+∞,0C.(][)+∞∞-,10,D.[]1,0 2．下列函数为偶函数的是( )A ．y ＝sin xB ．y ＝x 3C ．y ＝e xD ．y ＝ln x 2＋13.已知4.03=a ，2ln =b ，7.0log 2=c ，那么c b a ,,的大小关系为（ ）A.c b a >>B.c a b >>C.b a c >>D.b c a >> 4．函数x x x f cos )(-=在[0，＋∞)内( )A ．没有零点B ．有且仅有一个零点C ．有且仅有两个零点D ．有无穷多个零点5．如图，某几何体的主视图、左视图和俯视图分别是等边三角形、等腰三角形和菱形，则该几何体体积为( )．A ．．4 C ．．26．已知m ，n 是两条不同的直线，，β，γ是三个不同的平面，则下列命题正确的是( )．A ．若α⊥γ，α⊥β，则γ∥βB ．若m ∥n ，m ⊆α，n ⊆β，则α∥βC ．若m ∥n ，m ∥α，则n ∥αD ．若n ⊥α，n ⊥β，则α∥β 7、过两点A (2,)m -，B(m ，4)的直线倾斜角是45︒，则m 的值是（） A 1- B 3 B 1 D 3-8．已知圆C 与直线x －y ＝0及x －y －4＝0都相切，圆心在直线x ＋y ＝0上，则圆C 的方程为( )．A ．(x ＋1)2＋(y －1)2＝2B ．(x －1)2＋(y ＋1)2＝2C ．(x －1)2＋(y －1)2＝2D ．(x ＋1)2＋(y ＋1)2＝29． 已知扇形的周长是6 cm ，面积是2 cm 2，则扇形的圆心角的弧度数是 ( ) A ．1 B ．4 C ．1或4 D ．2或4 10． 角α的终边过点P (－1,2)，则sin α等于( )A.55B.255C ．－55D ．－25511． 已知0tan cos <θθ，那么θ是第几象限的角( )A ．第一或第二B ．第二或第三C ．第三或第四D ．第一或第四 12． cos629π的值为 ( ) A. 12 B ．－12C ．－32D ．3213． 把函数)25sin(π-=x y 的图像向右平移π4个单位，再把所得函数图像上各点的横坐标缩短为原来的12，所得的函数解析式为( )A ．)4310sin(π-=x yB ．)2710sin(π-=x yC ．)2310sin(π-=x yD ．)4710sin(π-=x y 14. 已知简谐运动f (x )＝A sin(ωx ＋φ) (|φ|<π2)的部分图像如图所示，则该简谐运动的最小正周期T 和初相φ分别为( )A ．T ＝6π，φ＝π6B ．T ＝6π，φ＝π3C ．T ＝6，φ＝π6D ．T ＝6，φ＝π315． 给出下列四个命题，其中不正确的命题为( )①若cos α＝cos β，则α－β＝2k π，k ∈Z； ②函数)32cos(π+=x y 的图像关于x ＝π12对称；③函数y ＝cos(sin x )(x ∈R)为偶函数； ④函数y ＝sin|x |是周期函数，且周期为2π. A ．①② B ．①④ C ．①②③ D ．①②④二，填空题（5小题，25分）16.函数)65ln()(2+-=x x x f 的单调增区间是______________．17.坐标原点到直线4x ＋3y=12的距离为 ． 18.))32ln(sin(π+=x y 的定义域为 ．19.已知31)12sin(=+πα，则)127cos(πα+的值为________． 20.设定义在区间⎪⎭⎫ ⎝⎛20π，上的函数x y cos 6=的图像与x y tan 5=的图像交于点P ,过点P 作x 轴的垂线，垂足为1P ，直线1PP 与函数x y sin =的图像交于点2P ，则线段21P P 的长为________．三，解答题（共4小题，50分） 21题（13分）(1)化简：)3sin()3cos()23sin()2cos()tan(αππαπααπαπ-----++；(2)已知)2cos()tan()2cos()sin()(x x x x x f +-+---=ππππ，求)331(π-f 的值． 22题(12分).函数1)sin()(++=ϕωx A x f (A >0，ω>0，22-πϕπ<<)在3π=x 处取最大值为3，其图像相邻两条对称轴之间的距离为π2，(1)求函数)(x f 的解析式； (2)设⎥⎦⎤⎢⎣⎡∈20x π，，)(x f 求的值域．23题（12分）.已知半径为5的圆C 的圆心在x 轴上，圆心的横坐标是整数，且与直线4x ＋3y －29＝0相切．(1)求圆C 的方程；(2)设直线ax －y ＋5＝0与圆C 相交于A ，B 两点，求实数a 的取值范围.24题（13分）.已知函数a x f x --=141)(. （1）求函数的定义域；（2）若()f x 为奇函数，求a 的值；（3）判断在()f x ),0(+∞上的单调性，并用定义证明.长安一中高一第二学期第一次月考数学试题答题纸二、填空题：（本大题共5小题，每小题5分，共25分）16. 17.18. 19.20.三、解答题：解答应写出文字说明，证明过程或演算步骤．21题（13分）（1）（6分）（2）（7分）22题（12分）23题（12分）24题（13分）。
2013-2014学年高一数学12月月考试题及答案(新人教A版 第274套)
西安市远东第一中学2013-2014学年度第一学期高一年级12月月考数学试题一、选择题：（每题4分，共40分）1．下列四个命题：①垂直于同一条直线的两条直线相互平行；②垂直于同一个平面的两条直线相互平行；③垂直于同一条直线的两个平面相互平行；④垂直于同一个平面的两个平面相互平行.其中错误的命题有…………………………………………………………………………（）A. 1个 B. 2个 C. 3 个 D. 4个2．在空间四边形各边上分别取四点，如果能相交于点，那么…………………………………………………………（）A．点不在直线上 B．点必在直线BD上C．点必在平面外 D．点必在平面内3．已知一个四棱锥的三视图如图所示，则该四棱锥的四个侧面中，直角三角形的个数是（）A．4 B．3C．2 D．14．三个平面把空间分成７部分时，它们的交线有…………………………（）A．１条 B．２条C．３条 D．１条或２条5.下列四个命题：①已知a、b、c三条直线,其中a、b异面, a∥c,则b、c异面。
②分别和两条异面直线都相交的两条直线一定是异面直线。
③过平面外一点有且只有一条直线与该平面垂直。
④过平面外一点有且只有一条直线与该平面平行。
其中正确的有……（）A.0个B. 1个C. 2个D. 3 个6．如图，在正方体中，分别为，，，的中点，则异面直线与所成的角等于（）A．45° B．60° C．90° D．120°7、有一个几何体的三视图及其尺寸如下（单位cm）,则该几何体的表面积及体积为（）A.24πcm2，12πcm3B.15πcm2，12πcm3C.24πcm2，36πcm3D.以上都不正确8．经过平面外两点与这个平面垂直的平面……………………………………………（） A．只有一个 B．至少有一个 C．可能没有 D．有无数个9. 若为一条直线，，，为三个互不重合的平面，给出下面三个命题：①，//，则//；②，，则；③，，则. ④，，则。
陕西省西安市第一中学2014-2015学年高一下学期期中考试数学试卷
陕西省西安市第一中学2014-2015学年高一下学期期中考试数学试卷西安市第一中学2014-2015学年度第二学期期中考试高一数学试题一、选择题：（每小题3分，共36分。
每道题只有一个正确答案，请将正确答案填涂在答题纸的相应位置。
）1、下列命题中正确的是（）A 、第一象限角必是锐角B 、终边相同的角必相等C 、相等的角终边必相同D 、不相等的角其终边必不相同2、数列0，1，0，-1，0，1，0，-1，…的一个通项公式是（）A 、21)1(+-nB 、cos 2n πC 、(1)cos 2n π+D 、(2)cos 2n π+ 3、集合{|}{|}2442k k M x x k Z N x x k Z ππππ==+∈==+∈，，，，则（） A 、M ?N B 、M ?N C 、M =N D 、φ=N M4、若a,b,c 成等比数列，m 是a,b 的等差中项，n 是b,c 的等差中项，则=+n c m a ( )A 、1B 、2C 、3D 、45、已知A 、B 、C 为三角形的三个内角，则下列各式中错误的是（）A 、()sin sin C A +B = B 、()cos cosC B +=-AC 、()tan tan C A +B =D 、sin cos 22C A +B = 6、已知等比数列{}n a 的公比13q =-，则13572468a a a a a a a a ++++++等于( ) A 、13- B 、3- C 、13 D 、3 7、已知1sin()63πα+=，则cos()3πα-的值为（）A 、12B 、12-C 、13D 、13-8、设{}n a 是等差数列，若273,13a a ==,则数列{}n a 前8项的和为( )A 、56B 、64C 、80D 、1289、要得到函数)42cos(π-=x y 的图像只需将2sin x y =图像（） A 、向左平移2π个单位 B 、向右平移 2π个单位≠ ≠C 、向左平移4π个单位D 、向右平移 4π个单位10、函数y=sin(4π-2x)的增区间是（） A 、[ k π-83π, k π+8π] （k z ∈） B 、[ k π+8π, k π+85π] （k z ∈） C 、[ k π-8π, k π+83π] （k z ∈） D 、[ k π+83π, k π+87π] （k z ∈） 11、已知等比数列{}n a 的公比为2, 前4项的和是1, 则前8项的和为（）A 、15B 、17C 、19D 、2112、若θ是直线l 的倾斜角，且sin cos θθ+=l 的斜率为（） A 、12- B 、12-或－2 C 、12或2 D 、－2 二、填空题：（每小题4分，共20分）13、若数列{}23n mn --是单调递增数列，则实数m 的取值范围是14、若3n f n π=()sin ，则1232015f f f f ++++()()()(）= 15、若-1、a 、b 、c 、-16成等比数列，则b=16、方程x=sinx 的解的个数为17、若x ，y ，z 成等差数列且公差不为0，xy ，yz ，zx 成等比数列，则等比数列xy ，yz ，zx 的公比为__ __三、解答题：（共44分，要求写出必要的推理过程）18、（本小题10分）扇形的周长是20，当扇形的圆心角为多少时扇形的面积最大。
陕西省西安市第一中学2013-2014学年高一下学期第一次月考物理试题 Word版含答案
西安市第一中学2013—2014学年度高一第二学期3月考试高一年级物理试题一、选择题：（共计58分。
1-14题为单选题，每题3分，；15-18为多选题，每题有一个以上的答案，全部选对得4分，少选得2分，不选或选错得0分。
）1.关于曲线运动，下列说法正确的是( )A.物体做曲线运动的速度方向时刻改变，故曲线运动不可能是匀变速运动B.物体只有受到一个方向时刻改变的力的作用才可能做曲线运动C.物体在一恒力作用下不可能做曲线运动D.曲线运动都是变速运动2．要想在最短的时间内渡过一条河流，则小船的船头应该（）A．垂直指向对岸 B．斜指向上游方向C．斜指向下游方向 D．不知水流速度无法判断3.一架飞机水平匀速飞行．从飞机上每隔l s释放一个铁球，先后释放4个，若不计空气阻力，从地面上观察4个小球( )A.在空中任何时刻总是排成抛物线，它们的落地点是等间距的B.在空中任何时刻总是排成抛物线，它们的落地点是不等间距的C.在空中任何时刻总在飞机正下方，排成竖直的直线，它们的落地点是等间距的D.在空中任何时刻总在飞机的正下方，排成竖直的直线，它们的落地点是不等间距的。
4．物体在平抛运动过程中，在相等的时间内，下列哪个量是相等的？（） A．位移 B．路程 C．平均速度 D．速度的变化量5.小球在离地面高为h处，以初速度v水平抛出，球从抛出到着地，速度变化量的大小和方向为( )，方向竖直向下，方向斜向下6.在高处以初速度v水平抛出一石子，当它的速度由水平方向变化为与水平方向成θ角时，石子水平方向运动的位移是( )A.2sinvgθB.2cosvθC.2tanvgθD.2tanvgθ7.如图所示，一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上.物体与斜面接触时速度与水平方向的夹角φ满足( )A.φ＝2θB.tan φ＝cotθC.tan φ＝tan θD.tan φ＝2tan θ8．物体做平抛运动，落到水平地面时，它的速度方向与水平方向的夹角θ的正切tan θ随时间的变化图象是下图中的（）9.如图所示，相对的两个斜面，倾角分别为37°和53°，在顶点两个小球A、B 以同样大小的初速度分别向左、向右水平抛出，小球都落在斜面上，若不计空气阻力，则A、B两个小球运动时间之比为( )A.1∶1B.4∶3C.16∶9D.9∶1610．关于匀速圆周运动的说法中，正确的是（）A．在相等时间内发生的位移总是相同的B．由于速度大小不变，故它属于匀速运动 C．匀速圆周运动时的角速度大小是不变的D．由于匀速圆周运动时的角速度是不变的，故线速度也不变。
陕西省西安市高一数学下学期第一次月考试题(有答案)
陕西省西安市高一数学下学期第一次月考试题分值： 100分 时间： 100分钟一、选择题（本题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．完成下列两项调查：①一项对“小彩旗春晚连转四小时”的调查中有10 000人认为这是成为优秀演员的必经之路，有9 000人认为太残酷，有1 000人认为无所谓.现要从中随机抽取200人做进一步调查.②从某中学的15名艺术特长生中选出3名调查学习负担情况，宜采用的抽样方法依次是（ ） A ．①简单随机抽样，②系统抽样 B ．①分层抽样，②简单随机抽样 C ．①系统抽样，②分层抽样 D ．①②都用分层抽样 2．根据《中华人民共和国道路交通安全法》规定：车辆驾驶员血液酒精浓度在20～80 mg/100 mL(不含80)之间，属于酒后驾车，处暂扣一个月以上三个月以下驾驶证，并处200元以上500元以下罚款；血液酒精浓度在80 mg/100 mL(含80)以上时，属醉酒驾车，处十五日以下拘留和暂扣三个月以上六个月以下驾驶证，并处500元以上2 000元以下罚款．据《法制晚报》报道，2009年8月15日至8月28日，全国查处酒后驾车和醉酒驾车共28 800人，如图是对这28 800人血液中酒精含量进行检测所得结果的频率分布直方图，则属于醉酒驾车的人数约为 ( )．A ．2 160B ．2 880C ．4 320D ．8 6403．下列说法正确的是 ( )．A ．任何事件的概率总是在(0，1)之间B ．频率是客观存在的，与试验次数无关C ．概率是随机的，在试验前不能确定D ．随着试验次数的增加，频率一般会越来越接近概率4四种正确的是( )．A ．蓝白区域大B ．红黄区域大C ．一样大D ．由指针转动圈数决定5．从1、2、3、4、5、6这6个数字中，一次性任取两数，两数都是偶数的概率是 ( )． A.12B.13C.14D.156．如果执行下面的算法框图，输入x ＝－2，h ＝0.5，那么输出的各个数的和等于( )．A．3 B．3.5 C．4 D．4.57．已知直线y＝x＋b，b∈[－2，3]，则直线在y轴上的截距大于1的概率为( )．A.15B.25C.35D.458. 如图是根据某校10位高一同学的身高(单位：cm)画出的茎叶图，其中左边的数字从左到右分别表示学生身高的百位数字和十位数字，右边的数字表示学生身高的个位数字，从图中可以得到这10位同学身高的中位数是( )．A．161 cm B．162 cm C．163 cm D．164 cm9．如图所示是一样本的频率分布直方图，则由图形中的数据，可以估计众数与中位数分别是 ( )．A．12.5 13B．12.5 12.5C．13 12.5D．13 1310. 甲、乙两位同学在高三的5次月考中数学成绩统计如茎叶图所示，若甲、乙两人的平均成绩分别为x甲，x乙，则下列叙述正确的是( )．A．x甲>x乙；乙比甲成绩稳定 B．x甲>x乙；甲比乙成绩稳定C．x甲<x乙；乙比甲成绩稳定 D．x甲<x乙；甲比乙成绩稳定二、填空题（本题共4小题，每小题4分，共16分)11、某鱼贩一次贩运草鱼、青鱼、鲢鱼、鲤鱼及鲫鱼分别为80条、2040条、20条，现从中抽取一个容量为20抽取样本，则抽取的青鱼与鲤鱼共有______条．12、如右图，面积为4的矩形ABCD中有一个阴影部分，若往矩形ABCD个点，落在矩形ABCD的非阴影部分中的点数为400个，试估计阴影部分的面积为。
陕西省西安市第一中学2016-20017学年高一上学期第一次月考数学试题
西安市第一中学2016～2017学年度第一学期月考高一数学试题一、选择题（每小题3分，共30分）1.已知集合，则集合（）A. B. C. D.2.如图所示,是全集,A, B是U的子集,则图中阴影部分所表示的集合是( )A. B. C. D.3.设全集,集合,,则=( )A. B. C. D.4.已知函数在区间上是减函数,则实数的取值范围是( )A. B. C. D.5.下列各组函数中,表示同一函数的一组是( )A. B.C.D.6.已知两个函数和的定义域和值域都是.其定义如右表:填写最后一个表格,其三个数依次为( )A.3,1,2B.2,1,3C.1,2,3D.3,2,17.化为分数指数幂结果是( )A. B. C. D.8.下列函数为偶函数的是( )A. B. C. D.9.已知函数＝x2＋bx＋c且，则()A．f (1)> c >f (－1) B．f (1) < c < f (－1)C．c > f (－1) > f (1) D．c < f (－1) < f (1)10.若一系列函数的解析式相同,值域也相同,但其定义域不同,则称这些函数为“同族函数”,那么解析式为,值域为的“同族函数”共有( )个 A.2 B.4 C.8 D.9二、填空题（每小题3分，共18分）11.设集合,则集合U的子集的个数是__________. 12．设集合，则集合等于___________. 13.函数的图像向左、向下分别平移2个单位，得到的图像，则函数_____________.14.已知函数则的最大值与最小值的差为_______.15.函数在上的最大值与最小值的和为-3，则函数在上的最小值是___________.16.设是方程的两个根，则=______.西安市第一中学2016～2017学年度第一学期月考高一数学答题纸题号 1 2 3 4 5 6 7 8 9 10 答案二、填空题（每小题3分，共18分）11. 12. 13.14．15. 16.三、解答题（共52分，解答应写出文字说明,证明过程或演算步骤)17.(本题满分10分)已知全集，，求：⑴；⑵；⑶；⑷18.(本题满分10分)已知点在幂函数的图像上,点在幂函数的图像上.⑴求出幂函数及的解析式；⑵在同一坐标系中画出及的图像；⑶观察⑵中的图像，写出当时，x的取值范围（不用说明理由）.19.(本题满分10分)已知函数是定义在R上的奇函数,且在区间上单调递减.（1）写出在R上的单调性（不用证明）；（2）若,请求出实数的取值范围.20.(本题满分10分)已知函数是常数)是奇函数,且满足.⑴求的值；⑵用定义证明在区间上的单调性；⑶试求函数在区间上的最小值.21.（本题满分12分）已知函数定义在上.⑴当时,求的最大值和最小值；⑵求实数的取值范围,使在上具有单调性；⑶求的值域.高一数学试题（2016-10-15）一、选择题（每小题3分，共30分）1.已知集合，则集合（）A. B. C. D.2.如图所示,是全集,A,B是U的子集,则图中阴影部分所表示的集合是( )A. B. C. D.3.设全集,集合,,则=( )A. B. C. D.4.已知函数在区间上是减函数,则实数的取值范围是( )A. B. C. D.5.下列各组函数中,表示同一函数的一组是( )A. B.C. D.6.已知两个函数和的定义域和值域都是.其定义如右表:填写最后一个表格,其三个数依次为( )A.3,1,2B.2,1,3C.1,2,3D.3,2,17.化为分数指数幂结果是( )A. B. C. D.8.下列函数为偶函数的是( )A. B. C. D.9.已知函数＝x2＋bx＋c且，则()A．f (1)> c >f (－1) B．f (1) < c < f (－1)C．c > f (－1) > f (1) D．c < f (－1) < f (1)10.若一系列函数的解析式相同,值域也相同,但其定义域不同,则称这些函数为“同族函数”,那么解析式为,值域为的“同族函数”共有( )个A.2B.4C.8D.9二、填空题（每小题3分，共18分）11.设集合,则集合U的子集的个数是__________. 12．设集合，则集合等于___________. 13.函数的图像向左、向下分别平移2个单位，得到的图像，则函数_____________.14.已知函数则的最大值与最小值的差为_______.15.函数在上的最大值与最小值的和为-3，则函数在上的最小值是___________.16.设是方程的两个根，则=______.一、选择题（每小题3分，共30分）题号 1 2 3 4 5 6 7 8 9 10 答案 D B C A B D B C B D二、填空题（每小题3分，共18分）11. 4 12. 13.14． 4 15. 0 16. 4.5三、解答题（共52分，解答应写出文字说明,证明过程或演算步骤)17.(本题满分10分)已知全集，，求：⑴；⑵；⑶；⑷答案：（1）；（2）；（3）；（4）。
陕西省西安市第一中学2013-2014学年高一下学期第一次月考生物试题 Word版含答案
西安市第一中学2013-2014学年度（下）第一次月考高一年级生物试题说明：１、本试卷包括第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。
卷面满分为100分。
考试时间为60分钟。
２、考生请将第Ⅰ卷选择题的正确选项填在答题纸的答题框内，第Ⅱ卷直接答在试卷上。
考试结束后，只收答题纸。
第Ⅰ卷（选择题共60分）一、选择题(每题只有一个选项符合题意。
每小题2分，共60分)1．下列属于相对性状的是（）A．玉米的黄粒和圆粒 B．家鸡的长腿和毛腿C．绵羊的白毛和黑毛D．豌豆的高茎和豆荚的绿色2．羊的毛色白色对黑色为显性，两只杂合白羊为亲本，接连生下了3只小羊是白羊，若它们再生第4只小羊，其毛色（）A．一定是白色的B．是白色的可能性大C．一定是黑色的D．是黑色的可能性大3．基因型为Aa的水稻自交后，子一代中的纯合体占其总数的（）A．25% B．50% C．75% D．100%4．将具有一对等位基因的杂合体，连续自交3次，在F3代中纯合体的比例为（）A．1/8 B．7/8 C．7/16 D．9/165．采用下列哪一组方法，可以依次解决①～④中的遗传学问题（）①鉴定一只白羊是否纯种②在一对相对性状中区分显隐性③不断提高抗病小麦的纯合度④检验杂种F1的基因型A．杂交、自交、测交、测交 B．测交、杂交、自交、测交C．测交、测交、杂交、自交 D．杂交、杂交、杂交、自交6. 某个体的基因型为AABbDdeeFf，这些基因分别位于5对同源染色体上，问此个体自交，F1中可能的基因型及表现型种类数：（）A．基因型9种，表现型8种 B．基因型16种，表现型9种C．基因型4种，表现型8种 D．基因型27种，表现型8种7．下列细胞中含有同源染色体的是（）①体细胞②初级精母细胞③次级卵母细胞④精子⑤精原细胞⑥受精卵A.①②⑤B.①②⑥C.①②③④D.①②⑤⑥8．一个有色盲儿子的正常女人，她的父母的基因型不可能是（）A.X B Y，X B X BB.X B Y，X B X bC.X b Y，X B X BD.X b Y，X B X b 9．用两个圆形南瓜做杂交实验，子一代均为扁盘状南瓜。
陕西省西安市重点高一下学期第一次月考数学试题(解析版)
高一下学期第一次月考数学试题一、单选题1．已知向量，，则（ ） ()2,1AB =-()1,3BC =- AC = A ．3 B ．4C ．5D ．6【答案】C【分析】由题知，进而求模即可.()3,4AC =-【详解】解：由题意可得. ()3,4AC AB BC =+=- 5=故选：C2．下列说法正确的是（ ）A ．若，则 a b =r r a b =±B ．零向量的长度是0C ．长度相等的向量叫相等向量D ．共线向量是在同一条直线上的向量 【答案】B【分析】根据向量的相关概念逐一判断即可.【详解】A ：仅表示与的大小相等，但是方向不确定， a b =r r a b故未必成立，所以A 错误； a b =±B ：根据零向量的定义可判断B 正确；C ：长度相等的向量方向不一定相同，故C 错误；D ：共线向量不一定在同一条直线上，也可平行，故D 错误. 故选：B.3．已知向量，则（ ） (2,1)(2,4)a b ==-，a b -r r A ．2 B ．3C ．4D ．5【答案】D【分析】先求得，然后求得.a b -a b -r r 【详解】因为，所以. ()()()2,12,44,3a b -=--=- 5-= a 故选：D4．已知平面向量，，若，则实数（ ） (,1)a x →=(1,2)b →=//a b →→x =A ． B ．5C ．D ．2-125-【答案】C【分析】根据共线向量的坐标表示求解即可. 【详解】，，，(,1)a x →= (1,2)b →=//a b →→， 2110x ∴-⨯=解得， 12x =故选：C5．如图，在矩形中，，，为的中点，与交于点，则ABCD AB a = AD b = M CD BD AM N MN =（ ）A ．B ．C ．D ． 1163a b --1163a b -1163a b +1163a b -+【答案】A【分析】结合平面图形的几何性质以及平面向量的线性运算即可求出结果. 【详解】因为矩形，所以，所以，所以,又因为为ABCD //AB CD MND ANB DN DM NB AB=M CD 的中点，所以，即，因此，从而1122DM DC AB ==12DN DM NBAB ==12DN NB =，又因为，，()111111232363MN MD DN DB DA AB AB AB AB AD +=-+=-++=-=-AB a = AD b = 所以，1163M a b N =-- 故选：A.6．在中，若，则的形状为（ ） ABC ||AB AC AB AC ==-ABC A ．等边三角形 B ．等腰三角形 C ．直角三角形 D ．等腰直角三角形【答案】A【分析】根据向量的减法法则可得，由三边相等关系即可得出结果. AB AC CB -=【详解】因为，，AB AC CB -= ||AB AC AB AC ==-所以， AB AC CB == 所以为等边三角形． ABC 故选：A7．向量，则与的夹角为（ ） ()()1,1,1,0a b ==- a bA ．B ．C ．D ．6π4π34π23π【答案】C【分析】直接由向量夹角的坐标运算求解即可.【详解】由题意得：与的夹角为. cos ,a = a b 34π故选：C.8．已知的内角的对边分别为，若，，，则为（ ） ABC ,,A B C ,,a b c a =2b =60A =︒B A ．60° B ．60°或120° C ．30° D ．30°或150°【答案】C【分析】由正弦定理可得，即可得解. 1sin 2B =【详解】在中，，，， ABC a =2b =60A =︒所以由正弦定理得， 4sin sin b a B A ===所以， 1sin 42b B ==又，所以. ()0,120B ∈︒︒30B =︒故选：C.【点睛】本题考查了正弦定理解三角形的应用，考查了运算求解能力，属于基础题. 9．在中，角所对的边分别为，若，则（ ） ABC ,,A B C ,,a b c 22()a b c ab +-=C =A ． B ．或 6π3π23πC ．D ．或23π6π56π【答案】C【分析】化简得，再由余弦定理计算，即可求得答案. 222a b c ab +-=-cos C 【详解】由得，，22()a b c ab +-=222a b c ab +-=-由余弦定理得，2221cos 222a b c ab C ab ab +--===-因为，所以. ()0,C π∈23C π=故选：C10．已知为实数，向量，，，若，则（ ） x (1,2)a =- (,1)b x =- 2c a b =+b c ⊥ x =A ．或 B ．或C ．或D ．或133-1-3-11-3【答案】D【分析】利用向量坐标及向量垂直关系建立方程求参数.【详解】由，，得，(1,2)a =- (,1)b x =- 2(2,3)c a b x =+=-又，则有，b c ⊥(2)(1)30x x -+-⋅=即，解得或, 2230x x --==1x -3故选:D .11．在中，，，则外接圆的半径为（ ） ABC60A =︒BC =ABC A ．1 BCD ．2【答案】A【分析】利用正弦定理运算求解.【详解】由正弦定理，则， 2sin aRA ==1R =故外接圆的半径为1. ABC 故选：A.12．河水的流速为2，一艘小船想沿垂直于河岸方向以10的速度驶向对岸，则小船的静m /s m /s 水速度为（ ） A ．10 B ．C ．D ．12m /s /s /s m /s 【答案】B【分析】根据题意，得到，结合向量的运算，即可求解. 211,0ννννν=-⋅=【详解】设河水的流速为，小船在静水中的速度为，船的实际速度为，1v 2v v 则，，所以，112,10,v v v v ==⊥12ννν=+ 211,0ννννν=-⋅=），即小船在静水中的速度大小为.=/m s /)m s 故选：B.二、填空题13．在中， 分别是内角A ，B ，C 所对的边，若，则ABC a b c ，，sin :sin :sin 2:3:4A B C =_____．cos A =【答案】/0.875 78【分析】由正弦定理得三边之比，再用余弦定理求解.cos A 【详解】因为，由正弦定理得，sin :sin :sin 2:3:4A B C =::2:3:4a b c =设， 234(0)a k b k c k k ===>，，，由余弦定理得，222222291c 6472234s 8o b c a k k k bc A k +-+-===⨯⨯故答案为：7814．已知向量，且，则实数__________.()()3,1,1,2a b ==-()()a b a b λ-+∥ λ=【答案】1-【分析】首先求出的坐标，然后根据向量共线的坐标表示可建立方程求解. ,a b a b λ-+【详解】由题意得，因为，所以()()2,3,3,12a b a b λλλ-=+=+-()()a b a b λ-+∥ ，解得.()()21233λλ-=+1λ=-故答案为：1-15．已知向量，则在方向上的投影向量的模长是___________．(1,3),(2,4)a b ==-b a【分析】根据数量积、模的坐标表示求出、，再根据求出在方向上的投影向a b ⋅ a r 1a b a a a ⋅⋅b a量，从而求出其模；【详解】解：因为，所以，(1,3),(2,4)a b ==-()123410a b ⋅=⨯+⨯-=-，a ==所以在方向上的投影向量为， b a )()11,31,3a b a a a⋅⋅==--；=16．如图，1kg 的重物在两根细绳的支持下处于平衡状态，已知两根细绳与水平线分别成30°与60°角，则两根细绳受到的拉力分别为_____．（取g =10m/s 2）【答案】；5N 【分析】根据受力平衡的知识进行分解，结合三角函数求解.【详解】如图，设左右两根绳子的拉力大小分别为， 12F F ，由受力平衡可知：，10N OM '=所以， 12sin 305N cos30F OM F OM ''==== ，故答案为：；5N三、解答题17．如图，已知平行四边形ABCD 的三个顶点B ､C ､D 的坐标分别是（-1，3）､（3，4）､（2，2），(1)求向量BC ； (2)求顶点A 的坐标.【答案】(1) ()4,1BC = (2) ()2,1-【分析】（1）由点B ､C 的坐标即可求解的坐标；BC（2）设顶点A 的坐标为，由四边形ABCD 为平行四边形，有，从而即可求解. (),x y BC AD =【详解】（1）解：因为点B ､C 的坐标分别是（-1，3）､（3，4），所以； ()()()3,41,34,1BC =--=u u u r（2）解：设顶点A 的坐标为，(),x y 因为四边形ABCD 为平行四边形，D 的坐标是（2，2）， 所以，即，BC AD =()()4,12,2x y =--所以，解得，2421x y -=⎧⎨-=⎩21x y =-⎧⎨=⎩所以顶点A 的坐标为.()2,1-18．已知，.3a =4b = (1)若与的夹角为，求；a b60︒()2a b a +⋅ (2)若与不共线，当为何值时，向量与互相垂直？ a b k a kb + a kb -【答案】(1) 21(2)34k =±【分析】（1）结合向量数量积运算与运算律计算求解即可；（2）根据解方程即可得答案.()()0a kba kb +-=【详解】（1）解：()21229234212a b a a b a +⋅=+⋅=+⨯⨯⨯= （2）解：∵向量与互相垂直，a kb + a kb -∴，整理得，又，，()()0a kba kb +-= 2220a k b -= 3a =4b = ∴，解得.29160k -=34k =±∴当时，向量与互相垂直.34k =±a kb + a kb -19．在中，角A ，B ，C 的对边分别为a ，b ，c ，且． ABC a b c >>2sin 0b C -=（1）求角B 的大小；（2）若，，求c ． b =2a =【答案】(1) ．(2) ．3B π=1c =【分析】（1）利用正弦定理将边化成角，即可求得角； B（2）把，代入，化简后根据一元二次方程的解法求出2a =b =3B π=2222cos b a c ac B =+-c的值．【详解】解：（1， 2sin 0b C -=． 2sin sin 0C B C -=因为，所以， 0C π<<sin 0C ≠所以 sin B =因为，且， 0B π<<a b c >>所以．3B π=（2）因为，b =2a =所以由余弦定理，2222cos b a c ac B =+-得，2214222c c =+-⨯⨯即． 2210c c -+=所以．1c =【点睛】本题考查正弦定理、余弦定理的应用，特殊角的三角函数值，熟练掌握公式并会应用是解题的关键，属于基础题．20．已知两个非零向量与不共线，，，． a b 2OA a b =- 3OB a b =+ 5OC ka b=+ （1）若，求k 的值； 20OA OB OC -+=（2）若A ，B ，C 三点共线，求k 的值． 【答案】（1）；（2）. 3k =-12k =【解析】(1)根据向量的计算求解即可.(2)根据A,B,C 三点共线可得,再根据系数的关系求解即可.AC AB λ=【详解】（1）∵,∴.22(2)35(3)0OA OB OC a b a b ka b k a -+=---++=+=3k =-（2）由题意知,.4AB OB OA a b =-=-+ (2)6AC OC OA k a b =-=-+∵A,B,C 三点共线,∴设,即,∴解得.AC AB λ= (2)64k a b a b λλ-+=-+ 2,64,k λλ-=-⎧⎨=⎩12k =【点睛】本题主要考查了向量的基本运算以及共线定理的应用,属于基础题型.21．在中，角A ，B ，C 的对边分别是a ，b ，c ，已知． ABC cos sin b b A B +=(1)求A ；(2)若，求的面积． 4a b ==ABC 【答案】(1)3π(2)【分析】（1）用正弦定理化简即可得到角A ； cos sin b b A B +=（2）先用余弦定理计算c ，再用面积公式计算面积.【详解】（1）由正弦定理，cos sin sin sin cos sin b b A B B B A A B +=⇒+=因为，所以，所以sin 0B >1cos A A +=1cos 2sin 6A A A π⎛⎫=-=- ⎪⎝⎭因为，所以，所以.()0,A π∈5,666A πππ⎛⎫⎛⎫-∈- ⎪ ⎪⎝⎭⎝⎭663A A p p p -=Þ=（2）由余弦定理，或（舍） 22222cos 211645a b c bc A c c c =+-Þ=+-Þ=1c =-所以11sin 4522ABC S bc A ==⨯⨯= 22．如图，一架飞机从地飞往地，两地相距.飞行员为了避开某一区域的雷雨云层，从A B 200km 机场起飞以后，就沿与原来的飞行方向成角的方向飞行，飞行到地，再沿与原来的飞行方向成θC角的方向继续飞行到达终点.45 km(1)求、两地之间的距离； A C (2)求.tan θ【答案】(1) (2) 37【分析】（1）利用余弦定理可直接求得的长；AC （2）利用余弦定理求出的值，结合同角三角函数的基本关系可求得的值. cos θtan θ【详解】（1）解：由余弦定理可得，(222222cos 20022004523200AC AB BC AB BC B =+-⋅=+-⨯⨯=所以，.AC =（2）解：由余弦定理可得 222cos 2AB AC BC A AB AC +-==⋅所以，为锐角，故 cos cos A θ==θsin θ==因此，. sin 3tan cos 7θθθ==。
陕西省西安市远东第一中学2013-2014学年高一数学12月月考试题 理 新人教A版
某某市远东第一中学2013-2014学年度第一学期高二年级12月月考数学（理科）试题一、选择题：（每小题4分，共48分）1.“x＞1”是“x2＞x”的（）A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件2. a＜0是方程ax2+2x+1=0至少有一个负数根的（）A.必要不充分条件B.充分不必要条件C.充分必要条件D.既不充分也不必要条件3若命题p:A B，则是（）A.x∈A且x BB.x A或x BC.x A且x BD.x∈A∪B4.已知条件p：(x+1)2＞4，条件q:x＞a,且的充分而不必要条件，则a的取值X围是（）A.a≥1B.a≤1C.a≥-3D.a≤-35.下列命题中是全称命题并且是真命题的是（）A.所有菱形的四条边都相等B.若2x为偶数，则任意x∈NC.若对任意x∈R，则x2+2x+1＞0D.是无理数6.已知命题p：所有有理数都是实数；命题q：正数的对数都是负数，则下列命题中为真命题是（）A.( )或B.C.( )且(D.( )或7.已知点O、A、B、C为空间不共面的四点，且向量a=++，向量b=+-，则与a、b不能构成空间基底的向量是（）A. B. C. D.或8.已知向量a,b满足|a|=2，|b|=3，|2a+b|=，则a与b的夹角为（） A.30° B.45° C.60°D.90°9.已知空间四边形ABCD的每条边和对角线的长都等于a,点E、F分别是BC、AD的中点，则·的值为（）A.a2B.C.D.10.已知A（4，1，3），B（2，-5，1），C为线段AB上一点，且=，则C点的坐标为( )A. B. C. D.11.已知=（1，5，-2），=（3，1，z），若⊥，=（x-1，y，-3），且BP⊥平面ABC，则实数x，y，z分别为（）A.，-，4B.，-，4C.，-2，4D.4，，-1512.如图所示，在棱长为2的正方体ABCD—A1B1C1D1中，O是底面ABCD的中心，E、F分别是CC1、AD的中点，那么异面直线OE和FD1所成角的余弦值等于（）A. B. C.D.二、填空题（本大题共6小题，每小题6分，共24分）13设集合A=则集合= .14.令p(x):ax2+2ax+1＞0,若对任意x∈R，p（x）是真命题，则实数a的取值X围是15.下列命题中：①若p、q为两个命题，则“p且q为真”是“p或q为真”的必要不充分条件；②若p为：存在x∈R，x2+2x+2≤0,则p为：任意x∈R，x2+2x+2＞0;③已知p是r的充分不必要条件，s是r的必要条件，q是s的必要条件，那么p是q成立的必要不充分条件④若a＜0,-1＜b＜0,则ab＞ab2＞a.所有正确命题的序号是16.已知a=（1-t，1-t，t），b=（2，t，t），则|b-a|的最小值为 .17.如图所示，已知正三棱柱ABC—A1B1C1的所有棱长都相等，D是A1C1的中点，则直线AD与平面B1DC夹角的正弦值为 .18.已知两平面的法向量分别为m=（0，1，0），n=（0，1，1），则两平面所成的二面角为_______某某市远东第一中学2013-2014学年度第一学期高二年级12月月考数学（理科）试题答题卡一、选择题：（每小题4分，共48分）题号 1 2 3 4 5 6 7 8 9 10 11 12 答案二、填空题（本大题共6小题，每小题6分，共24分）13_______________; 14__________________;15____________________;16_______________; 17__________________ 18___________________;三、解答题（本大题共3小题，共28分）19.（8分）设命题p：（4x-3）2≤1;命题q:x2-(2a+1)x+a(a+1)≤0,若p是q的必要不充分条件，某某数a的取值X围.20.(10分)如图所示，矩形ABCD和梯形BEFC所在平面互相垂直，BE∥CF，∠BCF=∠CEF=90°,AD=,EF=2.(1)求证:AE∥平面DCF;(2)当AB的长为何值时,二面角A—EF—C的大小为60°?21(10分)如图所示，已知长方体ABCD—A1B1C1D1中，AB=BC=2，AA1=4，E是棱CC1上的点，且BE⊥B1C.（1）求CE的长；（2）求证：A1C⊥平面BED；（3）求A1B与平面BDE夹角的正弦值.某某市远东第一中学2013-2014学年度第一学期高二年级12月月考数学（理科）参考答案一、选择题：（每小题4分，共48分）题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A B B A A D C C C B B D 二、填空题（本大题共6小题，每小题6分，共24分）13. ;14 0≤a<1 ;15②④ ;16 ;17 ;18答案45°或135°三、解答题（本大题共3小题，共28分）19.解设A={x|(4x-3)2≤1},B={x|x2-(2a+1)x+a(a+1)≤0},易知A={x|≤x≤1},B={x|a≤x≤a+1}.由p是q的必要不充分条件，从而p是q的充分不必要条件，即A B，∴故所某某数a的取值X围是［0，］.20；方法一（1）证明过点E作EG⊥CF交CF于G，连接DG.可得四边形BCGE为矩形，又四边形ABCD为矩形，所以AD EG，从而四边形ADGE为平行四边形，故AE∥DG.因为AE平面DCF，DG平面DCF，所以AE∥平面DCF.（2）解过点B作BH⊥EF交FE的延长线于H，连接AH.由平面ABCD⊥平面BEFC，AB⊥BC，得AB⊥平面BEFC，从而AH⊥EF，所以∠AHB为二面角A—EF—C的平面角.在Rt△EFG中，因为EG=AD=，EF=2，所以∠CFE=60°,FG=1,又因为CE⊥EF,所以CF=4,从而BE=CG=3.于是BH=BE·sin∠BEH=.因为AB=BH·tan∠AHB=×，所以当AB为时，二面角A—EF—C的大小为60°.方法二如图所示,以点C为坐标原点,以CB、CF和CD所在直线分别作为x轴、y轴和z轴，建立空间直角坐标系C—xyz.设AB=a，BE=b，CF=c，则C（0，0，0），A（，0，a），B（，0，0），E（，b，0），F（0，c，0）.（1）证明=（0，b，-a），=（，0，0），=（0，b，0），所以·=0，·=0，从而CB⊥AE，CB⊥BE.AE∩BE=E，所以CB⊥平面ABE.因为CB⊥平面DCF，所以平面ABE∥平面DCF，AE平面ABE.故AE∥平面DCF.（2）解因为=（-，c-b，0），=（，b，0）.·=0，||=2，所以解得所以E（，3，0），F（0，4，0）.设n=(1,y,z)与平面AEF垂直，则n·=0，n·=0，解得n=（1, ,）.又因为BA⊥平面BEFC，=（0，0，a），所以|cos〈n,〉|=，解得a=.所以当AB为时，二面角A—EF—C的大小为60°.21：解如图所示，以D为原点，DA、DC、DD1所在直线分别为x、y、z轴建立空间直角坐标系D—xyz.∴D（0，0，0），A（2，0，0），B（2，2，0），C（0，2，0），A1（2，0，4），B1（2，2，4），C1（0，2，4），D1（0，0，4）.设E点坐标为（0，2，t），则=（-2，0，t），=（-2，0，-4）.∵BE⊥B1C，∴·=4+0-4t=0.∴t=1，故CE=1.（2）证明由（1）得，E（0，2，1），=（-2，0，1），又=（-2，2，-4），=（2，2，0），∴·=4+0-4=0，且·=-4+4+0=0.∴⊥且⊥，即A1C⊥DB，A1C⊥BE，又∵DB∩BE=B，∴A1C⊥平面BDE. 即A1C⊥平面BED.（3）解由（2）知=（-2，2，-4）是平面BDE的一个法向量.又=（0，2，-4）, ∴cos〈,〉==.∴A1B与平面BDE夹角的正弦值为.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
西安市一中13-14学年上学期月考
高一数学《必修3》试题
一、选择题（每小题4分，共40分）
1. 某林场有树苗30 000棵，其中松树苗4 000棵，为调查树苗的生长情况，采用分层抽样的方法抽取一个容量为150的样本，则样本中松树苗的数量为
( )
A ．30
B ．25
C ．20
D ．15
2. 有一堆形状大小相同的珠子,其中只有一粒质量比其他的轻,某同学经过思考,认为根据科学的算法,利用天平(不用砝码),二次称量肯定能找到这粒质量较轻的珠子,则这堆珠子最多有( )粒
A.6
B.7
C.9
D.12
3. 下列说法正确的是( )
A ．任何事件的概率总是在(0,1)之间
B ．频率是客观存在的，与试验次数无关
C ．随着试验次数的增加，频率一般会越来越接近概率
D ．概率是随机的，在试验前不能确定
4. 将一个长与宽不等的长方形，沿对角线分成四个区域，如图所示涂上四种颜色，中间装个指针，使其可以自由转动，对指针停留
的可能性下列说法正确的是( )
A ．一样大
B ．蓝白区域大
C ．红黄区域大
D ．由指针转动圈数决定
5. 从1、2、3、4、5、6这6个数字中，不放回
地任取两数，两数都是偶数的概率是( )
A.12
B.13
C.14
D.15
6．执行下面的算法框图，输出的T 为（ ）
A.20
B.30
C.12
D.42
7. 设关于x 的一元二次方程x 2＋2ax ＋b 2＝0.
若a 是从0,1,2,3四个数中任取的一个数，b
是从0,1,2三个数中任取的一个数，则上述方
程有实根的概率( ) A.14 B.34 C.12 D.512
8．右面程序输出的结果是( )
A.66
B.65
C.55
D.54
9．如图所示是一样本的频率分布直方
图，
则由图形中的数据，可以估计众数与
中位数分别是( )
A ．12.5 12.5
B ．12.5 13
C ．13 12.5
D ．13 13
10．在等腰直角三角形中，过直角顶点C 在直角内随机作射线CM 交斜边AB 于点M ，则概率()P AM AC >=（ ）
A ．
B ．14
C ．38
D ．1-
二、填空题（每小题4分，共20分）
11．甲、乙两人下棋，甲获胜的概率是40%，甲不输的概率为90%，则甲、乙
两人下成平局的概率为________．
12．某鱼贩一次贩运草鱼、青苗、鲢鱼、鲤鱼及鲫鱼分别为80条、20条、40
条、40条、20条，现从中抽取
一个容量为20的样本进行质量检测，若
采用分层抽样的方法抽取样本，则抽取的
青鱼与鲤鱼共有________条．
13．小军、小燕和小明是同班同学，假设他们
三人早上到校先后的可能性是相同的，则
事件“小燕比小明先到校”的概率是____.
14．阅读下面的算法框图，若输入m ＝4，n ＝6， 则输出a 、i 分别是________.
15. 若连掷两次骰子,分别得到的点数是n m ,,
将n m ,作为点P 的坐标,则点P(n m ,)落在圆1622=+y x 内的概率
为_____.
西安市一中13-14学年上学期月考
高一数学《必修3》答题卷
一、选择题（每题5分，共40分）
二、填空题（每题4分，共20分）
11. ___________ 12.____________ 13. ____________
14.________________ 15._________________
三、解答题（每小题10分，共40分）
16．在一项农业试验中，A、B两种肥料分别被用于一种果树的生长.为了了解这两种肥料的效果,试验人员分别从施用这两种肥料的果树中随机抽取了10棵,下表给出了每一棵果树的产量(单位:kg)：
肥料A：25, 41, 40, 37, 22, 14, 19, 39, 21, 42；
肥料B：31，33，36，40，44，46，50，52，20, 48.
⑴请用茎叶图表示分别施用A、B两种肥料的果树的产量，并观察茎叶图估计
施用哪种肥料的果树产量的平均数大？哪个标准差小？
⑵分别计算施用A、B两种肥料的果树产量的平均数和方差，看看与你的估计
是否一致？你认为哪种肥料更能提高这种果树的产量?
17．为了了解学生的体能情况，某校抽取部分学生进行一分钟跳绳次数测试，所得数据整理后，画出频率分布直方图(如右)，图中从左到右各小长方形面积之比为2∶4∶17∶15∶9∶3，第二小组频数为12.
(1)学生跳绳次数的中位数落在哪个小组内？
(2)第二小组的频率是多少？样本容量是多少？
(3)若次数在110以上(含110次)为良好，试估计该学校全体高一学生的良好率是多少？
18.某地区50位居民的人均月用水量(单位:t)的分组及频数如下：[)[)[)[).15,5,4;20,4,3;10,3,2;5,2,1
⑴完成下面的频率分布表:
⑵画出其频率分布直方图和频率折线图：
19. 从A、B、C三个男生和D、E两个女生中，每次随机抽取1人，连续抽取2次.
⑴若采用不放回抽取，求取出的2人不全是男生的概率；
⑵若采用有放回抽取，求：
①2次抽到同一人的概率；
②抽取的2人不全是男生的概率.
高一数学试题答案
一、选择题（每小题4分，共40分）CCCBD BBDBC
二、填空题（每小题4分，共20分）
11. 50% 12. 6 13. 1/2 14. 12、3 15. 2/9
三、解答题（每小题10分，共40分）
16．解：⑴茎叶图如图：从图中可以看出：
B 的平均数较大；B 的标准差较小
⑵A 的平均数=A x 30；标准差为104.2；
B 的平均数=B x 40；标准差为90.6.
与估计一致. B 种肥料更能提高这种果树的产量.
17．解 (1)∵前三组频率和为2＋4＋1750＝2350<12
， 前四组频率之和为2＋4＋17＋1550＝3850>12
， ∴中位数落在第四小组内 (2)频率为：42＋4＋17＋15＋9＋3
＝0.08， 又∵频率＝第二小组频数样本容量， ∴样本容量＝频数频率＝120.08
=150. (3)由图可估计所求良好率约为：17＋15＋9＋32＋4＋17＋15＋9＋3
×100%＝88%.
18.解：
19．解： ⑴
710
=0.7； ⑵①15=0.2； ②1625=0.64。