斜拉桥拉索自振频率分析
振动频率法测量斜拉桥索力的影响因素研究

( 兰州交通大学 土木工程学 院, 甘肃 兰 州 7 3 0 0 7 0 )
摘 要 斜拉 索是 斜拉桥 的 主要 受力 构件 。在施 工 阶段 斜拉 索的 索力对主 梁的线形控 制及 内力的分布
起 决定性 作 用 ; 在成 桥及 运 营阶段 斜拉 索的索 力依 然影 响 着主 梁和 塔 柱 的 内力 和 线形 。通 过调 整拉 索
共 有 5种 规 格 : P E S 7 — 1 0 9 , P E S 7 — 1 3 9 , P E S 7 — 1 6 3 , P E S 7 —
假 定索 的边 界 条 件 为 两 端 铰 接 , 根据式 ( 1 ) 得 到
拉 索 的索力 为
4 T : T
1 9 9 , P E S 7 — 2 5 3 。斜 拉 索 在 塔 上 竖 向 间 距 为 1 . 5~
3 . 6 i n , 高度 2 . 5~ 3 . 5 i n , 横梁 与塔柱连接处设装 饰段 。
向坐标 ( 沿索 长方 向) ; W为 拉索单 位 长度重 量 ; g是 重 力加速度 ; E 1为 拉 索 的抗 弯 刚 度 ; T为 拉 索 的 索 力 ;
t 为 时 间。
斜 拉索 采用 直 径 7 m m 镀 锌 低 松 弛 平行 钢 丝 束 , 最 大索 长 1 1 8 . 9 2 9 I n , 最 大索质 量 9 . 0 8 6 t , 边 索与水 平 面最小 夹 角 为 2 6 。 , 斜拉 索 标 准 间距 为 8 . 0 m, 斜 拉 索
铁
2 0 1 7年 第 5期
道
建
筑
2 7
Ra i l wa y En g i n e e r i n g
桥梁结构自振频率分析

桥梁结构自振频率分析桥梁作为重要的交通基础设施,在现代社会发挥着关键的作用。
为了确保桥梁的安全性和稳定性,了解桥梁结构的自振频率是十分重要的。
本文将对桥梁结构自振频率的分析方法进行探讨。
一、概述桥梁结构的自振频率是指桥梁在自由振动状态下的频率。
当有外力作用于桥梁时,如果该外力的频率接近桥梁结构的自振频率,就会引发共振现象,对桥梁结构造成严重的破坏。
因此,准确计算和分析桥梁结构的自振频率对于桥梁设计和工程管理至关重要。
二、自振频率的分析方法1. 常规方法常规方法是通过对桥梁进行有限元分析来计算自振频率。
该方法可以精确计算桥梁的自振频率,但需要较为复杂的计算过程和大量的计算资源。
2. 经验公式经验公式是通过已有的桥梁结构的实测数据得出的近似计算公式。
这种方法可以用较简单的方式估算出桥梁的自振频率,适用于初步设计和快速评估。
三、影响自振频率的因素1. 桥梁的几何形状桥梁的几何形状对其自振频率有直接影响。
通常情况下,桥梁的自振频率与其长度、宽度、高度等几何参数有关。
2. 材料的物理性质桥梁材料的物理性质也是影响自振频率的重要因素。
不同材料具有不同的弹性模量和密度,这将直接影响桥梁的自振频率。
3. 桥梁的边界条件桥梁的边界条件也会对自振频率产生影响。
边界条件包括支座刚度、支座类型等,这些条件会改变桥梁的自由度,从而改变其自振频率。
四、自振频率的应用桥梁结构的自振频率不仅是用于评估桥梁的稳定性和安全性,还可以应用于其他方面。
例如,在桥梁的施工过程中,可以通过监测桥梁的自振频率来判断桥梁的质量和施工工艺的合理性。
五、案例分析以某桥梁为例,采用常规方法进行桥梁结构的自振频率分析。
通过有限元分析软件对桥梁进行建模,并设置边界条件和材料属性,最终得出桥梁的自振频率。
六、结论桥梁结构的自振频率分析是确保桥梁安全性和稳定性的重要手段。
常规方法和经验公式是常用的分析方法,根据实际情况选择适用的方法进行分析。
考虑桥梁的几何形状、材料的物理性质和边界条件等因素,可以更准确地计算桥梁的自振频率。
斜拉桥拉索振动及其抑振研究

拉索变成 了气动 不稳定 结构 。
二 、 拉 索 的 减振 措 施 l _ 气 动 控制 法 空 气 动 力 学 措 施 主 要 是 通 过 采 用 不 同 的 方 法 改 变拉 索 的 剖 面 形 状 来 改 善 其 空 气动 力 学 特 性 ,从 而 减 少或 抑 制 拉 索 的 风 雨 激 振 。 因为 风 雨激 振 的发 生 主 要 是 由 于 拉 索 表 明 水 线 的 形 成 而 引起 的 , 所 以 改 变拉 索 表 面特 性 如 粗 糙 度 等 可 以防 止 水 线 的 形成 , 使 拉 索 的 气 定 稳 定 性 得 到 了保 证 ,从 而 抑 制 了 风 雨 激 振 。 目前 主 要 有 以下 几 种 方 法 :( 1 ) 在 拉 索 表 面 的P E套管 上 沿轴 向 开设 凹 槽 或 增 加 U型 套 。 该方 法 可 以控 制 雨 水 在 拉 索 表 面 的轴 向流 动 ,可 以 避 免 因 为 积 水 改 变 拉 索 截 面 形 状 而 形 成 水 线 。对 于 这种 方
近 年 来 ,由 于经 济 建 设及 施工 工 艺 的 飞速 发 展 , 交 通 事 业 的建 设 日新 月 异 , 各 类 结 构 防 震 减 灾 工 作 日益 受 到 世 界 各 国 的重 视 。 桥 梁 作 为 重 要 的 交 通 枢 纽 和 生 命 线 工 程 ,其 各 类 桥 型 应 运 而 生 。 在 各 类 桥
的 现 象称 为尾 流 驰 振 。
3 . 风 雨激 振
减少不同拉索长度的垂度的振动 。就结构性状 和动
力特 性 而 言 , 辅 助 索 可 以 为 拉 索 提 供 中间 支撑 , 减 少 了拉 索 的有 效 长度 , 从 而增 大 了拉 索 的 固有 频 率 。 辅助 索 经 过 科 学 的 设 置 安 装 , 可 明显 地 提 高拉 索 的 基 本频 率 ,减 小 了 基 本 模 态 振 型 下 的 拉 索 随 全桥 模 态 发生 内 部共 振 的 可 能 性 。 设 置 辅 助 索 的 另 一 个 作
斜拉桥索力的频率法测试及其参数分析

工 程 技 术
斜拉桥 索力的频率法测试及其参数分析
李 红 ( 重庆交通 大学 土木工程 学院 重庆 4 00 4) 0 7 摘 要: 斜拉 索是斜 拉桥 的主要 承载 部件 , 章基 于频谱 法原理 定性分 析 了拉 索计算 长度 、 文 边界 条件 、 垂度 影响 、 温度 对斜拉 索 索力测 试 的影 响, 所得 的结论对 频率 法测试 索 力具 有指导 意史 。 关键 词 : 索力测试 频率 法 影响 因素 中 图分 类 号 : 4 6 u 4 文献 标 识 码 : A 文 章编 号 : 2 3 9 ( o o 1 () O 5 - 1 1 7 - 12 1 ) Ob- 0 4 0 6 7
一
2 影晌因素分析
2. 1计 算长度 的影 响 在施工阶段 , 减振 器未 安装 时 , 算 索 计 长 通 常 取 拉索 上 下 两 个 素孔 出 I处 锚 板 中 : 1 心 的 空 间距 离 。 安 装减 振 器 后 , 在 减振 器相 当于 一 个 附加 的 阻 尼 支 点 , 根拉 索 被 分 整 隔 成 中 间长 、 端短 的三 段 。 两 减振 器对 拉 索 的 约 束 作 用使 拉 索 的 自 由长 度 减 少 , 取 若 安 装 前 的 长 度 , 对 索 力 计 算 公式 进 行 修 需 正 , 考 虑 了 减振 器 的效 应 。 以 2 2 边界 条件 的影响 . 索的边界条件实际上是介于铰支和固 支之 间 , 为 接 近 固 支 的情 况 。 般 来 讲 , 较 一 当索力较小时 , 于铰 支; 索力较大时 , 偏 当 偏 于 固支 的 情 况 。 斜 拉桥 的斜 拉 索 而 言 , 对 索 力较 大 , 般 偏于 固支 的 情 况 。 一 当不 考 虑 垂 度 和 斜 度 的影 响 时 , 假 定 抗 弯 刚 度 为 可 零 , 种 边界 条件 下的 解 是 一致 的 , 虑 上 两 考 述 因 素 时 , 种 边 界 条件 下 索 力的 计 算 结 两 + :0 ( 果 亦 有 所 不 同 。 1 ) ox ox ol 当索 的 边 界 条 件 采 用 固结 时 候 , 索 其 式 中 : 为 横 向坐 标 ( y 垂直 于 索 长 度 方 力计 算 公 式 采 用两 端 固支 的 水 平 梁 模 拟斜 向)X ; 为纵 向坐 标 ( 索 长方 向)m为 单位 索 沿 ; 计 长的 质量 ; T为索 的张 力 ;Y 时 间 ; 为拉 索 拉索 , 算 公 式 是 : to EI 2p a O—c s /oh届) b +a )i d ih =0 o ̄ c s f+( 2s n f nc s 的抗 弯 刚 度 。 假 设 素 的 两端 为 铰 支 , 该 微 分 方 程 则 的解 r s修 正弹 性 模 量 ; E 为E n t E为 不考 虑 拉 索 垂 度 影 响 的 弹 性 模 量 ; v为 拉 索 单 位体 积 的重 量 ; 为 拉索张 力 , 拉索 T A为 横截 面 面积 ; 为拉 索 水平 投影 长 度 。 i l E 随拉 索索 的变化而变化 , 它带 入索力计算 公 将 式 可 以 得 到考 虑 垂 度 的 索 力T和 频率 f 关 的 系, 但是 计算 复杂 , 际 中不 常用 。 rh z i 实 Hi iu s 提 出 了无 量 纲 系数 K , 由下 式决 定 :
基于小波分析的斜拉索振动频率识别

浙江交通职业技术学院学报,第21卷第3期,2020年9月Journal of Zhejiang Institute of CommunicationsVol.21No.3,Sep.2020基于小波分析的斜拉索振动频率识别史慧彬1,刘舟峰1,钟昊茹2,徐洪东2,朱绪江2,郭健2(1.浙江舟山跨海大桥有限公司,浙江舟山316000; 2.浙江工业大学桥梁工程研究所,杭州310023)摘要:为了识别跨海斜拉桥拉索在外部因素作用下的振动频率,依托位于海域环境下的某跨海大桥健康监测系统,基于实测数据,采用了小波分析分别对20根斜拉索振的动信号进行分解及重构,再对重构信号进行频谱分析得到了斜拉索振动频率。
结果表明:小波变换非常适合对斜拉索振动这类含有稳态和非稳态成份的信号进行时频分析;不同尺度的小波重构信息及频谱图能很好的反应斜拉索的振动特征;应用小波频谱对信号进行处理以及采用峰值拾取法能够精确的识别斜拉索的频率。
以上利用小波分析对斜拉索振动频率的识别能为将来斜拉桥设计提供重要参考。
关键词:跨海大桥;斜拉索;小波分析;频率识别中图分类号:U448.27文献标识码:Adoi:10.3969/j.issn.1671-234X.2020.(B.001文章编号:1671-234X(2020)03-0001 0引言我国东南海域是台风和季风的多发区域,台风是威胁人类生存和发展的重要天气系统之一,平均每年登陆我国的台风就高达7.2次⑴。
20世纪以来,随着我国经济快速发展的需要,已建成多座大型跨海桥梁⑵,如东海大桥、杭州湾跨海大桥、青岛海湾大桥、舟山跨海大桥、港珠澳大桥等等。
不仅是我国,国外也有众多跨海桥梁建成,如日本多多罗大桥、俄罗斯岛大桥等。
这些跨海桥梁服役期间,都易受到风灾的影响,如浙江舟山海域的10m 高处基本风速达到40m/s以上,且冬季季风和夏季台风交替,无风期非常短,桥梁结构抗风问题突出。
特别是强/台风作用下拉索的强烈振动响应和风雨条件下拉索的激振一直是跨海桥梁建设和运营中需要重点解决的技术难题。
斜拉桥的索和塔对主梁竖向自振频率的影响

,一
、
、
为 了考察斜 拉桥 与对 应 的无索 的连续 梁 桥的 自 振频 率 的区别 , 考察 索 和 塔 对 该 自振 频 率 的贡献 程 度 , 以用 索 和塔 的变 形 能 与 主 粱变 形 能 之 比来 表 可
示。
这样 , 的变形 能 : 梁
2 五 , ) d = d P ( 出= I 3=
篡
。
( 1 2 )
(3 t)
面随跨 径不 变 , 样 E 为定 值 , 般 索 问 距 也 , 这 d 一
E 4
● d d
具参考价值 。’ 关键词 : 斜拉桥 ; 能量法 ; 自振频率 中圈分类号: 4 .7 U 伯 2 文献标识码 :A 文章编号 :0 4一 5 l0 7 2- O 8— 2 1 0 柏5 2 0 )s O 6 0
现代 意义上 的斜拉桥 出现才 5 时 间 , 中 0a的 在
拉 索长度 。。 d表 示 主 梁 的 , 标 C表 示 斜 拉 索 标 下 的, 下标 t 表示 塔 的。 由于索力 的 二 次 变 形 能 相 对 很 小 , 以忽 略 , 可
斜拉 索 的质 量相 对 于桥 面也 是一 个 微 小量 , 可 忽 也
国 已经取得 了突 飞猛 进 的发 展 , 种 桥 型 跨 径实 用 这 范 围 . 到几 ’米 , 到上 千米 。由于拉 索是 自锚 小 卜 大 式 地基 、 对 地形适 应能力 强 , 且桥 型美 观 , 多优 并 诸 点使 得其竞 争力越 来越强 。动 力特 性是斜 拉桥 十分
=
— ■一 。
二
m)出 a2 ,
2 斜拉 桥索 和塔对 ∞ 的 影响
二 兰: 兰 ㈤
假定主梁为一简支梁, 图 1有斜拉索在梁跨 见 ,
斜拉桥索力测试分析
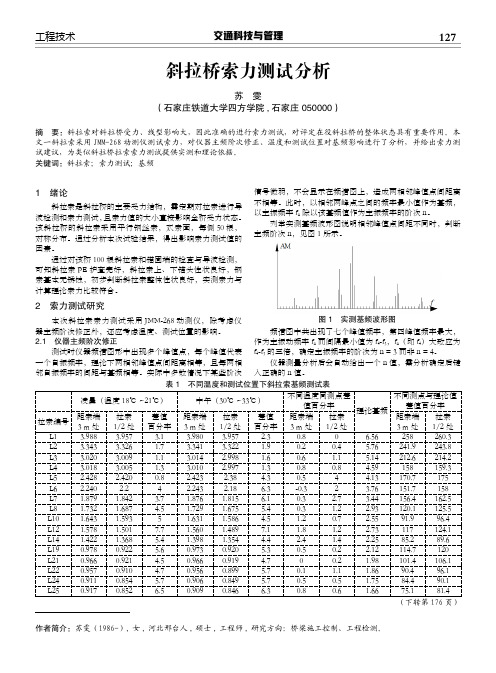
交通科技与管理127工程技术1 绪论 斜拉索是斜拉桥的主要受力结构,需定期对拉索进行导波检测和索力测试,且索力值的大小直接影响全桥受力状态。
该斜拉桥的斜拉索采用平行钢丝索,双索面,每侧50根,对称分布。
通过分析本次试验结果,得出影响索力测试值的因素。
通过对该桥100根斜拉索和锚固端的检查与导波检测,可知斜拉索PE护套完好,斜拉索上、下锚头性状良好,钢索基本无锈蚀,初步判断斜拉索整体性状良好,实测索力与计算理论索力比较符合。
2 索力测试研究 本次斜拉索索力测试采用JMM-268动测仪,除考虑仪器主频阶次修正外,还应考虑温度、测试位置的影响。
2.1 仪器主频阶次修正 测试时仪器频谱图形中出现多个峰值点,每个峰值代表一个自振频率,理论下两相邻峰值点间距离相等,且每两相邻自振频率的间距与基频相等。
实际中多数情况下某些阶次信号微弱,不会显示在频谱图上,造成两相邻峰值点间距离不相等。
此时,以相邻两峰点之间的频率最小值作为基频,以主振频率f n除以该基频值作为主振频率的阶次n。
列举实测基频波形图说明相邻峰值点间距不同时,判断主频阶次n,见图1所示。
图1 实测基频波形图 频谱图中共出现了七个峰值频率,第四峰值频率最大,作为主振动频率f n而间隔最小值为 f4-f3,f n(即f4)大致应为f4-f3的三倍,确定主振频率的阶次为n = 3而非n = 4。
仪器测量分析后会自动给出一个n值,需分析确定后键入正确的n值。
斜拉桥索力测试分析苏 雯(石家庄铁道大学四方学院,石家庄 050000)摘 要:斜拉索对斜拉桥受力、线型影响大,因此准确的进行索力测试,对评定在役斜拉桥的整体状态具有重要作用。
本文一斜拉索采用JMM-268动测仪测试索力,对仪器主频阶次修正、温度和测试位置对基频影响进行了分析,并给出索力测试建议,为类似斜拉桥拉索索力测试提供实测和理论依据。
关键词:斜拉索;索力测试;基频表1 不同温度和测试位置下斜拉索基频测试表凌晨(温度18℃~21℃)中午(30℃~33℃)不同温度同测点差值百分率理论基频不同测点与理论值差值百分率拉索编号距索端3 m处拉索1/2处差值百分率距索端3 m处拉索1/2处差值百分率距索端3 m处拉索1/2处距索端3 m处拉索1/2处L1 3.988 3.957 3.1 3.980 3.957 2.30.80 6.56 258260.3 L2 3.343 3.326 1.7 3.341 3.322 1.90.20.4 5.76 241.9243.8 L3 3.020 3.009 1.1 3.014 2.998 1.60.6 1.1 5.14 212.6214.2 L4 3.018 3.005 1.3 3.010 2.997 1.30.80.8 4.59 158159.3 L5 2.428 2.4200.8 2.423 2.38 4.30.54 4.13 170.7175 L6 2.240 2.24 2.243 2.18 6.3-0.32 3.76 151.7158 L7 1.879 1.842 3.7 1.876 1.815 6.10.3 2.7 3.44 156.4162.5 L8 1.732 1.687 4.5 1.729 1.675 5.40.3 1.2 2.93 120.1125.5 L10 1.643 1.5935 1.631 1.586 4.5 1.20.7 2.55 91.996.4 L12 1.578 1.5017.7 1.560 1.4897.1 1.8 1.2 2.73 117124.1 L14 1.422 1.368 5.4 1.398 1.354 4.4 2.4 1.4 2.2585.289.6 L190.9780.922 5.60.9730.920 5.30.50.2 2.12114.7120 L210.9660.921 4.50.9660.919 4.700.2 1.98 101.4106.1 L220.9570.910 4.70.9560.899 5.70.1 1.1 1.8690.496.1 L240.9110.854 5.70.9060.849 5.70.50.5 1.7584.490.1 L250.9170.852 6.50.9090.846 6.30.80.6 1.6675.181.4作者简介:苏雯(1986-),女,河北邢台人,硕士,工程师,研究方向:桥梁施工控制、工程检测。
振动频率法桥梁索力测量探讨

振动频率法桥梁索力测量探讨摘要:振动频率法在目前桥梁索力测量中得到普遍应用,在将其应用于平行钢绞线索索力测量时,仍存在一些问题。
本文依托实际桥梁中的拉索,对其进行探讨,得出了一些有意义的结论。
关键词:振动频率法平行钢绞线索索力不均匀性0 引言拉索作为斜拉桥重要组成构件,其索力状况对桥梁安全至关重要。
而成桥之后要复测拉索索力,只能选择振动频率法。
然而,运用振动频率法测平行钢绞线索索力时,尚存在以下问题:(1)平行钢绞线索施工时采用单根挂索和张拉,各钢绞线索力并不均等[1]。
(2)各鋼绞线两端离散,中间部分区域由于垂度不同接触。
基于以上问题,本文以某矮塔斜拉桥为依托,验证振动频率法测量平行钢绞线索索力的可行性。
1 工程概况选取不同长度的拉索共三根进行分析,其物理参数如下:1#拉索,斜度22.39°,拉索长度44.271m,初始张拉力9343KN,拉索尺寸;2#拉索,斜度16.20°,拉索长度76.558m,初始张拉力9160KN,拉索尺寸;3#拉索,斜度14.10°,拉索长度100.784m,初始张拉力9224KN,拉索尺寸。
拉索弹性模量均为1.95E+05 MPa,等效直径均为113.66mm。
考虑拉索张拉完成后可能存在的最不利情况,取单根钢绞线索力最大偏差为±5%。
运用midas软件,选取实桥斜拉索中相邻的7根钢绞线进行分析,分别建立整索、单根钢绞线、多根钢绞线接触耦合模型,对比其各阶振动频率,分析索力不均等及钢绞线离散对测量频率的影响。
斜拉索中各钢绞线垂度不同使得拉索中间区域各钢绞线相互接触,由于实桥拉索各钢绞线外侧都热挤PE护套,摩擦力很大,因此模型中采用弹性连接中的刚性来模拟钢绞线之间的接触。
由于各钢绞线之间的接触区域无法测得,而数值计算的结果往往跟实际情况也有很大偏差,因此本次模型研究采用先耦合中间两点,再逐步扩大接触区域的方法[2]。
分别为耦合中间两点、耦合中间1/3区域、耦合中间2/3区域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
斜拉桥拉索自振频率分析
摘要:应用数理方程知识和有限元理论,分别求得斜拉索自振频率的解析解和数值解,并将两种方法得到的结果进行比对,证明了解析法和有限单元法的可靠性,为拉索的风雨激振和参数共振分析提供基础。
关键词:斜拉桥;拉索;自振频率
Abstract: the application of mathematical equations knowledge and finite element theory, respectively given.according vibration frequency of stay-cables analytical solution and the numerical solution, and will by the two methods than the results, and proves the analytic method and finite element method of reliability, for the storm of the lasso excitation and parameter resonance analysis provides the foundation.
Keywords: cable-stayed bridge; The lasso; The natural frequency of vibration of
1. 引言
随斜拉桥跨度的不断增大,斜拉索变得越来越长,因为索的大柔度、小质量和小阻尼等特点,极易在风雨、地震及交通等荷载激励下发生振动[1]。
长拉索前几阶频率在0.2-0.3Hz时,模态阻尼比只有0.1%,更有可能发生大幅的摆动。
迄今,已有许多斜拉索风致振动的报导:日本结构工程协会(Japan Institute of Construction Engineering) 在1988 年一年内对日本的五座斜拉桥斜拉索振动进行了观测和测量,发现它们的最大振幅如下:Brotoni桥达600毫米,Kofin桥达1000毫米,Meikeh桥达600毫米,Aratsu桥达300毫米,大约为直径的两倍。
在国内,1992 年南浦大桥在一次风雨联合作用的情况下浦西岸尾部几根斜拉索发生了较大的振动;杨浦大桥尾索在风雨共振作用下也发生过剧烈的振动,最大振幅超过l米。
2001年,在南京长江二桥通车前,桥上斜拉索在风雨激振下发生大幅摆动,导致安装在梁端的部分油阻尼器损坏[3-5]。
目前对斜拉索风致振动的研究主要集中在单索的风致振动,已经发现的斜拉索可能的振动类型主要包括以下六类:(1) 顺向风振动;(2) 风雨激振;(3) 横风向驰振;(4) 涡激共振;(5) 参数共振。
1. 顺向风振动是拉索振动最常见的一种。
由于风速可以分解为平均风速和脉动风速,风对拉索的作用也表现为平均风引起的静内力、静位移和脉动风引起拉索的振动响应,包括动内力、动位移和振动加速度。
2. 在拉索的风致振动中,风雨激振是最激烈的形式之一。
风雨激振现象是由日本学者于1986年首先发现的。
其后在欧洲,我国等多个国家都观察到这一现象。
在干燥的气候条件下稳定的拉索,而在风和雨的共同作用下,由于雨线的出现,使拉索变得不再稳定。
拉索发生风雨激振的特点为大、中、小雨状态下皆可能发生拉索的风雨激振,一般长索发生风雨激振的可能性较大,而靠近塔柱处的短索发生这一振动的可能性较小,一般发生在包裹的具有光滑表面的拉索,风雨激振时,拉索常以单模态振动,振动的频率一般为拉索的一阶模态频率。
已经观察到有塔的背风面索面振动较大而塔的迎风面索面振动较小的情况。
在一座桥上,常有多根拉索同时发生风雨激振。
3. 横风向驰振是指拉索在垂直于风向上发生微小速度时,这个速度便和风速合成一个对索的迎风面形成一定角度的合成速度,同时产生垂直风向的力分量,这种作用不断加强,就会使拉索产生激烈的横风向振动,振幅可达1~10倍拉索的直径[8]。
拉索的横向风驰振属于发散性振动。
尾流驰振是拉索的另一种驰振形式,两索沿风向斜列时,来流方向的下游拉索将发生比上游拉索更强烈的一种风致振动。
上游拉索的尾流中存在一个不稳定驰振区,如果下游拉索正好位于这一不稳定区域内,其振动幅值就会不断加大,直至达到一个稳态大振幅的极限环。
当两拉索相距较远时,超出尾流驰振不稳定区时,就不会发生尾流驰振[2]。
4. 拉索的涡激共振。
风作用在圆截面拉索,产生交替脱落的漩涡此即所谓的卡门漩涡,拉索在横向风上被周期性驱动。
当涡旋的脱落频率与拉索的某阶自振频率相接近或相等时,出现频率锁定现象,引起拉索在横风向上较大的运动,即横风向涡激振[3]。
5. 参数振动。
对已建和在建的斜拉桥观测表明,在无风和风荷载很小的情况下,个别拉索有时会发生十分强烈的横向振动。
研究表明,当桥面的某阶振动频率接近拉索的振动频率的2倍时,拉索将可能发生自激共振现象,从而引起拉索的大幅振动,这种振动也称为参数振动[2]。
拉索的风雨激振和参数共振都是强非线性振动,能引起拉索的大幅振荡,对拉索具有相当大的破坏性。
对拉索进行动力学分析,其自振频率则是十分重要的参数。
与此同时,由风雨激振和参数共振发生的机理可知,这两种大幅振动的发生与拉索自身的振动频率密切相关,因此有必要对拉索自振频率进行分析。
2. 拉索自振频率解析解
运用数理方程知识,拉索的自振频率可由解析的方法计算得到,具体过程如下。
设有一根均匀、柔软而且有弹性的拉索,其长度为,建立如图1坐标系,设拉索被拉紧成直线状。
当它在平衡位置附近作垂直于方向的微小振动,并且在振动过程中拉索始终保持在同一平面,用表示拉索上任意一点,在任意时刻沿着垂直于方向的位移。
显然,拉索的微小横振动可以用函数来描述。
图1拉索示意图
在拉索上任取一小段弧长。
由于拉索的振动是微小的,故可以认为拉索在振动过程中并未伸长,即的长度。
由胡克定律知,拉索上各点处的张力的大小都相同且不随时间变化,即是常数。
又由于拉索是柔软的,因此拉索抵抗弯曲的能力非常小,可以忽略不计,即认为拉索的抗弯刚度为零,故的方向总是沿着拉索的切线方向。
任取拉索上微小的一段弧长为隔离体,在时刻的受力情况如图2所示。
图2拉索隔离体受力分析
由受力分析知,作用在微段上的力有:点处的张力,它在轴的分力为;点处的张力,它在轴的分力为;设拉索的单位长度质量为。
根据达朗伯原理得
;(1)
因为,故
(2)
又由于拉索做微小振动时,振幅很小,切线的倾角也很小,故就很小,以致<<1,可以忽略不计,因此有
(3)
同理
(4)
于是得
(5)
同除以得
(6)
令取极限得(7)。
