弹塑性力学第03章
第4讲-第三章 空间弹性问题的基本变量及方程_436907486

U
1 2
( xx xx
yy yy
zz zz
xy xy
yz yz
zx zx )d
若用指标形式来写变形体的应变能,则有
1
2
ijij d
1 2
((1111 12 12 13 13
21 21 22 22 23 23
31 31 3232 3333 )d
1 2
{ xx yy zz xy yz zx} 对 应于{ xx yy zz xy yz zx}
可以看出,其变形能应包括二个部分: 对应于正应力与正应变的变形能, 对应于剪应力与剪应变的变形能。
03:53
17
3.1 一般空间问题的基本变量及方程(直角坐标)
对应于正应力与正应变的应变能
如图所示,在xoy平面内考察由于主应力和主应变的作
xy yy yz b y 0 x y z
xz yz zz bz 0
x y z
xx
u , x
yy
v y
,
zz
w , z
xy
v x
u , y
yz
w y
v z
,
xx
1 E
xx
( yy
zz ) ,
yy
1 E
yy
( xx
zz ) ,
zz
1 E
zz
( xx
yy ) ,
zx
w x
u z
uu
vv
on
边界条件
ww
xxnx xyny xz nz px
xynx yyny yznz p y
xy
1 G
xy
,
yz
1 G
yz
弹塑性力学

ij 0 橡皮和铁盒之间无摩擦力 1 2 q, 3 q max 1 3 (1 2 ) q 1 2 2(1 )
ME6011 弹性塑性力学 21
3-3 3 3 Tresca和Mises屈服条件
研究塑性变形和作用力之间的关系及在塑性变形后 物体内部应力分布规律的学科称为塑性力学。 塑性力学问题的特点(4点) 应力与应变之间的关系(本构关系)是非线性的, 其非线性性质与具体材料有关; 应力与应变之间没有一一对应的关系,它与加载 历史有关; 在变形体中有弹性变形区 和塑性变形区,而在求 解问题时需要找出弹性区和塑性区的分界线;
xy yz
zx
xy
G
1 2 E 1 2 0 0 E
yz zxG NhomakorabeaG
1 1 1 2 [ x 0 ] x 0 [(1 ) x ] 0 E E E ex 应变偏量分量 sx 1 2G 应力偏量分量
ME6011 弹性塑性力学
9
不考虑材料强化性质
考虑材料强化性质
①理想弹塑性模型
E s ( s ) 韧性 ( s ) 材料
②线性强化弹塑性模型
( s ) E s E ( s ) ( s )
双线性强化模型
力学问题中各量间关系
ME6011 弹性塑性力学 3
• 本构关系
–反映应力应变之间的联系 映 –材料的固有特性:每一种材料,应力、应变有 着固有的关系 –广义Hook定律:线性 –增量理论:非线性,应变与应力状态和变形历 增量理论 非线性 应变与应力状态和变形历 史有关,研究应力和应变增强之间的关系
E
弹塑性力学课件第三章

zx C61x C62 y C63z C64 xy C65 yz C66 zx
C ij
ijkl kl
Cijkl Cijlk
2021/1/10
4
第三章 本构关系
一、线性弹性体的本构方程——具有一个弹性对称面的线
性弹性体
x
y
C11
C12 C22
C13 C23
C14 C24
2021/1/10
10
第三章 本构关系
一、线性弹性体的本构方程——各向同性弹性体
x
1 E
x
( y
z ) ,
xy
1 G
xy
y
1 E
y
( x
z ) ,
yz
1 G
yz
z
1 E
z
( x
y ) ,
zx
1 G
zx
ij 1Eij Ekkij
2021/1/10
11
第三章 本构关系 一、线性弹性体的本构方程——各向同性弹性体
0 x
0
y
z xy
C33 0 0
对
C44 0
0 z
0
xy
yz
zx
称
C55
0 C66
yz zx
2021/1/10
6
第三章 本构关系 一、线性弹性体的本构方程——正交各向异性弹性体
x y z xy
1 Ex
xy
1 Ey
对
xz
yz
弹塑性力学课件第三章
第三章 本构关系
本章学习要点:
掌握各项同性材料的广义Hooke定律 掌握弹性应变能密度函数的概念及计算 理解初始屈服、后继屈服以及加卸载的概 念 掌握几个常用的屈服条件 理解弹塑性材料的增量和全量本构关系的 基本概念
弹塑性力学课后答案

εij第二章 应力理论和应变理论2—3.试求图示单元体斜截面上的σ30°和τ30°(应力单位为MPa )并说明使用材料力学求斜截面应力为公式应用于弹性力学的应力计算时,其符号及正负值应作何修正。
解:在右图示单元体上建立xoy 坐标,则知σx = -10 σy = -4 τxy = -2 (以上应力符号均按材力的规定) 代入材力有关公式得:3030cos 2sin 22210410413cos 602sin 6073222226.768 6.77()104sin 2cos 2sin 602cos 60223132 3.598 3.60()22x yx yxy x y xy MPa MPa σσσσσατασστατα+-=+----+=++=--⨯+⨯=----+=⋅+=⋅-=-⨯-⨯=--代入弹性力学的有关公式得: 己知 σx = -10 σy = -4 τxy = +23030()cos 2sin 22210410413cos 602sin 6073222226.768 6.77()104sin 2cos 2sin 602cos 60222132 3.598 3.60()22x yx yxyx y xy MPa MPa s ss ss a tas s t a t a +-=++---+=++=--??=----+=-?=-?=??由以上计算知,材力与弹力在计算某一斜截面上的应力时,所使用的公式是不同的,所得结果剪应力的正负值不同,但都反映了同一客观实事。
2—6. 悬挂的等直杆在自重W 作用下(如图所示)。
材料比重为γ弹性模量为 E ,横截面面积为A 。
试求离固定端z 处一点C 的应变εz 与杆的总伸长量Δl 。
解:据题意选点如图所示坐标系xoz ,在距下端(原点)为z 处的c 点取一截面考虑下半段杆的平衡得:c 截面的内力:N z =γ·A ·z ;c 截面上的应力:z z N A z z A Aγσγ⋅⋅===⋅; 所以离下端为z 处的任意一点c 的线应变εz 为:δy题图1-3τxyx 30°10n24xO10yTτ30°δ30°zz zEEσγε==;则距下端(原点)为z 的一段杆件在自重作用下,其伸长量为:()22zzzzz z z z y zz l d l d d zd EEEγγγε=⎰⋅∆=⎰⋅=⎰=⎰=;显然该杆件的总的伸长量为(也即下端面的位移):()2222ll A l lW ll d l EEAEAγγ⋅⋅⋅⋅⋅=⎰∆=== ;(W=γAl )2—9.己知物体内一点的应力张量为:σij =50030080030003008003001100-⎡⎤⎢⎥+-⎢⎥⎢⎥--⎣⎦应力单位为kg /cm 2 。
弹塑性力学第03章

xy
v x
u
y
x
1 E
( x
y
)
y
1 E
( y
x
)
or
x
1
E 2
(
x
y
)
y
E 1 2
( y
x
)
xy
2 (1 E
)
x
y
)
xy
E 2 (1
)
xy
及
z 0, 畸变。这种畸变很小,
yzxz 0
并与z无关,而是x,y的
z E (xy)
函数。它可以从此式中 独立地求出。
§3-2 平面问题的应力函数解法
▪ 应力解法则以应力分量作为基本未知量,前面 已说过,应力分量必须满足平衡微分方程以及静力 边界条件,这是保证物体的平衡的充要条件,但这 仅仅是静力上可能的平衡,不是实际存在的平衡, 这组应力分量也不一定是真正的应力,而真正的应 力不仅要满足平衡微分方程与静力边界条件,还要 求与这组应力分量相应的应变分量满足应变协调方 程,这样才能既满足了物体的平衡又满足了物体的 连续,由此可知,应变协调方程在应力解法中是十 分重要的。以应力表示应变的物理方程代入应变协 调方程式中,得到以应力表示的协调方程。
▪ 问题:平面应力问题的以应力 表示的应变协调方程 类似三
维问题重新推导,能否直接用 三维的结论简化而来?
2y 2x 2xy x2 y2 xy
2(xy)(1) F xx F yy
2
2 x2
2 y2
应变协调方程(一般情况)
2 z 2 y 2 yz
y 2
z2
yz
2 x z2
2 z x 2
2. 取二次多项式为应力函数
弹塑性力学-03 几何方程

w z
0,
xy
u y
v x
0
yz
v z
w y
0
zx
w x
u z
0
u y z z y u0
刚体转动 v z x x z v0
刚体平移
w x y y x w0
,
3.1 位移与应变
5. 刚体位移
u y z z y u0 v z x x z v0 w x y y x w0
y
zdy
z
dz
C
dur
drD
o
By
A
dur du dv dw
dr dx dy dz
x
dr dx dy dz
du dx dv dy dw dz dur du dv dw
3.2 应变分析
1. 主应变
dx xdx yxdy zxdz dy xydx ydy zydz dz xzdx yzdy zdz
1 2
v z
w y
zx
1 w 2 x
u z
第三组方程
3.1 位移与应变
3. 应变概念 正应变
y 伸长为正
缩短为负
dz
x
=
du dx
dy
o
x
z
dx
du
3.1 位移与应变
3. 应变概念
剪应变
y
dz
dy xy
o
z
dx
直角变小为正 直角变大为负
x
3.1 位移与应变
●物体变形 微元变形即长度和角度的改变 y
( x )dx yxdy zxdz 0 xydx ( y )dy zydz 0 xzdx yzdy ( z )dz 0
(完整版)弹塑性力学习题题库加答案
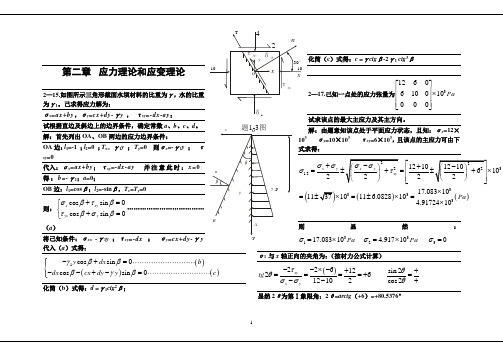
第二章 应力理论和应变理论2—15.如图所示三角形截面水坝材料的比重为γ,水的比重为γ1。
己求得应力解为:σx =ax+by ,σy =cx+dy-γy , τxy =-dx-ay ;试根据直边及斜边上的边界条件,确定常数a 、b 、c 、d 。
解:首先列出OA 、OB 两边的应力边界条件:OA 边:l 1=-1 ;l 2=0 ;T x = γ1y ; T y =0 则σx =-γ1y ; τxy =0代入:σx =ax+by ;τxy =-dx-ay 并注意此时:x =0 得:b=-γ1;a =0;OB 边:l 1=cos β;l 2=-sin β,T x =T y =0则:cos sin 0cos sin 0x xy yxy σβτβτβσβ+=⎧⎨+=⎩………………………………(a )将己知条件:σx= -γ1y ;τxy =-dx ; σy =cx+dy-γy 代入(a )式得:()()()1cos sin 0cos sin 0y dx b dx cx dy y c γβββγβ-+=⎧⎪⎨--+-=⎪⎩化简(b )式得:d =γ1ctg 2β;化简(c )式得:c =γctg β-2γ1 ctg 3β2—17.己知一点处的应力张量为31260610010000Pa ⎡⎤⎢⎥⨯⎢⎥⎢⎥⎣⎦试求该点的最大主应力及其主方向。
解:由题意知该点处于平面应力状态,且知:σx =12×103 σy =10×103 τxy =6×103,且该点的主应力可由下式求得:(()()31.233331210102217.0831******* 6.082810 4.9172410x yPa σσσ⎡++⎢=±=⨯⎢⎣⨯=⨯=±⨯=⨯则显然:3312317.08310 4.917100Pa Pa σσσ=⨯=⨯=σ1 与x 轴正向的夹角为:(按材力公式计算)()22612sin 22612102cos 2xyx ytg τθθσσθ--⨯-++====+=--+显然2θ为第Ⅰ象限角:2θ=arctg (+6)=+80.5376°题图1-3则:θ=+40.268840°16' 或(-139°44')2—19.己知应力分量为:σx =σy =σz =τxy =0,τzy =a ,τzx =b ,试计算出主应力σ1、σ2、σ3并求出σ2的主方向。
弹塑性力学-03应力应变关系
x
1 E
x
y
z
y
1 E
y
z
x
z
1 E
z
x
y
xy
xy
G
2(1 E
) xy
yz
yz
G
2(1 E
)
yz
zx
zx
G
2(1 E
)
zx
School of Engineering and Technology,China University of Geosciences
School of Engineering and Technology,China University of Geosciences
❖ 屈服曲线的性质:
1. 屈服曲线是一条封闭曲线,并且坐标原点被包围在内。
2. 由原点O向外作的射线与屈服曲线必相交,且只相交一次(材料的初 始屈服强度是唯一的)。
School of Engineering and Technology,China University of Geosciences
§3–1 拉伸应力 -- 应变曲线
二、真应力--应变曲线
T
P A
A'
TA
B A
A
o'
o
1
A
材料不可压缩: Al A0l0
T
P A0
l l0
T (1 )
School of Engineering and Technology,China University of Geosciences
x
z
1 E
z
x
y
xy
xy
G
2(1 E
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
▪ 问题:平面应力问题的以应力 表示的应变协调方程 类似三
维问题重新推导,能否直接用 三维的结论简化而来?
2 y 2 x 2 xy x 2 y2 xy
2 ( x
y)
(1
)
Fx x
Fy y
2
2 x 2
2 y 2
应变协调方程(一般情况)
2 z
y 2
2 y
z 2
2 yz
yz
2 x 2 z 2 xz
x
1 E
( x
y
)
y
1 E
( y
x )
or
x
E 1 2
( x
y )
y
E 1 2
( y
x )
xy
2(1 E
)
x
y
)
xy
E 2(1
)
xy
及
z0, 畸变。这种畸变很小,
yz xz 0
并与z无关,而是x,y的
z
E
( x
y)
函数。它可以从此式中 独立地求出。
弹性力学的基本方程 (一般情况)
E
21
E
yz xz
z
1 E
[
z
x
y
],
xy
21
E
xy
x
u x
,
yz
w y
v z
y
v , y
xz
u z
w
x
z
w , z
xy
v x
u
y
x 2G x , y 2G y , z 2G z ,
yz
G
yz
xz G xz
xy
G
xy
平面应力问题的应变协调方程
体受到垂直于z轴的外力作用时,这些横载面之间必然会产生
挤压力σz,由于σz为应力分量σx与σy的一种组合,因而它 不是独立的未知量,在求得σx和σy后,可由上式单独求解, 而基本方程中不包含σz。
横截面都可以看成对称截面,在对
称截面上的每一点只能在其自身平 面(与xOy平面平行)内移动,而沿 z方向的位移w为零,因而在整个柱 体内有w=0,由此在任意横截面内,
沿x轴和y轴方向的位移分量u及v均
与z无关,位移分量就简化为
u u(x, y)
v
v(
x,
y)
w 0
平面应变问题几何方程
x
u x
平衡(运动)微分方程
x x
yx y
zx z
Fx
0
2 t
u
2
xy x
y y
zx z
Fy
0
2v t 2
xz x
yz y
z z
Fz
0
2 t
w
2
几何方程——应变和位移的关系
物理方程——应力和应变的关系
x
y
1 E
[
x
y
z
],
1 E
[
y
x
z
],
yz xz
21
2
2
2
一点处的应力状态
平面应力问题
▪ 注意到切应力
互等性,可知,
只剩下平行于
xoy面的应力分
量: x , y , xy
x,
y的函数
z 0, yz 0, xz 0
x F1 (x, y), y F2 (x, y), xy F3 (x, y)
切应力互等定理
▪ 根据弹性体的形状与受力特点,弹性力学平面 问题可分成平面应力问题和平面应变问题两个类型。
一、平面应力问题
▪ 由于板很薄,外 力又不沿厚度方 向变化,应力沿 着板厚又是连续 分布的,因此, 可认为在板的内 部,这三个应力 分量是很小的, 不妨近似认为在 整个板内为零。
( z ) z 0, ( zy ) z 0, ( zx ) z 0
y 2 z 2 yz
2 x 2 z 2 xz
z 2 x 2 xz
2 y 2 x 2 xy
x 2 y 2 xy
x
yz
x
xz
y
xy
z
2
2
x
yz
y
y
x
z
xz
y
xy
z
2 2 y
xz
z
yz
x
xz
y
xy
z
2 2 z
xy
x
y
1 E
[
x
y
z
],
1 E
[
y
x
z
],
yz xz
21
E
21
E
yz xz
z
1 E
[
z
x
y
],
xy
21
E
xy
x
1
E
x
E
,
y
1
E
y
E
,
z
1
E
z
E
,
yz
2(1
E
)
yz
xz
2(1
E
)
xz
xy
2(1
E
)
xy
2 z
y 2
2
z 2
y
1
2 y 2
z 2
2 2 yz
yz
静力边界条件
f x xl yxm
f y xyl y m
应力边界条件(一般情况)
fx fy
xl xyl
yx y
m m
zx zy
n n
fz
xzl
y
z
m
z
n
二、平面应变问题
▪ 考察图示水坝或受内压的圆筒,它 们是母线与Oz轴平行且很长的柱体, 所受体力和面力垂直于Oz轴,而且
沿该轴方向均匀分布。对于这类物 体,不妨认为沿z方向是无限长的。 因而,柱体的任意一个垂直于z轴的
f1 (x, y)
y
v y
f 2 (x,
y)
xy
v x
u y
f3 (x, y)
z
w z
0
yz
w y
v z
0
xz
u z
w x
0
平面应变问题的应力分量
τ
yz
=τxz
=
0
z
1 E
[ z
(x
y )]
0
z ( x y )
σz在平面应变问题中不为零 。σz的存在说明了沿z方向 无限长的柱体的假设限制了每一个横截面的纵向位移。当柱
▪ 两相互垂直平面上的切应力数值相等,且均 指向(或背离)该两平面的交线,称为切应 力互等定理。(材料力学P61)
平面应力问题基本方程
▪ 在平面应力问题中,随着物理量的简化,基 本方程也随之简化 。
x x
yx y
Fx
0
xy x
y y
Fy
0
x
u x
y
v y
xy
v x
u
y
§3-1 平面应力问题和平面应变问题
▪ 严格说来,任何一个实际的弹性力学问题都是空 间问题(三维问题),从而要归结为求解复杂的偏 微分方程组的边值问题。但是,当弹性体的几何形 状和受力情况(包括约束条件)具有一定特点时, 只要经过适当的简化和力学的抽象处理,就可以归 结为所谓的弹性力学平面问题,在数学上属于二维 问题。这样处理,将使分析和计算工作量大为减少, 而所得结果却仍可以满足工程上对精度的要求。
z 2 x2 xz
2 y 2 x 2 xy
x2 y 2 xy
x
yz
x
xz
y
xy
z
2
2
x
yz
y
yz
x
xz
y
xy
z
2 2 y
xz
z
yz
x
xz
y
xy
z
2 2 z
xy
应力解法 以应力表示的应变 协调方程(一般情况)
2 z 2 y 2 yz
第三章 弹性力学平面问题
▪§3-1 平面应力问题和平面应变问题 ▪§3-2 平面问题的应力函数解法 ▪§3-3 代数多项式解答 ▪§3-4 若干典型实例 ▪§3-5平面问题的极坐标方程 ▪§3-6 平面轴对称应力问题 ▪§3-7 圆孔孔边应力集中 ▪§3-8 楔形体问题 ▪§3-9 半平面问题 ▪* §3-10 Airy应力函数的物理意义
