论角动量的质心轴定理
合集下载
角动量以及角动量守恒
dLz dt
Jz
d
dt
J z miri2 i
? 质点系的角动量定理 M 外
Z轴分量
Mz
dLz dt
dL dt
质元 mi : Fi 对O点的力矩
M i roi Fi
roi Fi roi Fiz
（垂直z轴）
roi Fi ri Fi riz Fi
（垂直z轴）
z
Mz
vi
Oi
ri mi
r 2
v dS dt dv
at dt
v v0 at
S
v0t
1 2
at 2
v2 v02 2aS
d
dt
d
dt
z
v dS
r d P
O 匀变速定轴转动
0 t
0t
1 t2
2
2 02 2
5.4 刚体定轴转动的角动量定理 角动量守恒
对定轴的力矩和角动量
Mz
dLz dt
?
Li
Li roi mivi roi vi
Rg
LO Rmgt
、质点的角动量定理
一 力矩
刚体绕 O z 轴旋转
F 作用在点 P ,
r
F
P 的径矢 .
对转轴Z 的力矩
M rF
M Fd Fr sin
d : 力臂
F
F
Fi 0 , Mi 0
5
M
O dM zrP* F
F
F
Fi 0 , Mi 0
刚体内作用力和反作用力的力矩 （一对内力）
圆盘半径为 R, 总质量为 m .
解: Jz r2dm r2 ds R r 2 2 rdr
1. 刚体转动惯性大小的量度
角动量及其守恒定律
m r2 r1 J0
22
因为 1 2， 1 1 2 E k 1 J 1 1 ( J 1 1 ) 1 2 2 相 E k1 E k 2 等 1 1 2 E k 2 J 2 2 ( J 2 2 ) 2 2 2 即系统的机械能不守恒。
23
人双臂收回过程中，内力做功，
J 2
l/2
r dr
2
1 12
l
3
0
1 12
ml
2
如转轴过端点垂直于棒 l 1 2 J r d r ml 2 0 3
例3 一质量为 m 、半径为 R 的均匀圆盘，求通 过盘中心 O 并与盘面垂直的轴的转动惯量 .
解 设圆盘面密度为 ， 在盘上取半径为 r ，宽为 d r 的圆环
v M (2 gh )
u l 2
1 2
M
h N
B
l 2 1 12
2
2
把M、N和跷板作为 一个系统, 角动量守恒
mvM l 2 J 2 mu
C l
m l 1 2 1 6 m ( 2 gh )
A l/2
ml
2
解得
mvMl 2 m l
2
2
12 ml
2
2 2 2
质量连续分布刚体的转动惯量
J
m
j
j j
r
2
r dm
2
d m ：质量元
例2 一质量为 m 、长为 l 的均匀细长棒，求 通过棒中心并与棒垂直的轴的转动惯量 .
O
l 2
O
dr
l 2
r
dr
O´
第六章、角动量定理
rc
ac
0
i
i
其中 rc 为质心系中质心位矢，它必为零。故
M 0
dL dt
质心系角动 量微分形式
即质点系相对质心的角动量的时间变化率等于外力相
对质心的外力矩总和。
t
0 M0dt L L0
质心系角动 量积分形式
注意：①质心系角动量定理虽与质点或质点系的角动量定理具
O
r
L0
mv
在直角坐标系中
i jk
Lx , Ly , Lz
x
y
z
px py pz
O
R
图6.2、圆锥摆的角动量
其中： p mv
3
二、力矩
作用力F，其作用点的位矢为r，它对O点的力矩被定义为
M rF
方向：由右手定则确定；
大小: M=rFsinθ。
在直角坐标系中，其分量表示
i jk
M x , M y , M z x y z
Fx F y Fz
图6.3、力矩
4
例6.1：试求作用在圆锥摆上的拉力T、重力
mg和合须明确指出是对那点或 那个轴的力矩；
o'
L
力矩
αT
o'点
拉力T 0
重力mg
合力F
mgLsinα× FLcosα×
正方向 量均为m，胶泥的质量为m’, 原来重
h
m' m vv
m
物与盘静止，让胶泥从h高处自由落 下，求胶泥粘到盘上后获得速度。
图v6o .8、题6.5图
解：把盘、重物、胶泥视为质点系，在胶
泥与盘的碰撞过程中，绳的拉力，盘与重物所受的重力对o轴
3-2质心运动定理、角动量守恒
L
O
●
rA r
●
A α m
●
v
证明： 不受外力，质点将做 匀速直线运动。 m在某一时刻经过A点时， 其对固定点O的角动量为
L rA mv rAmvsin r m v
固定点O到轨迹直线的垂直距离只有一 个值，所以角动量的大小恒定。 而角动量的方向恒垂直于固定点O和运动 轨迹所决定的平面。 所以m对任意固定点的角动量矢量保持不变。
力矩的大小：
力矩的方向： 角动量定理：
M r F rF sin
也由右螺旋法则确定。
dL M dt
质点所受的合外力矩等于它的角动量对时间的 变化率。 M 注意：定理中的力矩和角 动量是对惯性系中地同一 固定点而言的。
o
●
r
F
r
α
m
§3.7 角动量守恒定律
给上式两边同时乘以系统质量m
rC
mi ri
i
则：
mvc mi vi p
dvc dp p mvc 两边求导得： m mac dt dt dp F m a c dt
——质心运动定理
i
不管物体的质量如何分布，也不管外力作用在 物体的什么位置上，质心的运动就象是物体的质量 全部都集中于此，而且所有外力也都集中于此的一 个质点的运动一样。 实际上在质心位置处可能既无质量，又未受力。
i 1
m
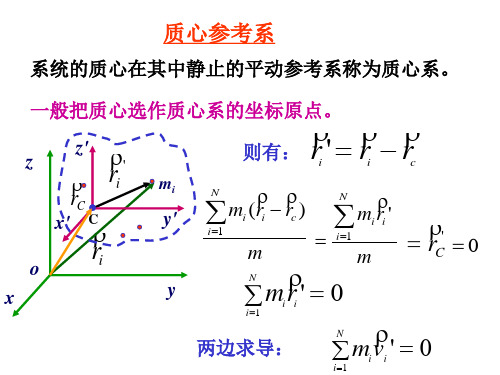
' rC
0
两边求导：
'0 mv i i
N i 1
z
z'
x'
o
rC
' ri
质点系角动量守恒定律
dL τ ，再考虑诸质点所受惯性力的力矩，即得 dt
dL τ i外 ri (mi ac ) dt 式中惯性力矩又可写作 mi ri dL ( mi ri) ac ( ) mac τ i外 m dt
此即质点系对质心的角动量定理，与惯性系中角动量定理具有完 全相同的形式。是表明质心系特殊和重要性的又一个例子。
第五章 角动量•关于对称性
前言 质点的角动量 质点系的角动量定理及角动量守恒定律 质点系对质心的角动量定理和守恒定律 对称性 • 对称性与守恒律 经典动力学的适用范围
§5.1 前
一、本章的基本内容及研究思路
言
角动量概念的建立和转动有密切联系，在研究物体的运动 时，人们经常可以遇到质点或质点系绕某一确定点或轴线运动 的情况，并且在这类运动中也存在着某些共同的重要规律。例 如，天文观测表明，行星绕日运动遵从开普勒第二定律，在近 日点附近绕行速度较快，远日点速度较慢，这个特点如果用角 动量及其规律很容易说明。特别是在有些过程中动量和机械能
当τ iz 0时,
Lz 常量.
§5.4 质点系对质心的角动量定理和 守 恒 定 律
前面给出的角动量定理和角动量守恒定律都相对于惯性系 而言，现在研究质心参考系中质点系角动量的变化规律。如图 （a），C xyz 即质心参考系。C 为质心，x ' , y ' 和 z 坐标轴
与惯性参考系 O xyz 的 x, y 和 z 轴总保持平行，而质心具有 加速度 ac 。 z
四、质点对轴的角动量定理和守恒定律（自阅）
§5.3 质点系的角动量定理及角动量守恒定 律
一、质点系角动量定理
设质点系由 N 个质点组成，对选定的某固定参考点，第 i 个 质 点的角动量定理的表达式为τ dLi
角动量角动量守恒定律jm
角动量守恒定律是自然界的一个基本定律.
20
角动量守恒现象举例
图1
图2
J ri2mi
i
M轴 0
J11 J22
L1
L2
L J
J1 J2
1 2
21
许多现象都可 以用角动量守恒来 说明.
花样滑冰 跳水运动员跳水
J11 J 22
J1 J2
若 M 0，则 L J =常量
or : J22 J11
19
M
M 轴外
d(J)
dt
dL dt
讨论
L J =常量
守恒条件 M 0
若 J 不变，不变；
J 22 J11
若 J 变， 也变，但 L J 不变.
内力矩不改变系统的角动量.
在冲击等问题中M in M exL 常量
碰撞后的瞬间：
M+N+板转动：
N
C
Bl
M+N具有相 u l
同的线速度： 2
M
h A
l/ 2
25
冲击前： vM (2gh)1 2
冲击后：u l
2
M、N和跷板组成的系统，角动量守恒
mvM
l 2
J
2mu l 2
M
1 ml2 1 ml2
12
2
质点：
L
r
4-3 角动量 角动量守恒定律
1
问题：
力的时间累积效应： 冲量、动量、动量定理．
力矩的时间累积效应： 冲量矩、角动量、角动量定理．
（角冲量）
§5.2 角动量定理及其守恒律
f1 r1 f1 r2 f 2 r 12 r1 r1 f1 r1 f 2 o (r1 r2 ) f1 r12 f1 0
f2
r2
内容
⒈质点系对点的角动量定理:
M外 dL dt
质点系在碰撞过程中对o轴的角动量守恒
o
⊙ 正方向
胶泥碰前速度
v0 2gh
h
m'
v m vo
m v
据角动量守恒
m' 2ghR (m'm)vR mvR
v
m' 2 gh m ' 2m
例1：人造地球卫星，绕地球作椭圆轨道运动， 地球在椭圆的一个焦点上，则卫星的( (A)动量不守恒，动能守恒． (B)动量守恒，动能不守恒． (C)对地心的角动量守恒，动能不守恒． (D)对地心的角动量不守恒，动能守恒． )
⒋质点对轴的角动量守恒定律：
若M z 0，则Lz = C
说 明
在应用角动量定理或角动 量守恒定律时，力矩和角动 量必须选取惯性系中的同一 参考点或同一参考轴.
o'
α L
T
o
F
mg
角动量守恒与选取的参考点或参考轴有关。
M o
Fl cos
L o'
mvl ,
例1
解得：v1 5.91104 m / s; v2 3.88 104 m / s
二、质点系的角动量
第i个质点对o点的角动量
Li ri P i
P2
r2
P 1
质点系对o点的角动量
dLi ri Fi ri f i 对 mi 使用角动量定理： dt
f2
r2
内容
⒈质点系对点的角动量定理:
M外 dL dt
质点系在碰撞过程中对o轴的角动量守恒
o
⊙ 正方向
胶泥碰前速度
v0 2gh
h
m'
v m vo
m v
据角动量守恒
m' 2ghR (m'm)vR mvR
v
m' 2 gh m ' 2m
例1：人造地球卫星，绕地球作椭圆轨道运动， 地球在椭圆的一个焦点上，则卫星的( (A)动量不守恒，动能守恒． (B)动量守恒，动能不守恒． (C)对地心的角动量守恒，动能不守恒． (D)对地心的角动量不守恒，动能守恒． )
⒋质点对轴的角动量守恒定律：
若M z 0，则Lz = C
说 明
在应用角动量定理或角动 量守恒定律时，力矩和角动 量必须选取惯性系中的同一 参考点或同一参考轴.
o'
α L
T
o
F
mg
角动量守恒与选取的参考点或参考轴有关。
M o
Fl cos
L o'
mvl ,
例1
解得：v1 5.91104 m / s; v2 3.88 104 m / s
二、质点系的角动量
第i个质点对o点的角动量
Li ri P i
P2
r2
P 1
质点系对o点的角动量
dLi ri Fi ri f i 对 mi 使用角动量定理： dt
质心系角动量定理
质心系角动量定理质心系角动量定理是指：在不受外力矩作用的情况下，质心系的角动量保持不变。
如果系统的总质量为M，质心的角动量为L_cm，则质心系角动量定理可以用以下数学表达式表示：dL_cm/dt = 0其中，dL_cm表示角动量的变化率，dt表示时间的微小变化量。
质心系角动量定理可以通过质心系动量矩阵的变化和角动量的定义来进行推导。
在质心系中，系统的总动量等于零，即：dP_cm/dt = 0其中，dP_cm表示动量的变化率。
由牛顿第二定律可知，总外力矩等于总动量的变化率，即：M*dV_cm/dt = dP_cm/dt其中，M表示系统的总质量，dV_cm表示质心速度的变化率。
又根据角动量的定义可以得到：L_cm = r_cm x P_cm其中，r_cm表示质心相对于某一点的位置矢量，P_cm表示质心的动量。
对上式求时间的导数，可得：dL_cm/dt = d(r_cm x P_cm)/dt根据向量的微分运算性质和叉乘的定义，可得：dL_cm/dt = (d(r_cm)/dt) x P_cm + r_cm x (dP_cm/dt)由于质心相对于某一点的位置矢量的导数为质心速度，即：d(r_cm)/dt = V_cm所以可以重新写成：dL_cm/dt = V_cm x P_cm + r_cm x (dP_cm/dt)由于质心系中系统的总动量等于零，即：dP_cm/dt = 0所以上式可以简化为：dL_cm/dt = V_cm x P_cm由于质心速度V_cm与质心的动量P_cm垂直，所以：V_cm x P_cm = 0于是可以得到：dL_cm/dt = 0这就是质心系角动量定理的数学表达式。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
论角动量的质心轴定理
质心轴定理是物理学中重要的定理，它指出：在一个多边形的质心处，所有质点的角动量之和等于零。
这个定理也被称为质心轴定理，因为它指出：在一个多边形的质心处，所有质点的角动量都沿着一条质心轴，这条质心轴是一个多边形的轴线。
质心轴定理对于研究多边形的稳定性和动量转移是非常重要的，因为它可以帮助我们确定多边形的稳定性，以及多边形内部的动量转移。
它可以帮助我们更好地理解多边形的属性，以及多边形的运动规律。
质心轴定理也可以帮助我们研究多边形的动量分配，它可以帮助我们确定每个质点的动量分配，以及多边形内部动量的分布情况。
这有助于我们更好地理解多边形的物理属性，以及多边形的动量分配规律。