运动微分方程
理想流体的运动微分方程

uz
uz
u x z
u y z
y
1 p
Z
z
du z dz
u z t
ux
u z x
uy
u z y
uz
u z z
写成矢量表达式为:
1 du F p dt
式中哈密顿算子:
i j k x y z
1.3.6.2 总流
对于粘性流体的总流,作稳定流动时的柏努利方程式为:
z1
p1
1 v1
2g
2
z2
p2
2v2
2g
2
hw
式中:
v1 , v 2 为截面的平均流速; 1 , 2为动能修正系数,通常由实验确定。
对于圆形管道中的稳定缓变流: 层流时 =2;
湍流时 =1.05~1.10;
由柏努利积分式:
U
1
dp
2
u
2
2
得
或
gz
1
gz
1
p
u
C
2
p
u
2
C
2
2
对于流线上任意两个质点1和2来说,有:
g z1 1
p1
u1
2
2
gz2
1
p2
u2 2
式中各项分别为单位质量的流体具有的位能,静压能及动能, J kg ( )。
1.3.5.2 理想流体稳定流动总流的柏努利方程 任何稳定流动的总流,都可以看成是无穷多微小流束 的总和。在总流中某一微小流束的不同有效截面上的物理 参数不一定相同。 (1)均匀流与缓变流 均匀流:如果有效断面或平均流速沿程不变,且流线为 平行直线这样的稳定流称为均匀流。 非均匀流:如果有效断面沿程变化,或者有效断面不变, 但各断面上速度分布改变,这种流动称为非均匀流。 缓变流:凡有效断面上流线间夹角很小,流线曲率半经 无限大,即流线趋近于平行线的流动称缓变流。
质点运动微分方程的初始条件

质点运动微分方程的初始条件
初始条件,又称初始条件问题,是指求解给定微分方程时必须满足的一组条件。
初始条件通常包括了物体的初始位置和速度,并由物理定律所确定。
在质点运动微分方程中,初始条件一般有:
1.位置初值:指定质点初始位置,一般由坐标系确定,如
x0=Ri(t=0);
2.速度初值:指定质点初始速度,一般由分数阶导数确定,如
v0=Ri′(t=0);
3.加速度初值:指定质点初始加速度,一般由二阶以上导数确定,如a0=Ri″(t=0)。
此外,还需要指定时间t的初值,一般由实验条件或特定问题确定。
运动微分方程和运动方程

运动微分方程和运动方程1. 引言运动微分方程和运动方程是描述物体运动的重要工具,它们在物理学、工程学和其他科学领域中得到广泛应用。
本文将介绍运动微分方程和运动方程的基本概念、应用领域以及解决问题的方法。
2. 运动微分方程运动微分方程是描述物体运动的微分方程。
它可以用来表示物体在一定时间内的位置、速度和加速度之间的关系。
在一维情况下,运动微分方程可以表示为:d2xdt2=a(t)其中,x(t)是物体在时刻t的位置,a(t)是物体在时刻t的加速度。
这个方程可以通过积分求解,得到物体的位置函数x(t)。
在二维和三维情况下,运动微分方程可以表示为:d2xdt2=a x(t)d2ydt2=a y(t)d2zdt2=a z(t)其中,x(t)、y(t)和z(t)分别是物体在时刻t的x、y和z坐标,a x(t)、a y(t)和a z(t)分别是物体在时刻t的x、y和z方向的加速度。
这个方程组可以通过积分求解,得到物体的位置函数x(t)、y(t)和z(t)。
3. 运动方程运动方程是描述物体运动的方程。
它可以用来表示物体在一定时间内的位置、速度和加速度之间的关系。
在一维情况下,运动方程可以表示为:x(t)=x0+v0t+12at2其中,x(t)是物体在时刻t的位置,x0是物体在时刻t=0的初始位置,v0是物体在时刻t=0的初始速度,a是物体在时刻t的加速度。
这个方程可以通过积分求解,得到物体的位置函数x(t)。
在二维和三维情况下,运动方程可以表示为:x(t)=x0+v0x t+12a x t2y(t)=y0+v0y t+12a y t2z(t)=z0+v0z t+12a z t2其中,x(t)、y(t)和z(t)分别是物体在时刻t的x、y和z坐标,x0、y0和z0分别是物体在时刻t=0的初始位置,v0x、v0y和v0z分别是物体在时刻t=0的初始速度,a x、a y和a z分别是物体在时刻t的x、y和z方向的加速度。
质点运动微分方程

质点运动微分方程质点运动微分方程是描述物体运动的基本方程。
它是基于牛顿第二定律推导出来的。
在强加一个力的作用下,质点的加速度与力成正比,其方向与力的方向一致。
通过利用微积分学中的知识,我们可以得到质点运动的微分方程。
质点运动微分方程在物理学和工程学中有着广泛的应用。
下面,我将详细介绍质点运动微分方程的原理和应用。
首先,让我们来看看质点运动微分方程的原理。
运动状态可以用位置矢量r(t)来描述。
在t时刻,质点所处的位置矢量为r(t)。
我们假设质点受到一个力F(t)的作用力,则根据牛顿第二定律,有以下方程:F(t) = ma(t)其中,m为质量,a(t)为加速度。
根据物理学中的定义,加速度a(t)等于位置矢量r(t)对时间t的二阶导数。
因此,我们可以用r(t)对t的二阶导数来表示质点的加速度a(t),如下所示:a(t) = d^2r(t)/dt^2将上述公式代入牛顿第二定律,得到质点运动微分方程:F(t) = m(d^2r(t)/dt^2)质点运动微分方程表明了力F(t)与位置矢量r(t)之间的关系。
这个方程的意义在于,给定一定的力,我们可以通过解方程来确定质点的运动状态。
因此,在物理学和工程学中,质点运动微分方程是解决运动问题的一个基本工具。
接下来,让我们来看看质点运动微分方程的应用。
质点运动微分方程在物理学和工程学中有着广泛的应用。
例如,在机械工程学中,我们可以用微分方程来描述物体的运动状态。
机械系统通常受到多个力的作用,因此需要解决多个微分方程,以确定系统的运动状态。
在电气工程学中,质点运动微分方程可以用来描述电路中电荷的运动状态。
在控制论中,微分方程可以用来描述物理系统的动态行为,并进一步设计控制算法。
总之,质点运动微分方程是描述物体运动的基本方程。
它可以用来解决物理学和工程学中的一些运动问题,例如机械系统的运动状态、电路中电荷的运动状态和控制系统的动态行为。
因此,熟练掌握质点运动微分方程,对于物理学和工程学的学习和应用非常重要。
理论力学10质点运动微分方程

= mgR 2,于是火箭在任意位置 x 处所受地球引力 F 的大
小为
m g R2 F = x2
(b)
(3)列运动方程求解,由于火箭作直线运动,
火箭的直线运动微分方程式为:m
分离变量积分式(c)
d2 dt
x
2
mg R2 x2
(c)
因 为
d d2 tx 2d dv td dv xd dx tvd dv x
其次,定律还指出,若质点的运动状态发生改 变,必定是受到其他物体的作用,这种机械作用就 是力。
第二定律(力与加速度关系定律)
质点的质量与加速度的乘积,等于作用于质点的 力的大小,加速度的方向与力的方向相同。
设质点M的质量为m,所受的力为F,由于力F的
作用所产生的加速度为a,如图10-1所示。则此定律
以上两例都是动力学的第一类基本问题,由此可
归纳出求解第一类问题的步骤如下:
(1) 取研究对象并视为质点; (2)分析质点在任一瞬时的受力,并画出受力图; (3) 分析质点的运动,求质点的加速度; (4) 列质点的运动微分方程并求解。
例10-3 以初速v0自地球表面竖直向上发射一质量 为 m 的火箭,如图10-6所示。若不计空气阻力,火箭所
解:取质量块为研究对象,并视其为质点。质
量块沿x方向作直线运动,弹性杆对质量块的作用相 当于一弹簧,图10-8(b)是该系统的计算模型。
设弹簧刚度系数
为 k ,任意位置时弹
a
在静力学中,我们研究了力系的简化和平衡问题, 但没有研究物体在不平衡力系作用下将如何运动。在 运动学中,我们仅从几何学的角度描述了物体的运动 规律及其特征,并未涉及物体的质量(Mass)及其所受 的力。因此,静力学和运动学都是从不同的侧面研究 了物体的机械运动。
理论力学第4节 刚体的定轴转动和平面运动微分方程

圆盘质心 加速度
aC
2M 3mR
FN
2)如果作用于圆盘的力偶矩 M
圆盘连滚带滑,所受摩擦力为
3 2
fmgR
时,则
F mgf
aC fg
2(M mgfR) mR2
0
d
dt
maC F
FN mg
1 mR 2 M FR
2
纯滚动 应满足
M C aC
mg F
FN
F f FN
M
3 2
fmgR
解得
F
2M 3R
,M
3 2
RF
,aC
2M 3mR
讨论
M
1)为使圆盘作纯滚动,应满足
作用于圆盘 的力偶矩
M
3 2
fmgR
C aC mg F
• 刚体绕定轴转动的运动微分方程:绕定轴转动的刚 体对转轴的转动惯量与其角加速度的乘积,等于作 用在刚体上的所有外力对转轴力矩的代数和。
例11-5 如图所示一均质圆盘质量 m = 100kg,半径 r = 0.5m,转速 n 擦因数 f = 0.6。开始加制动闸,使闸块对轮
dt
J C
n
M C (Fi(e) )
i1
式中 M 为刚体的质量,aC 为质心的加速度,J C为刚 体对通过质心Cz轴的转动惯量。
MaC
F (e) R
y
d(JC)
dt
JC
n
M C (Fi(e) )
i1
d
dt
d 2
流体运动微分方程
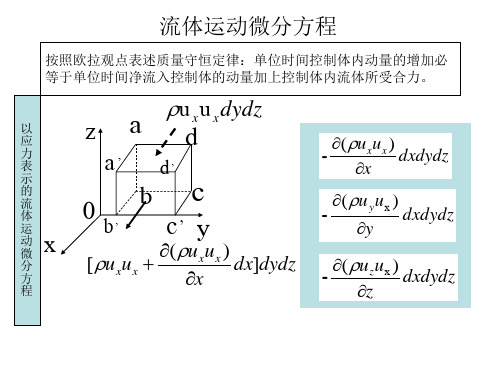
du du d 牛顿内摩擦定律 ,且 dy dy dt
d dt
流体为团运动时的角变形速度是纯剪切变形速度的两倍,顾有:
u y u x d 2 xy dt x y
则 xy yx
u y u x d ( ) dt x y
法向应力与线变形速度的关系
u x p xx p 2 x u y p yy p 2 y u z p zz p 2 z
d ux u 1 u x u x p u y u x u X [ ( ) ( ) ( x z )] dt x x x x y x y z z x
, p zz -p pzz
对于不可压缩均值流体,附加法向应力等于流体动力粘度与两倍的线变形速度 的乘积,即
u x p 2 xx 2 x u y , p yy 2 yy 2 y u z , p zz 2 zz 2 z
, xx
pxx pyy pzz
可以用任意一点三个相互垂直方 向上的 法向应力的平均值p的负 值作为黏性流体在该店的压强 黏性流体哥哥方向的法向应力等于 这个平均值加以个附加法向应力
1 p ( p xx p yy p zz ) 3
, p xx -p pxx
p yy -p p,yy
因此,切应力方向分量与角变形速度的关系
xy zy xz
粘性流体运动时存在切应力,所以法向 应力的大小与其作用面的方向有关,三个 相互垂直的法向应力大小一般不相等,即
u x u y yx ( ) 2 xy y x u y u yz ( z ) 2 zy y z u u zx ( x z ) 2 xz z x
运动微分方程的求解(共7页)

§2-3 运动(yùndòng)微分方程的求解1.求解步骤1)确定分析对象(隔离体)2)作受力分析(施力物、超距力、接触力),画隔离体图3)建立合适坐标系,写出方程解析式并给出初始位置、速度4)给出二阶常微分方程组的数字解5)阐明结果的物理含意与实质作用力为时间、位置、速度的函数;若力只是其中某一项的函数,则问题可加以简化。
2.常力作用下质点的运动〖例2-1〗求质点m在常力作用下的运动。
已知t=0时初位置和初速度分别为。
解:3.力只是时间的函数〖例2-2〗求自由电子-e在沿x轴的电场中的运动。
已知t=0时。
解:4.力只是速度的函数〖例2-3〗求在阻力正比于速度即的介质中抛物体的运动。
已知t=0时。
解:消去t得轨道方程为若阻力很小或距离很短(开始运动),即时,有轨道开始时接近抛物线,x趋于时y趋于无穷大,即为竖直直线。
5.力只是坐标的函数〖例2-4〗求做一维振动的弹性系数为k的弹簧振子的运动。
解:二维振动与利萨如图形。
6.复杂情况力为时间、坐标、速度的函数一维:(受迫振动)如LRC电路:为二阶常系数线性常微分方程,可用数值计算。
7.例题〖例2-5〗P39例1〖例2-6〗P41例3§2-4 加速(jiā sù)平动非惯性系动力学1.问题的提出在惯性系S中成立,在动系S’中是否成立?作加速平动的参照系为非惯性系。
2.改进的牛顿定律引入惯性力后牛顿定律仍成立。
3.讨论?为什么选择非惯性系:方便?惯性力与普通力的差别惯性力只是一种记号,它无施力物体,也无反作用力4.例题〖例2-7〗P44例质点运动(yùndòng)微分方程小结1.运动微分方程2.运动微分方程的解析式或3.理想光滑线约束力的求解4.平动加速非惯性系的加上惯性力后牛顿定律仍然成立处理5.例题〖例2-8〗P98补例1.4〖例2-9〗P99补例1.56.习题三〖P105习题1.21,1.27,1.32,1.33〗§2-5 质点的能量(néngliàng)积分1.第一积分直接求解运动微分方程是研究动力学问题的基本方法,但对具体问题解出微分方程有时比较困难。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
再根据an =v2/l,可求v=1.632m/s Nhomakorabeaql
T an
a mg
已知作用于质点的力,求质点的运动
例 图示质量为m的质点O带有电荷e,如已知质点在
均匀电场中所受力F=esinkt, k为常数。又质点的
初速为v0,与x轴夹角为q,且取坐标原点为起始位置。
2w
0
q2 2w 2(1 cosq )
将上式代入下式
mRq2
FN
FC
Fe
cos q
2
(2)
w
art
vr
FN M
ae arn qFC s
aC
Fe
OC
O'
R
FN
2mRw 2 (1 cosq ) FC
Fe
cos q
2
FC 2mwRq 2mwR
2w 2 (1 cosq ) 4mRw 2 cos q
z1 M0
Fe
M
h
W
分析质点M,取动坐标系
O1x1y1z1 ,固连于车厢。
a mar = F + Fe + FC
y1
mar = W + Fe
x1
mx1 0,
Fe = mae
my1 ma, mz1 mg
当 t = 0 时, x1 y1 0,z1 h,vx1 vy1 vz1 0
x1
0,
q
OC R
O'
解: ● 运动分析
分析小环。取动坐标系与大圆环固连,小环
M相对于大圆环的位置用弧坐标 s = Rq 表示。
● 受力分析
作用于小环M的力有大圆环的约束力FN。为了写出 小环的相对运动微分方程,还要加上相应的牵连惯
性力Fe和科氏惯性力FC。
Fe
mae
2mR cos q
2
w2
FC maC m2wvr 2mwRq
(3)
e(2g / u)t 1
e e (g / u)t
(g / u)t
于是物体速度随时间而变化的规律为
v uth( g t) u
th 是双曲正切。
x
dx
0
t u2 d[e( g / u)t e( g / u)t ]
0g
e e ( g / u)t
( g / u)t
物体的运动方程为
x
u2 ln e(gt / u) e(gt / u)
art vrFN
aC
w ae
arn
M
qFC
Fe
s
OC R
O'
由相对运动动力学基本方程
mar = W + FN + Fe+ FC
Fe
mae
2mR
q
cos 2
w2
•
FC maC m2wvr 2mwRq
mRq mRq2 FN
Fe FC
q
sin 2
Fe
cos
q
2
(1) ( 2)
由式(1)得
mRq 2mR sin q cos q
22
q w 2 sin q
(a)
w
art
vr
FN M
ae arn qFC s
aC
Fe
OC
O'
R
这就是小环 M 相对于大圆环的运动微分方程。
应用循环变换q q dq,将式( a )的变量分离并代
dq
入初始条件进行积分
q q dq dq
q w2 sin q
qqdq q w 2 sin qdq
第一章 质点运动微分方程
§1–1 质点运动微分方程 §1–2 质点动力学的两类问题 §1–3 质点相对运动基本方程
§1–1 质点运动微分方程
1 动力学基本定律——牛顿三定律
第一定律 不受力(平衡力系)作用的质点将永远保 持静止或作匀速直线运动。又称惯性定律。
两个基本概念:质点都有惯性,即保持原来运 动状态的性质;力是改变质点运动状态的原因。 (定性)
为了使铁球获得粉碎矿石的能量,铁球应在θ=θ0 时(如图)才掉下来。求滚筒每分钟的转数n。
q0 F
n
FN mg
视铁球为质点。铁球被旋 转的滚筒带着沿圆弧向上运动, 当铁球到达某一高度时,会脱 离筒壁而沿抛物线下落。
F = ma
铁球在未离开筒壁前m的vR2速度F,N 等
mg v
cos q Rw
πn
R
x v0t cosq
y
e mk
(t
sin kt) k
v0t
sin
q
弹簧-质量系统,物块的质量为m ,弹簧的刚度系
数为k,物块自平衡位置的初始速度为v0。求物块的
运动方程。
k
m
v0
mx+kx 0
w02
k m
l0
x v0
m sin k
kt m
mx=-k( x ) mg st
l0 k
kst mg
y1
1 2
at
2
,
z1
h
1 2
gt 2
z1
h
g a
y1
例题 一质量是m的小环M套在半径是R的光滑圆 环上,并可沿大圆环滑动,而大圆环在水平面内
以匀角速度w绕通过点O的铅垂轴转动。在初瞬 时,q = 0, q = 2 w ,试写出小环M相对于大圆 环的运动微分方程,并求出大圆环对小环M的约
束力。
M
w
u2
ln(ch
gt )
g
2
g
u
分析例 神州6号载人飞船回收过程中的动力学问题。 假设回收舱重为P, 回收舱在距离地面h处打开阻 力伞,此时速度为v0,回收舱受到的空气阻力与
速度成正比:F=cv,c为常数。求回收舱到达地
面时的速度和加速度。
例题粉碎机滚筒半径为R,绕通过中心的水平
匀速转动,筒内铁球由筒壁上的凸棱带着上升。
x v0
m sin k
kt m
1. 重力mg只改变了系统的平衡位置,对
运动规律并无影响。 2. 物块垂直悬挂时,
m
坐标原点选择不同对运动微分方程的影响
v0 这一问题请同学们自己研究。
例题 质量是m的物体M在均匀重力场中沿铅直线 由静止下落,受到空气阻力的作用。假定阻力F与速
度平方成比例,即F=v2 ,阻力系数单位取kg/m,
第二定律 质点的质量与加速度的乘积等于作用于
质点的力的大小,加速度的方向与力的方向相同。
即
ma F
此式即质点动力学的基本方程。 此定律给出:物体的受力与物体运动状态的
改变之间定量关系 (定量)。
ma F
力使物体产生沿其方向的加速度 F—作用在质点上的合力(共点力系的合力) a—质点相对惯性系的加速度(绝对加速度) 瞬时运动量的关系 适用范围(质点, 平动刚体)
动力学绪论
1 动力学的研究对象
动力学的研究对象:质点和质点系。 质点是指几何尺寸可以忽略不计,但具有一定质 量的物体。 质点系是由几个或无限个相互联系的质点组成的 系统。刚体是质点系的一种特殊情形。
2 动力学的研究内容
动力学是研究物体的机械运动与作用力之间的关系。 已知运动求力
已知力求运动 既有未知的运动量,又有未知力.
2
大圆环对小环的约束力为
FN
mRw 2[3(1
cosq )
4 cos q ]
2
本章小结
1.质点动力学的基本方程为
ma F
m
d 2r dt 2
F
2.质点动力学的两类问题
3.质点相对非惯性参考系矢量形式的微分方程为
m
d 2r dt 2
F
Fge
FgC
二是已知作用于质点的力,求质点的运动。
这类问题一般比较繁琐。求解这类问题时,首 先要列出质点运动微分方程式,然后进行积分,同 时利用运动的初始条件确定积分常数,求出质点的 运动规律。
具体求解步骤: 1. 明确研究对象 2. 分析受力----全部外力
分析运动----一般位置(运动描述的方法) 3. 建立方程并求解
2.运动微分方程
n
ma Fi i 1
m
d 2r dt 2
F
(1)质点运动微分方程在直角坐标轴上投影
m d 2 x
dt 2
n i 1
Fx i,
d 2 y
m dt2
n i 1
Fy i,
m
d 2z dt 2
n i 1
Fzi
(2) 质点运动微分方程在自然轴上投影
m dv dt
n i 1
Fi
m v2
n
Fni,
i 1
(3) 质点运动微分方程的复合运动形式
aa ae ar ac
m(ae ar ac ) F
§1–2 质点动力学的两类问题
一是已知质点的运动,求作用于质点的力。
求解这类问题时,只需根据已知的运动规律, 通过微分运算或通过复合运动求出质点的加速度; 从而按质点运动微分方程式求出未知力。
3 解决动力学问题的基本方法
质点运动微分方程-----质点 动力学普遍定理(三大动力学定理+达朗伯原理)
-----质点系 分析力学方法—虚位移原理
4 动力学的理论基础
牛顿定律的适用范围: 惯性坐标系; 速度远远小于光速; 宏观物体; 质点(平动刚体)
动力学理论有着广泛的应用。航天航空中的动力学计 算、结构的动荷响应、高速转动机械的动力学行为分 析等都需要有动力学的知识作为基础。
于筒壁上与其重合点的速度。即
30
m v2 R
