2018第三章-力系的平衡
第三章力系的平衡静定与超静定的概念

FCy
FE
FE=250N,
[CE]
整体]
F
q FQ
Fix=0, FAx=0
A
FAx
B
C
FAy 1 1
2
2
MA=0, –F·1+FB·2–FQ·4–M+FE·8=0
FB
ME
D 2m FE
FQ=4· FB=1500N q Fiy=0, FAy+FB+FE–F–FQ=0
FAy=–250N
例4-15:三根自重不计的杆组成构件如图示,巳知:F=600N,
得: FAx= –400N,
Fiy=0, FAy–F =0
得:FAy= 1000N,
M F3 [BD]
Miz 0
空间平行力系平衡方程
Fiz 0
Mix 0 Miy 0
例3-6:三轮平板车放光滑地面上,自重为:W,货重为F, 已知:F=10kN,W=8kN,试求各轮约束力的值。
解:这是空间平行力系。
z
Mix =0,
(200–80)W–200·FA =0; FA=4.8kN,
Miy =0,
y
FC
FAx= –2.8kN。
如校核方程: MCi=0, 应满足。
例3-9:图示雨蓬结构,因雨蓬对称结构可简化为平面结构,自
重不计,已知有力F作用,试求三根支撑杆的约束力。
解: 试用三力矩方程
B
MA 0,
M C 0,
2F1 5F 0, 1m
5F F1 2
1m
F2 4F 0 A
C 1m
3
M F3 2
0 32 42
FAx
B
3m
FAy
MD
第三章力系的平衡介绍

工 程 力 学
§3-2
平面力系的平衡条件
F1 Fn F3
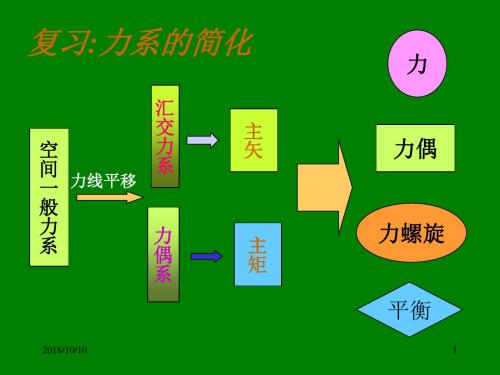
1、平面任意力系的平衡方程 F2 平面任意力系平衡的充要条件是: 力系的主矢和对任意点的主矩都等于零。
0 FR
第 三 章 力 系 的 平 衡
Mo 0
平面任意力系
FR ( Fx ) 2 ( Fy ) 2
M O M O (F )
2
0
F
x
0,
F
y
0,
F
z
0
即:汇交力系的平衡条件是力系中所有各力在各个坐
标轴中每一轴上的投影的代数和分别等于零。
工 程 力 学
三、空间平行力系的平衡方程
第 三 章 力 系 的 平 衡
F
z
0,
M (F ) 0, M (F ) 0
x
y
工 程 力 学
四、空间力偶系的平衡方程
第 三 章 力 系 的 平 衡
工 程 力 学
例:如图所示为一种起吊装置的结构简图。图中尺寸d , 载荷F, <FAD =60均为已知。若不计各杆自重,试求杆AF与杆AD在各 自的约束处所受的约束力。
第 三 章 力 系 的 平 衡
工 程 力 学
第 三 章 力 系 的 平 衡
工 程 力 学
例:滑轮支架系统如图所示。已知G,a,r,θ ,其余物体重 量不计,试求A和B的约束力。
工 程 力 学
3、平面汇交力系的平衡方程
F
x
0,
F
y
0
4、平面力偶系的平衡条件
第 三 章 力 系 的 平 衡
M 0
即:力偶系各力偶力偶矩的代数和等于零。
工 程 力 学
工程力学力系平衡

D
FC
l
A B
l
FP
D
第 三 种 情 形
l
C FA A l FCy l B l FP D
FCx
C
FA A
l
B
l
FP
D
第 三 种 情 形
FCy
FCx C
E
MA ( F ) = 0 : FCx l -FP 2l = 0 MC ( F ) = 0 : -FA l - FP 2l = 0 ME ( F ) = 0 : -FCy 2l -FA l = 0
A
F =0
x
l -FQ -FW x FTB lsin=0 2 l FP x+FQ 2 = 2 FW x F FTB= Q lsin l
F =0
y
FAx FTB cos=0 FQ 2 FW x FQl FW FAx= x cos30 = 3 l 2 l FAy-FQ-FP+FTB sin=0
例题
均质方板由六根杆支 撑于水平位臵,直杆 两端各用球铰链与扳 和地面连接。板重为 P,在A 处作用一水 平 力 F , 且 F=2P , 不计杆重。求各杆的 内力。
简单的刚体系统平衡问题
前面实际上已经遇到过一些简单刚体系统 的问题,只不过由于其约束与受力都比较简单, 比较容易分析和处理。 分析刚体系统平衡问题的基本原则与处理 单个刚体的平衡问题是一致的,但有其特点, 其中很重要的是要正确判断刚体系统的静定性 质,并选择合适的研究对象
平衡方程
根据平衡的充要条件
F1 M1 O
z
F2
M2
y Mn
FR =0 , MO=0
第3章平衡问题 矢量方法
M
F
iy
A
0
12 FBy 10 P 6 P 1 4P 2 2 P 5F 0
FBy 77.5kN
FAy FBy 2 P P 1P 2 0
解得
0
解得
FAy 72.5kN
F
ix
0
FAx F FBx 0
27
2018/10/10
2)取吊车梁,画受力图.
未知量个数和独立方程个数比较
• 未知量个数 = 独立方程个数
• 未知量个数 >独立方程个数
静 定
静不定
静不定次数 =未知量个数 - 独立方程个数 • 未知量个数 <独立方程个数
2018/10/10
不平衡 ???
9
静不定带来的问题:
1
2 G
3
• 3根绳子的受力相同吗?
图示结构在安装时会遇 到什么问题?
M O 0.
M x 0 M y 0 M z 0
投 影 式
力矩 式
2
2018/10/10
平面任意力系的平衡方程
M x 0 M y 0 Fz 0
设力系所在平面为O-xy
平 衡 方 程 有 三 种 形 式 2018/10/10
三矩式
2018/10/10
A, B, C 三个取矩点,不得共线
4
(2)汇交力系平衡方程
空 间 汇 交 力 系
MO 0
平 衡 方 程
Fx 0 Fy 0 Fz 0
平面汇交力系平衡方程
Fx 0 Fy 0
5
2018/10/10
定研究对象:滑轮 定问题性质:平面 受力分析 主动力简化
C·A上传 【理论力学】第三章 力系的平衡

FDC FDB
P
BE = CE DB = DC 则:FDB = FDC
DO DO DO ∑ Fiy FDB = 0; FDC FDA =0 DB DC DA
cm DB = 20 3, , DA = 20 5;cm
FDA
EO AO 0; ∑ Fiz = FDB 2 FDA P=0 DB DA
汇交力系
√2 FA = FC = — F = FB 力多边形自行封闭
2
r F r F
C
B
r FB
例3-2:已知物体的重量为 .求:(a)平衡时铅垂力 , - :已知物体的重量为P )平衡时铅垂力F, (b)维持平衡时 的最小值及其相应方向.不计构件自重. )维持平衡时F 的最小值及其相应方向.不计构件自重. 讨论题
3 联立求解 FDA = P = 745N , 3 FDB = FDC = 289N
避免解联立方程 改变坐标方向
立柱AB与绳 与绳BC 例3-8:起重机起吊重量 =1kN.求:立柱 与绳 ,BD,BE - :起重机起吊重量P . x' 的受力. 的受力.
解: B点有四个未知力汇交, 点有四个未知力汇交, 点有四个未知力汇交
§3-1 汇交力系的平衡 -
汇交力系简化的结果
汇交力系平衡的充要条件: 汇交力系平衡的充要条件: 充要条件 力系的合力等于零
r FR = 0
各力全部 汇交力系平衡的几何条件 力多边形自行封闭 首尾相连 几何条件: 汇交力系平衡的几何条件: 仅适用于平 力多边形法则 解析条件: 汇交力系平衡的解析条件 平衡方程 汇交力系平衡的解析条件: 面汇交力系 几何法 空间汇交力系: 合力投影定理
工程力学第三章-力系的平衡

将上式两边向x、y、z 轴投影,可得平衡方程
F F F
可以求解3个未知量。
x y
z
0 0 0
• 2.平面汇交力系
力系的平衡
• 力偶系的平衡方程 • 1.空间力偶系
平衡的充要条件(几何条件) M Mi 0 将上式两边向x、y、z 轴投影,可得平衡方程
M M M
可以求解3个未知量。
ix iy iz
0 0 0
• 2.平面力偶系
力系的平衡
• 平衡的充要条件:力偶系中各力偶矩的代数和等于零.
m 0
i
• 任意力系的平衡方程 空间任意力系: • 平衡的充要条件:力系的主矢和对任一点的主矩均为零。
FR 0
MO 0
G3 a
e
G 3(a b) FNAb G1e G 2L 0 G 3(a b) G1e G 2L FNA 2 b
由(1)、(2)式 得:
G1 G2 L
G1e G 2L G3 ab
3
A FN A b
B FN B
(2)空载时
不翻倒条件:FNB≥0 (4) 由 mA 0 得:
FAB = 45 kN
600
y B TBC 15 15 30 TBD
0 0 0
x
C
D
150
B
300
TBD=G E
A
E
FAB G
解题技巧及说明:
1、一般地,对于只受三个力作用的物体,且角度特殊时用 几 何法(解力三角形)比较简便。 2、一般对于受多个力作用的物体,且角度不特殊或特殊, 都用解析法。 3、投影轴常选择与未知力垂直,最好使每个方程中只有一 个未知数。
理论力学第3章 力系的平衡

基础部分——静力学第3 章力系的平衡主要内容:§3-7 重心即:力系平衡的充分必要条件是,力系的主矢和对任一点3-2-1 平衡方程的一般形式∑=iF F R ∑=)(i O O F M M 已知∑=iF F R ∑=)(i O O F M M 投影式:平衡方程i即:力系中所有力在各坐标轴上投影的代数和分别等于零;所有力对各坐标轴之矩的代数和分别等于零。
说明:¾一般¾6个3个投影式,3个力矩式;¾一般形式基本形式3-2-2 平面一般力系的平衡方程xy zOF1F2Fn平面内,¾一般形式¾3个2个投影式,1个力矩式;¾ABAzzCC附加条件:不垂直附加条件:不共线Bx二矩式的证明必要性充分性合力平衡AA 点。
B 点。
过ABBx故必有合力为零,力系平衡证毕平面问题3个3个 解题思路BAMFo45l l[例3-1] 悬臂梁,2解:M A 校核:0)(=∑F MB满足!解题思路?AyF AxF[例3-2] 伸臂梁F AxF AyF BF q 解:0=∑x F 0)(=∑F AM3(F −+0=∑yF3(F −+(F −+0)(=∑F AM=∑yF0=∑x F F AxF AyF BF q 思考:如何用其他形式的平衡方程来求解?0=∑x F 3(F −+0)(=∑F AMF AxF F BF q 0)(=∑F BM(F −+二矩式思考练习][练习FFlll F ACB DlllACB DM=F l[思考][思考]lll F ACB DlllACB DF见书P54例3-1—约束lllACB DF—约束CBADEFM—约束—约束—整体平衡局部平衡CB ADEFM研究对象的选取原则¾仅取整体或某个局部,无法求解;¾一般先分析整体,后考虑局部;¾尽量做到一个方程解一个未知力。
qCBAm2m2m2m2MBCM[例3-3] 多跨梁,求:如何选取研究对象?F CqF CFAxF AyM ABAqF'BxF'ByM A F Ax F AyF Bx F By解:先将分布力用合力来代替。
第三章 力系的平衡

FR =XR i+YR j
以及 F1+F2+…+Fn=(X1i+Y1j)+(X2i+Y2j)+…+(Xni+Ynj) =(X1+X2+…+Xn)i +(Y1+Y2+…+Yn)j
i a1
b1
x
F F F Xi Yj
x
y
式中:i、j——坐标轴x、y正向的单位矢量。
目录
第三章 力系的平衡\平面力系向一点的简化 【例3.1】 试计算图示各力在x轴和y轴上的投影。已知F1= F2
=100 N,F3=150 N, F4=200 N。
目录
第三章 力系的平衡\平面力系向一点的简化
第三章 力系的平衡
第三章 力系的平衡
本章介绍平面力系向一点简化的结果,由此得到平面力系的平 衡条件和平衡方程;在介绍力在空间直角坐标轴上的投影和力对轴 之矩的基础上,直接给出空间力系的平衡方程。着重于应用平衡方 程求解力系的平衡问题。最后介绍物体的重心、形心和静矩的概念 及其计算。本章是刚体静力分析的重点。
FRd1 sin MO
因 FR sin YR ,故
d1
MO YR 0.5 m目录第三章 力系的平衡\平面力系向一点的简化
2)力系向A点简化。主矢与上面 的计算相同。主矩为
MA=∑ MA (F) = -F×3m - W1×1.5m - W2×4m = -3150 kNm
其转向如图所示。
明,线分布荷载合力的大小等于荷载图的面积,合力的作用线通过 荷载图的形心,合力的指向与分布力的指向相同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平衡方程:
Fx 0
Mx(F )0
Fy 0
My(F )0
Fz 0
Mz(F ) 0
一、平面汇交力系
力系的平衡条件:主矢为零
平面汇交力系平衡方程:
Fx 0
平衡几何条件:
Fy 0
汇交力系的力多边形自行封闭
求解方法: 1、 几何法:利用力多边形自行封闭求解 2、 解析法:利用平衡方程求解
思考题1
若匀质杆AB长为2R,求AB的平衡位置。
AB与水平线夹角α=32.5°
二、平面力偶系 n
平面力偶系合成的结果 : M Mi i1 一个合力偶,其力偶矩等于原力偶系中 所有力偶矩之代数和。
平面力偶系的简化结果:主矩 Mo
平面力偶系的平衡条件: Mo = 0
平衡方程: M 0
例3 图中M, r 均为已知, 且 l=2r, 各杆自重不计。
例1 图a所示是汽车制动机
构的一部分。司机踩到制动
蹬上的力F =212 N,方向与
水平面成α = 45角。当平衡
时,DA铅直,BC水平,试
求拉杆BC所受的力。已知
EA=24 cm, DE=6 cm
O
点E在铅直线DA上 ,又B 、
C 、D都是光滑铰链,机构
的自重不计。
F
A
BE C D
24cm 6cm
F F2 60 Ay
Fy
FBy
0
F1
F2
sin
60
0
x 3、解方程,得
FAx
FBy
FAx 0.75 kN
FBy 3.56 kN FAy 0.261 kN
例7 如图所示为一悬臂梁,A 为固定端,设
梁上受强度为 q 的均布载荷作用,在自由端B 受一集中力 F 和一力偶 M 作用,梁的跨度为 l,求固定端的约束力。
FAx 32.89 kN, FAy 2.32 kN, M A 10.37 kN m
例9 图示三铰拱桥,由左右两段借铰链C连
接,又用铰链A,B与基础相连接。已知每 段重G = 40 kN,重心分别在D,E处,且桥 面受一集中载荷F =10 kN。设各铰链都是光 滑的,试求平衡时各铰链约束力。
3、联立求解。
FA
1 3.8
2G1
2.5G2
5.5G
A
G3 G1 B
G2
G
1.8 m 2.0 m 2.5 m
FA
FB
3.0 m
4、不翻倒的条件是:
FA≥0, 所以由上式可得
G≤
1 5.5
2G1
2.5G2
7.5
kN
故最大起吊重量为 Gmax= 7.5 kN
例6 外伸梁的尺寸及载荷如图所示,
F1=2 kN,F2=1.5 kN,M =1.2 kN·m, l1=1.5 m,l2=2.5 m,试求铰支座A及
FB
2、取整体为研究对象
Fx 0
30
Mq
F
A
C
B 60 D
FAx FB cos 60 F sin 30 0
l
MA
FAy M
Fy 0
FAy
FB
sin
60 2ql F cos
30
FAx
0
A
l
M AF 0
ll
l
q
30
F
C
B 60 D
FB
ll
l
M A M 2ql 2l FB sin 60 3l F cos 30 4l 0 解方程得:
FB
sin
F 750 N
解析法 1、取制动蹬 ABD 为研究对象
y
O 45°
2、画受力图
A
3、列出平衡方程
F
建立图示坐标系
Bx
DFB
Fx 0
FB FD cos F cos 45 0
Fy 0
FD sin F sin 45 0
联立求解得 FB 750 N
例2 利用铰车绕过定
滑轮B的绳子吊起一货 物重G = 20 kN,滑轮 由两端铰接的水平刚 杆AB和斜刚杆BC支持 于点B 。不计铰车的 自重,试求杆AB和BC 所受的力。
支座B的约束力。
F1
ll
F2
M
60
A B
l2
l1
解:1、 取梁为研究对象,受力分析如图。
2、 选取坐标系,列平衡方程。
F1 ll
M
A
B
Fx 0
F2
FAx F2 cos 60 0
60
MA(F) 0
l2
l1
FByl2 M F1l1 F2(l1 l2)sin 60 0
y FAy A
F1 M B
FR' 0
Mo 0
平面任意力系平衡方程基本形式:(一矩式)
Fx= 0 Fy = 0 MO(F)= 0
三个独立的平衡方程,可解 3 个未知量。
平衡方程其他形式:
B
Fx = 0 MA(F)= 0 MB(F)= 0
A
x
A、B 连线不垂直于x 轴
(两矩式)
MA(F)= 0 MB(F)= 0 MC(F)= 0 (三矩式)
y
FAy
l
l
A FAx
45
C
FC
x B F
3、解平衡方程,可得
FC 2F cos 45 28.28 kN
FAx FC cos 45 2F 20 kN
FAy F FC sin 45 F 10 kN
例5 一种车载式起重机,车重G1= 26 kN,起
重机伸臂重G2 = 4.5 kN,起重机的旋转与固 定部分共重G3 = 31 kN。尺寸如图所示。设伸 臂在起重机对称面内,且放在图示位置,试 求车子不致翻倒的最大起吊重量Gmax。
G3
G2
G
A
G1
B
1.8 m 2.0 m 2.5 m
FA
FB
3.0 m
解1:、取汽车及起重机为研究
对象,受力分析如图。
2、列平衡方程。
G3
G2
G
A
G1 B
F 0
1.8 m 2.0 m 2.5 m
FA
FB
3.0 m
FA FB G G1 G2 G3 0
MB F 0
G(2.5 m 3 m) G2 2.5 m G1 2 m FA(1.8 m 2 m) 0
y
F’Cy
F
F’Cx C
E
G
O FBx
B x
FBy
Fx 0,
FCx FBx 0
Fy 0,
FCy FBy F G 0
MC F 0,
F 3 m G 5 m FBy 6 m FBx 6 m 0 联立求解得: FCx = -FBx = 9.2 kN, FCy= 2.5 kN
M
F
q
45
B
A
l
解:1、 取梁为研究对象,受力分析如图
2、 选取坐标系,列平衡方程
q
M
F
45
Fx 0, FAx F cos 45 0
A
l
B
Fy 0, FAy ql F sin 45 0
M A F 0,
l M A ql 2 F cos 45 l M 0
y
M
3、 解方程,得
q FAx
45 F FAx F cos 45 0.707 F
A
l
B x FAy ql 0.707F
MA
FAy
MA
1 2
ql 2
0.707 Fl
M
课堂练习:梁AB上受到一个均布载荷和一
个力偶作用,已知载荷集度(即梁的每单位
长度上所受的力)q = 100 N/m,力偶矩大小 M = 500 N·m。求活动铰支座 D 和固定铰支座
忽略不计,求铰链A的约束力和杆DC所受的
力。
F
A
B
C
D
A
F 解:1、取AB杆为研究对象,
B
C
受力分析如图。
2、 列平衡方程:
D
y
FAy
l
l
AFAx
C 45 FC
建立如图所示的坐标系
Fx 0, FAx FC cos 45 0
Fy 0, FAy FC sin 45 F 0
x B
F MA F 0, FC cos 45 l F 2l 0
C B
A
C
A、B、C三点不
在同一条直线上
平面任意力系平衡方程讨论:
Fห้องสมุดไป่ตู้ = 0 Fy = 0 MO= 0
平面任意力系:三个独立的平衡方程,可解3个未知量
平面汇交力系:二个独立的平衡方程,可解2个未知量
平面平行力系:二个独立的平衡方程,可解2个未知量
平面力偶系: 一个独立的平衡方程,可解1个未知量。
第三章 力系的平衡
本章重点:
1、力系平衡方程及其应用 2、物体系统平衡问题分析 3、桁架内力分析
4、具有摩擦的平衡问题 5、重心
§3-1 力系的平衡方程
F2
z
F1
MO
z
FR′
y o
y o
x
Fn
x
空间任意力系向任意点O简化为: 主矢 FR′=∑Fi 主矩 MO=∑MO(Fi )
平衡的充分必要条件: FR' 0 Mo 0
(a)
解: 几何法 1、取制动蹬ABD为研究对象,
并画出受力图。
AF
2、作出相应的力多边形。
BE
O
FD
FB
D
(b)
I
F
FD
