高三数学选填专题限时训练
高考数学复习《30分钟选填》 (理科版) 限时训练(25)答案

限时训练(二十五)答案部分二、填空题:9.{}2,3,4- 10. 92314.2,⎡⎣解析部分1. 解析 解法一: ()()()()i 1i i 12i a b a b a b ++=-++=+,所以12a b a b -=⎧⎨+=⎩,解得3212a b ⎧=⎪⎪⎨⎪=⎪⎩.故选D.解法二: ()()()()12i 1i 12i 12i i 231i i 1i 1i 1i 222a b +-++-++====+++-.故选D. 2.解析 若1a =,则()1f x x =-,函数()f x 在[)1,+∞上单调递增;若函数()f x x a =-在区间[)1,+∞上为增函数,可得1a …,不一定得出1a =.所以“1a =”是“函数()f x x a =-在区间[)1,+∞上为增函数”的充分不必要条件.故选A. 3.解析 ππtan 2tan 236y x x ⎡⎤⎛⎫⎛⎫=-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,根据函数图像平移左加右减的规律,将tan 2y x =向右平移π6个单位长度可得πtan 26y x ⎡⎤⎛⎫=- ⎪⎢⎥⎝⎭⎣⎦πtan 23x ⎛⎫=- ⎪⎝⎭的图像.故选C.4.解析输出()440134710402862s +⨯=+++⋅⋅⋅+==.故选B.5.解析 91x ⎫-⎪⎭的通项为()92191C rr rr r T x x --+=-,令902r r --=,解得3r =,所以91x ⎫⎪⎭的常数项为()3391C 84-=-.故选C.6.解析 解法一(图像法):函数()f x 的图像如图所示,观察图像可得函数()f x 的零点个数为2. 故选B.解法二:令()()310x x +-=,解得3x =-或1x =(舍去);令2ln 0x -+=,解得2e x =,所以函数()f x 有2个零点.故选B.7.解析 由于()2y f x =-是由()y f x =向右平移2个单位长度得到的,且()2y f x =-在[]0,2上单调递减,所以()f x 在[]2,0-上单调递减.由题可得()()22b f f ==-,又因为210-<-<,所以()()()210f f f ->->,即b c a >>.故选A.8.解析 由定义的新运算可得()()()()1x y x y x y x y +⊗-=+-+,所以()()11x y x y +-+<,整理得2210x x y y -+++-<.因为此不等式对任意实数x 恒成立,所以()()2214110y y ∆=-⨯-+-<.解得3122y -<<,即y 的取值范围为31,22⎛⎫- ⎪⎝⎭.故选D. 9.解析 解方程得{}2,3A =,{}4,2B =-,所以{}2,3,4AB =-.10.解析 画出不等式组表示的平面区域如图所示,当直线z x y =+过A 点时,z 有最大值,联立方程105350x y x y -+=⎧⎨--=⎩,解得45x y =⎧⎨=⎩,即()4,5A ,所以max 9z =.1=011.解析 依题意,设抛物线22y bx =的焦点为A ,则,02b A ⎛⎫⎪⎝⎭,因为12:5:3F A F A =, 所以:5:322b b c c ⎛⎫⎛⎫+-=⎪ ⎪⎝⎭⎝⎭,化简得2c b =,所以c e a ====3=. 12.解析 利用正弦定理将cos cos b c B C =中边的关系转化为角的关系,得sin sin cos cos B CB C=,即tan tan B C =,又因为(),0,πB C ∈,所以B C =.因为cos A =()cos πcos2B C B -+=-=⎡⎤⎣⎦()22cos 1B --,所以222cos 13B -=-,得21cos 6B =,又由题可得cos 0B >,故cos B =. 13.解析 因为2AB =,60ABC ∠=, AD 为BC 边上的高,所以1BD =.又因为3CB =,所以13BD BC =.如图所示,13AD AB BD AB BC =+=+,所以111226AO AD AB BC ==+, 所以11,26λμ==,则23λμ+=.14.解析 设平面1AD Q 与直线BC 交于点P ,则P 为BC 的中点,连接,AP QP ,取1BB 的中点E ,11B C 的中点G ,连接11,,A G A E EG .如图所示.易证QP EG ∥,又因为QP ⊂平面1AD Q ,EG ⊄平面1AD Q ,所以//EG 平面1AD Q .同理1//A G 平面1AD Q ,又因为1AG EG G =,所以平面1A GE ∥平面1AD Q .由已知1A F ∥平面1AD Q ,所以1A F ⊂平面1A GE ,设1A F 与平面11BCC B 所成的角为θ,因为11A B ⊥平面11BCC B ,所以111tan A B B Fθ=,当点F 与点E 或点G 重合时,1B F 最大,tan θ有最小值,此时1111tan 212A B B F θ===;当点F 为EG 中点,即1B F EG ⊥时,1B F 最小,tan θ有最大值,此时CBPGED1C1B 1A 1DCBAQ111tan4A BB Fθ===所以tanθ的取值范围是2,⎡⎣.。
高三数学选填专题限时训练

高三数学选填专题限时训练一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}220A x x x =-<,101x B x x +⎧⎫=>⎨⎬-⎩⎭,则()AB =R( ).A.{}01x x << B.{}12x x < C.{}01x x < D.{}12x x <<2.已知12a -<<,复数z 的实部为a ,虚部为1,则z 的取值范围是( ). A.[)1,5B.⎡⎣C.D.()2,53.从正方形4个顶点及其中心这5个点中,任取2个点,则这2个点之间的距离不小于该正方形边长的概率为( ). A.35 B.25 C.15 D.3104.直线l :1y kx =+与圆O :221x y +=相交于,A B 两点,则“1k =”是“OAB △的面积为12”的( ).A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分又不必要条件 5.下列命题正确的是( ).A.函数sin 23y x π⎛⎫=+ ⎪⎝⎭在区间,36ππ⎛⎫- ⎪⎝⎭内单调递增B.函数44cos sin y x x =-的最小正周期为2πC.函数cos 3y x π⎛⎫=+ ⎪⎝⎭的图像是关于点,06π⎛⎫⎪⎝⎭成中心对称的图形D.函数tan 3y x π⎛⎫=+⎪⎝⎭的图像是关于直线6x π=成轴对称的图形 6.一几何体的三视图如图所示,则该几何体的体积为( ). A.13π B.12π C.2π D.π俯视图侧视图正视图7.执行如图所示的程序框图,则输出的结果为( ). A.1- B.1 C.2- D.28.已知双曲线M :22221x y a b -=和双曲线N :22221y x a b-=,其中0b a >>,且双曲线M 与N 的交点在两坐标轴上的射影恰好是两双曲线的焦点,则双曲线M 的离心率是( ). A.512+ B.512- C.532+ D.352- 9.已知正实数,m n 满足log log a a m n <()01a <<,则以下不等式成立的是( ). A.22mn< B.11m n m n <++ C.11ln ln m n< D.33m m n n +<+ 10.已知函数()122,0log ,0x a x f x x x ⎧⋅⎪=⎨>⎪⎩,若关于x 的方程()0f f x =⎡⎤⎣⎦有且仅有一个实数解,则实数a 的取值范围是( ). A.()(),00,1-∞ B.(),0-∞ C.()0,1 D.()()0,11,+∞11.点(),Q x y 在不等式组22211220y x x y x y --⎧⎪⎨--+⎪⎩所确定的区域内运动,点()1,0P -为定点,则线段PQ 的长度的最小值是( ).A.22 B.173 C.5 D.35512.已知点O 是ABC △的外心, 6AB =, 10AC =.若AO x AB y AC =+, 且2105x y +=,则ABC △的面积为( ).A.24B.2023 C.18或2023D.24或202 二、填空题:本大题共4小题,每小题5分,共20分. 把答案填写在题中的横线上.开始i =0,S =1,A =2是 否i =i +1 输出A 结束A =1−1Ai >2015?S =S ×A13. 在ABC △中,,,a b c 分别是内角,,A B C 的对边,若3A π=,1b =,ABC △则a 的值为 .14. 二项式712x x ⎛⎫+ ⎪⎝⎭的展开式中31x 的系数是 .15. 若数列{}n a 满足:114a =-,111n n n a a a --⋅=-()1n >,则2015a = . 16. 定义域为[],a b 的函数()y f x =图像的两个端点分别为,A B ,(),M x y 是()f x 图像上任意一点,其中()1x a bλλ=+-[]()0,1λ∈,向量()1ON OA OB λλ=+-,若不等式MNk 恒成立,则称函数()f x 在[],a b 上“k 阶线性近似”.若函数1y x x=-在[]1,2上“k 阶线性近似”,则实数k 的取值范围是 .答 案13.14.84 15.5 16. 32⎡⎫+∞⎪⎢⎣⎭1. 解析 (0,2)A =,(,1)(1,)B =-∞-+∞,故[]1,1B =-R.由数轴分析可得(]0,1AB =R.故选C.2. 解析 根据题意可设i z a =+,则z =因为12a -<<,则204a <,所以z ⎡∈⎣.故选B .3. 解析 如图所示,从图中5个点中任意选出2个点组成一条线段,有25C 10=(种)不同的选择方案,其中距离小于正方形边长的有4种, 则距离大于或等于正方形边长的有6种,其概率为P =63105=.故选A.4. 解析 当1k =时,易推知OAB △的面积为12,充分性成立; 当OAB △的面积为12时,由题可得1OA OB ==, 且11sin 22S OA OB AOB =∠=,所以2AOB π∠=,由图形性质转化到直线l 到圆心O 的距离d 为2,即d ==1k =±,必要性不成立.故选A. 5. 解析 当,36x ππ⎛⎫∈-⎪⎝⎭时,22,333x πππ⎛⎫+∈- ⎪⎝⎭,故不在sin y x =的某一单调增区间内,故A 错误;44cos sin y x x =-()()2222cos sin cos sin x x x x =-+22cos sin x x =-cos2x =,即T =π,故B 错误; 把6x π=代入cos 3y x π⎛⎫=+ ⎪⎝⎭,得0y =,故C 正确;正切函数没有对称轴,仅有对称中心,故D 错误.故选C.6. 解析 分析知该几何体为圆柱的一半,故体积为()2122V =⨯π⨯1⨯=π.故选D.2015,继续2015,继续2015,继续2015,继续2015,继续……为周期的循环, 故当20166723i ==⨯时,退出循环,因此2A =.故选D.8. 解析 如图所示,易知2a c +=,即212c e a ===.故选A.9. 解析 由题意得0n m <<,故根据2xy =在R 上单调递增,A 错误;作差比较或根据函数1xy x =+在()1,-+∞上单调递增,B 错误; 由题意得110m n<<,根据ln y x =在()0,+∞上单调递增,C 正确; 根据3y x x =+在R 上单调递增,D 错误.故选C. 评注 问题的本质就是研究函数的单调性.10. 解析 在()0f f x =⎡⎤⎣⎦中令()t f x =,则()0f t =. 若0a =,验证易知此时不符合题意;若0a ≠,分0a >,0a <讨论其图像大致如图所示.由()0f t =知,()1t f x ==,问题转化为()1t f x ==有且仅有一个实数解. 因此当0a <时,此式恒成立;当0a >时,()f x 与y 轴的交点()0,a 必须在1y =的下方,故01a <<. 综上所述:()(),00,1a ∈-∞.故选A.11. 解析 分解问题,211y x --21,123,1y x x y x x -+<⎧⇔⎨-⎩;xyaaa <0a >0123–1–2–3123–1–2–3OxO yc2a +c 2c22220x y x y--+⇔()()22110x y ---⇔()()20x y x y +-⇔- 020x y x y -⎧⎨+-⎩或020x y x y -⎧⎨+-⎩. 画出可行域,如图所示,分析知点P 到直线21y x =-+的距离为PQ 的最小值,故min 5PQ ==.故选D. 评注 ()()22110x y ---也可以等价为11x y --,采用分类讨论解决.12. 解析 解法一:以点A 为坐标原点,建立如图所示的平面直角坐标系. 设()00A ,,BAC θ∠=,则()6cos ,6sin B θθ,()10,0C . 取AC 的中点D ,连接OD ,则OD AC ⊥. 因为OD OA AD =+12AC xAB y AC =--=12y AC x AB ⎛⎫-- ⎪⎝⎭, 故OD AC ⋅12y AC xA AC B =⎡⎤⎛⎫--⋅⎪⎢⎥⎝=⎭⎣⎦212A C C y A xAB ⎛⎫-- ⎪⎝⎭⋅=110060cos 2y x θ⎛⎫-⨯- ⎪⎝⎭0=,即c 0106os 5x y θ-=-,把2105x y +=代入化简得6cos 02x x θ-=,得0x =或1cos 3θ=. ①当0x =时,12y =, 所以12AO AC =,所以O 点与D 点重合, 即ABC △为直角三角形,故168242S =⨯⨯=;y =②当1cos 3θ=时,sin 3θ=,故1sin 2S AB AC θ=⨯⨯⨯=. 综上所述,ABC △的面积为24或故选D.解法二(构造法):延长AB 到点E ,使52AE AB =,取AC 中点D . 因为2512522x AO AB y AC ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭225AE xy AD =+, 又因为2105x y +=,即2215xy +=,因此O ,E ,D 三点在一条直线上. 若O 与E 重合,则与O 在AB 的垂直平分线上矛盾;若O 与D 重合,即DA DB DC ==,所以ABC △为直角三角形, 且2B π∠=,故168242S =⨯⨯=; 若O 不与D ,E 重合,则由三点共线知ED AC ⊥. 因为5AD =,15AE =,故1cos 3A =,此时sin A =1sin 2S AB AC A =⨯⨯⨯=综上所述,ABC △的面积为24或故选D.E13. 解析1sin 2S bc A ===,故2c =. 由余弦定理得2222cos a b c bc A =+-11421232=+-⨯⨯⨯=,故a =14. 解析 展开式的第1r +项为()7171C 2rrrr T x x -+⎛⎫= ⎪⎝⎭7727C 2r r rx --=, 故令723r -=-,即5r =,所以31x的系数为5757C 221484-=⨯=. 15. 分析 通过常规的配凑无法实现,故尝试计算几个观察规律. 解析 因为111n n n a a a --⋅=-,且10n a -≠,故111n n n a a a ---=, 因此25a =,345a =,414a =-,55a =,…, 故数列{}n a 是以3为周期的数列.又因为201536712=⨯+,因此20155a =. 16.解析 由题意得()122M x λλλ=+-⨯=-+, 故12,22M λλλ⎛⎫---⎪-⎝⎭,[]0,1λ∈. ()1ON OA OB λλ=+-()()31,012,2λλ⎛⎫=+- ⎪⎝⎭332,22λλ⎛⎫=-- ⎪⎝⎭.3312222MN λλλ=--++-111222λλ=--+-()1132222λλ=-+--.令2t λ=-,则[]1,2t ∈,问题转化为1322t kt +-在[]1,2t ∈恒成立时,求k 的取值范围. 令13()22t g t t =+-,因为()1322t g t t =+-在⎡⎣上单调递减,在⎤⎦上单调递增,0故()min 32g t g==,()10g =,()20g =,故()max 0g t =,因此1330,222t t ⎡+-∈-⎢⎣,故32k ⎡⎫∈-+∞⎪⎢⎣⎭.。
高考数学复习《30分钟选填》 (理科版) 限时训练(33)答案

限时训练(三十三)答案部分一、选择题二、填空题13. 2 14.32- 15. 2316. 22π解析部分(1) 解析 依题{}02A x x =<<,{}3B y y =…画图 .故选C .评注 集合的交集、并集、补集等运算,集合间的关系以及集合的子集都是考查的热点,集合的考查属于基础题,它常与方程,不等式结合起来考,一般都属于送分题.解决集合的基本运算问题,还可以根据选项之间的差异利用特殊值法,数轴法进行排除确定正确选项.(2)解析 依题有:222=05+60a a a a ⎧--⎨-≠⎩⇒2123a a a a ==-⎧⎨==⎩或或.故选D . (3)解析 由向量模的公式可得a ,再由向量投影的概念可得a 在b 上的投影等于cos120︒a . 故选B.(4)解析 依题()()67867890a a a a a a a +++++<,即()()()7787783260a a a a a a +=+<,又因为P ,所以70a <,80a >,且78a a <.故选B. (5) 解析 因为()()2fx f x =-,所以函数关于1x =对称,()()2f x f x -=,()()222f x f x --=+,即()()2f x f x -=+,又因()f x 是奇函数,所以()()()2f x f x f x ==-+-,所以()()()24f x f x f x -+=+=,即()f x 是周期为4的奇函数,()00f =,()()112f f --=-=,()()200f f ==,()()231f f =-=()()400f f ==,()()()()()120175041420172f f f f f +⋅⋅⋅+=+⋅⋅⋅++=-⎡⎤⎣⎦.故选C.(6)解析 依题有:设AC x =,则BC =则1114233B A ACC V x -=⨯=,即224x x=-.x =值,所以1111222ABC A B C V Sh -===.故选C. (7)解析 依题,因为π2π2<<,所以0sin 21<<,213log 0b =<,11321122log log c =>,即c a b >>.故选B.(8)解析 6n=,3sin 60S =︒=;12n =,6sin303S =︒=; 24n =,12sin15120.2588 3.1086 3.10S =︒=⨯=>.所以24n =.故选C. (9)解析 ()()2x g x f x =+有三个零点,即()()02x g x f x =+=,()2xf x =-,即函数()y f x =与2x y =-有3个交点,当0x <时,有1个交点,当0x ≥时,22xx ax -=-在[)0,+∞上有2个交点,即方程有2个正根,121200x x x x ∆>⎧⎪+>⎨⎪⋅>⎩,得12a >,故选A .(10)解析 由俯视图知,底面积12222S =⨯⨯=,高3h ==, 所以1123233V Sh ==⨯⨯=.故选B. (11)解析 依题()cos f x x x '=,()cos f t t t '=,即()cos k g t t t ==,可知()g t 为奇函数,根据题中图像可排除B ,C ,又因为当0,2t ⎛⎫∈ ⎪⎝⎭π,()0g t >.故选A . (12)解析 由()10f =得2e 10a b -+-=,又()22e 2xf x ax b '=-+,令()()222e21e xg x f x ax a '==-++-,即()0g x =在()0,1内有2个零点,所以()22212e e 1xa x -=-+,当12x =时,222e e 10x -+<,所以只需()()0010g g >⎧⎪⎨>⎪⎩.故选A .(13)解析 作出可行域:目标函数从而变形为y kx z =-由题可知06z 剟,即函数y kx z =-的截距范围是[]6,0-,根据线性规划的知识则有可知2k =.评注 本题的关键是求出不等式组表示的可行域,理解代数式是表示直线的意义,然后在进行求解,此类题先画出不等式组表示的可行域,然后理解代数式的意义来求解.(14)解析 由题知,圆心21x k y k =⎧⎨=-⎩即圆心轨迹为21y x =-,又因为圆心与直线l 距离与tan()3πα-无关,即圆心轨迹与l 平行,所以32t -=,即32t =-. (15)解析 以E 为原点,AD 的垂直平分线为x 轴,AD 所在直线为y 轴,建立坐标系,可得24y x =.隐影部分面积为:10823=⎰,矩形的面积为4:,所求概率为82343=.(16)解析 由题只()()222015201722201620142018201620142016201420152017π22a a aa a a a a a aa++=⋅+⋅=+=…,故答案为2π2.32。
高考数学(理科)填空选择小题限时训练(4)

限时训练(四)一、选择题:本大题共 12小题,每小题 5分,共60分.在每个小题给出的四个选项中,只有一项是 符合题目要求的.1•在复平面内表示复数i 1 - 2i 的点位于( ). A.第一象限B.第二象限C.第三象限D.第四象限2•对任意等比数列fa n ?,下列说法一定正确的是()•A. a 1,a 3,a 9成等比数列B. a 2,a s ,a 6成等比数列C. a 2,a 4,a 8成等比数列D. a 3,a e ,a 9成等比数列3.下列函数中,最小正周期为n 且图像关于原点对称的函数是(A . y =cos 2xnI 2丿B . y 二 sin 2x -I 2丿C . y =sin2x+cos2(D . y = sinx + cosx4.已知向量 a =:i k,3 , b =]1,4 , c =]2,1 ,且 2 a- 3b _ c ,则实数 k 二( A . 9B. 0C.D .155.执行如图所示的程序框图,若输出 的值为6 ,则判断框内可填入的条件是(4 D. s56.已知命题8.设F 1,F 2分别为双曲线2 2-2 -^y ^ = 1 (a > 0,b > 0 )的左、右焦点,双曲线上存在一点 a bP 使得PF 』+ PF ? =3b, PF 1PF 2=9ab ,则该双曲线的离心率为().49•某次联欢会要安排 3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不 相邻的排法种数是( )• A. 72B. 120C. 144D. 16810.已知点A -2,3在抛物线C : y 2 = 2px 的准线上,过点A 的直线与C 在第一象限相切于点 B , 记C 的焦点为F ,则直线BF 的斜率为()•1 2 3 4_ xp :对-X 三R ,总有2 0 ;q : X .1”是’X2 ”的充分不必要条件•则下列命题为真命题的是()•A . p qB . 一p 一qc. 一pq D . p 一q7•某几何体的三视图如图所示,则该几何体的表面积为( )A. 54B. 60C. 66D. 72面积S满足1剟S 2,记a,b,c分别为A, B,C所对的边,则下列不等式成立的是()A. 2B. 3C. 4D. 3 11.已知△ ABC 的内角A,B,C 满足sin 2A sin A-B C 二sin C-A-B -,A. bc b c .8B. ab a >16,2C. 6剟abc 12D. 12剟abc 24xB. 3 3IL 2e‘412.设函数f x二e 2x -1 -ax a,其中a :;: 1,若存在唯一的整数X o使得f x° ::: 0,则a的取值范围是()•二、填空题:本大题共四小题,每小题5分,共20分.把答案填在题中的横线上.13.设全集U ={ N 1 剟n 10〉, A」1,2,3,5,8 },B = {1,3,5,7,9 },则(euAf]B= ______________14. 函数f (x )=log 2仮log 2(2x )的最小值为_________ .2 215. 设点M X0,1,若在圆O : x y =1上存在点N,使得• OMN =45,则x0的取值范围是____________ .16.如图所示,在正方体ABCD - AB1GD1中,点E是边BC的中点.点P在直线BD1(除B,D1两点)上运动的过程中,平面DEP可能经过的该正方体的顶点是 ______________ (写出满足条件的所有顶点).。
高三数学:2024届新结构“8+3+3”选填限时训练1_10(解析版)

2024届高三二轮复习“8+3+3”小题强化训练(1)一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1对两个具有线性相关关系的变量x 和y 进行统计时,得到一组数据1,0.3 ,2,4.7 ,3,m ,4,8 ,通过这组数据求得回归直线方程为y=2.4x -2,则m 的值为()A.3B.5C.5.2D.6【答案】A【解析】易知x =1+2+3+44=52,y =13+m4,代入y =2.4x -2得13+m 4=2.4×52-2⇒m =3.故选:A2已知m ,n 表示两条不同直线,α表示平面,下列说法正确的是()A.若m ⎳α,n ⎳α,则m ⎳nB.若m ⊥α,n ⊂α,则m ⊥nC.若m ⊥α,m ⊥n ,则n ⎳αD.若m ⎳α,m ⊥n ,则n ⊥α【答案】B【解析】线面垂直,则有该直线和平面内所有的直线都垂直,故B 正确.故选:B3已知向量a ,b 满足a =3,b =23,且a ⊥a +b,则b 在a 方向上的投影向量为()A.3B.-3C.-3aD.-a【答案】D【解析】a ⊥a +b ,则a ⋅a +b =a 2+a ⋅b =9+a ⋅b =0,故a ⋅b=-9,b 在a 方向上的投影向量a ⋅b a 2⋅a =-99⋅a =-a.故选:D .4若n 为一组从小到大排列的数1,2,4,8,9,10的第六十百分位数,则二项式3x +12xn的展开式的常数项是()A.7B.8C.9D.10【答案】A【解析】因为n 为一组从小到大排列的数1,2,4,8,9,10的第六十百分位数,6×60%=3.6,所以n =8,二项式3x +12x8的通项公式为T r +1=C r 8⋅3x 8-r ⋅12x r =C r 8⋅12 r⋅x8-r 3-r,令8-r 3-r =0⇒r =2,所以常数项为C 28×12 2=8×72×14=7,故选:A5折扇是我国古老文化的延续,在我国已有四千年左右的历史,“扇”与“善”谐音,折扇也寓意“善良”“善行”.它常以字画的形式体现我国的传统文化,也是运筹帷幄、决胜千里、大智大勇的象征(如图1).图2是一个圆台的侧面展开图(扇形的一部分),若两个圆弧DE ,AC 所在圆的半径分别是3和6,且∠ABC =120°,则该圆台的体积为()A.5023π B.9π C.7π D.1423π【答案】D【解析】设圆台上下底面的半径分别为r 1,r 2,由题意可知13×2π×3=2πr 1,解得r 1=1,13×2π×6=2πr 2,解得:r 2=2,作出圆台的轴截面,如图所示:图中OD =r 1=1,O A =r 2=2,AD =6-3=3,过点D 向AP 作垂线,垂足为T ,则AT =r 2-r 1=1,所以圆台的高h =AD 2-AT 2=32-1=22,则上底面面积S 1=π×12=π,S 2=π×22=4π,由圆台的体积计算公式可得:V =13×(S 1+S 2+S 1⋅S 2)×h =13×7π×22=142π3,故选:D .6已知函数f x =x 2-bx +c (b >0,c >0)的两个零点分别为x 1,x 2,若x 1,x 2,-1三个数适当调整顺序后可为等差数列,也可为等比数列,则不等式x -bx -c≤0的解集为()A.1,52B.1,52C.-∞,1 ∪52,+∞D.-∞,1 ∪52,+∞ 【答案】A【解析】由函数f x =x 2-bx +c (b >0,c >0)的两个零点分别为x 1,x 2,即x 1,x 2是x 2-bx +c =0的两个实数根据,则x 1+x 2=b ,x 1x 2=c 因为b >0,c >0,可得x 1>0,x 2>0,又因为x 1,x 2,-1适当调整可以是等差数列和等比数列,不妨设x 1<x 2,可得x 1x 2=-1 2=1-1+x 2=2x 1 ,解得x 1=12,x 2=2,所以x 1+x 2=52,x 1x 2=1,所以b =52,c =1,则不等式x -b x -c ≤0,即为x -52x -1≤0,解得1<x ≤52,所以不等式的解集为1,52.故选:A .7已知双曲线C :x 2a 2-y 2b2=1a >0,b >0 的左、右焦点分别为F 1,F 2,M ,N 为双曲线一条渐近线上的两点,A 为双曲线的右顶点,若四边形MF 1NF 2为矩形,且∠MAN =2π3,则双曲线C 的离心率为()A.3B.7C.213D.13【答案】C【解析】如图,因为四边形MF 1NF 2为矩形,所以MN =F 1F 2 =2c (矩形的对角线相等),所以以MN 为直径的圆的方程为x 2+y 2=c 2.直线MN 为双曲线的一条渐近线,不妨设其方程为y =bax ,由y =b a x ,x 2+y 2=c 2,解得x =a y =b ,或x =-a ,y =-b , 所以N a ,b ,M -a ,-b 或N -a ,-b ,M a ,b .不妨设N a ,b ,M -a , -b ,又A a ,0 ,所以AM =a +a 2+b 2=4a 2+b 2,AN =a -a 2+b 2=b .在△AMN 中,∠MAN =2π3,由余弦定理得MN 2=AM 2+AN 2-2AM AN ⋅cos 2π3,即4c 2=4a 2+b 2+b 2+4a 2+b 2×b ,则2b =4a 2+b 2,所以4b 2=4a 2+b 2,则b 2=43a 2,所以e =1+b 2a2=213.故选:C .8已知a =ln 1.2e ,b =e 0.2,c =1.2e 0.2,则有()A.a <b <cB.a <c <bC.c <a <bD.c <b <a【答案】C【解析】令f x =e x -ln x +1 -1,x >0,则f x =e x -1x +1.当x >0时,有e x >1,1x +1<1,所以1x +1<1,所以,f (x )>0在0,+∞ 上恒成立,所以,f (x )在0,+∞ 上单调递增,所以,f (x )>f (0)=1-1=0,所以,f (0.2)>0,即e 0.2-ln1.2-1>0,所以a <b令g x =e x -x +1 ,x >0,则g x =e x -1在x >0时恒大于零,故g x 为增函数,所以x +1ex <1,x >0,而a =ln 1.2e =1+ln1.2>1,所以c <a ,所以c <a <b ,故选:C二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9已知函数f x =sin 2x +3π4 +cos 2x +3π4,则()A.函数f x -π4 为偶函数 B.曲线y =f x 对称轴为x =k π,k ∈ZC.f x 在区间π3,π2单调递增D.f x 的最小值为-2【答案】AC【解析】f x =sin 2x +3π4 +cos 2x +3π4=sin2x cos 3π4+sin 3π4cos2x +cos2x cos 3π4-sin2x sin3π4=-22sin2x +22cos2x -22cos2x -22sin2x =-2sin2x ,即f x =-2sin2x ,对于A ,f x -π4 =-2sin 2x -π2=2cos2x ,易知为偶函数,所以A 正确;对于B ,f x =-2sin2x 对称轴为2x =π2+k π,k ∈Z ⇒x =π4+k π2,k ∈Z ,故B 错误;对于C ,x ∈π3,π2 ,2x ∈2π3,π ,y =sin2x 单调递减,则f x =-2sin2x 单调递增,故C 正确;对于D ,f x =-2sin2x ,则sin2x ∈-1,1 ,所以f x ∈-2,2 ,故D 错误;故选:AC10设z 为复数,则下列命题中正确的是()A.z 2=zz B.若z =(1-2i )2,则复平面内z对应的点位于第二象限C.z 2=z 2D.若z =1,则z +i 的最大值为2【答案】ABD【解析】对于A ,设z =a +bi ,故z =a -bi ,则z 2=a 2+b 2,zz =(a +bi )(a -bi )=a 2+b 2,故z 2=zz成立,故A 正确,对于B ,z =(1-2i )2=-4i -3,z =4i -3,显然复平面内z对应的点位于第二象限,故B 正确,对于C ,易知z 2=a 2+b 2,z 2=a 2+b 2+2abi ,当ab ≠0时,z 2≠z 2,故C 错误,对于D ,若z =1,则a 2+b 2=1,而z +i =a 2+(b +1)2=2b +2,易得当b =1时,z +i 最大,此时z +i =2,故D 正确.故选:ABD11已知菱形ABCD 的边长为2,∠ABC =π3.将△DAC 沿着对角线AC 折起至△D AC ,连结BD .设二面角D -AC -B 的大小为θ,则下列说法正确的是()A.若四面体D ABC 为正四面体,则θ=π3B.四面体D ABC 的体积最大值为1C.四面体D ABC 的表面积最大值为23+2D.当θ=2π3时,四面体D ABC 的外接球的半径为213【答案】BCD【解析】如图,取AC 中点O ,连接OB ,OD ,则OB =OD ,OB ⊥AC ,OD ⊥AC ,∠BOC 为二面角D AC -B 的平面角,即∠BOC =θ.若D ABC 是正四面体,则BD =BC ≠BO ,△OBD 不是正三角形,θ≠π3,A 错;四面体D ABC 的体积最大时,BO ⊥平面ACD ,此时B 到平面ACD 的距离最大为BO =3,而S △ACD=34×22=3,所以V =13×3×3=1,B 正确;S △ABC =S △DAC =3,易得△BAD ≅△BCD ,S △BAD=S △BCD=12×22sin ∠BCD =2sin ∠BCD ,未折叠时BD =BD =23,折叠到B ,D 重合时,BD =0,中间存在一个位置,使得BD =22,则BC 2+D C 2=BD 2,∠BCD =π2,此时S △BAD=S △BCD=2sin ∠BCD 取得最大值2,所以四面体D ABC 的表面积最大值为23+2 ,C 正确;当θ=2π3时,如图,设M ,N 分别是△ACD 和△BAC 的外心,在平面AOD 内作PM ⊥OD ,作PN ⊥OB ,PM ∩PN =P ,则P 是三棱锥外接球的球心,由上面证明过程知平面OBD 与平面ABC 、平面D AC 垂直,即P ,N ,O ,M 四点共面,θ=2π3,则∠PON =π3,ON =13×32×2=33,PN =ON tan π3=33×3=1,PB =PN 2+BN 2=12+233 2=213为球半径,D 正确.故选:BCD .三、填空题:本题共3小题,每小题5分,共15分.12设集合M =x log 2x <1 ,N =x 2x -1<0 ,则M ∩N =.【答案】x 0<x <12【解析】因为log 2x <1=log 22,所以0<x <2,即M =x log 2x <1 =x 0<x <2 ,因为2x -1<0,解得x <12,所以N =x 2x -1<0 =x x <12,所以,M ∩N =x 0<x <12 .故答案为:x 0<x <12 13已知正项等比数列a n 的前n 项和为S n ,且S 8-2S 4=6,则a 9+a 10+a 11+a 12的最小值为.【答案】24【解析】设正项等比数列a n 的公比为q ,则q >0,所以,S 8=a 1+a 2+a 3+a 4+a 5+a 6+a 7+a 8=a 1+a 2+a 3+a 4+q 4a 1+a 2+a 3+a 4 =S 41+q 4 ,则S 8-2S 4=S 4q 4-1 =6,则q 4>1,可得q >1,则S 4=6q 4-1,所以,a 9+a 10+a 11+a 12=q 8a 1+a 2+a 3+a 4 =S 4q 8=6q 8q 4-1=6q 4-1+1 2q 4-1=6q 4-1 2+1+2q 4-1 q 4+1=6q 4-1 +1q 4-1+2 ≥62q 4-1 ⋅1q 4-1+2 =24,当且仅当q 4-1=1q 4-1q >1 时,即当q =42时,等号成立,故a 9+a 10+a 11+a 12的最小值为24.故答案为:2414已知F 为拋物线C :y =14x 2的焦点,过点F 的直线l 与拋物线C 交于不同的两点A ,B ,拋物线在点A ,B 处的切线分别为l 1和l 2,若l 1和l 2交于点P ,则|PF |2+25AB的最小值为.【答案】10【解析】C :x 2=4y 的焦点为0,1 ,设直线AB 方程为y =kx +1,A x 1,y 1 ,B x 2,y 2 .联立直线与抛物线方程有x 2-4kx -4=0,则AB =y 1+y 2+2=k x 1+x 2 +4=4k 2+4.又y =14x 2求导可得y =12x ,故直线AP 方程为y -y 1=12x 1x -x 1 .又y 1=14x 21,故AP :y =12x 1x -14x 21,同理BP :y =12x 2x -14x 22.联立y =12x 1x -14x 21y =12x 2x -14x 22可得12x 1-x 2 x =14x 21-x 22 ,解得x =x 1+x 22,代入可得P x 1+x 22,x 1x 24 ,代入韦达定理可得P 2k ,-1 ,故PF =4k 2+4.故|PF |2+25AB=4k 2+4+254k 2+4≥24k 2+4 ×254k 2+4=10,当且仅当4k 2+4=254k 2+4,即k =±12时取等号.故答案为:102024届高三二轮复习“8+3+3”小题强化训练(2)一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1抛物线y =12x 2的焦点坐标为()A.18,0B.12,0 C.0,18D.0,12【答案】D 【解析】由y =12x 2可得抛物线标准方程为:x 2=2y ,∴其焦点坐标为0,12 .故选:D .2二项式3x 2-1x 47的展开式中常数项为()A.-7B.-21C.7D.21【答案】A 【解析】二项式3x 2-1x47的通项公式为Tr +1=C r 7⋅3x 27-r⋅-1x4r=Cr 7⋅-1 r⋅x14-14r 3,令14-14r 3=0⇒r =1,所以常数项为C 17⋅-1 =-7,故选:A3已知集合A =x log 2x ≤1 ,B =y y =2x ,x ≤2 ,则()A.A ∪B =BB.A ∪B =AC.A ∩B =BD.A ∪(C R B )=R【答案】A【解析】由log 2x ≤1,则log 2x ≤log 22,所以0<x ≤2,所以A =x log 2x ≤1 =x 0<x ≤2 ,又B =y y =2x ,x ≤2 =y 0<y ≤4 ,所以A ⊆B ,则A ∪B =B ,A ∩B =A .故选:A .4若古典概型的样本空间Ω=1,2,3,4 ,事件A =1,2 ,甲:事件B =Ω,乙:事件A ,B 相互独立,则甲是乙的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【答案】A【解析】若B =Ω,A ∩B =1,2 ,则P A ∩B =24=12,而P A =24=12,P B =1,所以P A P B =P A ∩B ,所以事件A ,B 相互独立,反过来,当B =1,3 ,A ∩B =1 ,此时P A ∩B =14,P A =P B =12,满足P A P B =P A ∩B ,事件A ,B 相互独立,所以不一定B =Ω,所以甲是乙的充分不必要条件.故选:A5若函数f x =ln e x -1 -mx 为偶函数,则实数m =()A.1B.-1C.12D.-12【答案】C【解析】由函数f x =ln e x -1 -mx 为偶函数,可得f -1 =f 1 ,即ln e -1-1 +m =ln e -1 -m ,解之得m =12,则f x =ln e x -1 -12x (x ≠0),f -x =ln e -x -1 +12x =ln e x -1 -x +12x =ln e x -1 -12x =f x故f x =ln e x -1 -12x 为偶函数,符合题意.故选:C6已知函数y =f (x )的图象恰为椭圆C :x 2a 2+y 2b2=1(a >b >0)x 轴上方的部分,若f (s -t ),f (s ),f (s +t )成等比数列,则平面上点(s ,t )的轨迹是()A.线段(不包含端点) B.椭圆一部分C.双曲线一部分D.线段(不包含端点)和双曲线一部分【答案】A【解析】因为函数y =f (x )的图象恰为椭圆C :x 2a 2+y 2b2=1(a >b >0)x 轴上方的部分,所以y =f (x )=b ⋅1-x 2a2(-a <x <a ),因为f (s -t ),f (s ),f (s +t )成等比数列,所以有f 2(s )=f (s -t )⋅f (s +t ),且有-a <s <a ,-a <s -t <a ,-a <s +t <a 成立,即-a <s <a ,-a <t <a 成立,由f 2(s )=f (s -t )⋅f (s +t )⇒b ⋅1-s 2a 22=b ⋅1-(s -t )2a 2⋅b ⋅1-(s +t )2a 2,化简得:t 4=2a 2t 2+2s 2t 2⇒t 2(t 2-2a 2-2s 2)=0⇒t 2=0,或t 2-2a 2-2s 2=0,当t 2=0时,即t =0,因为-a <s <a ,所以平面上点(s ,t )的轨迹是线段(不包含端点);当t 2-2a 2-2s 2=0时,即t 2=2a 2+2s 2,因为-a <t <a ,所以t 2<a 2,而2a 2+2s 2>a 2,所以t 2=2a 2+2s 2不成立,故选:A7若tan α+π4=-2,则sin α1-sin2α cos α-sin α=()A.65B.35C.-35D.-65【答案】C【解析】因为tan α+π4 =tan α+tan π41-tan αtan π4=tan α+11-tan α=-2,解得tan α=3,所以,sin α1-sin2αcos α-sin α=sin αsin 2α+cos 2α-2sin αcos α cos α-sin α=sin αcos α-sin α 2cos α-sin α=sin αcos α-sin 2α=sin αcos α-sin 2αcos 2α+sin 2α=tan α-tan 2α1+tan 2α=3-91+9=-35.故选:C .8函数f x =2ln xx,x >0sin ωx +π6,-π≤x ≤0,若2f 2(x )-3f (x )+1=0恰有6个不同实数解,正实数ω的范围为()A.103,4B.103,4 C.2,103D.2,103【答案】D【解析】由题知,2f 2x -3f x +1=0的实数解可转化为f (x )=12或f (x )=1的实数解,即y =f (x )与y =1或y =12的交点,当x >0时,f x =2ln xx ⇒f (x )=21-ln x x 2所以x ∈0,e 时,f (x )>0,f x 单调递增,x ∈e ,+∞ 时,f (x )<0,f x 单调递减,如图所示:所以x =e 时f x 有最大值:12<f (x )max =2e<1所以x >0时,由图可知y =f (x )与y =1无交点,即方程f (x )=1无解,y =f (x )与y =12有两个不同交点,即方程f (x )=12有2解当x <0时,因为ω>0,-π≤x ≤0,所以-ωπ+π6≤ωx +π6≤π6,令t =ωx +π6,则t ∈-ωπ+π6,π6则有y =sin t 且t ∈-ωπ+π6,π6,如图所示:因为x >0时,已有两个交点,所以只需保证y =sin t 与y =12及与y =1有四个交点即可,所以只需-19π6<-ωπ+π6≤-11π6,解得2≤ω<103.故选:D二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9已知复数z 1,z 2是关于x 的方程x 2+bx +1=0(-2<b <2,b ∈R )的两根,则下列说法中正确的是()A.z 1=z 2B.z 1z 2∈R C.z 1 =z 2 =1D.若b =1,则z 31=z 32=1【答案】ACD【解析】Δ=b 2-4<0,∴x =-b ±4-b 2i 2,不妨设z 1=-b 2+4-b 22i ,z 2=-b2-4-b 22i ,z 1=z 2,A 正确;z 1 =z 2 =-b 22+4-b 222=1,C 正确;z 1z 2=1,∴z 1z 2=z 21z 1z 2=z 21=b 2-22-b 4-b 22i ,b ≠0时,z 1z 2∉R ,B 错;b =1时,z 1=-12+32i ,z 2=-12-32i ,计算得z 21=-12-32i =z 2=z 1 ,z 22=z 1=z 2 ,z 31=z 1z 2=1,同理z 32=1,D 正确.故选:ACD .10四棱锥P -ABCD 的底面为正方形,P A 与底面垂直,P A =2,AB =1,动点M 在线段PC 上,则()A.不存在点M ,使得AC ⊥BMB.MB +MD 的最小值为303C.四棱锥P -ABCD 的外接球表面积为5πD.点M 到直线AB 的距离的最小值为255【答案】BD【解析】对于A :连接BD ,且AC ∩BD =O ,如图所示,当M 在PC 中点时,因为点O 为AC 的中点,所以OM ⎳P A ,因为P A ⊥平面ABCD ,所以OM ⊥平面ABCD ,又因为AC ⊂平面ABCD ,所以OM ⊥AC ,因为ABCD 为正方形,所以AC ⊥BD .又因为BD ∩OM =O ,且BD ,OM ⊂平面BDM ,所以AC ⊥平面BDM ,因为BM ⊂平面BDM ,所以AC ⊥BM ,所以A 错误;对于B :将△PBC 和△PCD 所在的平面沿着PC 展开在一个平面上,如图所示,则MB +MD 的最小值为BD ,直角△PBC 斜边PC 上高为1×56,即306,直角△PCD 斜边PC 上高也为1×56,所以MB +MD 的最小值为303,所以B 正确;对于C :易知四棱锥P -ABCD 的外接球直径为PC ,半径R =12PC =1222+12+12=62,表面积S =4πR 2=6π,所以C 错误;对于D :点M 到直线AB 距离的最小值即为异面直线PC 与AB 的距离,因为AB ⎳CD ,且AB ⊄平面PCD ,CD ⊂平面PCD ,所以AB ⎳平面PCD ,所以直线AB 到平面PCD 的距离等于点A 到平面PCD 的距离,过点A 作AF ⊥PD ,因为P A ⊥平面ABCD ,所以P A ⊥CD ,又AD ⊥CD ,且P A ∩AD =A ,故CD ⊥平面P AD ,AF ⊂平面P AD ,所以AF ⊥CD ,因为PD ∩CD =D ,且PD ,CD ⊂平面PCD ,所以AF ⊥平面PCD ,所以点A 到平面PCD 的距离,即为AF 的长,如图所示,在Rt △P AD 中,P A =2,AD =1,可得PD =5,所以由等面积得AF =255,即直线AB 到平面PCD 的距离等于255,所以D 正确,故选:BCD .11今年是共建“一带一路”倡议提出十周年.某校进行“一带一路”知识了解情况的问卷调查,为调动学生参与的积极性,凡参与者均有机会获得奖品.设置3个不同颜色的抽奖箱,每个箱子中的小球大小相同质地均匀,其中红色箱子中放有红球3个,黄球2个,绿球2个;黄色箱子中放有红球4个,绿球2个;绿色箱子中放有红球3个,黄球2个,要求参与者先从红色箱子中随机抽取一个小球,将其放入与小球颜色相同的箱子中,再从放入小球的箱子中随机抽取一个小球,抽奖结束.若第二次抽取的是红色小球,则获得奖品,否则不能获得奖品,已知甲同学参与了问卷调查,则()A.在甲先抽取的是黄球的条件下,甲获得奖品的概率为47B.在甲先抽取的不是红球的条件下,甲没有获得奖品的概率为1314C.甲获得奖品的概率为2449D.若甲获得奖品,则甲先抽取绿球的机会最小【答案】ACD【解析】设A 红,A 黄,A 绿,分别表示先抽到的小球的颜色分别是红、黄、绿的事件,设B 红表示再抽到的小球的颜色是红的事件,在甲先抽取的是黄球的条件下,甲获得奖品的概率为:P B 红∣A 黄 =P B 红A 黄 P A 黄=27×4727=47,故A 正确;在甲先抽取的不是红球的条件下,甲没有获得奖品的概率为:P B 红 ∣A 红 =P A 红 B 红 P A 红 =P A 黄B 红 +P A 绿B 红 P A 红 =27×37+27×1247=1328,故B 错误;由题意可知,P A 红 =37,P A 黄 =27,P A 绿 =27,P B 红∣A 红 =37,P B 红∣A 黄 =47,P B 红∣A 绿 =12,由全概率公式可知,甲获得奖品的概率为:P =P A 红 P B 红∣A 红 +P A 黄 ⋅P B 红∣A 黄 +P A 绿 ⋅P B 红∣A 绿 =37×37+27×47+27×12=2449,故C 正确;因为甲获奖时红球取自哪个箱子的颜色与先抽取小球的颜色相同,则P A 红∣B 红 =P A 红 ⋅P B 红∣A 红 P B 红=37×37×4924=38,P A 黄∣B 红 =P A 黄 ⋅P B 红∣A 黄P B 红=27×47×4924=13,P A 绿∣B 红 =P A 绿 ⋅P B 红∣A 绿 P B 红 =27×12×4924=724,所以甲获得奖品时,甲先抽取绿球机会最小,故D 正确.故选:ACD .三、填空题:本题共3小题,每小题5分,共15分.12已知△ABC 的边BC 的中点为D ,点E 在△ABC 所在平面内,且CD =3CE -2CA ,若AC =xAB +yBE,则x +y =.【答案】11【解析】因为CD =3CE -2CA ,边BC 的中点为D ,所以12CB=3BE -BC +2AC ,因为12CB =3BE -3BC +2AC ,所以52BC =3BE +2AC ,所以52BC =52AC -AB =3BE +2AC ,所以5AC -5AB =6BE +4AC ,即5AB +6BE =AC ,因为AC =xAB +yBE ,所以x =5,y =6,故x +y =11.故答案为:1113已知圆锥母线长为2,则当圆锥的母线与底面所成的角的余弦值为时,圆锥的体积最大,最大值为.【答案】①.63②.16327π【解析】设圆锥的底面半径为r ,圆锥的母线与底面所成的角为θ,θ∈0,π2 ,易知cos θ=r 2.圆锥的体积为V =13πr 2⋅4-r 2=43πcos 2θ⋅2sin θ=8π3cos 2θ⋅sin θ=8π31-sin 2θ sin θ令x =sin θ,x ∈0,1 ,则y =1-sin 2θ sin θ=-x 3+x ,y =-3x 2+1当y >0时,x ∈0,33,当y<0时,x ∈33,1 ,即函数y =-x 3+x 在0,33 上单调递增,在33,1上单调递减,即V max =8π333-33 3 =163π27,此时cos θ=1-323 =62.故答案为:62;163π2714已知双曲线C :x 2-y 23=1的左、右焦点分别为F 1,F 2,右顶点为E ,过F 2的直线交双曲线C 的右支于A ,B 两点(其中点A 在第一象限内),设M ,N 分别为△AF 1F 2,△BF 1F 2的内心,则当F 1A ⊥AB 时,AF 1=;△ABF 1内切圆的半径为.【答案】①.7+1##1+7②.7-1##-1+7【解析】由双曲线方程知a =1,b =3,c =2,如下图所示:由F 1A ⊥AB ,则AF 1 2+AF 2 2=F 1F 2 2=16,故AF 1 -AF 2 2+2AF 1 AF 2 =16,而AF 1 -AF 2 =2a =2,所以AF 1 AF 2 =6,故AF 2 2+2AF 2 -6=0,解得AF 2 =7-1,所以AF 1 =7+1,若G 为△ABF 1内切圆圆心且F 1A ⊥AB 可知,以直角边切点和G ,A 为顶点的四边形为正方形,结合双曲线定义内切圆半径r =12AF 1 +AB -BF 1 =12AF 1 +AF 2 +BF 2 -BF 1所以r =1227+BF 2 -BF 1 =1227-2 =7-1;故答案为:7+1,7-1;2024届高三二轮复习“8+3+3”小题强化训练(3)一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1有一组按从小到大顺序排列数据:3,5,x ,8,9,10,若其极差与平均数相等,则这组数据的中位数为()A.7B.7.5C.8D.6.5【答案】B【解析】依题意可得极差为10-3=7,平均数为163+5+x +8+9+10 =1635+x ,所以1635+x =7,解得x =7,所以中位线为7+82=7.5.故选:B .2已知集合A =x x -1 >2 ,B =x log 4x <1 ,则A ∩B =()A.3,4B.-∞,-1 ∪3,4C.1,4D.-∞,4【答案】A【解析】由x -1 >2,得x <-1或x >3,所以A =x x <-1或x >3 ,由log 4x <1,得0<x <4,所以B =x 0<x <4 ,所以A ∩B =x 3<x <4 .故选:A .3已知向量a =(2,0),b =sin α,32,若向量b 在向量a 上的投影向量c =12,0 ,则|a +b |=()A.3B.7C.3D.7【答案】B【解析】由已知可得,b 在a 上的投影向量为a ⋅b |a |⋅a |a |=2sin α2×2(2,0)=(sin α,0),又b 在a 上的投影向量c =12,0 ,所以sin α=12,所以b =12,32,所以a +b =52,32 ,所以|a +b |=52 2+322=7.故选:B .4如图是两个底面半径都为1的圆锥底面重合在一起构成的几何体,上面圆锥的侧面积是下面圆锥侧面积的2倍,AP ⊥AQ ,则PQ =()A.74B.262C.52D.3【答案】C【解析】设两圆锥的高OP =x ,OQ =y ,则AP =x 2+1,AQ =y 2+1,由AP ⊥AQ ,有AP 2+AQ 2=PQ 2,可得x 2+1+y 2+1=x +y 2,可得xy =1,又由上下圆锥侧面积之比为2:1,即π×1×P A =2×π×1×QA ,可得P A =2QA ,则有x 2+1=2y 2+1,即x 2=4y 2+3,代入y =1x整理为x 4-3x 2-4=0,解得x =2(负值舍),可得y =12,OP =x +y =2+12=52.故选:C .5已知Q 为直线l :x +2y +1=0上的动点,点P 满足QP=1,-3 ,记P 的轨迹为E ,则()A.E 是一个半径为5的圆B.E 是一条与l 相交的直线C.E 上的点到l 的距离均为5D.E 是两条平行直线【答案】C【解析】设P x ,y ,由QP=1,-3 ,则Q x -1,y +3 ,由Q 在直线l :x +2y +1=0上,故x -1+2y +3 +1=0,化简得x +2y +6=0,即P 轨迹为E 为直线且与直线l 平行,E 上的点到l 的距离d =6-112+22=5,故A 、B 、D 错误,C 正确.故选:C .6已知x +1 x -1 5=a 0+a 1x +a 2x 2+a 3x 3+a 4x 4+a 5x 5+a 6x 6,则a 1+a 3的值为()A.-1B.1C.4D.-2【答案】C【解析】在x +1 x -1 5=a 0+a 1x +a 2x 2+a 3x 3+a 4x 4+a 5x 5+a 6x 6中,而x +1 x -1 5=x x -1 5+x -1 5,由二项式定理知x -1 5展开式的通项为T r +1=C r 5x 5-r (-1)r ,令5-r =2,解得r =3,令5-r =3,r =2,故a 3=C 35(-1)3+C 25(-1)2=0,同理令5-r =1,解得r =4,令5-r =0,解得r =5,故a 1=C 45(-1)4+C 55(-1)5=4,故a 1+a 3=4.故选:C7已知P 为抛物线x 2=4y 上一点,过P 作圆x 2+(y -3)2=1的两条切线,切点分别为A ,B ,则cos ∠APB 的最小值为()A.12B.23C.34D.78【答案】C【解析】如图所示:因为∠APB =2∠APC ,sin ∠APC =AC PC=1PC,设P t ,t 24,则PC 2=t 2+t 24-3 2=t 416-t 22+9=116t 2-4 2+8,当t 2=4时,PC 取得最小值22,此时∠APB 最大,cos ∠APB 最小,且cos ∠APB min =1-2sin 2∠APC =1-21222=34,故C 正确.故选:C8已知函数f x ,g x 的定义域为R ,g x 为g x 的导函数且f x +g x =3,f x -g 4-x =3,若g x 为偶函数,则下列结论一定成立的是()A.f -1 =f -3B.f 1 +f 3 =65C.g 2 =3D.f 4 =3【答案】D【解析】对于D ,∵g x 为偶函数,则g x =g -x ,两边求导可得g x =-g -x ,则g x 为奇函数,则g 0 =0,令x =4,则f 4 -g 0 =3,f 4 =3,D 对;对于C ,令x =2,可得f 2 +g 2 =3f 2 -g 2 =3 ,则f 2 =3g 2 =0 ,C 错;对于B ,∵f x +g x =3,可得f 2+x +g 2+x =3,f x -g 4-x =3可得f 2-x -g 2+x =3,两式相加可得f 2+x +f 2-x =6,令x =1,即可得f 1 +f 3 =6,B 错;又∵f x +g x =3,则f x -4 +g x -4 =f x -4 -g 4-x =3,f x -g 4-x =3,可得f x =f x -4 ,所以f x 是以4为周期的函数,所以根据以上性质不能推出f -1 =f -3 ,A 不一定成立.故选:D二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9下列结论正确的是()A.若a <b <0,则a 2>ab >b 2B.若x ∈R ,则x 2+2+1x 2+2的最小值为2C.若a +b =2,则a 2+b 2的最大值为2D.若x ∈(0,2),则1x +12-x ≥2【答案】AD【解析】因为a 2-ab =a (a -b )>0,所以a 2>ab ,因为ab -b 2=b (a -b )>0,所以ab >b 2,所以a 2>ab >b 2,故A 正确;因为x 2+2+1x 2+2≥2的等号成立条件x 2+2=1x 2+2不成立,所以B 错误;因为a 2+b 22≥a +b 2 2=1,所以a 2+b 2≥2,故C 错误;因为1x +12-x =12(x +2-x )1x +12-x =122+2-x x +x 2-x ≥12(2+2)=2,当且仅当1x =12-x,即x =1时,等号成立,所以D 正确.故选:AD10若函数f x =2sin 2x ⋅log 2sin x +2cos 2x ⋅log 2cos x ,则()A.f x 的最小正周期为πB.f x 的图像关于直线x =π4对称C.f x 的最小值为-1D.f x 的单调递减区间为2k π,π4+2k π ,k ∈Z【答案】BCD【解析】由sin x >0,cos x >0得f x 的定义域为2k π,π2+2k π ,k ∈Z .对于A :当x ∈0,π2时,x +π∈π,32π 不在定义域内,故f x +π =f x 不成立,易知f x 的最小正周期为2π,故选项A 错误;对于B :又f π2-x =2cos 2x ⋅log 2cos x +2sin 2x ⋅log 2sin x =f x ,所以f x 的图像关于直线x =π4对称,所以选项B 正确;对于C :因为f x =sin 2x ⋅log 2sin 2x +cos 2x ⋅log 2cos 2x ,设t =sin 2x ,所以函数转化为g t =t ⋅log 2t +1-t ⋅log 21-t ,t ∈0,1 ,g t =log 2t -log 21-t ,由g t >0得,12<t <1.g t <0得0<t <12.所以g t 在0,12 上单调递减,在12,1 上单调递增,故g (t )min =g 12=-1,即f (x )min =-1,故选项C 正确;对于D :因为g t 在0,12 上单调递减,在12,1 上单调递增,由t =sin 2x ,令0<sin 2x <12得0<sin x <22,又f x 的定义域为2k π,π2+2k π ,k ∈Z ,解得2k π<x <π4+2k π,k ∈Z ,因为t =sin 2x 在2k π,π4+2k π 上单调递增,所以f x 的单调递减区间为2k π,π4+2k π ,k ∈Z ,同理函数的递增区间为π4+2k π,π2+2k π ,k ∈Z ,所以选项D 正确.故选:BCD .11已知数列a n 的前n 项和为S n ,且2S n S n +1+S n +1=3,a 1=α0<α<1 ,则()A.当0<α<13-14时,a 2>a 1B.a 3>a 2C.数列S 2n -1 单调递增,S 2n 单调递减D.当α=34时,恒有nk =1S k -1 <54【答案】ACD【解析】由题意可得:S n +1=32S n +1,a 1=α,由S n +1=32S n +1可知:S n +1=1⇔S n =1,但S 1=α∈0,1 ,可知对任意的n ∈N *,都有S n ≠1,对于选项A :若0<α<13-14,则a 2-a 1=S 2-2a 1=32α+1-2α=3-2α-4α22α+1=4α+1+13 13-14-α2α+1>0,即a 2>a 1,故A 正确;对于选项B :a 3-a 2=S 3-2S 2+S 1=6α+32α+7-62α+1+α=α-1 4α2+32α+39 2α+1 2α+7<0,即a 3<a 2,故B 错误.对于选项C :因为S n +1-1=-2S n -1 2S n +1,S n +1+32=3S n +32 2S n +1,则S n +1-1S n +1+32=-23⋅S n -1S n +32,且S 1-1S 1+32=α-1α+32<0,可知S n -1S n+32是等比数列,则S n -1S n +32=α-1α+32⋅-23n -1,设A =α-1α+32<0,t =232n -2,可得S 2n =3-3At 3+2At =3253+2At -1 ,S 2n -1=1+32At 1-At =521-At-32,因为At =A 232n -2,可知A 23 2n -2 为递增数列,所以数列S 2n -1 单调递增,S 2n 单调递减,故C 正确;对于选项D :因为S n +1=32S n +1,S n +1-34=32S n +1-34=33-2S n 42S n +1,由S 1=α=34,可得S 2-34>0,即S 2>34,则S 2≤65,即34<S 2≤65;由34<S 2≤65,可得S 3-34>0,即S 3>34,则S 3<65,即34<S 3<65;以此类推,可得对任意的n ∈N *,都有S n ≥S 1=α=34,又因为S n +1-1S n -1=22S n +1,则S n +1-1 ≤22α+1S n -1 =45S n -1 ,所以∑nk =1S k -1 ≤541-45 n <54,故D 正确.故选:ACD .三、填空题:本题共3小题,每小题5分,共15分.12在(1+ax )n (其中n ∈N *,a ≠0)的展开式中,x 的系数为-10,各项系数之和为-1,则n =.【答案】5【解析】由题意得(1+ax )n 的展开式中x 的系数为aC 1n =-10,即an =-10,令x =1,得各项系数之和为(1+a )n =-1,则n 为奇数,且1+a =-1,即得a =-2,n =5,故答案为:513已知椭圆C :x 2a 2+y 2b2=1a >b >0 的左、右焦点分别F 1,F 2,椭圆的长轴长为22,短轴长为2,P 为直线x =2b 上的任意一点,则∠F 1PF 2的最大值为.【答案】π6【解析】由题意有a =2,b =1,c =1,设直线x =2与x 轴的交点为Q ,设PQ =t ,有tan ∠PF 1Q =PQ F 1Q=t3,tan ∠PF 2Q =PQ F 2Q=t ,可得tan ∠F 1PF 2=tan ∠PF 2Q -∠PF 1Q =t -t31+t23=2t t 2+3=2t +3t ≤2t 23t =33,当且仅当t =3时取等号,可得∠F 1PF 2的最大值为π6.故答案为:π614已知四棱锥P -ABCD 的底面为矩形,AB =23,BC =4,侧面P AB 为正三角形且垂直于底面ABCD ,M 为四棱锥P -ABCD 内切球表面上一点,则点M 到直线CD 距离的最小值为.【答案】10-1【解析】如图,设四棱锥的内切球的半径为r ,取AB 的中点为H ,CD 的中点为N ,连接PH ,PN ,HN ,球O为四棱锥P-ABCD的内切球,底面ABCD为矩形,侧面P AB为正三角形且垂直于底面ABCD,则平面PHN截四棱锥P-ABCD的内切球O所得的截面为大圆,此圆为△PHN的内切圆,半径为r,与HN,PH分别相切于点E,F,平面P AB⊥平面ABCD,交线为AB,PH⊂平面P AB,△P AB为正三角形,有PH⊥AB,∴PH⊥平面ABCD,HN⊂平面ABCD,∴PH⊥HN,AB=23,BC=4,则有PH=3,HN=4,PN=5,则△PHN中,S△PHN=12×3×4=12r3+4+5,解得r=1.所以,四棱锥P-ABCD内切球半径为1,连接ON.∵PH⊥平面ABCD,CD⊂平面ABCD,∴CD⊥PH,又CD⊥HN,PH,HN⊂平面PHN,PH∩HN=H,∴CD⊥平面PHN,∵ON⊂平面PHN,可得ON⊥CD,所以内切球表面上一点M到直线CD的距离的最小值即为线段ON的长减去球的半径,又ON=OE2+EN2=10.所以四棱锥P-ABCD内切球表面上的一点M到直线CD的距离的最小值为10-1.故答案为:10-12024届高三二轮复习“8+3+3”小题强化训练(4)一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1已知双曲线的标准方程为x 2k -4+y 2k -5=1,则该双曲线的焦距是()A.1B.3C.2D.4【答案】C【解析】由双曲线方程可知a 2=k -4,b 2=5-k ,所以c 2=k -4+5-k =1,c =1,2c =2.故选:C2在等比数列a n 中,a 1+a x =82,a 3a x -2=81,前x 项和S x =121,则此数列的项数x 等于()A.4B.5C.6D.7【答案】B【解析】由已知条件可得a 1+a x =82a 3a x -2=a 1a x =81,解得a 1=1a x =81 或a 1=81a x =1 .设等比数列a n 的公比为q .①当a 1=1,a x =81时,由S x =a 1-a x q 1-q =1-81q1-q=121,解得q =3,∵a x =a 1q x -1=3x -1=81,解得x =5;②当a 1=81,a x =1时,由S x =a 1-a x q 1-q =81-q 1-q =121,解得q =13,∵a x =a 1q x -1=81×13x -1=35-x =1,解得x =5.综上所述,x =5.故选:B .3对任意实数a ,b ,c ,在下列命题中,真命题是()A.“ac 2>bc 2”是“a >b ”的必要条件B.“ac 2=bc 2”是“a =b ”的必要条件C.“ac 2=bc 2”是“a =b ”的充分条件D.“ac 2≥bc 2”是“a ≥b ”的充分条件【答案】B【解析】对于A ,若c =0,则由a >b ⇏ac 2>bc 2,∴“ac 2>bc 2”不是“a >b ”的必要条件,A 错.对于B ,a =b ⇒ac 2=bc 2,∴“ac 2=bc 2”是“a =b ”的必要条件,B 对,对于C ,若c =0,则由ac 2=bc 2,推不出a =b ,“ac 2=bc 2”不是“a =b ”的充分条件对于D ,当c =0时,ac 2=bc 2,即ac 2≥bc 2成立,此时不一定有a ≥b 成立,故“ac 2≥bc 2”不是“a ≥b ”的充分条件,D 错误,故选:B .4已知m 、n 是两条不同直线,α、β、γ是三个不同平面,则下列命题中正确的是()A.若m ∥α,n ∥α,则m ∥nB.若α⊥β,β⊥γ,则α∥βC.若m ∥α,m ∥β,则α∥βD.若m ⊥α,n ⊥α,则m ∥n【答案】D【解析】A选项:令平面ABCD为平面α,A1B1为直线m,B1C1为直线n,有:m∥α,n∥α,但m∩n=B1,A错误;B选项:令平面ABCD为平面β,令平面B1BCC1为平面α,令平面A1ABB1为平面γ,有:α⊥β,β⊥γ,而α⊥β,B错误;C选项:令平面ABCD为平面α,令平面A1ABB1为平面β,C1D1为直线m,有:m∥α,m∥β,则α∥β,而α⊥β,C错误;D选项:垂直与同一平面的两直线一定平行,D正确.故选:D5将甲、乙等8名同学分配到3个体育场馆进行冬奥会志愿服务,每个场馆不能少于2人,则不同的安排方法有()A.2720B.3160C.3000D.2940【答案】D【解析】共有两种分配方式,一种是4:2:2,一种是3:3:2,故不同的安排方法有C48C24C222!+C38C35C222!A33=2940.故选:D6若抛物线y2=4x与椭圆E:x2a2+y2a2-1=1的交点在x轴上的射影恰好是E的焦点,则E的离心率为()A.2-12 B.3-12 C.2-1 D.3-1【答案】C【解析】不妨设椭圆与抛物线在第一象限的交点为A,椭圆E右焦点为F,则根据题意得AF⊥x轴,c2=a2-a2-1=1,则c=1,则F1,0,当x=1时,y2=4×1,则y A=2,则A1,2,代入椭圆方程得12a2+22a2-1=1,结合a2-1>0,不妨令a>0;解得a=2+1,则其离心率e=ca=12+1=2-1,故选:C.7已知等边△ABC 的边长为3,P 为△ABC 所在平面内的动点,且|P A |=1,则PB ⋅PC 的取值范围是()A.-32,92B.-12,112C.[1,4]D.[1,7]【答案】B【解析】如下图构建平面直角坐标系,且A -32,0 ,B 32,0 ,C 0,32,所以P (x ,y )在以A 为圆心,1为半径的圆上,即轨迹方程为x +322+y 2=1,而PB =32-x ,-y ,PC =-x ,32-y ,故PB ⋅PC =x 2-32x +y 2-32y =x -34 2+y -34 2-34,综上,只需求出定点34,34 与圆x +322+y 2=1上点距离平方范围即可,而圆心A 与34,34 的距离d =34+32 2+34 2=32,故定点34,34与圆上点的距离范围为12,52,所以PB ⋅PC ∈-12,112.故选:B 8设a 、b 、c ∈0,1 满足a =sin b ,b =cos c ,c =tan a ,则()A.a +c <2b ,ac <b 2B.a +c <2b ,ac >b 2C.a +c >2b ,ac <b 2D.a +c >2b ,ac >b 2【答案】A【解析】∵a 、b 、c ∈0,1 且a =sin b ,b =cos c ,c =tan a ,则c =tan a =tan sin b ,先比较a +c =sin b +tan sin b 与2b 的大小关系,构造函数f x =sin x +tan sin x -2x ,其中0<x <1,则0<sin x <1,所以,cos1<cos sin x <1,则f x =cos x +cos xcos 2sin x -2=cos x -2 cos 2sin x +cos x cos 2sin x,令g x =cos x -1-12x 2 ,其中x ∈0,1 ,则g x =x -sin x ,令p x =x -sin x ,其中0<x <1,所以,p x =1-cos x >0,所以,函数g x 在0,1 上单调递增,故g x >g 0 =0,所以,函数g x 在0,1 上单调递增,则g x =cos x -1-12x 2 >0,即cos x >1-12x 2,因为x ∈0,1 ,则0<sin x <sin1,所以,cos sin x >1-12sin 2x =1-121-cos 2x =121+cos 2x ,所以,cos 2sin x >141+cos 2x 2,因为cos x -2<0,所以,cos x -2 cos 2sin x +cos x <14cos x -2 1+cos 2x 2+cos x=14cos 5x -2cos 4x +2cos 3x -4cos 2x +5cos x -2 =14cos x -1 3cos 2x +cos x +2 <0,所以,对任意的x ∈0,1 ,f x =cos x -2 cos 2sin x +cos xcos 2sin x <0,故函数f x 在0,1 上单调递减,因为b ∈0,1 ,则f b =sin b +tan sin b -2b <f 0 =0,故a +c <2b ,由基本不等式可得0<2ac ≤a +c <2b (a ≠c ,故取不了等号),所以,ac <b 2,故选:A .二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9某大学生做社会实践调查,随机抽取6名市民对生活满意度进行评分,得到一组样本数据如下:88、89、90、90、91、92,则下列关于该样本数据的说法中正确的是()A.均值为90B.中位数为90C.方差为2D.第80百分位数为91【答案】ABD【解析】由题意可知,该组数据的均值为x =88+89+90+90+91+926=90,故A 正确;中位数为90+902=90,故B 正确;方差为s 2=1688-90 2+89-90 2+90-90 2×2+91-90 2+92-90 2 =53,故C 错误;因为6×80%=4.8,第80百分位数为91,故D 正确.故选:ABD .10设M ,N ,P 为函数f x =A sin ωx +φ 图象上三点,其中A >0,ω>0,ϕ <π2,已知M ,N 是函数f x 的图象与x 轴相邻的两个交点,P 是图象在M ,N 之间的最高点,若MP 2+2MN ⋅NP=0,△MNP 的面积是3,M 点的坐标是-12,0 ,则()A.A =2B.ω=π2C.φ=π4D.函数f x 在M ,N 间的图象上存在点Q ,使得QM ⋅QN <0【答案】BCD【解析】MP 2+2MN ⋅NP =MP 2-2NM ⋅NP =MP 2-2NM ⋅12NM =T 4 2+A 2 -T 22=A 2-3T 216=0,而S △MNP =AT 4=3,故A =3,T =4=2πω,ω=π2,A 错误、B 正确;-12⋅π2+φ=k π,φ=k π+π4(k ∈Z ),而ϕ <π2,故φ=π4,C 正确;显然,函数f x 的图象有一部分位于以MN 为直径的圆内,当Q 位于以MN 为直径的圆内时,QM⋅QN<0,D 正确,故选:BCD .11设a 为常数,f (0)=12,f (x +y )=f (x )f (a -y )+f (y )f (a -x ),则().A .f (a )=12B .f (x )=12成立C f (x +y )=2f (x )f (y )D .满足条件的f (x )不止一个【答案】ABC 【解析】f (0)=12,f (x +y )=f (x )f (a -y )+f (y )f (a -x )对A :对原式令x =y =0,则12=12f a +12f a =f a ,即f a =12,故A 正确;对B :对原式令y =0,则f x =f x f a +f 0 f a -x =12f x +12f a -x ,故f x =f a -x ,对原式令x =y ,则f 2x =f x f y +f y f x =2f x f y =2f 2x ≥0,故f x 非负;对原式令y =a -x ,则f a =f 2x +f 2a -x =2f 2x =12,解得f x =±12,又f x 非负,故可得f x =12,故B 正确;对C :由B 分析可得:f x +y =2f x f y ,故C 正确;对D :由B 分析可得:满足条件的f x 只有一个,故D 错误.故选:ABC .三、填空题:本题共3小题,每小题5分,共15分.12在复平面内,复数z =-12+32i 对应的向量为OA ,复数z +1对应的向量为OB ,那么向量AB 对应的复数是.。
高考数学复习《30分钟选填》 (理科版) 限时训练(40)答案
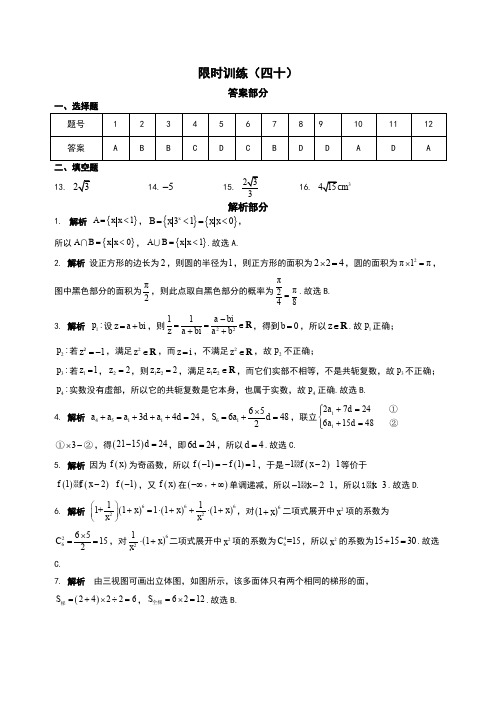
限时训练(四十)答案部分一、选择题二、填空题13. 5-3解析部分1.解析{}1A x x=<,{}{}310xB x x x=<=<,所以{}0A B x x=<,{}1A B x x=<.故选A.2. 解析设正方形的边长为2,则圆的半径为1,则正方形的面积为224⨯=,圆的面积为2π1π⨯=,图中黑色部分的面积为π2,则此点取自黑色部分的概率为ππ248=.故选B.3. 解析1:p设iz a b=+,则2211iia bz a b a b-==∈++R,得到0b=,所以z∈R.故1p正确;2:p若z1=-2,满足2z∈R,而z i=,不满足2z∈R,故2p不正确;3:p若1z1=,2z2=,则12z z2=,满足12z z∈R,而它们实部不相等,不是共轭复数,故3p不正确;4:p实数没有虚部,所以它的共轭复数是它本身,也属于实数,故4p正确.故选B.4.解析45113424a a a d a d+=+++=,61656482S a d⨯=+=,联立11272461548a da d+=⎧⎪⎨+=⎪⎩①②3⨯-①②,得()211524-=d,即624d=,所以4d=.故选C.5. 解析因为()f x为奇函数,所以()()111f f-=-=,于是()121f x--剟等价于()()()121f f x f--剟,又()f x在()-∞+∞,单调递减,所以121x--剟,所以3x1剟.故选D. 6. 解析()()()66622111+1111x x xx x⎛⎫+=⋅++⋅+⎪⎝⎭,对()61x+二项式展开中2x项的系数为2665C152⨯==,对()6211xx⋅+二项式展开中2x项的系数为46C=15,所以2x的系数为151530+=.故选C.7. 解析由三视图可画出立体图,如图所示,该多面体只有两个相同的梯形的面,()24226S=+⨯÷=梯,6212S=⨯=全梯.故选B.第2页/共5页8. 解析 因为要求A 大于1000时输出,且框图中在“否”时输出,所以“”中不能输入1000A >,排除A ,B.又要求n 为偶数,且n 的初始值为0,所以“”中n 依次加2可保证其为偶.故选D.9. 解析 1:cos C y x =,22π:sin 23⎛⎫=+ ⎪⎝⎭C y x .首先曲线1C ,2C 统一为一三角函数名,可将1:cos C y x =用诱导公式处理.πππcos cos sin 222⎛⎫⎛⎫==+-=+ ⎪ ⎪⎝⎭⎝⎭y x x x .横坐标变换需将1=ω变成2=ω,即112πππsin sin 2sin 2224C y x y x x ⎛⎫⎛⎫⎛⎫=+−−−−−−−−−−→=+=+→ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭上各坐短到原的倍点横标缩来2ππsin 2sin 233y x x ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭.注意ω的系数,左右平移需将2=ω提到括号外面,这时π4+x 平移至π3+x , 根据“左加右减”原则,“π4+x ”到“π3+x ”需加上π12,即再向左平移π12.故选D. 10. 解析 解法一:设直线1l 的斜率为k ,则直线2l 的斜率为1k-,设()11,A x y ,()22,B x y , ()33,D x y ,()44,E x y ,直线()11l k x =-,直线()21:1l y x k =--.联立()241y x y k x ⎧=⎪⎨=-⎪⎩,消去y 整理得()2222240k x k x k -++=,所以2122224424k AB x x p k k+=++=+=+,同理 22342124441k DE x x p k k+=++==+,从而22184+16AB DE k k ⎛⎫+=+ ⎪⎝⎭…,当且仅当1k =± 时等号成立.故选A.解法二:设AB 的倾斜角为θ,抛物线的准焦距为p .作1AK 垂直准线于点1K ,2AK 垂直x 轴于点2K ,如图所示.易知11cos 22AF GF AK AK AF p p GP pθ⎧⎪⋅+=⎪⎪=⎨⎪⎛⎫⎪=--= ⎪⎪⎝⎭⎩(几何关系)(抛物线定义),所以cos AF p AF θ⋅+=, 即1cos p AF θ=-,同理1cos p BF θ=+,所以22221cos sin p pAB θθ==-.又DE 与AB 垂直,即DE 的倾斜角为π2θ+,2222πcos sin 2p pDE θθ==⎛⎫+ ⎪⎝⎭. 而24y x =,即2p =,所以22112sin cos AB DE p θθ⎛⎫+=+ ⎪⎝⎭2222sin cos 4sin cos θθθθ+=224sin cos θθ=241sin 24θ== 21616sin 2θ≥,当π4θ=时取等号,即AB DE +的最小值为16.故选A. 11. 解析 设235x y z t ===,两边取对数得ln 2ln3ln5ln x y z t ===,则2ln 2ln 2tx =3ln 3ln 3t y =,5ln 5ln 5t z =,ln 0t >.设()ln x f x x=,()()2ln 1ln x f x x -'=,当()0,e x ∈时, ()0f x '<,()f x 单调递减;当()e,x ∈+∞时,()0f x '>,()f x 单调递增.而()24ln x f t =, ()33ln y f t =,()55ln z f t =.由e<3<4<5,得325y x z <<.故选D.12. 解析 设首项为第1组,接下来两项为第2组,再接下来三项为第3组,以此类推. 设第n 组的项数为n ,则n 组的项数和为()12n n +,由题意得,100N >,令()11002n n +>,得14n ≥且*n ∈N ,即N 出现在第13组之后,第n 组的和为122112nn -=--,n 组总共的和为 ()12122212n n n n +--=---,若要使前N 项和为2的整数幂,则()12n n N +-项的和21k -应与2n --互为相反数,即()*21214k n k n -=+∈N ,≥,()2log 3k n =+,得n 的最小值为295n k ==,, 则()2912954402N ⨯+=+=.故选A.13. 解析 ()22222(2)22cos602+=+=+⋅⋅⋅+a b a b a a b b 221222222=+⨯⨯⨯+=444++=12,所以2+==a b第4页/共5页14. 解析 不等式组21210x y x y x y +⎧⎪+-⎨⎪-⎩………表示的平面区域如图所示,由32z x y =-,得322zy x =-,求z 的最小值,即求直线322z y x =-的纵截距的最大值,当直线322zy x =-过图中点A 时,纵截距最大, 由2121x y x y +=-⎧⎨+=⎩,解得点A 的坐标为(1,1)-,此时3(1)215z =⨯--⨯=-. 15. 解析 如图所示,OA a =,AN AM b ==.因为60MAN ∠=,所以AP =,OP =tan AP OP θ==.又因为tan b a θ=,所以b a =,解得223a b =,则e ===.16. 解析 由题意,联结OD ,交BC 于点G ,如图所示,则OD BC ⊥,OG =, 即OG 的长度与BC 的长度成正比.设OG x =,则BC =,5DG x =-,三棱锥的高h =,2132ABC S x =⋅⋅=△,则13ABC V S h =⋅△令()452510f x x x =-,50,2x ⎛⎫∈ ⎪⎝⎭,()3410050f x x x '=-,令()0f x '>,即4320x x -<,2x <,当()0f x '<,得522x <<,所以()f x在()0,2上单调递增,在52,2⎛⎫ ⎪⎝⎭上单调递减.故()()280f x f =≤,则V =,所以体积的最大值为3.。
高三数学综合复习:选择填空限时练(二)

选择填空限时练(二)(推荐时间:45分钟)一、选择题1. 设两集合A ={x |y =ln(1-x )},B ={y |y =x 2},则用阴影部分表示A ∩B 正确的是( )答案 A解析 A ={x |y =ln(1-x )}=(-∞,1), B ={y |y =x 2}=[0,+∞),A ∩B =[0,1),故选A. 2. i 为虚数单位,则⎝⎛⎭⎪⎫1+i 1-i 2 014=( )A .-iB .-1C .iD .1答案 B解析 ⎝ ⎛⎭⎪⎫1+i 1-i 2 014=i 2 014=i 2=-1.3. 设{a n }是等比数列,则“a 1<a 2<a 3”是“数列{a n }是递增数列”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件 答案 C解析 设等比数列{a n }的公比为q ,若a 1<a 2<a 3,则q >0,且a 1<a 1q <a 1q 2,解得a 1>0,q >1,或a 1<0,0<q <1,所以数列{a n }为递增数列;反之,若数列{a n }是递增数列,显然有a 1<a 2<a 3,所以a 1<a 2<a 3是数列{a n }是递增数列的充要条件.故选C. 4. 平面向量a 与b 的夹角为60°,a =(2,0),|b |=1,则|a +2b |的值为( )A. 3 B .2 3C .4D .12答案 B解析 由已知|a |=2,|a +2b |2=a 2+4a ·b +4b 2 =4+4×2×1×cos 60°+4=12, 所以|a +2b |=2 3.5. 已知函数f (x )=x 2-ln|x |x,则函数y =f (x )的大致图象为( )答案 A解析 依题意,①当x >0时, f ′(x )=2x -1-ln x x 2=2x 3+ln x -1x 2,记g (x )=2x 3+ln x -1,则函数g (x )在(0,+∞)上是增函数, 注意到g (e -2)=2e -6-3<0,g (1)=1>0, 函数g (x )在(e -2,1)上必存在唯一零点x 0, e -2<x 0<1,g (x 0)=0, 当x ∈(0,x 0)时,f ′(x )<0; 当x ∈(x 0,+∞)时,f ′(x )>0,即函数f (x )在(0,x 0)上是减函数,在(x 0,+∞)上是增函数; ②当x <0时,f (x )=x 2-ln (-x )x,f (-1)=1>0,结合各选项知,选A.6. 阅读下边的程序框图,运行相应的程序,则输出i 的值为 ( )A .3B .4C .5D .6答案 B解析 第一次循环,i =1,a =2; 第二次循环,i =2,a =5; 第三次循环,i =3,a =16; 第四次循环,i =4,a =65>50; ∴输出i =4.7. 设函数f (x )和g (x )分别是R 上的偶函数和奇函数,则下列结论恒成立的是( )A .f (x )+|g (x )|是偶函数B .f (x )-|g (x )|是奇函数C .|f (x )|+g (x )是偶函数D .|f (x )|-g (x )是奇函数答案 A解析 由题意知f (x )与|g (x )|均为偶函数.A 项,偶+偶=偶;B 项,偶-偶=偶,错;C 项与D 项分别为偶+奇=偶,偶-奇=奇,均不恒成立.8. 已知抛物线C :y 2=4x 的焦点为F ,直线y =2x -4与C 交于A ,B 两点,则cos ∠AFB等于( )A.45B.35 C .-35D .-45答案 D解析 方法一 由⎩⎪⎨⎪⎧ y =2x -4,y 2=4x ,得⎩⎪⎨⎪⎧ x =1,y =-2或⎩⎪⎨⎪⎧x =4,y =4.令B (1,-2),A (4,4),又F (1,0),∴由两点间距离公式得|BF |=2,|AF |=5,|AB |=3 5. ∴cos ∠AFB =|BF |2+|AF |2-|AB |22|BF |·|AF |=4+25-452×2×5=-45.方法二 由方法一得A (4,4),B (1,-2),F (1,0), ∴F A →=(3,4),FB →=(0,-2), ∴|F A →|=32+42=5,|FB →|=2.∴cos ∠AFB =F A →·FB →|F A →|·|FB →|=3×0+4×(-2)5×2=-45.9. 已知O 是坐标原点,点A (-1,1),若点M (x ,y )为平面区域⎩⎪⎨⎪⎧x +y ≥2,x ≤1,y ≤2上的一个动点,则OA →·OM →的取值范围是( )A .[-1,0]B .[0,1]C .[0,2]D .[-1,2]答案 C解析 OA →·OM →=-x +y ,令z =-x +y ,做出可行域,求线性规划问题.10.已知一空间几何体的三视图如图所示,则该几何体的体积为 ( )A.65π cm 3 B .3π cm 3 C.23π cm 3D.73π cm 3 答案 D解析 由三视图可知,此几何体是一个底面半径为1 cm 、高为3 cm 的圆柱的上部去掉一个半径为1 cm 的半球所形成的几何体,所其体积为V =πr 2h -23πr 3=3π-23π=73π(cm 3).11.函数f (x )=A sin(ωx +φ)(A >0,ω>0)的图象如图所示.为了得到g (x )=-A cos ωx (A >0,ω>0)的图象,可以将f (x )的图象( ) A .向右平移π12个单位长度B .向右平移5π12个单位长度C .向左平移π12个单位长度D .向左平移5π12个单位长度答案 B解析 由图象知,f (x )=sin ⎝⎛⎭⎫2x +π3,g (x )=-cos 2x ,代入B 选项得sin ⎣⎡⎦⎤2⎝⎛⎭⎫x -5π12+π3=sin ⎝⎛⎭⎫2x -π2=-sin ⎝⎛⎭⎫π2-2x =-cos 2x . 12.记圆O :x 2+y 2=π2内的正弦曲线y =sin x 与x 轴围成的区域为D ,随机往圆O 内投一个点A ,则点A 落在区域D 内的概率是( )A.42 B.43 C.22 D.23 答案 B解析 结合图形可得,D 区域面积为2ʃπ0sin x d x=2() |-cos x π0=4,由几何概型可得概率为42=43. 二、填空题13.已知sin α=12+cos α,且α∈⎝⎛⎭⎫0,π2,则cos 2αsin ⎝⎛⎭⎫α-π4的值为________. 答案 -142解析 将sin α-cos α=12两边平方,得2sin α·cos α=34,(sin α+cos α)2=74,sin α+cos α=72,cos 2αsin ⎝⎛⎭⎫α-π4=cos 2α-sin 2α22(sin α-cos α)=-2(sin α+cos α)=-142. 14.已知各项不为零的等差数列{a n }的前n 项和为S n .若m ∈N *,且a m -1+a m +1-a 2m =0,S 2m -1=38,则m =________. 答案 10解析 a m -1+a m +1=2a m ,得2a m -a 2m =0,又a m ≠0.所以a m =2,则S 2m -1=(2m -1)(a 1+a 2m -1)2=(2m -1)a m =2(2m -1)=38,所以m =10.15.已知f (x )=a ln x +12x 2(a >0),若对任意两个不等的正实数x 1,x 2都有f (x 1)-f (x 2)x 1-x 2>2恒成立,则a 的取值范围是________. 答案 [1,+∞)解析 由k =f (x 1)-f (x 2)x 1-x 2知f ′(x )=ax +x ≥2,x ∈(0,+∞)恒成立.即a ≥x (2-x )恒成立,因为x (2-x )的最大值为1.所以a ≥1.16.在△ABC 中,M 是BC 的中点,AM =1,点P 在AM 上且满足AP →=2PM →,则AP →·(PB →+PC →)=________. 答案 49解析 由AP →=2PM →知,P 为△ABC 的重心, 所以PB →+PC →=2PM →,则AP →·(PB →+PC →)=2AP →·PM →=2|AP →||PM →|cos 0°=2×23×13×1=49.。
高考数学复习《30分钟选填》 (理科版) 限时训练(24)答案

限时训练(二十四)答案部分二、填空题:9.180 10. 24 11.13 12. 14.1,e ⎡⎫+∞⎪⎢⎣⎭解析部分1.解析 函数lg y x =的定义域为{}0A x x =>,则(]0,1AB =.故选C.2.解析 若复数()()2231i z m m m =+-+-为纯虚数,则2230m m +-=,且10m -≠,解得3m =-.故选A.3.解析 由πsin 222sin 23y x x x ⎛⎫=+=+⎪⎝⎭,得最小正周期2ππ2T ==,振幅2A =.故选B. 4.解析 由题意还原几何体,如图所示,则该几何体是圆柱体的16,其体积213π22π6V =⨯⨯⨯=. 故选D.5.解析 由20x …,得x ∈R ,故命题p 为假命题;由向量的三角形法则知,当⊥a b 时, -=+a b a b ,因此充分性成立,将-=+a b a b 平方得40=a b ,则⊥a b ,必要性成立, 故命题q 为真命题,故选项D 中,“p ⌝真,q ⌝假”,所以“()()p q ⌝∧⌝为假命题”.故选D. 6.解析 由函数()f x 的解析式作出函数图像,如图所示.可知()f x 为偶函数,则()()()()()21221f a f a f f a f -+⇔剟,即()()1f a f …,由图像知1a …,得11a -剟. 故选C.7.解析根据上表可得()1202010122012112s +⨯=+++++=+=.故选B.8.解析 当2n =时,将24n =个正整数1,2,3,4任意排成数表,由数表行列的对称性及题意可知,所有数表的特征值均在以下三个数表的特征值中取得.特征值为44min 2,,3,233⎧⎫=⎨⎬⎩⎭;特征值为434min 2,,4,323⎧⎫=⎨⎬⎩⎭;特征值为33min 2,3,,422⎧⎫=⎨⎬⎩⎭.综上所述,数表的所有可能的“特征值”最大值为4433max ,,3322⎧⎫=⎨⎬⎩⎭.故选D. 9.解析 由题可得总体中每个个体被抽到的概率为19,所以总体中的个体数2018019n ==.10.解析 依题意可得1212142PF PF PF PF ⎧+=⎪⎨-=⎪⎩,解得1286PF PF ⎧=⎪⎨=⎪⎩或1268PF PF ⎧=⎪⎨=⎪⎩,又1210F F =,故2221212PF PF F F +=,所以12PF F △为直角三角形,因此121211682422PF F S PF PF ==⨯⨯=△.11.解析 依题意,可行域如图所示,直线10x ky +-=恒过定点()1,0,若要将可行域分成面积相等的两部分,则直线10x ky +-=必过AB 的中点()0,3,则310k -=,即13k =. 图212.解析 将极坐标方程化成直角坐标方程得,曲线1:1C x =,()222:24C x y -+=.设圆心为()2,0D , 直线1x =与x 轴交于点C ,连接AD,如图所示,则2AB AC ===2=13.解析 由切割线定理得2AD AB AC =⋅,即23=,解得AB =所以BC AC AB =-=O 到AC=14.分析 对于复合函数零点问题利用图像法与换元法求解. 解析 令()t f x =,则函数()y f t =,其图像如图所示.若()1f t =-,则1e t =或10k t k--=<. 当1k t k--=时,函数()t f x =有两个零点,若使得函数()()1y f f x =+有四个零点, 则当1e t =时,函数()t f x =也要有两个零点,故1e k ….所以实数k 的取值范围是1,e ⎡⎫+∞⎪⎢⎣⎭.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三数学选择题、填空题限时训练一、选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一 项是符合题目要求的.1.已知i 是虚数单位,若复数()1i a +()2i +是纯虚数,则实数a 等于 ( ). A. 2 B.12 C. 12- D. 2- 2.下列全集U =R ,集合{}02A x x =<<,{}210B x x =->,那么UAB =( ).A. {}01x x << B. {}01x x< C. {}12x x << D. {}12x x <3.已知圆的方程为()()22124x y -+-=,那么该圆圆心到直线31x t y t =+⎧⎨=+⎩,(t 为参数)的距离为( ).A.B.C.D. 4.已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为( ).正(主)视图 侧(左)视图俯视图 A. 1B. 2C. 3D. 45.等比数列{}n a 中,10a >,则“13a a <”是“36a a <”的( ). A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件6.从甲、乙等5名志愿者中选出4名,分别从事A ,B ,C ,D 四项不同的工作,每人承担一项.若甲、乙二人均不能从事A 工作,则不同的工作分配方案共有 ( ).A.60种 B. 72种 C. 84种 D. 96种7.设直角ABC △,0P 是斜边AB 上一定点,满足0116P B AB ==,则对于边AB 上任一点P ,恒有00PB PC P B PC ⋅⋅,则斜边AB 上的高是( ). A.4B.C. D. 28.已知F 为抛物线2y x =的焦点,点A ,B 在该抛物线上且位于x 轴的两侧,2OA OB ⋅=(其中O 为坐标原点),则ABO △与AFO △面积之和的最小值是( ). A. 2 B. 3C.8D. 二、填空题:本大题共6小题,每小题5分,共30分. 把答案填在题中的横线上. 9. 已知tan 2α=,那么πtan 3α⎛⎫-= ⎪⎝⎭________,sin 2α=________. 10. 已知直线:4l mx y -=,若直线l 与直线()12x m m y +-=垂直,则m 的值为________;若直线l 被圆22:280C x y y +--=截得的弦长为4,则m 的值为________. 11. 在直角三角形ABC 中,90C ∠=,2AB =,1AC =,若32AD AB =,则CD CB ⋅=____________.12.若函数()()()2 1 01 0x x f x x ⎧-⎪=⎨-<⎪⎩,则满足()()244f x f x -的x 的取值范围为________.13. 已知向量(),a b =m,=n ,若1⋅=m n ,则=m _______.14. 如图所示,水平地面ABC 与墙面BCD 垂直,E 、F 两点在线段BC 上,且满足4EF =,某人在地面ABC 上移动,为了保证观察效果,要求他到E ,F 两点的距离和不得小于6,把人的位置记为P ,点R 在线段EF 上,满足1RF =,点Q 在墙面上,且QR 垂直BC ,且2RQ =,由点P 观察点Q 的仰角为θ,则tan θ的最大值是____________.答 案一、选择题二、填空题9. 811;45 10.①0或2;②2± 11. 9212. (,2-∞-+13. 1 14.151. 解析 ()()1i 2i 2i 2i a a a ++=++-,由题意得20120a a -=⎧⎨+≠⎩,解得212a a =⎧⎪⎨≠-⎪⎩.故选A.2. 解析 {}11B x xx =><-或,所以{}11UB x x=-.把UB 与集合A 在数轴表示出来,如图所示.由图可知,{}01UAB x x=<.故选B.3. 解析 由题意得直线的普通方程为2y x =-.可得圆心()1,2到直线的距离2d ==.故选C. 4. 解析 由三棱锥的三视图,还原三棱锥的立体图形,如图所示.由图可知,有4个直角三角形.故选D.R QPFE DCBA5. 解析 在等比数列{}n a 中,设公比为q .由13a a <,可得211a a q <,由10a >,可得21q >.① 由36a a <,可得2511a q a q <,由10a >,可得31q >.②综上可知,由①不一定能推出②.由②一定可以推出①.所以①是②的必要不充分条件.故选B. 6. 解析 解法一(特殊位置法):由甲、乙二人均不能从事A 工作,可知A 工作有13C 种分配方法,则剩余的B ,C ,D 三项工作有34A 种分配方法.所以由分步乘法计数原理,可得不同的工作分配方案有1334C C 72⋅=(种).解法二(特殊元素法):甲参加,乙不参加,有1333C A 18⋅=(种)分配方案;同理,乙参加,甲不参加,有18种分配方案; 甲、乙均参加,有213323C C A 36⋅⋅=(种)分配方案.由分类加法计数原理,可得共有18183672++=(种)分配方案.7. 解析 取BC 的中点M ,连接0P M ,PM ,如图所示.由PB PM MB =+,PC PM MC =+,可得()()222BC PB PC PM MB PM MC PM ⎛⎫⋅=++=- ⎪⎝⎭.MP 0PCBA同理可得220002BC P B P C P M ⎛⎫⋅=- ⎪⎝⎭.由00PB PCP B PC ⋅⋅,得220PMP M .可知0P M AB ⊥.在Rt ABC △与0Rt MBP △中,0B BBCA MP B∠=∠⎧⎨∠=∠⎩,可得0ABC MBP △∽△, 所以AB BCMB BP =,由题意可知01BP =,6AB =,可得6MB BC ⋅=,即226MB =,得MB =由勾股定理得0P M=由M 为BC 的中点,可得斜边AB 上的高为故选C.8. 解析 由题意作图,如图所示.设()2,A m m ,()2,B n n ,其中0m >,0n <.则()2,OA m m =,()2,OB n n =,222OA OB m n mn ⋅=+=,解得1mn =(舍)或2mn =-. 设直线AB l 的方程为()()()()222m n y n m n x n --=--,即()()2m n y n x n +-=-,令0y =,解得2x mn =-=,所以C 点坐标为()2,0C.()112222AOB AOC BOC S S S m n m n =+=⨯⋅+⨯⋅-=-△△△,111248AOF S m m =⨯⋅=△, 则199292238888AOB AOF m S S m n m m n m mm+=-+=-=+⋅=△△, 当且仅当928m m =,即43m =时等号成立.故ABO △与AFO △面积之和的最小值为3.故选B. 9. 解析πtan tan21π83tan π3111tan tan 3ααα--⎛⎫-====⎪⎝⎭+⋅. 22222sin cos 2tan 224sin 22sin cos sin costan 1215ααααααααα⨯=====+++.10. 解析 由两条直线互相垂直得到()10m m m --=,即220mm -=,所以0m =或2.圆C 的方程化为()2219x y +-=,所以圆心为()0,1,圆的半径3r =,所以圆心到直线l 的距离d ===2m =±.11. 解析 解法一:如图所示.因为90C ∠=,22AB AC ==,所以30ABC ∠=,BC=.因为32AD AB =,所以1BD =.()2931cos302CD CB CB BD CB CB BD CB ⋅=+⋅=+⋅=+= 解法二:以C 点为原点,CA 所在轴为x 轴,CB 所在轴为y 轴建立平面直角坐标系.则()0,0C ,()1,0A ,(B ,可得1,22D ⎛⎫- ⎪ ⎪⎝⎭,则1,22CD ⎛=- ⎝⎭,(CB =,可得92CD CB ⋅=. 12. 解析根据()f x 的解析式,画出它的图像,如图所示.A CBD解法一:要想求()()244f x f x -的解集,只需求出()()244f x f x -<的补集即可.要想求()()244f x f x -<,只需求24044x x x>⎧⎨>-⎩,解得2x >-+所以()()244f x f x -的解集为(,2-∞-+. 解法二:当()()244f x f x ->时,则224044x x x⎧->⎪⎨->⎪⎩,解得22x -<<-+当()()244f xf x -=时,则244x x -=或24040x x ⎧-⎨⎩,解得2x -或2x =-+综上可得()()244f x f x -的x的取值范围为(,2-∞-+. 13. 解析 由()222222a b m =-+=-n ,得222m n +=,又1⋅=m n , 故2220+-⋅m n m n =,即()20-=m n ,得=m n ,则1==m n .14. 解析 由点P 到E ,F 两点的距离和不得小于6,可知点P 的轨迹为椭圆C 及椭圆C 外的一点.由2tan QR PR PRθ==,可知当PR 取最小值时,tan θ最大,则点P 一定在椭圆C 上.假设E ,F 为线段BC 上固定的两点,设EF 的中点O 为原点,作OH EF ⊥,以O 为原点,EF所在轴为x 轴,OH 所在轴为y 轴,建立平面直角坐标系,如图所示.由4EF =,可得椭圆C 的方程为22195x y +=,点P 在椭圆C 上,设()00,P x y ,则2200195x y +=.由1RF =,得()1,0R .则)033PR x ===-.可得当2944 29x==⨯时,PR取得最小值.min2PR==.所以tanθ15 =.。
