理论力学(附答案)-谢传峰、王琪-动力学部分
理论力学习题答案 谢传峰、王琪 高等教育出版社
− F4 cos 450 ⋅ a − F6 cos 450 ⋅ a = 0 F1 ⋅ a + F6 cos 450 ⋅ a − F sin 450 ⋅ a = 0 F1 ⋅ a + F3 ⋅ a − F sin 450 ⋅ a = 0 F3 ⋅ a + F5 ⋅ a − F4 cos 450 ⋅ a = 0
静力学部分
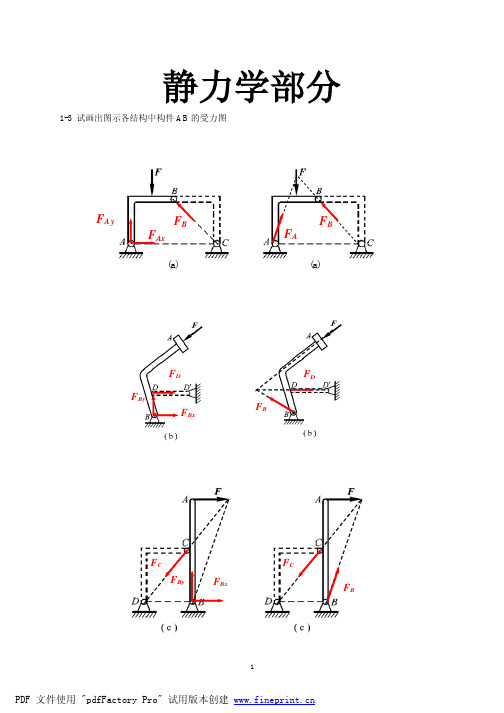
1-3 试画出图示各结构中构件 AB 的受力图
FA y FAx
FB
FA
FB
(a)
(a)
FD FBy FBx FB
FD
FC FBy FBx
FC FB
1
PDF 文件使用 "pdfFactory Pro" 试用版本创建
1-4 试画出两结构中构件 ABCD 的受力图
即棒料左侧脱离 V 型槽,与题意不符,故摩擦系数
8
PDF 文件使用 "pdfFactory Pro" 试用版本创建
2-33 均质杆 AB 长 40cm,其中 A 端靠在粗糙的铅直墙上,并用绳子 CD 保持平衡,如图所示。设
BC = 15cm, AD = 25cm ,平衡时 α 角的最小值为 45o 。试求均质杆与墙之间的静摩擦因数 f s 。
FBx
1-8 在四连杆机构的 ABCD 的铰链 B 和 C 上分别作用有力 F1 和 F2, 机构在图示位置平衡。 试求二力 F1 和 F2 之间的关系。 解:杆 AB,BC,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。 解法 1(解析法) 假设各杆受压,分别选取销钉 B 和 C 为研究对象,受力如图所示: 由共点力系平衡方程,对 B 点有:
F4 = F1 =
2 F 2
理论力学答案解析[谢传峰版]
![理论力学答案解析[谢传峰版]](https://img.taocdn.com/s3/m/dc43c06e33687e21af45a930.png)
静力学1-3 试画出图示各结构中构件AB 的受力图F AxF A yF B(a)(a)F AF BF D F BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5bF AxF A y F D F ByF A F BxF B F AF Ax F A y F DxF Dy WT EF CxF C yWF AxF A yF B y F Cx F Dy F Bx T EN’F BF DF A N F AF BF D1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F 对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =FF450302-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):=∑M 0)45sin(100=-+⋅⋅M a F A θaM F A 354.0= 其中:31tan =θ。
理论力学答案(谢传峰版)精编版
静力学1-3 试画出图示各结构中构件AB 的受力图F AxF A yF B(a)(a)F AF BF D F BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5bF AxF A y F D F ByF A F BxF B F AF Ax F A y F DxF Dy WT EF CxF C yWF AxF A yF B y F Cx F Dy F Bx T EN’F BF DF A N F AF BF D1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F 对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =FF450302-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):=∑M 0)45sin(100=-+⋅⋅M a F A θaM F A 354.0= 其中:31tan =θ。
理论力学课后习题答案

理论力学课后习题答案理论力学课后习题答案引言:理论力学是物理学的基础课程之一,对于理解和应用物理学的原理和方法具有重要意义。
在学习理论力学的过程中,课后习题是巩固知识、提高能力的重要途径。
本文将针对理论力学课后习题进行解答,帮助读者更好地理解和掌握这门课程。
第一章:牛顿力学1. 一个物体以初速度v0沿直线运动,加速度为a,求物体的位移与时间的关系。
答:根据牛顿第二定律F=ma,可得物体所受合力F=ma=mv/t,其中m为物体的质量,v为物体的速度,t为时间。
由此可得物体的位移s=vt+1/2at^2。
2. 一个质点在重力作用下自由下落,求它在t时刻的速度和位移。
答:在重力作用下,质点的加速度为g,即a=g。
根据牛顿第二定律F=ma,可得质点所受合力F=mg。
根据牛顿第一定律,质点的速度随时间的变化率为v=g*t,位移随时间的变化率为s=1/2gt^2。
第二章:拉格朗日力学1. 一个质点沿半径为R的圆周运动,求它的动能和势能。
答:质点的动能由动能定理可得,即K=1/2mv^2,其中m为质点的质量,v为质点的速度。
质点的势能由引力势能可得,即U=-GmM/R,其中G为引力常数,M为圆周的质量。
2. 一个质点在势能为U(r)的力场中运动,求它的运动方程。
答:根据拉格朗日方程可得,质点的运动方程为d/dt(dL/dv)-dL/dr=0,其中L=T-U,T为质点的动能,U为质点的势能。
第三章:哈密顿力学1. 一个质点在势能为U(x)的力场中运动,求它的哈密顿量和哈密顿运动方程。
答:质点的哈密顿量由哈密顿定理可得,即H=T+U,其中T为质点的动能,U为质点的势能。
质点的哈密顿运动方程为dp/dt=-dH/dx,其中p为质点的动量。
2. 一个质点在势能为U(x)的力场中运动,求它的哈密顿正则方程。
答:质点的哈密顿正则方程为dx/dt=dH/dp,dp/dt=-dH/dx,其中x为质点的位置,p为质点的动量。
结论:通过对理论力学课后习题的解答,我们可以更深入地理解和应用物理学的原理和方法。
理论力学课后答案-谢传峰、王琪-动力学第九章、第十章

1 2
2l m dx(
x sin )2 0 2l
2 ml 2
2 sin2 3
O C
系统的动能 T T1 T2 。 取 900 为势能零点,则系统的势能为:
V mgl cos
则拉格朗日函数:
L T V 2 ml2 (2
2 sin2 ) mgl cos 3
x
楔块 B 的速度 vB ,以及 B 相对于 A 的相对速度
满足如下的矢量关系(方向如图所示):
vB vA vBr
系统的动能为:
vBr vA
T
1 2
m
Av
A
2
1 2
mBvB 2
P1 2g
x 2
P2 2g
[(x
s cos)2
(ssin)2 ]
1 2g
(P1
P2 )x 2
度
转动。物体的质心 G 在垂直于 O1O2 的直线上,O3G l 。设 O1O2 和 O3G 是物体过 O3
点的惯量主轴,转动惯量为 J1 和 J 2 ,物体对另一过 O3 点的惯量主轴的转动惯量为 J 3 ,试
求物体的动能表达式并建立物体的运动微分方程。 解:
以该物体为研究对象,有一个自由度,取 O3G 和 OC 的夹角 为广义坐标。若以框架 O1O2OC 为动系,则物体的相对运动是以角速度 绕轴 O1O2 的定轴转动,牵连运动是以角 速度
垂直于 O1O2 的平面
z’
O3
θ G
y’
坐标系 O3 x y z 的三个坐标轴为过 O3 点的三个惯量主轴,则系统的动能为:
T
理论力学答案(谢传峰版)61453
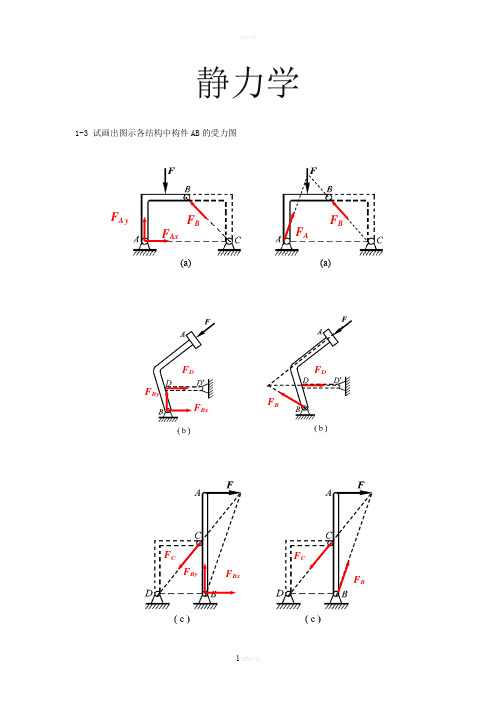
静力学1-3 试画出图示各结构中构件AB 的受力图F AxF A yFB(a)(a)F AF BF D F BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5bF AxF A yF D F ByF A F BxF B F AF Ax F A yF Dy T E F CxF C yN’F BF DF ANF AF BF D1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F 对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
45030对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):=∑M 0)45sin(100=-+⋅⋅M a F A θaM F A 354.0= 其中:31tan =θ。
习题课A(10月28日PPT)北航理论力学王琪

习题课I
2009-10-28 1
BUAA
对于刚体: •主矢 •主矩
平衡条件
基本原理与定理
{F1 , F2 , L , Fn } = {FR , M O }
FR = ∑Fi = ∑Fi '
i =1 n n
M O = ∑ M i = ∑ ri × Fi
n
i =1
n
FR = 0, M O = 0
1
2
C
D
设:杆1的长度为L
2009-10-28
dL < 0
28
BUAA
C D
E
C D 设:CD杆的长度为L dL > 0
2009-10-28 29
BUAA
思考题:系统如图所示。若人重W < > 板重P且人有足够大的 力量。下列两种情况中,哪个系统能在图示位置维持平衡?
(a)
(b)
A:图(a)
2009-10-28
z
F1
o
FR
F2
y
⎧ ∑ M l1 = 0 ⎪ ⎨ ∑ M l2 = 0 ⎪ ⎩ ∑ M l3 = 0
确定三根轴的位置
4
x
2009-10-28
Fn
BUAA
题8:给出空间平行力系平衡方程的三矩式
z
FR
Fi
y
o
x
MO
⎧∑ M x = 0 ⎪ ⎨∑ M y = 0 ⎪ ⎩∑ M L = 0
如何确定L轴?
2009-10-28
F1
D:力螺旋
F2
3
BUAA
题5:空间汇交力系的平衡方程独立的充分必要条件:
⎧ ∑ Fx = 0 ⎪ ⎨∑ Fy = 0 ⎪ ⎩ ∑ Fz = 0
习题课II北航理论力学王琪

A: 速度的模增加;
2009-11-18
B: 速度的模减小
10
理论力学
讲解过
A
演示过
o
过
θ
u
x
2009-11-18
11
理论力学
试题:已知图示瞬时圆盘中心O的速度和加速度,求此瞬时 AB 杆的角速度和角加速度。
动点:圆盘中心O A 动系:AB杆 速度分析
aa
vr a n e o ve t a e v B Ra a
2009-11-18 2
理论力学
•元功(elementary work):
虚位移原理
δW = F • vd t = F • d r
等效力系作功定理: 若作用于刚体上的力系等效 即:{F1 , F2 , L , Fn } = { P1 , L , Pm } = {FR , M O } 则
n m
∑W (F ) = ∑W ( P ) = W (F ) + W ( M
• 点的复合运动
– 绝对运动、相对运动、牵连运动 – 绝对速度、相对速度、牵连速度 – 绝对加速度、相对加速度、牵连加速度、科氏加速度
• 基本定理与方程
– 速度合成定理、加速度合成定理 – 质点动力学方程(惯性参考系和非惯性参考系)
2009-11-18 6
理论力学
基本公式
&⎫ vx = x ⎪ &⎬ vy = y ⎪ &⎭ vz = z
反映速度方向的变化
mar = ∑ F + Fe + FC
7
理论力学
• •
解决问题的方法与基本步骤
受力分析-根据约束条件和已知量,,确定力的方向、分析哪些是未知量 运动分析-利用几何性质和约束条件,建立运动学(包括几何、速度和 加速度)关系,确定系统的自由度和未知量数目。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
m 2R4 x2
(x2
R
2
)
5 2
,
FN
mg
m 2R5x
(x2
R
2
)
5 2
1-13 解:动点:套筒 A;
动系:OA 杆; 定系:机座; 运动分析: 绝对运动:直线运动; 相对运动:直线运动; 牵连运动:定轴转动。 根据速度合成定理
va ve vr
va
ve
vr
有: va cos ve ,因为 AB 杆平动,所以 va v ,
2014-北航考研-永爱渣渣
《动力学 I》第一章 运动学部分习题参考解答
1-3 解:
运动方程: y l tan ,其中 kt 。
将运动方程对时间求导并将 300 代入得 v y l lk 4lk
cos2 cos2 3
a y 2lk 2 sin 8 3lk 2
ve
va
R
, va
vr
R
,1
ve O1 A
R 2R
0.5
根据加速度合成定理有
aa aet aen ar aC
(b)
将(b)式在垂直于 O1A 杆的轴上投影得
v02l 2 x3
(负号说明滑块 A 的加速度向上)
取套筒 A 为研究对象,受力如图所示,根据质点矢量形式的运动微分方程有:
ma F FN mg
将该式在 x, y 轴上投影可得直角坐标形式的运动微分方程: mx mg F cos my F sin FN
x
(
x2
2R4x R2)2
(d)
由上式可知滑块 A 的加速度方向向左,其大小为
aA
2R4 x (x2 R2)2
取套筒 A 为研究对象,受力如图所示, 根据质点矢量形式的运动微分方程有:
ma F FN mg
将该式在 x, y 轴上投影可得直角坐标形式的
运动微分方程:
v vr1 e1
ve2
v r2
根据速度合成定理有
x
va1 ve1 vr1 ,
va2 ve2 vr2
由于动点 M 的绝对速度与动系的选取无关,即 va2 va1 ,由上两式可得:
ve1 vr1 ve2 vr2
(a)
4
2014-北航考研-永爱渣渣
将(a)式在向在 x 轴投影,可得:
由此可得 v cos
ve
,OC
杆的角速度为
ve OA
, OA
l cos
,所以
v cos2 l
当 450 时,OC 杆上 C 点速度的大小为 v C
a
av cos 2 45 0 l
av 2l
1-15 解:动点:销子 M
动系 1:圆盘 动系 2:OA 杆 动系:机座; 运动分析: 绝对运动:曲线运动 相对运动:直线运动 牵连运动:定轴转动
解:设 B 点是绳子 AB 与圆盘的切点,由于绳子相对圆盘无滑动,所以 vB R ,由于绳子
始终处于拉直状态,因此绳子上 A、B 两点的速度在 A、B 两点连线上的投影相等,即:
vB vA cos
因为
(a)
cos x2 R2 x
将上式代入(a)式得到 A 点速度的大小为:
(b)
ve1 sin 300 ve2 sin 300 vr2 cos300
由此解得:
vr2
tan 300 (ve2
ve1 )
OM
tan 300 (2
1)
bsin 300 cos2 300
(3
9)
0.4m /
s
ve2 OM2 0.2 3
vM va2 ve22 vr22 0.529m / s
1-17 解:动点:圆盘上的 C 点;
动系:OA 杆; 定系:机座; 运动分析:绝对运动:圆周运动;
相对运动:直线运动(平行于 O1A 杆); 牵连运动:定轴转动。 根据速度合成定理有ve va来自vrva ve vr
(a)
将(a)式在垂直于 O1A 杆的轴上投影以及在 O1C 轴上投影得:
va cos 300 ve cos 300 , va sin 300 ve sin 300
vA R
x x2 R2
(c)
由于 vA x ,(c)式可写成: x x2 R2 Rx ,将该式两边平方可得:
x2 (x2 R2 ) 2R2x2
将上式两边对时间求导可得:
2xx(x2 R2 ) 2xx3 2 2R2xx 将上式消去 2x 后,可求得:
s v0 , 2ss 2xx
由此解得: x sv0 x
(a)
vo
vo
F
y
FN
mg
(a)式可写成: xx v0 s ,将该式对时间求导得:
xx x 2 sv0 v02
(b)
将(a)式代入(b)式可得: ax
x
v02 x 2 x
cos3
9
1-6
证明:质点做曲线运动,所以 a at an ,
设质点的速度为 v ,由图可知:
cos vy an ,所以: a an v
va
vy
将vy
c , an
v2
代入上式可得 a v3 c
v y v y a
an
x o
证毕
1-7
证明:因为
v2 an
mx F cos my F sin FN mg
其中:
yB
R O
F
FN
A
vA
x
mg
sin R , x
cos
x2 R2 , x
x
(x2
2R4x R2)2
,
y
0
3
2014-北航考研-永爱渣渣
将其代入直角坐标形式的运动微分方程可得
F
其中: cos x ,sin l
x v02l 2 , y 0
x2 l2
x2 l2
x3
将其代入直角坐标形式的运动微分方程可得: F m(g v02l 2 ) 1 ( l )2
x3
x
1-11
O
A
x
vB
B
OR
A
x vA
2
2014-北航考研-永爱渣渣
, an
a sin
av v
所以: v3 av
证毕
y o
at a
an
x
1
2014-北航考研-永爱渣渣
1-10
解:设初始时,绳索 AB 的长度为 L ,时刻 t 时的长度 为 s ,则有关系式:
s L v0t ,并且 s 2 l 2 x 2
将上面两式对时间求导得:
