(完整版)超越对数
(完整版)超越对数

超越对数生产函数L·christensen、D·jorgenson和Lau于1973年提出超越对数生产函数,该函数模型是一种易于估计和包容性很强的变弹性生产函数模型,它在结构上属于平方反映面模型,可有效研究生产函数中投入要素的交互影响、各种投入技术进步的差异。
通过超越对数生产函数模型,可以分析投入要素的产出弹性和要素的替代弹性。
其形式为:LnYt =β+βKLnKt+βLLnLt+βKK(LnKt)2+βLL(LnLt)2+βKLLnKt•LnLt(1)公式中:Yt——t年产出;Kt 、Lt——t年资本存量、劳动力投入量;β——需要估计的系数。
(1)要素投入的产出弹性资本投入的产出弹性为:ηK =dY/Y dLnYt==βK+βKLLnLt+2βKKLnKt(2)dK/K dLnKt劳动投入的产出弹性为:ηL =dY/Y dLnYt==βL+βKLLnKt+2βLLLnLt(3)dL/L dLnLt(2)要素的替代弹性替代弹性可以定义为:在技术水平和投入要素的价格不变的情况下,边际技术替代率的相对变动所引起的生产要素投入的比例的相对变动,即投入要素比例的变动的百分比与边际技术替代率的变动百分比的比值。
要素之间可替代程度的高低可用要素替代弹性(the elasticity of substitution)来描述,其具体含义是:一种生产要素价格变化以后,它与另一种生产要素相互替代率的变化。
要素替代弹性在0与无穷大之间变化,当0时,说明两种要素之间完全不能互相替代,如固定投入比例生产函数(里昂惕夫生产函数),当替代弹性无穷大时,说明两种要素之间可以完全替代。
资本、劳动2种投入的替代弹性计算如下:资本和劳动的替代弹性为:σKLKd()L=K()LMPPL∂Y=MPPK∂Ld(K MPPLMPPL))d()g(L MPPKMPPK=(4)MPPLMPPLK()d()g()MPPKMPPKL∂YηLK=•(5)∂KηKL由于结合式( 4)、式(5 )可得,σKL⎛MP L ⎫⎛ηL K ⎫K d ()d (g )⎪d () ⎪ MP K ηηK L L g ηL =ηL g ⎪=L g ⎪(6)=-1-1d (MP L )ηK ηK MP d (K )⎪ηK d (K )⎪K⎝L ⎪⎭ ⎝L ⎪⎭d (ηL ηηg K )d 因为KL=η(L L +Kg η)K d (K η(7)KL L)d (K L)d (ηL η)=-ηL 12d (ηK )+d (ηL )(8)KηKηKd (K K 1L )=-L 2dL +LdK (9)将式(8),式(9)代入式(7)得:d (ηL ηL L )η)-η2d (η1K )+d (ηL )-ηL d (ηK )1d (ηK=KηK=η2+KdL ηKdLd (K L)-K 1L 2dL +LdK -K 1dKL 2+L dL将式(10)代入(6)得资本与劳动的替代弹性:-1σ=⎛ ⎛⎫KL1+-β+ηK βη-η-1⎫⎝ ⎝KL ηLL ⎪(L K )⎪L⎭⎪⎭(10)(11)。
对数函数专题

二、对数定义:一般地,如果a (a>0,a ≠1)的b 次幂等于N,即a b =N 。
那么就称b 是以a 为底N 的对数,记作:log a N=b注:底数a 的取值?真数N 的取值?(1)log a 1=0 log a a=1恒等式 (2)b=log a a b, b a log a b = 常用对数:N 10log 简记 lg N 自然对数 N e log 简记 ln N.四则运算:N M MN a a log log log a +=N M NM a a log log log a -= M M a nlog log na =简记:积商变加减,指数往前提 1.计算:21g21g25(+= )A .1B .2C .3D .4 2.3log 132的值为( ) A .13 B .12 C .−2 D .23.下列等式成立的是( ).A .log 2(8-4)=log 2 8-log 2 4B .log 28log 24=log 284C .log 2 23=3log 2 2D .log 2(8+4)=log 2 8+log 2 4 换底公式: b NN a a b log log log =b a log 1b log a =b log mn b log a n a m = 以上公式如何证明?如何记忆?为师教你记:真数加底(新)变分子 原底加底(新)变分母 1.若2x =3,则x 等于( )A .log 32B .lg2−lg3C .lg2lg3D .lg3lg22.2lg2log 10⋅的值为( ) A .1- B .0 C .1 D .23.求值:log 98⋅log 23=______.4.函数y =log x (3−2x)的定义域是( )A .(−∞,32)B .(0,32)C .(0,1)∪(1,32)D .(0,1) 5.若3log 8a =,1.22b =, 3.10.3c =,则( ) A .c a b >> B .a b c >> C .b a c >> D .a c b >>。
高考数学复习专题课件六个超越函数的性质和应用PPT

(Ⅱ)证明: x2 随着 a 的减小而增大; x1
(Ⅲ)证明: x1 x2 随着 a 的减小而增大.
【解析】(Ⅰ)由 f x x aex 0 ,有 a x .设 g x x ,
ex
ex
由题意可知直线 y a 与函数 g x
x 的图像有两个不同的交点, ex
ex e
e
解得
x2
ln( 3 a
1)
,因此,当
x2
ln( 3 a
1)
时,
f
(x2 )
0
.
这样,当 0 a 1时, f x 有两个零点.
(202X年新课标I卷文21).
已知函数 f (x) (x 2)ex a(x 1)2 .
(I)讨论 f (x) 的单调性;
(II)若 f (x) 有两个零点,求 a 的取值范围.
函数
y
x ex
的图像的
交点,数形结合,则第
一、二问将迎刃而解.
【例题 1】(2014 年全国高考天津卷理科第 20 题)
已知函数 f x x aex a R , x R .
已知函数 y f x 有两个零点 x1 , x2 ,且 x1 x2 .
(Ⅰ)求 a 的取值范围; (Ⅱ)证明: x2 随着 a 的减小而增大;
综上所述, ex (ln x 1) sin x 0 成立.
2.函数y
x ex
的性质与应用
函数 y x 的性质和应用. ex
【函数的性质】
y 1 x ,当 x 1时, y 0 ;当 x 1时, y 0 . ex
所以函数
y
x ex
在 (,1) 上单调递增,在 (1, ) 上单调递减.
2025高考数学必刷题 第10讲、对数与对数函数(教师版)

第10讲对数与对数函数知识梳理1、对数式的运算(1)对数的定义:一般地,如果(0x a N a =>且1)a ≠,那么数x 叫做以a 为底N 的对数,记作log a x N =,读作以a 为底N 的对数,其中a 叫做对数的底数,N 叫做真数.(2)常见对数:①一般对数:以(0a a >且1)a ≠为底,记为log Na ,读作以a 为底N 的对数;②常用对数:以10为底,记为lg N ;③自然对数:以e 为底,记为ln N ;(3)对数的性质和运算法则:①1log 0a =;log 1aa =;其中0a >且1a ≠;②log Na a N =(其中0a >且1a ≠,0N >);③对数换底公式:log log log c a c bb a=;④log ()log log a a a MN M N =+;⑤log log log aa a MM N N=-;⑥log log (m na a nb b m m=,)n R ∈;⑦log a b a b =和log b a a b =;⑧1log log a b b a=;2、对数函数的定义及图像(1)对数函数的定义:函数log a y x =(0a >且1)a ≠叫做对数函数.对数函数的图象1a >01a <<图象性质定义域:(0)+∞,值域:R过定点(10),,即1x =时,0y =在(0)+∞,上增函数在(0)+∞,上是减函数当01x <<时,0y <,当1x ≥时,y ≥当01x <<时,0y >,当1x ≥时,0y≤【解题方法总结】1、对数函数常用技巧在同一坐标系内,当1a >时,随a 的增大,对数函数的图象愈靠近x 轴;当01a <<时,对数函数的图象随a 的增大而远离x 轴.(见下图)必考题型全归纳题型一:对数运算及对数方程、对数不等式【例1】(2024·四川成都·成都七中校考模拟预测)1ln3411e 812-+=______.【答案】1-【解析】114ln3144111e81331)33112⨯-+-+=-++=--=-.故答案为:1-【对点训练1】(2024·辽宁沈阳·沈阳二中校考模拟预测)已知lg 2a b +=-,10b a =,则=a ______.【答案】110/0.1【解析】由题设1log 10lg a b a ==,则1lg 2lg a a+=-且0a >,所以22lg 2lg 1(lg 1)0a a a ++=+=,即lg 1a =-,故110a =.故答案为:110【对点训练2】(2024·上海徐汇·位育中学校考模拟预测)方程()2lg(2)lg 3x x -=-的解集为________.【答案】{}|1x x =-【解析】因为()2lg(2)lg 3x x -=-,则22232030x x x x ⎧-=-⎪->⎨⎪->⎩,解得=1x -,所以方程()2lg(2)lg 3x x -=-的解集为{}|1x x =-.故答案为:{}|1x x =-【对点训练3】(2024·山东淄博·统考二模)设0,0p q >>,满足()469log log log 2p q p q ==+,则pq=__________.【答案】12/0.5【解析】令()469log log log 2p q p q k ==+=,则4,6,29k k k p q p q ==+=,所以22469k k kp q +=⋅+=,整理得2222133kk k ⎛⎫⎛⎫⋅+= ⎪ ⎪⎝⎭⎝⎭,解得2132k k =(负值舍去),所以421632k k k k p q ===.故答案为:12.【对点训练4】(2024·天津南开·统考二模)计算34223log 32log 9log log 64⋅-+的值为______.【答案】8【解析】原式2523223222233=log 2log 3log log 65log 2log 3log log 644⋅-+=⋅-+2222365log log 65log 5log 88344=-+=+=+=.故答案为:8.【对点训练5】(2024·全国·高三专题练习)若14log 2a =,145b =,用a ,b 表示35lo g 28=____________【答案】11ab a++-【解析】因为145b =,所以14lo g 5b=,1414143514141414log 28log 14log 21log 28log 35log 14log 5log 21ab a++===+-+-.故答案为:11ab a++-.【对点训练6】(2024·上海·高三校联考阶段练习)若123==a b m ,且112a b-=,则m =__________.【答案】2【解析】123a b m == ,且112a b-=,0m ∴>且1m ≠,123log ,log a m b m ∴==,11log 12,log 3m m a b ∴==,11log 12log 3log 42m m m a b∴-=-==,2m ∴=.故答案为:2.【对点训练7】(2024·全国·高三专题练习)()()()226622lg 3lg 2log 3log 2lg 3lg 2⋅+++=____________;【答案】1【解析】原式()()226662lg 3lg 2log 3l l lg 6g og 2⋅=⋅++()()226666log 3log 22log 3log 2=++⋅()266log 3log 2=+()26log 61==.故答案为:1.【对点训练8】(2024·全国·高三专题练习)解关于x 的不等式2)l g (o 24xx <-解集为_____.【答案】1(0,)2【解析】不等式222log 24log 24(log 2)(4)202x x x x xx -⇔--<<<<⇔,解240x ->,即222x <,有21x <,解得12x <,解224x x -<,即22220x x +->,化为2)(21)0(2x x +->,有21x >,解得0x >,因此102x <<,所以不等式2)l g (o 24xx <-解集为1(0,2.故答案为:1(0,2【对点训练9】(2024·上海杨浦·高三上海市杨浦高级中学校考开学考试)已知函数()f x 是定义在R 上的奇函数,当0x >时,()2log f x x =,则()2f x ≥-的解集是__________.【答案】][14,0,4⎡⎫-⋃+∞⎪⎢⎣⎭【解析】当0x <时,0x ->,所以()2()log f x x -=-,因为函数()f x 是定义在R 上的奇函数,所以()2()()log f x f x x =--=--,所以当0x <时,()2()log f x x =--,所以()22log ,0()0,0log ,0x x f x x x x ⎧--<⎪==⎨⎪>⎩,要解不等式()2f x ≥-,只需20log 2x x >⎧⎨≥-⎩或()20log 2x x <⎧⎨--≥-⎩或002x =⎧⎨≥-⎩,解得14x ≥或40x -≤<或0x =,综上,不等式的解集为][14,0,4∞⎡⎫-⋃+⎪⎢⎣⎭.故答案为:][14,0,4∞⎡⎫-⋃+⎪⎢⎣⎭.【对点训练10】(2024·上海浦东新·高三华师大二附中校考阶段练习)方程42log 17xx +=的解为_________.【答案】4x =【解析】设函数()42log x f x x =+,()0,x ∈+∞,由于函数42,log xy y x ==在()0,x ∈+∞上均为增函数,又()4442log 416117f =+=+=,故方程42log 17xx +=的解为4x =.故答案为:4x =.【解题方法总结】对数的有关运算问题要注意公式的顺用、逆用、变形用等.对数方程或对数不等式问题是要将其化为同底,利用对数单调性去掉对数符号,转化为不含对数的问题,但这里必须注意对数的真数为正.题型二:对数函数的图像【例2】(2024·全国·高三专题练习)已知函数()log a y x b =+(a ,b 为常数,其中0a >且1a ≠)的图象如图所示,则下列结论正确的是()A .0.5a =,2b =B .2a =,2b =C .0.5a =,0.5b =D .2a =,0.5b =【答案】D【解析】由图象可得函数在定义域上单调递增,所以1a >,排除A ,C ;又因为函数过点(0.5,0),所以0.51b +=,解得0.5b =.故选:D【对点训练11】(2024·全国·高三专题练习)函数()log (1)2a f x x =-+的图象恒过定点()A .(2,2)B .(2,1)C .(3,2)D .(2,0)【答案】A【解析】当2x =时(2)log 122a f =+=,即函数图象恒过(2,2).故选:A【对点训练12】(2024·北京·统考模拟预测)已知函数()()22log 1f x x x =--,则不等式()0f x <的解集为()A .()(),12,-∞+∞B .()()0,12,⋃+∞C .()1,2D .()1,+∞【答案】B【解析】由题意,不等式()0f x <,即()22log 10x x --<,等价于()22log 1x x <-在()0,∞+上的解,令()2log g x x =,()()21h x x =-,则不等式为()()g x h x <,在同一坐标系下作出两个函数的图象,如图所示,可得不等式()0f x <的解集为()()0,12,⋃+∞,故选:B【对点训练13】(2024·北京·高三统考学业考试)将函数2log y x =的图象向上平移1个单位长度,得到函数()y f x =的图象,则()f x =()A .()2log 1x +B .21log x +C .()2log 1x -D .21log x-+【答案】B【解析】将函数2log y x =的图象向上平移1个单位长度,得到函数21log y x =+.故选:B.【对点训练14】(2024·北京海淀·清华附中校考模拟预测)不等式32log (1)(2)0x x x --->的解集为__________.【答案】{}13x x <<【解析】由3312log (1)(2)0log (1)(2)2x x x x x x --->⇒>--,在同一直角坐标系内画出函数()()31log ,(1)(2)2f x xg x x x ==--的图象如下图所示:因为()()331f g ==,所以由函数的图象可知:当(1,3)x ∈时,有()()f x g x >,故答案为:{}13x x <<【对点训练15】(多选题)(2024·全国·高三专题练习)当102x <≤时,4log xa x ≤,则a 的值可以为()A2B .2C .3D 【答案】ABC【解析】分别记函数()4x f x =,()log a g x x =由图1知,当1a >时,不满足题意;当01a <<时,如图2,要使102x <≤时,不等式4log xa x ≤恒成立,只需满足11((22f g ≤,即1214log 2a≤,即12log 2a ≤,解得12a ≤<.故选:ABC【解题方法总结】研究和讨论题中所涉及的函数图像是解决有关函数问题最重要的思路和方法.图像问题是数和形结合的护体解释.它为研究函数问题提供了思维方向.题型三:对数函数的性质(单调性、最值(值域))【例3】(2024·全国·高三专题练习)已知函数3()log (1)f x ax =-,若()f x 在(,1]-∞上为减函数,则a 的取值范围为()A .(0,)+∞B .(0,1)C .(1,2)D .(,1)-∞【答案】B【解析】设函数1y ax =-,因为()f x 在(,1]-∞上为减函数,所以1y ax =-在(,1]-∞上为减函数,则0a -<解得0a >,又因为10y ax =->在(,1]-∞恒成立,所以min 10y a =->解得1a <,所以a 的取值范围为01a <<,故选:B.【对点训练16】(2024·新疆阿勒泰·统考三模)正数,a b 满足2224log log a bb a -=-,则a与2b 大小关系为______.【答案】2a b </2b a>【解析】因为2224log log a bb a -=-,所以22222222log 4log 2log log 212log 21a b b ba b b b +=+=++-=+-,设2()2log x f x x =+,则()(2)1f a f b =-,所以()(2)f a f b <,又因为2x y =与2log y x =在(0,)+∞上单调递增,所以2()2log x f x x =+在(0,)+∞上单调递增,所以2a b <.故答案为:2a b <.【对点训练17】(2024·全国·高三专题练习)已知函数()()log 0,1a f x x a a =>≠在[]1,4上的最大值是2,则a 等于_________【答案】2【解析】当1a >时,函数()log a f x x =在[]1,4上单调递增,则()4log 42a f ==,解得2a =,当01a <<时,函数()log a f x x =在[]1,4上单调递减,则()1log 12a f ==,无解,综上,a 等于2.故答案为:2.【对点训练18】(2024·全国·高三专题练习)若函数()log a f x x =(0a >且1a ≠)在1,42⎡⎤⎢⎥⎣⎦上的最大值为2,最小值为m ,函数()(32g x m =+[0,)+∞上是增函数,则a m -的值是____________.【答案】3【解析】当1a >时,函数()log a f x x =是正实数集上的增函数,而函数()log a f x x =在1,42⎡⎤⎢⎥⎣⎦上的最大值为2,因此有(4)log 42a f ==,解得2a =,所以21log 12m ==-,此时()g x 在[)0,∞+上是增函数,符合题意,因此()213a m -=--=;当01a <<时,函数()log a f x x =是正实数集上的减函数,而函数()log a f x x =在1,42⎡⎤⎢⎥⎣⎦上的最大值为2,因此有11log 222a f ⎛⎫== ⎪⎝⎭,2a =,所以44m ==-,此时()g x =-在[)0,∞+上是减函数,不符合题意.综上所述,2a =,1m =-,3a m -=.故答案为:3.【对点训练19】(2024·全国·高三专题练习)若函数2()log (1)a f x x ax =-+有最小值,则a的取值范围是______.【答案】()1,2【解析】当01a <<时,外层函数log a y u =为减函数,对于内层函数21u x ax =-+,240a ∆=-<,则0u >对任意的实数x 恒成立,由于二次函数21u x ax =-+有最小值,此时函数()()2log 1a f x x ax =-+没有最小值;当1a >时,外层函数log a y u =为增函数,对于内层函数21u x ax =-+,函数21u x ax =-+有最小值,若使得函数()()2log 1a f x x ax =-+有最小值,则2401a a ⎧∆=-<⎨>⎩,解得12a <<.综上所述,实数a 的取值范围是()1,2.故答案为:()1,2.【对点训练20】(2024·河南·校联考模拟预测)写出一个同时具有下列性质①②③的函数:()f x =_____.①()()()1212f x x f x f x =+;②当,()0x ∈+∞时,()f x 单调递减;③()f x 为偶函数.【答案】12log x (不唯一)【解析】性质①显然是和对数有关,性质②只需令对数的底01a <<即可,性质③只需将自变量x 加绝对值即变成偶函数.故答案为:12log x (不唯一)【对点训练21】(2024·重庆渝中·高三重庆巴蜀中学校考阶段练习)函数()214log 2y x x =--的单调递区间为()A .1,2⎛⎫-∞ ⎪⎝⎭B .(),1-∞-C .1,2⎛⎫+∞ ⎪⎝⎭D .()2,+∞【答案】B【解析】函数()214log 2y x x =--的定义域为(,1)(2,),-∞-⋃+∞令22t x x =--,又14log y t =在定义域内为减函数,故只需求函数22t x x =--在定义域()(),12,-∞-⋃+∞上的单调递减区间,又因为函数22t x x =--在(),-1∞-上单调递减,()214log 2y x x ∴=--的单调递区间为(),1-∞-.故选:B【对点训练22】(2024·陕西宝鸡·统考二模)已知函数()()lg lg 2f x x x =+-,则()A .()f x 在()0,1单调递减,在()1,2单调递增B .()f x 在()0,2单调递减C .()f x 的图像关于直线1x =对称D .()f x 有最小值,但无最大值【答案】C【解析】由题意可得函数()()lg lg 2f x x x =+-的定义域为(0,2),则()()2lg lg 2lg(2)f x x x x x =+-=-+,因为22y xx =-+在(0,1)上单调递增,在(1,2)上单调递减,且lg y x =在(0,)+∞上单调递增,故()f x 在(0,1)上单调递增,在(1,2)上单调递减,A ,B 错误;由于()2lg(2)lg ()f x x x f x -=-+=,故()f x 的图像关于直线1x =对称,C 正确;因为22y xx =-+在1x =时取得最大值,且lg y x =在(0,)+∞上单调递增,故()f x 有最大值,但无最小值,D 错误,故选:C【对点训练23】(2024·全国·高三专题练习)若函数2,1,()2log ,1x a a x f x a x x ⎧+≤=⎨+>⎩在R 上单调,则a 的取值范围是()A .()0,1B .[2,)+∞C .10,(2,)2⎛⎫+∞ ⎪⎝⎭D .()0,1[2,)⋃+∞【答案】D【解析】若()f x 在R 上单调递增,则122log 1a a a a >⎧⎨+≤+⎩,解得[2,)a ∈+∞,若()f x 在R 上单调递减,则0122log 1a a a a <<⎧⎨+≥+⎩,解得(0,1)a ∈.综上得(0,1)[2,)a ∈+∞ .故选:D【解题方法总结】研究和讨论题中所涉及的函数性质是解决有关函数问题最重要的思路和方法.性质问题是数和形结合的护体解释.它为研究函数问题提供了思维方向.题型四:对数函数中的恒成立问题【例4】(2024·全国·高三专题练习)已知函数()29x f x x +=,()2log g x x a =+,若存在[]13,4x ∈,任意[]24,8x ∈,使得()()12f x g x ≥,则实数a 的取值范围是___________.【答案】13,4∞⎛⎤- ⎥⎝⎦【解析】若()f x 在[3,4]上的最大值max ()f x ,()g x 在[4,8]上的最大值max ()g x ,由题设,只需max max ()()f x g x ≥即可.在[3,4]上,9()6f x x x =+≥=当且仅当3x =时等号成立,由对勾函数的性质:()f x 在[3,4]上递增,故max 25()4f x =.在[4,8]上,()g x 单调递增,则max ()3g x a =+,所以2534a ≥+,可得134a ≤.故答案为:13,4∞⎛⎤- ⎥⎝⎦.【对点训练24】(2024·全国·高三专题练习)若1,22x ⎡⎤∀∈⎢⎥⎣⎦,不等式2122log 0x x x ax -+<恒成立,则实数a 的取值范围为___________.【答案】(),5-∞-【解析】因为1,22x ⎡⎤∀∈⎢⎥⎣⎦,不等式2122log 0x x x ax -+<恒成立,所以12log 2a x x <-对1,22x ⎡⎤∀∈⎢⎥⎣⎦恒成立.记()12log 2f x x x =-,1,22x ⎡⎤∈⎢⎥⎣⎦,只需()min a f x <.因为12log y x =在1,22x ⎡⎤∈⎢⎥⎣⎦上单调递减,2y x =-在1,22x ⎡⎤∈⎢⎥⎣⎦上单调递减,所以()12log 2f x x x =-在1,22x ⎡⎤∈⎢⎥⎣⎦上单调递减,所以()()min 25f x f ==-,所以5a <-.故答案为:(),5-∞-【对点训练25】(2024·全国·高三专题练习)已知函数2()23=-+f x x x ,2()log g x x m =+,对任意的1x ,2[1x ∈,4]有12()()f x g x >恒成立,则实数m 的取值范围是___________.【答案】(,0)-∞【解析】函数22()23(1)2=-+=-+f x x x x 在[1,4]上单调递增,2()log g x x m =+在[1,4]上单调递增,∴()()min 12f x f ==,()()max 42g x g m ==+,对任意的1x ,2[1x ∈,4]有12()()f x g x >恒成立,∴()()min max f x g x >,即22m >+,解得0m <,∴实数m 的取值范围是(),0∞-.故答案为:(,0)-∞.【对点训练26】(2024·全国·高三专题练习)已知函数()()2223,log f x x x g x x m =-+=+,若对[][]122,4,16,32x x ∀∈∃∈,使得()()12f x g x ,则实数m 的取值范围为___________.【答案】(],1-∞-【解析】因为对[][]122,4,16,32x x ∀∈∃∈,使得()()12f x g x ≥,所以()()12min min f x g x ≥,因为()223x x x f =-+的对称轴为1x =,所以()f x 在[]2,4上单调递增,所以()()min 23f x f ==,又因为()2log g x x m =+在[]16,32上单调递增,所以()()min 164g x g m ==+,所以34m ≥+,所以1m ≤-,即(],1m ∈-∞-,故答案为:(],1-∞-.【对点训练27】(2024·全国·高三专题练习)已知函数()()()2log 2log 30,1a a f x x x a a =++>≠.(1)若()32f =,求a 的值;(2)若对任意的[]8,12x ∈,()6f x >恒成立,求a 的取值范围.【解析】(1)因为()32f =,所以()2log 32log 332a a ++=,所以()2log 310a +=,所以log 31a =-,解得13a =.(2)由()6f x >,得()2log 2log 30a a x x +->,即()()log 3log 10a a x x +->,即log 3a x <-或log 1>a x .当01a <<时,log 12log log 8a a a x ≤≤,则log 83a <-或log 121a >,因为log 12log 10a a <=,则log 121a >不成立,由log 83a <-可得318a ⎛⎫< ⎪⎝⎭,得112a <<;当1a >时,log 8log log 12a a a x ≤≤,则log 123a <-或log 81a >,因为log 12log 10a a >=,则log 123a <-不成立,所以log 81a >,解得18a <<.综上,a 的取值范围是()1,11,82⎛⎫⋃ ⎪⎝⎭.【对点训练28】(2024·全国·高三专题练习)已知2()32log f x x =-,2()log g x x =.(1)当[]1,4x ∈时,求函数[]()1()y f x g x =+⋅的值域;(2)对任意12,2n n x +⎡⎤∈⎣⎦,其中常数n N ∈,不等式()2()f x f kg x ⋅>恒成立,求实数k 的取值范围.【解析】(1)因为2()32log f x x =-,2()log g x x =,[]()1()y f x g x =+⋅令()()()222242log log 2log 12y h x x x x ==-⋅=--+,∵[]1,4x ∈,∴[]2log 0,2x ∈,所以当2log 1x =,即2x =时取最大值()max 2h x =,当2log 0x =或2,即1x =或4x =时取最小值()min 0h x =,∴函数()h x 的值域为[]0,2.(2)由()()2f x fk g x ⋅>⋅得()()22234log 3log logx x k x -->⋅,令2log t x =,∵12,2n n x +⎡⎤∈⎣⎦,∴[]2log ,1t x n n =∈+,∴()()343t t k t -->⋅对一切的[],1t n n ∈+恒成立,①当0n =时,若0=t 时,R k ∈;当(]0,1t ∈时,()()343t t k t--<恒成立,即9415k t t<+-,函数9415t t+-在(]0,1t ∈单调递减,于是1t =时取最小值-2,此时2x =,于是(),2k ∈-∞-;②当1n =时,此时[]1,2t ∈时,()()343t t k t--<恒成立,即9415k t t<+-,∵9412t t +≥,当且仅当94t t =,即32t =时取等号,即9415t t+-的最小值为-3,(),3k ∈-∞-;③当2n ≥时,此时[],1t n n ∈+时,()()343 t t k t--<恒成立,即9415k t t<+-,函数9415t t +-在[],1t n n ∈+单调递增,于是t n =时取最小值9415n n-+,此时2n x =,于是9,415k n n ⎛⎫∈-∞-+ ⎝⎭.综上可得:当0n =时(),2k ∈-∞-,当1n =时(),3k ∈-∞-,当2n ≥时,9,415k n n ⎛⎫∈-∞-+⎪⎝⎭【解题方法总结】(1)利用数形结合思想,结合对数函数的图像求解;(2)分离自变量与参变量,利用等价转化思想,转化为函数的最值问题.(3)涉及不等式恒成立问题,将给定不等式等价转化,借助同构思想构造函数,利用导数探求函数单调性、最值是解决问题的关键.题型五:对数函数的综合问题【例5】(多选题)(2024·湖北·黄冈中学校联考模拟预测)已知1a >,1b >,21a aa =-,2log 1bb b =-,则以下结论正确的是()A .22log aa b b+=+B .21112log ab+=C .2a b -<-D .4a b +>【答案】ABD【解析】对于A ,由题意知,a ,b 是函数1()111x h x x x ==+--分别与函数()2x f x =,2()log g x x =图象交点的横坐标,由1y x=的图象关于y x =对称,则其向上,向右都平移一个单位后的解析式为1()11h x x =+-,所以()h x 的图象也关于y x =对称,又()f x ,()g x 两个函数的图象关于直线y x =对称,故两交点(),2aa ,()2,logb b 关于直线y x =对称,所以2log a b =,2a b =,故A 正确;对于B ,结合选项A 得21aa b a ==-,则ab a b =+,即111a b +=,即21112log a b +=成立,故B 正确;对于C ,结合选项A 得2log (24)a b b b b -=-<<,令2()log b b b ϕ=-,则1()10ln 2b b ϕ'=-<,所以2()log b b b ϕ=-在(2,4)上单调递减,则2()log 442b ϕ>-=-,故C 错误;对于D ,结合选项B 得11()24b aa b a b a b a b⎛⎫+=++=++> ⎪⎝⎭(a b¹,即不等式取不到等号),故D 正确.故选:ABD.【对点训练29】(2024·海南海口·统考模拟预测)已知正实数m ,n 满足:ln e ln m n n n m =-,则nm的最小值为______.【答案】2e 4【解析】由ln e ln mn n n m =-可得:e ln ln mm n n=+,所以ln e ln ln m n n m --=,ln ln e ln ln e ln m n m m n m m m -+-=+=+,设()e x f x x =+,()e 10xf x '=+>,所以()f x 在R 上单调递增,所以()()ln ln f m n f m -=,则ln ln m n m -=,所以e ln ln mn m=,所以e m n m =,所以2e m n m m =,令()()()2243e 2e e e 2,xx x x x x x g x g x x x x-⋅-⋅=='=,令()0g x '>,解得:2x >;令()0g x '<,解得:02x <<;所以()g x 在()0,2上单调递减,在()2,+∞上单调递增,所以()()2mine 24g x g ==.故n m 的最小值为2e 4.故答案为:2e 4.【对点训练30】(多选题)(2024·广东惠州·统考一模)若62,63a b ==,则()A .1ba>B .14ab <C .2212+<a b D .15b a ->【答案】ABD【解析】因为63,62b a ==,所以66log 3,log 2b a ==,则1a b +=,选项A ,6226log 3log 3log 21log 2b a ==>=,故A 正确;选项B ,因为666log 3log 2log 61a b +=+==,且0,0,a b a b >>≠,所以21()24a b ab +<=,故B 正确;选项C ,因为22211()2121242a b a b ab ab +=+-=->-⨯=,故C 错误;选项D ,因为()666324355log log log 61232b a -==>=,故D 正确,故选:ABD .【对点训练31】(2024·河南·高三信阳高中校联考阶段练习)已知1x ,2x 分别是方程e 3x x +=和ln 3x x +=的根,若12x x a b +=+,实数a ,0b >,则271b ab+的最小值为()A .1B .73C .679D .2【答案】D【解析】e 3,e 3x x x x +==-;ln 3,ln 3x x x x +==-.函数e x y =与函数ln y x =的图象关于直线y x =对称,由3y x y x=-⎧⎨=⎩解得32x y ==,设33,22A ⎛⎫⎪⎝⎭,则123232x x +=⨯=,即3a b +=,()()22222273211717171333b b b b b b ab b b b bb b -+++++==-=----221173b b b +⎛⎫=-+ ⎪-⎝⎭,令211b t +=,则121t b -=,则222712117731132121b b t ab b b t t ⎛⎫ ⎪++⎛⎫ ⎪=-+=-+ ⎪ ⎪-⎝⎭--⎛⎫-⨯ ⎪ ⎪⎝⎭⎝⎭4417726465t t ⎛⎫⎛⎫⎪ ⎪ =-+≥-= ⎪ ⎪+- ⎝⎭⎝,当且仅当6418,8211,,333t t b b a b t ===+==-=时等号成立.故选:D【对点训练32】(2024·全国·高三专题练习)若1x 满足25x x =-,2x 满足2log 5x x +=,则12x x +等于()A .2B .3C .4D .5【答案】D【解析】由题意1152xx -=,故有2225log x x -=故1x 和2x 是直线5y x =-和曲线2x y =、曲线2log y x =交点的横坐标.根据函数2x y =和函数2log y x =互为反函数,它们的图象关于直线y x =对称,故曲线2x y =和曲线2log y x =的图象交点关于直线y x =对称.即点(x 1,5﹣x 1)和点(x 2,5﹣x 2)构成的线段的中点在直线y =x 上,即12125522x x x x +-+-=,求得x 1+x 2=5,故选:D.【对点训练33】(2024·全国·高三专题练习)已知1x 是方程32x x ⋅=的根,2x 是方程3log 2x x ⋅=的根,则12x x ⋅的值为()A .2B .3C .6D .10【答案】A【解析】方程32x x ⋅=可变形为方程23x x =,方程3log 2x x ⋅=可变形为方程3log 2x x=,1x 是方程32x x ⋅=的根,2x 是方程3log 2x x ⋅=的根,2025高考数学必刷题1x ∴是函数3x y =与函数2y x =的交点横坐标,2x 是函数3log y x ==与函数2y x =的交点横坐标, 函数3x y =与函数3log y x =互为反函数,∴函数3log y x =与函数2y x =的交点横坐标2x 等于函数3x y =与函数2y x =的交点纵坐标,即12(,)x x 在数2y x =图象上,又2y x = 图象上点的横纵坐标之积为2,122x x ∴=,故选:A。
高中常见六大超越函数图像性质简单应用

表给出 ′ 在各区间上的正负,并得出f(x)的单调性与极值;
(4)确定f(x)的图象所经过的一些特殊点,以及图象的
变化趋势;
(5)画出f(x)的大致图象.
ex
y
x
x
y x
e
y x.ln x
y
ln x
1
(1,)
e
0
e
e
e
e
解:由题意得:eax - x 0可得:
lnx
ax lnx,
a
x
ln x
构造函数g(x )
,h(x ) a ,结合两个函数图像
x
1
可得:a - ,
0
e
四.课堂小结
谈谈本节课你的收获有哪些?
五.作业布置
基础教育精品课
探究六大超越函数
年 级:高中三年级
主讲人:张争
学
学
科:数学
校:罗山县莽张高中
教学目标:
1.经历探究六大超越函数极值、最值,图像及性质过程。
2.会求超越函数极值、最值,并画出图像。
3.利用导数解决与函数有关的问题。
一、复习导入
上节课我们学习了利用导数来研究简单函数的极值和最值,让我们来回
x
f(x)
x2
x2
令f(x) 0可得:x e
当x (0,e),f(x ) 0,f (x )单调递增
当x (e ,),f (x ) 0,f (x )单调递减
1
f (x )有极大值,f(e)
e
问题2:两个函数的最值找不出来怎么办?
4.3对数(AB分层训练)解析版 2023-2024学年高一数学重难点突破
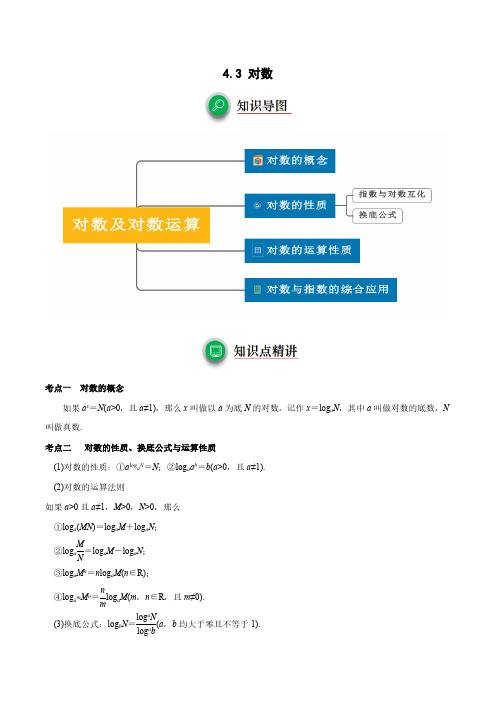
4.3 对数考点一 对数的概念如果a x =N (a >0,且a ≠1),那么x 叫做以a 为底N 的对数,记作x =log a N ,其中a 叫做对数的底数,N 叫做真数.考点二 对数的性质、换底公式与运算性质(1)对数的性质:①a log a N =N ;②log a a b =b (a >0,且a ≠1).(2)对数的运算法则如果a >0且a ≠1,M >0,N >0,那么①log a (MN )=log a M +log a N ;②log a M N=log a M -log a N ;③log a M n =n log a M (n ∈R);④log a m M n =n mlog a M (m ,n ∈R ,且m ≠0).(3)换底公式:log b N =log a N log a b(a ,b 均大于零且不等于1).(一) 求对数型函数的定义域问题例1.(1)、下列对数式中,与指数式79x =等价的是( )A .7log 9x =B .9log 7x =-C .7log 9x =D .log 97x =【答案】C【分析】根据指数式与对数式的关系直接判断即可.【详解】对于A ,7log 9x =等价于97x =,A 错误;对于B ,9log 7x =-等价于79x -=,B 错误;对于C ,7log 9x =等价于79x =,C 正确;对于D ,log 97x =等价于()790,1x x x =>≠,D 错误.故选:C.(2).(2021·全国·高一专题练习)(多选)下列选项中错误的是( )A .零和负数没有对数B .任何一个指数式都可以化成对数式C .以10为底的对数叫做自然对数D .以e 为底的对数叫做常用对数【答案】BCD【分析】对于A :由对数的定义即可判断;对于B :用对数的定义即可判断;对于C :由常用对数的定义即可判断;对于D :由自然对数的定义即可判断.【详解】对于A :由对数的定义可知:零和负数没有对数.故A 正确;对于B :只有符合0a >,且10a N ≠>,,才有log x a a N x N =⇔=,故B 错误;对于C :以10为底的对数叫做常用对数,故C 错误;对于D :以e 为底的对数叫做自然对数,故D 错误.故选:BCD.【变式训练1-1】、(2021·江西省吉水中学高一阶段练习)使式子()211log 2x x --有意义的x 的取值范围是( )A .()2,+∞B .1,22⎛⎫ ⎪C .(),2-∞D .()1,11,22⎛⎫ ⎪(二) 对数与指数互化例2.(1)、(2021·全国·高一单元测试)(多选题)下列指数式与对数式互化正确的是( )A .45625=与4log 6255=B .2100.01-=与lg 0.012=-C .41162-⎛⎫= ⎪⎝⎭与41log 162-=D .1293=与91log 32=(2)、(多选题)(2021·全国高一专题练习)下列指数式与对数式互化正确的一组是( )A .0101=与lg 1=0B .1327-=13与log 2713=-13C .log 39=2与129=3D .log 55=1与51=5【答案】ABD【分析】根据指数式与对数式互化的结论逐个分析可得答案.【详解】对于A ,0101=lg10⇔=,A 正确;对于B ,132711127log 333-=⇔=-,B 正确;对于C ,23log 9239=⇔=,C 不正确;对于D ,15log 5155=⇔=,D 正确.故选:ABD.(三) 解对数方程例3.(1)、(2021·江苏·淮安市淮安区教师发展中心学科研训处高一期中)若2log 3x =-,则x =_______.【答案】18##0.125【变式训练3-2】、(2022·安徽·合肥一六八中学模拟预测(文))方程()3ln log 0x =的解是( )A .1B .2C .eD .3【答案】D【分析】利用指数与对数的转化即可得到结果.【详解】∵()3ln log 0x =,∴03log e 1x ==,∴3x =.故选:D.例4.(2023·全国·高一假期作业)求下列各式中x 的值.(1)()()345log log 1log x =(2)()()345l 0log lo og g x =【答案】(1)645x =;(2)625.【分析】(1)利用对数式与指数式的关系化简即可;(2)利用对数式与指数式的关系化简即可.【详解】(1)由()()345log log 1log x =可得,()453log log x =,则354l 6g 4o x ==,所以645x =.(2)由()()345l 0log lo og g x =可得,()45log log 1x =,(四) 用对数型公式及换底公式化简求值例5.(1)、(2020·全国高一课时练习)log513+log53等于()A.0B.1C.-1D.log510 3【答案】A【解析】因为555511log log 3log 3log 1033⎛⎫+=⨯== ⎪⎝⎭.故选:A.【变式训练5-2】、(2021·上海市行知中学高三开学考试)已知实数,x y 满足:32272x y ⎛⎫== ⎪⎝⎭,则11x y +=________.(五) 与对数有关的条件求值问题例7、(2020·浙江高一课时练习)已知二次函数2()(lg )24lg f x a x x a =++的最小值为3,求()2log 5a +log 2log 50a a ⋅的值.【答案】1.【解析】∵2()(lg )24lg f x a x x a =++的最小值为3,∴lg 0a >,min 21111()lg 24lg 4lg 3lg (lg )lg lg f x f a a a a a a a ⎛⎫⎛⎫=-=⨯+⨯-+=-= ⎪ ⎪⎝⎭⎝⎭,即24(lg )3lg 10a a --=,∴(4lg 1)(lg 1)0a a +-=,则lg 1a =,∴10a =.∴()222log 5log 2log 50(lg5)lg 2lg50(lg5)lg 2(lg51)lg5(lg5lg 2)lg 21a a a +⋅=+⋅=++=++=.例8、(2021·安顺市第三高级中学(文))(1)已知2lg(2)lg lg x y x y -=+,求x y 的值.(2)设1x 满足2ln 3x x +=,2x 满足ln(1)21x x --=求12x x +的值.【答案】(1)4x y =;(2)1.【分析】(1)利用对数运算化简已知条件,因式分解然后求得x y的值.(2)利用换元法化简已知条件,结合函数()2ln f x x x =+的单调性求得121x x =+.【详解】(1)由2lg(2)lg lg x y x y -=+得2lg(2)lg()x y xy -=,∴2(2)x y xy-=∴22540x xy y -+=,∴()(4)0x y x y --=,即1x y=或4.又0,0,20x y x y >>->, ∴1x y =舍去,故4x y=.(2)由题意得()11222ln 3,ln 121x x x x +=--=,()()22ln 1213x x -+-=,令21x t -=,则2ln 3t t +=.∵()2ln f x x x =+在(0,)+∞单调递增,∴1t x =,∴121x x =+.【点睛】本小题主要考查对数运算,考查对数型函数的单调性,属于中档题.(六) 对数的综合应用例11.(1)、(2023秋·河北保定·高三校联考开学考试)在百端待举、日理万机中,毛泽东主席仍不忘我国的教育事业.1951年9月底,毛主席在接见安徽参加国庆的代表团时,送给代表团成员——渡江小英雄马毛姐一本精美的笔记本,并在扉页上题词:好好学习,天天向上.这8个字的题词迅速在全国传播开来,影响并指导着一代代青少年青春向上,不负韶华.他告诉我们:每天进步一点点,持之以恒,收获不止一点点.把学生现在的学习情况看作1.每天的“进步率”为3%,那么经过一个学期(看作120天)后的学习情况为()12013%34.711+≈,如果每天的“迟步率”为3%,同样经过一个学期后的学习情况为()12013%0.026-≈,经过一个学期,进步者的学习情况是迟步者学习情况的1335倍还多,按上述情况,若“进步"的值是“迟步”的值的10倍,要经过的天数大约为(保留整数)(参考数据:lg103 2.013≈,lg 97 1.987≈)( )A .28B .38C .60D .100【答案】B(2)、(2022·广东汕头·高三阶段练习)核酸检测分析是用荧光定量PCR 法,通过化学物质的荧光信号,对在PCR 扩增进程中成指数级增加的靶标DNA 实时监测,在PCR 扩增的指数时期,荧光信号强度达到阀值时,DNA 的数量X 与扩增次数n 满足0lg lg(1)lg n X n p X =++,其中0X 为DNA 的初始数量,p 为扩增效率.已知某被测标本DNA 扩增12次后,数量变为原来的1000倍,则扩增效率p 约为( )(参考数据:0.250.2510 1.778,100.562-≈≈)A .22.2%B .43.8%C .56.2%D .77.8%()2429a a ∴==;故答案为:9.【变式训练11-2】.(2022·江西·高二开学考试)《中华人民共和国国家标准污水综合排放标准》中一级标准规定的氨氮含量允许排放的最高浓度为15mg/L .某企业生产废水中的氨氮含量为450mg/L ,现通过循环过滤设备对生产废水的氨氮进行过滤,每循环一次可使氨氮含量减少13,要使废水中的氨氮含量达到国家排放标准,最少要进行循环的次数为( )(参考数据:lg 20.3010≈,lg30.4771≈)A .8B .9C .10D .11。
专题07 经典超越不等式
专题07 经典超越不等式一、结论(1)对数形式:1ln (0)x x x ≥+>,当且仅当1x =时,等号成立. (2)指数形式:1()xe x x R ≥+∈,当且仅当0x =时,等号成立.进一步可得到一组不等式链:11ln xe x x x >+>>+(0x >且1x ≠) 上述两个经典不等式的原型是来自于泰勒级数:2112!!(1)!n xxn x x e e x x n n θ+=++++++;2311ln(1)(1)()231n n n x x x x x o x n +++=−+−+−++; 截取片段:1()x e x x R ≥+∈ln(1)(1)x x x +≤>−,当且仅当0x =时,等号成立; 进而:ln 1(0)x x x ≤−>当且仅当1x =时,等号成立二、典型例题1.(2022·江苏苏州·高三期末)已知11a b >+> 则下列不等式一定成立的是( ) A .b a b ->B .11a b a b+>+ C .1e 1ln bb a a+<− D .ln ln a b b a +<+【答案】C 【解析】取10,8a b ==,则b a b -<,故A 选项错误;取3a =,13b =,11a b a b+=+,则B 选项错误;取3a =,1b =,则ln 3a b +=,2ln 1ln31ln 3b a e +=+<+=,即ln ln a b b a +>+, 故D 选项错误;关于C 选项,先证明一个不等式:e 1x x ≥+,令e1xy x =−−,e 1x y '=−,于是0x >时0y '>,y 递增;0x <时0y '<,y 递减; 所以0x =时,y 有极小值,也是最小值0e 010−−=, 于是e 10x y x =−−≥,当且仅当0x =取得等号,由e 1x x ≥+,当1x >−时,同时取对数可得,ln(1)x x ≥+, 再用1x −替换x ,得到1ln x x −≥,当且仅当1x =取得等号,由于11a b >+>,得到e 1bb >+,ln 1a a <−,111ln e b a b a -+\>>,即1e 1ln bb a a+<−, C 选项正确. 故选:C.【反思】对于指数形式:1()xe x x R ≥+∈,当且仅当0x =时,等号成立,该不等式是可以变形使用的:111111()1,111x xx x x xx x x e x e x x R e x x e e x <−−>⎧⎯⎯⎯→≤⎪⎪−≥+∈⎯⎯⎯→≥−+≥−⎨⎪⎯⎯⎯→≥⎪−⎩当替换当即注意使用时x 的取值范围;同样的还可以如下处理:1()x e x x R ≥+∈两边同时取对数:ln(1)(1)x x x ≥+>−,同样可以变形使用:"1"""ln(1)(1)1ln (0)1ln (0)x x x x x x x x x x x −≥+>−⎯⎯⎯⎯⎯→−≥>⎯⎯⎯⎯⎯⎯⎯→−≤−>替换左右两边同乘以“-1?;11111ln (0)1ln (0)1ln ln x xx x x x x x x x x x x−−≤−>⇔−≤>⎯⎯⎯⎯⎯⎯→−≤⇔≤用“”替换“”注意使用时x 的取值范围.2.(2021·安徽·高三阶段练习(文))已知函数()()1xf x e ax a R =−−∈.(1)若对0x ∀>,都有()0f x >,求实数a 的取值范围;(2)若a 、0b >,且1a b +=,求证:对任意0x ≥,都有:()()11xe ax bx ≥++.【答案】(1)1a ≤(2)证明见解析 【解析】(1)由0x >时:()10xf x e ax =−−>又:()xf x e a '=−,①若1a ≤时,由0x >,故e 1x >,所以对任意0x >,都有:()0xf x e a '=−>此时函数()g x 在()0,∞+上单调递增,故对任意0x >,都有:()()100xf x e ax f =−−>=满足条件.②若1a >时,由0x >,故:()0ln xf x e a x a '=−=⇒=故可得:故函数f x 在0,ln a 上单调递减,在ln ,a +∞上单调递增,故:()()ln 00f a f <=不满足条件0x ∀>,都有()0f x >, 综上,实数a 的取值范围为1a ≤.(2)由(1)可知,当1a =时,对任意0x ≥,都有:()10xf x e x =−−≥,故对任意0x ≥,都有:1x e x ≥+,又a 、0b >,故对任意0x ≥,都有:10ax e ax ≥+>,10bx e bx ≥+>又1a b +=,故:()()()11a b xax bx ax bxx e e ee e ax bx ++⋅===≥++故对任意0x ≥,都有:()()11xe ax bx ≥++.【反思】注意在解答题中1x e x ≥+不能直接使用,需要证明后才可以使用,才可以进一步变形得到有利于解题的不等式.三、针对训练 举一反三一、单选题1.(2022·广东韶关·一模)已知sin11e ,sin1,cos1a b c −===,则( ) A .a c b << B .a b c << C .c b a <<D .c a b <<2.(2022·山西运城·(理))已知命题p :0x ∃>,ln 1x x >−;命题q :R x ∀∈,||e 1x ≥则下列命题中为真命题的是( ) A .p q ⌝∧B .p q ∧C .p q ∧⌝D .()p q ⌝∨3.(2021·广东肇庆·)下列不等式中,不恒成立的是( ) A .23()x e x x R +≥+∈ B .()21ln 11()()x x x +>+>−C .()1ln )2(2x x x +≤+>−D .1si )n 8(xe x x R ≥+∈4.(2021·安徽·东至县第二中学(理))下列不等式正确的个数有( )个. ①1x e x ≥+;②1ln x x −≥;③1(1),()x x x x x e +>+> A .0B .1C .2D .35.(2020·黑龙江哈尔滨·(理))下列四个命题中的假命题为( ) A .x R ∀∈,1x e x ≥+ B .x R ∀∈,1x e x −≥−+ C .00x ∃>,00ln 1x x >−D .00x ∃>,001ln1x x >− 6.(2019·湖北·(文))下列不等式中正确的是①sin ,(0,)x x x <∈+∞;②1,x e x x R ≥+∈;③ln ,(0)x x x <∈+∞,. A .①③ B .①②③ C .② D .①②7.(2020·全国·(理))已知命题p :0x ∀>,1x e x >+,命题q :(0,)x ∃∈+∞,ln x x ≥,则下列命题正确的是 A .p q ∧B .()p q ⌝∧C .()p q ∧⌝D .()()p q ⌝∧⌝8.(2021·安徽·毛坦厂中学高三阶段练习(理))设ln1.01a =, 1.0130b e=,1101c =,(其中自然对数的底数 2.71828e =)则( )A .a b c <<B .a c b <<C .c b a <<D .c a b <<9.(2022·全国·高三专题练习)若正实数a ,b 满足22ln ln 222+≥+−ba b a ,则( )A .124+=a b B .122−=−a b C .2a b > D .240b a −<二、填空题10.(2020·广东·高三阶段练习)已知函数()ln f x x =的反函数为()g x ,若实数m 、n 满足()()2f m g n m n −≥−−,则m n += ____.11.(2020·北京·中关村中学)已知函数()1x f x e ax =−−,()ln 1g x x ax =−−,其中01a <<,e 为自然对数的底数,若0(0,)x ∃∈+∞,使()()000f x g x >,则实数a 的取值范围是___________. 三、解答题12.(2022·浙江·高三专题练习)证明以下不等式: (1)1x e x ≥+; (2)ln 1≤−x x ; (3)1ln(1)x e x −>+.13.(2022·全国·高三专题练习)已知()()()1ln 1f x x x =++. (1)求函数()f x 的单调区间; (2)设函数()()221g x x f x x =−+,若关于x 的方程()g x a =有解,求实数a 的最小值; (3)证明不等式:()()*111ln 1123n n N n+<++++∈.。
2024年新高一数学初升高衔接《对数及其运算》含答案解析
第16讲 对数及其运算模块一 思维导图串知识模块二 基础知识全梳理(吃透教材)模块三 核心考点举一反三模块四 小试牛刀过关测1.理解对数的概念,掌握对数的基本性质;2.掌握指数式与对数式的互化,能应用对数的定义和性质解方程;3.理解对数的运算性质,能用换底公式将一般对数转化成自然对数或常用对数;4.会运用运算性质进行一些简单的化简与证明.知识点 1 对数的概念与性质1、对数的概念:如果x a N =(0a >且1a ≠),那么数x 叫做以a 为底N 的对数,记作x =log a N ,其中a 叫作对数的底数,N 叫作真数.2、常用对数与自然对数名称定义记法常用对数以10为底的对数叫做常用对数lg 自然对数以无理数 2.71828e =⋅⋅⋅为底的对数称为自然对数ln3、对数的性质(1)当0a >,且1a ≠时,x a N =⇔log a x N =;(2)负数和0没有对数,即0>N ;(3)特殊值:1的对数是0,即log 1a =0(0a >,且1a ≠);底数的对数是1,即log 1a a =(0a >,且1a ≠);(4)对数恒等式:log a N a N =;(5)log ba ab =.知识点 2 对数的运算性质及应用1、运算性质:0>a ,且1≠a ,0,0>>N M (1)N M MN a a a log log )(log +=;(2)N M NMa a alog log log -=;(3)M n M a na log log =2、换底公式(1)换底公式:abb c c a log log log =(a >0,且a ≠1;c >0,且c ≠1;b >0).(2)可用换底公式证明以下结论:①ab b a log 1log =; ②1log log log =⋅⋅a c b c b a ;③b b a na n log log =;④b n mb a ma n log log =; ⑤b b a alog log 1-=.知识点 3 对数运算常用方法技巧1、对数混合运算的一般原则(1)将真数和底数化成指数幂形式,使真数和底数最简,用公式log log m n a a nM b m=化简合并;(2)利用换底公式将不同底的对数式转化为同底的对数式;(3)将同底对数的和、差、倍运算转化为同底对数真数的积、商、幂;(4)如果对数的真数可以写成几个因数或因式的相乘除的形式,一般改写成几个对数相加减的形式,然后进行化简合并;(5)对数真数中的小数一般要化成分数,分数一般写成对数相减的形式.2、对数运算中的几个运算技巧(1)lg 2lg 51+=的应用技巧:在对数运算中如果出现lg 2和lg 5,则一般利用提公因式、平方差公式、完全平方公式等使之出现lg 2lg 5+,再应用公式lg 2lg 51+=进行化简;(2)log log 1a b b a ⋅=的应用技巧:对数运算过程中如果出现两个对数相乘且两个对数的底数与真数位置颠倒,则可用公式log log 1a b b a ⋅=化简;(3)指对互化的转化技巧:对于将指数恒等式xyza b c ==作为已知条件,求函数(),,f x y z 的值的问题,通常设(0)x y za b c k k ===>,则log a x k =,log b y k =,log c z k =,将,,x y z 值带入函数(),,f x y z 求解.考点一:对数的概念及辨析例1.(23-24高一上·全国·专题练习)(多选)下列选项中错误的是( )A .零和负数没有对数B .任何一个指数式都可以化成对数式C .以10为底的对数叫做自然对数D .以e 为底的对数叫做常用对数【变式1-1】(23-24高一上·贵州贵阳·月考)使式子(31)log (2)x x --有意义的x 的取值范围是( )A .2x >B .123x <<C .123x <<且23x ≠D .2x <,【变式1-2】(23-24高一上·吉林延边·期中)在对数式()()3log 5a b a -=-中,实数a 的取值范围是( )A .()(),35,-∞⋃+∞B .()3,5C .()3,4D .()()3,44,5【变式1-3】(22-23高一上·江苏宿迁·期中)在下列四个命题中,正确的是( )A .若M N =则log log a a M N =;B .若log log a a M N =,则M N =;C .22log log a a M N =,则M N =;D .若M N =,则22log log a a M N =.考点二:对数式与指数式互化例2.(23-24高一上·新疆乌鲁木齐·期末)将3log 0.81x =化成指数式可表示为( )A .30.81x =B .0.813x =C .0.813x=D .30.81x=【变式2-1】(23-24高一上·黑龙江哈尔滨·期中)将328=化为对数式正确的是( )A .2log 38=B .2log 83=C .8log 23=D .3log 28=【变式2-2】(23-24高一上·江苏连云港·期中)已知)4x =,则x =( )A .2-B .0C .2D .4【变式2-3】(23-24高一上·江西宁冈·期中)(多选)下列指数式与对数式的互化,正确的一组是( )A .0e 1=与ln1=0B .131273-=与2711log 33=-C .2log 42=与1242=D .5log 5=1与155=考点三:利用对数性质解对数方程例3.(23-24高一·江苏·假期作业)方程()()2lg 1lg 22x x -=+的根为( )A .3-B .3C .1-或3D .1或3-【变式3-1】23-24高一上·山东烟台·月考)方程()3log 941xx -=+的实数解为.【变式3-2】(23-24高一上·广东深圳·期中)已知a ,b 是方程22(ln )3ln 10x x -+=的两个实数根,则log log a b b a +=.【变式3-3】(23-24高一上·全国·练习)已知a ,b 是方程3273log log 433x x +=-的两个根,试给出关于a ,b 的一个结论.考点四:利用对数运算性质化简例4.(23-24高一下·云南昆明·期中)下列等式正确的是( )A .22(lg5)2lg2(lg2)1+-=B .335log 5log 2log 93⋅⋅=C.ln 2eπ+=D122.535[(0.064)]1-=【变式4-1】(23-24高一下·浙江·期中)化简()2151515155log 91log 3log 5log log 155⎛⎫+-⋅= ⎪⎝⎭.【变式4-2】(23-24高一上·贵州毕节·期末)计算:(1)2+00.5281(log 8log 2)(3)16⋅-;(2)ln3427log 9log 8lg 4lg 25e+⋅++.【变式4-3】(24-25高一上·全国·课后作业)计算:(1)420.5251log log 3log 95+-;(2)()2323223log 2log 3log 2log 3log 3log 2+--.考点五:用已知对数表示其他对数例5.(23-24高一下·江苏盐城·期末)若lg2a =,lg3b =,则用a ,b 表示lg12=( )A .2a bB .2abC .2+a bD .2a b+【变式5-1】(23-24高一上·江苏淮安·期中)已知25a=,则lg 2=( )A .1aa +B .1a a -C .11a +D .1a a -【变式5-2】(23-24高一上·江苏宿迁·期末)已知2log 3a =,27b =,用a ,b 表示42log 56为( )A .3b a b++B .3b a b+C .31b a b +++D .31b a b ++【变式5-3】(23-24高一上·甘肃武威·月考)已知lg2,lg3a b ==,则30log 18=( )A .21a bb +-B .21a b b ++C .21a b b --D .21a b b -+考点六:利用换底公式证明等式例6.(23-24高一上·山东淄博·期末)设a ,b ,c 都是正数,且346a b c ==,那么下列关系正确的是( )A .2a b c+=B .2ac bc ab+=C .1112a b c+=D .112a b c+=【变式6-1】(23-24高一上·全国·随堂练习)求证:28log 643log 64=.【变式6-2】(23-24高一上·全国·随堂练习)设0a >,0b >,0α≠,且1a ≠,1b ≠,利用对数的换底公式证明:(1)1log log a b b aαα=;(2)log log a a b b αββα=.【变式6-3】(23-24高一上·河北石家庄·月考)设000a b a >>≠,,,且11a b ≠≠,,利用对数的换底公式证明:(1)log log a a b b αββα=;(2)1log log a b b aαα=;(3)计算:若2log 32x =,求33x x -+的值.一、单选题1.(23-24高一上·全国·专题练习)在()log 5a b a =-中,实数a 的取值范围是( )A .5a >或a<0B .01a <<或15a <<C .01a <<D .15a <<2.(23-24高一下·湖南株洲·月考)若lg a (0a >)与lgb (0b >)互为相反数,则( )A .1a b +=B .0a b -=C .1ab =D .1ab=3.(23-24高一上·全国·课后作业)将31128⎛⎫= ⎪⎝⎭化为对数式正确的是( )A .121log 38=B .121log 38=C .181log 32=D .311log 28=4.(23-24高一下·陕西西安·月考)1lg 22+=( )A .12B .1C .lg 5D.5.(23-24高一上·北京·月考)若1ab >,则下列等式中正确是的是( )A .()lg lg lg ab a b=+B .lg lg lg a a bb ⎛⎫=- ⎪⎝⎭C .()21lg()lg 2a b a b +=+D .()1lg log 10ab ab =6.(23-24高一上·天津·期末)化简2345log 3log 4log 5log 8⨯⨯⨯的值为( )A .1B .3C .4D .8二、多选题7.(23-24高一上·贵州安顺·期末)下列运算正确的有( )A .lg 2lg 3lg 5+=B .33log 10010log 10=C .4log 545=D .34log 4log 31⋅=8.(23-24高一上·吉林延边·期中)下列命题中正确的是( )A .已知25a=,8log 3b =,则34a b -=259B .222(lg 2)3lg 2lg 5(lg 5)lg 2++-的值为1C .若3log 41x =,则44x x -+的值为103D .若23m n k ==且112m n+=,则k =6三、填空题9.(23-24高一下·上海嘉定·月考)已知2log 3a =,25b =则12log 45= .(用含,a b的式子表示)10.(23-24高一下·云南昆明·期中)若4312,log 12a b ==,则11a b+=.11.(23-24高一上·辽宁沈阳·期末)设m ,n 是方程()23lg lg 10x x -+=的两个实根,则mn =.四、解答题12.(22-23高一上·新疆喀什·期末)求值:(1)0113410.027167-⎛⎫-+ ⎪⎝⎭;(2)ln 2145log 2lg 4lg e 2+++.(3)()()48392log 3log 3log 2log 2++13.(23-24高一上·安徽蚌埠·期末)(1)若3515a b ==,求55a b+的值;(2)求值:()()22327lg 5lg 2lg 503π++⨯--.第16讲 对数及其运算模块一 思维导图串知识模块二 基础知识全梳理(吃透教材)模块三 核心考点举一反三模块四 小试牛刀过关测1.理解对数的概念,掌握对数的基本性质;2.掌握指数式与对数式的互化,能应用对数的定义和性质解方程;3.理解对数的运算性质,能用换底公式将一般对数转化成自然对数或常用对数;4.会运用运算性质进行一些简单的化简与证明.知识点 1 对数的概念与性质1、对数的概念:如果x a N =(0a >且1a ≠),那么数x 叫做以a 为底N 的对数,记作x =log a N ,其中a 叫作对数的底数,N 叫作真数.2、常用对数与自然对数名称定义记法常用对数以10为底的对数叫做常用对数lg自然对数以无理数 2.71828e =⋅⋅⋅为底的对数称为自然对数ln3、对数的性质(1)当0a >,且1a ≠时,x a N =⇔log a x N =;(2)负数和0没有对数,即0>N ;(3)特殊值:1的对数是0,即log 1a =0(0a >,且1a ≠);底数的对数是1,即log 1a a =(0a >,且1a ≠);(4)对数恒等式:log a N a N =;(5)log ba ab =.知识点 2 对数的运算性质及应用1、运算性质:0>a ,且1≠a ,0,0>>N M (1)N M MN a a a log log )(log +=;(2)N M NMa a alog log log -=;(3)M n M a na log log =2、换底公式(1)换底公式:abb c c a log log log =(a >0,且a ≠1;c >0,且c ≠1;b >0).(2)可用换底公式证明以下结论:①ab b a log 1log =; ②1log log log =⋅⋅a c b c b a ;③b b a na n log log =;④b n mb a ma n log log =; ⑤b b a alog log 1-=.知识点 3 对数运算常用方法技巧1、对数混合运算的一般原则(1)将真数和底数化成指数幂形式,使真数和底数最简,用公式log log m n a a nM b m=化简合并;(2)利用换底公式将不同底的对数式转化为同底的对数式;(3)将同底对数的和、差、倍运算转化为同底对数真数的积、商、幂;(4)如果对数的真数可以写成几个因数或因式的相乘除的形式,一般改写成几个对数相加减的形式,然后进行化简合并;(5)对数真数中的小数一般要化成分数,分数一般写成对数相减的形式.2、对数运算中的几个运算技巧(1)lg 2lg 51+=的应用技巧:在对数运算中如果出现lg 2和lg 5,则一般利用提公因式、平方差公式、完全平方公式等使之出现lg 2lg 5+,再应用公式lg 2lg 51+=进行化简;(2)log log 1a b b a ⋅=的应用技巧:对数运算过程中如果出现两个对数相乘且两个对数的底数与真数位置颠倒,则可用公式log log 1a b b a ⋅=化简;(3)指对互化的转化技巧:对于将指数恒等式xyza b c ==作为已知条件,求函数(),,f x y z 的值的问题,通常设(0)x y za b c k k ===>,则log a x k =,log b y k =,log c z k =,将,,x y z 值带入函数(),,f x y z 求解.考点一:对数的概念及辨析例1.(23-24高一上·全国·专题练习)(多选)下列选项中错误的是( )A .零和负数没有对数B .任何一个指数式都可以化成对数式C .以10为底的对数叫做自然对数D .以e 为底的对数叫做常用对数【答案】BCD【解析】对于A :由对数的定义可知:零和负数没有对数.故A 正确;对于B :只有符合0a >,且10a N ≠>,,才有log xa a N x N =⇔=,故B 错误;对于C :以10为底的对数叫做常用对数,故C 错误;对于D :以e 为底的对数叫做自然对数,故D 错误.故选:BCD.【变式1-1】(23-24高一上·贵州贵阳·月考)使式子(31)log (2)x x --有意义的x 的取值范围是( )A .2x >B .123x <<C .123x <<且23x ≠D .2x <,【答案】C【解析】由式子(31)log (2)x x --有意义,则满足31031120x x x ->⎧⎪-≠⎨⎪->⎩,解得123x <<且23x ≠.故选:C.【变式1-2】(23-24高一上·吉林延边·期中)在对数式()()3log 5a b a -=-中,实数a 的取值范围是( )A .()(),35,-∞⋃+∞B .()3,5C .()3,4D .()()3,44,5 【答案】D【解析】要使对数式()()3log 5a b a -=-有意义,需满足303150a a a ->⎧⎪-≠⎨⎪->⎩,解得34a <<或45a <<,所以实数a 的取值范围是()()3,44,5 .故选:D.【变式1-3】(22-23高一上·江苏宿迁·期中)在下列四个命题中,正确的是( )A .若M N =则log log a a M N =;B .若log log a a M N =,则M N =;C .22log log a a M N =,则M N =;D .若M N =,则22log log a a M N =.【答案】B【解析】对A ,若0M N =≤,则log ,log a a M N 均无意义,故A 错;对B ,若log log a a M N =,说明0M N =>,则B 项正确;对C ,若22log log a a M N =,则22M N =,不一定能推出M N =,故C 错;对D ,若0M N ==,则22log ,log a a M N 无意义,故D 错.故选:B考点二:对数式与指数式互化例2.(23-24高一上·新疆乌鲁木齐·期末)将3log 0.81x =化成指数式可表示为( )A .30.81x =B .0.813x =C .0.813x=D .30.81x=【答案】A【解析】把对数式3log 0.81x =化成指数式,为30.81x =.故选:A .【变式2-1】(23-24高一上·黑龙江哈尔滨·期中)将328=化为对数式正确的是( )A .2log 38=B .2log 83=C .8log 23=D .3log 28=【答案】B【解析】328=化为对数式为2log 83=,故选:B .【变式2-2】(23-24高一上·江苏连云港·期中)已知)4x =,则x =( )A .2-B .0C .2D .4【答案】C【解析】由)4x =得42x =,即22x x =,又0x >且1x ≠,所以2x =,故选:C .【变式2-3】(23-24高一上·江西宁冈·期中)(多选)下列指数式与对数式的互化,正确的一组是( )A .0e 1=与ln1=0B .131273-=与2711log 33=-C .2log 42=与1242=D .5log 5=1与155=【答案】ABD【解析】根据指数式与对数式的互化公式log Na ab b N =⇔=(0a >且1,0)a N ≠>可知,ABD 正确;对于C ,22log 4242=⇔=,故C 错误.故选:ABD考点三:利用对数性质解对数方程例3.(23-24高一·江苏·假期作业)方程()()2lg 1lg 22x x -=+的根为( )A .3-B .3C .1-或3D .1或3-【答案】B【解析】由()()2lg 1lg 22x x -=+,得2212210220x x x x ⎧-=+⎪->⎨⎪+>⎩,即2223010220x x x x ⎧--=⎪->⎨⎪+>⎩,解得3x =,所以方程()()2lg 1lg 22x x -=+的根为3.故选:B【变式3-1】23-24高一上·山东烟台·月考)方程()3log 941xx -=+的实数解为.【答案】3log 4【解析】由()3log 941x x -=+,得()133log 94log 3x x +-=,所以1943x x +-=,即()23433x x -=⋅,即()()34310x x-+=,所以34x =或31x =-(舍去),所以3log 4x =.故答案为:3log 4.【变式3-2】(23-24高一上·广东深圳·期中)已知a ,b 是方程22(ln )3ln 10x x -+=的两个实数根,则log log a b b a += .【答案】52/2.5【解析】方法一:因为a ,b 是方程()22ln 3ln 10x x -+=的两个实数根,由韦达定理得1ln ln 2a b ⋅=,3ln ln 2a b +=,则()()()()2222ln ln ln ln 2ln ln ln ln ln ln 5log log 2ln ln ln ln ln ln ln ln 2a b a b a b a b a b b a b a a b a b a b a b ++-⋅++=+===-=⋅⋅⋅,即5log log 2a b b a +=;方法二:因为22310t t -+=的根为1t =或12t =,不妨设ln 1a =,1ln 2b =,则e a =,b =,所以e 15log log log 222e a b b a +=+=+=.故答案为:52.【变式3-3】(23-24高一上·全国·练习)已知a ,b 是方程3273log log 433x x +=-的两个根,试给出关于a ,b 的一个结论 .【答案】1081a b +=(答案不唯一)【解析】根据换底公式有33333log log lo 7g l 343og 32x x +=-,即33114133log log x x ++=-+,令3g 1lo x t +=,则1433t t +=-,解得1t =-或3t =-.所以31log 1x +=-或31log 3x +=-,解得19x =或181x =.故答案为:1081a b +=(答案不唯一)考点四:利用对数运算性质化简例4.(23-24高一下·云南昆明·期中)下列等式正确的是( )A .22(lg5)2lg2(lg2)1+-=B .335log 5log 2log 93⋅⋅=C.ln 2e π+=D122.535[(0.064)]1-=【答案】A【解析】对于A 中,由2222(lg5)2lg2(lg2)(1lg2)2lg2(lg2)1+-=-+-=,所以A 正确;对于B 中,由335lg5lg22lg3log 5log 2log 93lg3lg3lg5⋅⋅=⋅⋅≠,所以B 错误;对于C中,由ln 27e log 825ππ=++-≠,所以C 错误;对于D 中,122.513551515[(0.064)](0.4)122222--=+⨯=+⨯≠,所以D错误.故选:A【变式4-1】(23-24高一下·浙江·期中)化简()2151515155log 91log 3log 5log log 155⎛⎫+-⋅= ⎪⎝⎭.【答案】1【解析】原式()()()()22221515151515151515log 3log 9log 5log 5log 32log 3log 5log 5=+⋅+=+⋅+()21515log 3log 5=+()215log 151==.故答案为:1.【变式4-2】(23-24高一上·贵州毕节·期末)计算:(1)2+00.5281(log 8log 2)(3)16⋅-;(2)ln3427log 9log 8lg 4lg 25e+⋅++.【答案】(1)0;(2)6【解析】(1)原式=1122234937(1()1021644+-=+-=(2)原式=3+log 23⋅log 32+lg100=3+1+2=6.【变式4-3】(24-25高一上·全国·课后作业)计算:(1)420.5251log log 3log 95+-;(2)()2323223log 2log 3log 2log 3log 3log 2+--.【答案】(1)0;(2)2【解析】(1)420.5251log log 3log 95+-22222251log log 95log 3log 4log 0.5=+-2225log log 3log 53=+-225log 35log 103⎛⎫=⨯÷== ⎪⎝⎭;(2)()2323223log 2log 3log 2log 3log 3log 2+--2ln 2ln 3ln 2ln 2ln 3ln 3ln 3ln 2ln 3ln 3ln 2ln 2⎛⎫=+-⋅-⋅ ⎪⎝⎭2222ln 2ln 3ln 2ln 322ln 3ln 2ln 3ln 2⎛⎫⎛⎫⎛⎫⎛⎫=++--= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.考点五:用已知对数表示其他对数例5.(23-24高一下·江苏盐城·期末)若lg2a =,lg3b =,则用a ,b 表示lg12=( )A .2a bB .2abC .2+a bD .2a b+【答案】D【解析】由对数运算性质可得()2lg12lg 34lg3lg4lg3lg2lg32lg22a b =⨯=+=+=+=+,故选:D.【变式5-1】(23-24高一上·江苏淮安·期中)已知25a=,则lg 2=( )A .1aa +B .1a a -C .11a +D .1a a -【答案】C 【解析】由25a=得,2lg 51lg 2log 5lg 2lg 2a -===,则1lg 21a =+,故选:C .【变式5-2】(23-24高一上·江苏宿迁·期末)已知2log 3a =,27b =,用a ,b 表示42log 56为( )A .3b a b++B .3b a b+C .31b a b +++D .31b a b ++【答案】C【解析】因为27b =,所以2log 7=b ,2222242222222log 56log 7log 8log 73log 23log 56log log 7742log log log l g 62o ++==+=++31+=++b b a .故选: C.【变式5-3】(23-24高一上·甘肃武威·月考)已知lg2,lg3a b ==,则30log 18=( )A .21a bb +-B .21a b b ++C .21a b b --D .21a b b -+【答案】B 【解析】30lg18lg2lg92log 18lg30lg311a bb ++===++,故选:B.考点六:利用换底公式证明等式例6.(23-24高一上·山东淄博·期末)设a ,b ,c 都是正数,且346a b c ==,那么下列关系正确的是( )A .2a b c +=B .2ac bc ab+=C .1112a b c+=D .112a b c+=【答案】C【解析】由346a b c k ===,得3log a k =,4log b k =,6log c k =,1log 3k a=,1log 4k b =,1log 6k c =,则11log 4log 222k k b ==,根据log 3log 2log 6k k k +=可知,1112a b c+=.故选:C 【变式6-1】(23-24高一上·全国·随堂练习)求证:28log 643log 64=.【答案】证明见解析【解析】左边622log 26log 26===,右边362263log 23log 263==⨯⨯=,所以左边=右边,得证.【变式6-2】(23-24高一上·全国·随堂练习)设0a >,0b >,0α≠,且1a ≠,1b ≠,利用对数的换底公式证明:(1)1log log a b b aαα=;(2)log log a a b b αββα=.【答案】(1)证明见解析;(2)证明见解析【解析】(1)log 1log log log b a b b b b a aααα==,所以等式成立;(2)log log log log log log a a a a a a b b b b a a αββαββαα===,所以等式成立.【变式6-3】(23-24高一上·河北石家庄·月考)设000a b a >>≠,,,且11a b ≠≠,,利用对数的换底公式证明:(1)log log a a b b αββα=;(2)1log log a b b aαα=;(3)计算:若2log 32x =,求33x x -+的值.【答案】(1)证明见解析;(2)证明见解析;(3)174【解析】(1)因为log log log log log a a a a a a b b b b a a αββββα===,所以命题log log a ab b αββα=得证.(2)因为log 1log log log b a a b b b b a aαα==,所以命题1log log ab b a αα=得证.(3)因为2log 32x =,所以22322log 22log 4log 3log 3x ===,故1333log 4log 4log 4117333343444x x---+=+=+=+=,即33x x -+的值为174.一、单选题1.(23-24高一上·全国·专题练习)在()log 5a b a =-中,实数a 的取值范围是( )A .5a >或a<0B .01a <<或15a <<C .01a <<D .15a <<【答案】B【解析】由对数的定义可知5001a a a ->⎧⎪>⎨⎪≠⎩,解得05a <<,且1a ≠,故选:B .2.(23-24高一下·湖南株洲·月考)若lg a (0a >)与lg b (0b >)互为相反数,则( )A .1a b +=B .0a b -=C .1ab =D .1a b=【答案】C【解析】因为lg a (0a >)与lg b (0b >)互为相反数,所以lg lg lg 0a b ab +==,所以1ab =.故选:C.3.(23-24高一上·全国·课后作业)将31128⎛⎫= ⎪⎝⎭化为对数式正确的是( )A .121log 38=B .121log 38=C .181log 32=D .311log 28=【答案】B【解析】31128⎛⎫= ⎪⎝⎭化为对数式:121log 38=,故选:B 4.(23-24高一下·陕西西安·月考)1lg 22+=( )A .12B .1C .lg 5D.【答案】A【解析】11111lg 2lg 2lg 5lg(25)22222+=+=⨯=.故选:A5.(23-24高一上·北京·月考)若1ab >,则下列等式中正确是的是( )A .()lg lg lg ab a b=+B .lg lg lg a a bb ⎛⎫=- ⎪⎝⎭C .()21lg()lg 2a b a b +=+D .()1lg log 10ab ab =【答案】D【解析】当0,0a b <<时,ABC 均不成立,由换底公式知D 正确.故选:D .6.(23-24高一上·天津·期末)化简2345log 3log 4log 5log 8⨯⨯⨯的值为( )A .1B .3C .4D .8【答案】B【解析】由题意可得:2345ln 3ln 4ln 5ln 8ln 83ln 2log 3log 4log 5log 83ln 2ln 3ln 4ln 5ln 2ln 2⨯⨯⨯=⨯⨯⨯===.故选:B.二、多选题7.(23-24高一上·贵州安顺·期末)下列运算正确的有( )A .lg 2lg 3lg 5+=B .33log 10010log 10=C .4log 545=D .34log 4log 31⋅=【答案】CD【解析】对A ,lg 2lg 3lg 6+=,故A 错误;对B ,33log 1002log 10=,故B 错误;对C ,4log 545=正确;对D ,34log 4log 31⋅=正确.故选:CD8.(23-24高一上·吉林延边·期中)下列命题中正确的是( )A .已知25a=,8log 3b =,则34a b -=259B .222(lg 2)3lg 2lg 5(lg 5)lg 2++-的值为1C .若3log 41x =,则44x x -+的值为103D .若23m n k ==且112m n+=,则k =6【答案】ABC 【解析】因为25a=,则2log 5a =,且821log 3log 33b ==,则22253log 5log 3log 3a b -=-=则()22252log 253log 9332542229a b a b--====,故A 正确;()()222(lg 2)3lg 2lg 5(lg 5)lg 22lg 2lg 5lg 2lg 5lg 22lg 2lg 5lg 2++-=++-=+-lg 2lg 51=+=,故B 正确;由3log 41x =可得431log 3log 4x ==,则44log 3log 31104444333x x --+=+=+=,故C 正确;因为23m n k ==,则23log ,log m k n k ==,则11log 2,log 3k k m n==,所以11log 2log 3log 62k k k m n+=+==,所以k =D 错误;故选:ABC 三、填空题9.(23-24高一下·上海嘉定·月考)已知2log 3a =,25b =则12log 45=.(用含,a b的式子表示)【答案】22a b a ++【解析】因为25b =,所以2log 5b =,又2log 3a =,所以()()2222122222log 59log 45log 5log 9log 45log 12log 34log 3log 4⨯+===⨯+222222log 52log 3log 32log 2a ba ++=++=.故答案为:22a b a ++10.(23-24高一下·云南昆明·期中)若4312,log 12ab ==,则11a b +=.【答案】1【解析】因为312a =,所以3log 12a =,所以121212341111log 3log 4log 121log 12log 12a b +=+=+==.故答案为:1.11.(23-24高一上·辽宁沈阳·期末)设m ,n 是方程()23lg lg 10x x -+=的两个实根,则mn =.【答案】1000【解析】()23lg lg 10x x -+=,即()2lg 3lg 10x x -+=,设lg t x =,由题意lg lg m n ,是方程2310t t -+=的两个根,由根与系数关系得lg lg 3m n +=,即lg 3mn =,所以1000mn =.故答案为:1000.四、解答题12.(22-23高一上·新疆喀什·期末)求值:(1)0113410.027167-⎛⎫-+ ⎪⎝⎭;(2)ln 2145log 2lg 4lg e 2+++.(3)()()48392log 3log 3log 2log 2++【答案】(1)53-;(2)52;(3)2【解析】(1)()()()111113443344410.027160.32147--⎛⎫⎡⎤-+=-+- ⎪⎣⎦⎝⎭10521433=-+-=-(2)2ln 221245log 2lg 4lg e log 2lg 2lg 5lg 222-+++=++-+13352lg 2lg 5lg 22lg 2lg 512222=-++-+=++=+=(3)()()()()232483932232log 3log 3log 2log 22log 3log 3log 2log 2++=++223311log 3log 3log 2log 232⎛⎫⎛⎫=++ ⎪⎪⎝⎭⎝⎭2343log 3log 2232⎛⎫⎛⎫=⋅= ⎪ ⎪⎝⎭⎝⎭13.(23-24高一上·安徽蚌埠·期末)(1)若3515a b ==,求55a b+的值;(2)求值:()()22327lg 5lg 2lg 503π++⨯--.【答案】(1)5;(2)13π-【解析】(1)因为3515a b ==,所以35log 15,log 15==a b ,3551,1lo 1g 15l g 1o 1a b ==,则()()15151535551155log 3log 55log 355log 15log 15a b ⎛⎫+=+=+=⨯= ⎪⎝⎭;(2)()()()()()22223331027lg 5lg 2lg 503π3lg 5lglg 105π35++⨯--=++⨯⨯-+()()()()()22223lg 51lg 51lg 5π312πlg 51lg 513π=++-⨯+-+=-++-=-.。
高考数学 热点题型和提分秘籍 专题09 对数与对数函数
专题09 对数与对数函数【高频考点解读】1.理解对数的概念及其运算性质,知道用换底公式能将一般对数转化为自然对数或常用对数;了解对数在简化运算中的作用.2.理解对数函数的概念,理解对数函数的单调性,掌握对数函数图象通过的特殊点.3.知道对数函数是一类重要的函数模型.4.了解指数函数y =a x与对数函数y =log a x 互为反函数(a >0,且a ≠1). 【热点题型】题型一 对数式的运算 【例1】 求值:(1)log 89log 23;(2)(lg 5)2+lg 50·lg 2; (3)12lg 3249-43lg 8+lg 245.【提分秘籍】1.化同底是对数式变形的首选方向,其中经常用到换底公式及其推论. 2.结合对数定义,适时进行对数式与指数式的互化.3.利用对数运算法则,在积、商、幂的对数与对数的和、差、倍之间进行转化. 【举一反三】(1)若2a =5b=10,求1a +1b的值;(2)若x log 34=1,求4x+4-x的值.【热点题型】题型二对数函数图象及应用【例2】若实数a,b,c满足log a2<log b2<log c2,则下列关系中不可能成立的是( ) A.a<b<c B.b<a<cC.c<b<a D.a<c<b【提分秘籍】由对数函数的图象确定参数的方法已知对数型函数的图象研究其解析式及解析式中所含参数的取值范围问题,通常是观察图象,获得函数的单调性、对称性、奇偶性、经过的特殊点等,由此确定函数解析式以及其中所含参数的取值范围.【举一反三】已知函数若a、b、c互不相等,且f(a) =f(b)=f(c),则abc 的取值范围是( )(A)(1,10) (B)(5,6)(C)(10,12) (D)(20,24)【热点题型】题型三对数函数性质及应用例3.函数y=log a x(a>0,且a≠1)在[2,4]上的最大值与最小值的差是1,则a的值为________.【提分秘籍】1.比较对数式大小的方法(1)若底数为同一常数,则可由对数函数的单调性直接进行判断;若底数为同一字母,需对底数进行分类讨论.(2)若底数不同,真数相同,则可以先用换底公式化为同底后,再进行比较.(3)若底数与真数都不同,则常借助1,0等中间量进行比较.2.当对数函数底数大小不确定时要注意分a>1与0<a<1两种情况讨论.【举一反三】(1)(设a=log32,b=log52,c=log23,则( )A.a>c>b B.b>c>aC.c>b>a D.c>a>b(2)已知函数f(x)=|log2x|,正实数m,n满足m<n,且f(m)=f(n),若f(x)在区间[m2,n]上的最大值为2,则m,n的值分别为( )A.12,2 B.12,4C.22, 2 D.14,4【热点题型】题型四复合对数函数图象的应用【例4】已知函数f(x)=log a(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )A .0<a -1<b <1 B .0<b <a -1<1 C .0<b -1<a <1 D .0<a -1<b -1<1【举一反三】函数f (x )=-2ln 1+x1-x的图象可能是( )【热点题型】题型五 与对数函数有关的复合函数单调性应用例5、若f (x )=lg(x 2-2ax +1+a )在区间(-∞,1]上递减,则a 的取值范围为( ) A .[1,2) B .[1,2] C .[1,+∞) D .[2,+∞)【答案】A 【提分秘籍】1.求与对数函数有关的复合函数的单调性的步骤 (1)确定定义域;(2)弄清函数是由哪些简单初等函数复合而成的,将复合函数分解成简单初等函数y =f (u ),u =g (x );(3)分别确定这两个函数的单调区间;2.已知复合函数单调性求参数范围时,要注意真数大于0这一条件. 【举一反三】设0<a <1,函数f (x )=log a (a 2x-2a x-2),则使f (x )<0的x 的取值范围是( ) A .(-∞,0) B .(0,+∞) C .(-∞,log a 3)D .(log a 3,+∞)【高考风向标】1.(2014·天津卷) 函数f (x )=lg x 2的单调递减区间是________.2.(2014·安徽卷) ⎝ ⎛⎭⎪⎫1681-34+log 354+log 345=________.3.(2014·浙江卷)在同一直角坐标系中,函数f(x)=x a(x>0),g(x)=log a x的图像可能是( )4.(2014·福建卷)若函数y=log a x(a>0,且a≠1)的图像如图所示,则下列函数图像正确的是( )5.(2014·广东卷) 等比数列{a n }的各项均为正数,且a 1a 5=4,则log 2a 1+log 2a 2+log 2a 3+log 2a 4+log 2a 5=________.6.(2014·辽宁卷) 已知a =2-13,b =log 213,c =log 1213,则( )A .a >b >cB .a >c >bC .c >b >aD .c >a >b7.(2014·山东卷) 已知函数y =log a (x +c )(a ,c 为常数,其中a >0,a ≠1)的图像如图11所示,则下列结论成立的是( )图11A.a>1,x>1 B.a>1,0<c<1C.0<a<1,c>1 D.0<a<1,0<c<18.(2014·四川卷)已知b>0,log5b=a,lg b=c,5d=10,则下列等式一定成立的是( )A.d=ac B.a=cdC.c=ad D.d=a+c9.(2014·重庆卷)若log4(3a+4b)=log2ab,则a+b的最小值是( )A.6+2 3 B.7+2 3C.6+4 3 D.7+4 3【随堂巩固】1.已知函数f(x)=a x+log a x(a>0且a≠1)在[1,2]上的最大值与最小值之和为log a 2+6,则a的值为( )A.12B.14C.2 D.42.已知x =lnπ,y =log 52,z =e -12,则( )A .x <y <zB .z <x <yC .z <y <xD .y <z <x3.若f (x )=log a x 在[2,+∞)上恒有f (x )>1,则实数a 的取值范围是( )A.⎝ ⎛⎭⎪⎫12,1B.⎝ ⎛⎭⎪⎫0,12∪(1,2) C .(1,2) D.⎝ ⎛⎭⎪⎫0,12∪(2,+∞)4.已知函数f (x )满足:当x ≥4时,f (x )=⎝ ⎛⎭⎪⎫12x;当x <4时,f (x )=f (x +1),则f (2+log 23)=( )A.124 B.112C.18D.385.设函数f (x )=若f (m ) <f (-m ),则实数m 的取值范围是( )A .(-1, 0)∪(0,1)B .(-∞,-1)∪(1,+∞)C .(-1,0)∪(1,+∞)D .(-∞,-1)∪(0,1)6.|1+lg 0.001|+ lg 213-4lg 3+4+lg 6-lg 0.02的值为________.7.已知函数f (x )=⎩⎪⎨⎪⎧ 3x +1,x ≤0log 2x ,x >0,则使函数f (x )的图象位于直线y =1上方的x 的取值范围是______________.8.设函数f (x )定义在实数集上,f (2-x )=f (x ),且当x ≥1时,f (x )=ln x ,则f ⎝ ⎛⎭⎪⎫13,f ⎝ ⎛⎭⎪⎫12,f (2)的大小关系为________.(用“<”表示)9.若f(x)=x2-x+b,且f(log2a)=b,log2f(a)=2(a≠1).(1)求f(log2x)的最小值及对应的x值;(2)x取何值时,f(log2x)>f(1),且log2f(x)<f(1).∴x的取值为(0,1).10.已知函数f(x)=log a(x+1)-log a(1-x),a>0且a≠1.(1)求f(x)的定义域;(2)判断f(x)的奇偶性并予以证明.11.已知函数f(x)=log4(ax2+2x+3).(1)若f(x)定义域为R,求a的取值范围;(2)若f(1)=1,求f(x)的单调区间.。
(完整版)计量经济学期末考试及答案,推荐文档
《计量经济学》课程期末考试题(二)一、单项选择题(每小题1分,共20分)1、计量经济研究中的数据主要有两类:一类是时间序列数据,另一类是【 】A 、总量数据B 、 横截面数据C 、平均数据D 、 相对数据2、计量经济学分析的基本步骤是【】A 、 设定理论模型→收集样本资料→估计模型参数→检验模型B 、设定模型→估计参数→检验模型→应用模型C 、个体设计→总体设计→估计模型→应用模型D 、确定模型导向→确定变量及方程式→估计模型→应用模型3、在模型的经济意义检验中,不包括检验下面的哪一项【 】A 、 参数估计量的符号 B 、参数估计量的大小C 、 参数估计量的相互关系D 、参数估计量的显著性4、计量经济学模型用于政策评价时,不包括下面的那种方法【 】A 、工具变量法B 、 工具—目标法C 、政策模拟D 、 最优控制方法5、在总体回归直线E 中,表示【 】x y10)ˆ(ββ+=1βA 、 当x 增加一个单位时,y 增加个单位1βB 、当x 增加一个单位时,y 平均增加个单位1βC 、当y 增加一个单位时,x 增加个单位1βD 、当y 增加一个单位时,x 平均增加个单位1β6、用普通最小二乘法估计经典线性模型,则样本回归线通过t t t u x y ++=10ββ点【 】A 、 (,)B 、 (x ,) x y y ˆC 、(,)D 、 (x ,y)x yˆ7、对于,统计量服iki k i i i e x x x y +++++=ββββˆˆˆˆ22110 ∑∑----)1/()ˆ(/)ˆ(22k n yyky yi ii从【】A 、 F(k-1,n-k)B 、 F(k,n-k-1)C 、 t(n-k)D 、t(n-k-1)8、下列说法中正确的是:【 】A 、如果模型的很高,我们可以认为此模型的质量较好2RB 、如果模型的较低,我们可以认为此模型的质量较差2RC 、如果某一参数不能通过显著性检验,我们应该剔除该解释变量D 、如果某一参数不能通过显著性检验,我们不应该随便剔除该解释变量9、容易产生异方差的数据是【 】A 、时间序列数据 B 、横截面数据C 、修匀数据D 、 年度数据10、假设回归模型为,其中var()=,则使用加权最小二i i i u x y ++=βαi u 22i x σ乘法估计模型时,应将模型变换为【 】A 、B 、 x ux x y ++=βα222x ux x x y ++=βαC 、D 、xu x xx y ++=βαxu xx y ++=βα11、如果模型存在序列相关,则【 】t t t u x b b y ++=10A 、 cov (,)=0 B 、 cov (,)=0(t ≠s )t x t u t u s u C 、cov (,)≠0D 、cov (,)≠0(t ≠s )t x t u t u s u 12、根据一个n=30的样本估计i i i e x y ++=10ˆˆββ后计算得DW=1.4,已知在5%的置信度下,L d =1.35,=1.49,则认为原模型【 】U d A 、不存在一阶序列自相关 B 、 不能判断是否存在一阶自相关C 、存在正的一阶自相关D 、 存在负的一阶自相关13、已知样本回归模型残差的一阶自相关系数接近于-1,则DW 统计量近似等于【 】A 、 0B 、 1C 、 2D 、 414、在线性回归模型中,若解释变量和的观测值成比例,即有,1X 2X i i kX X 21=其中k 为非零常数,则表明模型中存在【 】A 、不完全共线性B 、 完全共线性C 、 序列相关D 、 异方差15、假设回归模型为,其中为随机变量,与高度相关,i i i u X Y ++=βαi X i X i u 则β的普通最小二乘估计量【 】A 、无偏且一致B 、 无偏但不一致C 、有偏但一致D 、 有偏且不一致16、在工具变量的选取中,下面哪一个条件不是必需的【 】A 、 与所替代的随机解释变量高度相关B 、与随机误差项不相关C 、与模型中的其他解释变量不相关D 、与被解释变量存在因果关系17、如果联立方程模型中某个结构方程包含了所有的变量,则这个方程【 】A 、 恰好识别B 、 不可识别C 、不确定D 、 恰好识别18、结构式方程中的系数称为【 】A 、 短期影响乘数B 、 长期影响乘数C 、结构式参数D 、 简化式参数19、下列生产函数中,要素的替代弹性不变的是【 】A 、线性生产函数B 、 投入产出生产函数C 、C —D 生产函数D 、 CES 生产函数20、线性支出系统的边际预算份额和扩展线性支出系统的边际消费倾向的j β*j β关系是【 】A 、B 、=*j j ββ=*j β*jβ∑C 、=D 、=j β*jβ∑j β∑**jj ββ二、多选题(每题有2~5个正确答案,多选、少选和错选均不得分;每题1分,共5分)1、对计量经济模型的计量经济学准则检验包括【 】A 、 误差程度检验B 、 异方差检验C 、序列相关检验D 、超一致性检验E 、多重共线性检验2、用普通最小二乘法估计模型的参数,要使参数估计量具备t t t u x y ++=10ββ最佳线性无偏估计性质,则要求:【 】A 、B 、 (常数)0)(=t u E 2)(σ=t u VarC 、D 、服从正态分布0),cov(=j i u u t u E 、 x 为非随机变量,且0),cov(=t t u x 3、下列哪些方法可以用于异方差性的检验【】A 、 DW 检验法 B 、 戈德菲尔德——匡特检验 C 、 怀特检验 D 、 戈里瑟检验E 、冯诺曼比检验4、D -W 检验不适用于下列情况下的序列自相关检验【】A 、模型包含有随机解释变量B 、 样本容量<15C 、含有滞后的被解释变量D 、 高阶线性自回归形式的序列相关E 、 一阶线性形式的序列相关5、 结构式方程的识别情况可能是【】A 、不可识别B 、 部分不可识别C 、 恰好识别D 、过度识别E 、 完全识别三、判断题(正确的写“对”,错误的写“错”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
超越对数生产函数
L·christensen 、D ·jorgenson 和Lau 于1973年提出超越对数生产函数,该函数模型是一种易于估计和包容性很强的变弹性生产函数模型,它在结构上属于平方反映面模型,可有效研究生产函数中投入要素的交互影响、各种投入技术进步的差异。
通过超越对数生产函数模型,可以分析投入要素的产出弹性和要素的替代弹性。
其形式为:
t t KL t LL t KK t L t K t LnL LnK LnL LnK LnL LnK LnY •+++++=ββββββ220)()((1)
公式中:t Y ——t 年产出;
t t L K 、——t 年资本存量、劳动力投入量;
β——需要估计的系数。
(1)要素投入的产出弹性 资本投入的产出弹性为:
t KK KL K K LnK βββη2LnL dLnK dLnY dK/K dY /Y t t
t
++===
(2) 劳动投入的产出弹性为:
t LL KL L L LnL βββη2LnK dLnL dLnY dL/L dY /Y t t
t
++===
(3) (2)要素的替代弹性 替代弹性可以定义为:在技术水平和投入要素的价格不变的情况下,边际技术替代率的相对变动所引起的生产要素投入的比例的相对变动,即投入要素比例的变动的百分比与边际技术替代率的变动百分比的比值。
要素之间可替代程度的高低可用要素替代弹性(the elasticity of substitution)来描述,其具体含义是:一种生产要素价格变化以后,它与另一种生产要素相互替代率的变化。
要素替代弹性在0与无穷大之间变化,当0时,说明两种要素之间完全不能互相替代,如固定投入比例生产函数(里昂惕夫生产函数),当替代弹性无穷大时,说明两种要素之间可以完全替代。
资本、劳动2种投入的替代弹性计算如下:
资本和劳动的替代弹性为:
KL
()(
)(
)()()()()()L L
K K
L L K K MPP K MPP K d d d L MPP MPP L K MPP MPP K d L MPP MPP L σ==g g (4)
由于
L L K K MPP K
Y
Y L
K MPP L
ηη∂∂==•∂∂ (5) 结合式( 4)、式(5 )可得,
11
()()()()()()L L L L K L K KL
L K K K K MP K K d d d MP L L MP K K d d d L L MP ηηηηησηηη--⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪=
== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭
g g g g (6) 因为
(
)()
()()
L L K L K K K
d d L
K
K K L d d L
L
ηη
ηηηη=+g g (7) 21(
)()()L L K L K K K
d d d ηηηηηηη=-+ (8) 21
(
)K K d dL dK L L L
=-+ (9) 将式(8),式(9)代入式(7)得:
2
2
22()()
1
1(
)()()11()L
L L K L K L K
K K
K K d d d d d dL dL
K K K dK
d dL dK L
L L
L L dL
ηηηηηηηηηηηη-+-+=
=
-+-+
(10)
将式(10)代入(6)得资本与劳动的替代弹性:
()1
11K KL
KL LL L K L ησββηηη--⎛⎫⎛⎫=+-+- ⎪ ⎪ ⎪⎝⎭⎝⎭
(11)。
