Sobolev_Hardy不等式与临界双重调和问题

合集下载

一类带Hardy项和Sobolev临界项的椭圆方程组变号解

要
研究了一类￣：ｒｙ项和ＳｂｌＨａｄｏｏｅｖ临界项的椭圆方程组，在集合上建立极小化序列及其紧性，当参数／，１
ｍ满足一定条件时，用变分法和分析技巧证明了变号解的存在性．运关键词变号解；性；ｂｌ紧ｏＳｏｅｖ临界项；ｒｙ项Ｈａｄ０１５２文献标识码７．５Ａ文章编号、１７ —３１２１）３Ｏ０一４６２４２（ＯＯＯ一１ｏ０
（Ｉ・Ｉｘ的完备化空间．Ｉ）ｄ
１问题的引入
考虑如下椭圆方程组：
３ｎ
本文研究范围在积空间Ｈ ×Ｈ上，问题（）在空间Ｈ ×Ｈ上对应的能量泛函为：
Ｊ（）：一 Biblioteka ，ｉ（ｕ・１一ｆＩｌＶ２ｖ。ｚ＋－卜△ ＝Ｉ’ ｎ＋Ｖ∈，１。ＩＩ１一＿＋ａ，（）１。一。一三一Ｉｚ３。．尸ＺｔｄｄｌＯＥＯ一，．一ｘａ
ＡｂｔａｔＡｉｄｏｌｐｉｙｔｍｓｉｖｌｉｇＨａｄｅｍｓａｄｔｅｃｉｃｌＳｂｌｖｅｐｎｎｓｉｔｄｅ．ｅｓｒｃｋｎｆｅｌｔｃｓｓｅｎｏｖｎｒｙｔｒｎｈｒｔａｏｏｅｘｏｅｔｓｓｔｉｄＴｈｉｉｌ
ＩＩ－＋ＩＩ一￣ｄ－（一 “２口）ｘｖ
收稿日期２１－５００００－５
作者简介

带有临界Sobolev-Hardy指数的奇异非齐次双调和问题

带有临界Sobolev-Hardy指数的奇异非齐次双调和问题康东升【期刊名称】《中南民族大学学报（自然科学版）》【年(卷),期】2005(024)002【摘要】Let Ω( )RN be a smooth bounded domain such that0∈Ω,N≥5,0≤s＜4,2* (s): =2(N-s)/N-4 is the critical Sobolev-Hardy exponent ,f(x) is a given function. By using the variational principle ,we prove the existence of solutions for the singular critical inhomogeneous problem △2u-μ x/|x|4=|u|2*(s)-2/|x|su+λu+f(x)with Dirichlet boundary condition on ( )Ω under some assumptions on f(x) ,λ and μ.%设Ω是RN(N≥5)中的有界光滑区域,0∈Ω,0≤s＜4,2*(s):=2(N-s)/N-4是临界Sobolev-Hardy指数,f(x)是一个给定的函数.利用变分原理,证明了当f(x),λ,μ满足一定条件时,带有Dirichlet边值条件的奇异临界非齐次问题△2u-μu|x|4=|u|2*(s)-2/|x|su+λu+f(x)解的存在性.【总页数】5页(P79-83)【作者】康东升【作者单位】中南民族大学,计算机科学学院,武汉,430074【正文语种】中文【中图分类】O175.25【相关文献】1.带非齐次项和Sobolev-Hardy临界指数的奇异椭圆方程的多解 [J], 姚仰新;沈尧天2.带有临界Sobolev-Hardy指数的非齐次椭圆方程解的存在性 [J], 康东升;赵占平;邓引斌3.带非齐次项和Sobolev-Hardy临界指数的奇异椭圆方程的多解 [J], 穆罕麦德;沈尧天;姚仰新4.带有临界Sobolev指数的奇异双调和问题 [J], 胡丽平;周世国5.带有加权Hardy-Sobolev临界指数的非齐次Neumann边界奇异的多解问题[J], 商彦英; 王聪因版权原因，仅展示原文概要，查看原文内容请购买。

【国家自然科学基金】_指数不等式_基金支持热词逐年推荐_【万方软件创新助手】_20140729

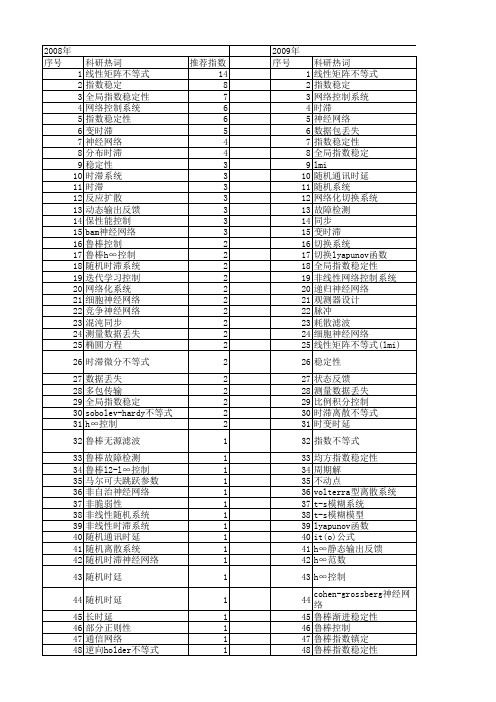
107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 1 young不等式 1 108 模糊细胞神经网络 vmo函数 1 109 模糊模型 treynor比率 1 110 模糊bam神经网络 slpmm(sequentially linear programming 1 matrix method) 111 概周期解 slpmm 1 112 椭圆问题 razumikhin定理 1 113 标准神经网络模型 puma560机器手臂 1 114 李雅普诺夫函数 p-阶拉普拉斯方程 1 115 有界时滞 markov跳跃参数 1 116 时滞系统 lyapunov稳定性 1 117 时滞相关 lyapunov泛函 1 118 时滞区间系统 lyapunov函数 1 119 时滞依赖 lyapunov-krasovskii泛函 1 120 时变时滞 lurie系统 1 121 数据丢失 lmi 1 122 数据丢包 li-yau抛物不等式 1 123 收敛速度. l2-l∞性能 1 124 控制与调度协同设计 jacobsthal不等式 1 125 指数镇定 ito类型随机时滞系统 1 126 指数同步 h值 1 127 执行器故障 h∞范数 1 128 微分中值定理 h∞滤波 1 129 微分不等式 harnack估计 1 130 异步动态系统 hardy不等式 1 131 广义网络控制系统 halanay不等式 1 132 平均驻留时间 halanay-type不等式 1 133 常微分方程组 h2控制 1 134 岩石可钻性 cohen-grossberg随机神经网络 1 135 岩屑 cohen-grossberg神经网络 1 136 局部场神经网络 chen系统 1 137 对数律 bamcg模型 1 138 存在性 139 奇异摄动系统 140 多李亚普诺夫函数 141 多奇异 142 多包传输 143 多临界 144 复杂网络 145 周期性 146 吸引子 147 变分法 148 反应扩散 149 参数不确定性 150 动态神经网络 151 加性增益摄动 152 分散控制 153 分布时滞 154 分布参数 155 凹函数 156 全连续算子 157 伴随推移映射 158 临界位势 159 临界hardy-sobohv指数 160 中立型

带有临界Sobolev—Hardy指数的非齐次椭圆方程解的存在性

＜１ “＞０
，
∈
，
ｃ』ｎ
中给出．
吉ｃｎ ≤ 【Ｉ』Ｖｕ
“ ∈ Ｗ（）， ’
【
“＝０，
∈ａ，
其中＞０ｐ＜：（，
），２Ｒ Ⅳ ≥ ３是ｚｇＣ（）
这两个重要的不等式我们在引理２１和引理２２．．
点．又设
Ｍ：一｛ ∈ Ｈ； ≠ ０（（， “ “ ， “） “＞＝０｝，
在ｉ问题的讨论中，于其中的奇异项，文对一
收稿日期：０２０ — １２０ — １２．基金项目：国家自然科学基金资助项目（Ｏ１３）１１０６．７作者简介：东升（７）男，南确山人，士研究生，教授，要从事微分方程研究康１６一，河９博副主
受上面这些文献的启发，文讨论下列问题本
包含０的有界区域，明了在一定条件下解的存在证
性．献［］则讨论了问题文２
一
＋
…
∈
，
ｊ △一一 “
ｌ
其中ｏ
，
“ ，一ｏ
＋ｍ ∈
∈ａ。
维普资讯
华中师范大学学报（自然科学版）
第３６卷
．
Ⅵ
：一
∈ ： “。（１ｄＯＭＩＩｑ）｝ＩＩ一』２一＞’

具有临界Sobolev-Hardy项的拟线性p-重调和方程解的存在性

具有临界Sobolev－Hardy项的拟线性p－重调和方程解的存在性作者：任艳桑彦彬来源：《河北科技大学学报》2019年第02期摘要：为了研究一类带有Hardy项和多临界Sobolev-Hardy指数的拟线性p-重调和方程解的存在性，借助于Ekeland变分原理，给出上述问题解的存在性定理。

首先，将方程对应的变分泛函定义在约束集Mη（通常称为Nehari流形）上，使得该泛函下方有界。

其次，利用纤维映射将上述集合Mη划分为M+η，M0η和M-η等3部分，并分别研究每部分的性质，证明了M+η和M-η中泛函极小值的存在性。

最后，利用隐函数定理，得到在参数满足一定条件下，存在极小化序列{un}，满足（PS）c条件，从而完成了该方程解的存在性的证明。

所得结论可为判定解的结构和性质提供理论依据。

关键词：非线性泛函分析;临界Sobolev-Hardy项;拟线性p-重调和方程;Ekeland变分原理;解的存在性中图分类号：O175.25文献标志码：AAbstract：In order to study a class of quasilinear p-biharmonic equations with Hardy terms and multi-critical Sobolev-Hardy exponents， the existence theorem of the solutions to the above problem is established by means of the Ekeland variational principle. Firstly， to guarantee the variational functional is bounded from below，it is restricted on a set ;Mη （usually called Nehari manifold）. Secondly，the set Mη ;is divided into three parts ;M+η，M0η ;and M-η ;by using fibering maps. Moreover，the existence of minimum in ;M+η and M-η ;is proved by stu dying the properties of the two subsets. Finally， by using implicit function theorem， it is found that there exists a minimizing sequence {un} ;making the （PS）c ;conditions hold when the parameters satisfy certain conditions. Therefore， the existence of the solutions to the problem is proved. The conclusions provide a theoretical basis for judging the structure and properties of the solutions.Keywords：nonlinear functional analysis; critical Sobolev-Hardy terms; quasilinear p-biharmonic equations; Ekeland's variational principle; existence of the solution3結论本文讨论了一类具有临界指数的p-重调和方程，运用变分方法和Ekeland变分原理，建立了其解的存在性定理，可为判定解的结构和性质提供理论依据。

R3双临界Kirchhoff型方程正解的存在性

R3双临界Kirchhoff型方程正解的存在性宋雅倩;张福伟;刘进生【摘要】利用变分方法研究了R3上具有双临界非线性项的Kirchhoff型方程正解的存在性。

首先证明了该问题的能量泛函满足山路引理的几何条件，从而证明了能量泛函存在(PS)c 序列，进而通过(PS)c 序列的有界性与弱极限的非平凡性及径向对称空间的性质证明了此(PS)c 序列具有强收敛子列，因此证明了能量泛函存在非平凡临界点，于是此问题存在非平凡解，最后证明了此非平凡解是正解。

%The existence of positive solutions for Kirchhoff type problem with multiple critical nonlineari-ties was investigated by using variationalmethod.Firstly,it was proved that the energy functional pos-sessed mountain pass geometry and got a (PS)c sequence.Then,it was demonstrated that the (PS)c se-quence contained strong convergent subsequence through the boundedness of the (PS)c sequence,the non triviality of weak limit,and the property of radial symmetryspace.Therefore,the energy functional has at least one nontrivial critical point and the problem has at least one nontrivial solution.Consequent-ly,it is achieved that the nontrivial solution is positive.【期刊名称】《中北大学学报（自然科学版）》【年(卷),期】2016(037)006【总页数】5页(P576-580)【关键词】Kirchhoff型方程;双临界非线性项;山路引理;正解【作者】宋雅倩;张福伟;刘进生【作者单位】太原理工大学数学学院，山西太原 030024;太原理工大学数学学院，山西太原 030024;太原理工大学数学学院，山西太原 030024【正文语种】中文【中图分类】O175.2本文主要考虑以下双临界Kirchhoff型方程解的存在性. 其中常数a,b>0,2*= 6, 2*(s)=6-2s, s∈(0,1). 而其内积与范数分别为‖u‖.由于Kirchhoff型方程的重要性，近年来，很多学者研究了如下的Kirchhoff型问题[1-8]非平凡解的存在性. 同时，也有学者研究带有Sobolev临界指数的Kirchhoff 型方程[9-13]文献[14]运用山路引理证明了RN中双临界p-Laplace方程正弱解的存在性，其中常数受此启发,本文主要研究双临界Kirchhoff 型方程(1)正解的存在性. 主要结论为定理 1 对任意a,b>0,s∈(0,1), 方程(1)在D1,2(R3)中至少存在一个正解.在径向空间R3)={u∈D1,2(R3)|u(x)=u(|x|)}中考虑问题(1). 由文献[14]知故对任意的R3), 方程(1)对应的能量泛函‖‖有意义且R3),R).引理 1 能量泛函φ满足山路引理的几何条件. 即1) φ(0)=0，并且存在α,ρ>0，当‖u‖=ρ时，有φ(u)≥α>0.2) 存在R3)，满足‖e‖>ρ，并且φ(e)<0.证明 1) 显然φ(0)=0. 由Sobolev嵌入定理，令故‖‖‖‖u‖6-‖u‖2*(s),注意到2*(s)=6-2s, s∈(0,1)，从而存在α, ρ>0，当‖u‖=ρ时，有φ(u)≥α>0.2) 取定R3)， u>0, t>0，那么,从而存在充分大的t0>0，使得‖t0u‖>ρ且φ(t0u)<0. 令e=t0u，则‖e‖>ρ且φ(e)<0.由引理 1 知，存在序列{un}⊂R3)，使得φ(un)→c, φ′(un)→0，其中R3))|γ(0)=0,φ(γ(1))<0},即{un}是泛函φ的一个(PS)c序列.为了证明φ满足(PS)c条件，本文在引理2～引理8中研究了(PS)c序列的结构. 引理 2 若{un}为φ的(PS)c序列，则{un}有界.证明由于φ(un)→c, φ′(un)→0且4<2*(s)<6，则‖un‖2,故{un}有界.对任意的0<r<R，以下记引理 3 当2≤q<+∞时，紧嵌入到Lq(A).证明若由文献[15]知存在C1>0，使得所以连续嵌入L∞(A). 设序列{vn}在中有界，则在中vn⇀v，由于紧嵌入L2(A)，从而在L2(A)中vn→v，又C2∫A|vn-v|2→0,其中常数C2>0. 从而紧嵌入到Lq(A).引理 4 设{un}是φ的(PS)c序列，若在R3) 中un→0，则(un)2=0.证明因在R3)中un⇀0，所以在中un⇀0，而由引理3知紧嵌入到Lq(A)，其中2≤q<+∞. 又在A中有界，且2<2*(s)<+∞，故在L6(A)及L2*(s)(A)中un→0，从而令R3\{0})，满足η(x)=η(|x|)，0≤η ≤1且η|A=1. 任给n∈N，有R3). 由于‖un‖L2(Supp(η2))=0，故式中：C(η)为正常数[14].由引理2， {un}有界. 故由式(5)～式(8)得b∫R3|un|2∫R3|(η un)|2+o(1),从而‖η un‖2=o(1),故‖ηun‖2=0，即(un)2=0.对任意的δ>0，令,(un)2,由引理4可知，α,β,γ的取值与δ无关.引理 5 设{un}是φ的(PS)c序列，α,β,γ定义如上所述. 若在R3)中un⇀0，则).证明对于任意δ>0，令R3)满足η(x)=η(|x|), 0≤η≤1且η|Bδ(0)=1. 由于‖ηun‖2，由引理 4 可得|un|2+o(1).令n→∞，得同理可证.由于R3)和结合引理4知a∫Bδ(0)|un|2+b∫R3|un|2∫Bδ(0)|un|2-,从而,由α,β,γ定义可知αγ≤α+β. 于是结论成立.命题1 设{un}是φ的任意一个(PS)c序列，若在R3)中un⇀0，则对任意的δ>0，都存在ε0>0，使得或证明假设任给ε>0，存在α, β满足0<α<ε, 0<β<ε. 由于2*(s)>4，故从而存在满足故这与引理5矛盾. 故任给δ>0，存在ε0>0，使得α=β=0或α≥ε0. 由α的定义可知，或.引理 6 设{un}是φ的(PS)c序列，若在R3)中， un⇀0，则.证明用反证法. 假设由Hardy不等式，对任意的u∈D1,2(R3)有|u2|，所以D1,2(R3)连续嵌入到L2(R3,|x|-2)，由于{un}有界，由Hölder不等式及Hardy不等式得,所以‖‖un‖4+o(1).从而c≤0，这与c>0矛盾. 故引理 7 设{un}是φ的(PS)c序列，若在R3)中un⇀0，则有在命题1中已给出)，对任意的ε∈(0,ε1)，存在{rn}，使得R3)，且也为φ的(PS)c序列，同时对任意n∈N，有ε.证明令由引理6知λ>0. 令取ε∈(0,ε1)，则任给n∈N，存在rn>0，使得ε. 令即得ε.引理在R3)中的弱极限.证明因在R3)中有界，则在R3)中⇀若由命题1知或,这与引理7矛盾.定理1的证明首先证明设B∈R3满足∫R3||2→B2. 由引理8知则∫R3||2≤B2. 假设∫R3||2<B2，由于则对于任给φR3)，,φ〉=∫R3aφ+bB2∫R3φφ.所以|||2+bB2∫R3|,即又易知当t>0充分小时，因此存在t*∈(0,1)，满足易见从而|<|,矛盾. 故∫R3|||2，即又由于b∫R3||2∫R3‖‖2)‖‖2,从而‖‖2=0，即再由强极值原理得最后由对称临界原理可知，也是泛函φ在D1,2(R3)中的临界点，所以方程 (1)在D1,2(R3) 中存在正解.【相关文献】[1]Sun J J, Tang C L. Resonance problems for Kirchhoff type equations[J]. Discrete and Continous Dynamical Sys., 2013(5): 2139-2154.[2]Cheng B T. New existence and multiplicity of nontrivial solutions for nonlocal elliptic Kirchhoff type problems[J]. J. Math. Anal. Appl., 2012, 394: 488-495.[3]Cheng B T, Wu X. Existence results of positive solutions of Krichhoff problems[J]. NonlinearAnal., 2009(71): 4883-4892.[4]Yang Y, Zhang J H. Nontrivial solutions of a class of nonlocal problems via local linking theory[J]. J. Appl. Math. Lett., 2010(23): 377-380.[5]Sun J, Liu S B. Nontrivial solutions of Kirchhoff type problems[J]. J. Applied Mathematics Letters, 2012, 25: 500-504.[6]Li Y H, Li F Y, Shi J P. Existence of a positive solution to Kirchhoff type problems without compactness conditions[J]. J. Differential Equations, 2012, 253: 2285-2294.[7]Liang Z P, Li F Y, Shi J P. Positive solutions to Kirchhoff type equations with nonlinearity having prescribed asym ptotic behavior[J]. Ann. I. H. Poincaré-AN, 2014, 31(1): 155-167. [8]He X M, Zou W M. Existence and concentration behavior of positive solutions for a Kirchhoff equation in R3[J]. J. Differential Equations, 2012, 252: 1813-1834.[9]Li G B, Ye H Y. Existence of positive solutions for nonlinear Kirchhoff type problems in R3 with critical Sobolev exponent[J]. Mathematical Methods in the Applied Sciences, 2014, 37(16): 2570-2584.[10]Figueiredo G M. Existence of a positive solution for a Kirchhoff problem type with critical growth via truncation argument[J]. J. Math. Anal. Appl., 2013, 401: 706-713. [11]Xu J X, Zhang F B. Multiplicity and concentration of positive solutions for a Kirchhoff type problem with critical growth[J]. J. Differential Equ., 2012(253): 2314-2351.[12]Brezis H, Nirenberg L. Positive solutions of nonlinear elliptic problems involvingcritical Sobolev exponent[J]. Comm. Pure Appl. Math., 1983, 36: 437-477.[13]Alves C O, Correa F J S A, Figueiredo G M. On a class of nonlocal elliptic problems with critical growth[J]. Differ Equ. Appl., 2012(2): 409-417.[14]Roberta F, Patrizia P, Ferdric R. On a p-Laplace equation with multiple critical nonlinearities[J]. Journal De Mathematiques Purest Appliquees, 2009, 91: 156-177. [15]Badiale M, Serra E. Semilinear elliptic equations for beginners[J]. Springer London, 2011: 226.。

带有临界项的Choquard方程的基态解

带有临界项的Choquard方程的基态解龙雷;黄永艳【摘要】考虑了一类带有临界项的Choquard方程.首先通过山路定理和集中紧性理论得到了非平凡解的存在性,然后证明了基态解的存在性.【期刊名称】《重庆理工大学学报（自然科学版）》【年(卷),期】2019(033)005【总页数】5页(P213-217)【关键词】Choquard方程;临界项;基态解【作者】龙雷;黄永艳【作者单位】山西大学数学科学学院,太原030006;山西大学数学科学学院,太原030006【正文语种】中文【中图分类】O177.91本文主要考虑下面的Choquard方程[1-9]：-Δu+u=λ(Iα*|u|p)|u|p-2u+|u|2*-2u, x∈RN(1)其中:N≥3;α∈(0,N);λ>0;p是介于上下临界之间且不包含上下临界的数，上临界是指(N+α)/(N-2)，下临界是指(N+α)/N。

Iα是一个Riesz势函数，即若λ=1，且没有临界项，方程(1)是Choquard-Pekar方程：-Δu+u=(Iα*|u|p)|u|p-2ux∈RN(2)当N=3,α=2,p=2时，方程(2)描述了带电粒子与未知电磁场之间的相互作用，在天体力学、量子力学、统计物理学中都有广泛的应用，可参考文献[4，9]。

Lieb [1]和Lion [2]最早证明了方程(2)非平凡解的存在性。

目前，已经有一系列关于Choquard-Pekar方程的结果，可参考文献[5]。

Seok [3]用扰动理论证明了下面Choquard方程径向对称解的存在性：-Δu+u=(Iα*|u|p)|u|p-2u+λ|u|2*-2u其中x∈RN。

最近，Schaftingen等[6]证明了当非线性项 f(x,u)=f(u)满足一定条件时，下面Choquard方程基态解的存在性：-Δu+u=(Iα*|u|(N+α)/N)|u|(α-N)/Nu+f(x,u)x∈RN受上述结果的启发，本文研究当λ≥λ0时，Choquard方程(1)基态解的存在性。

【国家自然科学基金】_椭圆问题_基金支持热词逐年推荐_【万方软件创新助手】_20140730

107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160
科研热词推荐指数椭圆曲线 13 椭圆曲线密码体制 4 椭圆方程 4 有限元 4 临界指数 4 应力强度因子 3 存在性 3 二阶椭圆问题 3 非协调元 2 能量正交形函数空间 2 秘密共享 2 正解 2 椭圆外区域 2 收敛性 2 形式群 2 弹流润滑 2 弱解 2 密钥托管 2 密码学 2 奇异椭圆方程 2 代理签名 2 sobolev-hardy不等式 2 jacobi椭圆函数 2 helmholtz方程 2 高阶辅助方程 1 高速列车 1 高级加密标准 1 驱动力 1 饱和执行器 1 风浪 1 预计算表法 1 非线性椭圆随机偏微分方程 1 非线性椭圆方程 1 非平面 1 非局部问题 1 非分歧扩域 1 静态与动态分析 1 集中紧性原理 1 集中紧性 1 随机稳定性 1 间隙 1 门限方案 1 门限密码 1 锥形齿 1 边界识别 1 边界元法 1 边界元 1 辐射方向图 1 轮对 1 车辆/轨道耦合动力学 1 车轮椭圆化 1 跳变系统 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106

sobolev不等式证明

sobolev不等式证明Sobolev不等式是数学中的一种重要的不等式，它在偏微分方程、函数空间、概率论等领域中都有广泛的应用。

本文将详细介绍Sobolev不等式的定义、证明和应用。

一、Sobolev不等式的定义Sobolev不等式是指对于任意一个充分光滑的函数$f(x)$，都存在一个常数$C$，使得下面的不等式成立：$$\|f\|_{L^p(\mathbb{R}^n)} \leq C\|\nablaf\|_{L^q(\mathbb{R}^n)}$$其中$p>1$，$q$是$p$的共轭指数，即$\frac{1}{p}+\frac{1}{q}=1$。

$\|\cdot\|_{L^p}$和$\|\cdot\|_{L^q}$分别表示$L^p$和$L^q$范数。

二、证明为了证明Sobolev不等式，我们需要先引入一个引理：引理：对于任意一个充分光滑的函数$f(x)$，有如下估计：$$|f(x)| \leq C\left(\int_{\mathbb{R}^n} |\nablaf(y)|^2dy\right)^{\frac{1}{2}}$$其中$C$是一个与$f(x)$无关的常数。

证明：由Cauchy-Schwarz不等式可得：$$|f(x)| = \left|\int_{\mathbb{R}^n} f(x)\frac{\nabla f(y)}{\|\nabla f(y)\|}\cdot\frac{\nabla f(y)}{\|\nabla f(y)\|}dy\right|$$再利用Holder不等式，得到：$$|f(x)| \leq \left(\int_{\mathbb{R}^n} |\nablaf(y)|^2dy\right)^{\frac{1}{2}} \left(\int_{\mathbb{R}^n}|f(x)|^2\frac{1}{\|\nabla f(y)\|^2}dy\right)^{\frac{1}{2}}$$因为$\|\cdot\|$是$L^p$范数，所以$\frac{1}{p}+\frac{1}{q}=1$。

无界域上带Hardy项和临界非线_省略_项的半线性椭圆问题的全局紧性结果_金玲玉

中国科学A辑:数学2009年第39卷第7期:840∼854 无界域上带Hardy项和临界非线性项的半线性椭圆问题的全局紧性结果金玲玉①,邓引斌②∗①华南农业大学理学院,广州510642②华中师范大学数学系,武汉430079E-mail:ybdeng@收稿日期:2008-01-10;接受日期:2009-01-06;*通信作者国家自然科学基金(批准号:10631030,10871075)、中国教育部博士专项基金(批准号:20060511001)和华南农业大学校长基金(批准号:4900-k07418)资助项目摘要本文讨论了下面一类带Hardy项和临界非线性项的半线性椭圆问题:−Δu−μu2∗−2u+k(x)|u|q−2u,|x|2+a(x)u=|u|(∗)u∈H1(R N)的全局紧性结果及其正解的存在性,其中2∗=2N/(N−2)是临界的Sobolev指标,2<q< 2∗,0 μ<¯μ (N−2)2/4,a(x),k(x)∈C(R N).通过对问题(∗)所对应的能量泛函进行紧性分析,在a(x)和k(x)满足一定条件下,得到了此问题正解的存在性.关键词椭圆方程紧性正解无界域MSC(2000)主题分类35J10,35J20,35J601引言考虑如下非线性椭圆问题:−Δu−μu2∗−2u+k(x)|u|q−2u,|x|2+a(x)u=|u|(1)u∈H1(R N),其中2∗=2N/(N−2)是临界Sobolev指数,0 μ<¯μ (N−2)2/4,2<q<2∗,且a(x),k(x)∈C(R N).众所周知,在研究R N上含临界指标的半线性椭圆问题正解的存在性时,必须克服由R N 的平移不变性和临界Sobolev指数所引起的升缩平移不变性带来的困难.实际上,这些不变性使得Sobolev嵌入失去紧性,所以标准的变分方法不能直接应用.为了克服这些困难,人们通常采用非紧性分析方法,具体找出问题中非紧性因素(导致Sobolev嵌入失去紧性的因素),然后通过逐一排除这些因素,得到对应问题正解的存在性.引用格式:金玲玉,邓引斌.无界域上带Hardy项和临界非线性项的半线性椭圆问题的全局紧性结果.中国科学A, 2009,39(7):840–854Jin L Y,Deng Y B.A global compact result for a semilinear elliptic problem with Hardy potential andcritical nonlinearities on R N.Sci China Ser A,2009,52,DOI:10.1007/s11425-009-0075-x中国科学A 辑:数学第39卷第7期早在上世纪80年代,Struwe [1]和Lions [2]讨论了一类带临界Sobolev 非线性项的椭圆问题,得到了问题在有界域上的全局紧性结果.Br´e zis 和Nirenberg [3]通过验证方程的能量泛函小于某个能量水平,得到了一类带临界Sobolev 非线性项的椭圆问题正解的存在性.1995年,Pierrotti 和Terracini [4]通过紧性分析方法,讨论了一类带Neumann 边值条件和临界非线性项的椭圆问题.2003年,Cao 和Peng [5]讨论一类带临界非线性项和Hardy 项的椭圆问题,得到了问题的全局紧性结果,并阐述了由问题中的Hardy 项导致的一些新的爆破(blow up)现象.近二十年来,无界域上的椭圆问题也是人们讨论的焦点.例如Lions [2,6]对于R N 上的某些非线性椭圆方程以及对应的一些极小化问题建立了集中紧性原理.Benci 和Cerami [7]讨论了无界域上一类带次临界指标的椭圆问题,得到了问题的全局紧性结果.Zhu 和Cao 在文献[8]中也得到了一些类似的结果.最近Smets [9]研究了下面问题:−Δu −μu |x |2=K (x )u 2∗−1,u >0,u ∈D 1,2(R N),(2)其中2∗=2NN −2,K (x )满足一定条件.Smets 在文献[9]中建立了问题(2)的一个全局紧性结果,并通过这一紧性结果得到了该问题解的存在性.在建立该紧性结果时,问题(2)所对应的变分泛函的任意一个PS 序列{u n }的定义域被分为两部分,一部分限制在球B (R )上,另一部份限制在R N \B (R )上.限制在球内的序列{u n }可以认为是紧的(集中紧性原理的情形之一).而在球外部分可通过Kelvin 变换转化到球内来.在这里,Kelvin 变换能成功的应用是由于问题(2)的右边仅含临界非线性项.本文建立了问题(1)所对应的变分泛函的PS 序列的一个全局紧性结果,通过这个紧性结果,得到了问题(1)正解的存在性.由于问题(1)在无穷远处的极限方程存在正解,这使得该问题中出现了除Hardy 项和临界Sobolev 指标外的第三种非紧性因素,所以不能应用Kelvin 变换.同时这三种非紧性因素在处理的时候会互相影响,这进一步增加了问题的难度.本文中采用的主要方法和技巧参见文献[1,2,5,6,8,9].为表达方便,这里先给出一些记号和假设.记H 1(R N )为标准的Sobolev 空间且范数为u H 1(R N )= R N(|∇u |2+|u |2)dx 1/2,定义D 1,2(R N )={u ∈L 2loc (R N );∇u ∈L 2(R N )},且范数为 u D 1,2(R N )=(R N |∇u |2dx )1/2.设B (x,r )为以x 为心,r 为半径的球,B (x,r )C 表示集合B (x,r )的补集.本文一致假定a (x ),k (x )满足如下条件:(a)0 a (x )∈C (R N ),0 k (x )∈C (R N );(b)lim |x |→∞a (x )=¯a>0,inf x ∈R N a (x )=ˆa >0,lim |x |→∞k (x )=¯k >0.设问题(1)所对应的能量泛函为I (u )=12 R N |∇u |2−μu 2|x |2+a (x )u 2 dx −12∗R N |u |2∗dx −1q R Nk (x )|u |q dx,u ∈H 1(R N ).841金玲玉等:无界域上带Hardy 项和临界非线性项的半线性椭圆问题的全局紧性结果问题(1)在无穷远处的极限方程为:−Δu +¯a u =|u |2∗−2u +¯k|u |q −2u,u ∈H 1(R N),(3)对应的变分泛函为I ∞=12 R N (|∇u |2+¯a |u |2)dx −12∗ R N |u |2∗dx −1q R N¯k|u |q dx,u ∈H 1(R N );问题(1)含Hardy 项和临界Sobolev 项的极限方程为:−Δu −μu |x |2=|u |2∗−2u,u ∈D 1,2(R N ),(4)对应的变分泛函为I μ=12 R N |∇u |2−μ|u |2|x |2 dx −12∗ R N|u |2∗dx,u ∈D 1,2(R N );问题(1)仅含临界Sobolev 项的极限方程为:−Δu =|u |2∗−2u,u ∈D1,2(R N),(5)对应的变分泛函为I 0=12R N|∇u |2dx −12∗R N|u |2∗dx,u ∈D 1,2(R N ).众所周知,方程(5)的正解集合可如下表示:Uε,y(x ):=ε(2−N )/2U 0x −yε,其中U 0(x ):=c (N )(1+|x |2)2−N 2,c (N )>0是某个常数,且这些解是下面最佳常数S =inf u ∈D 1,2(R N )\{0} R N |∇u |2dx ( R N |u |2∗dx )2/2∗的可达函数.这里S 的具体值参见文献[10].当0<μ<¯μ时,Terracini [11]证明了问题(4)的所有正解可以表示为U εμ(x ):=ε2−N 2U μ x ε,其中U μ(x ):=c μ(N )1|x |√¯μ−β(1+|x |2β√¯μ)N −22,c μ(N )>0为某个适当的常数,β:=√¯μ−μ,且这些解为极小问题S μ=infu ∈D 1,2(R N )\{0} R N (|∇u |2−μu 2|x |2)dx ( R N |u |2∗dx )2/2∗的达到函数.显然,S μ关于参数μ递减且lim μ→¯μS μ=0.为方便起见,定义D 0:=R N12|∇U 0|2−12∗U 2∗0 dx =1N S N/2,D μ:= R N12|∇U μ|2−μ2U 2μ|x |2−12∗U 2∗μ dx =1N S N/2μ.定义N = u ∈H 1(R N )\{0} RN(|∇u |2+¯a |u |2−|u |2∗−¯k |u |q )dx =0,842中国科学A 辑:数学第39卷第7期J ∞=inf u ∈NI ∞(u ).当N 4时,问题(3)至少有一个正解(参见文献[12]);当N =3时,4<q <6=2∗,问题(3)也至少存在一个正解.因此N =∅.本文的主要结果可归结为下面定理:定理1.1假定a (x ),k (x )满足条件(a)和(b),且当N =3时,4<q <6,而当N 4时2<q <2∗.设{u n }是问题(1)所对应的能量泛函I (u )在水平值d 0处的正的PS 序列,则存在非负整数l 1,l 2,l 3和l 1个序列{R jn}⊂R +(1 j l 1),2l 2个序列{r j n }⊂R +,{x j n }⊂R N \{0}(1 j l 2),l 3个序列{y j n }⊂R N(1 j l 3)以及函数0 u ∈H 1(R N ),0<u j ∈H 1(R N )(1 j l 3)使得•I (u )=0,I ∞ (u j )=0(1 j l 3);•当n →∞时,R jn →0或者∞(1 j l 1);•当n →∞时,x j n →x j ∈R N {∞},r jn →0或者∞且r j n |x j n|→0(1 j l 2);•当n →∞时,|y jn |→∞(1 j l 3);•d =I (u )+l 1D μ+l 2D 0+ l 3i =1I ∞(u i);•当n →∞时,u n −u −l 1 j =1U R j n μϕ1−l 2 j =1U r j n ,x jn 0ϕ2−l 3j =1u j (x −y j n ) H 1(R N )=o (1);(6)其中ϕ∈C ∞0(R N )满足0 ϕ 1,|∇ϕ| 2,当x ∈B (0,1)时ϕ≡1,当x ∈B (0,2)c 时ϕ≡0且ϕ1= 1,如果R jn→∞(n →∞),ϕ,如果R jn →0(n →∞),(1 j l 1)ϕ2= 1,如果r j n →∞(n →∞),ϕ,如果r jn →0(n →∞).(1 j l 2)特别地,如果u ≡0,则u 是问题(1)的非负解,且当l i =0(i =1,2,3)时,(6)中对应的总和应为零.注记(i)由于问题(3)的所有解都是径向解(参见文献[13]),并且问题(3)的径向解是唯一的(参见文献[14,15]).因此有I ∞(u j )=J ∞.(ii)类似于文献[9]中的推论3.3可得如下结论:对于I (u )的任意一个PS 序列,如果此序列的能量水平不能写成m 1D μ+m 2D 0+m 3J ∞,m 1,m 2,m 3∈N ∪{0}的形式,则问题(1)存在一个非零解.(iii)如果定理1.1中的PS 序列{u n }是变号的,也可以得到一个类似的定理.但是到目前为止还不能得到极限方程(4)和(5)的变号解的具体形式,所以这个定理没有多大的意义.同样对于情形μ<0,用类似的方法也可得到类似定理.(iv)(6)式中的截断函数ϕ1,ϕ2是为了保证U R jn μϕ1,U r j n,x j n0ϕ2∈L 2(R N ),显然,当N 4时,ϕ1,ϕ2的作用尤其重要.另外,在处理变号的PS 序列时,由于不知道方程(4)和(5)变号解的具体形式,不能轻易的决定变号解是否属于L 2(R N ),所以截断函数也必不可少.(v)此非紧性分析证明了任何爆破的PS 序列(弱收敛而不强收敛的序列)中有以下三843金玲玉等:无界域上带Hardy 项和临界非线性项的半线性椭圆问题的全局紧性结果种爆破因素:U εn ,y n 0(x ),且|y n |εn →∞,或者U εn ,y nμ(x )且|y n |εn→0(n →∞),或者u (x −y n )∈H 1(R N ),且|y n |→∞(n →∞),其中u 是问题(3)的解.利用上面的紧性结果和山路定理[16]可得如下推论:推论1.2假定max {2,N√¯μ+β,N −2β√¯μ}<q <2∗,a (x )和k (x )满足条件(a)和(b),此外¯a a (x ),k (x ) ¯k >0,k (x )≡¯k.(7)则问题(1)存在非零的解u ∈H 1(R N )且满足I (u )<min {1N S N/2μ,J ∞}.2一些预备的引理为了证明本文的主要结论,下面给出几个预备引理(其中一些引理的证明可参见对应的参考文献).引理2.1[8,引理2.1]设{ρn }n 1是L 1(R N )中序列且满足:ρn 0,lim n →∞R Nρn dx =λ>0,(8)其中λ>0是固定的常数.则存在子序列{ρn k }满足下面条件之一:(i)(消失):对于R <+∞,lim k →∞sup y ∈R Ny +B Rρn k (x )dx =0.(9)(ii)(不消失):∃α>0,R <+∞,{y k }⊂R N 使得lim k →+∞y k +B Rρn k (x )dx α>0.引理2.2[8,引理2.3]设1<p ∞,1 q <∞,且当p <N 时,q =NpN −p.假设u n 在L q (R N )中有界,∇u n 在L p (R N )中有界且当n →∞时sup y ∈R Ny +B R|u n |q dx →0,则u n →0于L α(R N ),这里α是介于q 和NpN −p之间的常数.引理2.3[9,引理2.3]设Ω是R N 中含零点的有界邻域,0<μ<(N −2)24,V ∈L N/2(Ω)且g ∈L s (Ω),s 2.若u ∈H 10(Ω)是−Δu −μu|x |2−V (x )u +νu =g 的一个弱解,这里ν是一个使线性算子的左边为正算子的常数,则有u ∈ p<p limL p loc (Ω),其中p lim =mins 2,2∗1− 1−4μ(N −2)2.引理2.4设u 为方程(1)的任意解,则u ∈p<p lim L p loc (R N),其中p lim =2∗1− 1−4μ(N −2)2.844中国科学A 辑:数学第39卷第7期证明对于0<R <∞,设φ∈C ∞0(B (R ))为截断函数且 φ ∞=1,当x ∈B (R/2)时,φ≡1.令g (x )=−2∇u ∇ϕ−u Δϕ+νw ,V (x )=|u |2∗−2+k (x )|u |q −2−a (x ).定义w =uφ则−Δw −μw|x |2−V (x )w +νw =g (x ).(10)由u ∈H 1(R N )可得|u |2∗−2,|u |q ∈L N/2(B (R )).(11)根据条件(a)、(b)和(11)可得V (x )∈L N/2(B (R )).利用Br´e zis-Kato 定理和椭圆正则理论,有u ∈W 2,p (B (R )\{0})且p <∞,因此w ∈C 1(B (R )\{0}).既然∇φ≡0于B (R/2),−2∇u ∇φ−u Δφ∈C 1(B (R ))并且g 的L p 正则性取决于w ,所以从g ∈L 2出发,重复使用引理2.3可提高w 的正则性,g 的正则性也随之不断地提高.依此下去,可以完成引理2.4的证明.引理2.5设{u n }是I 的PS 序列且能量水平为d ∈R ,则d 0且{u n }是H 1(R N )中有界序列.此外,I 的任一水平为0的PS 序列强收敛于0.证明由Hardy 不等式[17],a (x ) 0,¯a >0,inf R N a (x )=ˆa >0,可得RN|∇u n |2+a (x )|u n |2−μu 2n |x |2 dx c u n 2H 1(R N ),因此d +1+o ( u n ) I (u n )−1qI (u n ),u n= 12−1q R N |∇u n |2+a (x )|u n |2−μ|u n|2|x |2 dx + 1q −12∗R N|u n |2∗dxC u n 2H 1(R N ),所以{u n }在H 1(R N )中有界.由d =lim n →∞I (u n )−1q I (u n ),u n C lim sup n →∞u n 2H 1(R N ),所以d 0.假设d =0,由上面的不等式可得lim n →∞u n H 1(R N )=0.设{u n }是I 的PS 序列.至多取子列(仍记为{u n })有u n u 0弱收敛于H 1(R N )(n →∞).从而可导出I (u 0)=0.令v n =u n −u 0,则v n 0弱收敛于H 1(R N )(n →∞).引理2.6{v n }是I 的PS 序列且水平为d 0=d −I (u 0).证明根据Brizis-Lieb 引理[18]和序列的弱收敛性,当n →∞时,可得RN |v n |q dx =R N |u n |q dx − R N|u 0|q dx +o (1),2 q 2∗;(12) R N (|∇v n |2+|v n |2)dx = R N (|∇u n |2+|u n |2)dx − R N(|∇u 0|2+|u 0|2)dx +o (1);(13)R N |v n |2|x |2dx = R N |u n |2|x |2dx − R N |u 0|2|x |2dx +o (1).(14)845金玲玉等:无界域上带Hardy 项和临界非线性项的半线性椭圆问题的全局紧性结果因此I (v n )=I (u n )−I (u 0)+o (1)=d −I (u 0)+o (1).另一方面,由于||u n |2∗−2u n −|u 0|2∗−2u 0−|u n −u 0|2∗−2(u n −u 0)| c ||u n −u 0|2∗−2u 0+|u 0|2∗−2(u n −u 0)|,根据引理2.4可得u 0∈p<p limL p loc (R N),p lim =2∗1− 1−4μ(N −2)2.因此对于任一试验函数v ∈C ∞0(R N ),RN |v n|2∗−2v n v −|u n |2∗−2u n v +|u 0|2∗−2u 0vdx cR N(|v n |2∗−2|u 0|+|u 0|2∗−2|v n |)|v |dxc v 2∗( u 0 L p loc (R N )v n 2∗−2L ploc (R N )+ u 0 2∗−2L p loc(R N ) v n L p loc(R N ))=o (1)(n →∞),(15)其中1p+2∗−2p+12∗=1,1p+2∗−2p+12∗=1,2∗<p <p lim .则R N|v n |2∗−2v n vdx =R N|u n |2∗−2u n vdx −R N|u 0|2∗−2u 0vdx +o (1)(n →∞).(16)类似可得R N|v n |q −2v n vdx =R N|u n |q −2u n vdx −R N|u 0|q −2u 0vdx +o (1)(n →∞).(17)由于lim |x |→∞k (x )=¯k,所以∀ε>0充分小,存在常数M 0>0使得|k (x )−¯k|<ε,∀|x |>M 0.(18)根据(17)和(18)我们导出RN k (x )(|v n |q −2v n v −|u n |q −2u n v +|u 0|q −2u 0v )dx R N (k (x )−¯k )(|v n |q −2v n v −|u n |q −2u n v +|u 0|q −2u 0v )dx+ R N ¯k (|v n |q −2v n v −|u n |q −2u n v +|u 0|q −2u 0v )dx|x |<M 0(k (x )−¯k )(|v n |q −2v n v −|u n |q −2u n v +|u 0|q −2u 0v )dx+ |x |>M 0(k (x )−¯k )(|v n |q −2v n v −|u n |q −2u n v +|u 0|q −2u 0v )dx+o (1) cR N(|v n |q −2v n v −|u n |q −2u n v +|u 0|q −2u 0v )dx +o (1)=o (1)(n →∞).(19)由弱收敛性可得,当n →∞时, RN v n v |x |2dx = R N u n v |x |2dx −RN u 0v|x |2dx +o (1),(20) R N∇v n ∇vdx = R N∇u n ∇vdx − R N∇u 0∇vdx +o (1).(21)因此当n →∞时, v,I (v n ) = v,I (u n ) − v,I (u 0) =o (1).846中国科学A 辑:数学第39卷第7期引理2.7设{v n }⊂H 1(R N )是泛函I 水平为d 的PS 序列且v n 0(n →∞)弱收敛于H 1(R N ).如果存在序列r n ⊂R +,r n →0(n →∞)使得¯v n (x ):=r N −22n v n (r n x ) v 0弱收敛于D 1,2(R N ),¯vn (x )→v 0几乎处处于R N 且v 0≡0,则v 0是(4)的解且z n :=v n −v 0(x r n)r 2−N2n ϕ是I 水平为d −I μ(v 0)的PS 序列,其中ϕ∈C ∞0(R N )且0 ϕ 1,|∇ϕ| 2,当x ∈B (0,1)时,ϕ≡1;当x ∈B (0,2)C 时,ϕ≡0.证明首先证明v 0是问题(4)的解且I (z n )=I (v n )−I μ(v 0).固定球B (0,r ),任取试验函数φ∈C ∞(B (0,r ))可得, φ,I μ(v 0) =R N ∇v 0∇φdx − R N |v 0|2∗−2v 0φdx −R Nμv 0φ|x |2dx = R N ∇¯v n ∇φdx − R N |¯v n |2∗−2¯v n φdx −R Nμ¯v n φ|x |2dx+r n 2R N a (r n x )φ¯v n dx −r N −N −22qn RN k (r n x )φ|¯v n |q −2¯v n dx +o (1)= R N ∇v n ∇φn dx − R N |v n |2∗−2v n φn dx −RN μv n φn|x |2dx +R Na (x )φn v n dx − R Nk (x )φn |v n |q −2v n dx +o (1)=o (1)(n →∞),其中φn (x )=r 2−N2n φ(x/r n ).由于当n →∞时, ∇φ 2= φn H 1(R N )+o (1),所以v 0是问题(4)的解.设ϕ∈C ∞0(R N )满足0 ϕ 1和|∇ϕ| 2,且当x ∈B (0,1)时,ϕ≡1,当x ∈B (0,2)C 时,ϕ≡0.令z n (x )=v n (x )−r 2−N 2n v 0 xr nϕ(x )∈H 1(R N ),则¯z n =r N −22nz n (r n x )=¯v n −v 0(x )ϕ(xr n ).显然z n 0弱收敛于H 1(R N )(n →∞).以下证明{z n }是I 水平为d −I μ(v 0)的PS 序列.令ϕn (x )=ϕ(r n x ).注意到|∇v 0|∈L 2(R N ),因此当n →∞时,R N|∇v 0(ϕn −1)|2dx 2 R N |∇v 0|2(ϕn −1)2dx +2R N |v 0|2|∇(ϕn −1)|2dx2 R N \B (0,r −1n )|∇v 0|2dx +8r 2nB (0,2r −1n )\B (0,r −1n )|v 0|2dx2R N \B (0,r −1n )|∇v 0|2dx +8 cB (0,2r −1n )\B (0,r −1n )|v 0|2∗dx2/2∗=o (1).(22)易见,R N|v 0|2(1−ϕ2n )|x |2dx{|x | 1r n}|v 0|2|x |2dx c{|x | 1r n}|∇v 0|2dx =o (1)(n →∞).(23)由于当n →∞时,v 0xr nr 2−N 2n ϕ 0弱收敛于H 1(B (0,2)),847金玲玉等:无界域上带Hardy项和临界非线性项的半线性椭圆问题的全局紧性结果所以v0xr nr2−N2nϕ→0于L p(B(0,2))(n→∞),1 p<2∗.(24)根据Br´e zis-Lieb引理和(22)–(24)式可得I(z n)=I(v n)−Iμ(v0).由z n 0弱收敛于H1(R N)可得 I (z n),φ =o(1)(n→∞).证毕.3非紧性分析本节将借助于集中紧性原理,对泛函I的PS序列进行精细的分析,进而完成定理1.1的证明.定理1.1的证明设{u n}是泛函I的一个PS序列,由引理2.5可得{u n}是有界的.当n→∞时,至多取子列(仍记为{u n})有,u n u弱收敛于H1(R N),u n→u强收敛于L p loc(R N),1 p<2∗,u n→u几乎处处于R N.令v n=u n−u.根据引理2.6可得{v n}是I的PS序列,且当n→∞时,v n 0弱收敛于H1(R N),I(v n)=I(u n)−I(u)+o(1),(25)I (v n)=I (u n)−I (u)+o(1)(n→∞),(26)v n H1(R N)= u n H1(R N)− u H1(R N)+o(1)(n→∞).(27)如果 v n 2H1(R N)→0(n→∞),由(25)–(27)式,定理1.1证毕(此时只需取l1=l2=l3=0).不失一般性可设当n→∞时, v n 2H1(R N)→l>0.情形a v n L2(R N)→0(n→∞).首先我们断言:如果 v n L2(R N)→0,则对于所有的q∈[2,2∗)都有 v n L q(R N)→0.事实上,由v n∈L2(R N)∩L2∗(R N),根据L p-范数的插值不等式有v n∈L r(R N)且v n L r(R N) v n θL2(R N) v n 1−θL2∗(R N),(28)其中1r=θ2+1−θ2∗,0<θ<1.并且由2<q<2∗,存在常数θq∈(0,1)使得1q=θq2+1−θq2∗.由{v n}在L2∗(R N)中有界,可得v n L q(R N) v n θL2(R N) v n 1−θL2∗(R N)c v n θL2(R N)=o(1)(n→∞).因此有I(v n)=Iμ(v n)+o(1),I (v n)=I μ(v n)+o(1)(n→∞).从而导出{v n}是泛函Iμ的PS序列.根据文献[9]中定理3.1,存在两个整数k,l和l个序列{R j n}⊂R+(1 j l),2k个序列{r j n}⊂R+,{x j n}⊂R N\{0}(1 j k)使得d=I(v n)+I(u)+o(1)=Iμ(v n)+I(u)+o(1)=lDμ+kD0+I(u)+o(1)(n→∞),(29)un−u−kj=1U r j n,x j n−lj=1U R j n,0μD1,2(R N)→0(n→∞),(30)848中国科学A 辑:数学第39卷第7期其中R j n →0或者∞(1 j l ),x j n →x j ∈RN{∞}和r jn |x j n |→0(1 j k ).根据文献[9]中定理3.1,显然有r jn →0或者∞(n →∞)(1 j k ).如果r j n →0(1 j k )(n →∞),类似于引理2.7,可得R N|∇(U 0(ϕj n −1))|2dx =o (1)(1 j k )(n →∞),(31)其中ϕj n =ϕ(r jn (x +x j n )).如果R jn →0(1 j l )(n →∞),可得R N |(∇U μ(ϕj n −1))|2dx =o (1), RN |U μ|2(1−ϕj n )|x |2dx =o (1)(1 j l )(n →∞),(32)其中ϕj n =ϕ(R jn x ).如果R jn →∞(1 j l )(n →∞),则sup y ∈R NB (y,R )|∇U R j n μ|2+|U R j n μ|2dx =o (1)(n →∞),∀0<R <∞.(33)如果r jn →∞(1 j k )(n →∞),则sup y ∈R NB (y,R )|∇U r j n ,x j n 0|2+|U r j n ,x j n 0|2dx =o (1)(n →∞),∀0<R <∞.(34)由引理2.2可推出当n →∞时,R N|U R jn μ|2dx =o (1),R N|U r j n,x j n 0|2dx =o (1).(35)现在由(30)–(32)和(35)式,可得对于l 1=l,l 2=k,l 3=0,表达式(6)成立.情形b当n →∞时,v n L 2(R N )→a >0.(36)根据引理2.1,存在子列仍记为{v n }使得下面两种情形之一成立.(i)消失.根据引理2.1可得,当n →∞时,sup y ∈R Ny +B R(|∇v n |2+|v n |2)dx →0,∀0<R <∞,根据Sobolev 不等式和引理2.2可得,当n →∞时,R N|v n |p dx →0,∀1<p <2∗,这与(36)式矛盾.所以消失不可能发生.(ii)不消失.根据引理2.1,存在α>0,0<¯R<∞,{y n }⊂R N 使得lim inf n →∞y n +B ¯R (|∇v n |2+|v n |2)dx α>0.(37)不失一般性选取序列|y n |→∞(n →∞).否则,{v n }是紧的,且 v n L 2(R N )→0(n →∞).这与(36)式矛盾.下面假设|y n |→∞(n →∞).第1步除去Hardy 项引起的爆破.如果存在0<δ<∞使得对于某个R ∈(0,∞)有{|x |<R }v 2n|x |2dx δ>0.(38)849根据Hardy 不等式可得{|x |<R }|∇v n |2−μv 2n|x |2dx (¯μ−μ)δ>0.于是对于充分小的δ1∈(0,(¯μ−μ)δ),存在r n ∈R +,使得 B (0,1/r n )|∇v n |2−μv 2n |x |2dx = B (0,1)|∇¯v n |2−μ¯v 2n |x |2dx =δ1,(39)其中¯v n =r N −22nv n (r n x ),δ1为待定常数.由于 ¯v n D 1,2(R N )= v n D 1,2(R N ),所以当n →∞时,至多取子列(仍记为¯v n )有¯v n v 0弱收敛于D 1,2(R N ),H 1loc (R N ),¯v n →v 0强收敛于L p loc (R N ),1 p <2∗.下面证明v 0≡0.否则若v 0=0,则对于任意的h ∈C ∞0(B (0,1)),当n →∞时可以导出R N |∇(¯v n h )|2dx = R N ∇¯v n ∇(h 2¯v n )dx + R N ¯v 2n |∇h |2dx =R N∇¯v n ∇(h 2¯v n )dx +o (1) I (v n ) h 2¯v n + R N μh 2¯v 2n |x |2dx + R N ¯v 2∗n h 2dx +o (1)(40) S −1 B (0,1)¯v 2∗n dx 2/N R N|∇(¯v n h )|2dx +4μ(N −2)2 R N |∇(¯v n h )|2dx +o (1),根据最佳常数S μ的定义和(39)式可得下面不等式B (0,1)|¯v n |2∗dx 2/2∗ S −1μ B (0,1)|∇¯v n |2−μ¯v 2n |x |2 dx =S −1μδ1.选取δ1满足S −1μδ1<[(1−4μ(N −2)2)S ](N −2)/2,则由(40)式,可选取某个τ∈(0,1)使得R N |∇(¯v n h )|2dx (1−τ) R N|∇(¯v n h )|2dx +o (1)(n −→∞).因此B (0,r )|∇¯v n |2dx =o (1),0<r <1.(41)由(41)式和Hardy 不等式可得, B (0,1)¯v 2n |x |2dx = B (0,r )¯v 2n |x |2dx + {r |x |<1}¯v 2n|x |2dx o (1)+1r 2{r |x |<1}¯v 2n dx =o (1)(n →∞).(42)显然(41)、(42)式与(38)、(39)式矛盾.由于v n 0于H 1(R N ),¯v n v 0≡0于H 1(R N ),可得r n →0(n →∞).定义z n =v n −v 0(x r n)r 2−N 2nϕ,根据引理2.7,可得z n 是I 的PS 序列且满足I (z n )=I (v n )−I μ(v 0)+o (1)(n →∞),(43)其中ϕ∈C ∞0(R N ),0 ϕ 1,|∇ϕ| 2且当x ∈B (0,1)时,ϕ≡1;当x ∈B (0,2)c 时,ϕ≡0.如果仍存在δ>0,使得 {|x |<R }z 2n|x |2dx δ>0,重复第1步的做法,显然这种循环一定在有限次停止.因此可得泛函I 一个新的PS 序列,不失一般性,仍记为{v n }且满足当n →∞时, {|x |<R }v 2n|x |2dx =o (1),∀R ∈(0,∞).(44)850第2步构造I ∞的PS 序列.令¯v n =v n (x +y n ).由于 ¯v n H 1(R N )= v n H 1(R N ) c ,故存在子列,仍记为{v n }使得当n →∞时,¯v n v 0弱收敛于H 1(R N ),¯v n →v 0强收敛于L p loc (R N ),1 p <2∗.∀φ∈C ∞0(R N ),根据(44)式可得R N ¯v n φ|x +y n |2dx = R N v n φn |x |2dx =|x |>R v n φn|x |2dx +o (1) 1R 2R N v 2n dx 1/2 R Nφ2n dx 1/2+o (1)(n →∞),其中φn =φ(x −y n ).令R →∞,则R N¯v n φ|x +y n |2dx =o (1).(45)类似地,可以证明R N¯v 2n|x +y n |2dx =o (1)(n →∞).(46)由于v n 0弱收敛于H 1(R N )且lim n →∞a (x +y n )=¯a ,因此当n →∞时,o (1)= R Na (x )v n φn dx = R N¯a ¯v n φdx +R N[a (x +y n )−¯a ]¯v n φdx,R N [a (x +y n )−¯a ]¯v n φdxcR N|a (x +y n )−¯a |2φ2dx 1/2=o (1),即R N¯a ¯v n φdx =o (1)=R Na (x )v n φn dx (n →∞).(47)同理可以证明R Nk (x )|v n |q −2v n φn dx =R N¯k |¯v n |q −2¯vn φdx =o (1)(n →∞).(48)由(45)–(48)式,可得{v n }是泛函I 的PS 序列,I (v n ),φn +o (1)= I ∞ (¯v n ),φ =o (1)(n →∞).(49)于是{¯v n }为I ∞(u )的一个非负的PS 序列,v 0是问题(3)的弱解.第3步证明v 0≡0.由(36)式可知存在序列{y n }满足(37)式且∃0<R <∞,B (y n ,R )|v n |2dx =c +o (1)>0(n →∞),(50)其中c ∈(0,a ]是一个常数.假设v 0=0,对于0<R <∞可得B (0,R )|¯v n|2dx =B (y n ,R )|v n |2dx =o (1)(n →∞),这与(50)式矛盾.事实上,我们还可以得到 v n L q (R N )→ν>0.否则,假设v n L q (R N )→0(n →∞),∀2<q <2∗.(51)851由于{¯v n}是I∞的PS序列,故由(51)式知v0是下面方程−Δu+¯a u=u2∗−1,u>0,u∈H1(R N)(52)的非负解.由Phozoaev不等式易证v0≡0.矛盾.第4步除去由无界域引起的无穷远处的爆破.令z n=¯v n−v0.由(46)式可得I(v n)=12R N(|∇v n|2+a(x)|v n|2)dx−μ2R Nv2n|x|2dx−12∗R N|v n|2∗dx−1qR Nk(x)|v n|q dx=12R N(|∇¯v n|2+a(x+y n)|¯v n|2)dx−μ2R N|¯v n|2|x+y n|2dx−12∗R N|¯v n|2∗dx−1qR Nk(x+y n)|¯v n|q dx=12R N(|∇¯v n|2+¯a|¯v n|2)dx−12∗R N|¯v n|2∗dx−1qR N¯k|¯v n|q dx+o(1)(n→∞).因此z n H1(R N)= ¯v n 2H1(R N)− v0 2H1(R N)+o(1)(n→∞),(53)I(z n)=I∞(¯v n)−I∞(v0)+o(1)=I(v n)−I∞(v0)+o(1)(n→∞).(54)所以z n 0弱收敛于H1(R N)(n→∞),且z n是泛函I的PS序列.若 z n L2(R N)→c> 0(n→∞),则重复第2步到第4步的做法.此循环过程一定在有限次后停止.现在我们得到了I的新的PS序列,不失一般性仍记为{v n},且v n L2(R N)→0(n→∞).因此回到了情形a且{v n}是Iμ的PS序列.重复有限次循环后,定理1.1证明完毕.推论1.2的证明由于I(tu)=t22R N|∇u|2−μu2|x|2dx+R Na(x)u2dx−|t|2∗2∗R N|u|2∗dx−|t|qqR Nk(x)|u|q dx,则对于某个固定的u∈H1(R N),u≡0,当t→∞时,I(tu)→−∞.而R N |u|q dx C u q H1(R N),R N|u|2∗dx C u 2∗H1(R N),则I(u) c u 2H1(R N)−C( u q H1(R N)+ u 2∗H1(R N)).故存在充分小的r0>0使得I(u)|∂B(0,r0)ρ>0.所以I(u)满足山路引理的几何条件.定义cμ=:infγ∈Γsupt∈[0,1]I(γ(t)),其中Γ={γ∈C([0,1],H1(R N)):γ(0)=0,γ(1)=ψ0∈H1(R N)}.选取ψ0使得∀t 1, I(tψ0) 0.852下面验证I (u )满足局部PS 条件.根据注解(ii)只需验证c μ<min1N S N/2,1N S N/2μ,J ∞=min 1NS N 2μ,J ∞ ,μ 0.(55)设ϕ(x )∈C ∞0(Ω)且当|x | R 时,ϕ(x )=1;当|x | 2R 时,ϕ(x )=0.令u ε(x )=ϕ(x )U εμ(x ),v ε(x )=u ε(R N|u ε|2∗dx )1/2∗.下证max t>0I (tv ε)<1N S N/2μ.(56)事实上,v ε(x )满足如下估计式[19]:R N|∇v ε|2−μv2ε|x |2 dx =S μ+O (ε2β);R N |v ε|2dx =⎧⎪⎪⎨⎪⎪⎩O (ε2),β>1,O (ε2β|log ε|),β=1,O (ε2β),β<1, R N |v ε|qdx =⎧⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎩O (εβq),q <N √¯μ+β,O (εβq |log ε|),q =N √¯μ+β,O (εN −√¯μq),q >N √¯μ+β.由于2∗>q >max {2,N√¯μ+β,N −2β√¯μ},则 R N|v ε|q dx =O (εN −√¯μq ),O (ε2)+O (ε2β)+O (ε2β|log ε|)=o (εN −√¯μq ).(57)设I (t εv ε)=max t>0I (tv ε),易证t ε是一致有界的[2].因此,对给定充分小的ε>0可得,max t>0I (tv ε)=I (t εv ε)max t>0 t 22 R N |∇v ε|2−μv 2ε|x |2+¯av ε2 dx −t 2∗2∗ R N|v ε|2∗dx −O (εN −√¯μq)=1N S N2μ+O (ε2β)−O (εN −√¯μq)+⎧⎪⎪⎨⎪⎪⎩O (ε2),β>1,O (ε2|log ε|),β=1,O (ε2β),β<1,<1NS N 2μ,这样完成了(56)式的证明.由c μ的定义可得c μ<1N S N2μ.接下来证明c μ<J ∞.(58)设{u 0}是J ∞的可达函数且I ∞(u 0)=J ∞.令g (t )=I ∞(tu 0)=12t 2 R N|∇u 0|2+¯a u 20−μu 20|x |2 dx −t 2∗2∗ R N |u 0|2∗dx −t q q R N ¯k |u 0|q dx,g (t )=t R N |∇u 0|2+¯au 20−μu 20|x |2 dx −t 2∗−1 R N |u 0|2∗dx −t q −1R N¯k |u 0|q dx.因此∀t ∈(0,1),g (t ) 0;∀t 1,g (t ) 0.所以g (1)=I ∞(u 0)=max lI ∞(u );其中l ={tu 0,t 0,u 0固定}.(59)853显然存在t0>0使得sup t 0I(tu0)=I(t0u0),因此由(59)式以及函数a(x),k(x)满足的条件得J∞=I∞(u0) I∞(t0u0)>I(t0u0)=sup t 0I(tu0).这样有(58)式成立.由(58)和(56)式易得(55)式.致谢作者衷心感谢匿名审稿人对于本文提出的许多宝贵意见.本文的部分结果是邓引斌教授访问香港中文大学数学所时完成.参考文献1Struwe M.A global compactness result for elliptic boundary value problems involving limiting nonlinearities.Math Z,187:511–517(1984)2Lions P L.The concentration-compactness principle in the calculus of variations,The locally compact cases, Part I.Ann Inst H Poincar´e Anal Non Lin´e aire,1:109–145(1984)3Br´e zis H,Nirenberg L.Positive solutions of nonlinear elliptic equations involving critical m Pure Appl Math,36:437–477(1983)4Pierrotti D,Terracini S.On a Neumann problem with critical exponent and critical nonlinearity on the m Partial Diﬀerential Equations,20:1155–1187(1995)5Cao D,Peng S.A global compactness result for singular elliptic problems involving critical Sobolev expo-nent.Proc Amer Math Soc,131:1857–1866(2003)6Lions P L.The concentration-compactness principle in the calculus of variations,The locally compact cases, Part II.Ann Inst H Poincar´e Anal Non Lin´e aire,1:223–283(1984)7Benci V,Cerami G.Positive solutions of semilinear elliptic problem in exterior domains.Arch Ration Mech Anal,99:283–300(1987)8Zhu X,Cao D.The concentration-compactness principle in nonlinear elliptic equations Acta Math Sci SerB Engl Ed,9:307–323(1989)9Smets D.Nonlinear Schr¨o dinger equations with Hardy potential and critical nonlinearities.Trans Amer Math Soc,357:2909–2938(2005)10Aubin T.Probl´e mes isop´e rimetriques et espaces de Sobolev.J Diﬀerential Geom,11:573–598(1976)11Terracini S.On positive solutions to a class of equations with a singular coeﬃcient and critical exponent.Adv Diﬀerential Equations,2:241–264(1996)12Deng Y,Guo Z,Wang G.Nodal solutions for p-Lapalace equations with critical growth.Nonlinear Anal, 54:1121–1151(2003)13Gidas B,Ni W M,Nirenberg L.Symmetry of positive solutions of nonlinear elliptic equations in R N.Adv Math Suppl Stud,7A:209–243(1981)14Deng Y,Cao D.Uniqueness of the positive solution for singular nonlinear boundrary value problems.Systems Sci Math Sci,1:25–32(1993)15Kwong M K,Zhang L Q.Uniqueness of the positive solution ofΔu+f(u)=0in an annulus.Diﬀential Integral Equations,4:583–599(1991)16Ambrosetti A,Rabinowitz P H.Dual variational methods in critical point theory and applications.J Funct Anal,14:349–381(1973)17Garcia Azorero J P,Peral Alonso I.Hardy inequalities and some critical elliptic and parabolic problems.J Diﬀerential Equations,144:441–476(1998)18Br´e zis H,Lieb E.A relation between pointwise convergence of functions and convergence of functionals.Proc Amer Math Soc,88:486–490(1983)19Cao D,Peng S.A note on the sign-changing solutions to elliptic problem with critical Sobolev and Hardy terms.J Diﬀerential Equations,193:424–434(2003)854。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

∫
∫
Α u d x →- ∞ ( t →+ ∞ 时) , Α 8 故ϖ R o > 0, 使得 e= R ou | B Θ= {u ∈H 2 }, J ( e) ≤0. 0 ( 8 ) ‖u ‖< Θ 2 ( ) ( ) 定义 c= inf m axJ u , D 表示 H 0 8 中连接 0 和 e 的道路的集合, 则 c≥Β> 0, J 关于 c # ∈D u ∈#
2 解的存在性
首先给出关于 H a rdy 不等式和 H a rdy 2Sobo lev 不等式的两个引理, 这两个引理在定理证明中将起到重要作用, 它们的证明参见 [ 2 ]、 [ 4 ]. 1, p (R N ) , 则有引理 2. 1 (H a rdy 不等式) 设 1< p < N , u ∈ W
Sobo lev2 H a rdy 不等式和变分方法, 得到它的解的存在性的一些结果.
关键词: Sobo lev2 H a rdy 不等式; 双重调和方程; 变分法; 解的存在性.
M R ( 2000) 主题分类: 35J 30; 35J 70 中图分类号: O 175. 25 文献标识码: A
u ∈L p (R N ) , x p u p ( 2) N )p p dx ≤ ( R N - p x p ( 3) 常数 ( ) p 是最优的 . N - p
( 1)
∫
∫
R
N
u
p
dx ,
N - s 3 引理 2. 2 ( Sobo lev 2 H a rdy 不等式) 若 1< p < N , 0 ≤s ≤p , p ≤q ≤p ( s ) = p, 则 N - p
∫
1
△u △Υ d x - Λ f Υ d x. ∫ ∫ x dx = ∫ u Υ △u △Υ d x - Λ f Υ d x. ∫ ∫ x dx = ∫
8 8
s
u 1Υ
2
8
8
2
8
s
8
两式相减可得
110
数学物理学报 V o l . 23A △ (u ∫
8
1
- u 2 ) △Υ d x - Λ
有
( 1) 存在常数 C > 0, 使得对任意 u ∈ W ( ∫ x
8
1, p 0
( 8 ) , 都有
u
1, p 0
q s
dx ) q ≤ C (
1
∫
8
u
p
d x ) p.
u x
s q
1
( 2) 若 p ≤q < p 3 (s) , 则从 W 定理 1. 1 的证明
( 8 ) 到 L q ( 8 ) 的映射: u →
= 0,
∫
8
u x
2
s
dx ≤ C 1
∫
8
u
2
dx ≤ C 2
∫△u
8
2
2
d x , u ∈ H 2 0 (8 ) ,
由此可以定义 Λ0 = 则 Λ0 > 0, 且对任意 u ∈H 2 0 ( 8 ) , 都有 Λ0
2 u ∈H 0 ( 8 ) u ≠0
∫△u dx , m in u ∫ x dx
∫
8 8
u1 - u2 Υ d x = 0. s x
取Υ = u 1 - u 2 可得
∫
8
△ (u 1 - u 2 ) 2dx - Λ
∫
(u 1 - u 2 ) 2
x
s
d x = 0.
但 L = △2 - Λ
I < Λ0 时是正算子, 故有 u 1 ≡u 2 a. e. 在 8 中 . s, 当 Λ x
p = u x
s
+
u
p- 2
u,
x ∈8,
5u = 0, 5Μ
x ∈ 58 ,
0 ≤ s < 2.
( 1. 5)
2N , 0 < Λ < Λ0 , N - 4
则当 N ≥8- s 时, ( 1. 5) 至少存在一个非平凡解 u ∈H 2 0 ( 8 ). 在后面的内容中, 我们将运用变分方法给出上述三个定理的证明.
2 0
x ∈ 58 , Λ < Λ0 , 0 ≤ s ≤ 2.
( 1. 3)
△2 u = Λ u=
u x
s
+
u
Α - 2
u,
x ∈8,
5u = 0, 5Μ
2N , N - 4
x ∈ 58 ,
0 ≤ s ≤ 2.
( 1. 4)
Λ < Λ0 , 2 < Α< 则 ( 1. 4) 至少存在一个非平凡解 u ∈H 2 0 ( 8 ). 定理 1. 3 考虑问题 △2 u = Λ u=
有界区域, 得到了方程多个解的存在结果. 在这些问题的讨论中, 对于其中的奇异项, 一个重要的方法就是利用 H a rdy 不等式
∫
R
N
u x
p p
dx ≤ (
q s
p )p N - p
∫
R
N
u
p
dx , u ∈W
1, p
(R N ) ,
及 Sobo lev 2 . H a rdy 不等式
∫
(
8
u x
N o. 1 康东升等: Sobo lev 2 H a rdy 不等式与临界双重调和问题 - △p u = Κ u
r- 2
107
u+ Λ
u x
q- 2 s
u,
x ∈8, x ∈ 58.
u = 0, 其中 Κ , Λ 是两个正参数, 0≤s≤p , 1< p ≤q ≤
N - s Np 3 , 8 是包含 0 的 p , p ≤ r≤p = N - p N - p
( 在 H 2 ( ) = 0 ( 8 ) 中, 我们使用等价范数 ‖u ‖ = ‖u ‖H 2 0 8
∫△u
8
2
dx ) 2 , p =
1
2N 是 N - 4
2 p . 记H 2 0 ( 8 ) 的对偶空间为 H Sobo lev 嵌入 H 0 ( 8 ) →L ( 8 ) 的临界指数 p 表示 Sobo lev 空间 L ( 8 ) 中的范数.
J (u n ) -
f u d x. ∫ ) dx f u d x. ∫ 1 f u d x. 2∫
8
n
8
n
1 lim f u n d x 2 n →∞ 8
∫
1 1 ( u ) , u = J ( u ). f u dx = J (u ) J′ 2 8 2 最后证明解的唯一性. 设 u 1 , u 2 ∈H 2 ∈H 2 0 ( 8 ) 是 ( 1. 3 ) 的解, 则对任意 Υ 0 (8 ) , 有 = -
∫
8
∫x
8
2
∫
8
下面证明
J (u ) = J (u n ) =
2 v ∈H 0 ( 8 )
inf J ( v ).
un s ) dx x un x
2
s
(u n ) , u n J′
∫ ( △u = ∫
8
1 2
( △u n
- Λ
2
2
8
n
- Λ
1 (u n ) , u n = J′ n 8 2 1 (u n ) , u n ] = inf J ( v ) = li m J ( u n ) = lim [ J ( u n ) 2 J ′ 2 n →∞ n →∞ 2 v ∈H 0 ( 8 )
un u 2 s 2_ s 2 在 L ( 8 ) 中, x x ( 4) u n →u a. e. 在 8 中 .
( 3)
这里 “→” 表示强收敛,“_ ” 表示弱收敛. 这样 u ∈H 2 0 ( 8 ) 就是 ( 1. 3 ) 的一个弱解, 即对任 2 意Υ ∈H 0 ( 8 ) , 都有 uΥ △u △Υ d x = Λ f Υ d x. s dx +
dx ) q ≤ C (
1
∫
8
s
u
p
dx ) p , u ∈W
1
1, p 0
(8 ) ,
受它们的启发, 本文讨论下列问题 △2 u = Λ u=
u u x
+ f (x , u ) ,
x ∈8, x ∈ 8.
( 1. 1)
Μ 这里 8 < R N 是包含 0 的有界光滑区域, 0 ≤s ≤2, u ∈H 2 0 ( 8 ). 由 Sobo lev 2 H a rdy 不等式和 Sobo lev 嵌入不等式可知存在常数 C 1 > 0, C 2 > 0, 使得
是紧的.
N o. 1 康东升等: Sobo lev 2 H a rdy 不等式与临界双重调和问题
109
对于 u ∈H 2 0 ( 8 ) , ( 1. 3 ) 对应的能量泛函是 2 1 u ( △u 2 - Λ J (u ) = s ) dx 2 8 x
∫
2
f u dx , ∫
8
2ቤተ መጻሕፍቲ ባይዱ
( △u ∫
- 2 0
( 8 ). 我们用‖・‖p
本文的主要结果可以表述为以下几个定理定理 1. 1 考虑问题
108
数学物理学报 V o l . 23A △2 u = Λ u=
u x
s
+ f (x ) ,
x ∈8,
5u = 0, 5Μ f ( x ) ∈ H -0 2 ( 8 ) , 则 ( 1. 3) 有唯一的一个解 u ∈H ( 8 ). 定理 1. 2 考虑问题