自动控制04c根轨迹绘制的基本法则
自动控制原理 根轨迹法

n
i
|
注意
• 相角方程是决定系统闭环根轨迹的充分 必要条件 • 用相角方程绘制根轨迹; • 模值方程主要用来确定已知根轨迹上某 一点的K*值 • 例4-1,4-2
4.2 根轨迹绘制的基本法则
• 法则1: 根轨迹的分支数:根轨迹在[s]平面上的分支数 等于闭环 特征方程的阶数n,也就是分支数与闭环极点的 数目相同。
q
h
f
l
结论:1 零点、 2 极点、3 根轨迹增益
b0 ( s z1 )(s z 2 ) ( s zm ) G( s) H ( s ) K* a0 ( s p1 )(s p2 ) ( s pn )
• 根轨迹增益:
(s z ) (s p )
• 法则6: 根轨迹的起始角(从极点pk)和终止角(到零点zk) :
起始角:
例2 证2
m n
pk ( 2k 1) ( pk z j ) ( pk pi )
j 1 i 1 i k
终止角:
zk ( 2k 1) ( z k p i ) ( z k z j )
i
nm
0 ( 1) ( 2) 1 30
a
(2k 1)π π π , , π nm 3 3
d1 0.42, d 2 1.58(舍去)
s j
1 1 1 0 d d 1 d 2
1 G(s)H(s) 0即(s 3 3s 2 2s K * ) j 3 3 2 2 j K * 0
s2
0
常规根轨迹的绘制法则(P138) 终止于开环零点或。 1 根轨迹起始于开环极点或, 根轨迹对称实轴 2 根轨迹的条数为特征根的个数, 3 ∣n-m∣条渐近线对称于实轴,均起于实轴上的σa 点,
根轨迹的绘制法则

▼
a
6、 根轨迹的渐近线 ——有独立的(n-m)条
渐近线包括 ⑴ 渐近线的倾角 设在无穷远处有特征根sk ,则s平面上所有开环有限零点 渐近线的倾角 渐近线的交点 两方面内容
-zi和极点-pj到sk的矢量辐角都相等,即:i=j=
代入幅角条件,得:
本 节 返 回
根轨迹的绘制法则
绘制根轨迹的一般法则
本 章 返 回
根轨迹的绘制法则
绘制根轨迹的一般法则
绘制根轨迹应确定以下几个方面的内容: (9项) 起点、终点、根轨迹数、实轴上的根轨迹、
分离点和汇合定、根轨迹的渐近线、根轨迹的出射
本 节 返 回
角和入射角、根轨迹和虚轴的交点、根轨迹的走向。 注意:实际绘制根轨迹时应根据具体情 况有选择性地考虑以上9项内容。
本 节 返 回
本 章 返 回
4.2 根轨迹的绘制方法
5、分离点与会合点
D' (s) N(s) N' (s)D(s) 0
注意:
求出s=-d后,应把它代入特征方程计算Kd, 只有Kd为正值, s=-d才是分离点或会合点。 6、根轨迹的渐近线
本 节 返 回
180 (1 2 ) 渐近线的倾角: nm
本 节 返 回
N (s) D(s)
j 1 i 1 n
m
( s zi )
sm sn
i 1 n j 1
m
zi s m 1
z
i 1 n j 1
m
i
本 章 返 回
(s p j )
p j s n 1
p
自动控制原理 第四章 根轨迹法
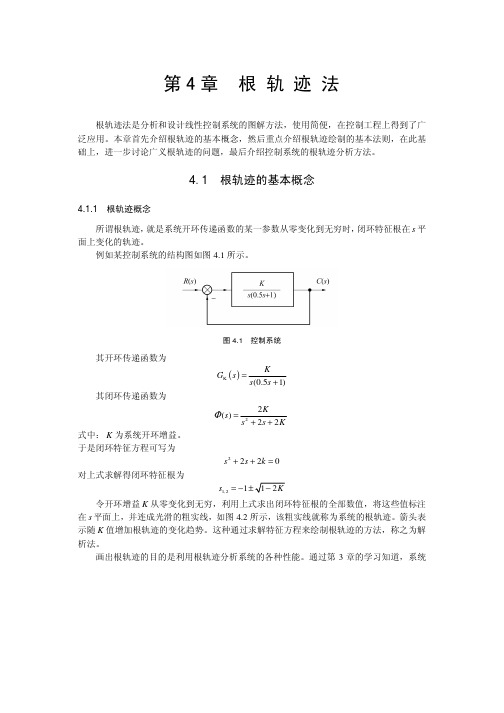
第4章 根 轨 迹 法根轨迹法是分析和设计线性控制系统的图解方法,使用简便,在控制工程上得到了广泛应用。
本章首先介绍根轨迹的基本概念,然后重点介绍根轨迹绘制的基本法则,在此基础上,进一步讨论广义根轨迹的问题,最后介绍控制系统的根轨迹分析方法。
4.1 根轨迹的基本概念4.1.1 根轨迹概念所谓根轨迹,就是系统开环传递函数的某一参数从零变化到无穷时,闭环特征根在s 平面上变化的轨迹。
例如某控制系统的结构图如图4.1所示。
图4.1 控制系统其开环传递函数为()K (0.51)KG s s s =+其闭环传递函数为22()22Ks s s KΦ=++式中:K 为系统开环增益。
于是闭环特征方程可写为2220s s k ++=对上式求解得闭环特征根为1,21s =−令开环增益K 从零变化到无穷,利用上式求出闭环特征根的全部数值,将这些值标注在s 平面上,并连成光滑的粗实线,如图4.2所示,该粗实线就称为系统的根轨迹。
箭头表示随K 值增加根轨迹的变化趋势。
这种通过求解特征方程来绘制根轨迹的方法,称之为解析法。
画出根轨迹的目的是利用根轨迹分析系统的各种性能。
通过第3章的学习知道,系统第4章 根轨迹法·101··101·特征根的分布与系统的稳定性、暂态性能密切相关,而根轨迹正是直观反应了特征根在复平面的位置以及变化情况,所以利用根轨迹很容易了解系统的稳定性和暂态性能。
又因为根轨迹上的任何一点都有与之对应的开环增益值,而开环增益与稳态误差成反比,因而通过根轨迹也可以确定出系统的稳态精度。
可以看出,根轨迹与系统性能之间有着比较密切的联系。
图4.2 控制系统根轨迹4.1.2 根轨迹方程对于高阶系统,求解特征方程是很困难的,因此采用解析法绘制根轨迹只适用于较简单的低阶系统。
而高阶系统根轨迹的绘制是根据已知的开环零、极点位置,采用图解的方法来实现的。
下面给出图解法绘制根轨迹的根轨迹方程。
根轨迹绘制的基本法则

规则七、 根轨迹与虚轴的交点:交点和相应的Kr值 利用劳斯判据求出。 根轨迹与虚轴的交点对应于临界稳定状态,此时系统 出现虚根。 在例4-2-2中,系统闭环特征方程式为:
1 Kr ( s 5) s ( s 1)( s 2)
1 3 6 2K r 3 5K r
0,
s( s 1)( s 2) K r ( s 5) 0
同理可证明入射角。
例4-2-3
设系统开环零极点图如图4-7。p
0 0
j
3
确定根轨迹离开共轭复数根的出射角。
其中 ( p3 z1 ) 85 , ( p3 p1 ) 135
( p3 p2 ) 45 , ( p3 p4 ) 90
0 0
×●
P3
P2 × ●
n m j j 1 i 1
i
nm
对例4-2-2,渐近线与实轴夹角为:
l 180 n m
180 l 2
( l 1,3,) 90 , 90 ( 270 )
0
0 0
交点坐标为:
1 2 ( 5 ) 2
1 , 即(1,j0)。
j
●
× × ×
﹣2 ﹣1
P3
s0 点为从 p3 出发的根轨迹上一点。
z ( p1 p 2 p 3 p 4 ) 180 l
0
j
×●
z
P3
P1
p 3 180 l z ( p1 p 2 p 4 )
0
P2
×●
Z1
×
01 P
P2
P2 × ●
绘制根轨迹的基本法则

4.2 绘制根轨迹的基本法则本节讨论根轨迹增益*K (或开环增益K )变化时绘制根轨迹的法则。
熟练地掌握这些法则,可以帮助我们方便快速地绘制系统的根轨迹,这对于分析和设计系统是非常有益的。
法则1 根轨迹的起点和终点:根轨迹起始于开环极点,终止于开环零点;如果开环零点个数m 少于开环极点个数n ,则有)(m n -条根轨迹终止于无穷远处。
根轨迹的起点、终点分别是指根轨迹增益0=*K 和∞→时的根轨迹点。
将幅值条件式(4-9)改写为∏∏∏∏==-==--=--=mi inj j mn m i i nj jsz sp sz s ps K 1111*|1||1||)(||)(|(4-11)可见当s=j p 时,0*=K ;当s=i z 时,∞→*K ;当|s|∞→且m n ≥时,∞→*K 。
法则2 根轨迹的分支数,对称性和连续性:根轨迹的分支数与开环零点数m 、开环极点数n 中的大者相等,根轨迹连续并且对称于实轴。
根轨迹是开环系统某一参数从零变到无穷时,闭环极点在s 平面上的变化轨迹。
因此,根轨迹的分支数必与闭环特征方程根的数目一致,即根轨迹分支数等于系统的阶数。
实际系统都存在惯性,反映在传递函数上必有m n ≥。
所以一般讲,根轨迹分支数就等于开环极点数。
实际系统的特征方程都是实系数方程,依代数定理特征根必为实数或共轭复数。
因此根轨迹必然对称于实轴。
由对称性,只须画出s 平面上半部和实轴上的根轨迹,下半部的根轨迹即可对称画出。
特征方程中的某些系数是根轨迹增益*K 的函数,*K 从零连续变到无穷时,特征方程的系数是连续变化的,因而特征根的变化也必然是连续的,故根轨迹具有连续性。
法则3 实轴上的根轨迹:实轴上的某一区域,若其右边开环实数零、极点个数之和为奇数,则该区域必是根轨迹。
设系统开环零、极点分布如图4-5 所示。
图中,0s 是实轴上的点,)3,2,1(=i i ϕ是各开环零点到0s 点向量的相角,)4,3,2,1(=j j θ是各开环极点到0s 点向量的相角。
自控c4(2) 自动化控制

渐近线与实轴的交点位置σ a 和 与实轴正方向的交角 ϕ 分别为 a
σa =
2 k+1 ϕa = π n− m
∑ p − ∑z
i =1 i j =1
n
m
j
n−m
(k = 0,1,2,L, n− m−1)
例4-2 已知系统的开环传递函数为 -
G(s) H(s) =
Kr (s+ 2) s (s+1)(s+ 4)
二、绘制根轨迹的基本规则 根轨迹的起点与终点; 1.根轨迹的起点与终点; 根轨迹的分支数; 2.根轨迹的分支数; 实轴上的根轨迹; 3.实轴上的根轨迹;
4.根轨迹的渐近线; 根轨迹的渐近线; 5.根轨迹在实轴上的分离点; 根轨迹在实轴上的分离点;
根轨迹的起始角和终止角; 6.根轨迹的起始角和终止角; 根轨迹与虚轴的交点。 7.根轨迹与虚轴的交点。
=1
∏| s+ p |
i=1 i
m j=1
j=1 n
或
∏| s+ z
j=1
n j i i=1
i=1 m
i
= Kr
j
|
满足相角 条件的表 达式为: 达式为:
∑∠(s+ z ) − ∑∠(s+ p ) = (2k +1)180°
(k = 0,±1,±2,L )
综上分析,可以得到如下结论: 综上分析,可以得到如下结论: ⑴ 绘制根轨迹的相角条件与系统开环根 的大小无关。 即在s 平面上, 轨迹增益值 Kr的大小无关 。 即在 s 平面上 , 所有满足相角条件点的集合构成系统的根 轨迹图。 轨迹图 。 即相角条件是绘制根轨迹的主要 依据。 依据。 ⑵ 绘制根轨迹的幅值条件与系统开环根 值的大小有关。 轨迹增益 Kr值的大小有关。即 Kr值的变化 会改变系统的闭环极点在s 会改变系统的闭环极点在s平面上的位置
(自动控制)第四章:根轨迹法

动态性能:从根轨迹图可以分析出系统的工作状态,
如过阻尼状态、欠阻尼状态……
根轨迹增益、闭环零极点与开环零极点的关系 l f
* G(s)= KG
∏( s-p ) i i=1
f i i 1 H q
q
∏( s-z ) i i=1
;
l
j=1 * H (s)= KH h
f l m
∏(s-zj )
C(s)
C ( s) 2k 2 R ( s ) S 2 S 2k
特征方程(闭环):
S2+2s+2k=0
k s(0.5s+1)
特征根:s1,2= -1±√1-2k k=0时, s1=0, s2=-2
K:0 ~ ∞
0<k<0.5 时,两个负实根 ;若s1=-0.25, s2=? k=0.5 时,s1=s2=-1 0.5<k<∞时,s1,2=-1±j√2k-1 j
注意:一组根对应同一个K;
K一变,一组根变; K一停,一组根停;
-2
-1
0
由以上分析,s1、s2两条根轨迹反映了系统特征根随参 数k变化的规律,组成了系统的根轨迹。 1.二阶系统有两个特征根,它的根轨迹有两条分支; 一个n阶系统的根轨迹则应有n条分支。 2.k=0时的闭环极点,s1=0、s2=-2正好是开环传递函 数的两个极点,因此说,系统开环极点就是它各条根轨 迹的起点。 3. k=∞时的闭环极点,是根轨迹的终点。 4.特征方程的重根点是根轨迹的分支离开负实轴进入复 数平面的分支点。
a.系统响应单调上升(ξ>1)系统具有两个不相等的负实根┈ 过阻尼响应。 b.系统响应衰减振荡(0<ξ<1)系统具有一对负实部的共 轭复根┈欠阻尼响应。
自动控制原理4.2 绘制根轨迹的基本法则

§4—2 绘制根轨迹的基本法则
绘制根轨迹的基本法则(续)
根轨迹在s平面上的分支数=闭环特征方程的阶 数。即:分支数=闭环极点数=开环极点数n(n≥m) 或=开环零点数m(m>n)。
二、根轨迹的起点和终点:
根轨迹起始于开环极点,终止于开环零点。 若n>m,则有(n-m)条终止于无穷远处。 若m>n,则有(m-n)条起始于无穷远处。
同理可得 :
zk
2k 1
n
z
k
i 1
pi
m
zk
j 1
zj
jk
共轭复数的开环零极点才需计算出射角和入射角,
实数开环零极点不用计算,一般为:0°, 180°,
±90°, ±60°与±120°, ±45°与±135°等.
§4—2 绘制根轨迹的基本法则
sd sd
1 2
0.473
3.527舍
j
-5
sd2
sd1
-1
0
§4—2 绘制根轨迹的基本法则
六、根轨迹与虚轴的交点:
根轨迹与虚轴相交,表示闭环极点中有一部分 位于虚轴上,即闭环特征方程有纯虚根±jω, 系统 处于临界稳定。
1、将s j,代入1 G( j)H( j) 0
3
2
Kg
0
Kg
6,
Kc 3
2、用劳斯判据:
§4—2 绘制根轨迹的基本法则
s3 1
2
s2 3
Kg
s1 6 K g
0
3
s0 K g
当 s1 行 等 于0时 , 可 能 出现共轭虚根,令
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分离点的概念:若干根轨迹在复平面上的某一点相遇后 又分开,称该点为分离点;分离角定义为根轨迹进入分 离点的切线方向与离开分离点的切线方向之间的夹角。
分离点的坐标d是如下方程的解,分离角为 (2k 1) / l
点数m时,有 n条根m轨迹分支沿着与实轴交角为 交点为a
的一组渐 a近线趋向无穷远处,且有
a
(2k 1)
nm
(k 0,1,2, , n m 1)
n
m
pi z j
和
a
i 1
j 1
nm
证明:渐近线就是s值很大时的根轨迹,因此渐近线也一 定对称于实轴。将开环传递函数写成多项式比值形式,得
m
G(s)H (s)
m 1
n1
j1 d Z j i1 d Pi
(4-20)
必须说明的是,方程只是必要条件而非充分条件,也就是
说它的解不一定是分离点,是否是分离点还要看其它规则。
实轴上分离点的位置可用重根法和极值法求得。
1)重根法
j 1 3
j) (1)
1.67
各渐近线与实轴的交角分别为
a
(2k 1)
nm
60
a
(2k 1)
nm
180
(k 0)
(k 1)
a
(2k 1)
nm
300
(k 2)
以上交角可用量角器s平面上绘出,或者用a atga
算出各渐近线与虚轴的交点来决定。
法则4 根轨迹在实轴上的分布 实轴上具有根轨迹的区间 是:其右方开环系统的零点数和极点数的总和为奇数。共 轭复数的开环零点、极点对确定实轴上的根轨迹无影响。
K
(s
j 1
z
j
)
n
(s
i1
pi )
K
sm b1sm1 sn a1sn1
bm1s bm an1s an
m
n
式中 b1 z j , a1 pi
j 1
i 1
当 s 时,上式可近似为
G(s)H(s)
K
s nm (a1 b1 )s nm1
令
G(s)H(s) 1
得渐近线方程
G(s)
K (s 1)
s(s 4)(s2 2s 2)
试根据已介绍的基本法则,确定绘制根轨迹的有关数据。
解:将开环零点、极点标注在s平面的直角坐标系上,以“×”表示 开环极点,以“○”表示开环零点。在根轨迹绘制过程中,由于需 要对相角和模值进行图解测量,所以横坐标与纵坐标必须采用相同 的比例尺。
在无穷远处。的确,当 s 时,
n
K
lim i1
s
pi
lim s nm
s
m
j 1
s
z
j
s
具有有限值的零点为有限零点,处于无穷远处的零点叫无限零点,则 根轨迹必终于开环零点。这时,开环零点数和开环极点数相等。
法则2 根轨迹的连续性与对称性:根轨迹是连续且对称于 实轴的曲线。
法则3 根轨迹的渐近线:当开环有限极点数 大n 于有限零
区间[-20,-5]右方的开环零点数和极点数总和为5,区间[1,-0.5]右方的开环零点数和极点数总和为3。故实轴上根 轨迹在上述区间内。
法则5 根轨迹的分离点和分离角
当K*从零变到无穷大时,根轨迹可能出现先会 合后分离,这样的点称分离点。分离点对应闭环重 极点,也就是闭环特征式的重根。
显然,位于实轴上的两个相邻的开环极点之间 一定有分离点,因为任何一条根轨迹不可能开始于 一个开环极点终止于另一个开环极点。同理,位于 实轴上的两个相邻的开环零点之间也一定有分离点。
a1
b1
)
1 nm
s[1
a1 b1
1
] (K )nm
s
(n m)s
→
s
a1 b1
K e 1 nm
(2k 1) j
nm
(n m)
(K ,s ,k 0,1, ,n m 1)
n
m
→
pi z j
a
i 1
j 1
nm
,
a
(2k 1)
nm
举例说明
例1 设控制系统如图4-5所示,其开环传递函数为
s pi
(i 1,2, , n)
说明K*=0时,闭环特征方程式的根就是开环传递函数的极 点,所以根轨迹必起于开环极点。
将特征方程改写成如下形式
1 K
n
(s
i1
pi )
m
(s
j 1
zj)
0
当 K 时,可得
s zj
( j 1,2, , m)
所以根轨迹必终于开环零点。
实际系统中,m n ,因此有 n m 条根轨迹的终点将
4-2 根轨迹绘制的基本法则
一、绘制根轨迹的基本法则
法则1 根轨迹的起点和终点:根轨迹起于开环极点,终于
开环零点。
证明:根轨迹起点是指根轨迹增益K*=0的根轨迹,而终点则
是指 K 的根轨迹。设系统闭环传递函数为(4-6),
则闭环系统的特征方程式为
n
m
(s
i 1
pi
)
K
(s
j 1
z
j
)
0
式中 K 可以从零变到无穷。当K*=0时,有
(s1 p3 ) 180
180º的奇数满足根轨迹方程的相角条件。故实轴上的点若在根轨迹 上,其右方实轴上的开环零点和极点综合必为奇数。
举例说明
例2
设系统开环传递函数为
G(s)
s
2
(s
K (s 0.5) 1)(s 5)(s
20)
试求实轴上的根轨迹。
解 系统的开环零点为 0.5 ,开环极点为-1,-5,-20以 及原点(两重根)。如图所示。
证明:如下图所示,成对出现的开环共轭复数零点或极点 对实轴上任一试探点s1构成的两向量的相角之和在任何情 况下都等于0或360º,即
(s1 p1) (s1 p2 ) 0,360
s1左方实轴上任一开环零点或极点对该点构成的向量的相角为0º
(s1 z1) 0
s1右方实轴上任一开环零点或极点对该点构成的向量的相角为180º
由法则1,根轨迹起于G(s)的极点 p1 0, p2 4 ,p3 1 j
和 p4 1 j , 终于 G(s) 的有限零点 z1 1 以及无穷远处。
由法则2,根轨迹的分支数有4条,它们是连续的且对称于实轴。
由法则3,有 n m 3 条根轨迹渐近线,它们的交点为
4
a
i1
pi 3
z1
(0 4 1
snm (1 a1 b1 ) K s
→
s(1
a1
b1
)
1 nm
1
(K )nm
s
根据二项式
a1 b1
1
1
(
1
1)(a1 b1 )2
s
(n m)s 2! n m n m
s
当 s 时,近似有
(1 a1
b1
)
1 nm
1
a1 b1
s
(n m)s
→
s(1
