第一届启智杯真题及答案详解
启智杯真题2013真题和答案

1.在下面的算式中,不同的汉子代表 1—9 中不同的数字,那么,“为了一切学生”的各 字分别代表了什么数字?写出一种答案,说明你的分析过程.
2.从 1、2、3、4、5、6、7、8、9 这 9 个数字中选出 8 个不同的数字分别填入下面两个 算式的方框内(每个数字只许用一次) ,使它们都成立,简述理由 .
5.答案:400=43+45+47+49+51+53+55+57(8 个连续的奇数之和) 400=31+33+35+37+39+41+43+45+47+49(10 个连续的奇数之和) 400=1+3+5+7+…+33+35+37+39(20 个连续的奇数之和) 400 可以写成最多 20 个连续奇数之和,因为如果连续奇数多于 20 个,则这些奇数的中 间(平均数小于 400 21 ,即小于 19,但是小于 19 的奇数只有 9 个,总数不会多于 20 个). 本问题的解答思路可以有多种: 比如:将 400 分别表示成 8 个、10 个、20 个连续的奇数之和,可以从 10 个连续奇数的 平均值出发向两边延伸:由于 400 10 40 ,所以这 10 个连续奇数的中间两个应该是 39 与 41 , 以 此 两 边 各 延 伸 4 个 , 于 是 得 到 从 31 到 49 的 10 个 连 续 奇 数 . 验 算 知 31+33+35+37+39+41+43+45+47+49=400. 6.答案:从侧面(前后左右)看,共有(16)个正方形; 从上面往下看有(5)个正方形; 从下面往上看有(5)个正方形. 7.答案:以下三种答案写出两种即可,其它答案如果合理,比照该评分标准给分 分类依据一:一类是围成的几何体每一个面均为多边形(多面体) ;另一类围成的面有 圆弧面(旋转体) 分类结果一:共分 2 类;一类是 1,3,4,5,7,9,10;另一类是 2,6,8,11 分类依据二: 一类是有两个面为平行平面 (柱体与台体) ; 另一类是有一个尖端 (锥体) ; 第三类表面没有平面图形(球) 分类结果二:共分 3 类;一类是 1,2,4,5,6,7,10;另一类是 3,8,9;第三类 11 分类依据三:按是否为柱体、锥体、台体、球分类. 分类结果三:共分 4 类;第一类是 1,5,6,7;第二类是 3,8,9;第三类是 2,4, 10;第四类 11.
“启智杯”训练题(附答案)

1.一张三角形纸片,请你剪去一个角,还剩几个角?怎么剪?答案如图所示:2.规定四个碗可换一个炒饭,某小队28人来吃饭,问至少买多少碗炒饭才能保证每人一碗?答案:三个空碗=一炒饭(不含碗)所以只需花钱买21碗,然后21个碗可换4碗炒饭共28碗。
3.2011个碗,碗口朝下,每次翻动4个,能否经过若干次翻动,使所有碗口全部碗口朝上?每次五个呢?答案:2011个碗口全向下,需翻动奇数次,但4的倍数均为偶数,所以不行。
每次翻动5个,依次翻2011/5次即可。
1、一刀可将薄饼切成两块,2刀最多切成四块,7刀最多切成几块?答:2、有一堆小朋友,如果8人一组,多2人;如果9人一组,多3人;如果10人一组,多4人,求最少几个小朋友?答:每8人一组差6人,每9人一组差6人,每10人一组差6人,所以:[8,9,10]360-6=354(人)3、在一长方形纸上有2011个点,这些点任意三点都不在同一条直线上,现在以这20 11个点及长方形四个顶点为顶点,将长方形纸片剪开,最多剪出几个三角形?答:4+(2011-1)X2=40241、下面是一串打乱顺序的数字,请找出规律。
3 5 13 21 1 1 2 8答:1 1 2 3 5 8 13 212、有三封不同的信,四个信箱可供传递,共有多少种投信方式?答:4X4X4=64(种)3、 A、B不同,求A+B。
答:A=38 B=83A+B=38+83=1211、一根钢管锯成5段,用20分钟;锯成12段用多少时间?答:20/(5-1)=5(分)5X(12-1)=55(分)2、答:(7+4+2)X2=263、一群男生女生在一起游戏,一个女生说:“我看到的男同学比女同学多一人”,一男生说:“我们男生我能看到6人。
”问,共多少个学生?答:男:6+1=7(人)女:7-1=6(人)共:7+7=14(人)1、一猴子爬树,每爬上5米,下落4米,树高14米,爬几次能上到树顶?答:(14-5)/(5-4)=99+1=10(次)2、移动2根火柴,使4个正方形变6个。
2011年第二届启智杯(小学组)真题

线
密封线内不要答题
年级
封
姓名 密
2、汉字“数”、“学”、“好”分别表示不同的数字,根据下列所给算式,则“数”表示数字 “好”表示数字 . 学好 学好 学好 + 学好 数学
、“学”表示数字
、 6、在同一个布袋里有红色、黄色、蓝色袜子各 15 只,最少要拿 (注意:袜子不分左右).
只才能保证其中至少有 2 双颜色不同的袜子
则“启”表示 、“智”表示 、“杯”表示 .
1/4
2/4
学校
பைடு நூலகம்
8、如图所示,长方形的长:宽= 4:3,将该长方形划分为四个三角形,其面积分别是 、 、 、 .若 = + = .则 : =______.
12、有一家公司董事长想从他手下四个得力助手中挑选一名担任策划部总经理,他给他们出了以下问题:把一闲置 的圆形土地平均分成四块,要求每块都与其它三块相连(即有公共的边).请你在下列所给图中至少画出 2 个符 合要求的分割方法.
线
9、a,b,c,d 为正整数,满足算式
,则 d=
.
(1)
(2)
(3)
10、观察下面的算式:
0×0=0-0,1× =1- ,
,
,….
根据算式反映出的规律,再写出满足这个规律的两个算式_____.
13、A,B,C,D 四个盒子中分别放有 6,5,4,3 个球,第一个小朋友找到放球最少的盒子,从其它的盒子中 各取 1 个球放入这个盒子中,然后第二个小朋友又找到一个放球最少的盒子,从其它的盒子中各取 1 个球放入这 个盒子中,……如此进行下去,当第 2011 个小朋友放完后,A,B,C,D 四个盒子中的球数依次是多少个?
2011 年第二届启智杯(小学组)真题
历届 最近十年 (新知杯)上海市初中数学竞赛试卷及答案(含模拟试题及解答)

新 知 杯 模 拟 试 题一、填空题(第1-5小题每题8分,第6-10题每题10分,共90分)1. 对于任意实数b a ,,定义b a *=b b a a ++)(,已知5.285.2=*a ,则实数a 的值是_________。
2. 在三角形ABC 中,,其中,,a CA a BC b AB 2122==-=b a ,是大于1的整数,则=-a b 。
3. 一个平行四边形可以被分成92个边长为1的正三角形,它的周长可能是 。
4. 已知关于x 的方程02)2()3(2234=++++++k x k x k x x 有实根,并且所有实根的乘积为-2,则所有实根的平方和为 。
5. 如图,直角三角形ABC 中1=AC ,2=BC ,P 为斜边AB 上一动点。
BC PE ⊥,CA PF ⊥,则线段EF 长的最小值为 。
6. 设b a ,是方程01682=++x x 的两个根,d c ,是方程01862=+-x x 的两个根,则()()()()d b d a c b c a --++的值为 。
7. 在平面直角坐标系中有两点()1,1-P ,()2,2Q ,函数1-=kx y 的图像与线段PQ 延长线相交(交点不包括Q ),则实数k 的取值范围是 。
8. 方程2009=xyz 的所有整数解有 组。
9. 如图,四边形ABCD 中CD BC AB ==,78=∠ABC ,162=∠BCD 。
设BC AD ,延长线交于E ,则=∠AEB _________________.EEC10. 如图,在直角梯形ABCD 中,90=∠=∠BCD ABC ,10==BC AB ,点M 在BC上,使得ADM ∆是正三角形,则ABM ∆与DCM ∆的面积和是________________。
二、(本题15分)如图,ABC ∆中,90=∠ACB ,点D 在CA 上,使得,,31==AD CD 并且,BAC BDC ∠=∠3求BC 的长。
第1~6届启智杯真题+答案
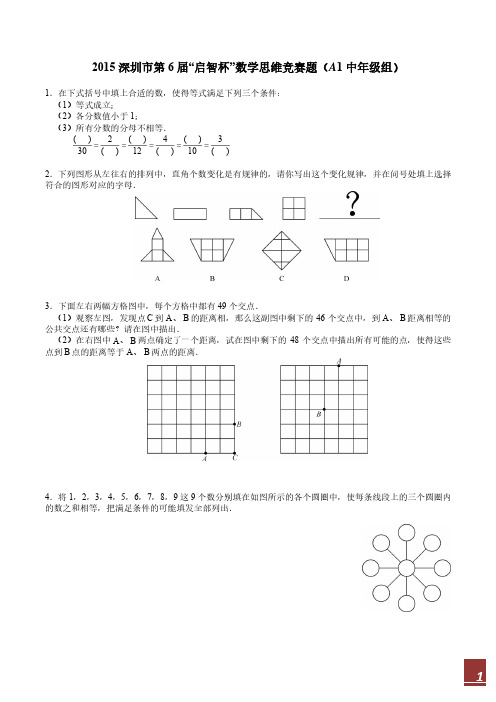
6.已知 a 1 1 1 23
1 ,b 1 2 4 5 7 8
672
369
2014 2015 .求 a b 的值,写出计算过程. 2016
7.下图左边是一个 4 4 的正方形去掉六个1 1的小正方形后剩下的“十字”形图形,右边的六个图形也是有 1 1的小正方形拼成的图形,这些图形中,选择两块可以在平面上移动(可转动,但不翻动)拼成左边“十 字”形图形,请把所有可能选出两块的拼法画在“十字”形图形上,并标出拼图组件所对应的字母.
7.在一个孤岛上生活着三种怪物:奇虎、奇狮、奇豹,数量分别为 2010、2015、2020 个.这些怪物有一种 古怪的习性:它们任何两种怪物一旦见面,就双方都变成第三种怪物(比如,一个奇虎和一个奇狮见面,就 都变成奇豹),见一种怪物见面则不会产生变化.问,如此下去,它们是否有可能到某种时刻全部变成同一 种怪物?请说明理由.
10.右边乘法算式中,只有四个位置源自的数已知,它们分别是 2,0,1,5,请你在空白位置填上数字,使 得算式能够成立,写出所有可能成立的算式.
3
11.如下图,在正方形 ABCD 的四个顶点 A 、 B 、 C 、 D 上按照顺时针方向依次进行如下标注:首先在顶 点 A 、 B 上分别标注数 1、2,之后将 AB 两点的标注数之和(1+2=3)标注在下一个顶点 C 处,再将 BC 两 点的标注数之和(2+3=5)标注在下一个顶点 D 处.接下来再把 A 点的标注数 1 擦去,将 CD 两点的标注数 之和(3+5=8)标注在 A 点,如此下去,请问:对 A 点进行第 2015 次标注的数被 3 除的余数是多少?说明 你的依据.
2015 深圳市第 6 届“启智杯”数学思维竞赛题(A1 中年级组)
第 届启智杯真题 答案

2015深圳市第6届“启智杯”数学思维竞赛题(A1中年级组)1.在下式括号中填上合适的数,使得等式满足下列三个条件:(1)等式成立;(2)各分数值小于1;(3)所有分数的分母不相等.()2()4()330()12()10()2.下列图形从左往右的排列中,直角个数变化是有规律的,请你写出这个变化规律,并在问号处填上选择符合的图形对应的字母.3.下面左右两幅方格图中,每个方格中都有49个交点.(1)观察左图,发现点C到A、B的距离相,那么这副图中剩下的46个交点中,到A、B距离相等的公共交点还有哪些?请在图中描出.(2)在右图中A、B两点确定了一个距离,试在图中剩下的48个交点中描出所有可能的点,使得这些点到B点的距离等于A、B两点的距离.4.将1,2,3,4,5,6,7,8,9这9个数分别填在如图所示的各个圆圈中,使每条线段上的三个圆圈内的数之和相等,把满足条件的可能填发全部列出.5.期末考试,在语数英三门课程中,聪聪有一门得了满分,她的同学甲、乙、丙在猜测到底哪一门得了满分.甲认为不是语文,乙认为是数学或英语,丙认为是英语.实际上,这三个同学的看法至少有一种是正确的,也至少有一种是错误的.请问,聪聪到底是哪门课考了满分?说明你的答案与推理过程.6.已知111124578201420151236723692016a b,.求a b的值,写出计算过程.7.下图左边是一个44的正方形去掉六个11的小正方形后剩下的“十字”形图形,右边的六个图形也是有11的小正方形拼成的图形,这些图形中,选择两块可以在平面上移动(可转动,但不翻动)拼成左边“十字”形图形,请把所有可能选出两块的拼法画在“十字”形图形上,并标出拼图组件所对应的字母.8.一个数各个位置上的数字加起来的和叫做数字和,如123的数字和是1+2+3=6.如果一个数的数字和不是一位数,就将其数字和再求数字和.如:456,4+5+8=17,1+7=8,如果最后得到的结果是1,则称这个数为“孤独数”.请问从1到2015的自然数中“孤独数”有多少个?写出结果及推理的过程.9.甲、乙、丙三人在A、B两块相邻的地植树,A地要植400棵,B地要植600棵.已知甲、乙、丙每天分别能植树30,34,38棵.甲在A地植树,丙在B地植树,乙先在A地植树,然后转到B地植树.三个人在两块地上的植树活动要求同一天开始同一天结束,乙应在开始后第几天从A地转到B地?A、B两地哪一块最先结束植树活动?写出答案及分析过程.10.右边乘法算式中,只有四个位置上的数已知,它们分别是2,0,1,5,请你在空白位置填上数字,使得算式能够成立,写出所有可能成立的算式.11.如下图,在正方形ABCD的四个顶点A、B、C、D上按照顺时针方向依次进行如下标注:首先在顶点A、B上分别标注数1、2,之后将AB两点的标注数之和(1+2=3)标注在下一个顶点C处,再将BC两点的标注数之和(2+3=5)标注在下一个顶点D处.接下来再把A点的标注数1擦去,将CD两点的标注数之和(3+5=8)标注在A点,如此下去,请问:对A点进行第2015次标注的数被3除的余数是多少?说明你的依据.12.某电脑动态屏保是这样设计的:开始共有2015只小鸟,随机编成若干列,每列数量不限.从第一列开始,每两列一组依次连续从屏幕左侧进入屏幕,移动至右侧从屏幕消失.如果消失的两列数量不同,就从后面增补一列小鸟(2015只小鸟以外),其数量为前面消失两列的数量之差(多的减少);如果消失的两列数量相同,则直接消失不予增补.如此下去,小鸟数量和列数都会越来越少,如果最后完全消失,则屏保结束;如果最后剩下1列,则电脑再随机增补100只新的小鸟,依然随机编排,并依前述规则进入和退出屏幕.问:如此下去,这个屏保会否在某个时刻结束?说明你的理由.2015深圳市第6届“启智杯”数学思维竞赛题(A 2高年级组)1.规定:符号“▼”为选择两个数中较大的数的运算,符号“▲”为选择两个数中较小的数的运算.比如5▼3=5,7▼10=10,3▲7=3.计算:1 3.141320154214201570.33?3 1.234▲▼▼▲▼▲2.一列数,其前七项依次为1,1,3,4,5,9,7,第8项是什么?说明理由.3.如图所示,圆周上的两个点1A 、2A 将圆等分成2份,在这两个点处写上14;圆周上的两个点3A 、4A 再将两段半圆弧等分,在点3A 、4A 处分别写上相邻2个数之和;如此继续这样操作,问能否出现圆周上所有数字之和2015?若可能,请求出经过了多少次操作?若不能,请说明理由.4.右图是四朵对称的小黄花相互连接于一个边长为4的正方形内,如果四朵黄花所围出的中间白色区域的面积为1.2,问一朵黄花的平面面积是多少?说明理由.(注:黑白印刷下,每一朵黄花是指图中虚线所包围的部分,包括其中的小圆内)5.如图,在正五边形ABCDE的五个顶点A、B、C、D、E上按顺时针方向依次进行如下标注:首先在顶点A、B上分别标注1、2,之后将A、B两点的标注数之和123标注在下一个顶点C处,再将B、C两点的标注数这和235标注在下一个顶点D处.再将C、D两点的标注数之和358标注在下一个顶点E处.接下来再把A点的标注数1擦去.将D、E两点的标注数之和5813标注在A点,如此下去,请问:对A点进行第2015次标注的数被5除的余数是多少?说明你的依据.6.某边远山区发生一起谋杀案,警方抓捕了三个嫌疑人A、B、C.法官问A是否杀了人,但A呜哩哇讲了一通方言,法官听不懂,就问另两位能讲普通话的嫌疑人B和C,他们懂这种方言.B说:“A告诉你,他没有杀人” .C说:“不对,A承认是他杀了人” .法官相信,在询问过程中,非罪犯是不会撒谎的,撒谎的一定是罪犯.请问:到底谁是罪犯?请说明理由.7.在一个孤岛上生活着三种怪物:奇虎、奇狮、奇豹,数量分别为2010、2015、2020个.这些怪物有一种古怪的习性:它们任何两种怪物一旦见面,就双方都变成第三种怪物(比如,一个奇虎和一个奇狮见面,就都变成奇豹),见一种怪物见面则不会产生变化.问,如此下去,它们是否有可能到某种时刻全部变成同一种怪物?请说明理由.8.在平面上用长度为5cm的火柴棒摆正方形,摆出1个边长为5cm的正方形需要4根火柴,摆出2015个这样的正方形最少需要多少根火柴?说明你的摆法(不必画图).9.有一个魔术是这样表演的:表演者将一副扑克牌去掉大小鬼共52张放入一暗箱,另有足够多的备用扑克牌.请一位观众上台,让他们从暗箱中随意取出若干张牌,算出这些牌的点数之和的个位数(规定J、Q、K的点数分别为11、12、13),然后从备用牌中拿来一张点数为这个个位数的扑克牌放进暗箱(如果个位数是0则不放),这个过程称为一次“置换”.如此下去,经过多次置换,暗箱里的扑克牌数量会越来越少,直至剩下一张.此时,魔术师非常自信地报出最后剩下的这张牌的点数,请问你能确定它的点数是几吗?为什么?10.如图所示,是一块上、下两面边长为28厘米的正方形蛋糕,其上表面和四周表面分别均匀覆盖着两种不同的糖霜,其厚度相同.如果用刀将其平均切分成7块体积相等,且覆盖有等量两种糖霜的小蛋糕,那么该怎样切?请在给出的平面图(下图右)上画出你的切割示意图,并做简要说明分割的理由.11.在棋盘上滚动骰子,使骰子的一面和棋盘格的大小相等,然后将骰子以棱为轴,滚动到邻近的棋盘格,每滚动一次,骰子朝上一面的数字就会变化.如果骰子的初始位置如左图,当骰子滚动六次到达对角顶点时(如右图),那么,第一步、第四步、第六步朝上的面分别是几点?(说明:骰子的相对两个面的点数之和为7)12.钢筋原材料每根长10米,每套钢筋架子用长2.4米、2米和1.5米的钢筋各一段.现需要绑好钢筋架子20套,至少要用去原材料多少根?总共浪费多少米?请填写下表以确定你的切割方案.2014深圳市第5届“启智杯”数学思维竞赛题(A组)1.观察如下几个等式:(1)331;(2)57313;(3)79113135;……你发现了什么规律?请据此写出第100个式子.2.有一个2014位数,其从左到右第2、3位数字分别为2、3,第11、30、2014位数字分别为4、5、6.如果其任何相邻的五位数字之和全相等,请问该数的第一位数字是几?全部2014位数字之和是多少?写出结果,并写出分析过程.3.一个非零自然数,如果从左到右顺读和从右到左逆读,都是一样的,则这个数称为“对称数”,如4,55,171,4994,12321等都是对称数,而332不是对称数.那么全部非零自然数(从1开始)从小到大的第2014这个对称数是多少?写出结果,并写出分析过程.4.把一张纸片裁剪成8份,称第1次操作;取其中一张再把它裁剪成8份,称第2次操作;如此继续下去,……,能否经过若干次操作后正好剪出了2014张纸片?若不能,请说明理由;若能,则需要经过多少次操作?写出结果,并写出分析过程.5.有如下三组数:A组:13,16,110,115;B组:1,3,5,7,9;C组:0.7,1.4,2.1,2.8,3.5,4.2,4.9.从每一组中各取一个数,相乘得到一个乘积,求这140个乘积的总和是多少?写出过程和结果.6.如图所示,五个圆中有部分的圆彼此相切(两个圆有且只有唯一一个公共点称两个圆相切),且总共只有三种不同长度的直径.若图中阴影部分的面积和为72cm,求最大圆内空白处的总面积.7.如图所示,正方形ABCD和正方形BEFG边长分别为a和b,25a b,若ACF△的面积是26cm,求CEF△的面积.8.通过折线的手段将一个正方形的每边两等分(对折)、四等分(再对折)、八等分(再对折)等等,都是轻而易举的(如图,虚线为折痕).请问,你能否在正方形的每边四等分、八等分的基础上,通过折线将其每边三等分、七等分?能否五等分呢?若能,请在图中用虚线画出你的折痕(用字母标出折痕经过的点);若不能,请说明理由.9.请将1,2,3,4,…11,12共12个数填入下列“井”字图形的12个○内,要求:(1)每个数都用一次;(2)每个“口”字四个解上(如ABCD四个位置)四个数之和都相等,四条直线上(如ACFG四个位置)四个数之和也相等,且等于各个“口”字四个角上四个数之和.10.明明的QQ号是由五个不同的数字组成的五位数,他把号码口头告诉了A、B、C三位同学.可惜他们都没有记住.A记的是“23865”,B记的是“32856”,C记的是“56328”.如果ABC三人每个人记的五位数中,位置和数字均正确的都只有两位,而且位置不相邻,请问明明的QQ号是多少?写出结果,并写出分析过程.11.张老师、王老师、李老师三人的年龄为三个连续的自然数,其中张老师28岁,他们三人分别教数学、语文和英语.已经知道:(1)李老师比英语教师年龄大;(2)张老师和语文教师不同岁;(3)语文教师比王老师年龄小.请判断一下,数学、语文、英语教师分别是谁?他们的年龄各为多大?写出结果,并写出分析过程. 12.某疗养院有100个床位,床号为1、2、3、…、100,依次分布在三种不同类型的病房内:单人房、双人房、三人房(每种类型至少有1间,前几间是单人房,接下来几间是双人房,最后几间为三人房).(1)最少有多少间房?(2)最多有多少间房?(3)如果其中有13个单人房,并且52、53号床在同一个房间,58、59号床不在同一个房间,问这里共有多少个房间?写出结果,并写出分析过程.2013深圳市第4届“启智杯”数学思维竞赛题(A 组)1.在下面的算式中,不同的汉字代表1—9中不同的数字,那么,“为了一切学生”的各字分别代表了什么数字?写出一种答案,说明你的分析过程.987654为了一切学生一切为了学生为了学生一切2.从1、2、3、4、5、6、7、8、9这9个数字中选出8个不同的数字分别填入下面两个算式的方框内(每个数字只许用一次),使它们都成立,简述理由.3.在如图所示的33 的方格中,不同的汉字代表不同的数,每行、每列和两条对角线上各数的和相等.则每一行各数之和是多少?写出结果并说明理由.4.如图,根据前面2个图形中四个数的排列规律,在后面图形的空缺处填入适当的数并说明你发现的规律.5.请将400分别表示成8个、10个、20个连续的奇数的和的形式;400可以写成最多多少个连续奇数之和?为什么?6.下图由6个大小相同的正方体组成的几何体吊在空中,从上下左右前后各个角度观察;会看到不同个数的正方形.请将你的观察结果填入如下括弧内,不必说明理由.从侧面(前后左右)看,共有()个正方形;从上面往下看有()个正方形;从下面往上看有()个正方形.7.请对下列空间几何体进行分类,并指出两种分类标准(即分类依据)和分类结果,填入如下的横线上.分类依据一是_______________________________________________,每一类分别是(把同一类标号填在一起)________________________,共分__________类;分类依据二是_______________________________________________,每一类分别是(把同一类标号填在一起)________________________,共分__________类.8.给定一条长度为2013米的硬塑料管,请你按下列要求把它裁断(三个要求同时满足);(1)每段长都是整数米;(2)任意三段为边长都不能构成三角形;(3)最长的一段尽可能的长.请问:最多可以裁成多少段?说出你的裁截思路与结果.9.如图,在斜边长为20cm 的直角三角形ABC 中去掉一个正方形EDFB ,留下两个阴影部分直角三角形AED 和DFC .若8cm AD ,12cm CD ,则阴影部分面积为多少?给出答案并说明你的计算依据.10.某小学六年级一、二班老师A 、B 、C 、D 、E 、F 、G 、H 共8人依次围着一张圆桌吃饭,其中有数学、语文、英语老师各2人,自然、社会老师各1人;有班主任2人,分别是语文和数学老师.为了便于交流,他们同一个学科的两人坐邻座,两位班主任也坐邻座,但自然老师与社会老师不坐邻座.已知C 的左侧老师与C 在同一学科;C 的对面老师教语文.请问哪两位是班主任?11.请设计一个游戏:地面上摆放着若干颗石子,甲乙两人轮流从中取石子,每人每轮最少取2颗,最多取5颗,取到最后一颗石子者为胜.请设定这堆石子的颗数(至少50颗),使先取者有必胜的策略,并说明你的策略.12.某商场购进1000套夏季套装,分三个阶段销售. (1)第一阶段:新货上架,以每套1000元价格出售;(2)第二阶段:旺季热卖促销,买2套打8折(即每件800元),买3套打6.5折; (3)第三阶段:过季大甩卖,全场3折.各阶段销售情况如下表.已知在第二阶段商场促销活动中,卖给一个人3套比卖给一个人两套可以多赚100元.问该批服装进价如何?该商场在这批服装销售中共赚(毛利润)多少钱?请填写下表.2012深圳市第3届“启智杯”数学思维竞赛题(A组)1.如图所示的算式中,相同的汉字表示相同的一位数字,不同的汉字表示不同的一位数字,则我+爱+启+智+杯= .写出你的推算过程.杯智杯启智杯爱启智杯爱启智杯我爱启智杯2.有三个封口的袋子,里面都装着同样重量和大小的小球,A袋子内装着红球,B袋子内装着白球,C袋子内混合装着红球和白球.三个袋子分别贴有“红色”、“白色”、“混合色”的标签,可惜每一个标签都与袋子中球的实际颜色不符.现在允许你只打开一个袋子,从中摸出一球(不准看袋子里面),看着这个球的颜色,你能立刻为三个袋子贴上正确的标签吗?请说明你的具体操作方法.3.在6,9,15,19,21,27中,从不同的角度看,你会发现有一个与众不同的数,这个数是几?请你写出4个不同的答案,并说明理由.4.观察下列等式:1223113221;2335225332;3558338553以上每个等式中两边的数字是分别对称的,且每个等式中的两位数与三位数的数字之间具有相同的规律,我们称这类等式为“数字对称式”,请根据上述各式所反映的规律填空,使下列式子称为数字对称式.(1)62______________26;(2)______891198______.说明你发现的规律.5.如图所示,在四分之一圆内含有两个以半径为直径的半圆,求图中阴影部分的面积和空白处的面积之比.(π取3.14)6.如图所示,已知圆周上的五个点A、B、C、D、E依次间隔弧长为1、2、3、4厘米,而E和A之间的弧长为5厘米,有一根很长的直尺,该直尺上的整整长度处依次标上1厘米,2厘米、3厘米、4厘米…….现在将该圆放在直尺上,将点B放在标有0厘米的刻度处,让圆沿着直尺由左到右无滑动滚动前进,问在直尺的2012厘米处与圆周上对应的英文字母是.说明你的推算过程.7.将数字2、3、5、8、9、11书写在每一个骰子的六个表面上,做成6枚一样的骰子.分别取3枚这种同样的骰子叠放成如图A和B的两个柱体.问柱体A和柱体B的表面(不含底面)点数之和分别是多少?说明你的理由.8.用相同大小的正六边形来铺广场,按如上图所示的方式来铺设,中间的正六边形瓷砖记为A,定义它为第一层,在它的周围铺上同样大小的正六边形瓷砖,定义为第二层,在第二层的外围铺上同样大小的正六边形瓷砖,定义为第三层,……,按这种方式铺下去,当铺第15层时,用了块瓷砖.请说出你的规律.9.本题分为两个小题,每题各5分.请分别写出解题过程.(1)有三个连续的两位数,由小到大依次分别是3、4、5整除,那么这三个数各是几?(2)三个连续自然数,由小到大依次分别是7、10、13整除,那么,所有这三个自然数组中,最小的一组是多少?10.如图所示,在一块22cm cm 的方格网板上钉上9颗图钉.如果用线绳围成三角形,大小形状完全相同的算一类,问其中面积为212cm 的三角形有几类?分别在图中画出一个.每类各有多少个不同位置的三角形?一共有多少个?11.仔细观察右边的算式,答案649正好和上边的被减数946的数字排列相反.如果选另外三位数减掉297后,答案也正好和所选的三位数的数字顺序相反的话,可以选出若干组这样的三位数,那么一共可以选出多少个这样的三位数?说明它的特征.94629764912.国庆期间,天虹商场采取“买满200送100连环送”的酬宾活动,规则如下:(一)顾客在商场内消费每满200元就送100元购物券,多买多送(满400送200,以此类推),消费不足200元的部分不赠送.(二)购物券不能兑换现金,但可以与现金同等使用,用购物券购物同样享受满200送100. 问题:(1)如果你有1000元,最多能购买价值多少钱的商品?说明你的购买策略. (22011深圳市第2届“启智杯”数学思维竞赛题(A 组)1.今天是2011年12月03日,请在20111203八个数字之间添加+、-、×、÷四种运算符号中的某些符号,使得下面等式成立.2011120392.汉字“数”、“学”、“好”分别表示不同的数字,根据下列所给算式,则“数”表示数字_____,“学”表示数字_______,“好”表示数字________.学好学好学好学好数学3.“启”、“智”、“杯”各表示一个数字,同时满足下列等式: ① =22启智杯;② =4启智杯;③ =6启智杯则“启”表示________,“智”表示________,“杯”表示________.4.有一个孤岛,那里的人们在商品交易时有如下特殊的要求: (1)所有商品价格(单位:元)为整数,且不超过31元.(2)消费者支付款项时,每一种币值的钱币最多只能使用1枚,而且商家不找零钱. 问:为了保证公平交易(照实支付),至少应该生产__________种不同面值的钱币,请具体列举出来:_____________________________________.5.按照下图规律,写出第四个图中x ,y ,z 所表示的三个数.x =_____,y =_____,z =_____.请说明理由:_____________________________________________.427564117151051937x y z图一图二图三图四6.在同一个布袋里有红色、黄色、蓝色袜子各15只,最少要拿_________只,才能保证其中至少有2双颜色不同的袜子(注意:袜子不分左右).7.如图所示是2011年12月份的日期,现用一矩形在日历中任意框出6个数 ,请用一个等式表示a 、b 、c 、d 、e 、f 这6个数之间的关系是______________________.8.如上图所示,长方形的长:宽=4:3,将该长方形划分为四个三角形,其面积分别是1234S S S S 、、、.若1234=+=S S S S ,则23:S S =___________.9.a 、b 、c 、d 为正整数,满足等式13014311a b c d,则d =__________.10.观察下面的算式:0000,111122,222233,11112323,……根据算式反映出的规律,再写出满足这个规律的两个算式.________________________,_________________________.F11.半径为1的圆沿着半径为3的圆的内侧与外侧无滑动地滚动(如下图),当它们回到开始滚动的位置时: (1)哪个圆滚动的圈数多?为什么?________________________ (2)若点A 是内侧滚动圆上的一个定点(如甲图),请在甲图中画出点A 的运动路线.12.有一家公司董事长想从他四个得力助手中挑选一名担任策划部总经理,他给他们出了以下问题:把一闲置的圆形土地平均分成四块,要求每块都与其他三块相连(即有公共边).请你在下列所给图中至少画出2个符合要求的分割方法.13.A ,B ,C ,D 四个盒子中分别放有6,5,4,3,个球.第一个小朋友找到放球最少的盒子,从其它的盒子中各取1个球放入这个盒子中,然后第二个小朋友又找到一个放球最少的盒子,从其它的盒子中各取1个球放入这个盒子中,……如此进行下去,当第2011个小朋友放完后,A ,B ,C ,D 四个盒子中的球数依次是多少个?乙图甲图A2010深圳市第1届“启智杯”数学思维竞赛题(A组)1.一张三角形的纸片,请你剪去一个角,要求还剩三个角,想一想,该怎样剪?2.桌上放着八枚硬币,竖着放五枚,横着放四枚(如上图),请问:如果只许移动其中一枚,能否使横竖都成为五枚硬币?3.请在四个数字5之间,适当添加,,,,()这些符号,以使等式成立.(1)55551;(2)55552;(3)55553;(4)55554;(5)55555;(6)55556.4.下面是一组被打乱的数字,在被打乱之前它们之间有一个非常有趣的规律.你试着找找看,然后按其原有的规律重新把下面的数字排列起来,并说明原来的规律是什么.3,5,13,21,1,1,2,85.在下列题目中缺少一个图,你认为从左边选择哪一个图插入右边空挡比较合理?说明你的理由.()6.商店规定4个空汽水瓶可换一瓶汽水,某班28位同学春游,他们至少买多少瓶汽水才能确保每人有一瓶汽水喝?7.一位3米高的巨人,沿赤道(假定赤道是一个圆)环绕地球步行一周,那么他的脚底沿赤道圆周移动了一圈,他的头顶画出了一个比赤道更大的圆.已知地球赤道的半径是6371千米.在这次环球旅行中,这位巨人的头顶比他的脚底多走了多少米?我们可以这样来计算:巨人的脚底走过的圆,半径是6371千米.巨人的身高是3米,所以他的头顶走过的圆的半径比脚走过的圆的半径增加3米.若都用千米做长度单位,半径就增加0.003千米.取圆周率的近似值为3.14,那么两圆周长的差为:3.142(63710.003) 3.1426371 3.140.0030.01884()18.84()km m.结论是:环绕地球一周,巨人的头顶只比脚底多走18.84米.如果这位巨人打算再环绕月球表面步行一圈(假定这个圈是以月球球心为圆心的圆),那样一圈走下来,他的头顶比脚底多走了________米呢?8.我们知道:1条直线可以把一个平面分成两个部分,2条直线最多可以把一个平面分成四个部分,那么8条直线最多可以把一个平面分成________个部分.9.某人每天下午5点钟下班,由汽车按时到达接他回家.一天,他提前一个小时结束工作,因汽车未到达而步行回家,在途中遇到来接他的汽车又改为乘车,结果比平时早10分钟到家,此人步行分钟遇到接他的汽车.10.对于给定的有顺序的四个数:30,10,67,15.任意交换两个非相邻位置的数,算作一次操作(不允许交换两个相邻位置的数),能否利用三次操作,使得最后得到的四个数从左到右依次减小,写出具体的操作步骤.11.2009只茶杯,杯口朝下,每次翻动4只茶杯,能否经过若干次翻动,使所有茶杯全变为杯口朝上?每次翻动5只呢?12.在一张长方形纸片上有2009个点,加上4个顶点共有2013个点,这些点中任意3点都不在一条直线上.现在以这2013个点为顶点,把长方形纸片剪开,最多能剪出多少个三角形(任意两个三角形没有重叠)?。
启智杯考前模拟训练题50题有答案 的

启智杯考前模拟训练题50题1. 方兴超市购进一批食盐,第一个月售出这批食盐的40%,第二个月又售出420袋,这时已售出的和剩下的食盐的数量比是3:1,则方兴超市购进的这批食盐有 袋.【解析】 分百应用题,寻找量率对应,420所对应的率为140%25%35%--=,42035%1200÷=(袋)2. 已知甲乙两数的和是231,已知甲数的末位是0,如果把甲数末位0去掉,正好等于乙数,那么乙数是 ,甲数是 .【解析】 乙数:21;甲数:2103. 如图,三个图形的周长相等,则::a b c = .【解析】 45,:5:4b a b a ==,65,:5:6a c a c ==,得到::20:25:24a b c =4. 一瓶可乐2.5元,3个空瓶可以再换一瓶可乐.有30元,最多可以喝到 瓶可乐.【解析】 3个空瓶可以换一瓶,相当于买3瓶只花2瓶的钱(借一个空瓶还回去),30 2.52318÷÷⨯=(瓶)5. “12345678910111213…484950”是一个位数很多的多位数,从中划去80个数字,使剩下的数字(顺序不变)组成一个首位不为0的多位数,则这个多位数最大为多少?最小为多少?【解析】 (1)这个数的位数是9+2×41=91,所以划去80个数字后是11个11位数.(2)为了使这个多位数最大,应使前面的9尽量多,所以这个多位数最大为99997484950.(3)为了使这个多位数最小,除了使第一位是1之外,还应使前面的0尽量多,这个多位数最小为10000123440.a 2a c c c c c 2a a2b2b a6. 在右边的算式中,相同的符号代表相同的数字,不同的符号代表不同的数字,根据这个算式,可以推算出:+++d W V ☆=_______. +dd WW W W W W V V☆☆ 【解析】 比较竖式中百位与十位的加法,如果十位上没有进位,那么百位上两个“□”相加等于一个“□”,得到“□”0=,这与“□”在首位不能为0矛盾,所以十位上的“□+□”肯定进位,那么百位上有“□+□110+=+□”,从而“□”9=,“☆”8=.再由个位的加法,推知“○+△8=”.从而“+++=d W V ☆98825++=”.7. 在1~100中任意取出两个不同的数相加,其和是偶数的共有多少种不同的取法?【解析】 两个数的和是偶数,通过前面刚刚学过的奇偶分析法,这两个数必然同是奇数或同是偶数,而取出的两个数与顺序无关,所以是组合问题.从50个偶数中取出2个,有2505049122521C ⨯==⨯(种)取法; 从50个奇数中取出2个,也有2505049122521C ⨯==⨯(种)取法. 根据加法原理,一共有122512252450+=(种)不同的取法.8. 正方形ABCD 的面积为9平方厘米,正方形EFGH 的面积为64平方厘米,如图所示,边BC 落在EH 上,已知三角形ACG 的面积为6.75平方厘米.则三角形ABE 的面积为 平方厘米【解析】 连接EG ,AG 与EG 平行,阴影部分面积=三角形AEC 的面积,AB =3cm ,所以EC =6.7523 4.5cm ⨯÷=,()24.5332 2.25ABE S cm =-⨯÷=V .也可以用三角形AEC 的面积减去三角形ABC 的面积得到ABE 的面积26.75 4.5 2.25cm =-=9. a 、b 、c 是整数,则(a -b )/2、(b -c )/2、(c -a )/2中( )整数.A 、至少有一个B 、仅有一个C 、仅有两个D 、没有【解析】 若均为偶数,则有三个整数,而当奇奇偶或偶偶奇时,最少整数有一个,选A10. a #b =a +b -1 ,a !b =a ×b -1(1)求3![(6#8)#(6!2)];(2)x #(x !8)=61,求x ;【解析】 (1)68(2)7x =11. 由数字0,1,3,9可以组成多少个无重复数字的自然数?【解析】 满足条件的数可以分为4类:一位、二位、三位、四位数.第一类,组成0和一位数,有4个(0不是一位数,最小的一位数是1);第二类,组成二位数,有339⨯=个;第三类,组成三位数,有33218⨯⨯=个;第四类,组成四位数,有332118⨯⨯⨯=个.由加法原理,一共可以组成49181849+++=个数.12. 如图,这是一个棋盘,将一个白子和一个黑子放在棋盘线的交叉点上,但不能在同一条棋盘线上,则有 种不同的放法.【解析】 2516400⨯=种13. 如果a ,b 均为质数,且3741a b +=,则a b +=______.【解析】 根据题意a ,b 中必然有一个偶质数2,,当2a =时,5b =,当2b =时不符合题意,所以257a b +=+=.14. 有甲、乙两堆棋子,其中甲堆棋子多于乙堆.现在按如下方法移动棋子:第一次从甲堆中拿出和乙堆一样多的棋子放到乙堆;第二次从乙堆中拿出和甲堆剩下的同样多的棋子放到甲堆;第三次又从甲堆中拿出和乙堆同样多的棋子放到乙堆.照此移法,移动三次后,甲、乙两堆棋子数恰好都是32个.问甲、乙两堆棋子原来各有多少个?【解析】 我们从最后一步倒着分析.因为第三次是从甲堆拿出棋子放到乙堆,这样做的结果是两堆棋子都是32个,因此,在未进行第三次移动之前,乙堆只有32216÷=(个)棋子,而甲堆的棋子数是321648+=(个),这样再逆推下去,逆推的过程可以用下表来表示,表中的箭头表示逆推的方向.所以,甲堆原有44个棋子;乙堆原有20个棋子.采用列表法非常清楚.【答案】甲乙两堆棋子原来各有44个和20个15. 下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积.【解析】 所求面积等于图中阴影部分的面积,为2052082140-+⨯÷=()(平方厘米).16. 同学们,你玩过“扫雷”的游戏吗?在64个方格内一共有10个地雷,每格中至多有一个,对于填有数字的方格,其格内无地雷且与其相邻的所有方格中地雷的个数与该数字相等,你认为图中所标的数字_______是有雷的.【解析】 “扫雷”游戏主要考查观察能力和推理能力.先考虑标有①②的两个方格周边的情况.由于第六行有4个方格中的数字都是0,表示它们的周围没有雷,所以得到第五行前三列的3个方格都不是雷,而第四行第一列的方格中的数是1,表示它的周围有1个雷,所以标有①②的两个方格中恰好有1个雷,那么对于第三行第一列标有2的方格来说,它的周围有2个雷,其中一个在标有①②的两个方格中,另一个只能在第二行第二列的方格内.然后再看第二行第一列的方格,它的周围有1个雷,在第二行第二列的方格内,所以标有①的方格中没有雷,标有②的方格中有雷.再考虑标有③的方格的周边.由于第七行第一列的方格标有数字1,表示第八行第一、二列的两个方格中恰好有1个雷,而第七行第二列的方格标有数字2,说明它的周围有2个雷,那么一个雷在第八行第一、二列的两个方格中,另一个雷只能在标有③的方格中,所以标有③的方格中有雷.再看标有④⑤的方格的周边.由于第八行第七列的方格标有数字1,说明第八行第八列和第七行第八列的两个方格内恰有1个雷,而第七行第七列的方格也标有数字1,所以标有④的方格是没有雷的.而第六行第七列的方格标有数字3,说明它的周围有3个雷,所以标有⑤的方格是有雷的.所以图中所标数字为②、③、⑤的方格是有雷的.17. 如图3,每个小方块周围最多有8个小方块,外围没标数字的小方块是未探明的雷区,其中每个小方块最多有一个雷.内部的小方块没有雷,数字表示所在小方块周围的雷数.图中共有 个雷.【解析】 1612113332313312111234图318.7个完全相同的长方形拼成了图中阴影部分,图中空白部分的面积是多少平方厘米?【解析】由图可知,长方形的长是宽的4倍,宽的6倍是24厘米,则长方形的宽是4厘米,故图中空白部分的面积是44232⨯⨯=(平方厘米).19.敌人欲从河岸B进攻对岸A,河上有13座桥,为阻止敌人进攻决定将桥炸坏.至少炸掉座桥可将敌人拦阻在河岸B.【解析】3座:5、9、1020.一班和二班的人数之比是8:7,如果将一班的8名同学调到二班去,则一班和二班的人数比变为4:5.求原来两班的人数.【解析】一班:二班=8:724:21⨯=和不变153一班:二班=4:520:25⨯=95一班向二班调了4份为8人,故每份842÷=(人),一班:24248⨯=(人)⨯=;二班:2124221.自然数N是一个两位数,它是一个质数,而且N的个位数字与十位数字都是质数,这样的自然数有多少个?【解析】这样的自然数有4个:23,37,53,73.22.由于天气逐渐冷起来,牧场上的草不仅不生长,反而以固定的速度在减少.已知某块草地上的草可供20头牛吃5天,或可供15头牛吃6天.照此计算,可以供多少头牛吃10天?【解析】设1头牛1天的吃草量为“1”,那么每天自然减少的草量为:()()20105150+⨯=;10天吃完需要牛的⨯-⨯÷-=,原有草量为:()2051566510头数是:15010105÷-=(头).23.甲、乙两人同时从A点背向出发,沿400米的环形跑道行走,甲每分钟走80米,乙每分钟走50米,两人至少经过多长时间才能在A点相遇?【解析】甲、乙走一圈分别需要5分钟和8分钟,因此他们要是在A点再次相遇,两人都要走整圈数,所以所需的时间应是5和8的最小公倍数40分钟.24.长方形有四个角,剪掉一个角,还剩几个角?【解析】共有三种情况,如下图,分别剩下5、4、3个角.25.图中的三个图形都是由A、B、C、D(线段或圆)中的两个组合而成,记为A*B、C*D、A*D.请你画出表示A*C的图形.【解析】观察上图,第一个图形和第三个图形的共同之处是都有一条竖向线段,而它们共有的字母是A,因此A表示竖向线段;第二个图形与第三个图形的共同之处是都有一条横向线段,它们的共同字母是D,因此D表示横向线段.这样,由第一个图形可知B表示大圆,由第二个图形可知C表示小圆,从而A*C表示的图形应为竖向线段和小圆组合而成,即下图.26.用红、黄、蓝、白、黑、绿六种颜色分别涂在正方体的各个面上,每一个面只涂一种颜色.如图所示,现有涂色方式完全一样的四块小正方体拼成了一个长方体.试回答:每个小正方体中,红色面的对面涂的是什么色?黄色面的对面涂的是什么色?黑色面的对面是什么色?【解析】在能看见的9个面中红色出现的次数最多.观察图8—4中最上面的一个正方体,由于红色和黑色、黄色相邻,所以它的对面不可能是黑黄两色.同理,由第二个正方体可知,红色的对面不能是白色;由第三个正方体知,红色的对面不能是蓝色.所以红色的面的对面只可能是绿色.同理,黄色面的对面不可能是红色、黑色或白色,又已推知不可能是绿色,所以黄色面的对面只可能是蓝色.这样黑色面的对面就只可能是涂白色的了.27.图1是下面的表面展开图①甲正方体;②乙正方体;③丙正方体;④甲正方体或丙正方体.甲 乙 丙【解析】 从展开图可以看出,每个面上至少有一块阴影,从而排除丙;又每个面上没有相邻的两块阴影,从而排除乙.故选甲答案为①.28. 如右图所示,在一个正方形内画中、小两个正方形,使三个正方形具有公共顶点,这样大正方形被分割成了正方形区域甲,和L 形区域乙和丙.甲的周长为4厘米,乙的边长是甲的周长的1.5倍,丙的周长是乙的周长的1.5倍,那么丙的周长为多少厘米?EF 长多少厘米?【解析】 乙的周长实际上是正方形AHJE 的周长(我们可将乙与甲重合的两条线段分别向左、向下平移),同样的,丙的周长也就是正方形ABCD 的周长.由于4 1.56AE =⨯=,6 1.59AD =⨯=,所以丙的周长为9436⨯=厘米,642EF AE AF =-=-=(厘米).29. 在一块长方形的地里有一正方形的水池(如下图).试画一条直线把除开水池外的这块地平分成两块.【解析】 用连对角线的办法找出这块长方形地的中心O 和正方形水池的中心A .过O 、A 画一条直线,这条直线正好能把除开水池外的这块地平分为两块(如右上图).FEH BA AO30. 试将任意一个矩形分成三块,然后拼成一个三角形.【解析】 方方法二:31. 900000-9=________×99999.【解析】 832. 多米诺骨牌是由塑料制成的1×2长方形,共28张,每张牌上的两个1×1正方形中刻有“点”,点的个数分别为0,1,2,…,6个不等,其中7张牌两端的点数一样,即两个0,两个1,…,两个6;其余21张牌两端的点数不一样,所谓连牌规则是指:每相邻两张牌必须有一端的点数相同,且以点数相同的端相连,例如:现将一付多米诺骨牌按连牌规则连成一条链,如果在链的一端为6点,那么在链的另一端为多少点?并简述你的理由.【解析】 由连牌规则可知,在链的内部各种点数均成对相连,即所有点都有偶数个,而6点的个数为8,所以在链的两端一定有偶数个点,所以链的另一端也应为6.33. 甲、乙两个哲人将正整数5至11分别写在7张卡片上.他们将卡片背面朝上,任意混合之后,甲取走三张,乙取走两张.剩下的两张卡片,他们谁也没看,就放到麻袋里去了.甲认真研究了自己手中的三张卡片之后,对乙说:“我知道你的两张卡片上的数的和是偶数.”试问:甲手中的三张卡片上都写了哪些数?答案是否唯一.【解析】 甲手中的8张卡片上分别写了6,8和10.甲知道其余4张卡片上分别写了哪些数,但不知道它们之中的哪两张落到了乙的手中.因此,只有在它们之中任何两张卡片上的数的和都是偶数时,甲才能说出自己的断言.而这就意味着,这4张卡片上所写的数的奇偶性相同,亦即或者都是偶数,或者都是奇数.但是由于一共只有3张卡片上写的是偶数,所以它们不可能都是偶数,从而只能都是奇数.于是3张写着偶数的卡片全都落入甲的手中.答案是唯一的.34. 三个人同时前往相距30千米的甲地,已知三人行走的速度相同,都是5千米每小时;现在还有一辆自行车,但只能一个人骑,已知骑车的速度为10千米每小时.现先让其…………中一人先骑车,到中途某地后放车放下,继续前进;第二个人到达后骑上再行驶一段后有放下让最后那人骑行,自己继续前进,这样三人同时到达甲地.问,三人花的时间各为多少?【解析】 由于每人的速度相同,所以每人行走的路程相同,骑车的路程也要相同,这样每人骑车的距离都是1/3,所以时间就是20÷5+10÷10=5小时35. 张师傅开汽车从A 到B 为平地(见下图),车速是36千米/时;从B 到C 为上山路,车速是28千米/时;从C 到D 为下山路,车速是42千米/时. 已知下山路是上山路的2倍,从A 到D 全程为72千米,张师傅开车从A 到D 共需要多少时间?【解析】 方法一:设BC 距离为:[]28,4284=(千米),所以CD 距离为842168⨯=(千米),那么B -C -D 的平均速度为:()()8416884281684236+÷÷+÷=(千米/小时),和平路的速度恰好相等,说明A -B -C -D 的平均速度为36千米/小时,所以从A -D 共需要的时间为:72362÷=(小时)方法二:设上山路为x 千米,下山路为2x 千米,则上下山的平均速度是:22824236x x x x +÷÷+÷=()()(千米/时),正好是平地的速度,所以行AD 总路程的平均速度就是36千米/时,与平地路程的长短无关.因此共需要72362÷=(小时).36. 右图是一个园林的规划图,其中,正方形的43是草地;圆的76是竹林;竹林比草地多占地450平方米. 问:水池占多少平方米?【解析】 正方形的43是草地,那如果水池占1份,草地的面积便是3份;圆的76是竹林,水池占1份,竹林的面积是6份.从而竹林比草地多出的面积是(6-3=)3份.3份的面积是450平方米,可见1份面积是450÷3=150(平方米),即水池面积是150平方米.37. 地球表面的陆地面积和海洋面积之比是29∶71,其中陆地的四分之三在北半球,那么南、北半球海洋面积之比是( ).A . 284∶29B . 284∶87C . 87∶29D . 171∶113【解析】 解:设地球表面积为1,则北半球海洋面积为:0.5-0.29×34=1.134南半球海洋面积为:0.71-1.134=1.714南北半球海洋面积之比为:1.714∶1.134=171∶113 答案:D38. 对任意两个不同的自然数,将其中较大数换成这两数之差,称为一次变换.如对18和42可作这样的连续变换:18,42→18,24→18,6→12,6→6,6直到两数相同为止.问:对1234和4321作这样的连续变换最后得到的两个相同的数是 .【解析】 操作如下:1234,4321→1234,3087→1234,1853→1234,619→615,619→615,44714243前一数每次减少→…→,4→3,4→3,1→2,1→1,1实际上按此法操作最后所得两相同的数为开始两数的最大公约数.即1234与4321的最大公约数为1.此法也称为辗转相减法求最大公约数.39. 有一副扑克牌,一开始抓若干张(小于13张),然后进行下列操作:抓和手里现有的扑克牌数目相等的扑克牌,然后若扑克牌总数超过13张,则放回其中的13张,称为一次操作.进行了777次操作后,手里有7张牌,则一开始手里有多少张?【解析】 根据倒退法知道第777次操作后是7,那么第776次操作就是:()7132=10+÷,第775次操作就是102=5÷,找到规律是遇见奇数就是加13后除以2,遇见偶数就是直接除以2,所以操作后得到这样一串数为:7、10、5、9、11、12、6、3、8、4、2、1、7、10L L ,观察发现是12个一周期,所以77712=649÷L L ,所以第一次手里的数是8,一开始手里的数是4张扑克.40. 小华和爸爸分享“红、黑甜品”(红豆沙加芝麻糊).方法是:小华先将两勺红豆沙倒进盛载芝麻糊的碗中,搅匀后再取回两勺放入原先盛载红豆沙的碗中,混成后,爸爸问小华:“如果混合前红豆沙与芝麻糊的体积一样,那么混合后红豆沙含芝麻糊的分量与芝麻糊含红豆沙的分量比较,哪一个多?”.小华的正确答案是_____.【解析】 一样多41. 由于潮汐的长期作用,月球自转周期与绕地球公转周期恰好相同,这使得月球总是以相同的一面对着我们.在地球上最多能看到 50%的月球面积,从一张月球照片中最多能看到 50%的月球面积.(填“大于”、“小于”或“等于”)【解析】 小于; 小于方法一、一张静止的照片,能看到的球体面积的极限是一半,只有当距离球体无限远时才能看到球体表面积的一半.方法二、如果能看到一半,则能看到一半的直线为两条平行线,不可能相交.42. 刘刚、马辉、李强三个男孩各有一个妹妹,六个人进行乒乓球混合双打比赛.事先规定:兄妹二人不许搭伴.第一盘:刘刚和小丽对李强和小英;第二盘:李强和小红对刘刚和马辉的妹妹.问:三个男孩的妹妹分别是谁?【解析】 因为兄妹二人不许搭伴,所以题目条件表明:刘刚与小丽、李强与小英、李强与小红都不是兄妹.由第二盘看出,小红不是马辉的妹妹.将这些关系画在左下表中,由左下表可得右下表.刘刚与小红、马辉与小英、李强与小丽分别是兄妹.43. 甲、乙、丙、丁四个人的职业分别是教师、医生、律师、警察.已知:⑴教师不知道甲的职业;⑵医生曾给乙治过病;⑶律师是丙的法律顾问(经常见面);⑷丁不是律师;⑸乙和丙从未见过面.那么甲、乙、丙、丁的职业依次是: .【解析】 律师、教师、警察.由⑶可以知道丙不是律师,但是他见过律师,再由⑸知乙不是律师,又由⑷可知甲是律师.于是由⑴和⑶知丙不是教师,由⑵和⑸知丙不是医生,从而丙是警察.再由⑵知乙是教师,丁是医生.列表如下(列表的好处在于直观明了,不会犯错误):李强马辉刘刚小丽小红小英×√×××××√√44. 右边算式中,A 表示同一个数字,在各个□中填入适当的数字,使算式完整.那么两个乘数的差(大数减小数)是 ?11AA A ⨯【解析】 由11AA 能被11整除及只有11⨯,37⨯,99⨯的个位是1,所以A 可能为1,3,7或9,而且11AA 可分解成11与1个一位数和一个两位数的乘积.分别检验1111、1331、1771、1991,只有1771满足:177111723=⨯⨯,可知原式是77231771⨯=.所以两个乘数的差是772354-=.45. 电子数字0~9如图所示,右图是由电子数字组成的乘法算式,但有一些模糊不清,请将右图的电子数字恢复,并将它写成横式形式: .【解析】 ⑴可以看出乘积的百位可能是2或8,由于被乘数的十位和乘数都不能是9,最大可能为8,所以它们的乘积不超过898712⨯=,故乘积的首位不能为8,只能为2;⑵被乘数的十位和乘数要与图中相符,只能是0、2、6或8,0首先可以排除,所以可能为2、6或8;⑶如果被乘数的十位是6或8,那么乘数无论是2、6或8,都不可能乘出百位是2的三位数.所以被乘数的十位是2,相应得出乘数是8;⑷被乘数应大于200825÷=,可能为27、28或29,检验得到符合条件的答案:288224⨯=46. 有一道关于蜗牛爬墙的题:“日升六尺六,夜降三尺三,墙高一丈九,几日到顶端”.蜗牛第 天首次到顶端.【解析】 蜗牛一整天可升三尺三6.6 3.3 3.3-=,四天可升一丈三尺二,第五天白天即已经达到顶端.47. 现有5段铁链,每段上有4个封闭的铁环.现在要打开一些铁环,把这20个铁环焊接成一个一环套一环的圆圈.如果每打开一个铁环要2分钟,焊接上一个铁环要3分钟.那么焊成这个圆圈,至少需要________分钟.【解析】 把第一段的每个都打开之后用了428⨯=(分钟),下面用每个铁环把剩下的4 段铁链之间的两个相连,只需要4312⨯=(分钟).所以至少需要20分钟.48. 用数字1,1,2,2,3,3拼凑出一个六位数,使两个1之间有1个数字,两个2之间有2个数字,两个3之间有3个数字.【解析】 312132 23121349. 一城镇共有5000户居民,每户居民的小孩都不超过两个.其中一部分家庭每户有一个小孩,余下家庭的一半每户有两个小孩,则此城镇共有 个小孩.【解析】 5000户居民可以分为三部分:(1)只有1个小孩的;(2)有2个小孩的;(3)没有小孩的.其中(2)与(3)的居民相同,我们就可以将有2个小孩的家庭的其中1个孩子分给没有小孩的家庭,这样5000户居民每个家庭都有1个小孩,所以这城镇共有5000个小孩.50. 若干个同样的盒子排成一排,小明把五十多个同样的棋子分装在盒中,其中只有一个盒子没有装棋子,然后他外出了.小光从每个有棋子的盒子里各拿一个棋子放在空盒内,再把盒子重新排了一下.小明回来仔细查看了一番,没有发现有人动过这些盒子和棋子.问共有多少个盒子?【解析】 原来有个空的,说明现在也有个空的;现在空的说明原来这盒有1个,当然现在也必须有个盒子有1个;现在盒中有1个,说明原来是2个,当然现在也必须有个盒子有2个;……考虑50多,所以有0+1+2+3+4+5+6+7+8+9+10=55 共11个盒子.第8题。
2024“走进美妙的数学花园”数学竞赛一年级初赛试卷及答案
2024“走进美妙的数学花园”数学竞赛一年级初赛试卷1.2+4+6+8+10+12+14-1-3-5-7-9-11-13=( )。
2.观察下面的算式有什么规律,那么5★9=( )。
2★3=2+3+16★9=6+9+35★7=5+7+23.森林运动会开始了,小乌龟本来在队伍的第4名,经过不懈的努力,超过了第2名,此时他和倒数第3名之间还有11只小动物,那么一共有( )只小动物参加了森林运动会。
4.下图中只包含一个苹果的正方形有( )个。
5.小松鼠乐乐有80个松果,它计划以后每天吃掉9个松果,每天摘来8个松果,那么第30天结束后,乐乐还剩( )个松果。
6.观察下面的三个天平,已知苹果、香蕉的重量都是整数克,那么一个苹果和一根香蕉的重量加起来是( )克。
7.一年级一班选举班长,每人投票从甲、乙、丙三个候选人中选择一人,已知全班共有50人可参加投票,并且在计票过程中的某时刻,甲得到15票,乙得到13票,丙得到10票,如果得票比其他两人都多的候选人将成为班长,那么甲最少再得( )张票就能够保证当选。
8.下面图形表示一个8位数,任意相邻格子里的数字之和都等于18,那么第3个格子填的数是( )。
9.己知在下面的竖式中,相同的图形代表了相同的数字,不同的图形代表不同的数字,那么☆+△+O=( )。
10.相同的图形代表了相同的数,不同的图形代表不同的数。
根据下面的算式,那么★+◆+■=( )。
◆+■=35★+★+★=◆★+★+■=2711.如图8张大小相同的纸片依次放到桌面上,形成下面的图形,如果按照自下而上的排放次序将这些正方形依次编号为1-8,那么标有字母c和G的正方形编号加起来是( )。
12.为了回收空汽水瓶,商店规定:每3个空汽水瓶可以换1瓶汽水,佳佳有12元钱,每瓶汽水1元,如果商店可以借给他若干个空瓶,但要求她喝完全部汽水后要还,他最多可以喝到( )瓶汽水13.如图①,是一个3×3的方格表,每个方格(除了右下最后一个方格)都包含了1~8中某个数字和一个箭头,该箭头正好指向下一个数字所在方格的方向,但两个方格可以不相邻。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7. 解:不必问月球赤道的半径是多大,也用不着做计算,头顶只比脚底多走的路程还是只有 18.84 米。 因为在刚才解答环绕地球旅行的问题时,地球赤道的半径在计算过程中消去了,计算结果与脚底圆周 的半径无关。 8. 解:实验归纳:在 n 刀的基础上再增加一刀,就增加了 n 块。共 37 个
9. 解:如图,假定此人在 P 点遇到接他的汽车,也就 是说,与往常相比,汽车少车两个 PB(一个来回) , 结果少用 10 分钟, 说明走一个 PB 需 5 分钟.汽车到单 位应是 5 点钟,那么到 P 点是 4 点 55 分,也就是,此 人 4 点开始从办公室出来, 4 点 55 分在 P 点遇到汽车, 共走了 55 分钟。
6.商店规定 4 个空汽水瓶可换一瓶汽水,某班 28 位同学春游,他们至少买多少瓶汽水才能确保每人 有一瓶汽水喝?
1
理科教研部
7.一位 3 米高的巨人,沿赤道环绕地球步行一周。那么他的脚底沿赤道圆周移动了一圈,他的头顶画 出了一个比赤道更大的圆。已知地球赤道的半径是 6371 千米。在这次环球旅行中,这位巨人的头顶比 他的脚底多走了多少千米? 巨人的脚底走过的圆, 半径是 6371 千米。巨人的身高是 3 米,所以他的头顶走过的圆,半径增加 3 米。 都用千米做长度单位,半径增加的数量就是 0.003 千米。取圆周率的近似值为 3.14,那么两圆周长的 差=3.14×2×(6371+0.003)-3.14×2×6371=3.14×2×0.003=0.01884(千米)=18.84(米)。 结论是:环绕地球一周,巨人的头顶只比脚底多走 18.84 米。 如果这位巨人打算再环绕月球表面步行一圈,那样一圈走下来,他的头顶比脚底多走了________ 千米呢? 8.我们知道:1 刀可以把一个蛋糕切成两块,2 刀最多可以把一个蛋糕切成四块,那么 8 刀最多可以把 一个蛋糕切成________块。
17. 正解:本题的数字虽然多些,却很有规律:三次分糖的份数分别是 8、9、10,顺次加 1;每次余
下糖的块数分别是 2、3、4,也是顺次加 1。 由于 8-2=9-3=10-4=6,所以问题的条件可以换一种说法:如果平均分成 8 份,就会有一份缺 6 块;
5
理科教研部
如果平均分成 9 份,也会有一份缺 6 块;如果平均分成 10 份,还是有一份缺 6 块。 既然每次都缺 6 块,不妨暂借 6 块糖来,放进这堆糖里,那么糖的总数就是 8 的倍数,也是 9 的 倍数,又 是 10 的倍数。 8、9、10 的最小公倍数是 8×9×5=360, 因而这堆糖加上 6 块以后,至少是 360 块。 所以最后得到,这堆糖至只剩 6 个乒乓球,让对方先拿球,你一定能拿到第 6 个乒乓球。理由是: 如果他拿 1 个,你拿 5 个;如果他拿 2 个,你拿 4 个;如果他拿 3 个,你拿 3 个;如果他拿 4 个,你 拿 2 个;如果他拿 5 个,你拿 1 个。 我们再把 100 个乒乓球从后向前按组分开,6 个乒乓球一组。100 不能被 6 整除,这样就分成 17 组;第 1 组 4 个,后 16 组每组 6 个。3、这样先把第 1 组 4 个拿完,后 16 组每组都让对方先拿球,自 己拿完剩下的。这样你就能拿到第 16 组的最后一个,即第 100 个乒乓球。 策略:先拿 4 个,他拿 n 个,你拿 6-n,依此类推,保证你能得到第 100 个乒乓球。
5 5 5 5 5 5
5 5 1; 5 5 5 5 5 52; 5 3; 54; 5 5; 56.
4.下面是一组被打乱的数字,在被打乱之前它们之间有一个非常有趣的规律。你试着找找看,然后按 按其原有的规律重新把下面的数字排列起来,并说明原来的规律是什么。
3,5,13,21,1,1,2,8 5.在下列题目中缺少一个图,你认为从左边选择哪一个图插入右边空挡比较合理?说明你的理由。 ( )
12.在一张长方形纸片上有 2009 个点,加上 4 个顶点共有 2013 个点,这些点中任意 3 点都不在一条 直线上.现在以这 2013 个点为顶点,把长方形纸片剪开,最多能剪出多少个三角形?
13.复旦大学某班 A、B、C、D、E、F、G、H、I 共 9 名同学参加 2010 年上海世博会志愿者知识测试. 测试合格者进入志愿者选拔范围.测试结果只有一人合格.向他们询问谁合格.他们的回答如下: A:“ 是 E” ; B:“是我”; C:“是 B” ; G:“不是 B”; D:“ 不是 E”; H:“ 不是 B 也不是我”;
理科教研部
小学数学思维竞赛试题
1.一张三角形的纸片,请你剪去一个角,要求还剩三个角,想一想,该怎样剪?
2.桌上放着八枚硬币,竖着放五枚,横着放四枚(如图) ,请 问:如果只许移动其中一枚,能否使横竖都成为五枚硬币?
① ② ③ ④ ⑤ ⑥ ⑦ ⑧
3.请在四个数字 5 之间,适当添加 , , , , ( ) 这些符号,以使等式成立。 ( 1) 5 ( 2) 5 ( 3) 5 ( 4) 5 ( 5) 5 ( 6) 5
A 家
P
B 单位
4
理科教研部
10. 解: 第一步:交换 30 与 15,得到 15,10,67,30; 第二步:交换 67 与 15,得到 67,10,15,30; 第一步:交换 30 与 10,得到 67,30,15,10.
11. 一只茶杯,从杯口朝下翻成杯口朝上,需要翻动奇数次.那么 2009 只茶杯,要全部朝上,翻动的总 “杯次”应为奇数(奇数个奇数之和为奇数).但是,每次翻动 4 只茶杯(4 是偶数! )无论翻多少次,总 “杯次”都是偶数,所以做不到. 每次翻动 5 只则可以.把 2009 只茶杯排成一圈,从某一个茶杯开始,顺次翻下去,每次翻 5 只,翻 2009 次.这样共翻了 5 2009 个茶杯,每个茶杯翻动 5 次,所以全部变成杯口朝上了! 12. 观察可发现放入第 1 个点可剪出 4 个三角形,以后每增加一个点,可多剪出 2 个三角形,所以最多 可剪出 4+20082=4020 个小三角形! 13. 解:假设 A 说实话,则 F、G、H、I 也是说实话,这“ 与说实话的只有 3 个人”不符,所以 A 说了假话, 从而 E 不合格, F 说了假话, D 说了实话. 假设 B 说实话,则 C、D、E 也是说实话,这“与说实话的只有 3 个人”不符,所以 B 说了假话,从而 B 不合格,C 说了假话, G 说了实话. E 与 H 一定是一人说假话,一人说实话,从而 I 说假话,继而得出 H 说假话, E 说实话. 所以 H 是合格的. 14.B 15. A=( 38 16.解题思路: 本题实质问题是数字表示问题。由 1、2 两个数字可表示 1-3 三个数字。由 1、2、4 三个数字可表示 1-7 七个数字(即 1,2,1+2,4,4+1,4+2,4+2+1)。由 1、2、4、8 四个数字可表示 1-15 十五个数字。 依此类推。 参考答案: 把金条分成 1/7、2/7 和 4/7 三份。这样,第 1 天我就可以给他 1/7;第 2 天我给他 2/7,让他找回我 1/7; 第 3 天我就再给他 1/7,加上原先的 2/7 就是 3/7;第 4 天我给他那块 4/7,让他找回那两块 1/7 和 2/7 的金条;第 5 天,再给他 1/7;第 6 天和第 2 天一样;第 7 天给他找回的那个 1/7。 )、B=( 83 )
(B)
(C)
(D)
15.在下边的算式中 A、B 代表不同的数字,若算式成立,求出 A=(
)、B=(
)。
16.你让工人为你工作 7 天,给工人的回报是一根金条。金条平分成相连的 7 段,你必须在每天结束 时给他们一段金条,如果只许你两次把金条弄断,你如何给你的工人付费?
17.有一堆夹心糖,如果平均分成 8 份,最后多余 2 块;如果平均分成 9 份,最后多余 3 块;如果平 均分成 10 份,最后多余 4 块。这堆糖至少有多少块?
E:“ 是 B 或 H”; F:“ 是 E”; I:“H 所说的是事实”.
其中,说实话的只有 3 个人,那么请问合格的是
.
2
理科教研部
14.将如右图所示的圆心角为 90 的扇形纸片 AOB 围成圆锥形纸帽,使扇形的两条半径 OA 与 OB 重 合(接缝粘贴部分忽略不计) ,则围成的圆锥形纸帽是
(A)
18.假设排列着 100 个乒乓球,由两个人轮流拿球装入口袋,能拿到第 100 个乒乓球的人为胜利者。 条件是:每次拿球者至少要拿 1 个,但最多不能超过 5 个,问:如果你是最先拿球的人,你该拿几个? 以后怎么拿就能保证你能得到第 100 个乒乓球?
3
理科教研部
参考答案 1.
2. 只要将硬币①叠放在硬币⑤上就可以了. 3. 解:答案不唯一 (1) (5 5 ) (5 5) 1 ; (3) (5 5 5) 5 3 ; (5) (5 5) 5 5 5 ; (2) (5 5) (5 5) 2 ; (4) (5 5 5) 5 4 ; (6) 5 5 5 5 6 .
6
4. 答案不唯一:1,1,2,3,5,8,13,21.或 21,13,8,5,3,2,1,1 5. 选 A。逻辑角度:左圆右方;左外不变内变,右内不变外变;左黑变白,右白变黑。 6. 此规定等价于: 3 个空瓶=1 瓶汽水(不含瓶) 只需买 21 瓶汽水,其中 21 个空瓶可换 7 瓶汽水,共计 28 瓶.
9.某人每天下午 5 点钟下班,有汽车按时到达接他回家.一天,他提前一个小时结束工作,因汽车未到 达而步行回家, 在途中遇到来接他的汽车又改为乘车, 结果比平时早 10 分钟到家, 此人步行 钟遇到接他的汽车. 分
10.对于给定的有顺序的四个数:30,10,67,15. 任意交换两个非相邻位置的数,算作一次操作(不 允许交换两个相邻位置的数) ,能否利用三次操作,使得最后得到的四个数从左到右依次减小,写出具 体的操作步骤. 11.2009 只茶杯,杯口朝下,每次翻动 4 只茶杯,能否经过若干次翻动,使所有茶杯全变为杯口朝上? 每次翻动 5 只呢?
