篇电阻星形连接与角形连接的等效变换
星形电阻网络与三角形电阻网络的等效变换

resistance network )
R12 R23 R31 R
R1 R2 R3 RY
对称三端电阻网络的变换关系:
R 3RY
RY
1 3
R
例 在图示电路中,R1 = 1 , R2 =2 , R3=3 , R4=4 , R5=5 , R6=6 ,Us = 1 V。试求通过 电压源的电流I。
电桥不平衡 怎样处理?
等效条件: (设加撇为Δ网络中的变量)
i1 i1 , i2 i2 , i3 i3 , u12 u12 , u23 u23 , u31 u31
由Y网络可得
u12 i1R1 i2 R2
u23 i2 R2 i3 R3
i3 i2 i1
由此解得
i1
R1 R2
R3u12 R2 R3
比较上面两组式子可得出由星形电阻网络变换为等效的三角形电阻网络时电阻的计算式312312311231231212233123122331对称三端电阻网络symmetricalthreeterminalresistancenetwork312312v
§26 星形电阻网络与三角形电阻网 络的等效变换
提出问题
R3u12 R2 R3
R3 R1
R1 R2
R2u31 R2 R3
R3 R1
i2
u23 R23
u12 R12
i2
R1 R2
R1u23 R2 R3
R3 R1
R1 R2
R3u12 R2 R3
R3 R1
比较上面两组式子,可得出由星形电阻网络变换 为等效的三角形电阻网络时电阻的计算式
等效结果:
R12
R1
R2
R1 R2 R3
电阻星形连接与三角形连接的等效变换
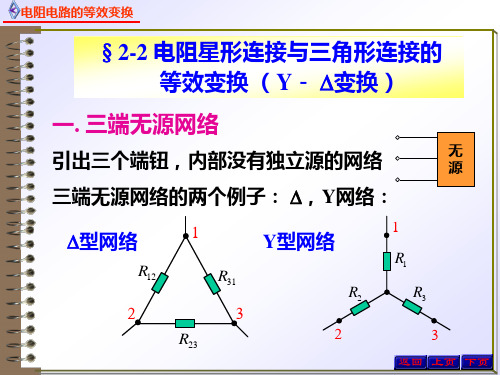
i1
u12 R12
u31 R31
i2
u23 R23
u12 R12
(1)
i3
u31 R31
u23 R23
由等效条件,比较式(3)与式(1),得由Y接接的变换结果
R12
R1 R2
R2 R3 R3
R3 R1
R23
R1 R2
R2 R3 R1
R3
R1
或
R31
R1 R2
R2 R3 R2
R3
R1
d
h
b
f
a
e
c
g
b
f
返回 上页 下页
电阻电路的等效变换
d
将等电位点短接,
a
e
画出等效电路:
h
c
g
b
f
b de a
cf h
Rag
R 3
R 6
R 3
g
5
R
6
返回 上页 下页
电阻电路的等效变换
(2)求Rab
d
由电路对称性,
h
找出等电位点:
a c
b
a
e
d、e等电位
c、f等电位
g
7
f
Rab 12 R
hg
1.5 (0.6 1.4)(1 1) 2.5 0.6 1.4 1 1
求得: i 10 10 4 R 2.5
返回 上页 下页
电阻电路的等效变换
+
10V -
i1
3 2
2
1.4
3
图(a)
5 Y→△ +
4
10V
-
1
i1
3
2
星三角电阻等效转化公式

星三角电阻等效转化公式在电学的世界里,有一个非常重要的知识点,那就是星三角电阻等效转化公式。
这可是个让不少同学挠头,但又十分关键的内容。
咱们先来说说什么是星型连接和三角型连接。
想象一下,电阻们就像是一群小伙伴,它们手拉手的方式不同,效果也就不一样啦。
星型连接呢,就像是一颗星星,三个电阻的一端连接在一起,另一端分别引出;而三角型连接,则像是一个三角形,三个电阻首尾相连。
那为什么要进行星三角电阻的等效转化呢?这就好比你在做一道数学题,有时候用一种方法算不出来,换个思路,可能就迎刃而解啦。
在电路分析中,不同的连接方式会影响电路的总电阻和电流等参数。
如果能灵活地进行星三角转换,就能让问题变得简单许多。
我记得有一次,在给学生们讲解这个知识点的时候,有个同学瞪着大眼睛,一脸迷茫地问我:“老师,这到底有啥用啊?”我笑了笑,跟他们说:“同学们,假设你们家里的电路出了问题,电工师傅要判断是哪里电阻出了毛病,如果不懂得星三角转换,那可就像在黑暗中摸索,找不到方向哦。
”接下来,咱们看看星三角电阻等效转化的公式。
星型转三角型,R₁₂ = R₁ + R₂ + R₁R₂/R₃,R₂₃ = R₂ + R₃ + R₂R₃/R₁,R₃₁= R₃ + R₁ + R₃R₁/R₂。
而三角型转星型,R₁ = R₁₂R₃₁/(R₁₂ +R₂₃ + R₃₁) ,R₂ = R₂₃R₁₂/(R₁₂ + R₂₃ + R₃₁) ,R₃ =R₃₁R₂₃/(R₁₂ + R₂₃ + R₃₁) 。
看着这些公式,是不是有点头疼?别担心,咱们慢慢来。
比如说,R₁₂ = R₁ + R₂ + R₁R₂/R₃这个公式,你可以这样理解,R₁和 R₂本来就是串联的,再加上 R₁R₂/R₃这一部分,就相当于把星型连接转换成了三角型连接。
为了让大家更好地掌握这个知识点,咱们来做几道练习题。
假设一个电路中,星型连接的电阻分别是 R₁ = 3Ω,R₂ = 4Ω,R₃ = 5Ω,那转换成三角型连接后,R₁₂、R₂₃和 R₃₁分别是多少呢?同学们,拿起笔来算算吧。
电工基础第二节3.2 电阻的星形与三角形连接的等效变换
1
作:习题二 2-6
返回本章开头
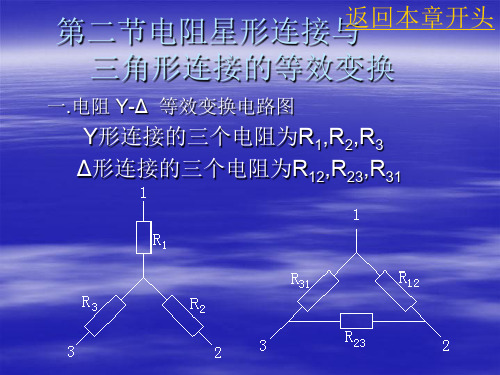
第二节电阻星形连接与返回本章开头 三角形连接的等效变换
一.电阻 Y-Δ 等效变换电路图
Y形连接的三个电阻为R1,R2,R3 Δ形连接的三个电阻为R12,R23,R31
二.电阻星形联结 转换 三角形联结
R12
R1R2
R2 R3 R3
R3 R1
R23
R1R2
R2 R3 R1
R3 R1
R31
R1R2
R2 R3 R2
R3 R1
便于记忆公式形
形联结电阻
形联结电阻两两乘积之和 形联结不相邻电阻
三.电阻三角形联结 转 换 星形联结
R1
R12
R12 R31 R23
R31
R2
R12
R12 R23 R23
R31
R3
R12
R31R23 R23
R31
便于记忆公式
形联结
形联结相邻电阻乘积 形联结电阻之和
四. Y形联结成△形联结三个电阻
相等 Y 等效公式
R0 3R
R
1 3
R
例2.求图2-a所示电路a.b两端的电阻
解: 将3个1电阻组成的星形连接等效变换为三角形连接,
得到图(b),由此得
Rab
31.5 3 1.5
电阻 等效电路
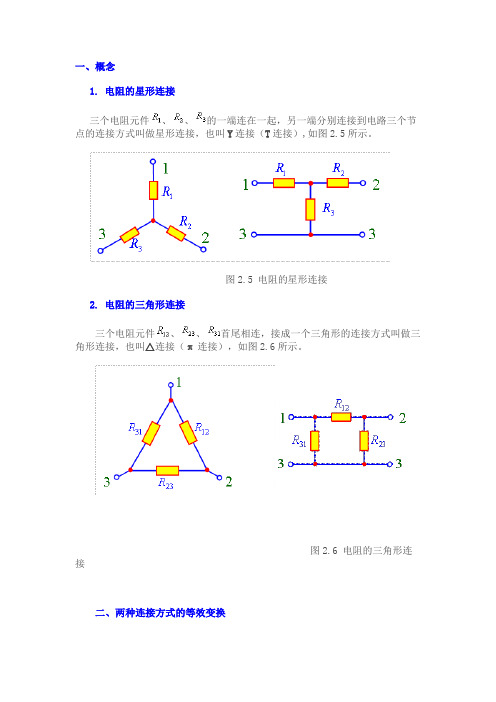
一、概念
1. 电阻的星形连接
三个电阻元件、、的一端连在一起,另一端分别连接到电路三个节点的连接方式叫做星形连接,也叫Y连接(T连接),如图2.5所示。
图2.5 电阻的星形连接
2. 电阻的三角形连接
三个电阻元件、、首尾相连,接成一个三角形的连接方式叫做三角形连接,也叫△连接(π连接),如图2.6所示。
图2.6 电阻的三角形连接
二、两种连接方式的等效变换
1. 等效变换条件:对应端口的电流、电压均相同
2. 等效变换结果:
①Y →△:
②△→ Y :
三、电阻星形与三角形等效变换步骤:
1. 确定星形或三角形的三个顶点;
2. 去掉在三个顶点内的电阻,换为另一种连接的三个电阻;注意:在三个顶点外的电阻不能动!
3. 计算替换换后的三个电阻阻值;
4. 再按电阻串并联进行等效化简、计算。
例2.5 在图2.7(a)中,求各电阻的电流。
解:将图(a)中顶点acd△连接等效变换为acdY联接,如图2.7(b),则。
电路原理2.2.1电阻的星形联结和三角形联结的等效变换 - 电阻星形连接与三角形连接的等效变换
返回 上页 下页
电阻电路的等效变换
由式(2)解得:
i1Y
u12Y R3 u31Y R2 R1R2 R2 R3 R3 R1
i2Y
u23Y R 1 u12Y R1R2 R2 R3
R3 R3
R1
(3)
i3Y
u31Y R2 u23Y R1 R1R2 R2 R3 R3 R1
G12
G1
G1G2 G2 G3
G23
G1
G2G3 G2 G3
G31
G1
G3G1 G2
G3返回
上页
下页
电阻电路的等效变换
由Y接 接的变换结果:
R12
R1 R2
R2 R3 R3
R3 R1
R23
R1 R2
R2 R3 R1
R3
R1
或
R31
R1 R2
R2 R3 R2
R3
R1
4
35 R1 3 2 5 1.5
32 R2 3 2 5 0.6
R3
3
2 2
5
5
1
返回 上页 下页
电阻电路的等效变换
+
10V -
i1
1.5
0.6 1
2
3
1.4
1
再用电阻串联和 并联公式,求出连接 到电压源两端单口的 等效电阻:
4
R 1.5 (0.6 1.4)//(1 1)
5 )
17
R23
(5
2+2 1+1 5
5 )
3.4;
R31
(
5
2+2 1+1 2
5 )
8.5
电阻的Y-△等效变换

等效变换的条件是:三端的电流与任何两 点之间的电压在变换前后保持相同,对外电路 的作用是完全一样的。
Y 联结转换为△联结的变换公式:
R12
R1
R2
R1 R2 R3
R23
R2
R3
R2 R3 R1
§3-8 电阻的Y-△等效变换
学习目标
掌握电阻Y-△等效变换的方法。
一、星形(Y)联结和三角形(△)联结
星形联结——把3个电 阻R1、R2、R3的一端联结 在一起,成为一个节点, 电阻的另外三端分别与电 路的不同部分联结的连接 方式,简称Y联结。
三角形联结——把3 个电阻R12、R23、R31联成 一个闭合的三角形,三角 形的三个顶点分别与电路 的不同部位相联结的联结 方式,简称△联结。
对称的Y联结和△联结的等效变换公式为:
1
RY = 3 RV
或
RV 3RY
[例3-12]
计算下图a所示电桥电路中的总电流I以及通 过桥上的电流IP。
解:由于图a所示电桥电路没有处于平衡状态,
故属于复杂直流电路,若按照一般的复杂直流电路
的解法求解非常复杂,更不能用电阻串并联的方法
求解。仔细观察不难发现,图中的三个电阻R2、R3、 R5正好构成对称的三角形接法,根据Y-△等效变 换原则,可把它们等效为星形接法,接成图b所示
的电路。其中
RY
1 3
RV
9 3
(3 )
这时原来的复杂直流电路已经等效成为简单
直流电路,此时的总电阻为:
Rcd = 15 3 / / 6 3 3=( 9 )
电阻网络中的三角形星形等效变换

电阻网络中的三角形星形等效变换在电路中,电阻网络是一个由电阻器连接而成的结构,用于控制电流和电压的传输。
在电阻网络中,基本的电路元件是电阻器,可以通过不同方式进行连接和变换,以达到不同的电流分布和电压分配的目的。
本文将介绍电阻网络中的三角形星形等效变换,以及其在电路设计和分析中的应用。
一、三角形到星形等效变换三角形到星形等效变换指的是将一个由三个电阻器连接而成的三角形电路转化为一个由三个电阻器连接而成的星形电路。
在三角形到星形等效变换中,需要满足以下条件:1. 三个电阻器的连接点形成一个等边三角形;2. 三角形的每个顶点连接一个电阻器;3. 三角形的一个顶点作为星形电路的中心连接点。
通过三角形到星形等效变换,可以改变电路的结构和性质,并简化电路的分析和计算。
二、星形到三角形等效变换星形到三角形等效变换是三角形到星形等效变换的逆过程,即将一个由三个电阻器连接而成的星形电路转化为一个由三个电阻器连接而成的三角形电路。
在星形到三角形等效变换中,需要满足以下条件:1. 三个电阻器连接到一个中心节点,形成一个星形电路;2. 两个相邻的电阻器连接到一个顶点,形成一个等腰三角形;3. 三个电阻器的连接点形成一个等边三角形。
通过星形到三角形等效变换,可以将星形电路转化为三角形电路,使得电路的分析更加简单和方便。
三、等效电阻的计算方法在电阻网络中,等效电阻是指将一个复杂的电路转化为一个简单的电阻网络,使得该电阻网络具有与原电路相同的电流-电压特性。
在三角形星形等效变换中,可以计算出等效电阻。
1. 三角形到星形等效变换中,等效电阻的计算公式为:Rt = R1 * R2 + R2 * R3 + R1 * R3其中,R1、R2、R3分别代表三个电阻器的阻值。
2. 星形到三角形等效变换中,等效电阻的计算公式为:Rt = R1 + R2 + R3其中,R1、R2、R3分别代表三个电阻器的阻值。
通过计算等效电阻,可以将复杂的电阻网络简化为一个等效电阻器,便于电路的计算和分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三篇电阻星形连接与三角形连接的等效变换
图 1 一 1 ( a )所示是一个桥式电路,显然用电阻串并联简化的办法求得端口ab 处的等效电阻是极其困难的。
如果能将连接在 1 、 2 、 3 、三个端子间的R12R23R31构成的三角形连接电路,等效变换为图 1 一 1 ( b )所示的由R1R2R3构成的星形连接电路,则可方便地应用电阻串并联简化的办法求得端口ab 处的等效电阻,这就是工程实际中经常遇到的星形、三角形等效变换问题(简称Y ―△变换)。
图1
在这里叙述Y ―△变换并非要求同学们掌握此变换,而是通过讲解,了解变换的过程意义,为课程后续内容的学习(三相电路)先行建立一个感性认识,从而为更进一步的学习奠定基础。
等效要解决的问题是:图 1 一 2 ( a )所示三角形连接(连接)与图1 一2 ( b )星形连接(Y 连接),就其1、2 、3 三个端子而言,要求对外等效。
要完成等效,应明确R1R2R3三个Y 连接电阻与R12R23R31三个连接电阻应满足什麽关系。
一种推导等效变换的办法是两电路在一个对应端子悬空的同等条件下,分别测两电路剩余两端子间的电阻,并要求测得的电阻相等。
式l 可方便地用来求三角形连接电阻等效的星形连接电阻。
若由星形连接求等效三角形连接的公式可将式!变换一下,即可得到。
