25-曲柄滑块-摇杆机构点水平运动速度分析2014.1.18
(2021年整理)曲柄滑块机构的运动分析及应用

曲柄滑块机构的运动分析及应用编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(曲柄滑块机构的运动分析及应用)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为曲柄滑块机构的运动分析及应用的全部内容。
机械原理课程机构设计实验报告题目:曲柄滑块机构的运动分析及应用小组成员与学号:刘泽陆(11071182)陈柯宇 (11071177)熊宇飞(11071174)张保开(11071183)班级: 1107172013年6月10日摘要 (4)曲柄滑块机构简介 (5)曲柄滑块机构定义 (5)曲柄滑块机构的特性及应用 (5)曲柄滑块机构的分类 (9)偏心轮机构简介 (10)曲柄滑块的动力学特性 (11)曲柄滑块的运动学特性 (12)曲柄滑块机构运行中的振动与平衡 (15)参考文献 (16)组员分工 (16)摘要本文着重介绍了曲柄滑块机构的结构,分类,用途,并进行了曲柄滑块机构的动力学和运动学分析,曲柄滑块机构的运动学特性分析,得出了机构压力表达式,曲柄滑块机构的运动特性分析,得出了滑块的位移、速度和加速度的运动表达式。
最后,对曲柄滑块机构运动中振动、平衡稳定性等进行了总结.关键字:曲柄滑块动力与运动分析振动与平稳性ABSTRACTThe paper describes the composition of planar linkage, focusing on the structure, classification, use of a slider—crank mechanism and making the dynamic and kinematic analysis, kinematics characteristics of the crank slider mechanism analysis for a slider—crank mechanism, on one hand , we obtain the drive pressure of the slider—crank mechanism ,on the other hand,we obtain the expression of displacement, velocity and acceleration of movement。
曲柄滑块机构运动分析

曲柄滑块机构运动分析一、相关参数在图1所示的曲柄滑块机构中,已知各构件的尺寸分别为mm l 1001=,mm l 3002=,s rad /101=ω,试确定连杆2和滑块3的位移、速度和加速度,并绘制出运动线图。
图1 曲柄滑块机构二、数学模型的建立1、位置分析为了对机构进行运动分析,将各构件表示为矢量,可写出各杆矢所构成的封闭矢量方程。
将各矢量分别向X 轴和Y 轴进行投影,得0sin sin cos cos 22112211=+=+θθθθl l S ll C(1) 由式(1)得2、速度分析将式(1)对时间t 求导,得速度关系C v l l l l =--=+222111222111sin sin 0cos cos θωθωθωθω(2) 将(2)式用矩阵形式来表示,如下所示⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-1111122222cos sin . 0 cos 1 sin θθωωθθl l v l lC(3) 3、加速度分析将(2)对时间t 求导,得加速度关系三、计算程序1、主程序%1.输入已知数据clear;l1=0.1;l2=0.3;e=0;hd=pi/180;du=180/pi;omega1=10;alpha1=0;%2.曲柄滑块机构运动计算for n1=1:721theta1(n1)=(n1-1)*hd;%调用函数slider_crank计算曲柄滑块机构位移、速度、加速度[theta2(n1),s3(n1),omega2(n1),v3(n1),alpha2(n1),a3(n1)]=slider_crank(theta1(n1),omega1,alpha1,l1,l2,e); endfigure(1);n1=0:720;subplot(2,3,1)plot(n1,theta2*du);title('连杆转角位移线图');xlabel('曲柄转角\theta_1/\circ');ylabel('连杆角位移/\circ');grid onsubplot(2,3,2)plot(n1,omega2);title('连杆角速度运动线图');xlabel('曲柄转角\theta_1/\circ');ylabel('连杆角速度/rad\cdots^{-1}');grid onsubplot(2,3,3)plot(n1,alpha2);title('连杆角加速度运动线图');xlabel('曲柄转角\theta_1/\circ');ylabel('连杆角加速度/rad\cdots^{-2}');grid onsubplot(2,3,4)plot(n1,s3);title('滑块位移线图');xlabel('曲柄转角\theta_1/\circ');ylabel('滑块位移/\m');grid onsubplot(2,3,5)plot(n1,v3);title('滑块速度运动线图');xlabel('曲柄转角\theta_1/\circ');ylabel('滑块速度/m\cdots^{-1}');grid onsubplot(2,3,6)plot(n1,a3);title('滑块加速度运动线图');xlabel('曲柄转角\theta_1/\circ');ylabel('滑块加速度/m\cdots^{-2}');grid on2、子程序function[theta2,s3,omega2,v3,alpha2,a3]=slider_crank(theta1,omega1,alpha1,l1,l2,e);%计算连杆2的角位移和滑块3的线位移s3=l1*cos(theta1)+l2*cos(theta2);theta2=asin((e-l1*sin(theta1))/l2);%计算连杆2的角速度和滑块3的线速度A=[l2*sin(theta2),1;-l2*cos(theta2),0];B=[-l1*sin(theta1);l1*cos(theta1)];omega=A\(omega1*B);omega2=omega(1);v3=omega(2);%计算连杆2的角加速度和滑块3的线加速度At=[omega2*l2*cos(theta2),0;omega2*l2*sin(theta2),0];Bt=[-omega1*l1*cos(theta1);-omega1*l1*sin(theta1)];alpha=A\(-At*omega+alpha1*B+omega1*Bt);alpha2=alpha(1);a3=alpha(2);四、程序运行结果及分析图2 运动规律曲线图从仿真曲线可以看出,当曲柄以w1=10rad/s匀速转动时,连杆的转角位移变化范围大约在-20~20度之间,在90°或270°有极值,呈反正弦变化趋势;连杆的角速度变化范围大约在-3.3~3.3rad/s,在0°或180°有极值,成反余弦变化趋势;连杆角加速度变化范围大约在-35~35rad/s2,在90°或270°有极值,呈正弦变化趋势。
曲柄滑块机构的运动分析及应用解读

机械原理课程机构设计实验报告题目:曲柄滑块机构的运动分析及应用小组成员与学号:刘泽陆(********)陈柯宇(11071177)熊宇飞(11071174)张保开(11071183)班级:1107172013年6月10日摘要 (3)曲柄滑块机构简介 (4)曲柄滑块机构定义 (4)曲柄滑块机构的特性及应用 (4)曲柄滑块机构的分类 (8)偏心轮机构简介 (9)曲柄滑块的动力学特性 (10)曲柄滑块的运动学特性 (11)曲柄滑块机构运行中的振动与平衡 (14)参考文献 (15)组员分工 (15)摘要本文着重介绍了曲柄滑块机构的结构,分类,用途,并进行了曲柄滑块机构的动力学和运动学分析,曲柄滑块机构的运动学特性分析,得出了机构压力表达式,曲柄滑块机构的运动特性分析,得出了滑块的位移、速度和加速度的运动表达式。
最后,对曲柄滑块机构运动中振动、平衡稳定性等进行了总结。
关键字:曲柄滑块动力与运动分析振动与平稳性ABSTRACTThe paper describes the composition of planar linkage, focusing on the structure, classification, use of a slider-crank mechanism and making the dynamic and kinematic analysis, kinematics characteristics of the crank slider mechanism analysis for a slider-crank mechanism, on one hand , we obtain the drive pressure of the slider-crank mechanism ,on the other hand,we obtain the expression of displacement, velocity and acceleration of movement. Finally, the movement of the vibration and balance stability of the crank slider mechanism are summarized.曲柄滑块机构简介曲柄滑块机构定义曲柄滑块机构是铰链四杆机构的演化形式,由若干刚性构件用低副(回转副、移动副)联接而成的一种机构。
曲柄滑块机构的运动分析及应用精编WORD版

曲柄滑块机构的运动分析及应用精编W O R D版IBM system office room 【A0816H-A0912AAAHH-GX8Q8-GNTHHJ8】机械原理课程机构设计实验报告题目:曲柄滑块机构的运动分析及应用小组成员与学号:刘泽陆(11071182)陈柯宇 (11071177)熊宇飞(11071174)张保开 (11071183)班级: 1107172013年6月10日摘要 (3)曲柄滑块机构简介 (4)曲柄滑块机构定义 (4)曲柄滑块机构的特性及应用 (4)曲柄滑块机构的分类 (8)偏心轮机构简介 (9)曲柄滑块的动力学特性 (10)曲柄滑块的运动学特性 (11)曲柄滑块机构运行中的振动与平衡 (14)参考文献 (15)组员分工 (15)摘要本文着重介绍了曲柄滑块机构的结构,分类,用途,并进行了曲柄滑块机构的动力学和运动学分析,曲柄滑块机构的运动学特性分析,得出了机构压力表达式,曲柄滑块机构的运动特性分析,得出了滑块的位移、速度和加速度的运动表达式。
最后,对曲柄滑块机构运动中振动、平衡稳定性等进行了总结。
关键字:曲柄滑块动力与运动分析振动与平稳性ABSTRACTThe paper describes the composition of planar linkage, focusing on the structure, classification, use of a slider-crank mechanism and making the dynamic and kinematic analysis, kinematics characteristics of the crank slider mechanism analysis for a slider-crank mechanism, on one hand , we obtain the drive pressure of the slider-crank mechanism ,on the other hand,we obtain the expression of displacement, velocity and acceleration of movement. Finally, the movement of the vibration and balance stability of the crank slider mechanism are summarized.曲柄滑块机构简介曲柄滑块机构定义曲柄滑块机构是铰链四杆机构的演化形式,由若干刚性构件用低副(回转副、移动副)联接而成的一种机构。
25-曲柄滑块-摇杆机构点水平运动速度分析2014.1.18

3 课程上机内容与要求
(1) 生成曲柄滑块机构的计算数值位移S3,速度V3与加速度a3关于φ的Excel数据文件,0≤φ≤2π, 增量∆φ=1/(2π)。
(2) 生成曲柄滑块机构的计算数值位移xD、yD,速度VDx、VDy与加速度aDx、aDy关于φ的Excel数据
2
文件,0≤φ≤2π,增量∆φ=1/(2π)。 (3) 生成曲柄摇杆机构的计算数值角位移ψ,角速度ω3与角加速度α3关于φ的Excel数据文件,0
连杆 2 上D点的位移xD、yD,速度VDx、VDy与加速度aDx、aDy分别为 xD = a cosϕ + c cos(θ − π + β ) (9) yD = a sinϕ + c sin(θ − π + β ) (10) VDx = −aω1 sin ϕ − cω2 sin(θ − π + β ) (11) VDy = aω1 cosϕ + cω2 cos(θ − π + β ) (12)
αL2 = [a cos(ϕ −ψ ) + bωL22 cos(ψ − λ) − cωL23] /[b sin(ψ − λ)] (24)
α2
=
(d2λ
/ dϕ 2 )(dϕ
/ dt)2
=
α
ω2
L2 1
,
α
3
=
(d 2ψ
/ dϕ 2 )(dϕ
曲柄摇杆机构的运动分析研究

曲柄摇杆机构的运动分析研究作者:黄帆来源:《科技视界》2016年第01期【摘要】本文介绍平面连杆机构运动分析杆组法,并针对曲柄摇杆机构的运动特性进行分析,给出了曲柄摇杆的数值参数设计方面的理论依据。
【关键词】曲柄摇杆;运动分析;急回特性【Abstract】This paper introduces the kinematic analysis of the planar linkage mechanism,analyzes the kinematic characteristics of the crank and rocker mechanism, and gives the theoretical basis of the numerical parameters design of the crank rocker.【Key words】Crank and rocker; Motion analysis; Quick return characteristics0 前言曲柄摇杆机构是一种典型的四杆机构之一,由曲柄、摇杆、连杆、机架组成的。
曲柄或摇杆通过直接接触将预定的运动传给从动件。
由于曲柄摇杆机构可以实现各种复杂的运动要求,而且具有结构简单紧凑的特点,所以广泛应用于各种自动化机器、仪器和装配线,例如在纺织机械、印刷机械以及一些控制系统等装置中,广泛应用着各种类型的曲柄摇杆机构。
具有急回特性的曲柄摇杆机构是常用的曲柄摇杆机构,曲柄的转动使从动件按预定的运动规律摆动。
由于曲柄摇杆机构的运动特征依赖于曲柄、摇杆、连杆的长度和行程速比的类型,在常规设计中,为了获得从动件的预定输出运动(位移、速度和加速度),必须合理选择从动件的类型和机构参数后精确地设计曲柄摇杆的数值参数。
1 平面连杆机构运动分析杆组法简介平面连杆机构的运动分析,早已有成熟的算法,其中阿氏杆组法最为简单有效。
大部分连杆机构都是在基本机构上增加一个或多个常用的阿氏杆组构成的。
曲柄滑块机构运动分析与力学计算
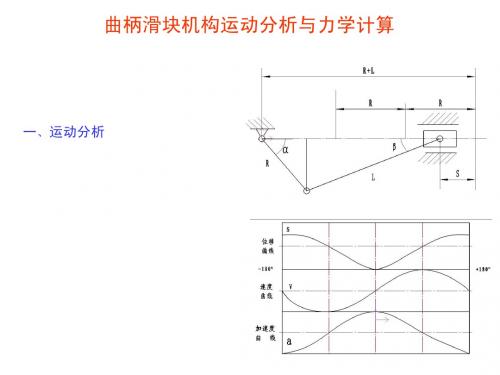
按压力行程计算扭矩作活塞 允许载荷曲线,在任何情况下
P R sin sin 2 m f M pac 2 M pac P R sin sin 2 m f 2
四、连杆的校验
M PAB R B PAB sin X 压弯组合 PAB cos M c F W PAB cos PAB R B PAB sin X F W c
Md
12
1
O
N21
R21
2
r fv r
F21
2
以轴颈中心为圆心,为半径作的圆称为摩擦圆, 为摩擦圆半径。
三、实际机构扭矩计算
理想机构:不计弹性变形;不计配合间隙 不计摩擦;不计惯性力
sin
(R A RB )
L m2
M ' 2 PAB
m 2 R A R sin( )
2
sin 2 )
M 1 PAB R (sin 2 M 1 ( P, , R, L ) PR(sin
2
ቤተ መጻሕፍቲ ባይዱ
sin 2 )在下死点 0
sin 2 )
设计(公称压力 )行程S g ; 设计(公称压力 )角 g 设计时扭矩要照此要求 进行计算 .
Q
转动副的摩擦 (轴颈摩擦)
曲柄滑块机构运动分析与力学计算
一、运动分析
S R L R co s L co s R( 1 co s ) L ( 1 co s ) L sin R sin sin
R sin L
曲柄滑块机构的结构
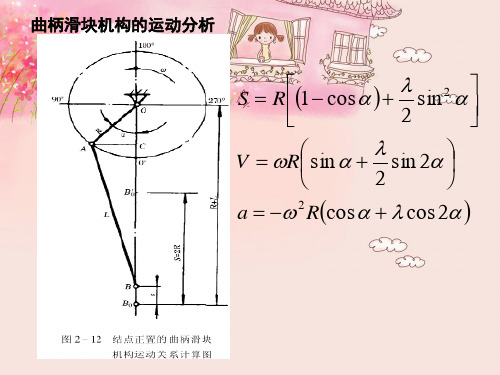
曲拐轴式曲柄滑块机构便于实现可调行程 且结构较简单,但由于曲柄悬伸,受力情
况较差,因此主要在中、小型机械压力机 上应用。
偏心齿轮工作时只传递扭矩,弯矩由芯轴承受,因此 偏心齿轮的受力比曲轴简单些,芯轴只承受弯矩,受
力情况也比曲轴好,且刚度较大。此外,偏心齿轮的
铸造比曲轴锻造容易解决,但总体结构相对复杂些。
为了保证滑块的运动精度,滑块的导向面应尽量长 ,因而滑块的高度要足够高,滑块高度与宽度的比 值,在闭式单点压力机上约为1.08~1.32 ,在开式压力机上则高达1.7左右。
滑块还应该越轻越好,质量轻的滑块上升时消耗的 能量小,可以减少滑块停止在上止点位置时的制动 力。
滑块还应有足够的强度,小型压力机的滑块常用HT200铸造。中 型压力机的滑块常用HT200或稀土球铁铸造,或用Q235钢板 焊接而成。
所以,偏心齿轮驱动的曲柄及滑块机构常用于大中型 压力机。
滑块与导轨结构
压力机上的滑块是一个箱形结构,它的上部与连杆连接,下面开有“ T”形槽或模柄孔,用以安装模具的上模。
滑块在曲柄连杆的驱动下,沿机身导轨上下往复运动,并直接承受上 模传来的工艺反力。
为了保证滑块底平面和工作台上平面的平行度,保 证滑块运动方向与工作台面的垂直度,滑块的导向 面必须与底平面垂直。(下平面的平面度,导向面的 平面度,下平面对导向面的垂直度,导向面对母线 的直线度)
综上所述,机身变形对冲压工艺的影响是至关重要的,必须给予重视 。不同刚度的压力机,在同样的工作负荷下,刚度小的变形大,刚度
大的变形小;而对同一台压力机,工作负荷越大,变形也越大。这是 在选择压力机时必须考虑的因素。
曲柄滑块机构的运动分析
S
R 1
cos
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
− a
a sinϕ cosϕ +
− ωL2b sin λ = −ωL3c sinψ ωL2b cos λ = ωL3c cosψ
⎬⎫ (19) ⎭
ωL3 = a sin(ϕ − λ) /[c sin(ψ − λ)] (20) ωL2 = a sin(ϕ −ψ ) /[b sin(ψ − λ)] (21)
λ = arctan 2[(c sinψ − a sinϕ) /(d + c cosψ − a cosϕ)] (18)
B
B2
y
B1
2
A
λ
φ θ2 1
A2
O1
3
1
P
图 2 曲柄摇杆机构
对式(15)求关于φ的一阶导数,得类速度方程及其解ωL2=dλ/dφ、ωL3=dψ/dφ分别为
cos λ − bαL2 sin sin λ + bαL2 cos
λ λ
= =
−cωL23 cosψ −cωL23 sinψ
− cαL3 sinψ + cαL3 cosψ
⎬⎫ ⎭
(22)
αL3 = [a cos(ϕ − λ) + bωL22 − cωL23 cos(ψ − λ)] /[c sin(ψ − λ)] (23)
3 课程上机内容与要求
(1) 生成曲柄滑块机构的计算数值位移S3,速度V3与加速度a3关于φ的Excel数据文件,0≤φ≤2π, 增量∆φ=1/(2π)。
(2) 生成曲柄滑块机构的计算数值位移xD、yD,速度VDx、VDy与加速度aDx、aDy关于φ的Excel数据
2
文件,0≤φ≤2π,增量∆φ=1/(2π)。 (3) 生成曲柄摇杆机构的计算数值角位移ψ,角速度ω3与角加速度α3关于φ的Excel数据文件,0
yD,速度VDx、VDy与加速度aDx、aDy。
D
机构的位移方程及其解分别为
a a
sin ϕ cosϕ
− b sinθ = 0 − b cosθ = S3
⎬⎫ (1) ⎭
S3 = a cosϕ + b2 − a2 sin2 ϕ (2) θ = arctan 2[a sinϕ /(a cosϕ − S3)] (3) 对位移方程求关于φ的一阶导数,得类速度方程及其解ωL2 =dθ/dφ、VL3=dS3/dφ分别为
αL2 = [a cos(ϕ −ψ ) + bωL22 cos(ψ − λ) − cωL23] /[b sin(ψ − λ)] (24)
α2
=
(d2λ
/ dϕ 2 )(dϕ
/ dt)2
=
α
ω2
L2 1
,
α
3
=
(d 2ψ
/ dϕ 2 )(dϕ
/ dt)2
=
α
ω2
L3 1
。
连杆 2 上P点的位移xP、yP,速度VPx、VPy与加速度aPx、aPy分别为 xP = a cosϕ + r cos(λ + θ2 ) (25) yP = a sin ϕ + r sin(λ + θ2 ) (26) VPx = −aω1 sin ϕ − rω2 sin(λ + θ2 ) (27) VPy = aω1 cosϕ + rω2 cos(λ + θ2 ) (28)
ω2 = dθ / dt = (dθ / dϕ)(dϕ / dt) = ωL2 ⋅ω1 ,V3 = dS3 / dt = (dS3 / dϕ)(dϕ / dt) = VL2 ⋅ω1 。 对类速度方程求关于φ的一阶导数,得类加速度αL2=d2θ/dφ2、aL3=d2S3/dφ2分别为 αL2 = (−a sinϕ + bωL22 sinθ ) /(b cosθ ) (7)
ω2 = (dλ / dϕ)(dϕ / dt) = ωL2 ⋅ω1 , ω3 = (dψ / dϕ)(dϕ / dt) = ωL3 ⋅ω1 。 对式(15)求关于φ的二阶导数,得类加速度方程及其解αL2=d2λ/dφ2、αL3=d2ψ/dφ2分别为
− −
a a
cosϕ sin ϕ
− bωL22 − bωL22
2 曲柄摇杆机构的运动分析
图 2 为分析连杆上点轨迹的曲柄摇杆机构。设曲柄 1 为主动件,令a、b、c和d分别表示曲柄 1、
连杆 2、摇杆 3 与机架 4 的长度,a=0.150 m,b=0.450 m,c=0.350 m,d=0.400 m,连杆 2 的角
位移为λ,摇杆 3 的角位移为ψ,连杆 2 上AP点与AB之间的夹角θ2=275°,AP=r=0.650 m。曲柄 1 的角速度ω1=1 rad/s。
连杆 2 上D点的位移xD、yD,速度VDx、VDy与加速度aDx、aDy分别为 xD = a cosϕ + c cos(θ − π + β ) (9) yD = a sinϕ + c sin(θ − π + β ) (10) VDx = −aω1 sin ϕ − cω2 sin(θ − π + β ) (11) VDy = aω1 cosϕ + cω2 cos(θ − π + β ) (12)
aL3 = −a cosϕ + bαL2 sinθ + bωL22 cosθ (8)
α2 = d2θ / dt 2 = (d2θ / dϕ 2 )(dϕ / dt)2 = αL2 ⋅ω12 , a3 = d2S3 / dt 2 = (d2S3 / dϕ 2 )(dϕ / dt)2 = aL3 ⋅ω12 。
曲柄摇杆机构的位移方程为
a a
cosϕ sin ϕ
+ b cos λ = d + c cosψ + b sin λ = c sinψ
⎬⎫ (15) ⎭
引入系数kA、kB和B kC分别为kA=-sinφ,kBB=d/a-cosφ,kC=(d2+c2+a2-b2)/(2ac)-(d/c) cosφ,得摇 杆 3 的角位移方程及其解ψ分别为
aDx = −aω12 cosϕ − cα2 sin(θ − π + β ) − cω22 cos(θ − π + β ) (13) aDy = −aω12 sin ϕ + cα2 cos(θ − π + β ) − cω22 sin(θ − π + β ) (14)
B β
ω1 1
A
φ
2
θ 3
C
S3 4
图 1 曲柄滑块机构
a −
cosϕ − a sinϕ
b(dθ / + b(dθ
dϕ) cosθ = 0 / dϕ) sinθ = dS3
/
dϕ
⎬⎫ (4) ⎭
ωL2 = a cosϕ /(b cosθ ) (5) VL3 = −a sin ϕ + bωL2 sinθ (6)
aPx = −aω12 cosϕ − rα2 sin(λ + θ2 ) − rω22 cos(λ + θ2 ) (29) aPy = −aω12 sin ϕ + rα2 cos(λ + θ2 ) − rω22 sin(λ + θ2 ) (30)
≤φ≤2π,增量∆φ=1/(2π)。 (4) 生成曲柄摇杆机构的计算数值位移xP、yP,速度VPx、VPy与加速度aPx、aPy关于φ的Excel数据
文件,0≤φ≤2π,增量∆φ=1/(2π)。
3
25−曲柄滑块机构与曲柄摇杆机构连杆上点的运动分析 2014.1.18
1 曲柄滑块机构的运动分析
图 1 所示为曲柄滑块机构,设曲柄 1 的杆长a=AB=0.090 m,连杆 2 的杆
长b=BC=0.300 m,连杆上BD的杆长c=0.420 m,BD的方位角β=40º,曲柄 1
W
的角速度ω1=1 rad/s。求滑块 3 的速度V3与加速度a3,连杆 2 上D点的位移xD、
1
kA sinψ + kB cosψ + kC = 0 (16)
ψ = 2 arctan 2[(kA + kA2 + kB2 − kC2 ) /(kB − kC )] ( 17) 由式(15)得连杆 2 的角位移 λ 为
