第四章条件异方差模型
应用回归分析,第4章课后习题参考答案
第4章违背基本假设的情况思考与练习参考答案4.1 试举例说明产生异方差的原因。
答：例4.1：截面资料下研究居民家庭的储蓄行为Y i=β0+β1X i+εi其中：Y i表示第i个家庭的储蓄额，X i表示第i个家庭的可支配收入。
由于高收入家庭储蓄额的差异较大，低收入家庭的储蓄额则更有规律性，差异较小，所以εi的方差呈现单调递增型变化。
例4.2：以某一行业的企业为样本建立企业生产函数模型Y i=A iβ1K iβ2L iβ3eεi被解释变量：产出量Y，解释变量：资本K、劳动L、技术A，那么每个企业所处的外部环境对产出量的影响被包含在随机误差项中。
由于每个企业所处的外部环境对产出量的影响程度不同，造成了随机误差项的异方差性。
这时，随机误差项ε的方差并不随某一个解释变量观测值的变化而呈规律性变化，呈现复杂型。
4.2 异方差带来的后果有哪些？答：回归模型一旦出现异方差性，如果仍采用OLS估计模型参数，会产生下列不良后果：1、参数估计量非有效2、变量的显著性检验失去意义3、回归方程的应用效果极不理想总的来说，当模型出现异方差性时，参数OLS估计值的变异程度增大，从而造成对Y的预测误差变大，降低预测精度，预测功能失效。
4.3 简述用加权最小二乘法消除一元线性回归中异方差性的思想与方法。
答：普通最小二乘估计就是寻找参数的估计值使离差平方和达极小。
其中每个平方项的权数相同，是普通最小二乘回归参数估计方法。
在误差项等方差不相关的条件下，普通最小二乘估计是回归参数的最小方差线性无偏估计。
然而在异方差的条件下，平方和中的每一项的地位是不相同的，误差项的方差大的项，在残差平方和中的取值就偏大，作用就大，因而普通最小二乘估计的回归线就被拉向方差大的项，方差大的项的拟合程度就好，而方差小的项的拟合程度就差。
由OLS 求出的仍然是的无偏估计，但不再是最小方差线性无偏估计。
所以就是：对较大的残差平方赋予较小的权数，对较小的残差平方赋予较大的权数。
条件异方差模型分析解析
第三节 自回归条件异方差(ARCH)模型金融时间序列数据通常表现出一种所谓的集群波动现象。
模型随机误差项中同时含有自相关和异方差。
一、ARCH 模型 （Auto-regressive Conditional Heteroskedastic —自回归条件异方差模型）对于回归模型t kt k t t x b x b b y ε++++= 110 （3.3.1） 若2t ε服从AR （q ）过程 t q t q t t νεαεααε++++=--221102 （3.3.2） 其中tν独立同分布，并满足0)(=t E ν , 2)(σν=tD 则称（3.3.2）式为ARCH 模型，序列t ε服从q 阶ARCH 过程，记为t ε～ARCH （q ）。
(3.3.1)和(3.3.2)称为回归—ARCH 模型。
注：不同时点t ε的方差2)(t t D σε=是不同的。
对于AR （p ）模型t p t p t t y y y εφφ+++=-- 11 （3.3.3） 如果tε～ARCH （q ），则（3.3.3）与（3.3.2）结合称为AR （p ）-ARCH （q ）模型。
ARCH （q ）模型还可以表示为 *t t h =εt ν (3.3.4)21022110jt q j q t q t t h -=--∑+=+++=εααεαεααα (3.3.5)其中，tν独立同分布，且0)(=t E ν,1)(=tD ν,00>α 0≥j α)2,1(q j = 且11<∑=q j j α（保证ARCH 平稳）。
有时，（3.3.5）式等号右边还可以包括外生变量，但要注意应保证th 值是非负的。
如：p t p t q t q t t h h h ----++++++=θθεαεαα 1122110 1011<+<∑∑==p j j q i iθα对于任意时刻t ，条件期望E （tε| ,1-t ε）=0)(*=t t E h ν （3.3.6）条件方差t t t t t h E h E ==-)(*),|(2212νεσ （3.3.7） （3.3.7）式反映了序列条件方差随时间而变化。
金融计量学期末复习试题——(综合)
一、 选择题。
1、在DW 检验中，当d 统计量为0时，表明（ ）。
A 、存在完全的正自相关B 、存在完全的负自相关C 、不存在自相关D 、不能判定 2、在检验异方差的方法中，不正确的是（ ）。
A 、 Goldfeld-Quandt 方法B 、ARCH 检验法C 、 White 检验法D 、 DW 检验法 3、t X 的2阶差分为 （ ）。
A 、2=t t t k X X X -∇-B 、2=t t t k X X X -∇∇-∇ C 、21=t t t X X X -∇∇-∇ D 、2-12=t t t X X X -∇∇-∇4、ARMA(p,q)模型的特点是（ ）。
A 、自相关系数截尾，相关系数拖尾B 、自相关系数拖尾，相关系数截尾C 、自相关系数截尾，相关系数截尾D 、自相关系数拖尾，相关系数拖尾 5、以下选项中，正确地表达了序列相关的是（ ）。
A 、 (,)0,i j Cov i j μμ≠≠ B 、 (,)0,i j Cov i j μμ=≠ C 、 (,)0,i j Cov X X i j =≠ D 、 (,)0,i j Cov X i j μ≠≠6、在线性回归模型中,若解释变量1i X 和2i X 的观测值有如1220i i X X +=的关系,则表明模型中存在( )。
A 、 异方差B 、 多重共线性C 、 序列自相关D 、 设定误差 7、如果样本回归模型残差的一阶自相关系数ρ接近于0，那么DW 统计量的值近似等于（ ）A 、0B 、1C 、2D 、48、当多元回归模型中的解释变量存在完全多重共线性时，下列哪一种情况会发生（ ） A 、OLS 估计量仍然满足无偏性和有效性； B 、OLS 估计量是无偏的，但非有效； C 、OLS 估计量有偏且非有效； D 、无法求出OLS 估计量。
9、在多元线性线性回归模型中，解释变量的个数越多，则可决系数R 2（ ）A 、越大；B 、越小；C 、不会变化；D 、无法确定 二、填空题。
时间序列计量经济学模型概述
时间序列计量经济学模型概述时间序列计量经济学模型是在经济学研究中广泛使用的一种方法，用于分析经济变量随时间的变化。
该模型基于时间序列数据，即经济变量在一段时间内的观测值。
时间序列计量经济学模型的核心是建立经济变量之间的关系，以解释和预测经济现象的变化。
其中最常用的模型是自回归移动平均模型（ARMA）、自回归条件异方差模型（ARCH）和季节性时间序列模型。
自回归移动平均模型（ARMA）是一个包含自回归项和移动平均项的线性模型。
该模型以过去的观测值和随机项为输入，预测当前观测值。
ARMA模型基于假设，即经济变量的行为受到历史观测值的影响。
自回归条件异方差模型（ARCH）是一种考虑了随时间变化方差的模型。
该模型通过引入一个条件异方差项，模拟经济变量中的波动性。
ARCH模型的应用范围广泛，特别是在金融市场波动性分析中。
季节性时间序列模型用于分析具有明显季节性特征的经济变量，如销售额、就业人数等。
这些模型通常基于季节、趋势和随机成分的组合，以预测未来观测值。
在建立时间序列计量经济学模型时，常常需要进行模型识别、参数估计和模型诊断等步骤。
识别模型的目标是确定适当的模型结构，参数估计则是利用历史数据估计模型的参数值。
模型诊断用于检验模型的拟合程度和误差分布是否符合模型假设。
时间序列计量经济学模型在经济研究中有广泛的应用，例如预测未来经济指标、分析经济周期和波动性、评估政策效果等。
它提供了一种量化的方法，使经济学家可以更好地理解和解释经济变量的演变。
时间序列计量经济学模型是经济学研究中一种重要的统计工具，广泛应用于宏观经济、金融市场和企业经营等领域。
它可以帮助我们理解和解释经济变量随时间的变化规律，进行预测和政策分析。
本文将进一步探讨时间序列计量经济学模型的相关概念和应用。
在构建时间序列计量经济学模型之前，首先需要了解时间序列数据的特点。
时间序列数据是按照时间顺序排列的一系列观测值，通常具有趋势性、季节性、周期性和随机性等特征。
中国通货膨胀的波动性与杠杆效应研究—基于条件异方差模型的实证分析
１Ａ ． ＲＭＡ 模型 。ＡＲＭＡ（ ｇ 表 达式 为 ： ｐ，）
口
反 映了金融 数据 时间序 列方差 波动 特 点 。Ｂ ｉ ｒ ］ ｏｌ — ｅ ｓ ｖ １ ８ ） 明 广 义 自回 归 条 件 异 方 差 模 型 ， ｌ （９６ 证 ｅ 即 Ｇ Ｃ 族 模型 能够更 好地 刻画 收益序 列残 差项 的 ＡＲ Ｈ
关 重要 的 。为 此 ， 文在借 鉴 上述研 究 的基础 上 ， 本 拟 采用条 件异 方 差模 型 结合 我 国 １ ９ ９ ４年 １月 ～２ ０ ０９ 年１ ２月 的居 民消 费价 格 指 数 对 中 国通货 膨 胀 的动 态演 化特征情 况进 行 研 究 ， 以期 揭 示 中 国通 货 膨 胀
ｇｅ １ ９ ） ｌ（ ９ ３ 比较 了允 许 利 好 消 息 和 利 坏 消 息对 未来
的波 动性有 不 同影 响 的非对称 波 动性模 型［ １ 。 虽然 国内外学 者就 通货膨 胀 的形 成 、 性 、 化 惯 演 机制 等 问题 从 不 同 侧 面 和 角 度 进 行 了有 成 效 的 研 究， 但是这些 研究 在 整 体 上缺 乏 对 通 货 膨胀 特 征 的 关注， 而这个 问题 对 帮 助 货 币 当局 就 通 货 膨胀 治 理
格变动 情况 ， 究表 明不 同商 品期 货市 场 的有 效性 研
略有差 异 ， 主要商 品 收益 波 动均 具 有 积 聚效 应 与 杠
杆效应 ［ 。张 成思 （０ ８ 分 析 了 １ ８ ～ ２ ０ １ ］ ２０ ） ９ ０ ０ ７年 中
国通货 膨胀情 况 ， 研究 表 明在低 通 胀 环 境 下我 国通
基于条件异方差模型和在险价值的我国银行间同业拆借利率风险度量
GARCH(1,1) TARCH(1,1)
表 3 样本数据失败次数表
失败次数 LR 检验的非拒绝域 失败次数 LR 检验的非拒绝域
a =90% 94 8 1 < N< 1 2 0 89 8 1 < N< 1 2 0
a =95% 41 3 7 < N< 6 5 38 3 7 < N< 6 5
a =99% 14 4 < N< 1 7 12 4 < N< 1 7
Log like lihood Schw arz crite rion
Prob. 0.0000 0.0000 0.0000 1207.666 - 2.707714
模型 GARCH(1,1) TARCH(1,1)
表 2 同业拆借利率日收益率的 VaR 估计结果
置信水平
90% 95% 99% 90% 95% 99%
2.由于数据序列不服从正态分布，具有 尖峰厚尾性，所以假设数据服从 t 分布。同 业拆借利率收益率的 VaR 计算公式为：
其中 VαRt 是在 t- 1 时刻预测的 t 时刻 的风险价值，Zα 是给定的置信水平 α 对应 的 t 分布的分位数，σt 是 t- 1 时刻预测的 t 时刻的同业拆借收益率的波动性，ωt-1 为 t- 1 时刻的资产价值。
冯科王德全2009应用armagarch及var方法对同业拆借利率作者简介男1963年生湖南岳阳人兰州大学数学与统计学院金融工程研究所所长兰州大学应用统计硕士专业学位教育指导分委员会委员硕士生导师副教授在证券投资风险管理银行管理等领域有深入的研究曾在工程数学学报统计与决策州理工大学学报兰州交通大学学报金融经济等刊物发表多篇论文
进行计算从而模拟未来的情景。在估计模 型中，历史模拟法采用的是全值估计方 法，即根据市场因子的未来价格水平进行 重新估计，计算出头寸的损益。这种方法 的优点有：容易理解和使用；可以用于任 何正态分布；可以有效处理那些难以计算 的金融工具的收益。缺点是：没有考虑金 融市场的变化；需要大量的历史数据；模 拟出的 VaR 波动性较大；对计算能力要
九、异方差模型
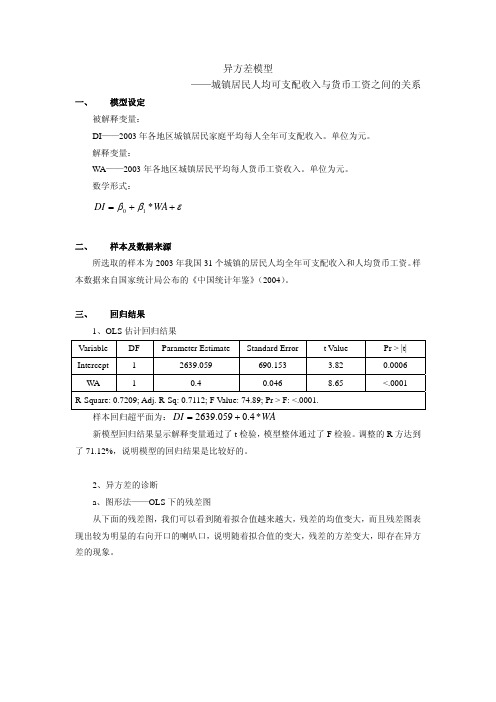
异方差模型——城镇居民人均可支配收入与货币工资之间的关系一、模型设定 被解释变量：DI ——2003年各地区城镇居民家庭平均每人全年可支配收入。
单位为元。
解释变量：WA ——2003年各地区城镇居民平均每人货币工资收入。
单位为元。
数学形式：εββ++=10WA DI *二、样本及数据来源所选取的样本为2003年我国31个城镇的居民人均全年可支配收入和人均货币工资。
样本数据来自国家统计局公布的《中国统计年鉴》（2004）。
三、回归结果1、OLS 估计回归结果 VariableDFParameter EstimateStandard Error t Value Pr > |t| Intercept 1 2639.059 690.153 3.820.0006WA 10.40.0468.65 <.0001R-Square: 0.7209; Adj. R-Sq: 0.7112; F Value: 74.89; Pr > F: <.0001.样本回归超平面为：WA DI *4.0059.2639+=新模型回归结果显示解释变量通过了t 检验，模型整体通过了F 检验。
调整的R 方达到了71.12%，说明模型的回归结果是比较好的。
2、异方差的诊断a 、图形法——OLS 下的残差图从下面的残差图，我们可以看到随着拟合值越来越大，残差的均值变大，而且残差图表现出较为明显的右向开口的喇叭口，说明随着拟合值的变大，残差的方差变大，即存在异方差的现象。
70008000900010000110001200013000-4000-200002000Fitted values R e s i d u a l slm(a$DI ~ a$WA)Residuals vs Fitted261129b 、White 检验利用White 检验的结果如下表所示Heteroscedasticity TestEquation Test Statistic DF Pr> ChiSq Variables DI White's Test12.9420.0016Cross of all varsWhite 检验的结果同样说明了异方差的存在，检验的P 值为0.0016，在1%的水平上能够通过显著性检验。
garch模型均值方程和方差方程
GARCH模型均值方程和方差方程一、引言在金融领域，预测和控制风险是至关重要的。
为了应对金融市场波动性的特点，学者们提出了各种模型。
其中，GARCH模型（Generalized Autoregressive Conditional Heteroskedasticity model）是一种常用的模型，用于建模和预测金融时间序列数据的波动性。
本文将深入探讨GARCH模型的均值方程和方差方程。
首先，我们将介绍GARCH模型的基本原理和概念。
然后，我们将详细讨论GARCH模型的均值方程和方差方程，并解释其含义和表示方式。
最后，我们将通过一个实例来说明如何应用GARCH模型进行波动性预测。
二、GARCH模型基本原理和概念2.1 GARCH模型的基本原理GARCH模型是一种条件异方差模型，它是对经典的自回归移动平均模型（ARMA）的扩展。
GARCH模型最初由Bollerslev（1986）提出，用于描述金融时间序列的波动性。
它的基本原理是：波动性不仅与过去的观测值相关，还与过去的波动性相关。
2.2 GARCH模型的关键概念在深入探讨GARCH模型的均值方程和方差方程之前，我们需要了解几个关键概念。
1.条件异方差：金融时间序列通常表现出波动性的不稳定性和聚集性。
条件异方差是指波动性在不同时间段内发生变化的现象。
2.自回归（AR）：自回归是指序列之间的相关性。
AR模型用过去的观测值来预测当前值。
3.移动平均（MA）：移动平均是指通过计算时间序列的平均数来平滑数据。
MA模型用过去的误差项来预测当前值。
4.自回归移动平均（ARMA）：ARMA模型结合了AR和MA模型，用于建模时间序列数据。
三、GARCH 模型的均值方程GARCH 模型的均值方程描述了时间序列数据的平均水平。
基本形式如下：Y t =μ+∑ϕi pi=1Y t−i +εt其中，Y t 表示时间t 的观测值，μ表示均值，ϕi 表示自回归系数，p 为自回归阶数，εt 表示误差项。
经济学实证研究中的时间序列分析方法比较
经济学实证研究中的时间序列分析方法比较时间序列分析是经济学实证研究中一种常用的方法，它对经济数据的时间变化进行建模和预测。
然而，由于经济学数据的特殊性和复杂性，选择合适的时间序列分析方法至关重要。
本文将比较几种常见的时间序列分析方法，包括自回归移动平均模型（ARMA）、自回归条件异方差模型（ARCH）、广义自回归条件异方差模型（GARCH）、ARIMA模型和向量自回归模型（VAR）。
ARMA模型是最基本的时间序列分析方法之一。
它假设数据的未来观测值是过去观测值的线性组合，同时考虑了残差项的随机性。
ARMA模型适用于平稳时间序列数据，其主要优点是简单易懂、计算效率高。
然而，ARMA模型无法应对非平稳时间序列数据和异方差性的存在。
ARCH模型是针对ARMA模型的不足提出的改进方法，它考虑了数据的条件异方差性。
ARCH模型假设数据的条件方差是过去观测误差的加权和，可用于对金融市场波动性进行建模。
然而，ARCH模型无法处理高度异方差的数据，且对时间序列结构的假设限制较多。
GARCH模型是ARCH模型的扩展，考虑了条件异方差和波动性的长期记忆。
GARCH模型在金融领域得到广泛应用，能够更好地对金融市场的波动进行建模。
然而，GARCH模型对参数估计的要求较高，对数据的拟合效果较为敏感。
ARIMA模型是一种广泛应用于短期时间序列预测的方法，包括自回归、差分和移动平均三个部分。
ARIMA模型能够适应一定程度的非平稳数据，并考虑了序列的趋势和季节性变化。
然而，ARIMA模型对数据具有一定的处理要求，在应用时需要仔细选择阶数和滞后期。
VAR模型是多变量时间序列分析的方法，适用于多个相关变量之间的关系分析与预测。
VAR模型的优点在于能够捕捉不同变量之间的动态联动关系，可以考虑更多的信息。
然而，VAR模型对变量之间的相关性和滞后期的选择有一定要求，模型的估计和解释较为复杂。
综上所述，经济学实证研究中的时间序列分析方法有多种选择，每种方法都有其适用的场景和局限性。
条件异方差模型
LM检验
总结词
LM检验（拉格朗日乘数检验）是另一种常用的检验条件异方差性的方法。
详细描述
LM检验基于残差的自回归模型，通过构造拉格朗日乘数统计量来检验残差是否存在条件异方差性。如果LM检验 的P值较小，则说明存在条件异方差性，适合使用条件异方差模型。
AIC准则
总结词
AIC准则（赤池信息准则）是一种用于模型 选择的准则，也可以用于选择适合的条件异 方差模型。
资产定价
资产定价
条件异方差模型可以用于资产定价，帮助投资者确定资 产的合理价格。
投资决策
基于资产定价结果，投资者可以做出更加明智的投资决 策，提高投资收益。
06
条件异方差模型的局限性与
未来发展
数据依赖性
模型的有效性依赖于数据的准确性和 完整性，如果数据存在误差或缺失， 可能导致模型预测结果的不准确。
贝叶斯估计法
贝叶斯估计法是一种基于贝叶斯定理 的参数估计方法，通过将模型中的未 知参数视为随机变量，并为其指定一 个先验分布，然后利用观测数据更新 该先验分布，从而得到未知参数的后 验分布。在条件异方差模型中，贝叶 斯估计法可以用来估计模型中的未知 参数。
VS
贝叶斯估计法的优点是灵活且能够处 理不确定性，可以考虑到未知参数的 不确定性，并为其提供一个概率描述。 然而，它对数据和先验分布的要求较 高，且计算复杂度较高，需要借助数 值计算方法进行求解。
TARCH模型
总结词
TARCH模型（门限自回归条件异方差 模型）是条件异方差模型的一种，用 于描述金融时间序列数据的波动性。
详细描述
TARCH模型由Zakoian于1994年提出， 它通过引入门限项来描述波动性的非 对称性。TARCH模型能够较好地拟合 金融时间序列数据的波动性，并预测 未来的波动情况。
条件异方差模型
测方差t2-1的说明。
通过在极E大V似iew然s函中数AR方C法H估模计型的是。在例扰如动，项对是于条G件A正R态CH分(1布,1的)，1假6t 定时下期，
按照通常的想法，自相关的问题是时间序列数据所特有， 而异方差性是横截面数据的特点。但在时间序列数据中，会 不会出现异方差呢？会是怎样出现的？
3
恩格尔和克拉格（Kraft, D., 1983）在分析宏观 数据时，发现这样一些现象：时间序列模型中的扰 动方差稳定性比通常假设的要差。恩格尔的结论说 明在分析通货膨胀模型时，大的及小的预测误差会 大量出现，表明存在一种异方差，其中预测误差的 方差取决于后续扰动项的大小。
大似然估计法进行估计。下面分别介绍这3种分布，其中的
代表参数向量。 1．对于扰动项服从正态分布的GARCH(1, 1)模型，它
的对数似然函数为
ln L(θ ) T ln( 2 π) 1
2
2
T t 1
ln
2 t
1 2
T t 1
( yt
x tγ ) 2
2（6.1.33）
t
这里的t2是ut的条件方差。
2 t
0
1
u
2 t
1
通常用极大似然估计得到参数0, 1, 2, , k(p)过程可以写为：
var(
u
t
)
2 t
0
1
u
2 t 1
u2
2 t2
经典单方程计量经济学模型(异方差性)
80%
适用范围
对数变换法适用于存在异方差性 的模型，尤其适用于解释变量和 被解释变量之间存在非线性关系 的情况。
04
异方差性与模型选择
异方差性与模型适用性
异方差性是指模型中误差项的 方差不为常数，而是随解释变 量的变化而变化。
在异方差性存在的情况下，经 典的单方程计量经济学模型可 能不再适用，因为模型假设误 差项的方差是恒定的。
为了使模型具有适用性，需要 选择能够处理异方差性的模型 ，例如广义最小二乘法、加权 最小二乘法等。
异方差性与模型预测能力
异方差性的存在会影响模型的预测能力，因为异方差性会导致模 型的残差不再独立同分布，从而影响模型的预测精度。
为了提高模型的预测能力，需要采取措施处理异方差性，例如使 用稳健的标准误、对误差项进行变换等。
在实践中，应该充分考虑异方差性的影响，采取适当 的措施进行修正，以提高模型的预测和推断能力。
02
异方差性的检验
图示检验法
残差图检验
通过绘制残差与拟合值的图形，观察残差的分布情况，判断是否 存在异方差性。如果残差随着拟合值的增加或减少而呈现有规律 的变化，则可能存在异方差性。
杠杆值图检验
将数据按照杠杆值（leverage）进行排序，并绘制杠杆值与残差的 图形。如果图形显示高杠杆值对应的点有异常的残差分布，则可能 存在异方差性。
经典单方程计量经济学模型(异 方差性)
目
CONTENCT
录
• 异方差性简介 • 异方差性的检验 • 异方差性的处理方法 • 异方差性与模型选择 • 经典单方程计量经济学模型中的异
方差性
01
异方差性简介
定义与特性
异方差性是指模型残差的方差不为常数，随着解释 变量的变化而变化。
Eviews数据统计与分析教程9章条件异方差模型ARCHGARCH
EViews统计分析基础教程
三、ARCH模型的其他扩展形式
2. TARCH模型
TARCH（Threshold ARCH）模型是门限自回归条件异 方差模型，可用来分析数据的剧烈波动性。 模型中条件方差的形式为
其中，dt-1是一个虚拟变量，满足的条件为 1 ，如果μt-1<0
dt-1= 0，如果μt-1>=0
EViews统计分析基础教程
一、自回归条件异方差模型（ARCH）
2.ARCH模型检验
（2）残差平方的相关图（Q）检验法
在EViews操作中，要实现残差平方的相关图（Q）检验，需 在 方 程 对 象 窗 口 中 选 择 “ View”|“Residual Tests”|“Correlogram – Q – statistics”选项。
GARCH（1，1）模型在金融领域应用广泛，可以对金融时 间序列的数据进行描述。
EViews统计分析基础教程
二、广义自回归条件异方差模型（GARCH）
2.GARCH模型的建立
当上述辅助回归方程进行ARCH效应检验时，如果ARCH的 滞后阶数q很大，检验结果依然显著，即残差序列依然存在 ARCH（q）效应。此时可采用GARCH（p，q）模型重新进 行估计。
在“Options”中输入ARCH和GARCH的阶数 。
在“Variance”的编辑栏中可列出方差方程中的外生变量。
EViews统计分析基础教程
一、自回归条件异方差模型（ARCH）
3.ARCH模型的建立
Options选项卡
如果选中“Backcasting”（回推） 中的复选框，MA初始扰动项 和GARCH项中的初始预测方 差将使用回推（“Backcasting”） 方法确定初始值。
什么是异方差性如何进行异方差性的检验与处理
什么是异方差性如何进行异方差性的检验与处理异方差性，它是统计学中一种常见的现象，指的是观测值的方差在不同的条件下不相等。
在数据分析和建模过程中，异方差性可能会导致模型参数估计不准确，假设检验无效以及预测效果下降等问题。
因此，了解异方差性并进行检验和处理是非常重要的。
1. 异方差性的表征异方差性通常表现为残差的方差与预测值的关系不稳定。
在回归分析中，当残差的方差与预测值的关系呈现出一定的模式时，可以初步判断存在异方差性。
常见的异方差性模式有以下几种：（1）线性模式：残差的方差与预测值呈线性关系，即残差的方差随着预测值的增大而增大或减小。
（2）指数模式：残差的方差与预测值呈指数关系，即残差的方差随着预测值的增大呈指数级别增大或减小。
（3）对数模式：残差的方差与预测值呈对数关系，即残差的方差随着预测值的增大呈对数级别增大或减小。
（4）多重峰值模式：残差的方差具有多个峰值，表示不同分组或条件之间存在不同的方差水平。
2. 异方差性的检验针对上述异方差性模式，可以进行一些统计检验来验证异方差性的存在。
常用的异方差性检验方法包括帕金森-斯皮尔曼检验（Park test）、布劳什-帕甘检验（Breusch-Pagan test）和韦斯特曼检验（White test）等。
这些检验方法都是基于残差的方差与预测值之间的关系建立的。
以布劳什-帕甘检验为例，该检验的原假设是残差的方差与预测变量之间不存在显著相关关系，即不存在异方差性。
在进行检验时，首先需要对模型进行拟合，并获得残差。
然后，根据拟合残差和预测变量的关系构建辅助回归模型，并进行显著性检验。
如果辅助回归模型的显著性检验结果小于设定的显著性水平（通常为0.05），则可以拒绝原假设，认为存在异方差性。
3. 异方差性的处理在实际数据分析中，如果检验结果表明存在异方差性，需要对数据进行处理以减小或消除其影响。
常用的异方差性处理方法包括以下几种：（1）对数或平方根变换：通过对原始数据进行对数或平方根变换，可以降低数据的异方差性。
计量经济学金玉国第四章
xi递增(或递减) (i=1,2,…,n)
2020/2/12
山东财经大学统计学院计量经济教研室
第21页
机动 目录 上页 下页 返回 结束
G-Q检验的步骤：
1.将n对样本观察值(xi , yi)按观察值xi的大小排队。 2.将序列中间的c个观察值除去，并将剩下的观察值
V a r ( u |x i)i 2 常 数 ( i 1 ,2 ,L ,n )
则称随机误差项u具有异方差性(Heteroscedasticity)。
如果被解释变量观测值的分散程度是随解释变量的 变化而变化的，如图4.1所示，可以把异方差看成是 由于某个解释变量的变化而引起的，则
V ar(ui2)i22f(xi)
第四章 回归模型中的 随机误差项问题
第一节 概述 第二节 异方差 第三节 自相关
第一节 概 述
一、古典假定
假定1：随机项ui具有零均值：
E(ui|xi)=0
i=1,2, …, n
假定2：随机项ui具有同方差：
Var (ui|xi)=u2
i=1,2, …, n
假定3：随机项ui无序列相关性：
Cov(ui , uj)=0 i≠j i,j= 1,2, …, n
2020/2/12
山东财经大学统计学院计量经济教研室
第14页
机动 目录 上页 下页 返回 结束
异方差产生的原因
1、模型中省略的解释变量
如果将某些未在模型中出现的重要影响因素归入随机误差 项，而且这些影响因素的变化具有差异性，则会对被解释 变量产生不同的影响，从而导致误差项的方差随之变化， 即产生异方差性。
异方差模型
从这，我们可以看出 ε t 是高峰和肥尾的。 估计 在 ε t = z t ht 中，若 zt 服从标准的正态分布，则伪似然估计 （Quasi-Maximum-Likelihood Estimator）的对数似然函数为：
LT = − T 1 T ln 2π − ∑ ln ht2 + zt2 2 2 t =1
2
值，即 E (rt | Ft −1 ) = μ t ，相应地可以定义 rt 的条件方差 ht ：
2
ht ≡ Var (rt | Ft −1 ) = E[(rt − μ t ) 2 | Ft −1 ] = E (ε t | Ft −1 )
2 2
(2)
式(2)是 GARCH 类波动率模型的核心部分，Engle(1982)首先提出了以 AR(q)结构 来对 ht 建模，这就是著名的自回归条件异方差模型(Auto-Regressive Conditional Heteroscedasticity,ARCH)。Engle 定义条件均值的残差序列 {ε t } 为：
无条件方差
E (ε t ) =
2
α0 1 − (α + β )
峰度 如果 1 − (α + β ) 2 − 2α 2 ，则峰度系数 E (ε t4 ) 3[1 − (α + β ) 2 ] == >3 [Var (ε t )]2 1 − (α + β ) 2 − 2α 2 从这，我们可以看出 ε t 是高峰和肥尾的。 估计 在 ε t = z t ht 中，若 zt 服从标准的正态分布，则伪似然估计 （Quasi-Maximum-Likelihood Estimator）的对数似然函数为：
可以写成为
ε t2 = α 0 + (α + β )ε t −1 2 + ε t2 − ht 2 − β (ε t2−1 − ht2−1 )
计量经济学四五章 李子奈
ii i i i i i i X X X X X X e εαααααα++++++=215224213221102~第四章异方差1.异方差的概念和类型概念：对于模型 如果出现 即对于不同的样本点，随机误差项的方差不再是常数，而互不相同，则认为出现了异方差性。
异方差一般可归结为三种类型：(1)单调递增型： σi 2随X 的增大而增大(2)单调递减型： σi 2随X 的增大而减小(3)复杂型： σi 2与X 的变化呈复杂形式2.几种异方差的检验方法（描述原理即可）（1）图示检验法①用X-Y 的散点图进行判断：看是否存在明显的散点扩大、缩小或复杂型趋势（即不在一个固定的带型域中）②用X-的散点图进行判断：看是否形成一斜率为零的直线（2）帕克(Park)检验与戈里瑟(Gleiser)检验选择关于变量X 的不同的函数形式，对方程进行估计并进行显著性检验，如果存在某一种函数形式，使得方程显著成立，则说明原模型存在异方差性。
（3）G-Q 检验先将样本一分为二，对子样①和子样②分别作回归，然后利用两个子样的残差平方和之比构造统计量进行异方差检验。
由于该统计量服从F 分布，因此假如存在递增的异方差，则F 远大于1；反之就会等于1（同方差）、或小于1（递减方差）。
（4）怀特（White ）检验怀特检验不需要排序，且适合任何形式的异方差。
以二元为例 先进行OLS 回归，得到 然后做辅助回归 可以证明，在同方差假设下，从该辅助回归所得到的可决系数R2与样本容量n 的乘积，渐进地服从自由度为辅助回归方程中解释变量个数的卡方分布：（R2为辅助回归的可决系数，h 为辅助回归法人解释变量的个数）如果存在异方差性，则表明确与解释变量的某种组合有显著的相关性，这时往往显示出有较高的可决系数并且某一参数的t 检验值较大。
3.异方差的后果（1）参数估计量非有效OLS 估计量仍然具有无偏性，但不具有有效性。
因为在有效性证明中利用了而且，在大样本情况下，尽管参数估计量具有一致性，但仍然不具有渐近有效性。
时间序列分析模型汇总
时间序列分析模型汇总时间序列分析是一种广泛应用于各个领域的统计分析方法，它用来研究一组随时间而变化的数据。
时间序列数据通常具有趋势、季节性和随机性等特征，时间序列分析的目的是通过建立适当的模型来描述和预测这些特征。
本文将汇总一些常用的时间序列分析模型，包括AR、MA、ARIMA、GARCH和VAR等。
1.AR模型（自回归模型）:AR模型是根据过去的观测值来预测未来的观测值。
它假设未来的观测值与过去的一系列观测值有关，且与其他因素无关。
AR模型的一般形式为：Y_t=c+Σ(φ_i*Y_t-i)+ε_t，其中Y_t表示时间t的观测值，c 为常数，φ_i为系数，ε_t为误差项。
2.MA模型（移动平均模型）:MA模型是根据过去的误差项来预测未来的观测值。
它假设未来的观测值与过去的一系列误差项有关，且与其他因素无关。
MA模型的一般形式为：Y_t=μ+ε_t+Σ(θ_i*ε_t-i)，其中Y_t表示时间t的观测值，μ为平均值，θ_i为系数，ε_t为误差项。
3.ARIMA模型（自回归积分移动平均模型）:ARIMA模型是AR和MA模型的组合，它结合了时间序列数据的趋势和随机性特征。
ARIMA模型的一般形式为：Y_t=c+Σ(φ_i*Y_t-i)+Σ(θ_i*ε_t-i)+ε_t，其中Y_t表示时间t的观测值，c为常数，φ_i和θ_i为系数，ε_t为误差项。
4.GARCH模型（广义自回归条件异方差模型）:GARCH模型用于建模并预测时间序列数据的波动性。
它假设波动性是由过去观测值的平方误差和波动性的自相关引起的。
GARCH模型的一般形式为：σ_t^2=ω+Σ(α_i*ε^2_t-i)+Σ(β_i*σ^2_t-i)，其中σ_t^2为时间t的波动性，ω为常数，α_i和β_i为系数，ε_t为误差项。
5.VAR模型（向量自回归模型）:VAR模型用于建模并预测多个时间序列变量之间的相互关系。
它假设多个变量之间存在相互依赖的关系，即一个变量的变动会对其他变量产生影响。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
19
因此，无条件均值、无条件方差不受误差过程（4.2）的影响。 3） t 的条件均值是
E ( t t 1 , t 2 ,) Et 1vt Et 1 ( 0 1 t21 )1/ 2 0
4） t 的条件方差是
E ( t2 t 1 , t 2 ,) 0 1 t21
ˆt2 q 1 ˆt21 0 1 ˆt2 2 ˆt21 q Et
方程(*)被称为自回归条件异方差(ARCH)模型。
条件异方差模型介绍
由 Engle (1982) 提出的一类乘积条件异方差模型：设定 白噪声扰动项 vt 为乘积扰动形式。如
t vt 0 1 t21
pValue = 0
ARCH_LM检验(Eviews) ARCH-LM效应检验结果
27
F统计量及T×R2统计量的P值都小于0.05，因此，在5% 的显著性水平下，深证综指收益率自回归模型的残差存 在ARCH效应。
残差平方相关图检验
28
残差
残差平方
ARCH模型定阶
ARCH Test: F-statistic Obs*R-squared 5.220573 44.68954 Probability Probability 0.000001 0.000002 Test Equation: Dependent Variable: RESID^2 Method: Least Squares Date: 10/21/04 Time: 21:27 Sample(adjusted): 2010 2254 Included observations: 245 after adjusting endpoints Variable Coefficient Std. Error t-Statistic C 0.000110 5.34E-05 2.060138 RESID^2(-1) 0.141549 0.065237 2.169776 RESID^2(-2) 0.055013 0.065823 0.835766 RESID^2(-3) 0.337788 0.065568 5.151697 RESID^2(-4) 0.026143 0.069180 0.377893 RESID^2(-5) -0.041104 0.069052 -0.595260 RESID^2(-6) -0.069388 0.069053 -1.004854 RESID^2(-7) 0.005617 0.069178 0.081193 RESID^2(-8) 0.102238 0.065545 1.559806 RESID^2(-9) 0.011224 0.065785 0.170619 RESID^2(-10) 0.064415 0.065157 0.988613 R-squared 0.182406 Mean dependent var Adjusted R-squared 0.147466 S.D. dependent var S.E. of regression 0.000627 Akaike info criterion Sum squared resid 9.19E-05 Schwarz criterion Log likelihood 1464.875 F-statistic Durbin-Watson stat 2.004802 Prob(F-statistic)
8
模型提出背景
9
深证综指日收益率峰度为3.755，高于正态分布的峰度值3，说明深证综 指具有一定的尖峰厚尾的特征，J-B检验也证实了深证综指日收益率的分 布显著异于正态分布。 View-Descriptive Statistics-Histogram and Stats
模型提出背景
10
Hist(x), histfit(x), normfit(x), normplot(x)
这个条件方差依赖于 t21 的值，如果 t21 值较大，在 t 处的条件方差将 也较大。因此，ARCH 模型能捕捉到 { yt } 的平缓期和波动期。
条件异方差模型介绍
现在可以分析 yt 的无条件均值、无条件方差：
a0 a1i t i ，可求出： 由于 yt 1 a1 i 0
2
当 代 计 量 经 济 模 型 体 系
单 序 列
时 间 序 列 分 析
截面数据回归
模型提出背景
波动模型种类
SV（随机波动）模型 SV-M 模型 MSSV 模型 LMSV 模型
3
波动模型
ACD（自回归条件久期）模型 MSACD 模型 SCD（随机条件久期）模型 MSSCD 模型
ARCH 模型 TARCH 模型 EARCH 模型 ABSARCH 模型 ARCH-M 模型 ABSARCH-M 模型 FIARCH 模型
第三章 条件异方差模型
模型提出背景
单位根检验 时间序列的加法、乘法模型， X12 季节调整 ARIMA（时间序列）模型 线性时间序列 SARIMA（季节时间序列）模型 GAR（广义自回归）模型 BL（双线性）模型 非线性时间序列 TAR、STAR（门限自回归、平滑转移）模型 ARCH、GARCH（自回归条件异方差）模型 向 量 序 列 波动模型 SV（随机波动）模型 ACD、 SCD（自回归、随机条件久期）模型 VAR、 VEC（向量自回归、误差修正）模型 单方程（线性、非线性） 、分位数回归模型 回 归 分 析 时间序列回归 联立方程模型（结构、简化型、递归模型） PANEL（面板数据）模型、空间计量模型 DS（离散选择）模型、有序响应、计数模型 LDV（受限因变量）模型（删失、截断模型） 蒙特卡罗模拟技术
模型提出背景
波动集群性
.15
-.10 250 500 750 1000 1250 1500
如图所示，为上证指数对数日收益率时间序列图，从 图中直观可见，收益率存在着丛集性效应(即一次大 的波动后往往伴随着大的波动，一次小的波动后往往 伴随着小的波动)。
模型提出背景
异方差性(heteroscedasticity)
15
条件异方差模型介绍
ARCH模型简介
1982年恩格尔（Engle）提出“条件异方差自回归模型，简 称ARCH模型 。ARCH模型获得了2003年诺贝尔经济学奖 被认为是最集中反映了方差变化特点，而被广泛应用于金 融数据时间序列分析的模型。 ARCH 理论是目前国际上前沿的用于金融市场资产定价的 理论。与传统的 CAPM 、 APT 理论相比， ARCH 是一种动 态非线性的股票定价模型，它突破了传统的方法论和思维 方式，摒弃了风险与收益呈线性关系的假定，反映了随机 过程的一个特殊性质方差随时间变化而变化。
20
1） yt 的无条件均值
Eyt a0 /(1 a1 )
i 0
2） yt 的无条件方差为 Var ( yt ) a12iVar ( t i ) ，则有 再由 t 的无条件方差是常量（ a0 /(1 a1 ) ）
1 Var ( yt ) 0 2 1 1 1 a1 3） yt 的条件均值： Et 1 yt a0 a1 yt 1
经典线性回归模型的一个重要假定是：总体回归函数 中的随机误差项满足同方差性，即它们都有相同的方差。 如果这一假定不满足，则称线性回归模型存在异方差性。
13
模型提出背景
异方差性的例子：
1. 调查不同规模公司的利润，发现大公司的利润波动 幅度比小公司的利润波动幅度大 2. 分析家庭支出时发现高收入家庭支出变化比低收入 家庭支出变化大。在分析家庭支出模型时，我们会发 现高收入家庭通常比低收入家庭对某些商品支出有更 大的方差。
4） yt 的条件方差
Var ( yt yt 1 , yt 2 ,) Et 1 ( yt a0 a1 yt 1 ) 2 Et 1 ( t2 ) 0 1 t21
ARCH 过程可以多种形式扩展。 Engle(1982)考虑了高阶 ARCH(q) 过程
t vt 0 i t2i
i 1 q
条件异方差模型例子
自回归条件异方差模型----ARCH模型
21
汇率
条件异方差模型例子
Tell Me Why 最炫民族风
22
条件异方差模型回顾
自回归条件异方差模型----ARCH模型
xt f (t , xt 1 , xt 2 , ) t t ht t 2 2 h 0 1 t 1 m t m t
16
条件异方差模型介绍
ARCH 模型 Engle(1982) 提出可以同时对一个序列的均值和方差建 模方法。 yt 1 的条件方差是： Var ( yt 1 yt ) Et ( yt 1 a0 a1 yt ) 2
Et ( t 1 ) 2
17
现在假设这个条件方差不是常量，预测这个条件方差的最简 单办法是把估计的残差的平方看作为 AR(q)过程 ˆt 2q vt ˆt 2 0 1 ˆt 21 2 ˆt 22 q (*) 这里 vt 是白噪声过程。由此可以预测 t+1 时的条件方差
GARCH 模型 TGARCH 模型 EGARCH-M 模型 ABSGARCH 模型 GARCH-M 模型 ABSGARCH-M 模型 FIGARCH 模型
模型提出背景
4
思考问题：
ARIMA模型是否适合拟合动态生产过程？ 对股票数据，利用ARIMA建模是否适合？ 传统的经济计量模型往往假设方差？
不变的，即在不同 时期方差保持一个 常数
模型提出背景
金融时间序列：尖峰厚尾、长记忆性、波动集群 性(丛集性或积聚性)、条件异方差性等特点
7
ACF随时间延迟以多 项式的速度缓慢衰 减至0，则称为长记 忆时间序列。
模型提出背景
尖峰厚尾(Leptokurtosis)：