多元函数微分学基础PPT课件
合集下载
多元函数微积分(课件)
3 V 为因变量的二元函数。根据问题的实际意义，函数的定义域为
D {(r,h) | r＞0,h＞0} 。
二元以及二元以上的函数统称为多元函数。
5
第、 一节 多元函数的概念、极限与连续性
、
2．二元函数的定义域 二元函数的定义域比较复杂，可以是坐标系中全部的区域，也可以是由曲线所围成的 部分区域。围成区域的曲线称为区域的边界。不包括边界的区域称为开区域，连同边 界在内的区域称为闭区域；开区域内的点称为内点，而边界上的点称为边界点。 如果一个区域 D 内任意两点之间的距离都不超过某一正常数 M ，则 D 称为有界区域， 否则称为无界区域。
、
【例 3】 求二元函数 z ln(x y) 的定义域 D 。 解 由对数函数性质可知 x 、 y 必须满足 x y＞0 。直线 x y 0 是它的边界，定义域 为不包括边界在内的开区域。
D {(x, y) | x y＞0}
二、多元函数的极限
定义 5.2 设二元函数 z f (x, y) ，如果当点 P(x, y) 以任意方式趋向于点 P0 (x0 , y0 ) 时，f (x, y) 总趋向于一个确定的常数 A ，则称 A 是二元函数 f (x, y) 当 (x, y) (x0, y0 ) 时的极限，记为
4
第、 一节 多元函数的概念、极限与连续性
、
一、多元函数的概念 1．二元函数的定义
定义 5.1 设 D 是平面上的一个非空点集，如果对于每个点 (x, y) D ，变量 z 按照一定的法 则总有确定的值和它对应，则称 z 是变量 x、y 的二元函数，记为 z f (x, y) 。其中 x、y 称 为自变量， z 称为因变量，自变量 x、y 的取值范围 D 称为函数的定义域。 【例 1】设圆锥体的底面半径为 r ，高为 h ，则体积V 1 πr2h 。这是一个以 r 、h 为自变量，
D {(r,h) | r＞0,h＞0} 。
二元以及二元以上的函数统称为多元函数。
5
第、 一节 多元函数的概念、极限与连续性
、
2．二元函数的定义域 二元函数的定义域比较复杂，可以是坐标系中全部的区域，也可以是由曲线所围成的 部分区域。围成区域的曲线称为区域的边界。不包括边界的区域称为开区域，连同边 界在内的区域称为闭区域；开区域内的点称为内点，而边界上的点称为边界点。 如果一个区域 D 内任意两点之间的距离都不超过某一正常数 M ，则 D 称为有界区域， 否则称为无界区域。
、
【例 3】 求二元函数 z ln(x y) 的定义域 D 。 解 由对数函数性质可知 x 、 y 必须满足 x y＞0 。直线 x y 0 是它的边界，定义域 为不包括边界在内的开区域。
D {(x, y) | x y＞0}
二、多元函数的极限
定义 5.2 设二元函数 z f (x, y) ，如果当点 P(x, y) 以任意方式趋向于点 P0 (x0 , y0 ) 时，f (x, y) 总趋向于一个确定的常数 A ，则称 A 是二元函数 f (x, y) 当 (x, y) (x0, y0 ) 时的极限，记为
4
第、 一节 多元函数的概念、极限与连续性
、
一、多元函数的概念 1．二元函数的定义
定义 5.1 设 D 是平面上的一个非空点集，如果对于每个点 (x, y) D ，变量 z 按照一定的法 则总有确定的值和它对应，则称 z 是变量 x、y 的二元函数，记为 z f (x, y) 。其中 x、y 称 为自变量， z 称为因变量，自变量 x、y 的取值范围 D 称为函数的定义域。 【例 1】设圆锥体的底面半径为 r ，高为 h ，则体积V 1 πr2h 。这是一个以 r 、h 为自变量，
高数课件21多元函数微分学
设两点为 P( x1, x2,, xn ), Q( y1, y2,, yn ),
| PQ | ( y1 x1)2 ( y2 x2 )2 ( yn xn )2 .
特殊地当 n 1, 2, 3时，便为数轴、平面、空间
两点间的距离．
n维空间中邻域、区域等概念
邻域： U (P0 , ) P | PP0 | , P Rn
1
2
重点
多元函数基本概念，偏导数， 全微分，复合函数求导，隐函 数求导，偏导数的几何应用， 多元函数极值。
难点
复合函数求导，多元函数极值。
函数的微分法从一元函数发展到 二元函数本质
上要出现一些新东西，但 从二元函数到二元以上
函数则可以类推，
因此这里基
本上只讨论二元函数。
一、多元函数的概念
设P0 ( x0 , y0 )是xoy 平面上的一个点， 是某 一正数，与点P0 ( x0 , y0 )距离小于 的点P( x, y) 的全体，称为点P0 的 邻域，记为U ( P0 , ) ，
4、 x2 1 y ；
x
1 y
5、 ( x, y) 0 x2 y2 1, y2 4x ；
6、 ( x, y) x 0, y 0, x 2 y ；
7、( x, y) x 0, x y x
( x, y) x 0, x y x；
8、 ( x, y) y 2 2x 0 .
3 x2 y2 1 2 x2 y2 4
x y2 0
x
y2
f ( x, y) arcsin(3 x2 y2 ) x y2
例1 求 解 所求定义域为
的定义域．
设函数z f ( x, y)的定义域为D ，对于任意 取定的P( x, y) D，对应的函数值为 z f ( x, y)，这样，以x 为横坐标、y 为纵坐 标、z 为竖坐标在空间就确定一点M ( x, y, z)， 当x 取遍D 上一切点时，得一个空间点集 {( x, y, z) | z f ( x, y), ( x, y) D}，这个点集称
多元函数微分法 PPT课件
x
y
z f [u( x, y), x, y]
z
x
y
z f u f , x u x x
两者的区别
变而对 x 的偏导数
z f u f . y u y y
把 z f (u, x, y) 中 的 u 及 y
把复合函数 z f [(x, y), x, y] 中的 y 看作不 看作不变而对 x 的
的偏导数都存在,函数在 z f (u, v) 对应点 (u, v) 可微，则 复合函数 z f [ ( x, y), ( x, y)] 在点 ( x, y ) 处存在对 x 、 y 的偏导数,且
z z u z v , x u x v x
z z u z v . y u y v y
z z u z v v 1 v vu x u ln u 1 y u y v y
xy(1 xy)
y
y 1
(1 xy) ln(1 xy)
y
xy (1 xy) [ ln(1 xy)] 1 xy
医用高等数学
推论:
”
医用高等数学
医用高等数学
第三节
多元函数微分法
一、复合函数微分法
二、隐函数微分法
医用高等数学
一、复合函数微分法
我们知道 : 如果函数u ( x )在点 x处可导 , 而 y f ( u)在 x点对应u处可导 , 则复合函数 y f [ ( x )] 在点 x处可导, 且其导数为
u
z
v
x
医用高等数学
全导数
例4-24 设 z e
u 2v
3 u sin x v x , 而 ， ,求
《多元函数的微积分》课件
最优化问题
在资源分配和生产计划中，多元函数微积分可以用于求解最优化问 题，例如最大化利润或最小化成本等。
风险评估
在金融学中，多元函数微积分可以用于评估投资风险和回报，以及 制定风险管理策略。
THANKS
感谢观看
多元函数的定义域
函数中各个自变量可以取值的范围。例如，对于函数z = f(x, y)，其定义域是x和y的所有可能取值的集合。
多元函数的值域
函数中因变量可以取值的范围。例如，对于函数z = f(x, y) ，其值域是z的所有可能取值的集合。
多元函数的几何意义
平面上的曲线
对于二元函数z = f(x, y)，其图像 在二维平面上表现为一条曲线。 例如，函数z = x^2 + y^2表示 一个圆。
体积计算
通过多元函数微积分，可以计算出由曲面围成的三维空间的体积 ，这在工程和科学领域中具有广泛的应用。
曲线积分
在几何学中，曲线积分是计算曲线长度的一种方法，而多元函数 微积分可以提供更精确和更高效的计算方法。
多元函数微积分在物理上的应用
力学分析
在分析力学中，多元函数微积分 被广泛应用于解决质点和刚体的 运动问题，例如计算物体的速度 、加速度和力矩等。
三维空间中的曲面
对于三元函数z = f(x, y, z)，其图 像在三维空间中表现为一个曲面 。例如，函数z = x^2 + y^2表 示一个球面。
多元函数的极限与连续性
多元函数的极限
当自变量趋近于某个值时，函数值的趋近值。例如，lim (x, y) → (0, 0) (x^2 + y^2) = 0，表示当(x, y)趋近于(0, 0)时，函数x^2 + y^2的值趋近于0。
《多元函数的微积分》 ppt课件
在资源分配和生产计划中，多元函数微积分可以用于求解最优化问 题，例如最大化利润或最小化成本等。
风险评估
在金融学中，多元函数微积分可以用于评估投资风险和回报，以及 制定风险管理策略。
THANKS
感谢观看
多元函数的定义域
函数中各个自变量可以取值的范围。例如，对于函数z = f(x, y)，其定义域是x和y的所有可能取值的集合。
多元函数的值域
函数中因变量可以取值的范围。例如，对于函数z = f(x, y) ，其值域是z的所有可能取值的集合。
多元函数的几何意义
平面上的曲线
对于二元函数z = f(x, y)，其图像 在二维平面上表现为一条曲线。 例如，函数z = x^2 + y^2表示 一个圆。
体积计算
通过多元函数微积分，可以计算出由曲面围成的三维空间的体积 ，这在工程和科学领域中具有广泛的应用。
曲线积分
在几何学中，曲线积分是计算曲线长度的一种方法，而多元函数 微积分可以提供更精确和更高效的计算方法。
多元函数微积分在物理上的应用
力学分析
在分析力学中，多元函数微积分 被广泛应用于解决质点和刚体的 运动问题，例如计算物体的速度 、加速度和力矩等。
三维空间中的曲面
对于三元函数z = f(x, y, z)，其图 像在三维空间中表现为一个曲面 。例如，函数z = x^2 + y^2表 示一个球面。
多元函数的极限与连续性
多元函数的极限
当自变量趋近于某个值时，函数值的趋近值。例如，lim (x, y) → (0, 0) (x^2 + y^2) = 0，表示当(x, y)趋近于(0, 0)时，函数x^2 + y^2的值趋近于0。
《多元函数的微积分》 ppt课件
多元函数全微分ppt课件-PPT精选文档
二 元 函 数 对 二 元 函 数 对 y y的 x和 和 对 的 偏 微 分 对 偏 改 变 量x
全改变量的概念
z f(x ,y )在 (x , y)的 如 果 函 数 点 某 邻 域 内 (x P x , y y)为 有 定 义 ， 并 设 这 邻 域 内 的 任 意 一 点 ， 则 称 这 两 点 的 函 数 值 之 差 f(x x , y y) f(x , y) x , y的 为 函 数 在 点 P对 应 于 自 变 量 改 变 量 全 z 改 变 量 （ 全 增 量 ） ， 记 为
0 0
0 , x 0 , y 0 . 即 lim z lim f ( x x , y y ) f ( x , y ) 0 , 0 0 0 0 0 x 0
x 0 y 0
y 0 lim f( x x ,y y )f(x ,y ) 0 0 0 0
( x , y ) z f ( x , y ) 故 函 数 在 点 处 连 续 . 0 0
定理 2 ：如果函数 z f (x , y)在点（ x ）可微 0, y 0 (x 则函数 z f (x , y) 的两个偏导数 fx 0, y 0), (x fy 存在，且 0, y 0) dz f ( x , y ) x f (x y x 0 0 y 0, y 0) (x , y )
0 0
即可微分定义中 z A x B y o ( ） A f ( x ,y ) ， B f ( x ,y ) x 0 0 y 0 0
P ( x , y ) 证： 如 0 0 z f ( x , y ) 果 函 数 在 点 可 微 分 ,
全改变量的概念
z f(x ,y )在 (x , y)的 如 果 函 数 点 某 邻 域 内 (x P x , y y)为 有 定 义 ， 并 设 这 邻 域 内 的 任 意 一 点 ， 则 称 这 两 点 的 函 数 值 之 差 f(x x , y y) f(x , y) x , y的 为 函 数 在 点 P对 应 于 自 变 量 改 变 量 全 z 改 变 量 （ 全 增 量 ） ， 记 为
0 0
0 , x 0 , y 0 . 即 lim z lim f ( x x , y y ) f ( x , y ) 0 , 0 0 0 0 0 x 0
x 0 y 0
y 0 lim f( x x ,y y )f(x ,y ) 0 0 0 0
( x , y ) z f ( x , y ) 故 函 数 在 点 处 连 续 . 0 0
定理 2 ：如果函数 z f (x , y)在点（ x ）可微 0, y 0 (x 则函数 z f (x , y) 的两个偏导数 fx 0, y 0), (x fy 存在，且 0, y 0) dz f ( x , y ) x f (x y x 0 0 y 0, y 0) (x , y )
0 0
即可微分定义中 z A x B y o ( ） A f ( x ,y ) ， B f ( x ,y ) x 0 0 y 0 0
P ( x , y ) 证： 如 0 0 z f ( x , y ) 果 函 数 在 点 可 微 分 ,
《高等数学教学课件》高数-第八章-多元函数微分学
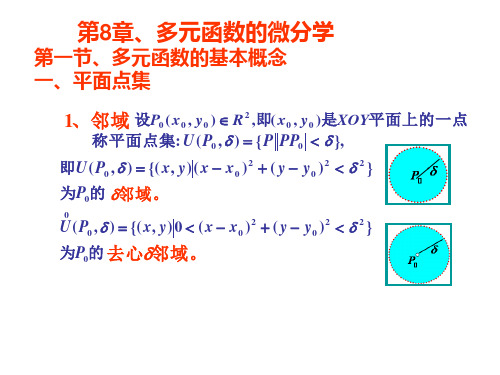
邻域U(P, ), 使U(P, ) E为空集,则
称点P为E的 外点。
边界点的定义：
若点P的任意的邻域内,既有属于E的点
也 有 不 属 于E的 点, 则 称 点P是E的 边 界 点 。
边界的定义：
E的边界点的全体称为E的 边 界 。
3、聚点、孤立点
设E是一个平面点集
聚点的定义：
若点P的任意邻域都含有E的无穷多个点，
为P0的 邻域。
0
U(P0 , ) {( x, y) 0 ( x x0 )2 ( y y0 )2 2 }
为P0的 去心邻域。
2、内点、外点、边界点
设E是一个平面点集.
内点的定义：
若点P E,并且存在P点的一个
邻域U(P, ), 使U(P, ) E,则称点P
为E的内点。
外点的定义： 若点P E,并且存在P点的一个
一切多元初等函数在其定义区域内是连续的。
例6、讨论下列函数的连续性
(1)、f
(
x,
y)
x
3 xy 2 2
y
2
x2 y2 0
解 0
x2 y2 0
当x 2 y 2 0时, f ( x, y) 3xy 是初等函数, x2 2y2
且 有 定 义, 连 续.
3kx 2
lim f ( x, y) lim
lim
x0
x2 2y4
02 2(1)4
. 2
y1
在有界闭区域上连续的多元函数的重要性质如下：
定理1、(最大最小值定理)
在有界闭区域D上连续的多元函数f , 在D上必有
最大值和最小值,亦即在D上有点P1和P2 , 使对D上任意
点P,恒有 f P1 f P f P2 , P D
称点P为E的 外点。
边界点的定义：
若点P的任意的邻域内,既有属于E的点
也 有 不 属 于E的 点, 则 称 点P是E的 边 界 点 。
边界的定义：
E的边界点的全体称为E的 边 界 。
3、聚点、孤立点
设E是一个平面点集
聚点的定义：
若点P的任意邻域都含有E的无穷多个点，
为P0的 邻域。
0
U(P0 , ) {( x, y) 0 ( x x0 )2 ( y y0 )2 2 }
为P0的 去心邻域。
2、内点、外点、边界点
设E是一个平面点集.
内点的定义：
若点P E,并且存在P点的一个
邻域U(P, ), 使U(P, ) E,则称点P
为E的内点。
外点的定义： 若点P E,并且存在P点的一个
一切多元初等函数在其定义区域内是连续的。
例6、讨论下列函数的连续性
(1)、f
(
x,
y)
x
3 xy 2 2
y
2
x2 y2 0
解 0
x2 y2 0
当x 2 y 2 0时, f ( x, y) 3xy 是初等函数, x2 2y2
且 有 定 义, 连 续.
3kx 2
lim f ( x, y) lim
lim
x0
x2 2y4
02 2(1)4
. 2
y1
在有界闭区域上连续的多元函数的重要性质如下：
定理1、(最大最小值定理)
在有界闭区域D上连续的多元函数f , 在D上必有
最大值和最小值,亦即在D上有点P1和P2 , 使对D上任意
点P,恒有 f P1 f P f P2 , P D
多元函数微分学(省公开课金奖全国赛课一等奖微课获奖课件
i1
i 1
❖几何上看，C0(S)是凸集，且表示包含集合S最小凸集或是包 含集合S全部凸集交集.
数理经济学（Mathematical Economics）, 刘树林, © 2005
16/311 6
ቤተ መጻሕፍቲ ባይዱ
Rn中凸集与凸集分离定理（续）
极点
定义4.1.11 设X Rn是凸集，称x X是X
极点，若对任意y，z X和
，定义
d(x, y)
n
(xi
yi )2
(x y) • (x y)
i1
则可验证映射d满足(M-1) (M-3)，故(R n，d)是一个度量空间．
数理经济学（Mathematical Economics）, 刘树林, © 2005
7/31 7
数学基础—几个空间
范数与赋范线性空间
设V是一个实线性空间，若V上实值函数‖.‖: x ‖x‖满足:
m
x
= (x1, x2, , xn)mlim xim
xi
i = 1，2，…，n．
❖定理 若
lim x m x lim y m y lim c m c
m
m
m
则
lim (c
m
m
x
m
ym)
cx
y
这里，m = 1，2，…，+ .
数理经济学（Mathematical Economics）, 刘树林, © 2005
易验证Rn满足(I-1) (I-3), 故是一个内积空间, 称作Euclidean 空间
数理经济学（Mathematical Economics）, 刘树林, © 2005
6/31 6
数学基础—几个空间
高等数学 多元函数微分法及其应用ppt课件
其余类推
fxy( x,
y)
lim
y0
fx(x, y
y) y
fx(x, y)
(2) 同样可得：三阶、四阶、…、以及n 阶偏导数。
(3) 【定义】二阶及二阶以上的偏导数统称为高阶偏导数。
【例
1】设 z
x3
y2
3 xy 3
xy
1，求二阶偏导数及
3z x 3
.
【解】 z 3x2 y2 3 y3 y, x
x2 y2 sin x2 y2 ( x2 y2 )3 2
y0
换元,化为一元 函数的极限
机动 目录 上页 下页 返回 结束
【阅读与练习】 求下列极限
5/51
x2
(1)lim sin( xy) (a 0); (2) lim (1 1 )x2 y2 ;
x0 x
x
x
ya
ya
1
(3)lim(1 sin xy)xy; x0
(2) 【复合函数求导链式法则】
①z
u
v
t t
dz z du z dv dt u dt v dt
全导数
u
x z z u z v y x u x v x
②z
v
x z z u z v
y y u y v y
③ z f (u, x, y)
u x z f f u
y x x u x
(
x,
y,
z)
lim
z0
z
.
机动 目录 上页 下页 返回 结束
10/51
4. 【偏导数的几何意义】 设 M0( x0 , y0 , f ( x0 , y0 )) 为曲面 z f ( x, y) 上一点, 如图
多元函数微分学基础PPT课件
rhvrhvrhrh这里是随着的变化而变化的当在一定范围内内取定一对数值时的对应值就随之确定611三角形面积见图其面积依赖于三角形的两条边及其夹角图611例2示意图xyzxy设有变量如果当变量在一定范围内任意取定一对数值时变量按照一定法则总有惟一确定的数值与之对应则称是的二元函数记作xy式中叫作自变量叫作因变量
(b)有界区域
(c)有界区域
图6-12 区域示意
若区域能延伸到无限远处，就称这区域是无界的，如 图6-12(c)所示，否则，它总可以被包含在一个以原点O为中 心，而半径适当大的圆内，这样的区域称为有界的，如图612(a)、(b)所示，围成区域的曲线叫区域的边界.
闭区域：连同边界在内的区域的曲线叫区域的边界.
同样,函数z f (x, y)在点(x0,y0 )处对y的偏导数定义为
lim f ( y0 y, y0 ) f (x0 ,y0 )
x0
y
记作 z , f , z (x ,y )或f (x ,y )等.
y x (x0 ,y0 )
(x0 ,y0 )
y 00
y 00
如果函数z f (x, y)在区域D内每一点(x,y)处对x的偏导数 都有存在,那么这个偏导数就是x, y的函数,称为函数z f (x, y) 对自变量x的偏导函数.记作
y
a x2 y2 a2
O ax
例 5 求二元函数z ln(x y)的定义域．
解 自变量x, y 所取的值必须满足不等式x y 0 , 即定义域为
D (x, y) | x y 0.
点集D 在 xOy 面上表示一个在直线上方的半平面(不 包含边界x y 0)，如下图所示，此时 D 为无界开区域．
(如右图所示)．
(b)有界区域
(c)有界区域
图6-12 区域示意
若区域能延伸到无限远处，就称这区域是无界的，如 图6-12(c)所示，否则，它总可以被包含在一个以原点O为中 心，而半径适当大的圆内，这样的区域称为有界的，如图612(a)、(b)所示，围成区域的曲线叫区域的边界.
闭区域：连同边界在内的区域的曲线叫区域的边界.
同样,函数z f (x, y)在点(x0,y0 )处对y的偏导数定义为
lim f ( y0 y, y0 ) f (x0 ,y0 )
x0
y
记作 z , f , z (x ,y )或f (x ,y )等.
y x (x0 ,y0 )
(x0 ,y0 )
y 00
y 00
如果函数z f (x, y)在区域D内每一点(x,y)处对x的偏导数 都有存在,那么这个偏导数就是x, y的函数,称为函数z f (x, y) 对自变量x的偏导函数.记作
y
a x2 y2 a2
O ax
例 5 求二元函数z ln(x y)的定义域．
解 自变量x, y 所取的值必须满足不等式x y 0 , 即定义域为
D (x, y) | x y 0.
点集D 在 xOy 面上表示一个在直线上方的半平面(不 包含边界x y 0)，如下图所示，此时 D 为无界开区域．
(如右图所示)．
《高等数学教学课件》高数-第八章-多元函数微分学
高数-第八章-多元函数微分学
目
CONTENCT
录
• 多元函数微分学概述 • 多元函数的导数与偏导数计算 • 多元函数微分学在几何上的应用 • 多元函数微分学在极值问题中的应
用
目
CONTENCT
录
• 多元函数微分学在约束最优化问题 中的应用
• 多元函数微分学在实际问题中的应 用
01
多元函数微分学概述
04
多元函数微分学在极值问题中的应用
极值的第一充分条件
总结词
极值的第一充分条件是多元函数微分 学中用于判断函数极值的重要定理。
详细描述
极值的第一充分条件表明，如果一个 多元函数在某一点的偏导数等于零， 并且这个点的海森矩阵（Hessian matrix）是正定的或负定的，那么这 个点就是函数的极值点。
多元函数的概念
80%
多元函数
设D是n维空间的一个区域，对D 中的任意点P，若存在实数x、y、 z...与之对应，则称f(x,y,z...)是D上 的多元函数。
100%
多元函数的定义域函数f(x Nhomakorabeay,z...)中所有自变量x、y 、z...的取值范围共同构成的集合 称为多元函数的定义域。
80%
多元函数的几何意义
在三维空间中，二元函数f(x,y)表 示曲面上的点P(x,y,f(x,y))的轨迹 。
偏导数的定义与性质
偏导数的定义
对于多元函数f(x,y,z...)，如果当 其他变量保持不变时，函数关 于某个特定变量的一阶导数存 在，则称这个导数为该函数在 该特定变量上的偏导数。
偏导数的几何意义
在三维空间中，二元函数f(x,y) 在点(x0,y0)处关于x的偏导数 表示曲面在点(x0,y0)处沿x轴 方向的切线斜率。
目
CONTENCT
录
• 多元函数微分学概述 • 多元函数的导数与偏导数计算 • 多元函数微分学在几何上的应用 • 多元函数微分学在极值问题中的应
用
目
CONTENCT
录
• 多元函数微分学在约束最优化问题 中的应用
• 多元函数微分学在实际问题中的应 用
01
多元函数微分学概述
04
多元函数微分学在极值问题中的应用
极值的第一充分条件
总结词
极值的第一充分条件是多元函数微分 学中用于判断函数极值的重要定理。
详细描述
极值的第一充分条件表明，如果一个 多元函数在某一点的偏导数等于零， 并且这个点的海森矩阵（Hessian matrix）是正定的或负定的，那么这 个点就是函数的极值点。
多元函数的概念
80%
多元函数
设D是n维空间的一个区域，对D 中的任意点P，若存在实数x、y、 z...与之对应，则称f(x,y,z...)是D上 的多元函数。
100%
多元函数的定义域函数f(x Nhomakorabeay,z...)中所有自变量x、y 、z...的取值范围共同构成的集合 称为多元函数的定义域。
80%
多元函数的几何意义
在三维空间中，二元函数f(x,y)表 示曲面上的点P(x,y,f(x,y))的轨迹 。
偏导数的定义与性质
偏导数的定义
对于多元函数f(x,y,z...)，如果当 其他变量保持不变时，函数关 于某个特定变量的一阶导数存 在，则称这个导数为该函数在 该特定变量上的偏导数。
偏导数的几何意义
在三维空间中，二元函数f(x,y) 在点(x0,y0)处关于x的偏导数 表示曲面在点(x0,y0)处沿x轴 方向的切线斜率。
《多元函数微分学》PPT课件
0 V .
14
定义1 设D是xOy平面上的点集, 若变量z与D
多 元
函
中的变量x, y之间有一个依赖关系, 使得在D内
数 的
基
每取定一个点P(x, y)时,按着这个关系有确定的
本 概
z值与之对应, 则称z是x, y的二元(点)函数.记为 念
z f ( x, y) (或z f (P) )
称x, y为自变量,称z为因变量,点集D称为该函数
P0 称为 E 的内点：如果存在一个正数 使得U (P0 ) E P0 称为 E 的外点：如果存在一个正数 使得
U (P0 ) E
P0 称为 E 的边界点：如果对任意一个正数 使得
U (P0 ) 中即有E中点又有非E中点
P0 即不是E的内点也不是E的外点
闭区域： G G G
12
（3）Rn 中的集合到 Rm的映射
的 基 本
和方法上都会出现一些实质性的差别, 而多元
概 念
函数之间差异不大. 因此研究多元函数时, 将以
二元函数为主.
24
3、多元函数的极限
多
讨论二元函数 z f ( x, y),当x x0 , y y0 ,
元 函
即P( x, y) P0 ( x0 , y0 )时的极限.
数 的 基
怎样描述呢? 回忆: 一元函数的极限
多 元 函 数
的
基
解 定义域是 ( x 1)2 y2 1且x2 y2 1
本 概
念
y
•
O
1
x
有界半开半闭区域
18
3 求 f ( x, y) arcsin(3 x2 y2的) 定义域． x y2
解
3 x2 y2 1
多元函数微分学(共184张PPT)
z
sin
x2
1 y2
1
• 在 点圆 都周 是x2间 断y2 点1，是上一没条有曲定线义，. 所以该圆周上各
• 性质1(最大值和最小值定理) 在有界闭区域 D上的多元连续函数，在D上一定有最大值和最小
值.
• 在D上至少有一点 及一点 ，使得 为最大 值而 为最小值，P 即1 对于一切P 2 P∈D，有f ( P1 )
•
P
于E的点，也有不属于E的点，
•
E
则称P为E的边界点（图8-2）.
•
设D是开集.如果对于D内的
• 图 8-1 任何两点，都可用折线连结起
上一页 下一页 返 回
•
来,而且该折线上的点都属于D,
•
P 则称开集D是连通的.
•
连通的开集称为区域或开区域.
•
E
开区域连同它的边界一起,称
•
为闭区域.
• 图 8-2
f( x x ,y ) f( x ,y ) A x ( x )
• 上式两边各除以 x ，再令 x 0而极限，就得
limf(xx,y)f(x,y)A • 从而 ，x 偏0导数 z 存 在x，而且等于A.同样可证
• =B.所以三式 x 成立.证毕.
z y
上一页 下一页 返 回
• 定理2(充分条件) 如果z=f(x,y)的偏导数
• 3.n维空间
• 设n为取定的一个自然数,我们称有序n元数组
•
的全体为n维空间,而每个有序n元数
(x1组,x2, ,xn) 称为n维空间中的一个点,数 称
(x1,x2, ,xn)
xi
上一页 下一页 返 回
• 为该点的第i个坐标,n维空间记为 .n
多元函数微分基本概念ppt课件
n 维向量. xi 称为 x 的第 i 个坐标 或 第 i 个分量.
10
Rn中两点x (x1,, xn ), y ( y1,, yn ) 的距离定义为
记作
特别, 点 x (x1, x2,, xn )与零元 0 的距离为
x x12 x22 xn2 当n 1,2,3时, x 通常记作 x .
显然, E 的内点必属于 E , E 的外点必不属于 E , E 的
边界点可能属于 E, 也可能不属于 E .
5
(2) 聚点
若对任意给定的 ,点P 的去心
E
邻域
内总有E 中的点 , 则
称 P 是 E 的聚点.
聚点可以属于 E , 也可以不属于 E (因为聚点可以为
E 的边界点 )
所有聚点所成的点集成为 E 的导集 .
6
(3) 开区域及闭区域
若点集 E 的点都是内点，则称 E 为开集；
E 的边界点的全体称为 E 的边界, 记作E ;
若点集 E E , 则称 E 为闭集；
若集 D 中任意两点都可用一完全属于 D 的折线相连 ,
则称 D 是连通的 ; 连通的开集称为开区域 ,简称区域 ; 开区域连同它的边界一起称为闭区域.
趋于不同值或有的极限不存在，则可以断定函数极限
不存在 .
例3. 讨论函数
f
(x,
y)
x2
xy y2
在点 (0, 0) 的极限.
解: 设 P(x , y) 沿直线 y = k x 趋于点 (0, 0) , 则有
lim
x0
f (x, y)
lim
x0
x2
kx2 k2x2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、二元函数的定义 先看下面的例子.
例1 圆柱体的体积V 和它的底面积半径r及高h之间的关系
为V r 2h
这里,V是随着r, h的变化而变化的.当r, h在一定范围内(r 0, h 0)内取定一对数值(r,h)时,V的对应值就随之确定.
例2 三角形面积(见图6-11)
C
S
1 2
bc
即1 x2 y2 9 ,函数定义域为
D (x, y) |1 x2 y2 9.点集 D
在 xOy平面上表示以原点为圆
心，半径为 3 的圆与以原点为
y
O1 3 x
圆心的单位圆所围成的圆环
域(包含边界曲线内圆 x2 y2 1， 但不包含边界曲线外圆x2 y2 9 )
O
1x
1 图6 14 x2 y2 1所确定区域
某点的邻域是指以该点为中心的一个圆形开区域.如点P0
(x0 , y0 )的一个 ( 0)邻域是指 {(x, y)|(x x0 )2 +(y y0 )< 2}
记作U (P0, ),在不需要强调邻域的半径的时,也可简记为U (P0 )
z
O
R
y
x 图6-15 例6示意图
三、二元函数的极限和连续性
1.二元函数的极限
函数的极限是研究当自变量变化时，函数的变化趋势， 但是二元函数的自变量有两个，所以自变量的变化过程比 一元函数要复杂得多.
现在把一元函数的极限概念推广到二元函数上.考虑当点 (x,y)趋近于点(x0,y0 )时函数z f (x, y)的变化趋势.虽然点P(x,
sin
A
b
a
其面积S依赖于三角形的两条 A
c
B
边b, c及其夹角A.
图6-11 例2示意图
一般地，二元函数的定义如下.
定义1 设有变量x,y,z,如果当变量x,y,在一定范围内任意 取定一对数值时,变量z按照一定法则,总有惟一确定的数值 与之对应,则称z是x, y的二元函数,记作z f (x, y)
二元函数z f (x, y)在点(x0, y0 )处的函数值记为
ቤተ መጻሕፍቲ ባይዱ
f (x0 , y0 )或z
(x0 , y0 ), z
x x0 y y0
例3 设z x2 2xy 3y2 ,求z . (2,3)
解 z (2,3) (2)3 2 (2) 3 3 32 31.
y
a x2 y2 a2
O ax
例 5 求二元函数z ln(x y)的定义域．
解 自变量x, y 所取的值必须满足不等式x y 0 , 即定义域为
D (x, y) | x y 0.
点集D 在 xOy 面上表示一个在直线上方的半平面(不 包含边界x y 0)，如下图所示，此时 D 为无界开区域．
开区域：不包括边界内的区域叫开区域. 一般没有必要区分开或闭时,通称区域,用字母D表示.
例如,由x y 0所确定的区域是无界开区域(见图6 13) 而由x2 y2 1所确定的区域是有界闭区域(见图6 14)
y
y
1
O
x
x y 0 图6 13 x y 0所确定区域
1
式中,x, y叫作自变量; z叫作因变量.x, y的变化范围叫作函数 的定义域.
类似,可定义三元函数W f (x, y, z)及三元以上的函数.二元 及二元以上的函数称为多元函数.
类似一元函数y f (x),用数轴上点P来表示数值x,而二元函数 z f (x, y)也可以用xOy平面上的点P(x, y)来表示一对有序实数x, y,于时函数z f (x, y)可简记为z f (P),这时z也可称为点P的函 数.(三元函数是否也可以看作点的函数)
(b)有界区域
(c)有界区域
图6-12 区域示意
若区域能延伸到无限远处，就称这区域是无界的，如 图6-12(c)所示，否则，它总可以被包含在一个以原点O为中 心，而半径适当大的圆内，这样的区域称为有界的，如图612(a)、(b)所示，围成区域的曲线叫区域的边界.
闭区域：连同边界在内的区域的曲线叫区域的边界.
y
O
x
例 6 求二元函数 z ln(9 x2 y2 ) x2 y2 1的定
义域．
解 这个函数是由ln(9 x2 y2 ) 和 x2 y2 1 两部
分构成，所以要使函数 z 有意义，x, y 必须同时满足
9 x2 y2 0,
x
2
y2
1
0,
为方便使用，将开区域内的点称为内点，将区域边界上的点 称为边界点.
例 4 求二元函数z a2 x2 y2 的定义域．
解 由根式函数的定义容易知道，该函数的定义域 为满足 x2 y2 a2 的x, y, 即定义域为
D (x, y) | x2 y2 a2 .
这里D 在xOy 面上表示一个以原点为圆心，a 为半 径的圆域．它为有界闭区域（如下图所示）.
对于一元函数，一般假定在某个区间上有定义进行讨论.对 于二元函数，类似地假定它在某平面区域内有定义进行讨论.
所谓区域（平面的）是指一条或几条曲线围成具有连通性的 平面一部分（见图6-35），所谓的连通性是指如果一块部分平面 内任意两点可用完全属于此部分平面的折线连结起来.
D1
D2
D3
(a)有界区域
y)趋近于点P0 (x0 ,y0 )的方式是多种多样的,如果用表示点P(x
, y)与点P0 (x0 ,y0 )之间的距离
(x x0 )2 ( y y0 )2
那么(x, y) (x0 ,y0 )的过程不论多么复杂,总可以用x x0, y y0
或 0来表示自变量的变化过程(x, y) (x0, y0 ).这样,可以提出
二元函数极限的定义如下.
(如右图所示)．
二、二元函数的几何意义
已经知道,一元函数y f (x)的图形,是平面上的一条曲线; 对于二元函数z f (x, y)的图形,则为空间的一个曲面.在前面 讲过的平面和曲面,都可以为二元函数图形的例子.
例6 函数z R2 x2 y2的图形是以原点为中心, R为半径, 在xOy平面上的半个球面(见图6 15.)
例1 圆柱体的体积V 和它的底面积半径r及高h之间的关系
为V r 2h
这里,V是随着r, h的变化而变化的.当r, h在一定范围内(r 0, h 0)内取定一对数值(r,h)时,V的对应值就随之确定.
例2 三角形面积(见图6-11)
C
S
1 2
bc
即1 x2 y2 9 ,函数定义域为
D (x, y) |1 x2 y2 9.点集 D
在 xOy平面上表示以原点为圆
心，半径为 3 的圆与以原点为
y
O1 3 x
圆心的单位圆所围成的圆环
域(包含边界曲线内圆 x2 y2 1， 但不包含边界曲线外圆x2 y2 9 )
O
1x
1 图6 14 x2 y2 1所确定区域
某点的邻域是指以该点为中心的一个圆形开区域.如点P0
(x0 , y0 )的一个 ( 0)邻域是指 {(x, y)|(x x0 )2 +(y y0 )< 2}
记作U (P0, ),在不需要强调邻域的半径的时,也可简记为U (P0 )
z
O
R
y
x 图6-15 例6示意图
三、二元函数的极限和连续性
1.二元函数的极限
函数的极限是研究当自变量变化时，函数的变化趋势， 但是二元函数的自变量有两个，所以自变量的变化过程比 一元函数要复杂得多.
现在把一元函数的极限概念推广到二元函数上.考虑当点 (x,y)趋近于点(x0,y0 )时函数z f (x, y)的变化趋势.虽然点P(x,
sin
A
b
a
其面积S依赖于三角形的两条 A
c
B
边b, c及其夹角A.
图6-11 例2示意图
一般地，二元函数的定义如下.
定义1 设有变量x,y,z,如果当变量x,y,在一定范围内任意 取定一对数值时,变量z按照一定法则,总有惟一确定的数值 与之对应,则称z是x, y的二元函数,记作z f (x, y)
二元函数z f (x, y)在点(x0, y0 )处的函数值记为
ቤተ መጻሕፍቲ ባይዱ
f (x0 , y0 )或z
(x0 , y0 ), z
x x0 y y0
例3 设z x2 2xy 3y2 ,求z . (2,3)
解 z (2,3) (2)3 2 (2) 3 3 32 31.
y
a x2 y2 a2
O ax
例 5 求二元函数z ln(x y)的定义域．
解 自变量x, y 所取的值必须满足不等式x y 0 , 即定义域为
D (x, y) | x y 0.
点集D 在 xOy 面上表示一个在直线上方的半平面(不 包含边界x y 0)，如下图所示，此时 D 为无界开区域．
开区域：不包括边界内的区域叫开区域. 一般没有必要区分开或闭时,通称区域,用字母D表示.
例如,由x y 0所确定的区域是无界开区域(见图6 13) 而由x2 y2 1所确定的区域是有界闭区域(见图6 14)
y
y
1
O
x
x y 0 图6 13 x y 0所确定区域
1
式中,x, y叫作自变量; z叫作因变量.x, y的变化范围叫作函数 的定义域.
类似,可定义三元函数W f (x, y, z)及三元以上的函数.二元 及二元以上的函数称为多元函数.
类似一元函数y f (x),用数轴上点P来表示数值x,而二元函数 z f (x, y)也可以用xOy平面上的点P(x, y)来表示一对有序实数x, y,于时函数z f (x, y)可简记为z f (P),这时z也可称为点P的函 数.(三元函数是否也可以看作点的函数)
(b)有界区域
(c)有界区域
图6-12 区域示意
若区域能延伸到无限远处，就称这区域是无界的，如 图6-12(c)所示，否则，它总可以被包含在一个以原点O为中 心，而半径适当大的圆内，这样的区域称为有界的，如图612(a)、(b)所示，围成区域的曲线叫区域的边界.
闭区域：连同边界在内的区域的曲线叫区域的边界.
y
O
x
例 6 求二元函数 z ln(9 x2 y2 ) x2 y2 1的定
义域．
解 这个函数是由ln(9 x2 y2 ) 和 x2 y2 1 两部
分构成，所以要使函数 z 有意义，x, y 必须同时满足
9 x2 y2 0,
x
2
y2
1
0,
为方便使用，将开区域内的点称为内点，将区域边界上的点 称为边界点.
例 4 求二元函数z a2 x2 y2 的定义域．
解 由根式函数的定义容易知道，该函数的定义域 为满足 x2 y2 a2 的x, y, 即定义域为
D (x, y) | x2 y2 a2 .
这里D 在xOy 面上表示一个以原点为圆心，a 为半 径的圆域．它为有界闭区域（如下图所示）.
对于一元函数，一般假定在某个区间上有定义进行讨论.对 于二元函数，类似地假定它在某平面区域内有定义进行讨论.
所谓区域（平面的）是指一条或几条曲线围成具有连通性的 平面一部分（见图6-35），所谓的连通性是指如果一块部分平面 内任意两点可用完全属于此部分平面的折线连结起来.
D1
D2
D3
(a)有界区域
y)趋近于点P0 (x0 ,y0 )的方式是多种多样的,如果用表示点P(x
, y)与点P0 (x0 ,y0 )之间的距离
(x x0 )2 ( y y0 )2
那么(x, y) (x0 ,y0 )的过程不论多么复杂,总可以用x x0, y y0
或 0来表示自变量的变化过程(x, y) (x0, y0 ).这样,可以提出
二元函数极限的定义如下.
(如右图所示)．
二、二元函数的几何意义
已经知道,一元函数y f (x)的图形,是平面上的一条曲线; 对于二元函数z f (x, y)的图形,则为空间的一个曲面.在前面 讲过的平面和曲面,都可以为二元函数图形的例子.
例6 函数z R2 x2 y2的图形是以原点为中心, R为半径, 在xOy平面上的半个球面(见图6 15.)