七年级数学上册 第5章 相交线与平行线 5.1 相交线 5.1.2 垂线练习 (新版)华东师大版
七年级数学上册第5章相交线与平行线5.1相交线2垂线习题课件新版华东师大版

二、垂线的性质 垂线的性质1 用三角尺或量角器画已知直线l的垂线: (1)如图1,画已知直线l的垂线,这样的直线能画_无__数__条. (2)如图2,过点A画直线l的垂线,这样的直线能画_一__条. (3)如图3,过点B画直线l的垂线,这样的直线能画_一__条.
【思考】(1)通过①的探究,能得到关于垂线的怎样的结论? 提示:直线l的垂线有无数条. (2)通过②③的探究,能得到关于垂线的怎样的结论? 提示:经过一点只能画一条直线与已知直线垂直. 【总结】 过一点__有__且__只_有__一__条__直线与已知直线垂直.
5.如图所示,AB是一条河流,要铺设管道将河水引到C,D两个 用水点,现有两种铺设管道的方案: 方案一:分别过C,D作AB的垂线,垂足分别为E,F,沿CE,DF 铺设管道; 方案二:连结CD交AB于点P,沿PC,PD铺设管道.
这两种铺设管道的方案哪一种更节省材料?为什么?
【解析】按方案一铺设管道更节省材料.理由如下:因为CE⊥ AB,DF⊥AB,而AB与CD不垂直,所以根据“垂线段最短”, 可知CE<CP,DF<DP,所以CE+DF<CP+DP,所以沿CE,DF 铺设管道更节省材料.
2.垂 线
1.了解垂线的概念,掌握垂线的性质.(重点) 2.理解点到直线的距离的概念. 3.会用三角尺或量角器过一点画一条直线的垂线,会用垂线的 性质解决问题. (难点)
一、垂直的概念及符号表示 1.当两条直线相交所构成的四个角中有一个角是_直__角__时,其他 三个角也都成为_直__角__,此时叫做这两条直线互相垂直,其中一 条直线是另一条直线的垂线,它们的交点叫做_垂__足__. 2.垂直的符号是_⊥__,直线AB与直线CD垂直,记作_A_B_⊥__C_D_,直线 m与直线n垂直,记作_m_⊥__n_.
七年级数学上册 第五章 相交线与平行线 5.1.2 垂线作业 (新版)华东师大版
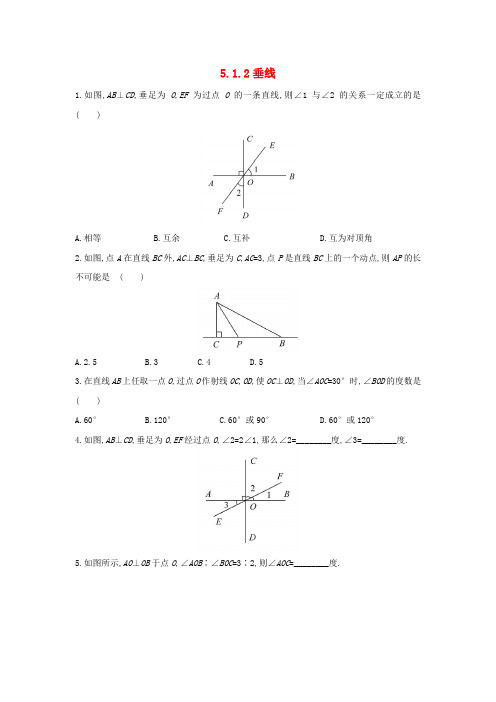
5.1.2垂线1.如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )A.相等B.互余C.互补D.互为对顶角2.如图,点A在直线BC外,AC⊥BC,垂足为C,AC=3,点P是直线BC上的一个动点,则AP的长不可能是( )A.2.5B.3C.4D.53.在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是( )A.60°B.120°C.60°或90°D.60°或120°4.如图,AB⊥CD,垂足为O,EF经过点O,∠2=2∠1,那么∠2=________度,∠3=________度.5.如图所示,AO⊥OB于点O,∠AOB∶∠BOC=3∶2,则∠AOC=________度.6.如图,BD⊥AC于D,DE⊥BC于E,若DE=9cm,AB=12cm,不考虑点与点重合的情况,则线段BD 的取值范围是________.7.如图所示,已知AO⊥OB于O,DO⊥OC于O,∠AOC=∠α,求∠BOD(用∠α表示).8.如图,CD⊥AB,垂足为D,AC⊥BC,垂足为C,线段AB,BC,CD的大小顺序如何?说明理由.参考答案:1.【解析】因为AB⊥CD,所以∠BOD=90°.又因为∠1+∠2+∠BOD=180°,所以∠1+∠2=90°,所以∠1与∠2互余.【答案】B2.A3.【解析】①如图1,当OC,OD在AB的同一侧时,因为OC⊥OD,所以∠COD=90°.又因为∠AOC=30°,所以∠BOD=180°-∠COD-∠AOC=60°;②如图2,当OC,OD在AB的两侧时,因为OC⊥OD,∠AOC=30°,所以∠AOD=60°,所以∠BOD=180°-∠AOD=120°.【答案】D4.【解析】因为AB⊥CD,所以∠2+∠1=90°.因为∠2=2∠1,所以2∠1+∠1=90°,所以∠1=30°,∠2=60°.因为∠1与∠3是对顶角,所以∠3=∠1=30°.【答案】60 305.【解析】因为AO⊥OB,所以∠AOB=90°.又因为∠AOB∶∠BOC=3∶2,所以∠BOC=60°,所以∠AOC=∠AOB+∠BOC=150°.【答案】1506.【解析】因为BD⊥AC,所以AB>BD,因为AB=12cm,所以BD<12cm.又因为DE⊥BC,所以BD>DE.因为DE=9cm,所以BD>9cm,所以9cm<BD<12cm.【答案】9cm<BD<12cm7.解:因为OA⊥OB于O,所以∠AOC+∠BOC=90°.因为∠AOC=∠α,所以∠BOC=90°-∠α.又因为OC⊥OD于O,所以∠COD=90°.因为∠BOD=∠COD+∠BOC,所以∠BOD=90°+90°-∠α=180°-∠α.8.解:AB>BC>CD.理由:因为CD⊥AB,垂足为D,所以BC>CD.因为AC⊥BC,垂足为C,所以AB>BC.所以AB>BC>CD.。
七年级数学上册 第5章 相交线与平行线5.1 相交线 2 垂线作业课件 华东师大级上册数学课件

2.有关垂线的基本事实及点到直线的距离 过一点,有且只有____一条直线与已知直线垂直.从直线外一点到这条直线的 的长垂度线,段叫做点到直线的距离.
练习2:如图,把水渠中的水引到水池C,先过C点向渠岸AB画垂线,垂足为 D,再沿垂线CD开沟才能使沟最短,其依据是 垂线段最短.为O,若∠1=35°, 则∠2=_5_5_°_.
9.如图,BA⊥BD,CB⊥CD,AD=8,BC=6, 则线段BD的长的取值范围是 6<BD<8.
10.已知:OA⊥OC,∠AOB∶∠AOC=2∶3,画出图形, 并求∠BOC的度数.
解:因为OA⊥OC,所以∠AOC=90°,因为∠AOB∶∠AOC=2∶3, 所以∠AOB=60°.因为∠AOB的位置有两种:一种是在∠AOC内, 一种是在∠AOC外.①当在∠AOC内时,∠BOC=90°-60°=30°; ②当在∠AOC外时,∠BOC=90°+60°=150°.
1.过点P向线段AB所在直线引垂线,正确的是( C )
2.如图,点O在直线AB上,若∠1=50°, 当∠2=___4_0度时,OC⊥OD.
3.如图,OA⊥OB,∠AOC=120°,则∠BOC等于__3_0_度.
4.如图,OA⊥m,OB⊥m,所以OA与OB重合,其理由是( C ) A.过两点只有一条直线 B.过一点只能作一条垂线 C.经过一点只有一条直线垂直于已知直线 D.垂线段最短
5.(2017·北京)如图,点P到直线l的距离是( B ) A.线段PA的长度 B.线段PB的长度 C.线段PC的长度 D.线段PD的长度
6.(2016·常州)已知△ABC,BC=6,AC=3,CP⊥AB,垂足为P, 则CP的长可能是( A) A.2 B.4 C.5 D.7
七年级数学第五章相交线与平行线同步练习和单元测试-新人教

M
AN
B
).
A、对顶角 B 、相等但不是对顶角 C 、邻补角 D 、互补但不是邻补角
6、下列说法正确的是(
).
A、有公共顶点的两个角是对顶角
B 、两条直线相交所成的两个角是对顶角
C、有公共顶点且有一条公共边的两个角是邻补角
D、两条直线相交所成的无公共边的两个角是对顶角
三、解答题
1 、如 图 6,三条直 线 AB、 CD、 EF 相交于 点 O,∠ 1=75 °,∠ 2=68°,求∠ COE 的度数。
2、如图 7, OE⊥ OF,∠ EOD和∠ FOH互补,求∠ DOH的度数。
3、已知图 8 中直线 AB、CD、 EF 相交于点 O, OF平分∠ BOD,∠ COB=∠ AOC+45°,求∠ AOF的度数。
4、如图 9,直线 AB、 MN、 PQ相交于点 O,∠ BOM是它的余角的 2 倍,∠ AOP=2∠ MO,Q 且有 OG⊥0A,
是
。
4、如图 3,直线 MN、 PQ被直线 EF所截,若∠ 1=∠ 2,则∠ MEF+∠ PFE=
°
图2
图3
二、选择题
1、如果相等的两个角的一边在一条直线上,另一边互相平行,那么这两个角(
)
A 、相等
B 、互补
C 、相等或互补
D 、不能确定
2、如图 5,∠ 1 和∠ 2 互补,那么图中平行的直线有(
∠ BOD,理由是
。
D
BC
E
O
A BC
A
D
图1
图2
4、自钝角的顶点引它的一边的垂线,把这两个角分成两个角,它们度数的比是
1: 2,则这个钝角的度数是
。
七年级数学下册第五章相交线与平行线5.1相交线5.1.2垂线同步练习含解析新版新人教版

5.1.2垂线基础闯关全练1.如图,直线AB、CD、EF相交于点O,且AB⊥CD,若∠BOE=35°,则∠DOF=( )A.65° B.45° C.35° D.55°2.如图,点O在直线AB上且OC⊥OD,若∠COA= 36°,则∠DOB的大小为( )A.36°B.54°C.55°D.44°3.下列选项中,过点P画AB的垂线CD,三角板放法正确的是( )A B C D4.在下图所示的各图中用三角板分别过点C画线段AB的垂线.(1)(2)(3)(4)5.如图,在立定跳远中,体育老师是这样测量运动员的成绩的,用一块直角三角板的一边附在起跳线上,另一边与拉直的皮尺重合,这样做的理由是( )A.两点之间,线段最短B.过两点有且只有一条直线C.垂线段最短D.过一点可以作无数条直线6.如图.想在河堤两岸搭建一座桥,图中四种搭建方式PA,PB,PC,PD中,最短的是_______. 7.下列图形中,线段PQ的长为点P到直线MN的距离的是( )A B C D8.如图.立定跳远比赛时,小明从点A起跳落在沙坑内B处,这次小明的跳远成绩是4.6米,则小明从起跳点到落脚点之间的距离( )A.大于4.6米 B.等于4.6米 C.小于4.6米 D.不能确定能力提升全练1.如图,∠ACB= 90°.CD⊥AB,垂足为点D,则下面的结论中,正确的有( )①BC与AC互相垂直②AC与CD互相垂直③点A到BC的垂线段是线段BC④点C到AB的垂线段是线段CD⑤线段BC是点B到AC的距离⑥线段AC的长度是点A到BC的距离A.2个 B.3个 C.4个 D.5个2.如图,已知直线CD、EF相交于点O.OA⊥OB,且OE平分∠AOC,若∠EOC= 60°,则∠BOF=______.3.如图,直线AB,CD相交于点O,∠DOE=∠BOD.OF平分∠AOE.(1)判断OF与OD的位置关系;(2)若∠AOC:∠AOD=1:5.求∠EOF的度数.三年模拟全练一、选择题1.如图所示,直线AB⊥CD于点D,直线EF经过点O.若∠1=26°,则∠2的度数是( )A.26° B.64° C.54° D.以上答案都不对2.如图,直线AB、CD相交于点O,OE⊥CD,∠AOE= 52°,则∠BOD等于( )A.24°B.26° C.36° D.38°二、填空题3.如图,已知AC⊥BC,CD⊥ AB.AC=3,BC=4,CD= 2.4,则点C到直线AB的距离等于______. 4.如图,当∠1与∠2满足_________条件时,OA⊥OB.三、解答题5.如图,直线AB与CD相交于点D,OP是∠BOC的平分线,OE ⊥AB,OF⊥ CD.(1)图中除直角外,写出三对相等的角:(2)已知∠EOC= 50°,求∠POF的度数,五年中考全练选择题.1.如图,直线AB,CD相交于点O,EO⊥CD.下列说法错误的是( ) A.∠AOD=∠BOC B.∠AOE+∠BOD=90°C.∠AOC=∠AOED.∠AOD+∠BOD= 180°2.如图,经过直线l外一点A画l的垂线,能画出( )A.1条B.2条C.3条D.4条3.如图所示,点P到直线l的距离是( )A.线段PA的长度 B.线段PB的长度C.线段PC的长度 D.线段PD的长度核心素养全练如图,随意画一个锐角∠MON和一个钝角∠M'O’N’,画出∠MON的平分线OP和∠M'O’N'的平分线O’P’.(1)在OP上任取一点A,画AB⊥OM,AC⊥ON,垂足分别为B,C;(2)在O'P’上任取一点A’,画A'B'⊥O'M’,A'C'⊥O'N',垂足分别是B’,C’;(3)通过度量线段AB,AC,A'B’,A'C'的长度,发现AB____AC,A'B'____ A'C’;(填“=”或“≠”)(4)通过上面的画图和度量,和同学们交流一下,有什么猜想?请用一句话表述出来.5.1.2垂线1.D∵AB⊥CD,∠BOE=35°,∴∠AOF=35°,∠AOD=∠BOC=90°,∴∠DOF= 90°-35°=55°.故选D.2.B∵OC⊥OD,∴∠COD= 90°,又∵∠AOC+∠COD+∠DOB= 180°.∴∠DOB= 180°-36°-90°= 54°.故选B. 3.C根据垂线的作法,将直角三角板的一条直角边与直线AB重合,另一条直角边过点P后沿该直角边画直线即可.4.解析5.C根据垂线段的性质:垂线段最短,故选C.6.答案PC解析根据“连接直线外一点与直线上各点的所有线段中,垂线段最短”与PC⊥AD.知PC最短.7.A对于选项A,PQ⊥MN,Q是垂足,故线段PQ的长为点P到直线MN的距离.8.A 跳远的成绩是点B 到起跳线的距离,即垂线段的长度为4.6米,结合题图知AB 的长大于4.6米.1.B .∵∠ACB=90°,∴AC ⊥BC,故①正确;AC 与DC 相交不垂直,故②错误;点A 到BC 的垂线段是线段AC .故③错误;点C 到AB 的垂线段是线段CD,故④正确;线段BC 的长度是点B 到AC 的距离,故⑤错误;线段AC 的长度是点A 到BC 的距离,故⑥正确.故选B . 2.答案30°解析∵OE 平分∠AOC,∠EOC=60°,∴∠AOE=∠COE= 60°,∠DOE= 180°-∠COE= 120°, ∴∠DOA= 60°,∵OA ⊥OB,∴∠DOA+∠BOD= 90°.∴∠DOB=30°, ∵∠DOF=∠EOC=60°,∴∠BOF=30°. 3.解析(1)因为OF 平分∠AOE,所以∠AOF=∠EOF=21∠AOE . 又因为∠DOE=∠BOD=21∠BOE,所以∠DOE+∠EOF=21(∠BOE+∠AOE)=21×180°=90°,即∠FOD=90°,所以OF ⊥OD.(2)设∠AOC=x .因为∠AOC:∠AOD=1:5, 所以∠AOD=5x,因为∠AOC+∠AOD= 180°, 所以x+5x= 180°,x=30°. 所以∠DOE=∠BOD=∠AOC=30°.又因为∠FOD= 90°.所以∠EOF= 90°-30°= 60°. 一、选择题1.B ∵∠1=26°,∠DOF 与∠1是对顶角, ∴∠DOF=∠1=26°,又∵AB ⊥CD.∴∠DOF+∠2=90°,∴∠2=90°-∠ DOF=90°-26°=64°.故选B.2.D 因为OE ⊥CD, ∠AOE =52°,所以∠AOC= 38°,则∠BOD=∠AOC= 38°,故选D . 二、填空题 3.答案2.4解析由题意得点C 到直线AB 的距离等于CD 的长,即点C 到直线AB 的距离等于2.4. 4.答案∠1+∠2= 90°解析当∠1+∠2= 90°时,∠AOB= 90°,根据垂直的定义得OA ⊥OB. 三、解答题5.解析(1)①∠AOD= ∠BOC,②∠COP= ∠BOP,③∠COE=∠ BOF 等. (2)∵OE ⊥AB,∴ ∠EOB=90°.∵∠ EOC= 50°,∴∠COB= ∠EOB- ∠EOC= 40°.∵OP 是∠BOC 的平分线,∴∠COP=21∠BOC=20°.∵OF ⊥CD, ∴∠COF=90°,∴∠POF= ∠COF-∠COP=70°. 选择题1.C 由对顶角相等知∠AOD=∠BOC,选项A 中说法正确;由对顶角相等知∠BOD=∠AOC .由EO ⊥CD 知∠AOE+∠AOC=90°,所以∠AOE+∠BOD=90°,选项B 中说法正确;由邻补角概念知∠AOD+∠BOD= 180°,选项D 中说法是正确的.只有选项C 中说法是错误的.2.A 同一平面内,过一点有且只有一条直线垂直于已知直线. 3.B 点P 到直线l 的距离就是点P 到直线l 的垂线段PB 的长度。
华东师大版数学七年级上册《5.1.2垂线》同步课时练习及答案

华东师大版数学七年级上册第5章相交线与平行线 5.1相交线5.1.2垂线同步课时练习题1.在同一平面内,下列语句正确的是()A.过一点有无数条直线与已知直线垂直B.和一条直线垂直的直线有两条C.过一点有且只有一条直线与已知直线垂直D.两直线相交,则一定垂直2.下列选项中,过点P画AB的垂线CD,三角尺放法正确的是()3.如图,OA⊥OB,若∠1=55°,则∠2的度数是()A.35°B.45°C.55°D.65°4.如图,点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为()A.35°B.45°C.55°D.65°5.过一条线段外一点画这条线段的垂线,垂足在()A.这条线段上B.这条线段的端点上C.这条线段的延长线上D.以上都有可能6.体育课上,老师测量跳远成绩的依据是()A.两直线间的距离B.两点之间,线段最短C.垂线段最短D.两点确定一条直线7.如图,OM⊥NP,ON⊥NP,所以ON与OM重合,理由是()A.两点确定一条直线B.经过一点有且只有一条直线与已知直线垂直C.过一点只能作一条直线D.垂线段最短8.如图,AB⊥AC,AD⊥BC,垂足分别为A,D,则图中能表示点到直线距离的线段共有()A.2条B.3条C.4条D.5条9.在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是()A.60°B.120°C.60°或90°D.60°或120°10.如图,已知AB⊥BD,CB⊥CD,AD=14cm,BC=10cm,若线段BD的长度为偶数,则线段BD的长度为()A.8cm B.10cm C.12cm D.14cm11.如图,直线AB,CD 相交于点O,若∠AOC=90°,则AB_____CD;若AB⊥CD,则∠AOC=∠COB=∠BOD=∠AOD=_________.12.如图,当∠1和∠2满足________________(只需填一个条件)时,OA⊥OB.13.如图所示,AC⊥l 1,AB⊥l 2,垂足分别为A,B,则A 点到直线l 2的距离是线段____的长,线段AC 的长是点____到直线____的距离.14.如图,OA 是北偏东30°方向的一条射线,若射线OB 与射线OA 垂直,则OB 的方位角是_____________.15.已知,AD⊥BD,AE⊥BE 且AD=3,BE=4,CD=2,BC=5,则点B 到AC 的距离为____,点A 到BC 的距离为____,点B 到AD 的距离为____.16.如图,O 为直线AB 上一点,∠AOC=13∠BOC,OC 是∠AOD 的平分线.(1)求∠COD 的度数;(2)判断OD 与AB 的位置关系,并说明理由.17.如图,直线AB 与CD 相交于点O,OE,OF 分别是∠BOD,∠AOD的平分线.(1)∠DOE 的补角是__________________;(2)若∠BOD=62°,求∠AOE 和∠DOF 的度数;(3)判断射线OE 与OF 之间有怎样的位置关系?并说明理由.参考答案:1---10CCACD CBDDC 11.⊥90°12.∠1+∠2=90°13.ABC l 114.北偏西60°15.43716.解:(1)设∠AOC=x°,则∠BOC=3x°,所以x°+3x°=180°,则x=45°.又OC 平分∠AOD,所以∠COD=∠AOC=45°(2)OD⊥AB,理由:由(1)知∠AOD=∠AOC+∠COD=45°+45°=90°,所以OD ⊥AB17.(1)∠AOE 或∠COE解:(1)因为OE 是∠BOD 的平分线,所以∠DOE=∠BOE,又因为∠BOE+∠AOE =180°,∠DOE+∠COE=180°,所以∠DOE 的补角是∠AOE 或∠COE(2)因为OE 是∠BOD 的平分线,∠BOD=62°,所以∠BOE=12∠BOD=31°,所以∠AOE=180°-31°=149°,因为∠BOD=62°,所以∠AOD=180°-62°=118°,因为OF 是∠AOD 的平分线,所以∠DOF=12×118°=59°(3)OE 与OF 的位置关系是OE⊥OF.理由如下:因为OE,OF 分别是∠BOD,∠AOD的平分线,所以∠DOE=12∠BOD,∠DOF=12∠AOD,因为∠BOD+∠AOD=180°,所以∠EOF=∠DOE+∠DOF=12(∠BOD+∠AOD)=90°,所以OE⊥OF。
七年级数学下册第五章相交线与平行线5.1相交线5.1.2垂线课时练习(pdf,含解析)(新版)新人教版

初中数学·人教版·七年级下册——第五章相交线与平行线5.1.2垂线测试时间:30分钟一、选择题1.如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC=55°,则∠AOD的度数为()A.115°B.125°C.135°D.145°2.如图,点P是直线a外的一点,点A、B、C在直线a上,且PB⊥a,垂足是B,PA⊥PC,则下列说法不正确的是()A.线段PB的长是点P到直线a的距离B.PA、PB、PC三条线段中,PB最短C.线段AC的长是点A到直线PC的距离D.线段PC的长是点C到直线PA的距离3.如图,要把小河里的水引到田地A处,则作AB⊥l,垂足为点B,沿AB挖水沟,水沟最短,理由是()A.两点之间线段最短B.两点确定一条直线C.垂线段最短D.过一点可以作无数条直线4.点P为直线MN外一点,点A、B、C为直线MN上三点,PA=5厘米,PB=4厘米,PC=2厘米,则P 到直线MN的距离()A.等于4厘米B.等于2厘米C.小于2厘米D.不大于2厘米5.直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOC=70°,则∠CON的度数为()A.65°B.55°C.45°D.35°二、填空题6.如图,直线AB,CD相交于点O,EO⊥AB,垂足为点O,若∠AOD=132°,则∠COE=.7.如图,直线AB,CD相交于点O,若∠EOD=40°,∠BOC=130°,那么射线OE与直线AB的位置关系是.8.如图,直线AB与CD相交于点O,OE⊥CD,垂足为O,∠AOE=55°,则∠DOB的度数是.9.如图,点O为直线AB上一点,∠AOC=55°,过点O作射线OD,使得OD⊥OC,则∠BOD的度数是.三、解答题10.如图,O为直线AB上一点,OC⊥OD.已知∠AOC的度数比∠BOD的度数的2倍多6°.(1)求∠BOD的度数;(2)若OE平分∠BOD,OF平分∠BOC,求∠EOF的度数.11.如图,直线AB,CD相交于点O,OE⊥AB,OF⊥CD.(1)若OC恰好是∠AOE的平分线,则OA是∠COF的平分线吗?请说明理由;(2)若∠EOF=5∠BOD,求∠COE的度数.12.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=50°,求∠BOE的度数;(2)若OF平分∠COB,那么OE⊥OF吗?一、选择题1.答案D∵EO⊥AB,∴∠BOE=90°.又∵∠COE=55°,∴∠COB=∠COE+∠BOE=145°.∵∠AOD=∠COB(对顶角相等),∴∠AOD=145°.故选D.2.答案C A.点到直线的距离即点到这一直线的垂线段的长度,故此选项中说法正确;B.根据垂线段最短可知此选项中说法正确;C.线段AP的长是点A到直线PC的距离,故此选项中说法错误;D.点到直线的距离即点到这一直线的垂线段的长度,故此选项中说法正确.故选C.3.答案C由题意可知,理由是垂线段最短.故选C.4.答案D∵PA=5厘米,PB=4厘米,PC=2厘米,∴P到直线MN的距离不大于2厘米.故选D.5.答案B∵ON⊥OM,∴∠MON=90°,∵OM平分∠AOC,∠AOC=70°,∴∠MOC=12∠AOC=35°,∴∠CON=90°-35°=55°,故选B.二、填空题6.答案42°解析∵∠AOD=132°,∴∠COB=132°,∵EO⊥AB,∴∠EOB=90°,∴∠COE=132°-90°=42°.7.答案垂直解析∵∠BOC=130°,∴∠AOD=∠BOC=130°,∴∠AOE=∠AOD-∠EOD=130°-40°=90°.∴OE⊥AB,即射线OE与直线AB的位置关系是垂直.8.答案35°解析∵OE⊥CD,∴∠COE=90°,又∵∠AOE=55°,∴∠AOC=90°-55°=35°,∵直线AB与CD相交于点O,∴∠DOB=∠AOC=35°.9.答案35°或145°解析如图所示,OD的位置有两种情况,①∵OD⊥OC,∴∠COD=90°,∵∠AOC=55°,∴∠BOD=35°.②∵OD'⊥OC,∴∠BOD'=145°.∴∠BOD的度数是35°或145°.三、解答题10.解析(1)设∠BOD=x°,则∠AOC=2x°+6°,∵OC⊥OD,∴∠COD=90°.∵∠AOC+∠COD+∠BOD=180°,∴2x+6+90+x=180,解得x=28,即∠BOD=28°.(2)∵OE平分∠BOD,∴∠BOE=12∠BOD=14°,∵OF平分∠BOC,∴∠BOF=12∠BOC=12×(90°+28°)=59°,∴∠EOF=∠BOF-∠BOE=59°-14°=45°.11.解析(1)OA是∠COF的平分线.理由如下:∵OE⊥AB,∴∠AOE=90°,∵OC恰好是∠AOE的平分线,∴∠AOC=12∠AOE=45°,∵OF⊥CD,∴∠COF=90°,∴∠AOF=∠COF-∠AOC=90°-45°=45°,∴OA是∠COF的平分线.(2)设∠AOC=x,则∠BOD=x,∵∠AOE=90°,∴∠COE=∠AOE-∠AOC=90°-x,∴∠EOF=∠COE+∠COF=90°-x+90°=180°-x,∵∠EOF=5∠BOD,∴180°-x=5x,解得x=30°,∴∠COE=90°-30°=60°.12.解析(1)因为OE平分∠BOD,所以∠BOE=12∠BOD,因为∠BOD=∠AOC=50°,所以∠BOE=12∠BOD=25°.(2)OE⊥OF.因为OE平分∠BOD,所以∠BOE=12∠BOD,因为OF平分∠COB,所以∠BOF=12∠BOC,所以∠EOF=∠BOE+∠BOF=12(∠BOD+∠BOC)=90°,所以OE⊥OF.。
七年级数学上册第5章相交线与平行线5.1相交线2垂线练习1华东师大版(2021年整理)

七年级数学上册第5章相交线与平行线5.1 相交线2 垂线同步练习1 (新版)华东师大版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(七年级数学上册第5章相交线与平行线5.1 相交线2 垂线同步练习1 (新版)华东师大版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为七年级数学上册第5章相交线与平行线5.1 相交线2 垂线同步练习1 (新版)华东师大版的全部内容。
5.1 2。
垂线一、选择题1.在同一平面内,经过一点能作几条直线与已知直线垂直()A.0条 B.1条C.2条 D.无数条2.如图K-47-1,OA⊥OB,若∠1=35°,则∠2的度数是()图K-47-1A.35° B.45° C.55° D.70°3.下列说法中错误的是()A.两直线相交,若有一组邻补角相等,则这两条直线垂直B.两直线相交,若有两个角相等,则这两条直线垂直C.两直线相交,若有一组对顶角互补,则这两条直线垂直D.两直线相交,若有三个角相等,则这两条直线垂直4.如图K-47-2,直线l1与l2相交于点O,OM⊥l1.若∠α=44°,则∠β等于( )图K-47-2A.56° B.46° C.45° D.44°5.如图K-47-3,已知直线AB,CD互相垂直,垂足为O,直线EF过点O,∠DOF∶∠BOF=2∶3,则∠AOE的度数为( )图K-47-3A.36° B.54° C。
48° D.42°6.如图K-47-4所示,P为直线l外一点,A,B,C三点均在直线l上,并且PB⊥l,有下列说法:①PA,PB,PC三条线段中,PB最短;②线段PB的长度叫做点P到直线l的距离;③线段AB的长度是点A到PB的距离;④线段AC的长度是点A到PC的距离.图K-47-4其中正确的有()A.1个 B.2个C.3个 D.4个7.P为直线m外一点,A,B,C为直线m上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线m的距离( )A.等于4 cm B.等于2 cmC.小于2 cm D.不大于2 cm二、填空题8.如图K-47-5所示,OA⊥OC,∠1=∠2,则OB与OD的位置关系是____________.图K-47-59.如图K-47-6,OA是北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB的方向是__________________.图K-47-610.如图K-47-7,AC⊥BC,CD⊥AB,垂足分别是C,D.(1)点C到直线AB的距离是线段________的长度;(2)点B到直线AC的距离是线段________的长度.图K-47-711.如图K-47-8,运动会上,甲、乙两名同学测得小明的跳远成绩分别为DA =4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5章相交线与平行线
5.1 相交线
2.垂线
1.画一条线段的垂线,垂足在( )
A.线段上
B.线段端点上
C.线段的延长线上
D.以上都有可能
2.[xx·北京]如图所示,点P到直线l的距离是( )
A.线段PA的长度
B.线段PB的长度
C.线段PC的长度
D.线段PD的长度
第2题图
3.如图,AB⊥AC,AD⊥BC,垂足分别为A、D,则图中能表示点到直线距离的线段共有( )
第3题图
A.2条
B.3条
C.4条
D.5条
4.两条直线相交所成的四个角中:
(1)若四个角都相等时,则这两条直线的位置关系是________;
(2)若有一组邻补角相等时,则这两条直线的位置关系是________.
5.如图,已知直角△ABC中,∠C=90°,AC=3 cm,BC=4 cm,AB=5 cm,则点A到BC的距离是线段________的长度,为________cm,点B到AC的距离是线段________的长度,为________cm.
6.如图,在下列图形中,分别过点C作直线AB的垂线.
7.[xx春·召陵区期中]如图所示,码头、火车站分别位于A、B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
8.如图,直线AB与CD相交于点O,O E⊥CD,O F⊥AB,∠D O F=65°,求∠B O E和∠A O C 的度数.
9.一辆汽车在直线型的公路MN上由M向N行驶,点A、B是分别位于公路MN两侧的两个村庄,如图.
(1)汽车行驶到公路M N上点C位置时,距离A村最近;行驶到点D位置时,距离B村最近,请在图中分别画出点C、D的位置;
(2)当汽车由M向N行驶的过程中,在公路的哪一段上距离A、B两村都越来越近?在哪
一段上距离
B 村越来越近,而距离A 村越来越远?(不必说明理由)
10.[xx 春·林甸县期末]如图,直线AB 、CD 相交于点O ,OM⊥A B. (1)若∠1=∠2,求∠NO D 的度数;
(2)若∠1=1
3
∠B O C ,求∠A O C 与∠MO D 的度数.
11.[xx·揭西县期末]如图,AB 与CD 相交于O ,O E 平分∠A O C ,O F ⊥AB 于O ,O G ⊥O E 于O ,若∠B O D =40°,求∠A O E 和∠F O G 的度数.
12.[xx 春·大石桥市校级期末]如图所示,直线AB 、CD 相交于点O ,O F 平分∠A O C ,
E O⊥CD 于点O ,且∠D O
F =160°,求∠B O E 的度数.
参考答案
1.D
2.C
3.D
4.相互垂直相互垂直
5. AC 3 BC 4
6.
解:如答图所示.
第6题答图
7. 解:如答图所示:
(1)沿AB走,两点之间线段最短;
(2)沿AC走,垂线段最短;
(3)沿BD走,垂线段最短.
第7题答图
8. 解:因为O E⊥CD,O F⊥AB,
所以∠B O E+∠D O B=90°,∠D O B+∠D O F=90°,所以∠B O E=∠D O F=65°,
∠D O B=90°-∠D O F=90°-65°=25°.
因为∠A O C与∠D O B是对顶角,
所以∠A O C=∠D O B=25° .
9. 解:(1)如答图,分别由A 、B 两点向MN 作垂线,垂足分别为C 、D 两点;
第9题答图
(2)汽车从M 向C 走时,离A 、B 两村都越来越近;在CD 上时离B 村越来越近,而离A 村越来越远.
10.
解:(1)∵OM⊥AB ,
∴∠A OM =∠1+∠A O C =90°. ∵∠1=∠2,
∴∠NO C =∠2+∠A O C =90°,
∴∠NO D =180°-∠NO C =180°-90°=90°. (2)∵OM⊥AB , ∴∠A OM =∠B OM =90°. ∵∠1=1
3
∠B O C ,
∴∠B O C =∠1+90°=3∠1, 解得∠1=45°,
∴∠A O C =90°-∠1=90°-45°=45°, ∠MO D =180°-∠1=180°-45°=135°. 11. 解:∵∠B O D =40°, ∴∠A O C =∠B O D =40°. 又∵O E 平分∠A O C ,
∴∠A O E =1
2∠A O C =20°,即∠A O E =20°.
∵O F ⊥AB 于O ,O G ⊥O E , ∴∠A O F =∠E O G =90°,
∴∠F O G =∠A O E =20°(同角的余角相等).
12. 解:∵∠D O F+∠C O F=180°,∠D O F=160°,
∴∠C O F=180°-∠D O F=180°-160°=20°.
∵O F平分∠A O C,
∴∠A O C=2∠C O F=40°,
∴∠D O B=∠A O C=40°.
∵E O⊥CD,
∴∠D O E=90°,
∴∠B O E=∠D O E+∠D O B=90°+40°=130°.
欢迎您的下载,资料仅供参考!。
