《激光原理及应用》陈家璧第版
陈家璧版光学信息技术原理及应用习题解答(7-8章)

陈家璧版光学信息技术原理及应用习题解答(7-8章)-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII第七章 习题解答1. 某种光盘的记录范围为内径80mm,外径180mm 的环形区域,记录轨道的间距为2um.假设各轨道记录位的线密度均相同记录微斑的尺寸为um,试估算其单面记录容量. (注: 内、外径均指直径)解: 记录轨道数为 25000002.0280180=⨯-=N单面记录容量按位计算为 ∑=⨯≈⨯+=Nn n M 110107.10006.0)002.040(2π bits = 17 Gb.按字节数计算的存储容量为 2.1GB.2. 证明布拉格条件式(7-1)等效于(7-17)式中位相失配= 0的情形, 因而(7-18)式描述了体光栅读出不满足布拉格条件时的位相失配。
证明: 将体光栅读出满足布拉格条件时的照明光波长(介质内) 和入射角 (照明光束与峰值条纹面间夹角)分别记为0和θ0, 则根据布拉格条件式(7-1)有: 2sin θ0= 0 其中为峰值条纹面间距.对于任意波长λa (空气中) 和入射角θr (介质内), 由(7-17)式, 位相失配 δ 定义为:24)cos(n K K ar πλθφδ--=其中n 0为介质的平均折射率, K = 2π/Λ为光栅矢量K 的大小,φ为光栅矢量倾斜角,其值为 22πθθφ++=sr ,θr 为再现光束与系统光轴夹角 (参见图7-9).当 δ = 0 时,有2422cos n K K a r s r πλθπθθ=⎪⎭⎫ ⎝⎛-++ 即:Λ=Λ=⎪⎭⎫ ⎝⎛-2422sin 0λππλθθn s rλ为介质中的波长. 由于角度2sr θθ-恰为照明光与峰值条纹面的夹角θ, ∑ ©亦即布拉格条件2Λ sin θ = λ.当读出光偏离布拉格角θo 和布拉格波长λo 的偏移量分别为∆θ和∆λ时,有[]0200200002044sin )sin(cos )cos( 4)()(cos n K n K K K n K K πλπλθθφθθφπλλθθφδ∆--∆--∆-=∆+-∆+-=利用布拉格条件式(7-17), 以及∆θ和∆λ很小时的近似关系 cos ∆θ≈1 和 sin ∆θ≈∆θ, 立即可得:δ =∆θK sin(φ-θ0) - ∆λK 2/4πn 0 即(7-18)式 原题得证。
陈家璧版-光学信息技术原理及应用习题解答(4-7章)

第四章习题4.1若光波的波长宽度为λΔ,频率宽度为νΔ,试证明:λλννΔΔ=。
设光波波长为nm 8632=.λ,nm 8-10⨯2=λΔ,试计算它的频宽νΔ。
若把光谱分布看成是矩形线型,那么相干长度?=c l 证明:参阅苏显渝,李继陶《信息光学》P349,第4.1题答案。
421.510c λνλ∆∆==⨯赫,32010()c c cl ct m ν===⨯∆4.2设迈克尔逊干涉仪所用的光源为nm 0589=1.λ,nm 6589=.2λ的钠双线,每一谱线的宽度为nm 010.。
(1)试求光场的复自相干度的模。
(2)当移动一臂时,可见到的条纹总数大约为多少?(3)可见度有几个变化周期?每个周期有多少条纹?答:参阅苏显渝,李继陶《信息光学》P349,第4.2题答案。
假设每一根谱线的线型为矩形,光源的归一化功率谱为()^1212rect rect νννννδνδνδν⎡--⎤⎛⎫⎛⎫=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦G (1)光场的复相干度为^1()()exp(2)1sin ()exp(2)[1exp(2)]2r j d c j j τνπντνδντπντπντ∞==+∆⎰G 式中12ννν-=∆,复相干度的模为ντπδνττ∆=cos )(sin )(c r 由于νδν∆ ,故第一个因子是τ的慢变化非周期函数,第二个因子是τ的快变化周期函数。
相干时间由第一个因子决定,它的第一个零点出现在δντ1=c 的地方,c τ为相干时间,故相干长度δλλδλλδντ22≈===cc l c c 。
(2)可见到的条纹总数589301.05893====δλλλcl N (3)复相干度的模中第二个因子的变化周期ντ∆=1,故可见度的变化周期数601.06==∆=∆==δλλδννττc n 每个周期内的条纹数9826058930===n N 4.3假定气体激光器以N 个等强度的纵模振荡,其归一化功率谱密度可表示为()()()()∑21-21--=+-1=N N n n NνννδνΔgˆ式中,νΔ是纵模间隔,ν为中心频率并假定N 为奇数。
激光原理及应用陈家璧主编习题解答

思考练习题11. 试计算连续功率均为1W 的两光源,分别发射λ=μm ,ν=3000MHz 的光,每秒从上能级跃迁到下能级的粒子数各为多少?答:粒子数分别为:188346341105138.21031063.6105.01063.61⨯=⨯⨯⨯⨯=⨯⨯==---λνc h q n 239342100277.51031063.61⨯=⨯⨯⨯==-νh q n2.热平衡时,原子能级E 2的数密度为n 2,下能级E 1的数密度为n 1,设21g g =,求:(1)当原子跃迁时相应频率为ν=3000MHz ,T =300K 时n 2/n 1为若干。
(2)若原子跃迁时发光波长λ=1μ,n 2/n 1=时,则温度T 为多高?答:(1)(//m n E E m m kTn n n g e n g --=)则有:1]3001038.11031063.6exp[2393412≈⨯⨯⨯⨯⨯-==---kT h e n n ν(2)K T Te n n kTh 3623834121026.61.0]1011038.11031063.6exp[⨯=⇒=⨯⨯⨯⨯⨯⨯⨯-==----ν3.已知氢原子第一激发态(E 2)与基态(E 1)之间能量差为×l0-18J ,设火焰(T =2700K)中含有1020个氢原子。
设原子按玻尔兹曼分布,且4g 1=g 2。
求:(1)能级E 2上的原子数n 2为多少?(2)设火焰中每秒发射的光子数为l08 n 2,求光的功率为多少瓦?答:(1)1923181221121011.3]27001038.11064.1exp[4----⨯=⨯⨯⨯-⨯=⇒=⋅⋅n n e g n g n kTh ν且202110=+n n 可求出312≈n(2)功率=W 918810084.51064.13110--⨯=⨯⨯⨯4.(1)普通光源发射λ=μm 波长时,如受激辐射与自发辐射光功率体密度之比q q 激自1=2000,求此时单色能量密度νρ为若干?(2)在He —Ne 激光器中若34/100.5m s J ⋅⨯=-νρ,λ为μm ,设μ=1,求q q 激自为若干? 答:(1)3173436333/10857.31063.68)106.0(2000188m s J h h c q q ⋅⨯=⇒⨯⨯⨯=⇒=---ννννρρπρπλρνπ=自激(2)943436333106.71051063.68)106328.0(88⨯=⨯⨯⨯⨯⨯==---πρπλρνπννh h c q q =自激5.在红宝石Q 调制激光器中,有可能将全部Cr 3+(铬离子)激发到激光上能级并产生巨脉冲。
《激光原理》教学大纲

《激光原理》课程教学大纲一、课程基本信息二、课程简介本课程是“光电器件加工”课程模块中的专业核心课程,以培养应用能力突出、能适应工作变化和具有创新素质的学生为目标,在教学内容上,将理论教学与案例教学有机地结合进行知识点讲解,注重培养学生运用基础物理知识分析解决激光相关问题的能力;在教学模式上,采用研讨式的教学模式,注重引导学生对激光技术相关领域的核心问题已有的解决方案进行分析比较,培养学生的问题分析能力。
在培养学生熟练掌握激光器结构、工作原理、调Q技术与锁模技术的基础上,提升学生的综合能力和解决复杂问题的能力,为学生成为新一代技术应用型人才奠定基础。
三、课程目标及对毕业要求(及其指标点)的支撑四、教学内容及进度安排五、课程考核六、教材及参考资料(一)课程教材1.《激光原理及应用》(第3版),陈鹤鸣等编著,电子工业出版社,2017(二)参考教材及网站1.《激光原理》(第7版),周炳琨等编著,国防工业出版社,2014。
2.《激光原理及应用》(第3版),陈家璧等编著,电子工业出版社,2013。
3.《激光原理及技术》,电子科技大学,刘志军等主讲,中国大学慕课。
编写人:审核人:审批人:审批日期:附件:各类考核与评价标准表(1)考试方式及占比:采用闭卷笔试,考试成绩100分,占课程考核成绩的60%。
(2)评定依据:考试成绩的评定根据试卷参考答案和评分标准进行。
(3)考试题型:可以包含单项选择题、填空题、简答题、计算题和设计题。
(4)考试内容:对学生综合运用激光物理的基本概念、基本原理进行问题分析能力的考核,不仅包括对各章节知识点的独立考核,还需要包括综合考虑多种激光器性能与控制的改善方案,实现技术分析和解决复杂工程问题能力的考核。
激光原理及应用(第2版)(陈家璧)课后答案(全)

5 10 4
7.6 109
5.在红宝石 Q 调制激光器中, 有可能将全部 Cr3+ (铬离子 )激发到激光上能级并产生巨脉冲。
设红宝石直径 0. 8cm,长 8cm,铬离子浓度为 2× 1018cm-3,巨脉冲宽度为 10ns。求: (1)
输出 0. 6943 m 激光的最大能量和脉冲平均功率;
(2) 如上能级的寿命
3.已知氢原子第一激发态
(E2)与基态 (E1)之间能量差为
- 18
1. 64× l0 J,设火焰 (T = 2700K) 中
含有 1020 个氢原子。设原子按玻尔兹曼分布,且
4g1= g2。求: (1)能级 E2 上的原子数 n2 为
多少? (2)设火焰中每秒发射的光子数为 l08 n2,求光的功率为多少瓦?
1 /c 1 / c 0 ,在一级近似下为:
0(1 ) c
c ,证明接收器接收到的频率
证明: 即证
1 1
c c
0
21
(1
)(1 c
c2 ) 2
0
12
(1
)(1 c
2 c2 )
0
(1 ) c
0
11.静止氖原子的 3S2 2P4 谱线的中心波长为 0. 6328 m,设氖原子分别以
的速度向着接收器运动,问接收到的频率各为多少?
答:( 1) nm / gm nn / gn
( Em En)
e n kT 则有: 2 n1
h
e kT
6.63 10 34 3 109
exp[
]1 1.38 10 23 300
( 2) n2 n1
h
e kT
6.63 10 34 3 108
exp[ 1.38 10 23
00.序再版说明前言目录(第二版)

序1960年发明激光到现在已经有近50年了。
这期间年来激光的理论与应用研究有了极大的发展,而且对人类社会产生了深刻的影响。
作为光的受激辐射,激光是一种极好的光源,它首先在测量领域得到了广泛的应用。
物理学中最基本的量值——米,改为激光在真空中的波长来定义,使有效数字提高到九位。
激光用来测长、测距、测速、测角、测量各种可以转换为光的物理量,发展出一个专门的学科——激光测量学,还使光学测量方法走出实验室成为工程测量的常规手段。
激光用于加工,始于激光打孔,很快就推广到切割、焊接、热处理、表面改性与强化,乃至激光快速成型、激光清洗和激光微加工,已经成为高科技产业不可缺少的加工方法。
激光医学近三十年来的发展和推广,给广大人民群众带来了福祉。
而激光在信息产业中的大量应用更是信息时代到来的主要原动力之一。
可以毫不夸张的说,现代社会的方方面面已经与激光的应用密不可分。
鉴于激光在现代科学技术中的如此重要作用,激光原理和它的各种应用技术已成为各行各业的技术人员都必须掌握的一门高新技术。
我国的重点高等院校从二十世纪七十年代就开设激光的理论与应用的课程,并开办了若干以激光器制造和应用为培养目标的理工科专业。
改革开放以来,推广到一般院校,目前国内高等院校不开设激光原理与应用课程的已很难找到。
各重点高校编写的涉及激光原理、技术和应用的有关教材,林林总总不下数十种。
但是其中多数激光原理的教材涉及到过多的物理原理,超越了大学普通物理的内容,教材只针对重点高校的要求,并不适于培养工程应用型人材的一般院校。
相对适用的流传较广的清华大学丁俊华先生的《激光原理和应用》是二十世纪八十年代初的讲稿,因为激光技术的快速发展,需要补充修订。
本书编者在多年为普通高校本科生讲授这门课程的基础上,重新编写《激光原理和应用》就是为了一般高等院校学生掌握应用激光技术的教学需要。
该书的特点在于着重阐明受激辐射的物理概念以及激光输出特性与激光器的参数之间的关系,以掌握激光器的选择和使用为主要目的。
激光原理及应用-陈家璧第二版
辐 2. 电子具有的量子数不同,表示有不同的电子运动状态
射 理 论
电子的能级,依次用E0,E1,E2,… En表示 基态:原子处于最低的能级状态 激发态:能量高于基态的其它能级状态 简并能级:能级有两个或两个以上的不同运动状态
概
简并度:同一能级所对应的不同电子运动状态的数目
要
与 3. 图(1-3)为原子能级示意图
激 光 产 生 的
En
激
E2
发 态
例:计算1s和2p态的简并度
条
E1
件
E0基态
第一章 上一页 回首页 下一页 回末页 回目录
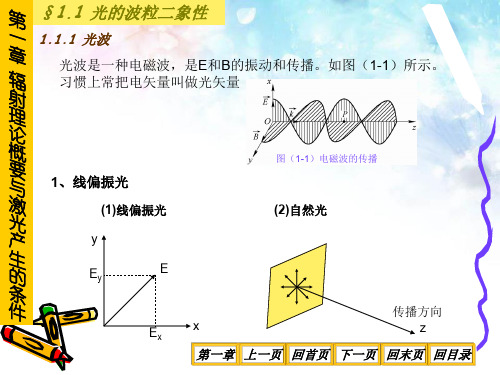
第 §1.1 光的波粒二象性
一 章
1.3.1 黑体热辐射
1. 绝对黑体又称黑体:某一物体能够完全吸收任何波长的电磁辐射。自
辐 然界中绝对黑体是不存在的
射 理 2. 空腔辐射体是一个比较理想的绝对黑体
ν
d
dVdv
概
在量子假设的基础上,由处理大量光子的量子统计理论得到真空中 ν
要
与温度T及频率 ν的关系,即为普朗克黑体辐射的单色辐射能量密度公式
与 激 光
式中k为波尔兹曼常数。
8ch3ν3
1
hν
e kT1
产 生
总辐射能量密度 :
0 νdν
的
条
件
第一章 上一页 回首页 下一页 回末页 回目录
第 §1.1 光的波粒二象性
一 章
1.3.2 光和物质的作用
自发辐射
辐
光与物质的相互作用有三种不同的基本过程:受激辐射
射 1. 自发辐射
受激跃迁
理 论 概
自发辐射: 高能级的原子自发地从高能级E2向低能级E1跃迁,同时放出能
陈家璧版 光学信息技术原理及应用习题解答(3-4章)

第三章 习题3.1 参看图3.5,在推导相干成像系统点扩散函数(3.35)式时,对于积分号前的相位因子⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+≈⎥⎦⎤⎢⎣⎡+2220202002exp )(2exp M y x d k j y x d k j i i试问(1)物平面上半径多大时,相位因子⎥⎦⎤⎢⎣⎡+)(2exp 20200y x d k j相对于它在原点之值正好改变π弧度?(2)设光瞳函数是一个半径为a 的圆,那么在物平面上相应h 的第一个零点的半径是多少?(3)由这些结果,设观察是在透镜光轴附近进行,那么a ,λ和d o 之间存在什么关系时可以弃去相位因子⎥⎦⎤⎢⎣⎡+)(2exp 20200y x d k j 3.2 一个余弦型振幅光栅,复振幅透过率为 00002cos 2121),(x f y x t π+=放在图3.5所示的成像系统的物面上,用单色平面波倾斜照明,平面波的传播方向在x 0z 平面内,与z 轴夹角为θ。
透镜焦距为f ,孔径为D 。
(1)求物体透射光场的频谱;(2)使像平面出现条纹的最大θ角等于多少?求此时像面强度分布;(3) 若θ采用上述极大值,使像面上出现条纹的最大光栅频率是多少?与θ=0时的截止频率比较,结论如何?3.3光学传递函数在f x = f y =0处都等于1,这是为什么?光学传递函数的值可能大于1吗?如果光学系统真的实现了点物成点像,这时的光学传递函数怎样?3.4当非相干成像系统的点扩散函数h I (x i ,y i )成点对称时,则其光学传递函数是实函数。
3.5 非相干成像系统的出瞳是由大量随机分布的小圆孔组成。
小圆孔的直径都为2a ,出瞳到像面的距离为d i ,光波长为λ,这种系统可用来实现非相干低通滤波。
系统的截止频率近似为多大?3.6 试用场的观点证明在物的共轭面上得到物体的像 解:如图设1∑是透过率函数为),(00y x t 的物平面,2∑是与1∑共轭的像平面,即有fd d i 1110=+ 式中f 为透镜的焦距,设透镜无像差,成像过程分两步进行:(1) 射到物面上的平面波在物体上发生衍射,结果形成入射到透镜上的光场l U ; (2) 这个入射到透镜上的光场经透镜作位相变换后,在透镜的后表面上形成衍射场'l U ,这个场传到像面上形成物体的像。
