统计学时间序列
统计学之时间序列
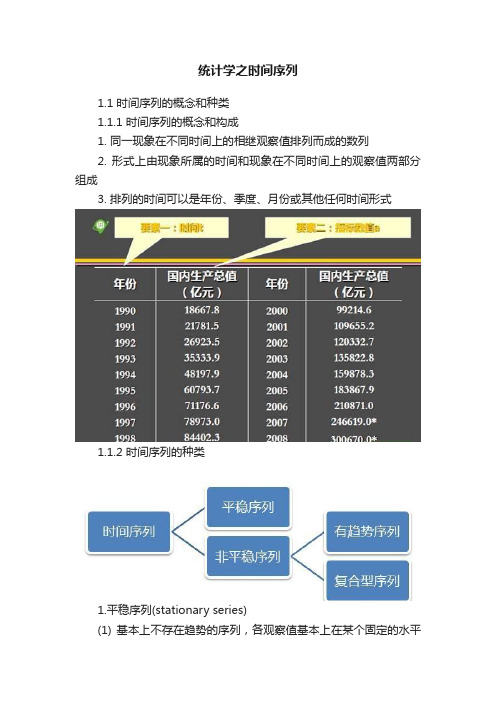
统计学之时间序列1.1 时间序列的概念和种类1.1.1 时间序列的概念和构成1. 同一现象在不同时间上的相继观察值排列而成的数列2. 形式上由现象所属的时间和现象在不同时间上的观察值两部分组成3. 排列的时间可以是年份、季度、月份或其他任何时间形式1.1.2 时间序列的种类1.平稳序列(stationary series)(1) 基本上不存在趋势的序列,各观察值基本上在某个固定的水平上波动(2) 或虽有波动,但并不存在某种规律,而其波动可以看成是随机的2.非平稳序列 (non-stationary series)(1) 有趋势的序列(2) 线性的,非线性的(3) 有趋势和季节性的序列(4) 有趋势、季节性和周期性的复合型序列1.1.3 时间序列的成分1.趋势(trend)(1) 持续向上或持续下降的状态或规律;(2) 既可以是线性趋势,也可以是非线性趋势2.季节性(seasonality)(1) 也称季节变动(Seasonal fluctuation)(2) 时间序列在一年内重复出现的周期性波动3.周期性(cyclity)(1) 也称循环波动(Cyclical fluctuation)(2) 围绕长期趋势的一种波浪形或振荡式变动4.随机性(random)(1) 也称不规则波动(Irregular variations)(2) 除去趋势、周期性和季节性之后的偶然性波动1.1.3.1 含有不同成分的时间序列1.1.3.2 一张图总结时间序列的成分1.2 时间序列的描述性分析1.2.1 图形描述1.2.2 水平指标分析1.2.2.1 发展水平和平均发展水平1. 发展水平:指时间序列中每一项指标数值2. 平均发展水平:又叫时序平均数,是把时间数列中各期指标数值加以平均而求得的平均数。
3. 一般平均数与序时平均数(1) 共同点:具有抽象性和代表性(2) 不同点:a) 计算的依据不同:前者是根据变量数列计算的,后者则是根据时间数列计算的。
统计学时间序列分析

统计学时间序列分析时间序列是经济学、金融学和其他社会科学领域中的一个重要分析对象。
通过对时间序列数据的分析,我们可以揭示数据之间的关系、趋势和周期性,从而为决策提供有力的支持和预测。
统计学时间序列分析是一种应用数学方法的工具,用于对时间序列数据进行建模和预测。
一、时间序列的基本概念时间序列是按时间顺序排列的一系列观测值的集合。
在时间序列分析中,我们关注数据之间的内在关系,而忽略其他因素的影响。
时间序列数据通常具有以下特征:1. 趋势性:时间序列数据的长期变化趋势。
2. 季节性:时间序列数据在一年内固定时间段内的重复模式。
3. 循环性:时间序列数据中存在的多重周期性波动。
4. 随机性:时间序列数据中的不规则、无法预测的波动。
二、时间序列分析的方法在进行时间序列分析时,我们可以采用以下方法来揭示数据的内在规律:1. 描述性统计分析:通过计算数据的均值、方差、相关系数等指标,对数据的整体特征进行描述。
2. 图表分析:通过绘制折线图、柱状图等图表,展示时间序列数据的变化趋势和周期性。
3. 分解模型:将时间序列数据分解为趋势项、季节性项和残差项,以揭示数据的内在结构。
4. 平滑法:通过移动平均法、指数平滑法等方法,消除时间序列数据的随机波动,从而揭示趋势和季节性成分。
5. 自回归移动平均模型(ARIMA):ARIMA模型是一种常用的时间序列分析方法,可以对数据进行预测和建模。
它综合考虑了自回归、移动平均和差分的影响因素。
三、时间序列分析的应用领域时间序列分析广泛应用于经济学、金融学、市场调研等领域,具体应用包括:1. 经济预测:通过对经济数据进行时间序列分析,可以预测未来的经济发展趋势,为政府决策提供参考。
2. 股票市场分析:时间序列分析可以帮助分析师预测股票市场的走势,制定投资策略。
3. 需求预测:通过对销售数据进行时间序列分析,可以预测产品的需求量,为企业的生产和供应链管理提供指导。
4. 天气预测:通过对气象数据进行时间序列分析,可以预测未来的天气状况,为农业、旅游等行业提供参考。
统计学时间序列

中间水平
动态比较时:基期水平y0、报告期水平y1。
二、平均发展水平
(二)平均发展水平 又叫序时平均数,动态平均数 序时平均数将指标在各时间上表现的差异加以抽
象,以一个数值来代表现象在这一段时间上的一般 发展水平。
是将时间数列中各时期的发展水平加以平均而得出的平 均数。 单位时间内的水平或速度 解决对比性问题(如日平均产量优于月总产量)
年末职工人数
(万人)
14792 14849 14849 14908 1时48点45指1标 466数8 列
国有经济单位职
工工资总额所占 78.45 77.55 77.78 45.06 相74对 .81指7标6.6数9 列
比重(%)
职工平均货币工 资(元)
2711
3371
4538
5500 平62均10指6标47数0 列
2. 时点数列的序时平均数
【课堂练习】1991年底~1996年底我国人口总数:
年份
年底人数
(亿人)
1991 1992 1993 1994 1995 1996
n 1
yi
i 1
n
2. 时点数列的序时平均数
时点序列序时平均数:所有(原则上无穷多)时 点上指标的平均数。
实际上只有有限个时点的数据,这些已知数据的 时点将时间分割成一系列时期。
时点序列序时平均数等于每个时期的代表值用时 期长度作为权重的加权算术平均。
n 1
n 1
tn y(t)dt
基本稳定在某个水平附件波动
3. 非平稳时间序列
各指标值受各种因素的影响,存在某种规律性 的变动
• 趋势性:增加或减少的趋势 • 季节性:随季节周期性波动
统计学中的时间序列

统计学中的时间序列时间序列(Time Series)是统计学中重要的研究对象之一,它描述了同一变量在不同时间点上的观测结果。
时间序列在许多领域都有广泛的应用,如经济学、金融学、气象学等。
通过对时间序列的分析,可以揭示出其中的规律和趋势,为决策和预测提供依据。
一、时间序列的基本概念时间序列是按照时间顺序排列的数据序列。
通常,时间序列中的观测值可以按照以下两个因素进行分类:1. 时间单位:观测点之间的时间间隔可以是固定的,如每日、每月、每年等,也可以是不规则的,如每小时、每分钟等。
2. 观测值类型:时间序列可以包含单变量(单个观测变量)或多变量(多个观测变量)。
二、时间序列的经典模型时间序列分析的目标是识别和建模数据中的模式和结构。
经典的时间序列模型包括以下几种:1. 自回归移动平均模型(ARMA):ARMA模型是将自回归模型(AR)和移动平均模型(MA)结合起来,它假设时间序列的当前观测值与过去的观测值和随机误差有关。
2. 自回归整合移动平均模型(ARIMA):ARIMA模型是在ARMA模型的基础上引入差分操作,用于消除时间序列的非平稳性。
3. 季节性模型:对于具有明显季节性变化的时间序列,可以采用季节性模型,如季节性ARIMA模型(SARIMA)。
4. 非线性模型:除了上述线性模型外,时间序列还可能具有非线性特征,因此可以采用非线性模型,如ARCH、GARCH模型等。
三、时间序列分析的方法时间序列分析主要包括以下几个步骤:1. 数据获取和预处理:从数据源获取时间序列数据,并对数据进行预处理,如处理缺失值、异常值等。
2. 数据可视化和描述性统计:通过绘制时间序列图、自相关图、偏自相关图等,对数据进行可视化和描述性统计,以了解数据的整体特征。
3. 模型识别和参数估计:根据观察到的时间序列图和自相关函数,选择适当的模型,并对模型的参数进行估计。
4. 模型检验和诊断:对所建立的模型进行检验,如检验模型的拟合优度、残差序列是否平稳等,并进行诊断,如检验残差是否具有自相关性等。
统计学 时间序列分析

三 11.0
四 12.6
五 14.6
六 16.3
七 18.0
月末全员人数(人) a 2000 2000 2200 2200 2300
b
要求计算:①该企业第二季度各月的劳动生产率 ; ②该企业第二季度的月平均劳动生产率; ③该企业第二季度的劳动生产率。
6.2 时间序列分析的水平指标
6.2.1 发展水平与平均发展水平 --相对数(平均数)时间序列
时间 1月1日 5月31日 8月31日 12月31日
社会劳动者 人数
362
390
416
420
解:则该地区该年的月平均人数为:
362390539041634164204
y 2
2
2
534
39.765万人
6.2 时间序列分析的水平指标
6.2.1 发展水平与平均发展水平 --相对数(平均数)时间序列
月份 工业增加值(万元)
6.1 时间序列概述
6.1.2 时间序列的种类
绝对数序列
时期序列
时
派生
时点序列
间
序 列
相对数序列
平均数序列
6.1 时间序列概述
6.1.2 时间序列的种类
年 份 1992 1993 1994 1995 1996 1997
职工工资总额 3939.2 4916.2 6656.4 8100.0时90期80数.0数94列05.3 (亿元)
解:①第二季度各月的劳动生产率:
四月份: y12 10 .6 2 0 1 20 0 00 0 2 0 0 603元 0人 0
五月份: y22 10 .6 4 0 1 20 0 20 0 2 0 0 60 9.4 5 元 2 人
统计学第9章(时间序列)

时间数列、相对数时间数列和平均数时间数列。
(一)绝对数时间数列 :是由一系列绝对数指标,即总
量指标,按时间顺序排列而成的数列。它是时间数列
中最基本的表现形式,用以反映事物在不同时间上所 达到的绝对水平。
1.时期数列:反映现象在各段时期内发展过程的总量
2.时点数列:反映现象在各时点所达到的水平
(二) 相对数时间数列:是由一系列相对数指标按时间 顺序排列而成的数列 。反映现象之间相互关系的
发展变化过程。
1. 静态相对数时间数列是由两个指标相应时期的水 平值对比计算形成的;如,人均国内生产总值。 2. 动态相对数时间数列是由同一指标不同时期水平 值对比计算形成的;如,国内生产总值发展速。
(三) 平均数时间数列:是由一系列平均数按时间顺序
排列而成的数列 。它反映现象一般水平的发展过
程和发展趋势。
2、编制时间数列的作用
1)描述事物的发展状况和结果。
2)研究事物的发展趋势和发展速度。
3)探索事物发展变化的特点和规律。
4)建立数学模型,对事物发展的未来状况
进行科学的预测。
时间序列的分析目的
分析目的
分析过去
描述动态变化
认识规律
揭示变化规律
预测未来
未来的数量趋势
二、时间数列的种类
按指标表现形式的不同,时间数列可分为绝对数
第九章
时间序列分析
第一节 时间序列的编制
一、时间序列的概念和作用 1 、定义:通常把反映某种事物在时间上变 化的统计数据,按照时间顺序排列起来得 到的序列称为时间序列,也称动态序列。 时间序列的两个基本要素:一个是被研究 现象所属时间,另一个是该现象在一定时 间条件下的统计指标数值。
我国人口和生产总值时间数列
统计学(时间序列分析)
时间序列分析本章内容第一节:时间序列及分析方法概述第二节:时间序列的指标分析法第三节:时间序列构成因素分析法一、时间序列的概念和要素时间序列分析就是从时间的发展变化角度,研究事物在不同时间上和一段时间内的发展状态,探索其随时间推移的演变趋势和变化规律,揭示其数量变化和时间的关系,探讨一特定时间序列的各种构成因素及组合模式,预测事物在未来时间上可能达到的数量规模和水平。
时间序列(动态数列)动态数列是指将同类社会经济现象在不同时间上发展变化的一系列统计指标,按时间先后顺序排列所形成的统计数列,亦称时间序列。
注意:时间数列由两个基本要素构成:一是被研究现象所属的时间(t);二是反映现象在各个时间上的发展水平,亦称动态水平(y)意义通过时间数列的编制和分析,可以从事物在不同时间上的量变过程中,认识社会经济现象的发展变化的方向、程度、趋势和规律,为制定政策、编制计划提供依据。
通过对时间数列资料的研究,可以对某些经济现象进行预测。
利用不同的时间数列对比,可以揭示各种社会现象的不同发展方向、发展规律及其相互之间的变化关系。
利用时间数列,可以在不同地区或国家之间进行对比分析。
二、时间序列(动态序列)的种类总量指标(绝对数)动态数列✓时期数列:由时期总量指标编制而成的动态数列数列中每一个指标,都是表示社会经济现象在一定时期内发展过程的总量数列中的各个指标是可以相加的。
每个指标数值的大小与时期长短有直接关系数列中每一个指标数值,通常都是通过连续不断的登记取得的。
✓时点数列:由时点总量指标编制而成的动态数列数列中的每一个指标数值,都表示社会经济现象在某一时点(时刻)上的数量。
数列中的每个指标不能相加。
数列中每个指标数值大小和“时点间隔”长短没有直接关系。
数列中每个指标数值通常都是定期(间断)登记取得的。
相对数动态数列:指一系列相对指标按照时间先后顺序排列所组成的动态数列。
(相对数动态数列一般是两个有联系的总量指标动态数列对比派生的数列)由两个时期数列对比而成的相对数动态数列;由两个时点数列对比而成的相对数动态数列;由一个时期数列和一个时点数列对比形成的相对数时间数列。
统计学第9篇(时间序列)
3. 不同方法计算的平均速度指标的比较 几何平均法(水平法) 方程式法(累计法)
计算简单
求解方程难
与中间水平无关,只与期 与各水平值有关,关注 初、期末水平有关,关注 各期水平的累计 期末水平
适用于发展比较平衡的数 适用于侧重于观察全期
列
累计总量指标平均发展
速度的计发展速度的计算
2.方程式法(累计法)
基本思路:假定现象从最初水平a0出发,每期按 平均速度发展,计算的各期水平之和等于实际各 期水平之和,即:
a 0 x a 0 x 2 a 0 x 3 a 0 x n a 1 a 2 a n
xx2x3 xnai a0
解这个高次方程式比较麻烦,在实际工作中,通 常是通过查《平均增长速度查对表》来求平均发 展速度。
环 比 发 展发速展 度速 是 报度告报基 期告期 水期平水水 与平平 前 一 期 水 平 之 比 , 说 明现象逐期发展程度
定基发展速度是报告期aa1 0水,aa平1 2 ,与a a2 3某, 一,固aan定n1时期水平之 比,说明现象在较长一段时期内总的发展程度
a1 , a2 , a3 ,, an
三、时间数列的编制原则
1.时间数列中的各个指标所属时间长短应前后一致。 2.时间数列中各指标所反映现象的总体范围应一致。 3.时间数列中各指标的经济内容应一致。 4.时间数列中各指标的计算口径应该相同。计算口径
主要是指计算方法、计算价格和计量单位等。
第二节 时间数列的基本分析指标
动态分析:现象发展的水平分析、现象发展的速度分析。 水平分析是速度分析的基础,速度分析是水平分析的深入
3
3
一般计算公式为 (首末折半法)
an i 1 1ai 2ai1a 21a2a3 an1a 2n
统计学课件第六章_时间序列分析
统计学课件第六章_时间序列分析第一章统计总论第二章统计调查第三章统计数据的整理与显示第四章统计指标第五章统计指数第六章时间序列分析第七章抽样推断第八章相关与回归分析第九章统计预测第十章统计的综合评价统计学概论内容第六章时间序列分析本章内容安排§6.1 时间序列编制及分析指标§6.2 时间序列的分解分析学习目标1. 时间序列及其分析指标的计算2. 时间序列的分解分析一、时间序列的编制二、时间序列的水平指标三、时间序列的速度指标§6.1 时间序列的编制及分析指标时间序列的编制1.同一现象(指标)在不同时间上的相继观察值排列而成的数列2.形式上由现象所属的时间和现象在不同时间上的观察值两部分组成3.排列的时间可以是年份、季度、月份或其他任何时间形式如将我国历年的某产品产量发展情况按时间先后顺序排列起来就是一个动态数列。
如表6—1所示。
由表6—1可看出,时间数列由两个基本要素构成:一是被研究现象所属的时间;二是反映现象在各个时间上的发展水平,亦称动态水平。
动态平均数时间序列静态平均数时间序列平均数时间序列由一个时期序列和一个时点序列对比形成的相对数时间序列由两个时点序列对比而成的相对数时间序列由两个时期序列对比而成的相对数时间序列相对数时间序列派生数列时点序列时期序列总量指标时间序列基本序列时间序列的种类时间序列的种类总量指标时间序列是指将反映某种社会经济现象的一系列总量指标按时间的先后顺序排列而形成的序列。
总量指标时间序列反映了社会经济现象总量在各个时期所达到的绝对水平及其发展变化过程。
有时期序列和时点序列之分.1、时期序列。
是指由时期总量指标编制而成的序列。
在时期序列中,每个指标都反映某社会经济现象在一定时期内发展过程的总量。
(一)总量指标(绝对数)时间序列如表6-2所列的1990年—2001年我国税收基本情况就是一个时期序列。
时期序列的特点:(l)序列中每一个指标,都是表示社会经济现象在一定时期内发展过程的总量。
统计学原理 第五章 时间序列
月份 实际产值 a 计划产值 b 计划完成程度 c
四 100 90 111
五 120 100 120
六 125 100 125
% 第二季度计划完成程度
实际产值a 计划产值b 100 120 125 90 100 100 118 .96%
% 第二季度计划完成程度
收盘价
解:
16.2元
16.7元
17.5元
18.2元
17.8元
a a
n 16.2 16.7 17.5 18.2 17.8 17.28(元) 5
(2)由时点数列计算 ①由连续时点数列计算
对于逐日记录的时 点数列,每变动一 次才登记一次
※间隔不相等时,采用加权算术平均法
a1f1 a2f2 a m fm a f1 f2 fm
n n
【例1】某工业企业2011年各季度工业总 产出计划完成进度
季度
实际工业总产出 计划工业总产出
因为
一
100 200
二
300 200
三
400 500
四
200 300
利润计划 实际利润a c 计划利润b 完成程度
【例2】某厂第二季度有关资料如下,试求该厂第二节度 的计划完成程度。
a ,a2 , , an 1, an
a2 a1, a3 a2 , ,an an 1
a2 a1, a3 a1, ,an a1
二者的关系:累积增长量=相应的逐期增长量之和
a
2
a1 a3 a2 an an 1 an a0
一季 度初
二季 度初
三季 度初
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.总量指标时期数列的序时平均数:算术平均法
发展 水平
y1 y 2 y n 1 y yi n n
y1 1
y yy 2
2
y
y
yi
y
y
…
y
yy n n
… …
i
… …
时期
1.总量指标时期数列的序时平均数:算术平均法
年 份
1991 1992 1993 1994 1995 1996
抽象的差异不同:
平均发展水平:同一现象的时间差异 一般平均数: 不同单位的标志值差异
平均发展水平的计算
序时平均数,要根据不同数列总量 指标数列(具体又分为时期数、时点数 )、相对指标数列和平均指标采用不同 的计算公式计算!
相对指标和平均指标由总量指标派 生,总量指标时间序列的序时平均数最 基本
f
( yi 为ti ~ ti 1时期代表值,f i ti 1 ti 是该时期长度) 【用时期长度为权重的时期代表值加权算术平均】 (每个最小间隔时间的指标已知,连续时点序列1) 【比如知道每天(非时点)指标实际上是每天的代表值】 (变动时登记,时期内恒等于期初指标,连续时点序列2) 【根据会计等知识判断,库存量等;时点一般无规律】
时间序列:
就是把不同时间的社会经济统计指标按时间 先后顺序排列所形成的数列; 又称动态数列或时间数列。; 描述现象发展变化的过程,是分析各种现象的 动态过程及其演化规律的重要依据
时间序列
—— 按时间顺序排列的 某项统计指标的一串数值。 如:1986—2000年间,我国逐年的 人均GDP, 构成一个时间序列。 记:y1 , y2 , … , yn ( n项 ) 或:y0 , y1 , y2 , … , yn ( n+1项 )
2.增长水平
累计增长量 平均增长量
发展水平
一、发展水平
(一)发展水平
时间序列中,各指标数值就是该指标所反映的 社会经济现象在所属时间的发展水平。
最初水平
最末水平
y 0 y1 y i y n 1 y n
中间水平
动态比较时:基期水平y0、报告期水平y1。
二、平均发展水平
(二)平均发展水平 又叫序时平均数,动态平均数 序时平均数将指标在各时间上表现的差异加以抽
派生性—由绝对数列派生而得 不可加性
相对
平均
复习
时点数列与时期数列 P154-158:1.1,1.2,2.1,2.2
时间序列的分类(指标的平稳性)
1. 随机性时间序列
各指标值的变动除了随机因素的影响外,不存 在某种规律性的变动
基本稳定在某个水平附件波动
2. 平稳时间序列
3. 非平稳时间序列
时点指标时间序列具有以下特点:
A ) 不可加性 。不同时点的总量指标不可相加, 这是因为把不同时点的总量指标相加后,无法解 释所得数值的时间状态。 B)指标数值的大小与时点间隔的长短一般没有直
接关系。在时点数列中,相邻两个指标所属时间
的差距为时点间隔。存在长期趋势时例外。 C)指标值采用间断统计的方式获得。
2. 时点数列的序时平均数
【课堂练习】某商业企业2004年第二季度某商品库存资料如 下,求第二季度的月平均库存额。 时间 库存量(百件) 3月末 66 4月末 72 5月末 64 6月末 68
【分析】库存量一般变动都会登记,但不会总是在月末变动, 因此是中间数据未知且等间隔,首尾折半法
1 y 0 y1 y 2 y n 1 1 yn 2
时间序列的种类(例)
年 份
职工工资总额
(亿元)
1992 1993 1994 1995 1996 1997
3939.2 4916.2 6656.4 8100.0 9080.0 9405.3 时期指标数列 14792 14849 14849 14908 14845 14668 时点指标数列
年末职工人数
时间数列的构成要素
1. 现象所属的时间(时间要素)
2. 不同时间的具体指标数值(数 据要素)。
t y
t 0 t1 y 0 y1
t2 ti tn y2 yi yn
时间序列(一个例子)
另见课本 P122 表5-1
时间序列的图形描述(线图P81)
时间序列的分类(指标的性质)
时间序列
时间序列(CPI)
时间序列
时间序列(上证综指日K线图)
时间序列
时间序列(中国年度、季度GDP)
时间序列
时间序列(中国年度、季度GDP增长率)
主要内容
5.1 时间序列概述
5.2 时间序列的水平分析 5.3 时间序列的速度分析 5.4 长期趋势变动分析 5.5 季节变动与循环波动分析
序时平均数:不同时间的指标的平均数。 时点指标:描述任意时刻的状态的指标。 时点指标序时平均数:所有时点上指标的 平均数 原则上时点无穷多,平均用积分
1 y t n t0
tn
t0
y (t )dt
2. 时点数列的序时平均数
实际上两种处理方式:
对时间进行分割(比如最小到天),已知每个 最小时点的数值(实际上是一段时间的代表值 ),则简单算术平均。【连续时点数列1】
平稳 性
平稳数列
非平稳数列
编制时间序列的基本原则
保证数列中各期指标数值的可比性
① 各期指标数值所属时间可比 ② 各期指标数值总体范围可比 ③ 各期指标数值经济内容可比 ④ 各期指标数值计算口径可比
第二节 时间序列的水平分析
一、发展水平
二、增长水平
时间序列的水平分析
时间序列的水平指标
1.发展水平 发展水平 平均发展水平 或序时(动态)平均数 逐期增长量
• •
各指标值受各种因素的影响,存在某种规律性 的变动
趋势性:增加或减少的趋势 季节性:随季节周期性波动
时间序列的分类(指标的平稳性)
平稳时间序列
各指标值的变动除了随机因素的影响外,不存在 某种规律性的变动 基本稳定在某个水平附件波动
平稳性数列?
时间序列的分类(指标的平稳性)
非平稳时间序列
一系列相对指标或平均指标按时间顺序排列 而成 相对指标时间序列反映社会经济现象之间相 互联系的发展过程。 平均指标时间序列反映社会现象发展的一般 趋势
时间序列的特点
序列 时点 时期
特
点
不可加性—不同时期资料不可加 无关联性—与时间的长短无关联 间断登记—资料的收集登记 可加性、关联性、连续登记
各指标值受各种因素的影响,存在某种规律性的 变动。 趋势性、季节性等
季节性数列
时间序列的分类(指标的平稳性)
非平稳时间序列(中国年度、季度GDP)
趋势性+季节 性数列
趋势性数列
时间序列的分类
总量指 标数列 质量指 标数列 时期数列 时点数列 时间 属性
时间 序列 分类
指标 性质
相对指标数列 平均指标数列
1 y t n t0
tn
t0
y (t )dt
1 n 1 yi n i 0
2. 时点数列的序时平均数
实际上两种处理方式:
只记录一些时点的指标。又分两种情况 1)、变动一次登记一次,则实际上所有时点的 指标都已知【连续时点数列2】 。
1 y t n t0
tn
t0
学习目标
掌握:时间序列的分类;时间序列的 水平分析(序时平均数)和速度分析 (平均发展速度与平均增长速度);
理解:长期趋势分析的方法和应用。 了解:季节变动和循环波动分析的原 理和应用。
第一节 时间序列的概念和分类
一、概念
二、分类 三、编制原则
第一节
时间序列的概念和分类
社会经济现象总是随着时间的推移而变化,呈 现动态性。统计对事物进行动态研究的基本方法 是编制时间序列。
② 时点指标时间序列
一系列时点指标按时间顺序排列而成 反映社会经济现象在某一时刻(瞬间)的情况。
时期序列列与时点序列
时期指标时间序列具有以下特点:
A)可加性,不同时期的总量指标可以相加; B ) 指标值的大小与所属时间的长短有 直
接关系(正相关)。
C)指标值采用连续统计的方式获得。
时期序列列与时点序列
y
i 0
n 1
yi yi 1 f 2
f
i 0
n 1
i 0
n 1
yi yi 1 2 n
y0 yn n 1 yi 2 i 1 n
2. 时点数列的序时平均数
时点序列序时平均数:所有(原则上无穷多)时 点上指标的平均数。 实际上只有有限个时点的数据,这些已知数据的 时点将时间分割成一系列时期。 时点序列序时平均数等于每个时期的代表值用时 期长度作为权重的加权算术平均。
国内生产总值 21618 26638 34634 46756 58478 67885 (亿元) 1991~1996 年平均国内生产总值:
1 y yi n 21618 26638 34634 46756 58478 67885 6 42 668 亿元
时期数列
2. 时点数列的序时平均数
象,以一个数值来代表现象在这一段时间上的一般 发展水平。
是将时间数列中各时期的发展水平加以平均而得出的平 均数。 单位时间内的水平或速度 解决对比性问题(如日平均产量优于月总产量)
平均发展水平与一般平均数
相同点: 忽略差异,反映一般水平 区别: 平均对象不同:
平均发展水平:时间序列动态平均 一般平均数: 变量数列静态平均
11.58 11.71 11.85 11.99 12.11 12.24
