直线方程教学课件PPT
合集下载
直线的方程ppt课件

y 2x3
(2)A(0,5),B(5,0) y 5 x 0 y x 5 05 50
(3)C(-4,-5),D(0,0)
y0 x0 5 0 4 0
y 5x 4
6
2.根据下列条件求直线方程
(1)在x轴上的截距为2,在y轴上的截距是3;
x
由截距式得:
y
1
23
整理得: 3x 2y 6 0
说明:
(1)这个方程是由直线上两点确定;
(2)当直线没斜率或斜率为0时,不能 用两点式来表示;
15
4.截距式: x y 1 ab
说明: (1)这一直线方程是由直线的纵截
距和横截距所确定; (2)截距式适用于纵,横截距都 存在且都不为0的直线;
16
课堂练习
<<教材>> P.41
练习1.2
书面作业
1
一.复习回顾 直线方程的点斜式和斜截式:
1.点斜式 y y1 k(x x1 ) 2.斜截式 y kx b
2
二、直线方程的两点式和截距式
提出问题
直线l经过P1(x1,y1),P2(x2,y2)(x1≠x2)两点, 求直线l的方程?
分析:直线l经过两点P1(x1,y1),P2(x2,y2)并且x1≠x2,
b0 0a
说明:
即: x y 1 ab
(1)这一直线方程是由直线的纵截距和横截 距所确定;叫直线方程的截距式.
(2)截距式适用于纵,横截距都存在且都不为0的 直线;
5
课堂练习:
1.求经过下列两点的直线的两点式方程,再化
斜截式方程.
(1)P(2,1),Q(0,-3)
y 1 x 2 3 1 0 2
▲ 式不▲能用点斜式表示,直线方程为x=x1
直线方程课件ppt

0。
解线性方程的步骤
首先将方程化为标准形式 ax + b = 0,然后根据 a 和 b 的值,使用 公式 x = -b/a(当 a≠0)或 x 无 解(当 a=0,b≠0)来求解。
线性方程的应用
线性方程是数学和实际生活中最基 础和最常用的方程之一,可用于解 决各种问题,如计算、建模等。
一次方程的解法
直线方程课件
目录
• 直线方程的基本概念 • 直线方程的解法 • 直线方程的应用 • 直线方程的拓展知识 • 练习题与答案
01 直线方程的基本概念
直线的定义
直线是由无数个点组成的几何图形, 这些点沿着同一直线排列,没有弯曲 或转折。
在平面几何中,直线是二维空间中最 基本的图形之一,具有方向和长度。
04 直线方程的拓展知识
直线的斜率与截距
斜率
直线在平面上的倾斜程度,表示 为直线方程 y = mx + b 中的 m 。
截距
直线与 y 轴交点的 y 坐标,表示 为直线方程 y = mx + b 中的 b 。
直线的点斜式和两点式
点斜式
通过直线上的一点和直线的斜率来表示直线方程,形式为 y - y1 = m(x - x1) 。
掌握高阶技能,如利用计算机软件进行辅助 解题等。
04
03
01
谢谢聆听
点斜式
y - y1 = m(x - x1),其中 (x1, y1)是直线上的一点, m是斜率。
两点式
y - y1 = (y2 - y1)/(x2 x1) * (x - x1),其中(x1, y1)和(x2, y2)是直线上的 两点。
02 直线方程的解法
线性方程的解法
线性方程的定义
线性方程是只包含一个变量的一 元方程,其一般形式为 ax + b =
解线性方程的步骤
首先将方程化为标准形式 ax + b = 0,然后根据 a 和 b 的值,使用 公式 x = -b/a(当 a≠0)或 x 无 解(当 a=0,b≠0)来求解。
线性方程的应用
线性方程是数学和实际生活中最基 础和最常用的方程之一,可用于解 决各种问题,如计算、建模等。
一次方程的解法
直线方程课件
目录
• 直线方程的基本概念 • 直线方程的解法 • 直线方程的应用 • 直线方程的拓展知识 • 练习题与答案
01 直线方程的基本概念
直线的定义
直线是由无数个点组成的几何图形, 这些点沿着同一直线排列,没有弯曲 或转折。
在平面几何中,直线是二维空间中最 基本的图形之一,具有方向和长度。
04 直线方程的拓展知识
直线的斜率与截距
斜率
直线在平面上的倾斜程度,表示 为直线方程 y = mx + b 中的 m 。
截距
直线与 y 轴交点的 y 坐标,表示 为直线方程 y = mx + b 中的 b 。
直线的点斜式和两点式
点斜式
通过直线上的一点和直线的斜率来表示直线方程,形式为 y - y1 = m(x - x1) 。
掌握高阶技能,如利用计算机软件进行辅助 解题等。
04
03
01
谢谢聆听
点斜式
y - y1 = m(x - x1),其中 (x1, y1)是直线上的一点, m是斜率。
两点式
y - y1 = (y2 - y1)/(x2 x1) * (x - x1),其中(x1, y1)和(x2, y2)是直线上的 两点。
02 直线方程的解法
线性方程的解法
线性方程的定义
线性方程是只包含一个变量的一 元方程,其一般形式为 ax + b =
直线的一般式方程--ppt课件精选全文完整版

x y 1 ab
bx ay (ab) 0
上述四式都可以写成直线方程的一般形式:
Ax+By+C=0, A、B不同pp时t课件为0.
2
ppt课件
3
Ax By C 0
问:所有的直线都可以用二元一次方程表示?
①当B≠0时 方程可化为 y A x C
BB
这是直线的斜截式方程,它表示斜率是
A1 B1 C1 A2 B2 C2
(B1 0, B2 0, )
l1与l2重合
A1 B1 C1 A2 B2 C2
A1 B1 A2 B2
l1与l2平行 l1与l2相交
(2)当l1 l2时,上述方程系数有何联系?
2
.l1
l ppt课件 2
A1A2
B1B2
014
练习1:已知直线l1:x+(a+1)y-2+a=0和 l2:2ax+4y+16=0,若l1//l2,求a的值.
o
x
ppt课件
7
二、二元一次方程的系数对直线的位置的影响: 在方程Ax+By+C=0中,A,B,C为何值时, 方程表示的直线: (1)平行于x轴;(2)平行于y轴;(3)与x轴重合;
y
l
(3) A=0 , B≠0 ,C=0
o
x
ppt课件
8
二、二元一次方程的系数对直线的位置的影响:
在方程Ax+By+C=0中,A,B,C为何值时,
a=1
练习2:已知直线l1:x-ay-1=0和 l2:a2x+y+2=0,若l1⊥l2,求a的值.
a=1或a=0
ppt课件
15
2.2.3直线的一般式方程(教学课件(人教版))

解(1)若方程不能表示直线,则 m2+5m+6=0 且 m2+3m=0.
解方程组
m 2+5m+6=0,得 m 2+3m=0,
m=-3
(2)由已知 m2m2-2+mm≠-0,3=-(m2-m),解由得已m知=-24mm12- .+1m=-2m3≠2+ 0,m-3,
例4(一般式下直线的平行与垂直问题)
BB
当B=0时, A≠0, 方程Ax+By+C=0可变形为 x C . A
由上可知, 关于x,y的二元一次方程Ax+By+C=0都表示一条直线.
综上可知, 在平面直角坐标系中, 任何关于x, y的二元一次方程Ax+By +C=0都表 示一条直线.
我们把关于x, y的二元一次方程Ax+By+C=0 (其中A, B不同时为0)叫做直线的 一般式方程, 简称一般式. 探究 在方程Ax+By +C=0中, A,B,C为何值时, 方程表示的直线:
两点式
过点P1(x1,y1), P2(x2,y2) (其中x1 ≠ x2, y1 ≠ y2)
直线方程 y y0 k( x x0 )
y kx b y y1 x x1 y2 y1 x2 x1
应用范围
不含与x轴垂
直的直线
不含与x轴垂
直的直线
不含与x, y轴
垂直的直线
截距式
过点P1(a,0), P2(0,b) (其中a≠0, b≠0)
已知A(2,2)和直线l:3x+4y-20=0.求: (1)过点A和直线l平行的直线方程;(2)过点A 和直线l垂直的直线方程.
解 (1)将与直线 l 平行的方程设为 3x+4y+C1=0,
又过点 A(2,2),所以 3×2+4×2+C1=0,所以 C1=-14.
直线的方程ppt课件
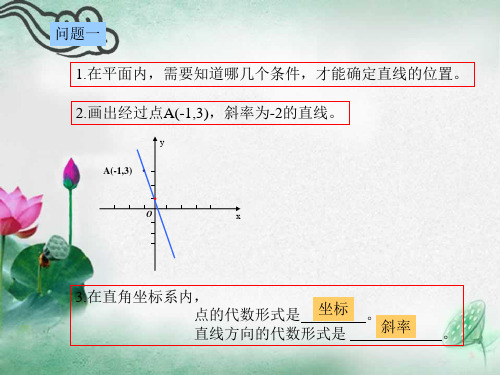
问题一
1.在平面内,需要知道哪几个条件,才能确定直线的位置。
2.画出经过点A(-1,3),斜率为-2的直线。
y
A(-1,3) .
.
O
x
3.在直角坐标系内, 点的代数形式是
坐标
。
直线方向的代数形式是 斜率 。
问题二
若直线l经过点A(-1,3),斜率为-2,点P(x,y)在直线l上运动,那么 点P的坐标x和y之间满足什么关系?
例2: 已知直线l 斜率为k,与y轴的交点是P(0,b),求直线l的方程。
解:由直线的点斜式方程,得 y b k(x 0) 即为 y kx b .
其中,b为直线与y轴交点的纵坐标。 我们称b为直线l 在y轴上的截距。
方程 y kx b 由直线l的斜率和它在y轴上的截距确定 。 所以,这个方程 y kx b 就也叫做直线的斜截式方程。
答 不能。从代数式的表达意义上讲“两点式”
方程使用的前提是x“1 x2 y且1 y2 ”。
它不能表示倾斜角90为 0和 的直线,即
当直线与x轴,y轴不平行时,可以用两点式 表示。
例1:
已知一直线经过两点 A(a, 0), B(0,b). 其中 Байду номын сангаас b 0
求这条直线的方程。
解:由直线的两点式方程,得 y0 xa b0 0a
填空
1.直线y=2x-4的斜率是 2 ,在y轴上的截距是 - 4 。
2.直线2x+y-4=0的斜率是 - 2 ,在y轴上的截距是 4 。
3.直线3x+2y=0的斜率是
3 2
,在y轴上的截距是 0
。
判断
1.直线的点斜式方程 y y1 k(x x1) 可以表示直角坐标系 中的任何一条直线。
1.在平面内,需要知道哪几个条件,才能确定直线的位置。
2.画出经过点A(-1,3),斜率为-2的直线。
y
A(-1,3) .
.
O
x
3.在直角坐标系内, 点的代数形式是
坐标
。
直线方向的代数形式是 斜率 。
问题二
若直线l经过点A(-1,3),斜率为-2,点P(x,y)在直线l上运动,那么 点P的坐标x和y之间满足什么关系?
例2: 已知直线l 斜率为k,与y轴的交点是P(0,b),求直线l的方程。
解:由直线的点斜式方程,得 y b k(x 0) 即为 y kx b .
其中,b为直线与y轴交点的纵坐标。 我们称b为直线l 在y轴上的截距。
方程 y kx b 由直线l的斜率和它在y轴上的截距确定 。 所以,这个方程 y kx b 就也叫做直线的斜截式方程。
答 不能。从代数式的表达意义上讲“两点式”
方程使用的前提是x“1 x2 y且1 y2 ”。
它不能表示倾斜角90为 0和 的直线,即
当直线与x轴,y轴不平行时,可以用两点式 表示。
例1:
已知一直线经过两点 A(a, 0), B(0,b). 其中 Байду номын сангаас b 0
求这条直线的方程。
解:由直线的两点式方程,得 y0 xa b0 0a
填空
1.直线y=2x-4的斜率是 2 ,在y轴上的截距是 - 4 。
2.直线2x+y-4=0的斜率是 - 2 ,在y轴上的截距是 4 。
3.直线3x+2y=0的斜率是
3 2
,在y轴上的截距是 0
。
判断
1.直线的点斜式方程 y y1 k(x x1) 可以表示直角坐标系 中的任何一条直线。
直线的参数方程ppt课件
返回首页
下一页
5.化直线l的参数方程
x=-3+t, y=1+ 3t
(t为参数)为普通方程,并求倾斜角,
说明|t|的几何意义.
上一页
返回首页
下一页
【解】 由xy= =- 1+3+3tt, 消去参数t,得
直线l的普通方程为 3x-y+3 3+1=0.
故k= 3=tan α,即α=π3,
几何意义为|
→ M0M
|=4,且
→ M0M
与e方向相反(即点M在直线l上点M0的左下
方).
上一页
返回首页
下一页
1.一条直线可以由定点M0(x0,y0),倾斜角α(0≤α<π)惟一确定,直线上
的动点M(x,y)的参数方程为
x=x0+tcos y=y0+tsin
α, α
(t为参数),这是直线参数方程的
上一页
返回首页
下一页
【解析】 将xy= =12- +23tt 化为y=-32x+72, ∴斜率k1=-32, 显然k=0时,直线4x+ky=1与上述直线不垂直, ∴k≠0,从而直线4x+ky=1的斜率k2=-4k. 依题意k1k2=-1,即-4k×-32=-1, ∴k=-6. 【答案】 -6
上一页
θ, θ
(θ为参数)交于A,B两点,求|PA|·|PB|.
上一页
返回首页
下一页
【解】 (1)直线l的参数方程为
x=-3+tcos56π=-3- 23t, y=3+tsin56π=3+2t
(t为参数).
上一页
返回首页
下一页
(2)把曲线C的参数方程中参数θ消去,得4x2+y2-16=0. 把直线l的参数方程代入曲线C的普通方程中,得 4-3- 23t2+3+12t2-16=0, 即13t2+4(3+12 3)t+116=0. 由t的几何意义,知 |PA|·|PB|=|t1·t2|, 故|PA|·|PB|=|t1·t2|=11136.
直线方程的几种形式-ppt课件

的正负确定直线
通过的象限.
y y=kx+b (k>0,b>0)
y=x y=kx=b (k>0,b<0)
o
x
当斜率大 于0时
y
当斜率
o
x
y=kx+b(k<0,b>0
小于0时
y=-x y=kx+b(k<0,b<0
重点与难点
• 1.重点: 求直线方程. • 2.难点:直线方程的互化及记忆有关结论和灵
y1 x1
(x x1)
当 y2 ≠ y1时可以写成:
y y1 x x1 y2 y1 x2 x1
这个方程是由直线上两点确 定的,叫做直线方程的两点式。
3.斜截式:已知直线 l的斜率是
k,与 y 轴的交点是 (0 , b) ( b 是直线
在轴上的截距)代入点斜式得直线 l
的方程:
y-b = k( x-0 )
y y
k
1
x x1
可化为
y y1 k(x x1)
可以验证,直线 l 上的每一个点的坐标
都是这个方程的解;反过来,以这个方程的
解为坐标的点都在直线 l 上,所以这个方程
就是过点 p 1
、斜率为 k
的直线 l
的方程。
这个方程是由直线上一点和直线的斜率 确定的,叫做直线方程的点斜式。
特属 情况
y
p1
l
1、当直线 l 的倾斜角为 零度 时(图 2)tg 00=0 , 即 k=0. 这时直线 的方程就是
y y1
o
x
图2
y
p1
o
x
图3
当直线 l 的倾斜角为 900 时,直线没有 斜率这时直线 l与y轴平行或重合,它的方
通过的象限.
y y=kx+b (k>0,b>0)
y=x y=kx=b (k>0,b<0)
o
x
当斜率大 于0时
y
当斜率
o
x
y=kx+b(k<0,b>0
小于0时
y=-x y=kx+b(k<0,b<0
重点与难点
• 1.重点: 求直线方程. • 2.难点:直线方程的互化及记忆有关结论和灵
y1 x1
(x x1)
当 y2 ≠ y1时可以写成:
y y1 x x1 y2 y1 x2 x1
这个方程是由直线上两点确 定的,叫做直线方程的两点式。
3.斜截式:已知直线 l的斜率是
k,与 y 轴的交点是 (0 , b) ( b 是直线
在轴上的截距)代入点斜式得直线 l
的方程:
y-b = k( x-0 )
y y
k
1
x x1
可化为
y y1 k(x x1)
可以验证,直线 l 上的每一个点的坐标
都是这个方程的解;反过来,以这个方程的
解为坐标的点都在直线 l 上,所以这个方程
就是过点 p 1
、斜率为 k
的直线 l
的方程。
这个方程是由直线上一点和直线的斜率 确定的,叫做直线方程的点斜式。
特属 情况
y
p1
l
1、当直线 l 的倾斜角为 零度 时(图 2)tg 00=0 , 即 k=0. 这时直线 的方程就是
y y1
o
x
图2
y
p1
o
x
图3
当直线 l 的倾斜角为 900 时,直线没有 斜率这时直线 l与y轴平行或重合,它的方
02教学课件_2.2.2 直线的两点式方程(共25张PPT)

可以确定一条直线。
这样,在直角坐标系中,给定一个点p0(x0,y0)和斜率k,可得出直线方程。
若给定直线上两点p1(x1,y1)p2(x2,y2),你能否得出直线的方程呢?
探究新知
1.直线的两点式方程
(1)直线的两点式方程的定义
y-y1 x-x1
=
y
-y
x2-x1
2
1
__________________就是经过两点
点的坐标还有限制条件吗?
答案:这个方程对两点的坐标没有限制,即它可以表示过任意两点的直线方程.
2.已知直线l过点A(3,1),B(2,0),则直线l的方程为
y-1
x-3
解析:由两点式,得0-1 = 2-3,化简得 x-y-2=0.
答案:x-y-2=0
.
二、直线的截距式方程
点睛:直线的截距式方程是直线的两点式方程的特殊情况,由直线的截距式方程
2
S 取最大值为-3×152+20×15+54 000=54 150(m2).
因此点 P 距 AE 15 m,距 BC 50 m 时所开发的面积最大,
最大面积为 54 150 m2.
归纳总结 二次函数最值问题,一方面要看顶点位置,另一方面还要看定义域的范围.结
合图形求解,有时并非在顶点处取得最值.
当堂检测
不垂直于x、y轴的直线
点P1 ( x1,y1 )和点P2 ( x2,y2 )
y1 y2 x1 x2
在x轴上的截距 a
在y轴上的截距 b
x y
1
a b
不垂直于x、y轴的直线
不过原点的直线
课堂小结
课堂小结:
-3
)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)两直线相交:夹角与直线到直线的角差别 (4)点到直线的距离
双基再现:
①若直线ax+by+c=0在第一 二 三象限,则
A.ab>0,bc>0 B.ab>0,bc<0
()
C.ab<0,bc>0 D.ab<0,bc<0
②平面上有相异的两点A(cosθ,sin2θ)和B.(0,1), 求经过A. B两点的直线的斜率及倾斜角的范围. ③过点A(1,4)且纵横截距的绝对值相等的直线 共有的条数()
A.B两点,求使三角形AOB面积取得最小 值时直线L的方程
⑥直线y=ax+2穿过以A(1,4)
B.(3,1)两点为 端点的线段,求a的取值范围 ⑦设A.B是x轴上的两点,点p的横坐标2, 且PA的绝对值等于PB的绝对值,若直线 PA的方程为x-y+1=0,则直线PB的方程是
一直线被两直线L1:4x+y+6=0,L2:3x-5y-
A.1 B.2
C.3
D.4
④过点p(2,-3),倾斜角比直线y=2x-1的倾斜 角大45°的直线的方程 A.3x+y-2=0 B.x+3y-2=0 C.3x+y+3=0 D.3x+y3=0
⑤若直线L1:ax+2y+6=0与直线L2:x+(a1)y+a2-1=0平行,则a等于( )
过点P(1,2)作直线L,交x,y轴的正半轴于
直线方程总复习 • 基本知识点:直线的倾斜角和斜率、直线的方 程、两条直线的位置关系、简单的线性规划。
重点:求直线方程 难点:对称问题.
.两直线位置关系.
直线系问题. 坐标法
重要的数学思想方法:数形结合
直线方程的五种形式 点斜式: y-y1=k(x-x1) 斜截式: y=kx+b
y y1 x x1 两点式: y2 y1 x2 x1
6=0截得的线段的中点恰好是坐标原点, 求该直线方程
m为何值时,下面三条直线
L1:4x+y=4,L2:mx+y=0,L3:2x-3my=4能围成 三角形。
直线L过点A(2,3),且被两平行线
L1:3x+4y-7=0和L2:3x+4y+8=0截得的线段 长为 3 2,试求直线的方程
在三角形ABC中,BC边上的高所在直线
适合斜率存在 适合斜率存在 适合与坐标轴不垂直
x y 截距式: 1 同上且不适合过原点 a b
一般式:Ax+By+C=0 适合所有直线
两条直线的位置关系:
(1)两直线平行的充要条件:
斜率相等,截距不等或
A1 B1 C1 A2 B2 C2
(2)两直线垂直的充要条件:
K1K2=-1或A1A2+B1B2=0
所以kAC=-1(为什么??) AC:y=-(x+1) KBC=-2 BC:y-2=-2(x-1) C(已知点A(2,0),B(0,6),o为原点
(1)若点C在线段OB上,且角BAC=Π/4,求三角 形ABC的面积; (2)若原点O关于直线AB的对称点为D,延长 BD到P,且PD的绝对值等于BD的绝对值2, 已知直线L:ax+10y+84-108 3 =0经过点P, 求直线L的倾斜角.
的方程为x-2y+1=0,A的平分线所在直线 的方程为y=0,若B点的坐标为(1,2),求点 A和点C的坐标
已知三角形ABC的一条内角平分线CD
的方程是2x+y-1=0,两个顶点A(1,2) B(-1,-1),求第三个顶点C的坐标
分析由
X-2y+1=0
y=0
y A o
B x
A(-1,0)
kAB==-1 因为x轴是A的平分线
