最新人教版七年级数学下册同步检测:平移1
人教版数学七年级下册5.4.1平移的概念、平移的性质说课稿

在学习本节课之前,学生已经具备了以下前置知识或技能:
1.基本的几何图形知识;
2.图形的对称、旋转等基本变换;
3.平行线、相似图形的性质。
可能存在的学习障碍有:
1.对平移定义的理解不够深入,容易与旋转、对称等变换混淆;
2.空间想象能力不足,难以理解平移的性质;
3.将平移变换应用于解决实际问题时,可能缺乏思路和技巧。
(五)作业布置
课后作业布置如下:
1.基础作业:布置一些与平移相关的基础题目,巩固学生对知识点的掌握。
2.提高作业:设计一些拓展性的题目,让学生在课后进行思考和探究,提升学生的应用能力。
3.实践作业:鼓励学生运用平移的性质,解决生活中的实际问题。
作业的目的是巩固所学知识,培养学生的自主学习能力和问题解决能力。
人教版数学七年级下册5.4.1平移的概念、平移的性质说课稿
一、教材分析
(一)内容概述
本节课选自人教版数学七年级下册第5章“图形的变换”,本节课主要讲解5.4.1平移的概念、平移的性质。在整个课程体系中,平移作为基本的几何变换之一,是学生在学习图形变换中的重要环节。通过本节课的学习,学生可以掌握平移的定义、性质和运用,为后续学习对称、旋转等其他图形变换打下基础。本节课的主要知识点有:
3.游戏互动:设计一个简单的平移变换游戏,让学生在游戏中体验平移的性质,为学习新知识做好铺垫。
(二)新知讲授
在新知讲授阶段,我将逐步呈现知识点,引导学生深入理解:
1.定义:通过动态展示几何图形的平移运动,让学生观察、思考,总结出平移的定义。
2.性质:引导学生从平移的定义出发,探讨平移的性质,如对应点、线段、角度的不变等,并通过实例加以验证。
(三)学习动机
七年级-人教版-数学-下册-第1课时-平移及其基本性质

平移
定义
性质
图形移动前后形状、大 小完全相同
对应点的连线平行(或 在同一条直线上)且相等
B A
B′ A′
C
C′
思考 如图,在所画出的相邻两个雪人中,找出三组对应点(例如,
它们的鼻尖 A 与 A′,帽顶 B 与 B′,纽扣 C 与 C′),连接这些对应 点,观察得出的线段,它们的位置、长短有什么关系?
可以发现,AA′∥BB′∥CC′, 并且 AA′=BB′=CC′.
B A
C
B′ A′
C′
它们的鼻尖 A 与 A′,帽顶 B 与 B′,纽扣 C 与 C′),连接这些对应 点,观察得出的线段,它们的位置、长短有什么关系?
B A
B′ A′
C
C′
思考 如图,在所画出的相邻两个雪人中,找出三组对应点(例如,
它们的鼻尖 A 与 A′,帽顶 B 与 B′,纽扣 C 与 C′),连接这些对应 点,观察得出的线段,它们的位置、长短有什么关系?
∵它们对应点的连线平行且相等, ∴它们是通过平移变换得到的.
图形平移的方向,不限于是水平的.
问题 平移在我们日常生活中是很常见的,利用平移也可以制作很多美
丽的图案,你能举出生活中一些利用平移的例子吗?
滑雪
火箭
汽车
例1 下列各组图形中,经过平移变换可以由一个图形得到 另一个图形的是( A ).
A
B
C
D
解析:平移是把一个图形整体沿某一直线方向移动一定的距离,
因此,平移前后图形的大小、形状都没变.只有选项 A 中一个三角
形是由另一个三角形经过平移得到的.
归纳
两法定平移 判断是不是平移,可根据平移的定义,看图形的形状、 大小是否发生了变化,是不是沿某一直线方向移动的. 除此之外,还有一个方法,根据平移的性质,即看连接 各组对应点的线段是否平行(或在同一条直线上)且相等.
(新人教版)数学七年级下册:5.4《平移》教案和习题(含答案)

《平移》教案一、教学目标1.经历观察、分析、操作、欣赏以及抽象、归纳等过程,以及与他人合作交流探索的过程,进一步发展空间观念,增强审美意识,学会用运动的观点分析问题.2.通过实例,认识图形平移,了解平移的特征,理解平移的含义,会进行点的平移.3.理解平移前后两个图形对应点连线平行且相等的性质,能解决简单的平移问题.二、教学重点与难点重点:图形平移的特征和作平移图形.难点:平移的性质探索和理解.三、教学过程(一)创设情境,引入新课1.感受平移,体验新知你坐过公车和搭过电梯吗?它是一种什么样的运动?这样的运动在生活中还有哪些现象?(活动1:学生讨论)2.观察图形,形成印象生活中有许多美丽的图案,他们都有着共同的特点,请同学们欣赏下面图案.观察上面图形,我们发现他们都有一个局部和其他部分重复,如果给你一个局部,你能复制他们吗?学生思考讨论,并回答问题.(1)它们有什么共同的特点?(2)能否根据其中的一部分绘制出整个图案?(活动2:师生交流.)这些美丽的图案是由若干个相同的图案组合而成的,每个图形都有“基本图形”,而“基本图形”是什么?如第一个图形是中间一个正方形,上、下有正立与倒立的正三角形,下排的左图中的“基本图形”是鸽子与橄榄枝;下排右图中的“基本图形”是上、下一对面朝右与面朝左的人头像组成的图案.3.实践探索,得出新知探究:设计一个简单的图案,利用一张半透明的纸附在上面,绘制一排形状,大小完全一样的图案如:引导学生找规律,发现平移特征,回答下面问题:1、图形经过平移后,_______图形的位置,________图形的形状,________图形的大小.(填“改变”或“不改变”)2、经过平移,每一组对应点所连成的线段________.归纳 (活动3:分组讨论)平移:(1)把一个图形整体沿某一方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同. (2)新图形中的每一点,都是由原图形中的某一个点移动后得到的,这两个点是对应点. (3)连接各组对应的线段平行且相等.图形的这种变换,叫做平移变换,简称平移简单归纳为两点:1.平移的方向. 2.平移的距离四、典例剖析,深化巩固1. 把鱼往左平移8cm.(假设每小格是1cm2)五、小结(学生回答):这节课你学了什么?知道了什么?学会了什么?六、课后作业必做题:教科书习题:3.6题《平移》习题1、决定平移的基本要素是____和____。
2020-2021人教版七年级数学下学期平移练习题

6、如图1,直线AB、CD相交于点O,
现将直线AB平移到直线EF位置,
那么,∠1与∠2的位置关系是
,角度关系是
。 图1
二、选择题
1、下面的每组图形中,左面的平移后可以得到右面的是( )
A B C D
2、三角形ABC从一个位置平移到另一个位置,则下列说法不正确的是( )
A、AB=A′B′ B、AB//A′B′ A A′
C、四边形BC B′C′为平行四边形
D、AA′>BB′>CC′ B C B′ C′
3、一个长方形ABCD沿PQ对折,A点落到A′位置,则( )
A、∠APQ≠∠A′PQ B、A′P > A′Q D C
C、PQ有可能平分∠A′QA A′
D、三角形 APQ和三角形APQ的面积相等 P
A Q B
4、已知 ,当 时, ;当 表示的数在1的基础上向左移动100个单位以后, 对应的值是( )
A、201 B、199 C、 D、
三、解答题
1、有一只小燕鱼正在自由的游动,它起始的位置如图所示:
6
5
4
3
2
1
0 1 2 3 4 5 6 7 8 9 10 11 1213
(1)请将组成小燕鱼轮廓的点的数对(x,y)填写在下面:
一、填空题
1、把一个图形沿某一个方向移动,会得到一个新的图形,新图形与原图形的和完全相同。
2、新图形中的每一点,都是由中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段且。
3、图形的移动,叫做,简称。
4、如图,线段AB经过平移到达DC位置, A D
那么图形ABCD为形。
5、在下图中画出原图形向右移动6个单位, B C
人教版七年级下册数学《平移》相交线与平行线研讨说课复习课件

课件
1、通过实例了解平移的概念; 2、理解并掌握平移的性质; 3、能按要求作出平移后的图形。
重点
理解并掌握平移的性质; 能按要求作出平移后的图形。
难点 理解并掌握平移的性质。
仔细观察下面这些美丽的图案,回答问题:
(1)这些图案有什么共同特点?
(2)这些图案能否根据其中的 一部分绘制出整个图案?若能, 你能否想象出是怎样绘制的?
知识
平移的概念及性质
考点
绘制平移图形 利用平移的性质解决问题
再见
人教版 数学 七年级 下册
5.4 平移
课件
导入新知
传送带上的电视 机在运送过程中发生 了什么变化?
学习目标
3. 能按要求作出简单平面图形平移后的图 形,培养观察和动手操作的能力. 2. 会找出平移前后图形中对应点和对应 线段. 1. 通过实例认识平移,理解平移的含义和 性质.
A'
所得的三角形就是平移后的 三角形.
B'
A C'
B
C
探究新知
归纳总结 平移作图是平移性质的应用.在具体作图时,应抓住作图 的“四部曲”——定、找、移、连. (1)定:确定平移的方向和距离; (2)找:找出表示图形的关键点; (3)移:过关键点作平行且相等的线段,得到关键点的 对应点; (4)连:按原图形顺序连接对应点.
移的方向、距离都相同.
(4)确定一个图形平移的方向和距离,只需确定其上一个点平移
的方向和距离即可.
探究新知
考 点 1 平移现象的识别
下列现象:(1)水平运输带上砖块的运动;(2)高楼电梯上上
平移
下下迎接乘客;(3)健身做呼啦圈运动;(4)火车飞驰在一段
平移
旋转
平直的铁轨上;(5)沸水中气泡的运动.
(新人教版)数学七年级下册:5.4《平移》练习题及解析
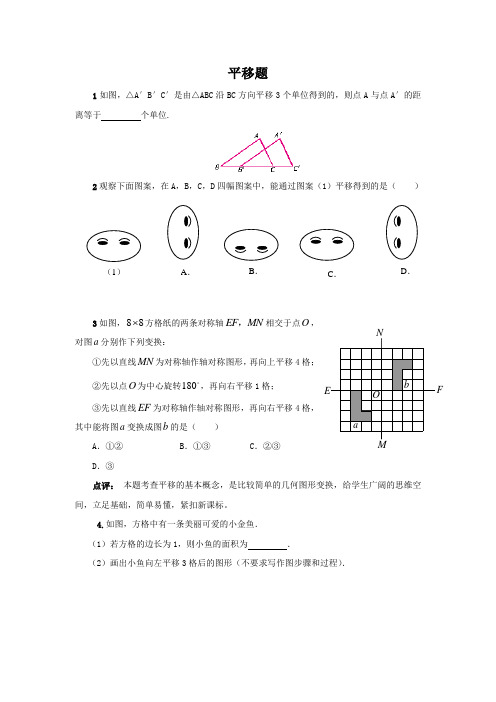
平移题
1如图,△A′B′C′是由△ABC沿BC方向平移3个单位得到的,则点A与点A′的距离等于个单位.
2观察下面图案,在A,B,C,D四幅图案中,能通过图案(1)平移得到的是()
3如图, 方格纸的两条对称 轴 相交于点 ,对图 分别作下列变换:
①先以直线 为对称轴作轴对称图形,再向上平移4格;
②先以点 为中心旋转 ,再向右平移1格;
7分析:题中具体指明了平移的距离是2cm,在平移方向上只说明了“水平方向”,并未指明向左还是向右,故应分向左平移还是向右平移两种情况。作平移时可利用五个关键点平移后的位置进行。
解:平移后的图形如图2-2所示,有两种情况。
8分析:此题移动方向与距离均未知,只要求移动三条线段成一个三角形时最少需移动的格数,那么首先我们应该知道移动后组成三角形的大致形状,因平移不改变图形形状和大小,只是位置发生变化,故易知三角形形状应是“◣”,由此作为突破口去探索,显然若只移两条线段,单移任一条或两条向居中位置移动,最少格数是一样的,但三条就不同了,应让三条尽最大可能的少“拐弯”,观察图3-1,应在三条线段的“中间”画出最后所形成的三角形,如图3-2,可得出三条线段平移成一个三角形至少要平移9格。
(新人教版)七年级下册数学:5.4《平移》练习题及答案
平移练习题◆回顾归纳1.平移的要素:(1)平移的_________;(2)平移的_________.2.(1)平移:将一个图形沿某个方向_________叫平移.(2)平移的性质:对应点的连结线段_________且_________.3.平移作图方法:(1)找出已知图形上的关键点;(2)过这些点沿指定_______平移,使平移_______等于已知距离;(3)依次作出各个_______点,连结所平移后的点得平移图形.◆课堂测控知识点平移(1)将线段AB•向北偏东方向平移5cm,•则点A•平移方向_______,•平移距离为______.(2)1.经过平移后的图形与______形状和大小都不改变.2.下列物体运动中平移的是_________(填序号).(1)打乒乓球的运动;(2)手表上指针的运动;(3)汽车在笔直公路上运动;(4)车轮的滚动.3.如图1所示的“田”字格可以看成由________平移得到的.图1 图2 图34.如图2所示,线段b向右平移3格,再向上平移______格,能与线段______重合.5.如图3所示,三角形ABC向下(右)平移_______格,再向右(下)平移_____得到三角形A′B′C′,图形的面积相等,形状不变.6.下列各组图形可以通过平移得到另一个图形的是()A B C D7.(经典题)如图4所示,长方形ABCD中,对角线AC,BD交于点O.DE∥AC,CE ∥BC.那么三角形EDC可以看成什么三角形平移得到的,指出平移方向,并求出平移距离?图4◆课后测控1.将正方形ABCD向北偏东30°方向平移4cm,•则对角线交点O•向________•平移______cm.2.如图5所示,BC垂直于水平面,高5.196m,现要建造阶梯,•每级台阶不超过20cm,则至少要建_______级台阶(不足20cm,按一级台阶计算)图5 图6 图73.在5×5方格纸中将图6(1)中的图形N平移后的位置如图6(2)中所示,那么正确的平移方法是()A.先向下移动1格,再向左移动1格B.先向下移动1格,再向左移动2格C.先向下移动2格,再向左移动1格D.先向下移动2格,再向左移动2格4.(互动探究题)如图7所示,在网格中,有三角形ABC,将A点平移到P点,画出三角形ABC平移后的图形.[解答](1)将A点向_______(或向______)平移______格(或_____格).(2)再向_____(或向_____)平移______格(或_______格),得点P.(3)同理B,C与A点平移次数方向距离一样,易得B′,C′.(4)连结PB′,PC′,B′C′得到三角形ABC平移后的三角形PB′C′.5.(经典题)如图所示,一块边长为8米的正方形土地,上面修了横竖各两条道路,宽都是1米,空白的部分种上各种花草,请利用平移的知识求出种花草的面积?◆拓展创新6.如图所示,在长方形ABCD中,AB=10cm,BC=6cm,试问将长方形ABCD•沿着AB方向平移多少才能使平移后的长方形与原来的长方形ABCD重叠部分的面积为24cm2?答案:回顾归纳1.(1)方向(2)距离2.(1)移动(2)平行或在同一条直线上,相等3.(2)方向;距离(3)对应课堂测控1.(1)北偏东;5cm (2)原图形 2.(3)3.小正方形包括中间四个小圆圈为基本图形4.2,c 5.3(或2),2(或3)6.C(点拨:A,B,D都不能通过平移得到)7.由三角形AOB,向右平移,平移距离为AD长.解题技巧:由平移图形的特征:大小,形状不变,猜想是△AOB.课后测控1.北偏东30°;4 2.26(点拨:519.620=26)3.C(点拨:或向左平移1格,再向下平移2格)4.(1)右;(下);4;(5)(2)下;(右);5;(4)(3),(4)图略5.将两条道路平移得到如图所示,则空白面积为(8-2)(8-2)=36(m2)思路点拨:运用平移思想方法是求这类面积问题最佳途径.6.设平行线段AE=x,A到E,E到F,则BE=AB-AE=10-x,因为BC=6,所以6(10-x)=24,•解得x=6,向右平移6cm.解题规律:扣住HEBC面积为24cm2,运用方程思想求解.。
专题5.4平移专项提升训练重难点培优拔尖特训七年级数学下册培优必刷题原卷版人教版
2022-2023学年七年级数学下册尖子生培优题典【人教版】专题5.4平移专项提升训练(重难点培优)班级:___________________ 姓名:_________________ 得分:_______________注意事项:本试卷满分120分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2022春•启东市期中)下列生活现象中,属于平移的是( )A.升降电梯的上下移动B.荡秋千运动C.把打开的课本合上D.钟摆的摆动2.(2022春•东莞市期中)下列选项中,由如图所示的“笑脸”平移得到的是( )A.B.C.D.3.(2022春•增城区期中)如图,已知△ABC的周长为20cm,现将△ABC沿AB方向平移2cm至△A′B′C′的位置,连接CC′,则四边形AB′C′C的周长为( )A.20cm B.22cm C.24cm D.26cm4.(2022春•白云区期中)如图,△ABC中,∠ABC=90°,沿BC所在的直线向右平移得到△DEF,下列结论中,错误的( )A.EC=CF B.∠A=∠D C.AC∥DF D.∠DEF=90°5.(2022春•海州区校级期末)如图,在△ABC中,BC=7,∠A=80°,∠B=70°,把△ABC沿RS的方向平移到△DEF的位置,若CF=4,则下列结论中错误的是( )A.DE=7B.∠F=30°C.AB∥DE D.EF=76.(2022春•海沧区校级期末)如图,将直角三角形ABC沿AB方向平移得到直角三角形DEF.已知AD=4,AE=13,则DB长为( )A.4B.5C.9D.137.(2022春•社旗县期末)如图,将△ABC沿着某一方向平移一定的距离得到△DEF,则下列结论:①AD =CF;②AC∥DF;③∠ABC=∠DFE;④∠DAE=∠AEB.其中正确的是( )A.仅①②B.仅①②④C.仅①②③D.①②③④8.(2022春•迁安市期末)如图,将△ABC沿直线AB向右平移后到达△BDE的位置,连接CE,则下面的结论①AC∥BE;②∠ACB=∠BED;③BD=AB;④∠CBE=∠BEC;⑤CE=BD;正确的个数是( )A.2B.3C.4D.59.(2022秋•二道区校级月考)如图,将直角三角形ABC沿BC方向平移得到直角三角形DEF.若AB=8cm,BE=4cm,DH=2cm,则图中阴影部分面积为( )A.28cm2B.29cm2C.30cm2D.32cm210.(2022•南京模拟)如图,若四个完全相同的小直角三角形按如图方式全部放置在大直角三角形ABC的内部,这四个小三角形的斜边刚好相接在斜边BC上,AB+AC=21,BC=15,则这四个小直角三角形的直角边之和为( )A.6B.15C.21D.36二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上11.(2022春•如皋市期中)如图,将△ABC沿BC所在直线向右平移得到△DEF,若EC=2,BF=10,则平移的距离为 .12.(2022•南京模拟)如图,将△ABC沿着射线AC的方向平移到达△CDE的位置,若AE=12cm,则线段BD的长是 cm.13.(2022春•榆次区期中)如图,将周长为18的△ABC沿BC方向平移3个单位长度得到△DEF,则四边形ABFD的周长为 .14.(2022春•息县期中)如图,将直角三角形ABC沿BC方向平移得到直角三角形DEF,其中AB=6,BE =3,DM=2,则阴影部分的面积是 .15.(2022春•景谷县期末)如图,校园里长为10米,宽为8米的长方形草地内修建了宽为1米的道路,则草地面积是 平方米.16.(2022春•武江区校级期末)如图,某住宅小区有一长方形地块,若要在长方形地块内修筑同样宽的两条道路,道路宽为2m,余下部分绿化,则绿化的面积为 .17.(2022春•耒阳市期末)要在台阶上铺设某种红地毯,已知这种红地毯每平方米的售价是20元,台阶宽为3米,侧面如图所示,购买这种红地毯至少需要 元.18.(2022春•庆云县期末)如图,两个直角三角形重叠在一起,将△ABC沿AB方向平移2cm得到△DEF,CH=2cm,EF=4cm,下列结论:①BH∥EF;②AD=BE;③BD=HF;④∠C=∠BHD,以上结论正确的有 (填序号).三、解答题(本大题共6小题,共66分.解答时应写出文字说明、证明过程或演算步骤)19.(2022春•盱眙县期中)如图,在边长为1个单位的正方形网格中,△ABC经过平移后得到△A'B'C',图中标出了点B的对应点B'.根据下列条件,利用网格点和无刻度的直尺画图并解答相关的问题保留画图痕迹:(1)画出△A'B'C';(2)连接AA'、CC',那么AA'与CC'的关系是 ,线段AC扫过的图形的面积为 ;20.(2022春•玄武区校级期中)如图,△ABC的顶点都在方格纸的格点上.(1)在△ABC中画出BC边上的中线AM,AB边上的高CN;(2)平移△ABC,使点B移动到点B'的位置,①画出平移后的△A′B′C′;②若连接AA′、BB′,则这两条线段之间的关系是 ;③平移过程中,AC边扫过的面积是 .21.(2022春•富阳区期中)在所给网格图(每个小格均为边长是1的正方形)中完成下列各题:(1)作出△ABC向右平移4格,向下3格后所得的△A1B1C1;(2)连接AA1,BB1,判断AA1,BB1的关系,并求△A1B1C1的面积.22.(2022春•高淳区校级期中)如图,每个小正方形的边长均为1,每个小方格的顶点叫格点.(1)画出△ABC中AB边上的高线CD,D为垂足;(2)画出△ABC向右平移3个单位后得到的△A1B1C1;(3)图中AB与A1B1的关系是 ;的面积是 .(4)S△ABC23.(2022春•吴江区校级期中)如图,直线AB∥CD,MN⊥AB分别交AB,CD于点M、N,射线MP、MQ分别从MA、MN同时开始绕点M顺时针旋转,分别与直线CD交于点E、F,射线MP每秒转10°,射线MQ每秒转5°,ER,FR分别平分∠PED,∠QFC,设旋转时间为t秒(0<t<18).(1)①用含t的代数式表示:∠AMP= °,∠QMB= °;②当t=4时,∠REF= °.(2)当∠MEN+∠MFN=130°时,求出t的值;(3)试探索∠EFR与∠ERF之间的数量关系,并说明理由;(4)若∠PMN的角平分线与直线ER交于点K,∠EKM的度数是 .24.(2022春•仓山区校级期中)如图1,已知两条直线AB,CD被直线EF所截,分别交于点E,点F,EM 平分∠AEF交CD于点M,且∠FEM=∠FME.(1)若2∠AEF=∠MFE,求∠AEF的度数;(2)如图2,点G是射线MD上一动点(不与点M,F重合),EH平分∠FEG交CD于点H,过点H 作HN⊥EM于点N,设∠EHN=α,∠EGF=β.①当点G在点F的右侧时,若β=50°,求α的度数;②当点G在运动过程中,α和β之间有怎样的数量关系?请写出你的猜想,并加以证明.。
人教版七年级数学下册 7-2-2用坐标表示平移(同步练习)
第7章平面直角坐标系7.2坐标方法的简单应用-7.2.2用坐标表示平移班级:姓名:知识点1用坐标表示点的平移1.将点A(2,1)向左平移2个单位长度得到点A',则点A'的坐标是()A.(0,1)B.(2,-1)C.(4,1)D.(2,3)2.把点A(-2,1)向上平移2个单位长度,再向右平移3个单位长度后得到B,点B的坐标是()A.(-5,3)B.(1,3)C.(1,-3)D.(-5,-1)3.点P(2,-3)先向左平移4个单位长度,再向上平移1个单位长度,得到点P'的坐标是.4.将点A(-3,-2)先沿y轴向上平移5个单位长度,再沿x轴向左平移4个单位长度得到点A',则点A'的坐标是.5.将点A(1,-3)向右平移2个单位长度,再向下平移2个单位长度后得到点B(a,b),则ab=.6.(1)如图,将点A向右平移几个单位长度可得到点B()A.3个单位长度B.4个单位长度C.5个单位长度D.6个单位长度(2)将点A向下平移5个单位长度后,将重合于图中的()A.点CB.点FC.点DD.点E(3)将点A先向右平移3个单位长度,再向下平移5个单位长度,得到A',将点B先向下平移5个单位长度,再向右平移3个单位长度,得到B',则A'与B'相距()A.4个单位长度B.5个单位长度C.6个单位长度D.7个单位长度(4)点G(-2,-2),将点G先向右平移6个单位长度,再向上平移5个单位长度,得到G',则G'的坐标为()A.(6,5)B.(4,5)C.(6,3)D.(4,3)7.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是()A.(2,5)B.(-8,5)C.(-8,-1)D.(2,-1)知识点2用坐标表示图形的平移8.将一个三角形的三个顶点的坐标分别向上平移1个单位长度,再向左平移4个单位长度所得点的坐标分别是(2,1),(-1,3),(4,-5),则平移前三个顶点的坐标分别是()A.(6,0),(3,2),(8,-6)B.(-1,-5),(2,-7),(3,-1)C.(1,5),(2,-7),(-3,1)D.(-1,5),(2,-7),(-3,1)9.如图,将三角形PQR向右平移2个单位长度,再向下平移3个单位长度,则点P平移后的坐标是()A.(-2,-4)B.(-2,4)C.(2,-3)D.(-1,-3)10.如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(-4,2),(-2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是.11.如图,三角形OAB 的顶点B 的坐标为(4,0),把三角形OAB 沿x 轴向右平移得到三角形CDE.如果CB=1,那么OE 的长为.12.如图,A,B 的坐标分别为(1,0),(0,2),若将线段AB 平移至A 1B 1,A 1,B 1的坐标分别为(2,a),(b,3),则a+b=.13.如图,梯形A'B'C'D'可以由梯形ABCD 经过怎样的平移得到?对应点的坐标有什么变化?综合点学科内综合14.如图,点A,B 的坐标分别为(1,2),(4,0),将三角形AOB 沿x 轴向右平移,得到三角形CDE,已知DB=1,则点C 的坐标为.15.如图,三角形A'B'C'是由三角形ABC 平移后得到的,已知三角形ABC 中一点P(x 0,y 0)经平移后对应点为P'(x 0+5,y 0-2).(1)已知A(-1,2),B(-4,5),C(-3,0),请写出A',B',C'的坐标;(2)试说明三角形A'B'C'是如何由三角形ABC平移得到的;(3)请直接写出三角形A'B'C'的面积为_____.拓展训练拓展点坐标中的规律探究16.如图,三角形DEF 是三角形ABC 经过某种变换后得到的图形,分别写出点A 与点D,点B 与点E,点C 与点F 的坐标,并观察它们的关系,如果三角形ABC 中任一点M 的坐标(x,y),那么它的对应点N的坐标是什么?第7章平面直角坐标系7.2坐标方法的简单应用-7.2.2用坐标表示平移答案与点拨1.A(点拨:点A'的横坐标为2-2=0,纵坐标为1,∴A'的坐标为(0,1).故选A.)2.B(点拨:∵A(-2,1)向上平移2个单位长度,再向右平移3个单位长度后得到B,∴1+2=3,-2+3=1;点B的坐标是(1,3).故选B.)3.(-2,-2)(点拨:点(2,-3)向左平移4个单位长度,横坐标为:2-4=-2,向上平移1个单位长度,纵坐标为:-3+1=-2,∴点P'(-2,-2).)4.(-7,3)(点拨:点A(-3,-2)先沿y轴向上平移5个单位长度,再沿x轴向左平移4个单位长度得到点A',∴A'的坐标是(-3-4,-2+5),即(-7,3).)5.-15(点拨:将点A向右平移2个单位长度,纵坐标不变,横坐标增加2,此时点的坐标为(3,-3),再向下平移2个单位长度,横坐标不变,纵坐标减2,此时的坐标为(3,-5),即点B坐标为(3,-5),∴a=3,b=-5,∴ab=3×(-5)=-15.)6.(1)B(2)D(3)A(点拨:先分别找到A',B'的位置,再观察它们之间的距离.)(4)D7.D(点拨:逆向思考,把点(-3,2)先向右平移5个单位长度,再向下平移3个单位长度可得到A点坐标.)8.A(点拨:将平移后各点横坐标加4,纵坐标减1,可得到平移前的点的坐标分别是:(2+4,1-1),(-1+4,3-1),(4+4,-5-1),即(6,0),(3,2),(8,-6).)9.A(点拨:由图形知点P的坐标为P(-4,-1),由平移规律得平移后P点的坐标是(-4+2,-1-3)即(-2,-4).故选A.)10.(5,4)(点拨:左眼坐标由(-4,2)到(3,4)是向右平移7个单位长度,又向上平移2个单位长度,右眼由(-2,2)作同样的平移得坐标为(5,4).)11.7(点拨:因为三角形OAB的顶点B的坐标为(4,0),所以OB=4,所以OC=OB-CB=4-1=3,因此平移的距离为3.因为把三角形OAB沿x轴向右平移得到三角形CDE,所以CE=OB=4,所以OE=OC+CE=3+4=7.)12.2(点拨:∵A,B的坐标分别为(1,0),(0,2),若将线段AB平移至A1B1,A1,B1的坐标分别为(2,a),(b,3),可知线段AB向右平移了1个单位长度,向上平移了1个单位长度,则a=0+1=1,b=0+1=1,则a+b=1+1=2.)13.可由ABCD向左平移7个单位长度,向上平移7个单位长度得到.各对应点的坐标横坐标减7,纵坐标加7.14.(4,2)(点拨:O与D是一对对应点,因此平移距离为OD=OB-DB=4-1=3,因此平行规律为向右平移3个单位长度,所以A(1,2)的对应点C的坐标为(4,2).)15.(1)A'(4,0),B'(1,3),C'(2,-2)(2)三角形ABC向右平移5个单位长度,再向下平移2个单位长度(或先下平移2个单位长度,再向右平移5个单位长度)即可得到三角形A'B'C'.(3)616.A(4,3),D(-4,-3),B(3,1),E(-3,-1),C(1,2),F(-1,-2);N(-x,-y)。
新人教版七年级数学下册同步练习5.4平移(练习卷+解析版)
18.(8 分)如图,在方格纸中,每个小正方形的边长均为 1 个单位长度有一个 △ABC,它的三个顶点均与小正方形的顶点重合. (1)将△ABC 向右平移 3 个单位长度,得到△DEF(A 与 D、B 与 E、C 与 F 对应),请在方格纸中画出△DEF; (2)在(1)的条件下,连接 AE 和 CE,请直接写出△ACE 的面积 S,并判断 B 是否在边 AE 上.
C、由图形可得其周长为:12cm,
D、由图形可得其周长为:12cm,
故最长的是 B.
故选:B.
3.下列生活现象中,属于平移的是( )
A.足球在草地上滚动
B.拉开抽屉
C.投影片的文字经投影转换到屏幕上
D.钟摆的摆动
解:A.足球在草地上滚动方向变化,不符合平移的定义,不属于平移
B.拉开抽屉符合平移的定义,属于平移;
解:∵将线段 DC 沿着 CB 的方向平移 7cm 得到线段 EF,
∴EF=DC=4cm,FC=7cm, ∵AB=AC,BC=12cm, ∴∠B=∠C,BF=5cm, ∴∠B=∠BFE, ∴BE=EF=4cm, ∴△EBF 的周长为:4+4+5=13(cm). 故答案为:13. 14.如图,∠1=70°,直线 a 平移后得到直线 b,则∠2﹣∠3= 110 °.
A.12
B.24
C.21
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.4《平移》检测题
一、选择题
1、在以下现象中:①温度计中液面上升或下降,②用打气筒打气时活塞的移动,③钟摆的摆动,④传送带带着瓶装饮料的移动。
其中平移的有( ) A 、①②④ B 、①③ C 、②③ D 、②④
2、如图所示ABC ∆平移到C B A '''∆, 则图中平行相等的线段有_____对( ) A 、3对 B 、4对 C 、5对 D 、6对
3、在平移过程中,对应线段( )
A 、互相平行且相等
B 、互相垂直且相等
C 、互相平行(或在同一条直线上)且相等
D 、相交且相等 4、如图,ABC ∆平移后得到FD
E ∆,则和BD 对应的线段是( ) A 、DC B 、DE C 、CE D 、以上都不对
(4题图) (5题图)
5、DEF ∆经过平移后得到ABC ∆,则C ∠的对应角和ED 的对应边分别是( ) A 、F ∠、AC B 、BOD ∠、BA C 、F ∠、BA D 、BOD ∠、AC 二、填空题
1、平移后,对应线段________________________________,对应角__________
2、如图DEF ∆,ABC ∆是沿BC 方向平移后的图形,试判断FCGD 四边形S 与GAB S E 四边形的面积关系是______________
B
B
E
C
D
A
3、如图,直角ABO ∆的周长为100,在其内部有4个小直角三角形,则这4个小直角三角形周长之和为( )
A 、90
B 、100
C 、110
D 、120
4、在长为a m ,宽为b m 的一块草坪上修了一条1m 宽的笔直小路,则余下草坪的面积可表示为__________m 2,现为增加美感,把这条小路改为竖直方向的宽恒为1m 的弯曲小路,则此时余下草坪的面积为__________ m 2
5、如图,平移ABC ∆可得到DEF ∆,若A ∠=50°,C ∠=60°,则E ∠=__________,
EDF ∠=__________,F ∠=__________,DOB ∠=__________
(4题图
6、如图,是一块钜形ABCD 的场地,长AB =101米,宽AD =52米,从A 、B 两处入口的中路宽都为1米,两小路汇合处路口宽为2米,其余部分种植草坪面积为__________米 2 三、解答题
1、如图,将Rt ABC ∆沿AB 方向平移AD 距离得到Rt DEF ∆,已知BE =5,EF =8,
CG =3,求图中阴影部分面积。
E
2、某商场重新装修后,准备在大厅的主楼梯上铺设一种红色的地毯,已知地毯每平方米40元,主楼梯道的宽为3米,问买地毯至少需要多少元?
3、如图,若要在长32m ,宽20m 的长方形地面上修筑同样宽2米的两条道路,余下的部分修草坪,草坪的面积是多少?
4、如图,把直角梯形ABCD 沿BA 方向平移得到梯形A B C D '''',CD 与B C ''相交于点E ,BC =20cm ,EC =5cm ,E C '
=4cm ,图中阴影部分的面积与哪个四边形的
面积相等,并求出阴影部分的面积。
参考答案
一.1.A 2.D 3.C 4.C 5.C
二.1.平行(或在同一条直线上)且相等,相等 2.相等 3.B 4.(ab-a)(ab-a)
5.70º, 50º, 60º 60º
6.5000
三.解答题1.S
阴= S
梯形BGFE
=
2
1
(5+8)×5=
2
65
2. 1008元
3. 540m2
4. 90cm2。
