必修3概率期末复习
必修3概率与统计复习导学(文)

概率与统计复习一、典型问题与方法(一)随机抽样:简单随机抽样、系统抽样、分层抽样简单随机抽样:各个个体被抽中的机会都相等,不放回抽取,常有抽签法、随机数法。
系统抽样:用简单随机抽样确定一个个体,再按一定规则(加间隔)抽取。
分层抽样的比较:已知总体内部组成结构,各层按比例抽取。
例1.1.为调查参加运动会的1000名运动员的年龄情况,从中抽查了100名运动员的年龄,就这个问题来说,下列说法正确的是()A.1000名运动员是总体B.每个运动员是个体C.抽取的100名运动员是样本D.样本容量是1002.一个总体中有100个个体,随机编号为0,1,2,…,99,依编号顺序平均分成10个小组,组号依次为1,2,3,…,10.现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k小组中抽取的号码个位数字与m+k的个位数字相同.若m=6,则在第7组中抽取的号码是3.甲校有3600名学生,乙校有5400名学生,丙校有1800名学生,为统计三校学生某方面的情况,计划采用分层抽样法,抽取一个样本容量为90人的样本,应在这三校分别抽取学生()A.30人,30人,30人B.30人,45人,15人C.20人,30人,10人D.30人,50人,10人4.某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点.公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为①;在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查为②. 则完成①、②这两项调查宜采用的抽样方法依次是()A.分层抽样法,系统抽样法B.分层抽样法,简单随机抽样法C.系统抽样法,分层抽样法D.简单随机抽样法,分层抽样法基础训练1.某单位有老年人28人,中年人54人,青年人81人.为了调查他们的身体状况,需从他们中抽取一个容量为36的样本,最适合抽取样本的方法是( ).A.简单随机抽样B.系统抽样C.分层抽样D.先从老年人中剔除一人,然后分层抽样2.某学校为了了解高一年级学生对教师教学的意见,打算从高一年级2007名学生中抽取50名进行抽查,若采用下面的方法选取:先用简单随机抽样从2007人中剔除7人,剩下2000人再按系统抽样的方法进行,则每人入选的机会()A. 不全相等B. 均不相等C. 都相等D. 无法确定3.有20位同学,编号从1至20,现在从中抽取4人作问卷调查,用系统抽样方法确定所抽的编号为()A.5,10,15,20B.2,6,10,14C.2,4,6,8D.5,8,11,144.某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点,公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为(1);在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查为(2)。
必修3第三章-概率-知识点总结和强化练习:

高中数学必修3 第三章 概率 知识点总结及强化训练一、 知识点总结3.1.1 —3.1.2随机事件的概率及概率的意义 1、基本概念:(1)必然事件:在条件S 下,一定会发生的事件,叫相对于条件S 的必然事件; (2)不可能事件:在条件S 下,一定不会发生的事件,叫相对于条件S 的不可能事件; (3)确定事件:必然事件和不可能事件统称为相对于条件S 的确定事件;(4)随机事件:在条件S 下可能发生也可能不发生的事件,叫相对于条件S 的随机事件;(5)频数与频率:在相同的条件S 下重复n 次试验,观察某一事件A 是否出现,称n 次试验中事件A出现的次数nA 为事件A 出现的频数;称事件A 出现的比例fn(A)=n n A为事件A 出现的概率:对于给定的随机事件A ,如果随着试验次数的增加,事件A 发生的频率fn(A)稳定在某个常数上,把这个常数记作P (A ),称为事件A 的概率。
(6)频率与概率的区别与联系:随机事件的频率,指此事件发生的次数nA 与试验总次数n 的比值n n A,它具有一定的稳定性,总在某个常数附近摆动,且随着试验次数的不断增多,这种摆动幅度越来越小。
我们把这个常数叫做随机事件的概率,概率从数量上反映了随机事件发生的可能性的大小。
频率在大量重复试验的前提下可以近似地作为这个事件的概率3.1.3 概率的基本性质 1、基本概念:(1)事件的包含、并事件、交事件、相等事件(2)若A ∩B 为不可能事件,即A ∩B=ф,那么称事件A 与事件B 互斥;(3)若A ∩B 为不可能事件,A ∪B 为必然事件,那么称事件A 与事件B 互为对立事件;(4)当事件A 与B 互斥时,满足加法公式:P(A ∪B)= P(A)+ P(B);若事件A 与B 为对立事件,则A ∪B 为必然事件,所以P(A ∪B)= P(A)+ P(B)=1,于是有P(A)=1—P(B)2、概率的基本性质:1)必然事件概率为1,不可能事件概率为0,因此0≤P(A)≤1; 2)当事件A 与B 互斥时,满足加法公式:P(A ∪B)= P(A)+ P(B);3)若事件A 与B 为对立事件,则A ∪B 为必然事件,所以P(A ∪B)= P(A)+ P(B)=1,于是有P(A)=1—P(B);4)互斥事件与对立事件的区别与联系,互斥事件是指事件A 与事件B 在一次试验中不会同时发生,其具体包括三种不同的情形:(1)事件A 发生且事件B 不发生;(2)事件A 不发生且事件B 发生;(3)事件A 与事件B 同时不发生,而对立事件是指事件A 与事件B 有且仅有一个发生,其包括两种情形;(1)事件A 发生B 不发生;(2)事件B 发生事件A 不发生,对立事件互斥事件的特殊情形。
高一数学必修三概率复习总结精品PPT课件

例3.甲、乙二人约定在 12 点到 5 点之间在某地会面,先到者 等一个小时后即离去设二人在 这段时间内的各时刻到达是等 可能的,且二人互不影响。求 二人能会面的概率。
解: 以 X , Y 分别表示甲乙二人到
达的时刻,于是 0X5,0Y5.
即 点 M 落在图中
的阴影部分。所有的 点构成一个正方形, 即有无穷多个结果。 由于每人在任一时刻 到达都是等可能的, 所以落在正方形内各 点是等可能的。
(3) 当事件A、B对立时, P(A)1P(B)
(4 )P (A B )= P (A )+ P (B )-P (A B )
古典概型
1)两个特征:
(1)试验中所有可能出现的基本事件只有 有限个;(有限性)
(2)每个基本事件出现的可能性相等。 (等可能性)
2)古典概型计算任何事件的概率 计算公式为:
15 5
(2)记“取出的鞋不成对”为D , P(D)= 1 - 3 = 4 15 5
例2、函数 f(x)=x2-x-2,x?[5,5] ,几那何概么型任主取要一有体点积x0型, 、使 面f积(x型0)、£长0 的度概型 率等,(解题关键是):找到本题中要
解:用区画到域出A是的函哪几数种何的几度图何量象度占,量的由,几图然何象后度得再量,考当的虑任比子取一
一九八四年,我终于考上长沙一所理工学院,当我把这一消息告诉母亲时,我不知母亲那一刻在想什么,我相信给她的那份震撼绝不亚于惊涛骇浪。她说的第一句话就是要去菩萨面前谢恩,要告慰我亲的在天之灵:“九满上大学了!” 因为我不停的升学,这个小心呵护我的母亲,不得不眼睁睁地看着我离开她,而且越来越远,越来越远……我十五岁以后,回家的时间仅仅是节假日或寒暑假,所谓想家,其实就是渴望母亲给我筹集的学费,回家吃顿饱饭……所以,在我的心中,故乡在慢慢地缩小,而母亲的身影却在不断放大! 大学毕业后,当我告诉母亲:我被分配到广州工作。母亲的神情是复杂的,既有欣慰也有失落,传统的“父母在,不远行”的思想,让她觉得儿子不应离开她,而母爱又使她觉得不应阻碍儿子的前程,母亲的失落只有我才感觉到,我知道,母亲是希望儿子留在故乡的。从我离开故乡到广州工作的时间里,母亲经常因挂念儿子而偷偷地落泪,特别是在她患病的时候,一有人提起我,母亲说话就会哽噫,这是我后来听嫂嫂说才知道的。虽然我离家离得断然绝然,但是,从我参加工作的那年开始,只要一休假,虽然要坐十几个小时人满为患的火车,虽然待在家里的时间只有两天三天,我也会带着疲惫和兴奋匆匆往家赶,因为那里有我的母亲。 参加工作后,母亲才终于结束农村对城市的支援,但这时的她,因为年龄的缘故,已经老态龙钟,走路也要借助拐杖。一九九五年,我把母亲从乡下接到广州,以为故人、故乡可以暂时从母亲的脑海里淡出,专事休养。其实不然,母亲就像一本故乡的活字典,昨天说二姐的身体,今天说五哥的夫妻关系。晚上看电视,明明是粤剧,她却说是湖南花鼓戏。当有晚辈从故乡来到广州,母亲便会急迫地向他打听村子里的情况,当听到一切安好时,脸上就会露出欣慰而放心的笑容;当听到村里有人生病或去世时,母亲的情绪就会非常低落,通常好几天都无法从担心和失落的心情里走出来。 母亲在广州还没住满一年,就匆匆地返回故乡了。每每当她得到我要回乡探亲的消息时,母亲的心情就会突然变得开朗起来,精神也比平日好了许多,整天兴奋地念叨:九满还有几天几天就要回来了。我一回到老人身边,母亲的一切就会以我为中心,看着忙前忙后的哥哥嫂嫂,看着满屋子乱串叫嚷着的侄男侄女,老人就会开心,就会快乐。当我在母亲身边坐下来,她总是拿着我的手,重复地对我说:九满,我没有什么要求,只是希望你多回来看看。所以我每次探亲,都会谢绝一切同学朋友聚会,就是想在母亲的身边多待上一点时间,以此减少母亲心里的挂念,多给自己一些尽孝的机会,来弥补距离的缺憾。 我离开故乡返回广州的那天,天还没亮,我总会听到一个不太清淅的声音,睁眼一看,母亲在为她临行的儿子准备我最喜欢的土产,看到母亲的样子,我真的好难过,作为她的儿子,我什么时候能做到像母亲这样关心她呢?临行时,母亲更是依依不舍,眼里饱含着泪花,一句话也说不出来,她很担心自己再也见不到她的小儿子了,我理解母亲的心情,在母亲面前,我祥装坚强,当我转身离开的那一霎那间,我的泪水便随意如流水!
数学必修3第3章概率章末复习课件人教新课标

)
(2,5 (2,6
)
)
(3,5 (3,6
)
)
(4,5 (4,6
)
)
(5,5 (5,6
)
)
(6,5 (6,6
)P(A)=)1/18
2,从10件产品(其中3件次品)中,一件一件 地不放回地任意取出4件,求4件中恰有一件次 品的概率。
错解: 因为第一次有10种取法,第二次有9种取法 …,由乘法原理可知从10件取4件共有 10×9×8×7种取法,故样本空间S中基本事 件总数有10×9×8×7个。
(4)随机事件:在条件S下可能产生也可能不产 生的事件,叫相对于条件S的随机事件;
(5)频数与频率:在相同的条件S下重复n次实验
,视察某一事件A是否出现,称n次实验中事件A出
现的次数nA为事件A出现的频数;称事件A出现的
比例fn(A)=
n A为事件A出现的概率:对于给定 n
的随机事件A,如果随着实验次数的增加,事件A 产生的频率fn(A)稳定在某个常数上,把这个常数记 作P(A),称为事件A的概率。
设A=“取出4件中恰有一件次品”,则A中含有C31 C73 种取法。
错解: 因为第一次有10种取法,第二次有9种取法…,由乘法 原理可知从10件取4件共有10×9×8×7种取法,故样本 空间S中基本事件总数有10×9×8×7个。
设A=“取出4件中恰有一件次品”,则A中含有C31 C73 种取法。
(1) 实验总所有可能出现的基本事件只有有限个; (2) 每个基本事件出现的可能性相等
我们将具有这两个特点的概率模型称为古典概率 模型,简称古典概率。
对于古典概型,任何事件的概率为: P(A)= A包含的基本事件的个数
基本事件的总数
必修3第三章《概率》复习课

数学
年级
高二
备课组组长
主备人
授课时间
2020年 月 日
单元
(第几单元)第三章总复习
课题
必修3第三章《概率》复习课
教材分析
随机事件的概率,随机现象的产生,频率与概率的关系与区别
课程标准
要求
通过本节课学习使学生掌握必然事件,不可能事件,确定事件,随机事件,频数与频率,概率的六种基本性质,古典概型,几何概型,互斥事件,对立事件等内容。
课前3分钟教育
课前三分钟防疫情及爱国主义教育
课型
复习课
教学目标
1、随机事件的概率;随机现象的发生;频率与概率的区别。
2、利用古典概型与几何概型可以求一些随机事件的概率;随机模拟。
教学重点
应用概率解决实际问题
教学难点
应用概率解决实际问题
教学方法
讲授法,归纳、总结、讨论、交流
学习方法
自主学习,合作学习
教学用具
教材书,课件,班班通,粉笔
课时数
2课时
设计
意图
师生
活动
师生 们共 同讨 论实 例, 提出 自己
的观 点, 老师, 学生进行 讨论。
首先
学生
们对
每一
个实
例提
出自
己的
观点,
然后
在老
师的
引导
下解
决问
题。
首先
学生
们对
每一
个实
例提
出自
己的
观点,
题。
首先第三章的有关内容与定义提问的形式来让学生想起。
(1)频率本身是随机的,在试验前___________确定,做同样次数的重复试验得到事件的频率会不同。
高中数学必修3概率复习
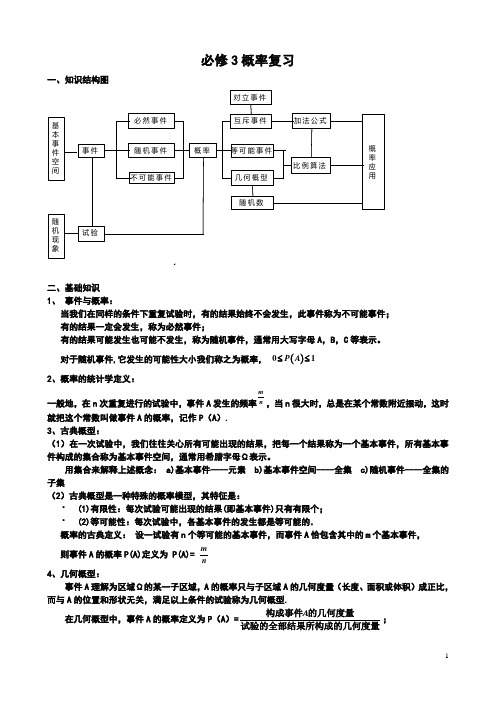
必修3概率复习一、知识结构图二、基础知识1、 事件与概率:当我们在同样的条件下重复试验时,有的结果始终不会发生,此事件称为不可能事件; 有的结果一定会发生,称为必然事件;有的结果可能发生也可能不发生,称为随机事件,通常用大写字母A ,B ,C 等表示。
对于随机事件,它发生的可能性大小我们称之为概率, ()01P A ≤≤ 2、概率的统计学定义:一般地,在n 次重复进行的试验中,事件A发生的频率mn,当n 很大时,总是在某个常数附近摆动,这时就把这个常数叫做事件A 的概率,记作P (A ). 3、古典概型:(1)在一次试验中,我们往往关心所有可能出现的结果,把每一个结果称为一个基本事件,所有基本事件构成的集合称为基本事件空间,通常用希腊字母Ω表示。
用集合来解释上述概念: a)基本事件----元素 b)基本事件空间----全集 c)随机事件----全集的子集(2)古典概型是一种特殊的概率模型,其特征是:• (1)有限性:每次试验可能出现的结果(即基本事件)只有有限个; • (2)等可能性:每次试验中,各基本事件的发生都是等可能的.概率的古典定义: 设一试验有n 个等可能的基本事件,而事件A 恰包含其中的m 个基本事件,则事件A 的概率P(A)定义为 P(A)=m n4、几何概型:事件A 理解为区域Ω的某一子区域,A 的概率只与子区域A 的几何度量(长度、面积或体积)成正比,而与A 的位置和形状无关,满足以上条件的试验称为几何概型.在几何概型中,事件A 的概率定义为P (A )=A 构成事件的几何度量试验的全部结果所构成的几何度量;5、事件的并:由事件A 和B 至少有一个发生(即A 发生,或B 发生,或A 、B 都发生)所构成的事件C ,称为事件A 与B 的并(或和)。
记作C=A B (或C=A+B )。
事件A B 是由事件A 或B 所包含的基本事件所组成的集合。
6、事件的交:把事件A 和B 同时发生所构成的事件D ,称为事件A 与B 的并(或和)。
人教b版数学必修三:第3章《概率》章末复习导学案(含答案)
章末复习课知识概览对点讲练知识点一互斥事件与对立事件互斥事件和对立事件,都是研究怎样从一些较简单的事件的概率的计算来推算较复杂事件的概率.应用互斥事件的概率加法公式解题,备受高考命题者的青睐,应用公式时一定要注意首先确定各个事件是否彼此互斥,然后求出各事件分别发生的概率,再求和.对于较复杂事件的概率,可以转化为求对立事件的概率.例1某公务员去开会,他乘火车、轮船、汽车、飞机去的概率分别为0.3、0.2、0.1、0.4.(1)求他乘火车或乘飞机去的概率;(2)求他不乘轮船去的概率.点评“互斥”和“对立”事件容易搞混.互斥事件是指两事件不可能同时发生.对立事件是指互斥的两事件中必有一个发生.变式迁移1互相输血,小明是B型血,若小明因病需要输血,问:(1)任找一个人,其血可以输给小明的概率是多少?(2)任找一个人,其血不能输给小明的概率是多少?知识点二 古典概型古典概型是一种基本的概型,也是学习其它概型的基础,在高考题中,经常出现此种概型的题目,解题时要紧紧抓住古典概型的两个基本特征,即有限性和等可能性.在应用公式P (A )=mn时,关键是正确理解基本事件与事件A 的关系,求出n 、m .例2 将一颗骰子先后抛掷2次,观察向上的点数,求(1)两次向上的点数之和为7或是4的倍数的概率;(2)以第一次向上的点数为横坐标x ,第二次向上的点数为纵坐标y 的点(x ,y )在圆x 2+y 2=20的内部(不包括边界)的概率.变式迁移2 任取两个一位数,观察结果,问: (1)共有多少种不同的结果?(2)取出的两数之和等于3的结果有多少种? (3)两数的和是3的概率是多少?知识点三 几何概型几何概型同古典概型一样,是概率中最具有代表性的试验概型之一,在高考命题中占有非常重要的位置.我们要理解并掌握几何概型试验的两个基本特征,即每次试验中基本事件的无限性和每个事件发生的等可能性,并能求简单的几何概型试验的概率.例3 甲、乙两船驶向一个不能同时停泊两艘船的码头,它们在一昼夜内到达该码头的时刻是等可能的.如果甲船停泊时间为1 h ,乙船停泊时间为2 h ,求它们中的任意一艘都不需要等待码头空出的概率.(保留小数点后三位)变式迁移3 在圆心角为90°的扇形中,以圆心O 为起点作射线OC ,求使得∠AOC 和∠BOC 都不小于30°的概率.课时作业一、选择题1.从装有2个红球和2个黑球的口袋中任取2个球,那么互斥而不对立的两个事件是( )A .至少有1个黑球与都是黑球B .至少有1个黑球与至少有1个红球C .恰有1个黑球与都是黑球D .至少有1个黑球与都是红球2.一个电路板上装有甲、乙两根熔丝,甲熔断的概率为0.85,乙熔断的概率为0.74,两根同时熔断的概率为0.63,则至少有一根熔断的概率是( )A .0.59B .0.85C .0.96D .0.743.将一个各个面上均涂有颜色的正方体锯成27个同样的大小的小正方体,从中任取一个小正方体,其中恰有3面涂有颜色的概率为( )A.19B.827C.427D.494.在5张卡片上分别写有数字1,2,3,4,5,然后将它们混和,再任意排列成一行,则得到的数能被2或5整除的概率是( )A .0.2B .0.4C .0.6D .0.85.已知实数x 、y ,可以在0<x <2,0<y <2的条件下随机取数,那么取出的数对(x ,y )满足(x -1)2+(y -1)2<1的概率是( )A.π4B.4πC.π2D.π3 二、填空题6.某射击选手射击一次,击中10环、9环、8环的概率分别为0.3、0.4、0.1,则射手射击一次,击中环数小于8的概率是________.7.某市公交车每隔10分钟一班,在车站停1分钟,则乘客等车时间不超过7分钟的概率为________.8.在平面直角坐标系xOy 中,设D 是横坐标与纵坐标的绝对值均不大于2的点构成的区域,E 是到原点的距离不大于1的点构成的区域,向D 中随机投一点,则所投点在E 中的概率是________.三、解答题9.袋中有红、黄、白3种颜色的球各1只,从中每次任取1只,有放回地抽取3次,求: (1)3只全是红球的概率; (2)3只颜色全相同的概率; (3)3只颜色不全相同的概率; (4)3只颜色全不相同的概率.10.在圆x 2+y 2-2x -2y +1=0内随机投点,求点与圆心距离小于13的概率.章末复习课对点讲练例1 解 (1)记“他乘火车去”为事件A 1,“他乘轮船去”为事件A 2,“他乘汽车去”为事件A 3,“他乘飞机去”为事件A 4,这四个事件不可能同时发生,故它们彼此互斥.故P (A 1∪A 4)=P (A 1)+P (A 4)=0.3+0.4=0.7. 所以他乘火车或乘飞机去的概率为0.7.(2)设他不乘轮船去的概率为P ,则P =1-P (A 2) =1-0.2=0.8.变式迁移1 解 (1)对任一人,其血型为A 、B 、AB 、O 型血的事件分别记为A ′、B ′、C ′、D ′,它们是互斥的.由已知,有P (A ′)=0.28,P (B ′)=0.29,P (C ′)=0.08,P (D ′)=0.35.因为B 、O 型血可以输给B 型血的人,故“可以输给B 型血的人”为事件B ′∪D ′.根据互斥事件的加法公式,有P (B ′∪D ′)=P (B ′)+P (D ′)=0.29+0.35=0.64. (2)由于A 、AB 型血不能输给B 型血的人,故“不能输给B 型血的人”为事件A ′∪C ′,且P (A ′∪C ′)=P (A ′)+P (C ′)=0.28+0.08=0.36.答 任找一人,其血可以输给小明的概率为0.64,其血不能输给小明的概率为0.36. 例2 解 (1)第一颗骰子先后抛掷2次,此问题中含有36个等可能的基本事件.记“两数之和为7”为事件A ,则事件A 中含有(1,6),(2,5),(3,4),(4,3),(5,2),(6,1),6个基本事件.∴P (A )=636=16.记“两数之和是4的倍数”为事件B ,则事件B 中含有(1,3),(2,2),(3,1),(2,6),(3,5),(4,4),(5,3),(6,2),(6,6),9个基本事件,∴P (B )=936=14.∵事件A 与事件B 是互斥事件,∴所求概率为P (A )+P (B )=512.(2)记“点(x ,y )在圆x 2+y 2=20的内部”为事件C ,则事件C 中共含有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),(4,1),11个基本事件,∴P (C )=1136.变式迁移2 解 (1)因为每次取出的数是0,1,2,…,9这十个数字中的一个,从而每次取数都有10种可能,所以两次取数共有等可能的结果总数为n =10×10=100(种).(2)记“两个数的和等于3”为事件A ,则事件A 的可能取法有第一次取的数分别为0,1,2,3,相应的第二次取的数分别为3,2,1,0,即事件A 包含4种结果.(3)事件A 的概率是P (A )=4100=0.04.例3 解 要使两船都不需要等待码头空出,当且仅当甲比乙早到达1 h 以上或乙比甲早到达2 h 以上,即y -x ≥1或x -y ≥2,设A 为“两船都不需要等待码头空出”,则A ={(x ,y )|y -x ≥1或x -y ≥2,x ∈[0,24],y ∈[0,24]}.A 为右图中阴影部分,Ω为边长是24的正方形,由几何概型定义知, 所求概率为P (A ) =A 的面积Ω的面积=(24-1)2×12+(24-2)2×12242=506.5576≈0.879. 变式迁移3 解 如图所示,设事件A 是“作射线OC ,使∠AOC 和∠BOC 都不小于30°”,μA =90°-30°-30°=30°,μΩ=90°,由几何概型的计算公式,得P (A )=μA μΩ=30°90°=13.故所求“使得∠AOC 和∠BOC 都不小于30°”的概率是13.课时作业1.C [结合互斥事件和对立事件的定义知,对于C 中恰有1个黑球,即1黑1红,与都是黑球是互斥事件.但不是对立事件,因为还有2个都是红球的情况,故应选C.]2.C 3.B4.C [最后一位数有5种结果,而能被2或5整除的有3种.] 5.A 6.0.2解析 P =1-0.3-0.4-0.1=0.2. 7.45 8.π169.解 (1)记“3只全是红球”为事件A .从袋中有放回地抽取3次,每次取1只,共会出现3×3×3=27种等可能的结果,其中3只全是红球的结果只有一种,故事件A 的概率为P (A )=127.(2)“3只颜色全相同”只可能是这样三种情况:“3只全是红球”(设为事件A ),“3只全是黄球”(设为事件B ),“3只全是白球”(设为事件C ),且它们之间是互斥关系,故“3只颜色全相同”这个事件可记为A ∪B ∪C .由于事件A 、B 、C 不可能同时发生,因此它们是互斥事件;再由于红、黄、白球个数一样,故不难得到P (B )=P (C )=P (A )=127,故P (A ∪B ∪C )=P (A )+P (B )+P (C )=19.(3)3只颜色不全相同的情况较多,如有两只球同色而另一只球不同色,可以两只同红色或同黄色或同白色;或三只球颜色全不相同,这些情况一一考虑起来比较麻烦.现在记“3只颜色不全相同”为事件D ,则事件D 为“3只颜色全相同”,显然事件D 与D 是对立事件.∴P (D )=1-P (D )=1-19=89.(4)要使3只颜色全不相同,只可能是红、黄、白各一只,要分三次抽取,故3次抽到红、黄、白各一只的可能结果有3×2×1=6种,故3只颜色全不相同的概率为627=29.10.解 圆x 2+y 2-2x -2y +1=0可化为(x -1)2+(y -1)2=1,则圆的圆心C (1,1),半径r =1,点与圆心距离小于13的区域是以C (1,1)为圆心,以13为半径的圆内部分.故点与圆心距离小于13的概率为P =π⎝⎛⎭⎫132π·12=19.。
高一数学必修三概率复习总结PPT课件
的区域长度 2 1 3,全部结果构成的区
域长度是 5
5
10 ,则
P A 3
1140
1、从装有2个红球和2个黑球的袋子
中任取2个球,那么互斥而不对立的
事件是( C ) A.至少有一个黑球与都是黑球
计算公式为:
P(A)=
A所包含的基本事件的个数 基本事件的总数
7
几何概型
1)几何概型的特点:
(1)试验中所有可能出现的结果(基本事件) 有无限多个. (2)每个基本事件出现的可能性相等.
2)在几何概型中,事件A的概率 的计算公式如下:
P(A)
构 成 事 件 A 的 区 域 长 度(面 积 或 体 积) 试 验 的 全 部 结 果 所 构 成的 区 域 长 度( 面 积 或 体 积 )
6、在长为10cm的线段AB上任取一点,并以 线段AP为一边作正方形,这个正方形的面
积介于25 cm2与 49 cm2 之间的概率为__1_/_5_
17
例3.甲、乙二人约定在 12 点到 5 点之间在某地会面,先到者 等一个小时后即离去设二人在 这段时间内的各时刻到达是等 可能的,且二人互不影响。求 二人能会面的概率。
B.至少有一个黑球与至少有一个红球
C.恰有一个黑中有10个铁钉,其中8个是 合格的,2个是不合格的,从中 任取两个恰好都是不合格的概率 是_1__/4_5____
3、在一个袋子中装有分别标注数
字1,2,3,4,5的五个小球,
现从中随机取出2个小球,则取出
,几那何概么型任主取要一有体点积x0型,、使面f积(x型0 )、£长0 的度概型 率等,(解题关键是):找到本题中要
北师大版数学必修三第3章概率章末归纳总结课件
每批邮箱数
60 130 265 306 1 233 2 130 4 700 6 897
名称里有数字的邮箱数 36 78 165 187 728 1 300 2 820 4 131
频率
(1)填写上表中的频率(精确到0.01); (2)中国人的邮箱名称里使用数字的概率是多少?
[解析] (1)由频率公式可算出,表格中应填的频率从左到右依次为:0.60、 0.60、0.62、0.61、0.59、0.61、0.60、0.60.
2
『规律总结』 一般地,若一个随机事件需要用两个连续变量[如本例中的 (x,y)]来描述,用这两个变量的有序实数对来表示它的基本事件,利用坐标平 面能顺利地建立与面积有关的几何概型.
〔跟踪练习 3〕 如图,M 是半径为 R 的圆周上一个定点,在圆周上等可能 1
地任取一点 N,连接 MN,则弦 MN 的长度超过 2R 的概率是__2____.
将长为l的木棒随机折成3段,求3段长度能构成三角形的概率. [思路分析] 构成三角形要用三边长的度量,设出两边,再表示第三边. [解析] 如图所示,设A=“3段长度能构成三角形”,x,y分别表示其中两 段的长度,则第3段的长度为l-x-y.
高中数学必修3概率章末复习
题型研修
章末复习
题型二 互斥事件与对立事件 1.互斥事件与对立事件的概念的理解
(1)互斥事件是不可能同时发生的两个事件;对立事件 除要求这两个事件不同时发生外,还要求二者必须有 一个发生.因此对立事件一定是互斥事件,但互斥事 件不一定是对立事件,对立事件是互斥事件的特殊情 况. (2)利用集合的观点来看,如果事件A∩B=∅,那么两 事件是互斥的,此时A∪B的概率就可用加法公式来 求,即为P(A∪B)=P(A)+P(B);如果事件A∩B≠∅, 那么可考虑利用古典概型的定义来解决,不能直接利
题型一 随机事件的概率 1.有关事件的概念
(1)必然事件:我们把在条件S下,一定会发生的事 件,叫做相对于条件S的必然事件,简称必然事件. (2)不可能事件:在条件S下,一定不会发生的事件, 叫做相对于条件S的不可能事件,简称不可能事件. (3)确定事件:必然事件与不可能事件统称为相对于条 件S确实定事件,简称确定事件.
知识网络 要点归纳 题型研修
题型研修
章末复习
例2 现有8名2021伦敦奥运会志愿者,其中志愿者A1,A2, A3通晓日语,B1,B2,B3通晓俄语,C1,C2通晓韩语,从 中选出通晓日语、俄语和韩语的志愿者各1名,组成一个 小组. (1)求A1被选中的概率; (2)求B1和C1不全被选中的概率.
知识网络 要点归纳 题型研修
S
446345453 5
知识网络 要点归纳 题型研修
题型研修
章末复习
其中 S≤4 的有 A1,A2,A4,A5,A7,A9,共 6 件,故该样本 的一等品率为160=0.6,从而可估计该批产品的一等品率为 0.6. (2)①在该样本的一等品中,随机抽取2件产品的所有可能结果 为{A1,A2},{A1,A4},{A1,A5},{A1,A7},{A1,A9}, {A2,A4},{A2,A5},{A2,A7},{A2,A9},{A4,A5},{A4, A7},{A4,A9},{A5,A7},{A5,A9},{A7,A9},共15种.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
古典概型与几何概型练习题
1.一个袋中装有5件正品1件次品. 从中随机取出两件,则取出的两件产品中既有正品又有次品的概率是( )
A .1
B .
21 C .31 D .3
2
2.设点),(q p ,其中3||≤p ,3||≤q ,则方程01222=+-+q px x 有两根的概率为 ( )
A .
36π B .36
1π- C .81π D .811π
-
3.一个袋中装有2个红球和2个白球,现从袋中取出1球,然后放回袋中再取出一球,则取出的两个球同色的概率是 ( ) A .
21 B .31 C .41 D .5
2
4.现有五个球分别记为A ,C ,J ,K ,S ,随机放进三个盒子,每个盒子只能放一个球,则K 或S 在盒中的概率是( ) A .
101 B .35 C .310 D .910
5.平面上有一组平行线,且相邻平行线间的距离为3 cm ,把一枚半径为1 cm 的硬币任意平掷在这个平面上,则硬币不与任何一条平行线相碰的概率是( )
A.14
B.13
C.12
D.23
6.把一颗骰子投掷两次,观察出现的点数,并记第一次出现的点数为a ,第二次出现的点数为b ,向量 m =(a ,b),n =(1,2),则向量m 与向量n 不共线的概率是( )
A .16
B .1112
C .112
D .118
7.如图所示,墙上挂有一边长为a 的正方形木板,它的四个角的空白部分都是以正方形 的顶点为圆心,半径为
2
a
的扇形,某人向此板投镖,假设每次都能击中木板,且击中 木板上每个点的可能性都一样,则他击中阴影部分的概率是 A .14π-
B .4π
C .18
π
- D .与a 的取值有关 8.从1,2,3,4,5这五个数中,不放回地任取两数,则两数都是奇数的概率是( ) A.
52 B.103 C.254 D.25
9 9. 在长为10 cm 的线段AB 上任取一点P ,并以线段AP 为边作正方形,这个正方形的面积介于25 cm 2与49 cm 2之间的概率为( ) A.103 B.5
1 C.
5
2
D.
5
4 10. 从一个不透明的口袋中摸出红球的概率为
1
5
,已知袋中红球有3个,则袋中共有除颜色外完全相同的球的个数为 ( )
A. 5
B. 8
C. 10
D.15
11.在10枝铅笔中,有8枝正品和2枝次品,从中不放回地任取2枝,至少取到1枝次品的概率是( )
A .29
B .1645
C .1745
D .25
12.一个袋子里装有编号为1,2,…,12的12个相同大小的小球,其中1到6号球是红色球,其余为黑色球.若从中任意摸出一个球,记录它的颜色和号码后再放回袋子里,然后再摸出一个球,记录它的颜色和号码,则两次摸出的球都是红球,且至少有一个球的号码是偶数的概率是( )
A .116
B .316
C .14
D .716
13.有100件产品,其中有5件次品,从中有放回地连抽两次,则第二次才抽到合格品的概率为( )
A .
1920
B .
19
200
C .
19
400
D .
29400
14.在100箱同种食品中,有20箱已过期,从中任取两箱,则取到的两箱均已过期的概率等于( )
A .
1
5
B .
110
C .
19
505
D .
19
495
15.在面积为S 的△ABC 的边AB 上任取一点P ,则△PBC 的面积不小于3
S
的概率是( )
A .
3
2 B .
13 C .4
3 D .
4
1
16.某校36名高级教师的血型分别是:A 型12人,B 型10人,AB 型8人,O 型6人,若从中随机选出2人,则恰好血型相同的概率为( ) A .
118
B .
1145
C .
145
D .
1118
17. 若过直角三角形ABC 的直角顶点A 任作一条直线l ,则l 与斜边BC 相交的概率为( ) A .
21 B .31
C .41
D .6
1 18.设M 是半径为R 的圆周上一定点, 在圆周上等可能地任取一点N, 连接MN,则弦MN 的长超过2R 的概率为( ) A .
51 B .41 C .31 D .2
1 19. 甲从正方形四个顶点中任意选择两个顶点连成直线,乙从该正方形四个顶点中任意选择两个顶点连成直线,则所得的两条直线相互垂直的概率是( ) A .
318 B .418 C .518 D .618 20.从标有1,2,3,4,5,6,7,8,9的9张纸片中任取2张,那么这2 张纸片数字之积为偶数的概率为( ) A.
12 B. 718 C. 1318 D. 1118
20.如图,在半径为R 的圆内随机撒一粒黄豆,它落在阴影部分内接正三角形上的概率是( )
A D
21. 在区间[0,π]上随机取一个数x ,则事件“sin 1x x ≤”发生的概率为( )
A .
14 B .13 C .12 D .23 22.抛掷红、蓝两颗骰子,若已知蓝骰子的点数为3或6时,则两颗骰子点数之和大于8的概率为( )
A .
13 B .12 C .536
D .512 23.有四所大学进行自主招生,同时向一所高中的已获省级竞赛一等奖的甲、乙、丙、丁4位学生发出录取通
知书.若这4名学生都愿意进这四所大学的任意一所就读,则仅有2名学生被录取到同一所大学的概率为( ) A .
12 B .916 C .1116
D .
7
24
二、填空题:
1.连续掷两次骰子,记第1次出现的点数为X ,第2次出现的点数为Y ,则满足1log 2=Y X 的概率为________. 2.在区间[0,2]内任取两个数a ,b ,那么函数f(x)=x 2+ax +b 2无零点的概率为_______. 3.一栋楼房有4个单元, 甲,乙两人住在此楼内 ,则甲,乙两人同住一单元的概率为____ ____
4.已知函数c bx x x f ++=2)(,其中40,40≤≤≤≤c b ,记函数)(x f 满足条件⎩⎨⎧≤-≤4
)2(12
)2(f f 为事件A ,则
事件A 发生的概率为___ _____
5.在一个袋子中装有分别标注数字1,2,3,4,5,的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为3或6的概率是__________
6.在区间(0,1)中随机地取出两个数,则两数之和大于
2
3
的概率是__________
7.如图,半径为10 cm 的圆形纸板内有一个相同圆心的半径为1 cm 的小圆.现将半径为1 cm 的一枚硬币抛到此纸板上,使硬币整体随机平落在纸板内(硬币不出纸板边界),则硬币落下后与小圆无公共点的概率为 . 三、解答题:
1. 有编号为1210,,A A A 的10个零件,测量其直径(单位:cm ),得到下面数据:
其中直径在区间[1.48,1.52]内的零件为一等品。
(1)从上述10个零件中,随机抽取一个,求这个零件为一等品的概率; (2)从一等品零件中,随机抽取2个.
(ⅰ)用零件的编号列出所有可能的抽取结果;(ⅱ)求这2个零件直径相等的概率.
2.将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为x ,第二次出现的点数为y .
(1)求事件“3x y +≤”的概率;(2)求事件“2x y -=”的概率.
3.一个口袋内装有大小相同的6个小球,其中2个红球,记为A 1、A2,4个黑球,记为B1、B2、B3、B4,从中一次摸出2个球.(Ⅰ)写出所有的基本事件;(Ⅱ)求摸出的两个球颜色不同的概率.
4.已知函数22()2,,.f x x ax b a b R =-+∈ (1)若a 是从集合{}0,1,2,3中任取的一个元素,b 是从集合{}0,1,2中任取的一个元素,求方程()0f x =有两个不相等实数根的概率1P ; (2)若a 是从区间[]0,2任取的一个数,b 是从区间[]0,3中任取的一个数,求方程()0f x =没有实数根的概率2P .
5.某校从参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[)50,40,
[)60,50…[]100,90后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: (Ⅰ)求分数在[)70,80内的频率,并补全这个频率分布直方图;
(Ⅱ)用分层抽样的方法在分数段为[)80,60的学生中抽取一个容量为
6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分
数段[)80,70的概率.
6.从0,1,2,3,4五个数字中,任意有放回地连续抽取三个数字,组成一个三位数
(I )求这个三位数各个数位上的数字完全不同的概率 (II )求这个三位数各个数位上的数字都不含3的概率; (III )求这个三位数各个数位上的数字中3恰好出现1次的概率。
7.2009年世界邮展在我市举行,邮展期间需从7名志愿者中选出会英语、俄语和日语的志愿者各一名组成一服务小组,已知这7名志愿者中1A 、2A 、3A 、4A 会英语,1B 、2B 会俄语,只有C 会日语 (1)求1B 被选中的概率;(2)求1B 和1A 不全被选中的概率。
8.已知,060.2,5AOB OA OB ∠=== 在线段OB 上任取一点C ;求AOC ∆为钝角三角形的概率:。
