第2章作业解答
第2章 递归与分治_作业答案讲解

具体执行过程:求最大值
0 1 2 3 4 5 6 7 8 9 10 11 12 13 24 -13 29 113 87 65 -9 36 14 76 44 83 67 5 0 1 2 3 4 5 6 24 -13 29 113 87 65 -9 0 1 2 3 24 -13 29 113 0 1 24 -13 2 3 29 113 4 5 6 87 65 -9 7 8 9 10 11 12 13 36 14 76 44 83 67 5 7 8 9 10 36 14 76 44 7 8 36 14 7 36 9 10 76 44 11 12 13 83 67 5 11 12 83 67 11 83 12 67 13 5
课后练习
• 练习2:分析如下时间函数的复杂度,并说明 原因。 1. 利用递归树说明以下时间函数的复杂度:
O(1) T ( n) 3T ( n ) O( n) 4 n1 n1
2. 利用主定理说明以下时间函数的复杂度:
T(n) = 16T(n/4) + n
T(n) = T(3n/7) + 1
课后练习
• 练习1:给定数组a[0:n-1], 1. 试设计一个分治法算法,找出a[0:n-1]中元素最 大值和最小值; 2. 写出该算法时间函数T(n)的递推关系式; 3. 分析该算法的时间复杂度和空间复杂度。
0 1 2 3 4 5 6 7 8 9 10 11 12 13 24 -13 29 113 87 65 -9 36 14 76 44 83 67 5
• 递归公式:
– 设n个元素的集合可以划分为F(n,m)个不同的由 m个非空子集组成的集合。 F(n,m) = 1, when n=0, n=m, n=1, or m=1 F(n,m) = 0, when n<m 否则 F(n,m)=F(n-1,m-1)+m*F(n-1,m)
第2章_作业 (1)

第二章作业一、单项选择题1、通常以( C )代表时间价值率。
A、通货膨胀补偿率B、风险报酬率C、利息率D、投资利润率2、财务管理的两个基本价值观念是( A )A、时间价值和风险收益B、利润和成本C、风险和利润D、时间价值和成本3、在存本付息的情况下,若想每年都得到利息1000,利率为5%,则现在应存入的本金应为( A )元。
(永续年金的计算问题)A、20000B、50000C、500000D、2000004、一定时期内连续发生在期末的等额支付款项,被称为( B )A、先付年金B、普通年金C、永续年金D、延期年金5、下面有关资金时间价值的表述,正确的是( A )A.资金时间价值的实质是资金周转使用后的增值额B.资金时间价值是推迟消费所获得的报酬C.资金时间价值只能用绝对数来表示D.资金时间价值的量无法进行计量(选择A,严格将来,时间价值是资金周转增值额的一部分,但是因为题目中没有使用“全部”的字样,可以理解为正确;B推迟消费获得的报酬不一定能获得报酬,比如资金不周转的情形。
)6、一项借款,期限一年,年利率8%,按复利计算每半年复利一次,则借款实际利率为( D )A、0.16%B、12.49%C、18.53%D、8.16%(已知名义利率求实际利率的情形)7、永续年金具有下列特征( C )A、每期期初支付B、每期不等额支付C、没有终值D、没有现值8、资金时间价值实质是( B )。
A、资金的自然增值B、资金周转使用后的增值C、不同时间的价值量D、对暂缓消费的报酬9、为在第三年末获得本利和100元,求每年末存入多少资金,计算时应采用(B)。
A、年金现值系数B、年金终值系数C、复利现值系数D、复利终值系数(100元是终值,所以用终值系数计算)10.每年年底存款100元,求第5年末的价值,可用( D )来计算.(终值计算问题)A.PVIF i,n B.FVIF i,n C. PVIFA i,n D.FVIFA i,n11、当利率为10%,计息期为5时,后付年金现值系数为3.791;计息期为6时,后付年金现值系数为4.355,那么利率为10%。
第2章作业-2 参考答案

二、综合题
1. 若X=-0.1110,Y=-0.1101,采用原码一位乘法运算求 X·Y=? 给出计算过程。
2.若X=-0.1101,Y=-0.1011 试利用补码Booth算法(比较 法)求X·Y=? 给出计算过程。
3. 将十进制数+76.75存入某微机中,试写出其IEEE754标准规 格化单精度浮点数形式。
第2章作业-2 参考答案
一、单项选择题: 1、两个浮点数相加,一个数的阶码值为7 ,另一个数的阶码值为9 ,则需要将阶码
值较小的浮点数的小数点( )。 A .左移1 位 B .右移1 位 C .左移2 位 D .右移2 位29 .
答案: C
2、如果某单精度浮点数、某原码、某补码、某移码的32位机器数均为 OxF0000000 。这些数从大到小的顺序是()。 A .浮原补移 B .浮移补原 C .移原补浮 D . 移补原浮 答案: D
说明
初始值,最后一位补0 Y4Y5=10 +[-X]补
右移一位 Y3Y4=01
+[X]补
右移一位 Y2Y3=10
+[-X]补
右移一位 Y1Y2=01
+[X]补
右移一位 Y0Y1=10 不移位
+[-X]补
3. 解:76.75 = 1001100.11 = 1.00110011 ×26 指数E = 7 + 127 = 133 = 1000 0101B 127是单精度浮点数应加的指数偏移量。
4. 某微机内存有一个单精度规格化浮点数(IEEE754标准)为 C2308000H,试写出其真值。
计算机组成原理
1. 解: X=-0.1110,Y=-0.1101 ,X*=0.1110,Y*=0.1101。 其中寄存器 B=X* ,计数器Cd=4。计算过程:
第2章拉压作业参考解答

aEADj + 4.5aEADj = 2aF , Dj = 2F 5.5EA
4. 再由 Hooke 定律:
FN1
=
EADj
=
2F 5.5
=
0.3636F
FN 2
= 1.5EADj
=
1.5´ 2F 5.5
2
(1)图(a)为开槽拉杆,两端受力 F=14kN,b=20mm,b0=10mm,δ=4mm。 (2)图(b)为阶梯形杆,AB 段杆横截面面积为 80mm2,BC 段杆横截面面积为 20mm2, CD 段杆横截面面积为 120mm2。 (3)图(c)为变截面拉杆,上段 AB 的横截面面积为 40mm2,下段 BC 的横截面面积为
DG
=
Dl2
-
2 3
Dl1
-
1 3
Dl3=6.89 ´10-4
m
5
2-15 求附图示圆锥形杆在轴向力 F 作用下的伸长量。弹性模量为 E。
解答 对于截面缓变的圆锥形杆可假设横截面上正应力均匀分布。横截面面积为
A(x)
=
1 4
p [d1l
-
(d1
-
d2 )x]2
/l2
ò ò ò Dl =
l
edx =
FN1
FN3
FN2
D
(2)
(b) 整体分析,示力图见附图(3)。
å M Ai = 0 : FN1 ´1 + 3´ 3´1.5 = 0
FN1 = -13.5kN
FAx A
FAy FN1
B
s1
=
FN 1 A1
=
-13.5 ´103 850 ´10-6
=
-15.88MPa
操作系统 第二章作业本(含答案)

第二章作业第一次作业:1.进程有哪三种基本状态?进程在三种基本状态之间转换的典型原因是什么?答:三种基本状态:就绪状态、执行状态、阻塞状态。
(1)就绪状态→执行状态:进程分配到CPU资源(进程调度);(2)执行状态→就绪状态:时间片用完(3)执行状态→阻塞状态:I/O请求(4)阻塞状态→就绪状态:I/O完成2.在Linux系统中运行下面程序,最多可产生多少个进程?画出进程家族树。
main(){fork();fork();fork();}答:最多可以产生7个进程。
其家族树为:3.试从动态性、并发性和独立性上比较进程和程序。
答:1)动态性是进程最基本的特性,可表现为由创建而产生,由调度而执行,因得不到资源而暂停执行,以及由撤销而消亡,因而进程由一定的生命期;而程序只是一组有序指令的集合,并存放于某种介质上,其本身并不具有运动的含义,因而是静态的;2)并发性是进程的重要特征,同时也是OS的重要特征。
引入进程的目的正是为了使其程序能和其它建立了进程的程序并发执行,而程序本身(没有建立PCB)是不能并发执行的;3)独立性是指进程实体是一个能独立运行、独立分配资源和独立接受调度的基本单位。
凡未建立PCB的程序,都不能作为一个独立的单位来运行。
4.分析下列代码的功能:答:sleep_on实现进程的睡眠过程;wake_up实现进程的唤醒过程。
第二次作业:1.同步机制应该遵循哪些基本准则?你认为整型信号量机制遵循了同步机制的哪些基本准则?答:同步机制应遵循四个基本准则:a. 空闲让进:当无进程处于临界区时,应允许一个请求进入临界区的进程立即进入自己的临界区,以有效地利用临界资源。
b. 忙则等待:当已有进程进入临界区时,其它试图进入临界区的进程必须等待,以保证对临界资源的互斥访问。
c. 有限等待:对要求访问临界资源的进程,应保证在有限时间内能进入自己的临界区,以免陷入“死等”状态。
d. 让权等待:当进程不能进入自己的临界区时,应立即释放处理机,以免进程陷入“忙等”状态。
第二章作业 参考答案
第二章作业2、画前驱图4、程序并发执行时为什么会失去封闭性和可再现性?答:程序在并发执行时,是多个程序共享系统中的各种资源,因而这些资源的状态将由多个程序分别来改变,致使程序的运行换去了封闭性,这样,某程序在执行时,必然会受到其它程序的影响。
程序在并发执行时,由于失去了封闭性,也将导致其再失去可再现性。
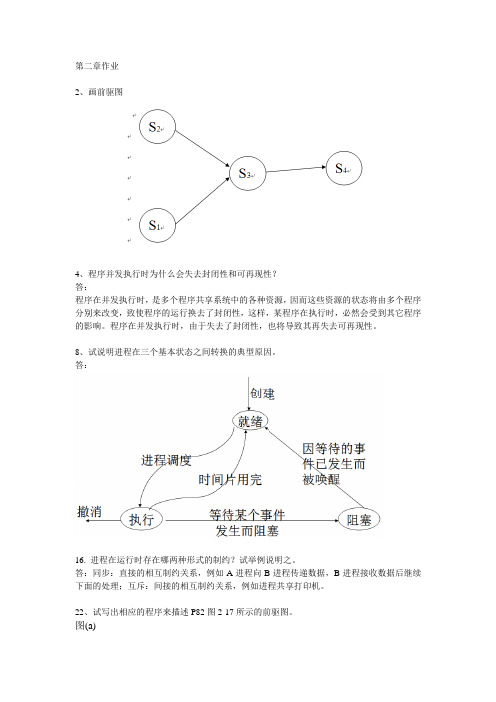
8、试说明进程在三个基本状态之间转换的典型原因。
答:16. 进程在运行时存在哪两种形式的制约?试举例说明之。
答:同步:直接的相互制约关系,例如A进程向B进程传递数据,B进程接收数据后继续下面的处理;互斥:间接的相互制约关系,例如进程共享打印机。
22、试写出相应的程序来描述P82图2-17所示的前驱图。
图(a)int a1=0,a2=0,a3=0,a4=0,a5=0,a6=0;a7=0;a8=0;parbeginbegin S1;V(a1);V(a2);end;begin P(a1);S2;V(a3);V(a4);end;begin P(a2);S3;V(a5);end;begin P(a3);S4;V(a6);end;begin P(a4);S5;V(a7);end;begin P(a5);S6;V(a8);end;begin P(a6);P(a7);P(a8);S7;end;parend图(b)int a1=0,a2=0,a3=0,a4=0,a5=0,a6=0;a7=0;a8=0;a9=0;a10=0;parbeginbegin S1;V(a1);V(a2);end;begin P(a1);S2;V(a3);V(a4);end;begin P(a2);S3;V(a5);V(a6);end;begin P(a3);S4;V(a7);end;begin P(a4);S5;V(a8);end;begin P(a5);S6;V(a9);end;begin P(a6);S7;V(a10);end;begin P(a7);P(a8);P(a9);P(a10);S8;end;parend28、在测量控制系统中的数据采集任务,把所采集的数据送一单缓冲区;计算任务从该单缓冲中取出数据进行计算。
第2章作业参考答案
2. 一批晶体管中有个 9 个合格品和 3 个不合格品,从中任取一个安装在电子设备上。若取 出不合格品不再放回,求取得合格品前已取出的不合格品个数的分布律和分布函数。 解:
X0 1 2
3
p 3/4 9/44 9/220 1/220
⎧ 0,
x<0
F (x) = ⎪⎪⎪⎨321/ 4/ ,22,
0≤ x <1 1≤ x < 2
求: (1) 系数 A,B; (2) X 落在区间(-1,1)的概率; (3) X 的概率密度。 解:
x∈R
7. 从一批子弹中任意抽出 5 发试射,若没有一发子弹落在靶心 2 厘米以外,则接受该批子 弹。设弹着点与靶心的距离 X(厘米)的概率密度为
f
(
x)
=
⎪⎧ ⎨
Axe−
x2
,
⎪⎩ 0,
0< x<3 其他
X
~
B
⎛ ⎜⎝
4,
1 5
⎞ ⎟⎠
, 故分布律为
P( X = k) = C4k (0.2)k (0.8)4−k , k = 0,1, 2, 3, 4
( ) (2)P X = k
=
C5k
*
C 4− 20
k
C245
k = 0,1,2,3,4
5. 临床观察表明,某药物产生副作用的概率为 0.002。现在 900 个患者服用该药物,求至 少有3例患者出现副作用的概率.
试求:(1)系数 批子弹被接受的概率。 解:
⎧ 0,
x<0
∫ ∫ (2) F(x) =
x −∞
f
(t)dt
=
⎪⎪ ⎨ ⎪
x2 0 1 − e−9
第二章作业题解答
第二章静电场习题解答2-1.已知半径为F = Cl的导体球面上分布着面电荷密度为A = p s0 cos的电荷,式中的炖0为常数,试计算球面上的总电荷量。
解取球坐标系,球心位于原点中心,如图所示。
由球面积分,得到2用打Q =护= J j p50cos OrsmOd Od(p(S) 0 0In x=j j psQSefsinGded00 0In n=PsF j J cos ageded(p0 0丸=sin20d0 = 0o2-2.两个无限人平面相距为d,分别均匀分布着等面电荷密度的异性电荷,求两平面外及两平面间的电场强度。
解对于单一均匀带电无限人平面,根据对称性分析,计算可得上半空间和卞半空间的电场为常矢量,且大小相等方向相反。
由高斯定理,可得电场大小为E = ^-2e0对于两个相距为的d无限大均匀带电平面,同样可以得到E] = E“耳=E3题2-2图因此,有2-3.两点电荷q、= 8C和q2 = -4C ,分别位于z = 4和),=4处,求点P(4,0,0)处的电场强度。
解根据点电荷电场强度叠加原理,P点的电场强度矢量为点Si和Si处点电荷在P处产生的电场强度的矢量和,即E r = Qi 弘 | ① R?4T V£0/?/ 4TT£0R] = r — r L = 4e v — 4e., R 、= J 4-0 " + 0-4 ~ = 4>/2 R 2 =r —r 2 =4e v -4e v , R 2 = J 4-0 ' + 0-4 ' = 4>/22-7. 一个点电荷+q 位于(-a, 0,0)处,另一点电荷-2q 位于(a,0,0)处,求电位等于零的 面;空间有电场强度等于零的点吗?解根据点电荷电位叠加原理,有々)=丄]鱼+鱼4矶丄忌」式中Rj =r-r L = x-\-a e v + ye v +e. R i = yl x + a 2 + r+^2 R 2 =r-r 2 = x ~a e v + ),e y+e r R? — yj x — ci + )r +代入得到式中代入得到心孟 _______ 1^x + a)2+ y 2+ z 22JaS+b+z 2(3x+d )(x+3a ) + 3),+3z ,=0根据电位与电场强度的关系,有电位为零,即令简化可得零电位面方程为要是电场强度为零,必有E x = 0, E y = 0, E : = 0一 (x+ d)[(x + d)2 + y 2 + ^2p + 2(—d)[(—d)2+ y 2 + 疋 -)^(x+n)2 + y 2 + z 2 2 +2y^(x-a)2 + y 2+ z 2丄-z[(x + d)2 + + 疋 2+2z[(x-d)2 +)*此方程组无解,因此,空间没有电场强度为零的点。
第二章课后作业答案
第二章线性表习题(答案)1.描述以下三个概念的区别:头指针,头结点,首元素结点。
首元结点是指链表中存储线性表中第一个数据元素a1的结点。
为了操作方便,通常在链表的首元结点之前附设一个结点,称为头结点,该结点的数据域中不存储线性表的数据元素,其作用是为了对链表进行操作时,可以对空表、非空表的情况以及对首元结点进行统一处理。
头指针是指向链表中第一个结点(或为头结点或为首元结点)的指针。
若链表中附设头结点,则不管线性表是否为空表,头指针均不为空。
否则表示空表的链表的头指针为空。
2.填空:(1)在顺序表中插入或删除一个元素,需要平均移动一半元素,具体移动的元素个数与插入或删除的位置有关。
(2)在顺序表中,逻辑上相邻的元素,其物理位置也相邻。
在单链表中,逻辑上相邻的元素,其物理位置不一定相邻。
(3)在带头结点的非空单链表中,头结点的存储位置由头指针指示,首元素结点的存储位置由头结点的next域指示,除首元素结点外,其它任一元素结点的存储位置由其直接前趋的next域指示。
3.已知L是无表头结点的单链表,且P结点既不是首元素结点,也不是尾元素结点。
按要求从下列语句中选择合适的语句序列。
a. 在P结点后插入S结点的语句序列是:(4)、(1)。
b. 在P结点前插入S结点的语句序列是:(7)、(11)、(8)、(4)、(1)。
c. 在表首插入S结点的语句序列是:(5)、(12)。
d. 在表尾插入S结点的语句序列是:(11)、(9)、(1)、(6)。
供选择的语句有:(1)P->next=S; (2)P->next= P->next->next; (3)P->next= S->next;(4)S->next= P->next; (5)S->next= L; (6)S->next= NULL;(7)Q= P; (8)while(P->next!=Q) P=P->next;(9)while(P->next!=NULL) P=P->next; (10)P= Q;(11)P= L; (12)L= S; (13)L= P;4.设线性表存于a[n]中且递增有序。
最新大连理工大学-机械设计基础-作业解答:第2章-平面四杆机构
连杆BC= (AC1+AC2)/2 = (34+82)/2 =58mm 。
2-10 设计加热炉门启闭的四杆机构:已知炉门上两活动铰链的 中心距为 50mm ,炉门打开成水平位置时,炉门温度较低的一 面朝上(如虚线所示)。固定铰链安装在 y-y 轴线上。
给定连杆位置设计四杆机构 例题课本图2-29
量取AD=96 mm, AB=68 mm, CD=112 mm。
结束语
谢谢大家聆听!!!
9
பைடு நூலகம்
(d) 50+100=150<100+90=190,以最短杆的对边作机架,因此是双摇 杆机构。
2-3 画出各机构的传动角和压力角。图中标注箭头的构件为 原动机。
压力角:作用在从动件上的力与作用点绝对速度直接所夹的锐角
解(1)由行程速度变化系数公式 代入数据 摇杆空回行程
(2)曲柄回转一周时间t 转速n为
解:(1)由题可知,CD在水平位置上下摆动10°是摇 杆机构的两个极限位置,由此可知
2-7 设计曲柄滑块机构:已知滑块的行程 s=50mm , 偏距 e=16mm ,行程速度变化系数 K=1.2 ,求曲柄 和连杆的长度。给定行程速度变化系数设计四杆机构 例题课本图2-27
量取AC1=34 mm,AC2=82 mm。
作用在从动件上的力与作用点绝对速度直接所夹的锐角解1由行程速度变化系数公式2曲柄回转一周时间t代入数据摇杆空回行程转速n为解
大连理工大学-机械设计基 础-作业解答:第2章-平面
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.3 试用下列各种方法计算水蒸气在10.3MPa 和643K 下的摩尔体积,并与水蒸气表查出的数据(3-10.0232m kg V =⋅)进行比较。
已知水的临界常数与偏心因子为c 647.3K T =,22.05MPa C p =,0.344ω=。
(1)理想气体方程;(2)RK 方程;(3)普遍化关系式 [解] 查得水蒸气的临界参数为c 647.3K T =,c 22.05MPa p =,0.344ω=33V 0.0232/417.6/m kg cm mol ==实验值(1) 用理想气体方程 3-1R 8.314643519.02(c m mo l )10.3T V p ⨯===⋅ 519.02-417.6V 24.3%417.6∆==(2) RK 方程0.5()RT ap V b T V V b =--+ ()(1)0.5()()k k k RTV b ap T V V b+⇒=+++2 2.576-2(8.314)(647.3)0.42748 1.428510(Pa m mol )22.05a M c ⨯=⨯=⨯⋅⋅3-18.314647.30.0866421.15(m mol )20.05b c ⨯=⨯=⋅()(1)70.5()()5345.90221.15 1.42851010.364321.15k k k V V V +∴=+⨯++取(0)3-18.314643519.02(cm mol )10.3RT V p ⨯===⋅为初值, 则,()1455.45V=,()2435.71V =,()3428.30V =,()44425.33V =()5424.11V = ()6423.61V = ()7423.4V =,31423.4cm m V mol -∴=∙423.4-417.6V 1.39%417.6∆==(3) 用普遍化关系式r 6430.993647.3T == r 10.30.46722.05p == 由于r 0.467p ≈较小,故采用普遍化Virial 系数关联(0) 1.61.6r 0.4220.4220.0830.0830.3440.993B T =-=-=- (1) 4.24.2r 0.1720.1720.1390.1390.03820.993B T =-=-=-()cC0.3440.3440.03820.357R Bp T =-+⨯-=- ()0.4671110.3570.832R R R 0.993c r c rpV Bp Bp pZ T T T T ⎛⎫∴==+=+=+-⨯= ⎪⎝⎭3-1ZR 0.8328.314643431.82(cm mol )10.3T V p ⨯⨯∴===⋅ 431.82-417.6V 3.41%417.6∆==2.10 一压缩机每小时处理600kg 4CH 及26C H 的等摩尔混合物。
气体在5MPa ,149℃下离开压缩机。
试问离开压缩机的气体体积流率为多少? 解:以1摩尔为计算基准,则x 1=0.5,x 2=0.5T=422.15K ,P=5MPa查表 4CH :()1c 190.58.19K P 4.604MPa 0.011 1c T ω=== 1422.152.215190.58r T ==26C H :()2c 305.33K P 4.87MPa 0.099 2c T ω=== 2422.151.3826305.33r T ==()()22c1118.314190.58RT 0.4572350.457235 4.604c c a P ⨯∴==⨯5622.493310M P a c m m o l -=⨯∙∙ ()()().501211110.26992-1.54226.3764601r T Tr -++=ωωα()()20.510.37646-1.542260.011-0.269920.0111 2.215=+⨯⨯⨯-0.8088=()10.6542Tr α∴=()5562111 2.4933100.6542 1.631110c a a Tr MPa cm mol α-=∙=⨯⨯=⨯∙∙ 31118.314190.580.0777960.07779626.77cm 4.604c c RT b mol P -⨯=⨯=⨯=∙ 同理:()()22c2228.314305.33RT 0.4572350.457235 4.87c c a P ⨯==⨯5626.050210M P a c m m o l -=⨯∙∙()()().502222210.26992-1.54226.3764601r T Tr -++=ωωα()()20.510.37646-1.542260.099-0.269920.0991 1.3826=+⨯⨯⨯-0.9077=()20.8239Tr α∴=()5562222 6.0502100.8239 4.984810c a a Tr MPa cm mol α-=∙=⨯⨯=⨯∙∙31228.314305.330.0777960.07779640.55cm 4.87c c RT b mol P -⨯=⨯=⨯=∙ 混合规则:112226.770.540.550.5m i i ib x b b x b x ==+=⨯+⨯∑3133.66cm mol -=∙2222112212x a x x a x a a x x a i ijij j i m ++==∑∑22221212112x a x x a a x a ++=525521.6311100.59848100.50.5 4.9848100.5=⨯⨯+⨯⨯+⨯⨯5623.079710M P a c m m o l-=⨯∙∙ 混合物状态方程为: 222mm m m m m m b V b V a b V RTP -+--= 则222mm m mm m b b V a P RT b V -+++=52m 8.314422.1533.66 3.07971040.5067.32V1132.9956m V ⨯=+⨯++-取()0318.314422.15701.95cm 5RTVmol P-⨯===∙为初值则,()()()123663.61 V 656.35 V 654.86V=== ()4654.55V = ()5654.49V =31654.49cm m V mol -∴=∙摩尔体积则:体积流率为:363160010654.491017.07m 23m nV h --=⨯⨯⨯=∙ 2.11 试计算含有30%(mol)氮气(1)-70%(mol)正丁烷(2)的气体混合物7g ,在188℃和 6.888MPa 条件下的体积。
已知:3-11114cm mol B =⋅,22265B =-31cm mol -⋅,129.5B =-31cm mol -⋅。
解:()()22111121222211223-1()20.31420.30.79.50.7265132.58(cm mol )N Ni j ij i j B y y B y B y y B y B ====++=⨯+⨯⨯⨯-+⨯-=-⋅∑∑()132.58 6.888110.7618R R 8.314461.5pV Bp Z T T -⨯==+=+=⨯3-1ZR 0.76188.314461.15424.03(cm mol )6.888m T V p ⨯⨯∴===⋅ 37424.0360.58(cm )49V ∴=⨯= 2.16 已知正常流体的饱和蒸气压可以用经验方程:lg s B p A T=+表示,其中p 的单位为MPa ,T 的单位是K ,试推导出该流体偏心因子表达式。
解:蒸汽压方程Slg Bp A T=+因 c c T T p p ==, 0.101325b T T p MPa ==, 代入以上蒸汽压方程,得c lg (1)lg0.101325(2)c b B p A T B A T ⎧=+⎪⎪⎨⎪=+⎪⎩联立方程组,确定式中常数A 、B 。
()()c c c lg lg 10.101325lg 10.101325br br c br br T p A p T T T p B T ⎧⎛⎫=- ⎪⎪-⎝⎭⎪⎨⎛⎫⎪= ⎪⎪-⎝⎭⎩其中bbr cT T T =则该蒸汽压方程对比态关联式为:S1lg 1r r p T θ⎛⎫=- ⎪⎝⎭其中,c lg 10.101325br br T p T θ⎛⎫= ⎪-⎝⎭ ,p c 单位为MPa 。
又r Sr0.71lg T p ω==--131110.77ωθθ⎛⎫∴=---=- ⎪⎝⎭。
