广义birkhoff方程的平衡稳定性
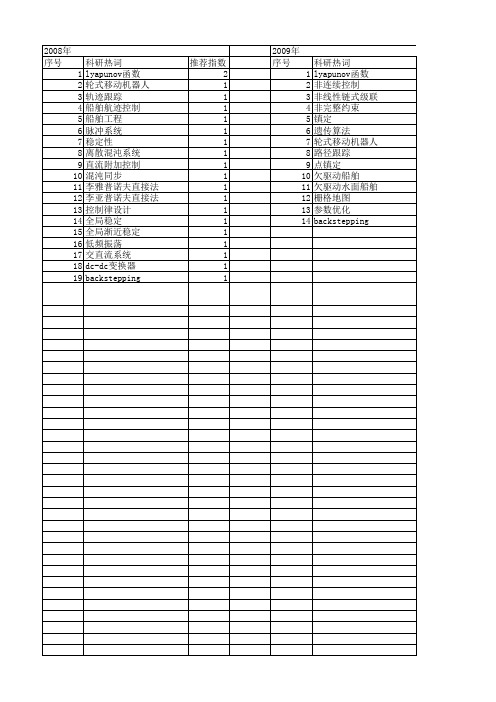
【国家自然科学基金】_lyapunov直接法_基金支持热词逐年推荐_【万方软件创新助手】_20140729
2014年 序号 1 2 3 4 5
2014年 科研热词 运动控制 轨迹跟踪 移动机器人 扩展卡尔曼滤波 lyapunov直接法 推荐指数 1 1 1 1 1
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
科研热词 lyapunov函数 非连续控制 非线性链式级联 非完整约束 镇定 遗传算法 轮式移动机器人 路径跟踪 点镇定 欠驱动船舶 欠驱动水面船舶 栅格地图 参数优化 backstepping
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12
科研热词 lyapunov直接法 路径跟踪 稳定自适应自动舵 神经网络 直接法 欠驱动船舶 斜拉索 广义birkhoff系统 平衡稳定性 一次近似法 mr阻尼器 lugre动态摩擦模型
科研热词 推荐指数 稳定性 5 边界控制 2 lyapunov直接法 2 非自治系统 1 轮式移动机器人 1 轨迹跟踪 1 视线坐标系 1 船舶 1 航向保持 1 自适应非线性输出反馈 1 自适应控制 1 自治广义birkhoff系统 1 纹波补偿 1 类拉格朗日方程 1 神经网络 1 直接法 1 滑模控制 1 柔性结构 1 柔性梁 1 李雅普诺夫(lyapunov)直接法 1 振动 1 扩展卡尔曼滤波 1 平衡稳定性 1 姿态稳定 1 变时滞 1 动态性能 1 中立型随机微分方程 1 不动点 1 一次近似法 1 rbf神经网络 1 lyapunov方法 1 lyapunov函数 1 hopfiled神经网络 1 buck变换器 1 3d刚体摆 1
微分方程中的稳定性与动力系统

微分方程中的稳定性与动力系统微分方程是数学中的重要分支,它描述了自然界和人类社会中许多现象的变化规律。
稳定性是微分方程中一个重要的概念,它指的是系统在某个状态下,当微小扰动施加在其上时,系统能够回到原来的状态。
而动力系统则是研究微分方程解的性质与行为的一种数学工具。
本文将探讨微分方程中的稳定性与动力系统的关系以及其应用。
一、稳定性的概念与分类稳定性是微分方程研究中常用的一个重要概念。
在微分方程中,稳定性分为三类:渐近稳定性、指数稳定性和有界稳定性。
渐近稳定性指的是当系统趋于稳定状态时,解会渐近地接近一个特定的值。
指数稳定性则是指当系统趋于稳定状态时,解以指数速度趋于一个特定值。
有界稳定性则是指解在稳定状态附近有界,不会趋于无穷大或无穷小。
二、动力系统的基本概念与性质动力系统是研究微分方程解的性质与行为的数学工具。
在动力系统中,解的性质可以通过相图来描述。
相图是在平面上描述状态变化的图形,每个点代表系统的一个状态,而解的轨迹则是相图上的一条曲线。
动力系统中的关键概念包括平衡点、极限环和吸引子等。
平衡点是动力系统中解保持恒定的点,极限环则是动力系统解在某个周期内反复变化的情况。
三、稳定性与动力系统的联系稳定性与动力系统密切相关,动力系统的稳定性分析是通过研究微分方程解的行为来进行的。
对于一个稳定的系统,解的轨迹将会以某种方式限制在特定的区域内,而对于不稳定的系统,则可能出现解趋于无穷大或无穷小的情况。
稳定性分析的方法主要有线性稳定性分析和Lyapunov稳定性分析。
线性稳定性分析通过线性化系统的方程来研究它的稳定性,而Lyapunov稳定性分析则通过构造Lyapunov函数来判断系统的稳定性。
四、应用案例:生态系统中的稳定性与动力系统稳定性与动力系统的理论在生态学中有广泛的应用。
生态系统是由生物体、环境和相互作用构成的复杂系统,稳定性是维持生态系统平衡的重要条件。
以食物链为例,假设有一个由食物链构成的生态系统,包括植物、食草动物和食肉动物。
状态空间与Birkhoff力学

状态空间与Birkhoff力学丁光涛【摘要】In this paper, we expound in three ways that Birkhoffian mechanics is the analytical mechanics in the state space. (1) In the reduction of Newton' s equations to the first-order form to obtain the Birkhoffian representation of the equations, it is declared that Birkhoffian variables are the general state variables which are transformed form the coordinate-velocity state variables. (2) Birkhoffian equations are the analytical equations of motion according as the structure of Lagrange's equations in the state space and of Birkhoff's equations are the same, and the Lagrangian in the state space can consist of Birkhoffian function and functions. (3) Since by noncanonical transformation the phase space as a particular state space can be transformed into the general state space, and Hamiltonian equation can be transformed into Birkhoffian equation, Birkhoffian mechanics can be regarded as the analytical dynamics in the state space.%本文从三方面论述Birkhoff力学是状态空间中的分析动力学:(1)从Newton运动微分方程一次化而引入Birkhoff表示的过程中,说明Birkhoff变量是从坐标-速度状态变量变换而来的,即Birkhoff变量本质上是系统的广义状态变量.(2)论证系统状态空间中Lagrange方程与Birkhoff方程具有相同的结构,状态空间中系统的Lagrange函数可以由Birkhoff函数和函数组构成,就是说Birkhoff方程是状态空间中系统的分析力学运动方程.(3)相空间是一种特殊的状态空间,经非正则变换成为一般的状态空间,而Hamilton方程经非正则变换成为Birkhoff方程,再次说明Birkhoff力学是状态空间中分析动力学.【期刊名称】《安徽师范大学学报(自然科学版)》【年(卷),期】2012(035)005【总页数】4页(P415-418)【关键词】分析力学;Birkhoff力学;一阶Lagrange力学;状态空间【作者】丁光涛【作者单位】安徽师范大学物理与电子信息学院,安徽芜湖241000【正文语种】中文【中图分类】O320引言三百多年来经典力学持续发展,成长为枝繁叶茂的参天大树,其理论体系的内容、模式、结构和方法的演变过程伴随着一系列的创新与突破,呈现出明显的阶段性:Newton力学、Lagrange力学、Hamilton力学、非完整力学以及Birkhoff 力学和广义Hamilton力学[1].1927年 Birkhoff 在《动力系统》中提出一个积分变分原理和一类新型运动方程[2],1978年,Santilli推广了这类方程,并建议命名为Birkhoff方程[3],文献[4]构建了Birkhoff系统动力学的基本理论框架.应当指出,在经典力学发展的不同阶段,描述力学体系运动的变量空间也随之改变,例如Newton力学主要研究质点和质点系在现实物理空间-Euclid空间中的运动;Lagrange力学研究力学系统在位形空间中的运动,Lagrange方程是广义坐标的二阶微分方程(组);Hamilton力学研究力学系统在相空间中的运动,Hamilton方程是正则共轭变量的一阶微分方程组,等等.状态空间是力学中重要的空间之一,相空间是其一种特殊情况[5,6],在状态空间中对约束的研究取得重要成果,深化了对约束完整性的认识[7,8].状态空间中分析动力学的研究也取得进展,给出了这种空间中系统的Lagrange函数和运动方程,讨论了它们与位形空间中Lagrange 函数和运动方程的关系[9,10].在研究过程中,我们发现,在不同符号和术语后面,Birkhoff力学和状态空间中分析动力学实质上是一致的,本文将从三个方面论述,Birkhoff力学是状态空间中分析动力学.1 状态变量和Birkhoff变量Santilli是从将Newton方程化成一阶形式入手,导出Birkhoff方程的[3].设Newton系统方程为(1)引入一组新变量yk如下(2)式中是一组任意选择的规则并充分光滑的函数,且(3)由此可以解出速度(4)代入方程(1),得到(5)方程(4)和(5)是方程(1)的一阶形式,写成统一的形式(6)(7)(8)aμ是Birkhoff变量.在经典力学中,狭义的状态空间是坐标—速度空间,式(2)定义的变量yk是狭义的状态变量坐标和速度的函数,选择特殊的函数(9)(10)式(7)定义aμ就是经典力学中狭义的状态变量,选择其他形式的函数Mk,则rk 和yk相当于狭义状态变量空间的变量变换,但保持了坐标不变,因此,式(7)定义的aμ仍是状态变量.在Birkhoff力学中变量aμ可以作一般的可逆变换aμ→a′μ=a′μ(t,a)(11)(12)显然,a′μ是新Birkhoff变量,又是广义形式的状态变量,式(11)是状态空间中变量变换.可以将从Newton方程化为一阶形式而引入Birkhoff变量的过程,在Lagrange 力学中重复进行,在把Lagrange方程化为一阶形式的同时,可以引入作为广义坐标和广义速度函数的Birkhoff变量aμ,换句话说,从位形空间变换得到的状态空间,其中状态变量实质上是Birkhoff变量.2 状态空间Lagrange方程和Birkhoff方程描述系统运动的空间可以从位形空间推广为状态空间,其动力学方程也可作相应的推广[10].在坐标—速度状态空间中,Lagrange函数是一阶Lagrange函数,Lagrange方程是一阶微分方程组.讨论一般情况,引入广义状态变量xμ(μ=1,2,…,2n),系统的状态演化规律是一阶微分方程组(13)已经证明,方程(13)可以构造出 Lagrange表示,即由方程(13)导出对应的一阶Lagrange函数[11,12](14)对应的Lagrange方程为(15)(16)而方程(15)与方程(13)等价.如果将系统状态变量xμ写成Birkhoff形式变量aμ,方程(13)写成(17)同样地,Birkhoff力学证明,方程(17)总可以表示成Birkhoff方程,即由方程(17)构造出Birkhoff函数B(t,a)和Birkhoff函数组Rμ(t,a),将方程(17)写成等价的Birkhoff方程(18)(19)Ωμν称为Birkhoff张量.方程(18)可以表示成Lagrange方程形式,只要由Rμ和B构成Lagrange函数[3,4](20)对应的一阶Lagrange方程就是Birkhoff方程(18).比较式(14)和式(20)中函数L,以及式(15)和式(18)方程,可以得到如下结论:Birkhoff方程是状态空间中Lagrange方程.3 相空间Hamilton方程和Birkhoff方程分析力学中以正则共轭变量qi和pi(i=1,2,…,n)为坐标的空间称为相空间,其中的系统运动微分方程为Hamilton方程(21)式中H=H(t,q,p)称为Hamilton函数,引入统一变量(22)方程(21)可以写成逆变型(23)或者写成协变型(25)(26)将式(22)aμ看作Birkhoff变量,并引入Birkhoff函数组和Birkhoff函数分别为B(t,a)=H(t,a)(27)直接可以验证方程(25)是方程(18)的特例,或者说,Hamilton系统是Birkhoff系统的特殊情形[3,4].文献[3]中已经阐明,Birkhoff方程是Hamilton方程的一种推广.相空间实质上是一种特殊类型的状态空间,一个体系的状态由相空间中一个点所确定.相空间中坐标变换与位形空间中坐标变换不同,前者将分为两大类型,一类称为正则变换,它将一组正则变量变换成新的一组正则变换,保持对所有的Hamilton函数的正则方程形式不变;另一类是非正则变换,不能保持变换后正则方程形式不变,导出的是Birkhoff方程[3].例如,对如下非正则的可逆变换(28)方程(25)的变换规则为=0其中(30)由式(29)可以导出Birkhoff方程如下(31)应当指出,相空间变量的非正则变换得到的虽然不再是正则变量,都仍是状态变量,这就是说,由Hamilton方程经非正则变换得到的Birkhoff方程是状态空间的运动微分方程.所有的Hamilton方程都可以通过变量变换成为Birkhoff方程,然而只有满足一定条件的Birkhoff系统才能变换为Hamilton系统[3,4],换句话说,不是所有的Birkhoff方程都能Hamilton化,状态空间中Birkhoff力学是比相空间中Hamilton力学具有更大的普遍性的分析动力学.参考文献:[1] 梅凤翔.经典约束力学系统的对称性与守恒量研究进展[J].力学进展,2009,39:37-43.[2] BIRKHOFF G D 1927 Dynamical Systems.Providence RI[M].AMS College Pub1,1927.[3] SANTILLI R M. Foundations of theoretical mechanics II[M]. NewYork:Springer-Verlag,1983.[4] 梅凤翔,史荣昌,张永发,吴惠彬.Birkhoff系统动力学[M].北京:北京理工大学出版社,1996.[5] ROSENBERG R M. Analytical mechanics[M]. New York: Pleum Press,1977.[6] 丁光涛.力学系统状态空间的探讨[J].安徽师范大学学报:自然科学版,2010,33(6):539-542.[7] 陈滨.状态空间非线性约束的完整性和非完整性[J].中国科学:A辑,1993,(23):839-846.[8] CHEN B, WANG L S, CHU S S, CHOU W T.A new classification of non-holonomic constraints[J]. Proc R Soc Lond A,1997,(453):631.[9] 丁光涛.状态空间中变分原理和状态方程[J].安徽师范大学学报:自然科学版,1989,(12):12-24.[10] 丁光涛.状态空间Lagrange函数和运动方程[J].中国科学G辑:物理学·力学·天文学,2009,(39):813-820.[11] 丁光涛,陶松涛.一阶Lagrange力学逆问题及其在非力学领域中的应用[J].科学通报,2008,(53):872-876.[12] 丁光涛.一阶Lagrange力学逆问题的直接解法.动力学与控制学报[J].2010,(8):193-196.[13] 李元成,梁景辉,梅凤翔.二阶Birkhoff系统的Hamilton化[J].固体力学学报,2002,(23):203-206.[14] 丁光涛.Birkhoff系统的Hamilton化[J].动力学与控制学报,2010,(8):8-11.。
一类滞后时变广义系统稳定性的拉什密辛型定理

一类滞后时变广义系统稳定性的拉什密辛型定理拉什米辛型(Lur'e–Khasminskii)定理,是一种极具影响力的系统稳定性定理,可以用来分析系统的动态特性。
它可以用来测定系统是否保持稳定性,并且可以用于研究这些系统的持续性。
拉什米辛型定理的思想和其他定理相似,但它却能够涵盖更大的范围。
它可以用于分析更加复杂的应用程序,使系统的特性,更加有效的分析和控制。
拉什米辛型定理属于滞后时变(time-varying)的广义系统稳定性定理。
它是由苏联理论计算机科学家YuriA.Lur'e(1966)和苏联理论计算机科学家AndreA.Khasminsky (1970)提出的,它重要的创新在于将普通时变系统的稳定性特性纳入到了范围更广的广义系统的稳定性特性的讨论学习之中。
拉什米辛型定理改进了之前其他稳定性定理,因为它从数学和技术的角度对系统稳定性进行了全面描述。
拉什米辛型定理可以用来研究时变系统的稳定性性质。
它可以通过调控输入值,控制和调节系统耦合参数而使时变系统保持稳定性。
例如,拉什米辛型定理可以用来分析控制和优化一类工程中的微分方程,以及控制温度变化的参数,这些都是需要采用时变系统的控制流程的应用环境。
此外,该定理还可以用来研究交通路线和动态仿真。
拉什米辛型定理的发展,极大地促进了时变系统的稳定性的研究,也为时变系统的稳定性设计和控制提供了指导方针。
它可以用来研究时变系统的稳定性特性,并且可以帮助人们把握系统在不同情况下的行为规律。
拉什米辛型定理是信息系统和微分Δ正则算法等系统稳定性研究和设计的基础。
该定理已经被用于测试电力系统的动态特性,以及对复杂控制问题进行建模和建模。
拉什米辛型定理的有效性和必要性得到了广泛的认可,它的适用范围也在不断扩大。
它的研究仍然在持续发展,新的定理也正在被开发出来,以期拓展该定理的使用范围。
拉什米辛型定理也在不断地为工程技术和科学研究提供更为全面和深入的支持和服务。
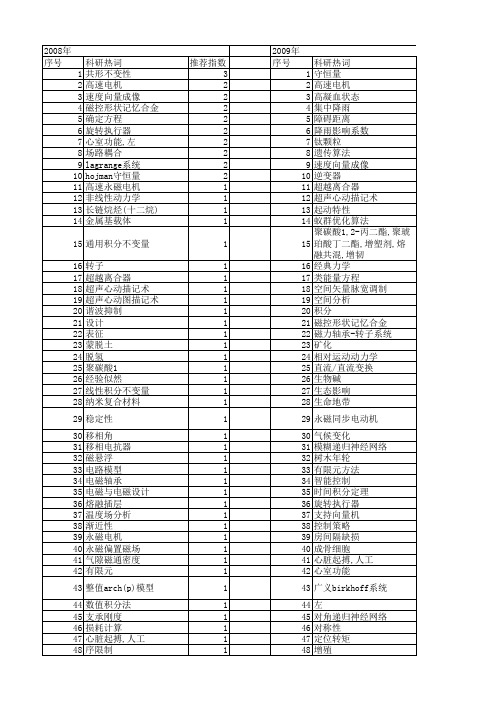
【国家自然科学基金】_凤翔_基金支持热词逐年推荐_【万方软件创新助手】_20140802
1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 高速电机 2 超声心动描记术 2 广义birkhoff系统 2 马来酸酐 1 非线性振动 1 随机响应 1 钴酞菁 1 认知与响应 1 血液动力学改变 1 血流向量成像 1 蓝宝石 1 综合设计 1 纳米线 1 积分 1 磁饱和 1 磁轴承 1 磁控溅射 1 电磁特性 1 活性碳纤维 1 波导膜 1 永磁转子 1 模型 1 梯度 1 有限元法 1 有限元分析 1 有限元 1 扩链 1 心脏起搏 1 心室功能,左 1 强度 1 弹性模量 1 弱非完整系统 1 应变率 1 左心室功能 1 屈服强度 1 封端 1 室性早搏复合征 1 太阳电池 1 多项式拟合 1 多场迭代 1 地震灾害 1 单心动周期全容积成像 1 势积分方法 1 加权平均反射率 1 分数维动力学 1 分子动力学 1 凤翔地区 1 减反射 1 农村居民 1 催化氧化 1 人工 1 二氧化碳-氧化环己烯共聚物 1
科研热词 守恒量 高速电机 高凝血状态 集中降雨 障碍距离 降雨影响系数 钛颗粒 遗传算法 速度向量成像 逆变器 超越离合器 超声心动描记术 起动特性 蚁群优化算法 聚碳酸1,2-丙二酯,聚琥珀酸丁二酯,增塑剂,熔 经典力学 类能量方程 空间矢量脉宽调制 空间分析 积分 磁控形状记忆合金 磁力轴承-转子系统 矿化 相对运动动力学 直流/直流变换 生物碱 生态影响 生命地带 永磁同步电动机 气候变化 模糊递归神经网络 树木年轮 有限元方法 智能控制 时间积分定理 旋转执行器 支持向量机 控制策略 房间隔缺损 成骨细胞 心脏起搏,人工 心室功能 广义birkhoff系统 左 对角递归神经网络 对称性 定位转矩 增殖 地震活动 地下水位 合成 变分原理
推荐指数 3 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
微分方程稳定性理论简介

第五节 微分方程稳定性理论简介这里简单介绍下面将要用到的有关内容:一、 一阶方程的平衡点及稳定性设有微分方程()dxf x dt= (1) 右端不显含自变量t ,代数方程()0f x = (2)的实根0x x =称为方程(1)的平衡点(或奇点),它也是方程(1)的解(奇解)如果从所有可能的初始条件出发,方程(1)的解()x t 都满足0lim ()t x t x →∞= (3)则称平衡点0x 是稳定的(稳定性理论中称渐近稳定);否则,称0x 是不稳定的(不渐近稳定)。
判断平衡点0x 是否稳定通常有两种方法,利用定义即(3)式称间接法,不求方程(1)的解()x t ,因而不利用(3)式的方法称直接法,下面介绍直接法。
将()f x 在0x 做泰勒展开,只取一次项,则方程(1)近似为:0'()()dxf x x x dt=- (4) (4)称为(1)的近似线性方程。
0x 也是(4)的平衡点。
关于平衡点0x 的稳定性有如下的结论:若0'()0f x <,则0x 是方程(1)、(4)的稳定的平衡点。
若0'()0f x >,则0x 不是方程(1)、(4)的稳定的平衡点0x 对于方程(4)的稳定性很容易由定义(3)证明,因为(4)的一般解是0'()0()f x t x t ce x =+ (5)其中C 是由初始条件决定的常数。
二、 二阶(平面)方程的平衡点和稳定性方程的一般形式可用两个一阶方程表示为112212()(,)()(,)dx t f x x dtdx t g x x dt⎧=⎪⎪⎨⎪=⎪⎩ (6)右端不显含t ,代数方程组1212(,)0(,)0f x x g x x =⎧⎨=⎩ (7) 的实根0012(,)x x 称为方程(6)的平衡点。
记为00012(,)P x x 如果从所有可能的初始条件出发,方程(6)的解12(),()x t x t 都满足101lim ()t x t x →∞= 202lim ()t x t x →∞= (8) 则称平衡点00012(,)P x x 是稳定的(渐近稳定);否则,称P 0是不稳定的(不渐近稳定)。
微分方程稳定性理论简介
任期5年的国家来说, 0.2.
24
对模型和参数的粗略检验 考察第一次 世界大战前夕欧洲的两个国家同盟——法 俄同盟和德奥匈同盟的军备竞赛情况.
两个同盟的经济实力大致相等,且约 为德国的3倍,因为德国的k 0.3,所以这
3. 由于相互敌视或领土争端,每一方 都存在着增加军备的固有潜力.
16
进一步假定前两个因素的影响是线性的,
第3个因素的影响是常数,那么x(t)和y(t)的变
化过程可用微分方程组
x(t) x ky g
Hale Waihona Puke y (t )lx y h
(1)
表示,其中的系数均大于或等于零. k, l是对方
军备刺激程度的度量; , 是己方经济实力制
15
模型的假设和构成 为了方便起见,用
军备表示军事力量的总和,如兵力、装备、 军事预算等. 甲乙双方在时刻t的军备分别 记作x(t)和y(t),假设它们的变化只取决于 下面3个因素:
1. 由于相互不信任及矛盾的发展,一 方军备越大,另一方军备增加得越快;
2. 由于各方本身经济实力的限制,任 一方军备越大,对军备增长的制约作用越 大;
12
军事分析家平可夫: 中日军备竞赛由隐形转向有形 /letter/ 加入日期 2005-5-24 9:02:37 点击次数: 3
防卫厅消息来源声称过去一年以来,航空自卫 队在日本排他经济水域周围监视中国军用飞机的次 数明显增多。它们大半是侦察机。在海上,中国海 军的最新型俄式“现代”导弹驱逐舰的活动也比较 频繁。冷战时代苏联海军太平洋舰队的“现代”级 导弹驱逐舰经常航行在东海海域,目前中国出现的 频率超过了俄罗斯海军。
平衡的稳定条件
利用:
d μi (T , P) = −sidT + vidP = d μ j (T , P) = −s jdT + v jdP
⇓
( ) dP = s j − si =
L
dT v j − vi T v j − vi
这就是克拉珀龙方程。
⎞ ⎟⎠T
ΔκT
必须自恰方程
ΔcP = Δα TvΔα ΔκT
第三章习题 三版:4,9,10,16 四版: 4,9,10,16
∫ ∫ ( ) dP =
LP
⇒ ln P = − L0
T
+
dT
T
dT RT 2
RT
RT 2
T0
T0
c1P − cP2
dT + A0.
如果温度也变化不大,则 c1P , cP2 可以看成常数,并且上式可以
积分为
ln P = A − B + C ln T. T
A, B, C 可以实验测定
超导相变 对正常态和超导态的吉布斯函数满足下列方程
∂si ∂P
⎞ ⎟⎠T
⎞ ⎟⎟⎠
dP dT
=
L T
+
cPj
−
cPi
−T
⎛⎛
⎜⎜⎝
⎜ ⎝
∂v j ∂T
⎞ ⎟ ⎠P
−
⎛ ⎜⎝
∂vi ∂T
⎞ ⎟⎠P
⎞ ⎟⎟⎠
dP dT
( ) =
L T
+
cPj
−
cPi
−
⎛⎛
⎜⎜⎝
⎜ ⎝
∂v j ∂T
微分方程中的稳定性理论研究
微分方程中的稳定性理论研究微分方程是数学和物理学中应用广泛的重要工具之一。
而稳定性理论作为微分方程中的核心内容之一,对于研究系统的长期行为和解的性质具有重要的意义。
本文将介绍微分方程中的稳定性理论的研究进展,并讨论其在实际问题中的应用。
一、稳定性理论的基本概念稳定性理论是研究微分方程解的长期行为的数学工具。
在微分方程的解中,稳定性指的是当初始条件发生微小变化时,解是否仍然保持在原来的状态附近。
稳定性理论可以分为以下几个方面:1. 渐近稳定性:当系统的解趋向于某一特定的值或集合时,称为渐近稳定。
对于线性系统,通常可以通过特征根的位置来判断解的渐近稳定性。
2. 指数稳定性:当系统的解以指数形式趋近于某一特定的值或集合时,称为指数稳定。
3. 非线性稳定性:对于非线性系统,稳定性分析更加复杂。
通常需要借助于拉格朗日函数或李雅普诺夫函数来判定。
二、稳定性理论的研究方法稳定性理论的研究方法可以分为两类:直接法和间接法。
1. 直接法:直接法是通过直接分析微分方程解的性质来判断系统的稳定性。
其中,线性系统可以通过特征根的位置来判断其稳定性。
对于非线性系统,可以利用稳定性的定义和拉格朗日函数或李雅普诺夫函数来判断。
2. 间接法:间接法是通过构造一些性质满足一定条件的函数来判断系统的稳定性。
常用的方法有:线性化方法、平衡点分析方法和Lyapunov方法等。
三、稳定性理论的应用领域稳定性理论在许多领域都有广泛的应用,下面以几个具体的应用领域为例进行介绍。
1. 动力系统:稳定性理论在动力系统中的应用非常广泛。
动力系统是描述物理系统或所研究问题的一种数学模型,通过动力学方程来描述系统的演化规律。
稳定性理论可以帮助我们分析动力系统的长期行为和解的性质。
2. 自然科学:稳定性理论在自然科学中的应用也非常丰富。
例如,在物理学中,稳定性理论被广泛应用于系统的能量稳定性分析;在生物学中,稳定性理论可以帮助研究生物系统的稳定性以及生态系统的演化。
第4章稳定性与李雅普诺夫方法
4.3 李雅普诺夫第二法
3、希尔维斯特判据
设实对称阵
p11 p12
P
p21
p22
pn1
p1n
,
pij
p ji
pnn
i 为其各阶顺序主子式,即
1 p11 ,
2
p11 p21
p12 , p22
,n P
矩阵P或V(x)定号性的充要条件是:
22
4.3 李雅普诺夫第二法
(1)若 i 0 (i 1, 2, , n), 则 P 正定;
要条件是整个状态空间只有一个平衡点。
线性系统:渐近稳定 大范围渐近稳定 非线性系统:一般小范围渐近稳定
6
4. 不稳定
4.1.2 稳定性的几个定义
对于某个实数 和任意
,在超球域
内始终存在状态 ,使得从该状态开始的运动轨迹要 突破超球域 。
7
4.1.2 稳定性的几个定义
此三个图分别表示平衡状态为稳定、渐近稳定 和不稳定时初始扰动所引起的典型轨迹。
28
4.3 李雅普诺夫第二法
说明: (1)V (x) 0 ,则此时 V (x) C,系统轨迹将在某个曲面上,
而不能收敛于原点,因此不是渐近稳定。 (2)V (x)不恒等于0,说明轨迹在某个时刻与曲面 V (x) 相C 交,
但仍会收敛于原点,所以是渐近稳定。
x0
x0
(3)稳定判据只是充分条件而非必要条件!
于是知系统在原点处不稳定。
33
4.3 李雅普诺夫第二法
4.3.3 对李雅谱诺夫函数的讨论 (1) V(x)是正定的标量函数,V(x)具有一阶连续偏导数; (2)并不是对所有的系统都能找到V(x)来证明该系统稳定 或者不稳定; (3)V(x)如果能找到,一般是不唯一的,但关于稳定性的 结论是一致的;
