高数习题集(附答案)
高等数学练习题(附答案)

《高等数学》专业年级学号姓名一、判断题.将√或×填入相应的括号内.(每题2分,共20分)()1.收敛的数列必有界.()2.无穷大量与有界量之积是无穷大量.()3.闭区间上的间断函数必无界.()4.单调函数的导函数也是单调函数.()5.若f (x )在x 0点可导,则f (x )也在x 0点可导.()6.若连续函数y =f (x )在x 0点不可导,则曲线y =f (x )在(x 0,f (x 0))点没有切线.()7.若f (x )在[a ,b ]上可积,则f (x )在[a ,b ]上连续.()8.若z =f (x ,y )在(x 0,y 0)处的两个一阶偏导数存在,则函数z =f (x ,y )在(x 0,y 0)处可微.()9.微分方程的含有任意常数的解是该微分方程的通解.()10.设偶函数f (x )在区间(-1,1)内具有二阶导数,且f ''(0)=f '(0)+1,则f (0)为f (x )的一个极小值.二、填空题.(每题2分,共20分)1.设f (x -1)=x ,则f (x +1)=.22.若f (x )=2-12+11x1x,则lim +=.x →03.设单调可微函数f (x )的反函数为g (x ),f (1)=3,f '(1)=2,f ''(3)=6则---------------------------------------------------------------------------------------------------------------------------------g '(3)=.4.设u =xy +2x,则du =.y35.曲线x =6y -y 在(-2,2)点切线的斜率为.6.设f (x )为可导函数,f '(1)=1,F (x )=f ()+f (x ),则F '(1)=.7.若1x2⎰f (x )0t 2dt =x 2(1+x ),则f (2)=.8.f (x )=x +2x 在[0,4]上的最大值为.9.广义积分⎰+∞0e -2x dx =.2210.设D 为圆形区域x +y ≤1,⎰⎰y D1+x 5dxdy =.三、计算题(每题5分,共40分)111+Λ+).1.计算lim(2+22n →∞n (n +1)(2n )2.求y =(x +1)(x +2)(x +3)ΛΛ(x +10)在(0,+∞)内的导数.23103.求不定积分⎰1x (1-x )dx .4.计算定积分⎰πsin 3x -sin 5xdx .3225.求函数f (x ,y )=x -4x +2xy -y 的极值.6.设平面区域D 是由y =x ,y =x 围成,计算⎰⎰Dsin ydxdy .y7.计算由曲线xy =1,xy =2,y =x ,y =3x 围成的平面图形在第一象限的面积.---------------------------------------------------------------------------------------------------------------------------------8.求微分方程y '=y -2x的通解.y四、证明题(每题10分,共20分)1.证明:arc tan x=arcsinx 1+x 2(-∞<x <+∞).2.设f (x )在闭区间[a ,b ]上连续,且f (x )>0,F (x )=⎰f (t )dt +⎰x xb1dt f (t )证明:方程F (x )=0在区间(a ,b )内有且仅有一个实根.《高等数学》参考答案一、判断题.将√或×填入相应的括号内(每题2分,共20分)1.√;2.×;3.×;4.×;5.×;6.×;7.×;8.×;9.√;10.√.二、填空题.(每题2分,共20分)21.x +4x +4; 2.1; 3.1/2;4.(y +1/y )dx +(x -x /y )dy ;25.2/3;6. 1;7.336;8.8;9.1/2;10.0.三、计算题(每题5分,共40分)n +1111n +1<++L +<1.解:因为(2n )2n 2(n +1)2(2n )2n 2且lim 由迫敛性定理知:lim(n →∞n +1n +1=0lim ,=0n →∞(2n )2n →∞n 2111++Λ+)=0222n (n +1)(2n )2.解:先求对数ln y =ln(x +1)+2ln(x +2)Λ+10ln(x +10)---------------------------------------------------------------------------------------------------------------------------------∴11210y '=++Λ+y x +1x +2x +10∴y '=(x +1)Λ(x +10)(3.解:原式=21210++Λ+)x +1x +2x +10⎰11-xd x =2⎰11-(x )2d x=2arcsin4.解:原式=x +c⎰πsin 3x cos 2xdxπ32=⎰π2020cos x sin xdx -⎰cos x sin xdx232ππ32=⎰sin xd sin x -⎰ππ2sin xd sin x32222-[sin 2x ]π=[sin 2x ]0π552=4/525.解:f x'=3x -8x -2y =0f y'=2x -2y =05π5故⎨⎧x =0⎧x =2或⎨⎩y =0⎩y =2当⎨⎧x =0''(0,0)=-2,f xy ''(0,0)=2''(0,0)=-8,f yy 时f xx⎩y =0---------------------------------------------------------------------------------------------------------------------------------Θ∆=(-8)⨯(-2)-22>0且A=-8<0∴(0,0)为极大值点且f (0,0)=0当⎨⎧x =2''(2,2)=-2,f xy ''(2,2)=2''(2,2)=4,f yy 时f xxy =2⎩Θ∆=4⨯(-2)-22<0∴无法判断6.解:D=(x ,y )0≤y ≤1,y 2≤x ≤y{}∴⎰⎰D1y sin y 1sin y sin y dxdy =⎰dy ⎰2dx =⎰[x ]y dyy 20y 0y y y =⎰(sin y -y sin y )dy1=[-cos y ]+10⎰1yd cos y 1=1-cos1+[y cos y ]0-⎰cos ydy 01=1-sin17.解:令u =xy ,v =y;则1≤u ≤2,1≤v ≤3x1x uJ =yuxv =2uv y vv-u 2v v =12v u2u v231dv =ln 3∴A =⎰⎰d σ=⎰du ⎰112v D8.解:令y =u ,知(u )'=2u -4x由微分公式知:u =y =e ⎰22dx 2(⎰-4xe ⎰-2dx dx +c )---------------------------------------------------------------------------------------------------------------------------------=e 2x (⎰-4xe -2x dx +c )=e 2x (2xe -2x +e -2x +c )四.证明题(每题10分,共20分)1.解:设f (x )=arctan x -arcsinx 1+x 221Θf '(x )=-21+x 1x 1-1+x 221+x -⋅1+x 2x 21+x 2=0∴f (x )=c-∞<x <+∞令x =0Θf (0)=0-0=0∴c =0即:原式成立。
高等数学考试题库和答案

高等数学考试题库和答案一、选择题1. 极限的定义是()。
A. 函数在某点的增量B. 函数在某点的导数C. 函数在某点的值D. 函数在某点的无穷小变化答案:D2. 函数f(x) = x^2 + 3x - 4在x = 1处的导数是()。
A. 6B. 2C. 5D. 4答案:C3. 曲线y = x^3 - 3x + 1在x = 1处的切线斜率是()。
A. 1B. -1C. 3D. -3答案:A4. 函数f(x) = sin(x)的不定积分是()。
A. -cos(x) + CB. cos(x) + CC. sin(x) + CD. -sin(x) + C答案:B5. 定积分∫(0 to 1) x^2 dx的值是()。
A. 1/3B. 1/2C. 1D. 2答案:A二、填空题6. 函数f(x) = 2x + 3在x = 2处的值是_________。
答案:77. 极限lim(x→0) (1 + x)^(1/x)的值是_________。
答案:e8. 函数f(x) = x^2的二阶导数是_________。
答案:29. 曲线y = e^x在x = 0处的切线方程是_________。
答案:y = x + 110. 定积分∫(0 to π/2) sin(x) dx的值是_________。
答案:1三、解答题11. 求函数f(x) = x^3 - 6x^2 + 9x + 5在区间[0, 3]上的极值点。
解:首先求导数f'(x) = 3x^2 - 12x + 9。
令f'(x) = 0,解得x = 1, 3。
检查二阶导数f''(x) = 6x - 12,f''(1) = -6 < 0,所以x = 1是极大值点;f''(3) = 6 > 0,所以x = 3是极小值点。
12. 求曲线y = ln(x)绕x轴旋转一周所形成的立体的体积。
解:使用圆盘法,体积V = ∫(1 to e) π[ln(x)]^2 dx。
高等数学考试题库及答案

高等数学考试题库及答案一、选择题(每题3分,共30分)1. 函数y=x^2+2x+1的导数是:A. 2x+2B. 2x+1C. 2xD. 2答案:A2. 以下哪个选项是无穷小量:A. 0B. 1C. ∞D. ∃答案:A3. 极限lim(x→0) (sin(x)/x)的值是:A. 0B. 1C. -1D. ∞答案:B4. 以下哪个函数是奇函数:A. y=x^2B. y=x^3C. y=xD. y=1/x答案:B5. 积分∫(0 to 1) x^2 dx的值是:A. 1/3B. 1/2C. 2/3D. 3/2答案:A6. 以下哪个选项是二阶导数:A. dy/dxB. d^2y/dx^2C. d^2y/dxD. d^3y/dx^3答案:B7. 函数y=e^x的不定积分是:A. e^xB. e^x + CC. ln(x) + CD. x^2 + C答案:B8. 以下哪个选项是二重积分:A. ∫∫f(x,y) dxdyB. ∫f(x) dxC. ∫∫f(x) dxD. ∫f(x,y) dydx答案:A9. 以下哪个选项是泰勒级数展开:A. Σ(-1)^n x^(2n)B. Σ(-1)^n x^nC. Σx^n / n!D. Σx^(2n+1) / (2n+1)!答案:C10. 以下哪个选项是定积分的性质:A. ∫(a to b) f(x) dx = ∫(a to b) g(x) dxB. ∫(a to b) f(x) dx = -∫(b to a) f(x) dxC. ∫(a to b) f(x) dx = ∫(a to c) f(x) dx + ∫(c to b) f(x) dxD. ∫(a to b) f(x) dx = ∫(a to b) f(-x) dx答案:C二、填空题(每题2分,共20分)1. 函数y=x^3的导数是________。
答案:3x^22. 极限lim(x→∞) (1/x)等于________。
高数习题集及答案

高数习题集及答案一、极限1. 求下列极限:- \( \lim_{x \to 0} \frac{\sin x}{x} \)- \( \lim_{x \to \infty} (1 + \frac{1}{x})^x \)2. 利用夹逼定理证明:- \( \lim_{n \to \infty} (1 + \frac{1}{n})^n = e \)答案:1. 对于第一个极限,我们可以使用洛必达法则或者直接利用三角函数的性质得到:\[ \lim_{x \to 0} \frac{\sin x}{x} = 1 \]对于第二个极限,我们可以使用重要极限:\[ \lim_{x \to \infty} (1 + \frac{1}{x})^x = e \]2. 利用夹逼定理,我们可以找到两个序列 \( a_n \) 和 \( b_n \) 使得:\[ a_n \leq (1 + \frac{1}{n})^n \leq b_n \]并且 \( \lim_{n \to \infty} a_n = e \) 和 \( \lim_{n \to \infty} b_n = e \),从而证明 \( \lim_{n \to \infty} (1 +\frac{1}{n})^n = e \)。
二、导数与微分1. 求下列函数的导数:- \( f(x) = x^3 - 2x^2 + x \)- \( g(x) = \ln(x) \)2. 利用导数求函数的单调区间:- 对于函数 \( h(x) = x^2 - 4x + 4 \),求其单调增区间。
答案:1. 对于 \( f(x) \) 的导数,我们有:\[ f'(x) = 3x^2 - 4x + 1 \]对于 \( g(x) \) 的导数,我们有:\[ g'(x) = \frac{1}{x} \]2. 对于函数 \( h(x) \),我们先求导:\[ h'(x) = 2x - 4 \]令 \( h'(x) > 0 \),解得 \( x > 2 \),因此 \( h(x) \) 在\( (2, \infty) \) 上单调增。
高等数学习题集及解答

高等数学习题集及解答第二章一、 填空题1、设()f x 在x a =可导,则0()()lim x f a x f a x x →+--=。
2、设(3)2f '=,则0______________(3)(3)lim 2h f h f h →--=。
3、设1()xf x e -=,则0_____________(2)(2)limh f h f h→--=。
4、已知00cos (),()2,(0)1sin 2x f x f x x x π'==<<-,则0_______________________()f x =。
5、已知2220x y y x +-=,则当经x =1、y =1时,_______________dydx =。
6、()x f x xe =,则_______________(ln 2)f '''=。
7、如果(0)y ax a =>是21y x =+的切线,则__________a =。
8、若()f x 为奇函数,0()1f x '=且,则0_________________()f x '-=。
9、()(1)(2)()f x x x x x n =+++,则_________________(0)f '=。
10、ln(13)x y -=+,则____________________y '=。
11、设0()1f x '=-,则0___________00lim(2)()x xf x x f x x →=---。
12、设tan x y y +=,则_________________________dy =。
13、设lny =_______________(0)y '''=。
14、设函数()y f x =由方程42ln xy x y +=所确定,则曲线()y f x =在点(1,1)处的切线方程是______________________。
完整)高等数学练习题附答案

完整)高等数学练习题附答案第一章自测题一、填空题(每小题3分,共18分)1.lim (sinx-tanx)/(3xln(1+2x)) = 1/22.lim (2x^2+ax+b)/(x-1) =3.a = 5.b = 123.lim (sin2x+e^(2ax)-1)/(x+1) = 2a4.若f(x)在(-∞,+∞)上连续,则a=05.曲线f(x) = (x-1)/(2x-4x+3)的水平渐近线是y=1/2,铅直渐近线是x=3/26.曲线y=(2x-1)/(x+1)的斜渐近线方程为y=2x-3二、单项选择题(每小题3分,共18分)1.“对任意给定的ε∈(0,1),总存在整数N,当n≥N时,恒有|x_n-a|≤2ε”是数列{x_n}收敛于a的充分条件但非必要条件2.设g(x)={x+2,x<1.2-x^2,1≤x<2.-x,x≥2},f(x)={2-x,x<1.x^2,x≥1},则g(f(x))=2-x^2,x≥13.下列各式中正确的是 lim (1-cosx)/x = 04.设x→0时,e^(tanx-x-1)与x^n是等价无穷小,则正整数n=35.曲线y=(1+e^(-x))/(1-e^(-x^2))没有渐近线6.下列函数在给定区间上无界的是 sin(1/x),x∈(0,1]三、求下列极限(每小题5分,共35分)1.lim (x^2-x-2)/(4x+1-3) = 3/42.lim x+e^(-x)/(2x-x^2) = 03.lim (1+2+3+。
+n)/(n^2 ln n) = 04.lim x^2sin(1/x) = 01.设函数$f(x)=ax(a>0,a\neq1)$,求$\lim\limits_{n\to\infty}\frac{1}{\ln\left(\frac{f(1)f(2)\cdotsf(n)}{n^2}\right)}$。
2.求$\lim\limits_{4x\to1}\frac{x^2+e\sin x+6}{1+e^x-\cosx}$。
大学高等数学习题及答案

高等数学(A)1习题1-11.求下列函数的自然定义域:(3)y =1-1-x 2x⎧1-x 2≥0⎧-1≤x ≤1解:由⎨,所以函数的定义域为:[-1,0)⋃(0,1]⇒⎨⎩x ≠0⎩x ≠0(7)y =arcsin(x -3)解:由-1≤x -3≤1⇒2≤x ≤4,所以函数的定义域为:[2,4]1(8)y =3-x +arctanx⎧3-x ≥0⎧x ≤3解:由⎨x ≠0⇒⎨x ≠0,所以函数的定义域为:(-∞,0)⋃(0,3]⎩⎩9.求下列函数的反函数:(1)y =3x +1解:由y 3=x +1⇒x =y 3-1,所以反函数为:y =x 3-11-xy =(2)1+x解:由y (1+x )=1-x ⇒x =1-x 1-yy =1+x1+y ,所以反函数为:习题1-21.下列各题中,哪些数列收敛?哪些数列发散?1(2){(-1)n }n 收敛.且极限为0.⎧n -1⎫(4)⎨⎬n +1⎩⎭收敛,且极限为12n -1(6){3n }2n -12n 1n收敛.且因为:3n =(3)-(3),知极限为0.习题1-3x |x |当x →0时的左、右极限,并说明它们在x →0时的极限4.求f (x )=,φ(x )=x x 是否存在.解:x →0lim -f (x )=lim -x →0x →0x x=lim -1=1,lim +f (x )=lim +=lim +1=1x →0x →0x x →0x x →0∴lim f (x )=1|x |-x |x |x=lim -lim(-1)=-1,lim φ(x )=lim =lim =lim +1=1x →0x →0x x →0x x →0-x →0+x →0+x x →0+x x →0∴lim φ(x )不存在.lim -φ(x )=lim -x →0习题1-44.求下列极限并说明理由.(1)lim x →∞2x +1x2x +1112x +1=2+,而lim =0,由定理1可知:lim =2.解:x x →∞x →∞x x x 1-x 2(2)lim x →∞1-x1-x 2(1-x )(1+x )1-x 2=1+x ,而lim x =0,由定理1可知:lim =1解:1-x =x →0x →01-x1-x 习题1-51.计算下列极限.x 2-32(2)x lim →3x +1解:lim x →x -3x →30===023x +1lim(x 2+1)4x →32lim(x 2-3)x 2-2x +1(3)lim x →1x 2-1x 2-2x +1(x -1)2x -1lim =lim =lim =0解:x →1x 2-1x →1(x +1)(x -1)x →1x +14x 3-2x 2+x (4)lim x →03x 2+2x 解:lim 4x -2x +x 4x -2x +1=lim =x →0x →03x 2+2x 3x +2322lim(4x 2-2x +1)x →0lim(3x +2)x →0=1=02x 2-1(7)lim x →∞2x 2-x -11)2x -11x →∞x lim =lim ==解:x →∞2x 2-x -1x →∞111122--2lim(2--2)x x x →∞x x 21-1x 2lim(1-x 2-6x +8(9)lim x →4x 2-5x +4x 2-6x +8(x -4)(x -2)(x -2)2lim =lim =lim 解:x →4x 2-5x +4x →4(x -4)(x -1)x →4(x -1)=3习题1-61.计算下列极限:1-cos2x lim (5)x →0x sin x 1-cos2x 2sin 2x sin xlim =lim =2lim =2⋅1=2解:x →0x sin x x →0x sin x x →0x 2.计算下列极限.-x )(1)lim(1x →0-1lim(1-x )=lim[(1+(-x ))]=e 解:x →0x →01x1-x -11x+2x )(2)lim(1x →02lim(1+2x )=lim[(1+2x )]=e 解:x →0x →01x12x 21x习题1-75.利用等价无穷小的性质,求下列极限:tan3xlim (1)x →02x tan3x ~3x ,∴lim 解:当x →0时,(3)lim x →0tan3x 3x 33=lim =lim =x →0x →02x x →022x 2tan x -sin xsin 3x 1x ⋅x 2tan x -sin x tan x (1-cos x )2=lim 1=1lim =lim =lim 333x →0x →0x →0x →02sin xsin x x 2解:1(x →0,tan x ~x ,1-cos x ~x 2,sin 3x ~x 3)2习题1-83.下列函数在指出的点处间断,说明这些间断点属于哪一类,如果是可去间断点,那么补充或改变函数的定义使它连续:x 2-1(1)y =x 2-3x +2,x =1,x =2解:在x =1点,lim y =lim x →1(x -1)(x +1)(x +1)=lim =-2x →1(x -1)(x -2)x →1(x -2)故x =1点为第一类中的可去间断点.如果补充f (1)=-2,则f (x )在x =2点连续。
高等数学题库习题集带答案
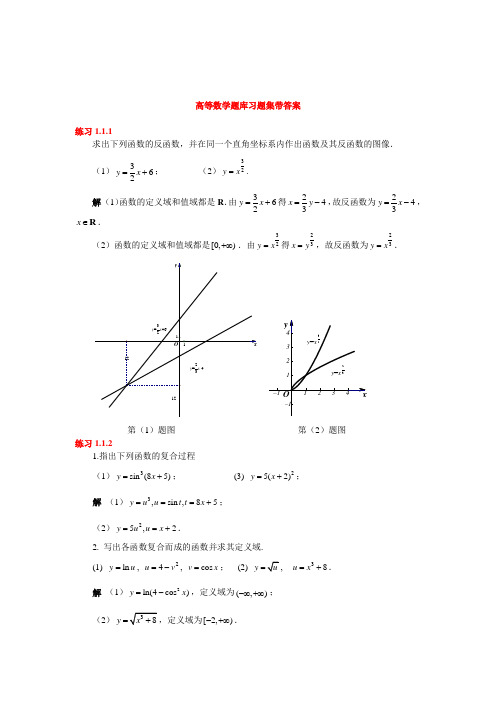
解
(2)
解
练习2.1.4
1.求函数 在 时函数的增量及微分.
解 ,
2.求下列函数的微分
(1) ;
解
(2) ;
解
(3) .
解
练习2.2.1求下列函数的单调区间
(1) ;
解函数 的定义域为 ,且
所以函数 在 上单调递增.
(2) ;
解函数的定义域为 , ,令 ,得 (舍负)
当 时, ,所以 为单减区间.
(1) , , ;
(2) , , .
解(1) .
(2) .
练习3.3.3
1.求函数 在区间 上的平均值.
解 .
2.有一根长度为 的细棒,其上任意点 处的密度 ,若细棒的一端与坐标原点重合,求细棒的平均密度.
解 .
高等数学练习题第四章及答案
练习4.1.1
1.试写出下列各微分方程的阶数
(1)一阶;(2)一阶;(3)二阶;(4)二阶.
(1)积分变量与积分区间;
(2)路程S的微元 ;
(3)路程S.
解(1)积分变量为 ,积分区间为 ;
(2) ;
(3)
练习3.3.2
1.求下列由曲线和直线围成的平面图形的面积
(1) , , ;
(2) , , ;
(3) , .
解(1) .
(2) .
(2) .
2.求下列由曲线和直线围成的平面图形绕x轴旋转而成的旋转体的体积
2.求微分方程 , , 的特解.
解两边积分得 ,
再积分得
代入 , 得, , .
所求微分方程的特解为 .
练习4.1.2
1.求解微分方程 .
解分离变量得 ,
两边积分得 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 函数与极限
§1 函数
必作习题
P16-18 4 (5) (6) (8),6,8,9,11,16,17
必交习题
一、一列火车以初速度0v ,等加速度a 出站,当速度达到1v 后,火车按等速运动前进;从
出站经过T 时间后,又以等减速度a 2进站,直至停止。
(1) 写出火车速度v 与时间t 的函数关系式;
(2) 作出函数)(t v v =的图形。
二、 证明函数1
2+=
x x y 在),(+∞-∞内是有界的。
三、判断下列函数的奇偶性: (1)x x x f 1sin
)(2= ;
(2)1
212)(+-=x x x f ;
(3))1ln()(2++=x x x f 。
四、 证明:若)(x f 为奇函数,且在0=x 有定义,则0)0(=f 。
§2 初等函数
必作习题
P31-33 1,8,9,10,16,17
必交习题
一、 设)(x f 的定义域是]1,0[,求下列函数的定义域:
(1))(x e f ;
(2))(ln x f ;
(3))(arcsin x f ;
(4))(cos x f 。
二、(1)设)1ln()(2x x x f +=,求)(x e
f -;
(2)设23)1(2+-=+x x x f ,求)(x f ;
(3)设x
x f -=
11)(,求)]([x f f ,})(1{x f f 。
)1,0(≠≠x x
三、设)(x f 是x 的二次函数,且1)0(=f ,x x f x f 2)()1(=-+,求)(x f 。
四、设⎩⎨⎧>+≤-=0,
20,
2)(x x x x x f ,⎩⎨⎧>-≤=0,0,)(2x x x x x g ,求)]([x g f 。
P42 3 (3) (4),4,5,6
必交习题
一、 写出下列数列的前五项 (1)3sin 31n n x n =
;
(2)n n n n x n ++++++=
22212111 ;
(3)n
x n x n n n
)1(1211122-=+++=-, 。
二、已知n
x n
n )1(1-+=,用定义证明:0lim =∞→n n x
P50 1 (2) (4),2(2),3,4,7,9
必交习题 一、用极限的定义证明:41
22 lim 21=--→x x x 。
二、用极限的定义证明:656 lim =+∞→x
x x 。
三、研究下列函数在0=x 处的左、右极限,并指出是否有极限: (1)x x x f ||)(=
;
(2)⎪⎩
⎪⎨⎧<+=>-=0,10,
00,1)(2x x x x x x f
四、用极限的定义证明:2)106( lim 22
=+-→x x x
§5 无穷大与无穷小 §6 极限运算法则
必作习题
P54-55 3,4,5; P63 1,2,3
必交习题
一、举例说明(当0→x 时):(1)两个无穷小的商不一定是无穷小;(2)无界量不一定为无穷
大量。
二、求下列数列的极限: (1))121( lim 2
22n n n n n -+++∞→ =
(2)n
n n n n 6565 lim 1
1++++∞→=
(3))3
)1(27191311( lim 11
--∞→-++-+-n n n =
三、求下列函数的极限: (1)1
1 lim 1--→x x x =
(2)h
x h x h 3
30)( lim -+→=
(3)))(( lim x a x x x -++∞
→=
(4))1311( lim 31x
x x ---→=
四、设21
2)1( lim 2334-=-++++∞→x x bx x a x ,求b a ,。
§7 极限存在准则 ,两个重要极限 §8 无穷小的比较
必作习题
P 71 1,2,4; P 74 1,2,3,4
必交习题
一、 求下列极限: (1) x
x x 3sin lim ∞→=
(2)a
x a x a x --→22sin sin lim =
(3)114sin lim 0-+→x x x =
(4)114 lim +∞→⎪⎭
⎫ ⎝⎛++x x x x =
(5)x
x x x 1011 lim ⎪⎭
⎫ ⎝⎛-+→=
二、用极限存在准则求证下列极限:
(1)设1(0=>i a i ~),m },,m ax {1m a a M =;证明: M a a a n n
m n n n =+++∞→ 21lim
(2)设31>x ,),2,1(3)1(31 =++=+n x x x n
n n 。
证明此数列收敛,并求出它的极限。
三、确定k 的值,使下列函数与k x ,当0→x 时是同阶无穷小: (1)
x x +-+111;
(2)53243x x -;
(3)x x sin 1tg 1--+。
四、已知11 lim 21=-++→x b a x x ,求b a 和. 。
三、用极限定义证明:
(1) 若)(∞→→n a x n ,则对任一自然数k ,也有)(∞→→+n a x k n ;
(2) 若)(∞→→n a x n ,则)(||||∞→→n a x n ,并举例说明反之未必成立;
(3) 若)(0||∞→→n x n ,则)(0∞→→n x n 。
四、 设数列}{n x 有界,又0 lim n =∞→n y ,证明0 lim n =∞
→n n y x 。
§9 函数的连续性与间断点
必作习题
P80 1,2,3
必交习题
一、当0=x 时下列函数)(x f 无定义,试定义)0(f 的值,使)(x f 在0=x 连续: (1)1111)(3-+-+=
x x x f ;
(2)x
x x f 1sin sin )(⋅=。
二、指出下列函数的间断点并判定其类型: (1)311)(x x x f ++=
;
(2))
1(||)(22--=x x x x x f ;
(3)⎪⎩
⎪⎨⎧≤<-+>=-0
1)1ln(0)(1
1x x x e x f x 。
三、确定b a 和,使函数)
1)(()(---=x a x b e x f x 有无穷间断点0=x ;有可去间断点1=x 。
四、设函数)(x f 在),(+∞-∞上有定义,且对任何21,x x 有
)()()(2121x f x f x x f +=+,
证明:若0)(=x x f 在连续,则),()(+∞-∞在x f 上连续。
§10 连续函数的运算与初等函数的连续性 §11 闭区间上连续函数的性质 必作习题 P85-86 1,2,3;
P91 1,2,3 必交习题
一、 欲使 ⎪⎩⎪⎨⎧->++-=-<+=1
)ln(111)(22x x x b x x x a x f ,,,
在1-=x 处连续,求b a ,。
二、求下列极限:
(1)x a
a x x ln )ln( lim 0-+→=
(2)x
x x e x 1
)( lim 0+→=
(3)x (x-x cos 21)
sin lim 33-→π
π=
(4)x x x 2sin 1
)(cos lim →=
三、证明方程=-x x 351至少有一根介于1和2之间。
四、设函数)(x f 在区间]2,0[a 上连续,)2()0(a f f =,证明在区间],0[a 上至少存在一
点0x 使得)()(00a x f x f +=。
