数据结构第七章(上)
数据结构第七章-图

*
V0
V7
V6
V5
V4
V3
V2
V1
若图的存储结构为邻接表,则 访问邻接点的顺序不唯一, 深度优先序列不是唯一的
V0
V1
V3
V2
V7
V6
V5
V4
V0,V1,V3,V4,V7,V2,V5,V6,
※求图G以V0为起点的的深度优先序列(设存储结构为邻接矩阵)
void DFSAL(ALGraph G, int i) {/*从第v个顶点出发,递归地深度优先遍历图G*/ /* v是顶点的序号,假设G是用邻接表存储*/ EdgeNode *p; int w; visited[i] =1; Visit(i); /*访问第v个顶点*/ for (p=G.vertices[i].firstarc;p;p=p->nextarc) {w=p->adjvex; /*w是v的邻接顶点的序号*/ if (!visited[w]) DFSAL(G, w); /*若w尚未访问, 递归调用DFS*/ } }/*DFSAL*/
在邻接表存储结构上的广度优先搜索
*
Q
V0
V1
V2
V3
V4
V7
V5
V6
V1
V2
V3
V0
V4
V7
V5
V6
V0
V7
V6
V5
V4
V3
V2
V1
7.3 图的遍历
7
0
1
2
V0
V2
V3
V1
data
firstarc
0
1
^
^
adjvex
next
3
《数据结构(C语言版 第2版)》(严蔚敏 著)第七章练习题答案

《数据结构(C语言版第2版)》(严蔚敏著)第七章练习题答案第7章查找1.选择题(1)对n个元素的表做顺序查找时,若查找每个元素的概率相同,则平均查找长度为()。
A.(n-1)/2B.n/2C.(n+1)/2D.n答案:C解释:总查找次数N=1+2+3+…+n=n(n+1)/2,则平均查找长度为N/n=(n+1)/2。
(2)适用于折半查找的表的存储方式及元素排列要求为()。
A.链接方式存储,元素无序B.链接方式存储,元素有序C.顺序方式存储,元素无序D.顺序方式存储,元素有序答案:D解释:折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
(3)如果要求一个线性表既能较快的查找,又能适应动态变化的要求,最好采用()查找法。
A.顺序查找B.折半查找C.分块查找D.哈希查找答案:C解释:分块查找的优点是:在表中插入和删除数据元素时,只要找到该元素对应的块,就可以在该块内进行插入和删除运算。
由于块内是无序的,故插入和删除比较容易,无需进行大量移动。
如果线性表既要快速查找又经常动态变化,则可采用分块查找。
(4)折半查找有序表(4,6,10,12,20,30,50,70,88,100)。
若查找表中元素58,则它将依次与表中()比较大小,查找结果是失败。
A.20,70,30,50B.30,88,70,50C.20,50D.30,88,50答案:A解释:表中共10个元素,第一次取⎣(1+10)/2⎦=5,与第五个元素20比较,58大于20,再取⎣(6+10)/2⎦=8,与第八个元素70比较,依次类推再与30、50比较,最终查找失败。
(5)对22个记录的有序表作折半查找,当查找失败时,至少需要比较()次关键字。
A.3B.4C.5D.6答案:B解释:22个记录的有序表,其折半查找的判定树深度为⎣log222⎦+1=5,且该判定树不是满二叉树,即查找失败时至多比较5次,至少比较4次。
(6)折半搜索与二叉排序树的时间性能()。
数据结构课后习题答案第七章
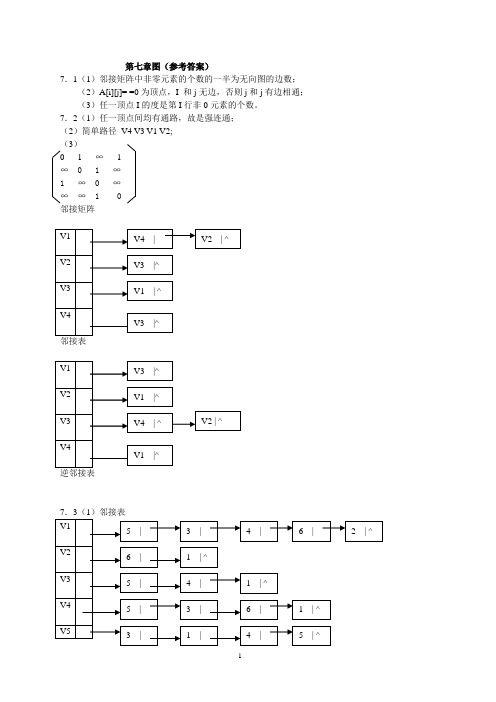
第七章图(参考答案)7.1(1)邻接矩阵中非零元素的个数的一半为无向图的边数;(2)A[i][j]= =0为顶点,I 和j无边,否则j和j有边相通;(3)任一顶点I的度是第I行非0元素的个数。
7.2(1)任一顶点间均有通路,故是强连通;(2)简单路径V4 V3 V1 V2;(3)0 1 ∞ 1∞ 0 1 ∞1 ∞ 0 ∞∞∞ 1 0邻接矩阵邻接表(2)从顶点4开始的DFS序列:V5,V3,V4,V6,V2,V1(3)从顶点4开始的BFS序列:V4,V5,V3,V6,V1,V27.4(1)①adjlisttp g; vtxptr i,j; //全程变量② void dfs(vtxptr x)//从顶点x开始深度优先遍历图g。
在遍历中若发现顶点j,则说明顶点i和j间有路径。
{ visited[x]=1; //置访问标记if (y= =j){ found=1;exit(0);}//有通路,退出else { p=g[x].firstarc;//找x的第一邻接点while (p!=null){ k=p->adjvex;if (!visited[k])dfs(k);p=p->nextarc;//下一邻接点}}③ void connect_DFS (adjlisttp g)//基于图的深度优先遍历策略,本算法判断一邻接表为存储结构的图g种,是否存在顶点i //到顶点j的路径。
设 1<=i ,j<=n,i<>j.{ visited[1..n]=0;found=0;scanf (&i,&j);dfs (i);if (found) printf (” 顶点”,i,”和顶点”,j,”有路径”);else printf (” 顶点”,i,”和顶点”,j,”无路径”);}// void connect_DFS(2)宽度优先遍历全程变量,调用函数与(1)相同,下面仅写宽度优先遍历部分。
王道数据结构 第七章 查找思维导图-高清脑图模板
每次调整的对象都是“最小不平衡子树”
插入操作
在插入操作,只要将最小不平衡子树调整平衡,则其他祖先结点都会恢复平衡
在A的左孩子的左子树中插入导致不平衡
由于在结点A的左孩子(L)的左子树(L)上插入了新结点,A的平衡因子由1增
至2,导致以A为根的子树失去平衡,需要一次向右的旋转操作。
LL
将A的左孩子B向右上旋转代替A成为根节点 将A结点向右下旋转成为B的右子树的根结点
RR平衡旋转(左单旋转)
而B的原左子树则作为A结点的右子树
在A的左孩子的右子树中插入导致不平衡
由于在结点A的左孩子(L)的右子树(R)上插入了新结点,A的平衡因子由1增
LR
至2,导致以A为根的子树失去平衡,需要两次旋转操作,先左旋转再右旋转。
将A的左孩子B的右子树的根结点C向左上旋转提升至B结点的位置
本质:永远保证 子树0<关键字1<子树1<关键字2<子树2<...
当左兄弟很宽裕时,用当前结点的前驱、前驱的前驱来填补空缺 当右兄弟很宽裕时,用当前结点的后继、后继的后继来填补空缺
兄弟够借。若被删除关键字所在结点删除前的关键字个数低于下限,且与此结点 右(或左)兄弟结点的关键字还很宽裕,则需要调整该结点、右(或左)兄弟结 点及其双亲结点及其双亲结点(父子换位法)
LL平衡旋转(右单旋转)
而B的原右子树则作为A结点的左子树
在A的右孩子的右子树中插入导致不平衡
由于在结点A的右孩子(R)的右子树(R)上插入了新结点,A的平衡因子由-1
减至-2,导致以A为根的子树失去平衡,需要一次向左的旋转操作。
RR
将A的右孩子B向左上旋转代替A成为根节点 将A结点向左下旋转成为B的左子树的根结点
数据结构第七章 树和森林

7.5 树的应用
➢判定树
在实际应用中,树可用于判定问题的描述和解决。
•设有八枚硬币,分别表示为a,b,c,d,e,f,g,h,其中有一枚且 仅有一枚硬币是伪造的,假硬币的重量与真硬币的重量不同,可能轻, 也可能重。现要求以天平为工具,用最少的比较次数挑选出假硬币, 并同时确定这枚硬币的重量比其它真硬币是轻还是重。
的第i棵子树。 ⑺Delete(t,x,i)在树t中删除结点x的第i棵子树。 ⑻Tranverse(t)是树的遍历操作,即按某种方式访问树t中的每个
结点,且使每个结点只被访问一次。
7.2.2 树的存储结构
顺序存储结构 链式存储结构 不管哪一种存储方式,都要求不但能存储结点本身的数据 信息,还要能够唯一的反映树中各结点之间的逻辑关系。 1.双亲表示法 2.孩子表示法 3.双亲孩子表示法 4.孩子兄弟表示法
21
将二叉树还原为树示意图
A BCD
EF
A
B
C
E
D
F
A
B
C
E
D
F
22
练习:将下图所示二叉树转化为树
1 2
4
5
3
6
2 4
1 53
6
23
7.3.2 森林转换为二叉树
由森林的概念可知,森林是若干棵树的集合,只要将森林中各棵树 的根视为兄弟,森林同样可以用二叉树表示。 森林转换为二叉树的方法如下:
⑴将森林中的每棵树转换成相应的二叉树。 ⑵第一棵二叉树不动,从第二棵二叉树开始,依次把后一棵二叉树 的根结点作为前一棵二叉树根结点的右孩子,当所有二叉树连起来 后,此时所得到的二叉树就是由森林转换得到的二叉树。
相交的集合T1,T2,…,Tm,其中每一个集合Ti(1≤i≤m)本身又是 一棵树。树T1,T2,…,Tm称为这个根结点的子树。 • 可以看出,在树的定义中用了递归概念,即用树来定义树。因此, 树结构的算法类同于二叉树结构的算法,也可以使用递归方法。
数据结构第七章课后习题答案 (1)

7_1对于图题7.1(P235)的无向图,给出:(1)表示该图的邻接矩阵。
(2)表示该图的邻接表。
(3)图中每个顶点的度。
解:(1)邻接矩阵:0111000100110010010101110111010100100110010001110(2)邻接表:1:2----3----4----NULL;2: 1----4----5----NULL;3: 1----4----6----NULL;4: 1----2----3----5----6----7----NULL;5: 2----4----7----NULL;6: 3----4----7----NULL;7: 4----5----6----NULL;(3)图中每个顶点的度分别为:3,3,3,6,3,3,3。
7_2对于图题7.1的无向图,给出:(1)从顶点1出发,按深度优先搜索法遍历图时所得到的顶点序(2)从顶点1出发,按广度优先法搜索法遍历图时所得到的顶点序列。
(1)DFS法:存储结构:本题采用邻接表作为图的存储结构,邻接表中的各个链表的结点形式由类型L_NODE规定,而各个链表的头指针存放在数组head中。
数组e中的元素e[0],e[1],…..,e[m-1]给出图中的m条边,e中结点形式由类型E_NODE规定。
visit[i]数组用来表示顶点i是否被访问过。
遍历前置visit各元素为0,若顶点i被访问过,则置visit[i]为1.算法分析:首先访问出发顶点v.接着,选择一个与v相邻接且未被访问过的的顶点w访问之,再从w 开始进行深度优先搜索。
每当到达一个其所有相邻接的顶点都被访问过的顶点,就从最后访问的顶点开始,依次退回到尚有邻接顶点未曾访问过的顶点u,并从u开始进行深度优先搜索。
这个过程进行到所有顶点都被访问过,或从任何一个已访问过的顶点出发,再也无法到达未曾访问过的顶点,则搜索过程就结束。
另一方面,先建立一个相应的具有n个顶点,m条边的无向图的邻接表。
数据结构(C语言版)_第7章 图及其应用
实现代码详见教材P208
7.4 图的遍历
图的遍历是对具有图状结构的数据线性化的过程。从图中任 一顶点出发,访问输出图中各个顶点,并且使每个顶点仅被访 问一次,这样得到顶点的一个线性序列,这一过程叫做图的遍 历。
图的遍历是个很重要的算法,图的连通性和拓扑排序等算法 都是以图的遍历算法为基础的。
V1
V1
V2
V3
V2
V3
V4
V4
V5
图9.1(a)
图7-2 图的逻辑结构示意图
7.2.2 图的相关术语
1.有向图与无向图 2.完全图 (1)有向完全图 (2)无向完全图 3.顶点的度 4.路径、路径长度、回路、简单路径 5.子图 6.连通、连通图、连通分量 7.边的权和网 8.生成树
2. while(U≠V) { (u,v)=min(wuv;u∈U,v∈V-U); U=U+{v}; T=T+{(u,v)}; }
3.结束
7.5.1 普里姆(prim)算法
【例7-10】采用Prim方法从顶点v1出发构造图7-11中网所对 应的最小生成树。
构造过程如图7-12所示。
16
V1
V1
V2
7.4.2 广度优先遍历
【例7-9】对于图7-10所示的有向图G4,写出从顶点A出发 进行广度优先遍历的过程。
访问过程如下:首先访问起始顶点A,再访问与A相邻的未被 访问过的顶点E、F,再依次访问与E、F相邻未被访问过的顶 点D、C,最后访问与D相邻的未被访问过的顶点B。由此得到 的搜索序列AEFDCB。此时所有顶点均已访问过, 遍历过程结束。
【例7-1】有向图G1的逻辑结构为:G1=(V1,E1) V1={v1,v2,v3,v4},E1={<v1,v2>,<v2,v3>,<v2,v4>,<v3,v4>,<v4,v1>,<v4,v3>}
数据结构-第7章图答案
7.3 图的遍历 从图中某个顶点出发游历图,访遍图中其余顶点, 并且使图中的每个顶点仅被访问一次的过程。 一、深度优先搜索 从图中某个顶点V0 出发,访问此顶点,然后依次 从V0的各个未被访问的邻接点出发深度优先搜索遍 历图,直至图中所有和V0有路径相通的顶点都被访 问到,若此时图中尚有顶点未被访问,则另选图中 一个未曾被访问的顶点作起始点,重复上述过程, 直至图中所有顶点都被访问到为止。
void BFSTraverse(Graph G, Status (*Visit)(int v)) { // 按广度优先非递归遍历图G。使用辅助队列Q和访问标志数组 visited。 for (v=0; v<G.vexnum; ++v) visited[v] = FALSE; InitQueue(Q); // 置空的辅助队列Q for ( v=0; v<G.vexnum; ++v ) if ( !visited[v]) { // v尚未访问 EnQueue(Q, v); // v入队列 while (!QueueEmpty(Q)) { DeQueue(Q, u); // 队头元素出队并置为u visited[u] = TRUE; Visit(u); // 访问u for ( w=FirstAdjVex(G, u); w!=0; w=NextAdjVex(G, u, w) ) if ( ! visited[w]) EnQueue(Q, w); // u的尚未访问的邻接顶点w入队列Q
4。邻接多重表
边结点
mark ivex
顶点结点
ilink
jvex
jlink
info
data
firstedge
#define MAX_VERTEX_NUM 20 typedef emnu {unvisited, visited} VisitIf; typedef struct Ebox { VisitIf mark; // 访问标记 int ivex, jvex; // 该边依附的两个顶点的位置 struct EBox *ilink, *jlink; // 分别指向依附这两个顶点的下一条 边 InfoType *info; // 该边信息指针 } EBox; typedef struct VexBox { VertexType data; EBox *firstedge; // 指向第一条依附该顶点的边 } VexBox; typedef struct { VexBox adjmulist[MAX_VERTEX_NUM]; int vexnum, edgenum; // 无向图的当前顶点数和边数 } AMLGraph;
数据结构第7章排序
7.2.1 冒泡排序
• 排序过程 – 将第一个和第二个元素的关键字进行比较,若为逆序 ,则将两个元素互换;接着比较第二个和第三个元素 的关键字,依次类推,直至最后两个元素的完成比较 ,这称为第一趟冒泡排序。第一趟排序分划出一组元 素个数为n-1的待排序列和一个关键字最大的元素。 – 第i趟对前n - i + 1个的元素进行类似的排序操作,得到 一组元素个数为n - i的待排序列和一个(在前n-i+1个元 素中)关键字最大的元素。 – 这样不断分划直至一趟分划时无元素互换为止。
34 28 81 79 63 28 34 81 79 63 28 34 79 81 63
第一趟
28 34 79 63 81
第二趟
28 34 63 79 81
初始
7.2.1 冒泡排序
• 冒泡排序算法
template<class ElemType> void BubbleSort(ElemType data[], int n) { int lastSwapIndex = n - 1; //用于记录最后一次交换的元素下标 int i, j; for (i = lastSwapIndex; i > 0;i = lastSwapIndex){ lastSwapIndex = 0; for (j = 0; j < i; j++) if (data[j] > data[j + 1]){ Swap(data[j],data[j + 1]); lastSwapIndex = j; } } }
数 据 结 构
第7章 排序
概述
• 什么是排序? – 排序是计算机内经常进行的一种操作,其目的是将一 组“无序”的元素序列调整为“有序”的元素序列。 – 假设含n个记录的序列为{ R1, R2, …, Rn },其相应的 关键字序列为 { K1, K2, …,Kn }。这些关键字相互之 间可以进行比较,即在它们之间存在着这样一个关系 : Kp1≤Kp2≤…≤Kpn (或≥) 按此关系将上面记录序列重新排列为: { Rp1, Rp2, …,Rpn } 的操作称作排序。
数据结构第七章 排序
name 张涛 赵亮
冯博远 王强 李燕
7.2
基本原理
插入排序
每次将一个待排序的对象,按其关键字大小, 插入到前面已经排序好的一组对象的适当位臵上, 直到对象全部插入为止。
直接插入排序(Insert Sort)
希尔排序(Shell Sort)
7.2.1
直接插入排序
R[1]---R[i-1]
08 08
16 16
第三次
08
16
21
25* 25
49
希尔排序中d(间隔量)的取法 Shell最初的方案是 d= n/2, d=d/2, 直到d=1; Knuth的方案是d= d/3+1;
其它方案有:都取奇数为好;d互质为好 等等。
希尔排序的稳定性
如序列: 21 25 排序后为:08 16
R[0]有两个作用:
其一: 进入查找循环之前,保存 R[i] 的副本,使之不至 于因记录的后移而丢失R[i]中的内容; 其二: 在 while 循环时,“监视”下标变量 j 是否越界, 一旦越界(j<0),R[0]自动控制while循环的结束, 从而 避免了在while 循环内的每一次都要检测 j 是否越界( 即 省略了循环条件j>=0)。 因此,把 R[0] 称为“监视哨”。
第七章 排 序
本章内容
排序的概念和有关知识
常用的几种排序方法的基本思想、排序过 程和算法实现 各种排序算法的时间复杂度分析
学生成绩表
学号 姓名 高数 英语 总分
005 010 002
018 004
Chen Lin Gao Hong Wang Na
ZhangYang Zhao Pen
84 69 90
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.2.2 邻接表 实现:为图中每个顶点建立一个单链表,第i个单 链表中的结点表示依附于顶点Vi的边(有向图中指 以Vi为尾的弧)。 邻接表的类型定义参见P163。
例: a c b d
表结点 头结点 邻接点的位 置,即序号
数据结构
adjvex nextarc vexdata firstarc adjvex nextarc 2 ^
G1 vexdata firstarc 1 a b 2 ^ 3 c 4 d
3 4 1 ^ ^
数据结构 例: a c d G2 e adjvex nextarc 4 ^ 3 4 3 3 ^ ^ 5 5 ^ ^ b
vexdata firstarc 2 1 a b 2 1 3 c 2 4 d 1 5 e 2
⎧1, 若(v i , v j )或 < v i , v j >∈ E A[i, j ] = ⎨ ⎩0,其它
例: 1 3 G1 2 4
⎡0 ⎢ ⎢0 ⎢0 ⎢ ⎢1 ⎣ 1 0 0 0 1 0 0 0 0⎤ ⎥ 0⎥ 1⎥ ⎥ 0⎥ ⎦
数据结构 例: 1 3 4 G2 5 2
⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 0 0 ⎤ ⎥ 1 ⎥ 1 ⎥ ⎥ 0 ⎥ ⎥ 0 ⎥ ⎦
⎧ω ij , 若(v i , v j )或 < v i , v j >∈ E 网的邻接矩 阵可定义为: A[i, j ] = ⎨∞,其它 ⎩
例: 1 3 7 5 2
⎡∞ ⎢ ⎢5 ⎢7 ⎢ ⎢∞ ⎢ ⎢3 ⎣ 5 ∞ ∞ 4 8 7 ∞ ∞ 2 1 ∞ 4 2 ∞ 6 3⎤ ⎥ 8⎥ 1⎥ ⎥ 6⎥ ⎥ ∞⎥ ⎦
数据结构
连通分量(强连通分量) 无向图G 的极大连通子图称为G的连通分量。 极大连通子图意思是:该子图是 G 连通子图,将G 的任何不在该子图中的顶点加入,子图不再连通。 V0 V1 V4 非 连 通 V3 V2 V5 连通分量 图
V0 V3 V1 V2 V4 V5
数据结构
有向图G 的极大强连通子图称为G的强连通分量。 极大强连通子图意思是:该子图是G的强连通子图 ,将D的任何不在该子图中的顶点加入,子图不再 是强连通的。
非 连 通 图 非 强 连 通 图
V2
V3
V2
V3
数据结构
权 某些图的边具有与它相关的数, 称之为权。 这种带权图叫做网络。 子图 设有两个图G=(V,{E})、G1=(V1,{E1}), 若V1⊆ V,E1 ⊆ E,则称 G1是G的子图。 例:(b)、(c) 是 (a) 的子图
V0 V2 V3 (a) V4 V3 (b) V1 V0 V2 V4 V3 (c) V1 V0 V2 V4 V1
V0 V1 V2 V3 V4 V0 V1
无向图G1
有向图G2
V2 V3
数据结构
连通图(强连通图) 在无(有)向图G=( V, {E} )中,若对任何两个顶 点 v、u 都存在从v 到 u 的路径,则称G是连通图 (强连通图)。 连 通 图 强 连 通 图
V0 V2 V3 V0 V4 V1 V3 V0 V2 V5 V1 V1 V0 V1 V4
数据结构
数据结构
7.1 图的定义和术语
图的定义:是一种多对多的结构关系,每个元素 图的定义: 可以有零个或多个直接前趋;零个或多个直接后 继。图是由顶点集合(vertex)及顶点间的关系集 合组成的一种数据结构: Graph=( V, R ) 其中 V = { v | v ∈ 某个数据对象}
是顶点的有穷非空集合; R ={VR}={(v, w) | v, w ∈ V } 图的类型定义参见P156
V0 V2 V3
V1ห้องสมุดไป่ตู้
V4
V0
V1
V2
V3
数据结构
路径、回路 无向图G =(V,{E})中的顶点序列v1,v2,… ,vk, 若(vi,vi+1)∈E( i=1,2,…k-1), v =v1, u =vk, 则 称该序列是从顶点v到顶点u的路径。 若v=u,则称该序列为回路。 例:
V0 V2 V3 V4 V1
数据结构
基本术语: 有向图与无向图 在有向图中,顶点对<v, w>是 有序的。在无向图中,顶点对(x, y)是无序的。 1 有向图 2 3 6 7 5 4 有向边又可称为弧, <vi,vj> 中vi称为狐尾或初始点,vj 狐尾 称为狐头或终端点。 狐头
V={1,2,3,4,5,6,7} VR={<1,3>,<1,2>,<3,7>,<3,6>,<2,5>,<2,6>, <2,4>,<5,7>,<6,7>}
在图G1中,V0,V1,V2,V3 是V0到V3的路径。 V0,V1,V2,V3,V0是回路。
数据结构
有向图G =(V,{E})中的顶点序列v1,v2,… ,vk, 若<vi,vi+1>∈E (i=1,2,…k-1), v =v1, u =vk, 则 称该序列是从顶点v到顶点u的路径。 若v=u,则称该序列为回路。 例: 有向图G2
强连通分量 V0 V1 V0 V1
V2
V3
V2
V3
权与网 图中边或弧所具有的相关数称为权。表明从一 个顶点到另一个顶点的距离或耗费。带权的图 称为网。
数据结构
生成树和生成森林 极小连通子图:该子图是G 的连通子图,在该子 极小连通子图 图中删除任何一条边,子图不再连通。 包含无向图G 所有顶点的极小连通子图称为G 的 生成树。对非连通图,则称由各个连通分量的生 成树的集合为非连通图的生成森林。
数据结构
1 3 4 5 6 7 2 无向图
V={1,2,3,4,5,6,7} VR={(1,3),(3,4),(4,5),(1,2),(2,6),(2,7),( 6,7),(5,6),(1,5),(1,7) }
数据结构
邻接点及关联 若无向图中存在边(v, u),则称顶点v 和u互为邻接点;边(v, u)依附于顶点v 和u;或者说边(v, u)和顶点v和u相关 联。 顶点的度、入度、出度 在无向图中: 顶点V的度 = 与V相关联的边的数目 在有向图中: 顶点V的出度=以V为狐尾的有向边数 顶点V的入度=以V为狐头的有向边数 顶点V的度= V的出度+V的入度
V2 V3 V0 V1
在图G2中,V0,V2,V3 是V0到V3的路径。 V0,V2,V3,V0是回路。
数据结构
简单路径和简单回路 在一条路径中,若除起点和终点外,所有顶点各不 相同,则称该路径为简单路径。 由简单路径组成的回路称为简单回路。 在图G1中,V0,V1,V2,V3 是简单路径。 V0,V1,V2,V4,V1不是简单路径。 在图G2中, V0,V2,V3,V0是简单回路。
8 4 5 1 6 3 4 2
邻接矩阵类型定义:
数据结构
#define INFINITY INT_MAX //最大值∞ #define MAX_VERTEX_NUM 20 typedef enum{DG,DN,AG,AN} GraphKind; typedef struct ArcCell //边或弧的结构 { VRType adj; // 顶点关系:0/1或权值 InfoType * info; //边或弧相关信息的指针 }ArcCell,AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_ NUM] typedef struct { VertexType vexs[MAX_VERTEX_NUM]; AdjMatrix arcs; //邻接矩阵 int vexnum,arcnum; GraphKind kind; }MGraph;
《 数据结构》
第七章(上)
第七章 图
7.1 图的定义和术语 7.2 图的存储结构 7.2.1 数组表示法 7.2.2 邻接表 7.3 图的遍历 7.3.1 深度优先搜索 7.3.2 广度优先搜索 7.4 图的连通性问题 7.4.3 最小生成树 7.5 有向无环图及其应用 7.5.1 拓扑排序 7.6 最短路径 7.6.1 从某个源点到其余各顶点的最短路径 7.6.2 每一对顶点之间的最短路径
数据结构
逆邻接表:有向图中对每个结点建立以Vi为弧头 的弧的单链表。
例: a b 1 c G1 d 2 3 4 vexdata a b c d firstarc adjvex nextarc 4 1 1 3 ^ ^ ^ ^
V0 V2 V3 V4 V3 V1 V0 V2 V4 V1 V3 V2 V0 V1 V4
连通图 G1
G1的生成树
图的几种基本操作参见P158。
数据结构
7.2.1 数组表示法 邻接矩阵:表示顶点间相联关系的矩阵。 邻接矩阵: 定义:设G=(V,{E})是有n≥1个顶点的图,G的邻接 矩阵A是具有以下性质的n阶方阵:
