第四章弯曲内力习题
弯曲内力习题与答案

弯曲力1. 长l的梁用绳向上吊起,如图所示。
钢绳绑扎处离梁端部的距离为x。
梁由自重引起的最大弯矩|M|max为最小时的x值为:(A) /2l;(B) /6l;(C…) 1)/2l。
l;(D) 1)/22. 多跨静定梁的两种受载情况如图(a)、(b)所示。
下列结论中哪个是正确的?(A) 两者的剪力图相同,弯矩图也相同;(B) 两者的剪力图相同,弯矩图不同;(C) 两者的剪力图不同,弯矩图相同;(D….) 两者的剪力图不同,弯矩图也不同。
3. 图示(a)、(b)两根梁,它们的(A) 剪力图、弯矩图都相同;(B…) 剪力图相同,弯矩图不同;(C) 剪力图不同,弯矩图相同;(D) 剪力图、弯矩图都不同。
4. 图示梁,当力偶M e的位置改变时,有下列结论:(A) 剪力图、弯矩图都改变;(B…) 剪力图不变,只弯矩图改变;(C) 弯矩图不变,只剪力图改变;(D) 剪力图、弯矩图都不变。
5. 图示梁C截面弯矩M C = ;为使M C =0,则M e= ;为使全梁不出现正弯矩,则M e≥。
6. 图示梁,已知F、l、a。
使梁的最大弯矩为最小时,梁端重量P= 。
7. 图示梁受分布力偶作用,其值沿轴线按线性规律分布,则B端支反力为,弯矩图为 次曲线,|M |max 发生在 处。
8. 图示梁,m (x )为沿梁长每单位长度上的力偶矩值,m (x )、q (x )、F S (x )和M (x )之间的微分关系为:S d ();d F x x = d ()d M x x = 。
9. 外伸梁受载如图,欲使AB 中点的弯矩等于零时,需在B 端加多大的集中力偶矩(将大小和方向标在图上)。
10. 简支梁受载如图,欲使A 截面弯矩等于零时,则=e21e /M M 。
1-10题答案:1. C 2. D 3. B 4. B 5. 28e2M ql -;42ql ;22ql 6. ⎪⎭⎫⎝⎛-a l a F 24 7. m 0/2;二;l /28. q (x );F S (x )+ m (x ) 9. 10. 1/211-60题. 作图示梁的剪力图和弯矩图。
材料力学典型例题及解析 4.弯曲内力典型习题解析

弯曲内力典型习题解析1 作图示简支梁的剪力图和弯矩图,并求出maxSF 和maxM。
解题分析:作剪力、弯矩图的基本方法是写出每一段梁上的剪力、弯矩方程,根据方程描点作图。
在能熟练地作剪力、弯矩图后,可采用如下简便作图法:在表中列出特殊截面(如有位移约束的截面、集中力作用截面等的剪力、弯矩值,再根据载荷集度与剪力、弯矩之间的微分关系判断各区段的内力图形状,连线相邻特殊截面对应的点。
下面按两种方法分别作图。
解I :1、求支反力qa F Ay =,qa F Cy 2=2、将梁分成AB 、BC 和CD 三个区段 以A 为原点,向右取x 坐标。
AB 段,如图d :qa F F Ay ==S ,()a x <<02qa(c)(b)(a)M(d)(e)MSSSM(f)题1图qax x F M Ay ==,()a x ≤≤0BC 段,如图e:)2()(S x a q a x q F F Ay −=−×−=,(a x a 2<<))/2()/2)((22a x q a x a x q x F M Ay +=−−+=,(a x a 2≤≤)CD 段,如图f:)()(S x a q F a x q F F Ay −=−−×−=,(a x a 32<<))/2()/2)((22a x q a x a x q x F M Ay +=−−+=,(a x a 32≤≤)3、按照步骤2所得各段梁的剪力、弯矩方程画出剪力图和弯矩图,如图b 和图c。
4、计算剪力和弯矩的最大值qa F 2maxS=, 2max23qa M=解II :1、计算支反力qa F Ay =,qa F Cy2=2、将梁分为AB 、BC 、CD 三个区段,计算每个区段起点和终点的力值。
3、根据载荷情况及微分关系,判断各力区的内力图形状,并以相应的图线连接起来,得到剪力图和弯矩图。
力区 A 截面 AB B 截面 BC C 截面 CD D 截面 载荷 F Ay 向上 q =0无集中力q =负常数 F 向下 q =负常数 F Dy 向上F S突跳F Ay水平(+)连续 下斜线(+) 突减F 下斜线(-) 突跳F DyM 0 上斜线 相切上凸抛物线转折上凸抛物线4、计算剪力弯矩最大值qa F 2maxS=, 2max23qa M=讨论:利用剪力弯矩方程作图时,注意坐标轴x 的正向一般由左至右。
最新弯曲的内力与强度计算习题

弯曲的内力与强度计算一、判断题1.如图1示截面上,弯矩M和剪力Q的符号是:M为正,Q为负。
()图12.取不同的坐标系时,弯曲内力的符号情况是M不同,Q相同。
()3、在集中力作用的截面处,Q图有突变,M连续但不光滑。
()4、梁在集中力偶作用截面处,M图有突变,Q图无变化。
()5.梁在某截面处,若剪力Q=0,则该截面的M值一定为零值。
()6.在梁的某一段上,若无荷载作用,则该梁段上的剪力为常数。
()7.梁的内力图通常与横截面面积有关。
()8.应用理论力学中的外力定理,将梁的横向集中力左右平移时,梁的Q 图,M图都不变。
()9.将梁上集中力偶左右平移时,梁的Q图不变,M图变化。
()10.图2所示简支梁跨中截面上的内力为M≠0,Q=0。
()图 2 图 311.梁的剪力图如图3所示,则梁的BC段有均布荷载,AB段没有。
()12.上题中,作用于B处的集中力大小为6KN,方向向上。
()13.右端固定的悬臂梁,长为4m,M图如图示,则在x=2m处,既有集中力又有集中力偶。
()图 4 图 514.上题中,作用在x=2m处的集中力偶大小为6KN·m,转向为顺时针。
()15.图5所示梁中,AB跨间剪力为零。
()16.中性轴是中性层与横截面的交线。
()17.梁任意截面上的剪力,在数值上等于截面一侧所有外力的代数和。
()18.弯矩图表示梁的各横截面上弯矩沿轴线变化的情况,是分析梁的危险截面的依据之一。
()19.梁上某段无荷载作用,即q=0,此段剪力图为平行x的直线;弯矩图也为平行x轴的直线。
()20.梁上某段有均布荷载作用,即q=常数,故剪力图为斜直线;弯矩图为二次抛物线。
()21.极值弯矩一定是梁上最大的弯矩。
()22.最大弯矩Mmax只可能发生在集中力F作用处,因此只需校核此截面强度是否满足梁的强度条件。
()23.截面积相等,抗弯截面模量必相等,截面积不等,抗弯截面模量必不相等。
()24.大多数梁都只进行弯曲正应力强度核算,而不作弯曲剪应力核算,这是因为它们横截面上只有正应力存在。
习题解答4(弯曲内力)

M2 FS2
M3 FS3
M2 = - F×1 = - 10 kN· m
F C
FS3 = F = 10 kN M3 = 0
P73 40-1(d) a = l
12 3 O(3Fa) F M
A
F A
B
12
C
3
FS1 M1
D FD
Fy = 0
FD = 10 kN
FS1 = - F = - 10 kN
3 qa2 2
FS 图
1 qa2 2
1 M(x) = - qa×(2a- a-x) 2 3 2 = qax - qa 2 BC段: FS(x) = q ×(2a-x) = 2qa - qx 1 M(x) = q×(2a-x)× (2a-x) 2 1 2 = - qx + 2qax - 2qa2 2 1 = - q× ( 2a- x) 2 2
A 1 ql 4 C B A C
B A
C
B
l/ 2
l/ 2
1 ql 2 1 ql FS 图(q) 2
FS 图(M0)
1 ql 4 1 ql2 8 1 ql2 8
FS 图
3 ql 4
1 ql2 32 5 ql2 1 ql2 32 4
1 ql2 8
M图
M 图 ( q)
M 图(M0)
P78 42-2-1 叠加法 (过程)
F M0(Fa) C B A F
A B C A
M0(Fa) C B
a
a
F
F
3Fa
FS 图
2Fa Fa
FS 图(F)
2Fa
FS 图(M0)
Fa
测试题-弯曲内力(答案)
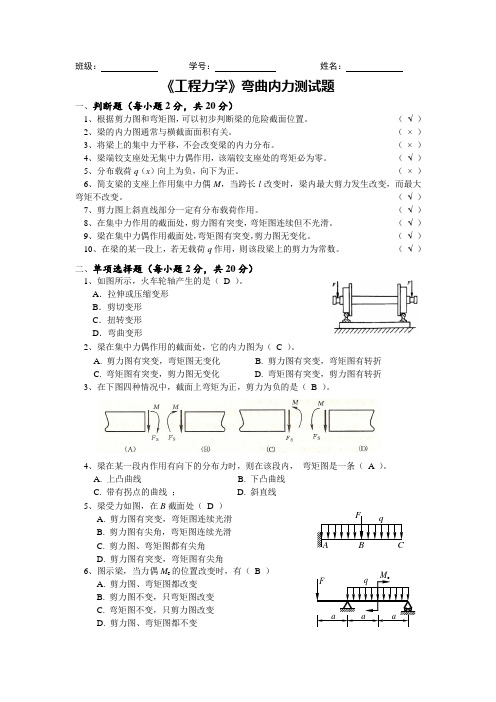
班级:学号:姓名:《工程力学》弯曲内力测试题一、判断题(每小题2分,共20分)1、根据剪力图和弯矩图,可以初步判断梁的危险截面位置。
(√)2、梁的内力图通常与横截面面积有关。
(×)3、将梁上的集中力平移,不会改变梁的内力分布。
(×)4、梁端铰支座处无集中力偶作用,该端铰支座处的弯矩必为零。
(√)5、分布载荷q(x)向上为负,向下为正。
(×)6、简支梁的支座上作用集中力偶M,当跨长l改变时,梁内最大剪力发生改变,而最大弯矩不改变。
(√)7、剪力图上斜直线部分一定有分布载荷作用。
(√)8、在集中力作用的截面处,剪力图有突变,弯矩图连续但不光滑。
(√)9、梁在集中力偶作用截面处,弯矩图有突变,剪力图无变化。
(√)10、在梁的某一段上,若无载荷q作用,则该段梁上的剪力为常数。
(√)二、单项选择题(每小题2分,共20分)1、如图所示,火车轮轴产生的是(D )。
A.拉伸或压缩变形B.剪切变形C.扭转变形D.弯曲变形2、梁在集中力偶作用的截面处,它的内力图为(C )。
A. 剪力图有突变,弯矩图无变化B. 剪力图有突变,弯矩图有转折C. 弯矩图有突变,剪力图无变化D. 弯矩图有突变,剪力图有转折3、在下图四种情况中,截面上弯矩为正,剪力为负的是(B )。
4、梁在某一段内作用有向下的分布力时,则在该段内,弯矩图是一条(A )。
A. 上凸曲线B. 下凸曲线C. 带有拐点的曲线;D. 斜直线5、梁受力如图,在B截面处(D )A. 剪力图有突变,弯矩图连续光滑B. 剪力图有尖角,弯矩图连续光滑C. 剪力图、弯矩图都有尖角D. 剪力图有突变,弯矩图有尖角6、图示梁,当力偶M e的位置改变时,有(B )A. 剪力图、弯矩图都改变B. 剪力图不变,只弯矩图改变C. 弯矩图不变,只剪力图改变D. 剪力图、弯矩图都不变F qCBAFM eaqa a7、若梁的受力情况对于梁的中央截面为反对称(如图),则下列结论中正确的是(D )A. 剪力图和弯矩图均为反对称,中央截面上剪力为零B. 剪力图和弯矩图均为对称,中央截面上弯矩为零C. 剪力图反对称,弯矩图对称,中央截面上剪力为零D. 剪力图对称,弯矩图反对称,中央截面上弯矩为零8、多跨静定梁的两种受载情况分别如图所示,力F靠近铰链,以下结论正确的是(C )A. 两者的剪力图和弯矩图完全相同B. 两者的剪力图相同,弯矩图不同C. 两者的剪力图不同,弯矩图相同D. 两者的剪力图和弯矩图均不相同9、多跨静定梁的两种受载情况如图所示,下列结论中正确的是(D )A. 两者的剪力图和弯矩图完全相同B. 两者的剪力图相同,弯矩图不同C. 两者的剪力图不同,弯矩图相同D. 两者的剪力图和弯矩图均不相同10、若梁的剪力图和弯矩图分别如图所示,则该图表明(C )A. AB段有均布载荷,BC段无载荷;B. AB 段无载荷,B截面处有向上的集中力,BC段有向下的均布载荷;C. AB 段无载荷,B截面处有向下的集中力,BC段有向下的均布载荷;D. AB 段无载荷,B截面处有顺时针的集中力偶,BC段有向下的均布载荷。
刘鸿文材料力学 I 第6版_4_弯取内力

(3) 在剪力Q为零处, 弯矩M取极值。
注意: 以上结论只在该 段梁上无集中力 或集中力偶作用 时才成立。
44
(4) 在集中力作用点: 剪力图有突变,突变值 即为集中力的数值,突 变的方向沿着集中力的 方向(从左向右观察); 弯矩图在该处为折点。
(5) 在集中力偶作用点: 对剪力图形状无影响; 弯矩图有突变,突变值 即为集中力偶的数值。
2
AC段: N 1 qa Q qa qy 2
M qa y 1 qy2
2
(3) 轴力图
(4) 剪力图
35
(4) 剪力图
(5) 弯矩图
BC段:
M 1 qa x
2
qa
AC段:
M qa y 1 qy2
特点: 2
在刚节点处,弯矩值连续 ;
Q
1 qa 2
36
特点: 在刚节点处,弯矩值连续; 可以利用刚节点的平衡, 对内力图进行校核。
(2) 求剪力方程和弯矩方程
需分段求解。
分为两段:AC和CB段。 AC段 取x截面,左段受力如图。
由平衡方程,可得:
Q(x) Pb l
(0 x a)
M (x) Pb x
(0 x a)
l
CB段 取x截面,
x
Q
M
17
CB段 取x截面, 左段受力如图。 由平衡方程,可得:
外侧均可,但需标出正 负号; (3) 弯矩画在受压侧。
32
例 5 刚架
已知:q,a。
求:内力图。
解:(1) 求支反力 结果如图。
(2) 求内力 BC段:
X 0
MQ
N Dx
N 0
弯曲内力习题课
0.5P
L
0.5P
0.5PL –
+
x
0.5P
L
L
0.5P
M2
0.5PL
[例3] 用简易作图法画下列各图示梁的内力图。
qa A a
q
解: 利用内力和外力的关系及
特殊点的内力值来作图。
a 特殊点(控制点):
端点、分区点(外力变化点)和
驻点等。
qa A a Fs
q
左端点: Fs qa; M 0 a x 线形:根据
例 题
[例1] qL 1 求图(a)所示梁1--1、2--2截面处的内力。 q 2 解:截面法求内力。 1--1截面处截取的分离体 2 b 如图(b)示。
1 a y qL A M1 x1 FS1
x
图(a)
Y qL F
S1
0
FS1 qL
mA( Fi ) qLx1 M1 0 M1 qLx1
dx
dFs x
dx 2 dM (x) d M ( x) ; q( x) FS (x) 2
dx
q x ;
– qa qa2
及集中载荷点的规律确定。
3 2 分区点A: F qa; M qa 2 qa S 2 3 2 M 的驻点: FS 0 ;M 2 qa
–
弯曲内力习题课
概念
平面弯曲——外力作用在梁的纵向对称平面内,使梁的 轴线弯曲后仍在此对称平面内的弯曲变形
P1 q P2
M
纵向对称面
弯曲内力
符号规定
剪力与弯矩的正负号规则
FS FS
剪力 FS一使截开部分梁段产生顺时针方向 弯矩M —— 使梁产生上凹、下凸变形的弯矩为 转动趋势者为正;逆时针方向转动者为负。 正;反之为负。
材料力学答案4弯曲内力
A
C
B 出剪力图和弯矩图。
x1
x2
解:1.确定约束力
FAy
l
FBy
M /l
M A=0, MB=0
Fs:
Ma / l
M:
FAy=M / l FBy= -M / l
2.写出剪力和弯矩方程
AC FS x1=M / l 0 x1 a
M x1=Mx1 / l 0 x1 a
剪力图和弯矩图
例1
1kN.m
A
C D B 解法2:1.确定约束力
FAY
Fs( kN) 0.89
1.5m
1.5m
2kN
1.5m
FBY
1.11
(+)
FAy=0.89 kN FFy=1.11 kN
(-)
2.确定控制面为A、C 、D、B两侧截面。
3.从A截面左侧开始画
剪力图。
19
剪力图和弯矩图
例1
x 5.确定控制面上的 弯矩值,并将其标在
M-x中。
22
剪力图和弯矩图
例2
q
D 解法2:1.确定约束力
A
B
FAy
9qa/4
4a
a qa FBy
FAy=
9 4
qa
,
FBy=
3 4
qa
Fs (+)
(-) qa
7qa/4
2.确定控制面,即A 、B、D两侧截面。
3.从A截面左测开始画
剪力图。
23
剪力图和弯矩图
Mb / l
CB FS x2 =M / l 0 x2 b
M x2 = Mx2 / l 0 x2 b
04章弯曲内力习题课
1KN 1KN
1KN
归纳:
1.根据微分关系作Q、M图步骤:
①求约束反力; ②确定分段,计算控制截面上的剪力和弯矩值;
③根据微分关系确定各段内力图形状;
④由② 、 ③作内力图。
2.控制截面的选择:
①分布荷载的起点和终点、集中力和集中力偶 作用点、支座点; ② M为极值(Q=0)的截面。
积分关系:
q(x) MA A QA QB B MB
q A
P=qa D
解:(1)支反力
R A qa 2
RB 5qa 2
2a
RB
B
a
RA
Q
qa / 2
C
qa
3 qa 2
qa QA RA 2 3 QB左 R A q 2a qa 2 QBD qa
MA 0
(2)作剪力图、弯矩图
M B qa 2
MC qa 2 8
②M 图 BC 段不为零 , 因为 BC
段Q=0,所以该段 M=常量。
Pa Pa P Q图 M图 Pa P
③在B、C点无集中力偶,M 图不应有突变;
Pa
例:已知梁的弯矩图,试画出梁的剪力图和荷载图。
1KN .m 1KN .m
A
B
2 KN .m 1m 3m
C
D
1m
2 KN 1KN
3KN .m
1KN .m
M D M A Q ( AD )
2a
a
qa / 3
1 5 5 25 2 0 qa a qa 2 3 3 18
M B左 M D Q ( DB ) 25 2 1 1 1 qa a qa 18 2 3 3 4 2 qa 3
(完整word版)南京工业大学工程力学弯曲内力习题答案
图示圆轴承受扭转力偶矩e M ,已知许用切应力[]100 MPa ,切变模量80 GPa G ,在轴2.5 m 长度内的最大许可扭转角为0.06 rad ,试求e M 的许可值。
试题答案:解:按强度条件e maxp 2[]M Wep2[]4241 N m M W由刚度条件e 1e 2p1p 2[]AC AB BCM l M l GI GIe3362 N m Me []3360 N m M1、试求图示各梁中指定截面上的剪力、弯矩值.解:题(a) A 截面-Q P 0,bF F M a b ==+ C 截面-Q P P ,b ab F F M F a b a b ==++ D 截面-Q P P ,a ab F F M F a b a b =-=++ B 截面-Q P 0,aF F M a b=-=+ 1mA 80φ60φ1.5mBCM e题(b) A 截面-0Q 0,M F M a b==+ C 截面-0Q 0,M aF M M a b a b ==++ D 截面-0Q 0,M bF M M a b a b =-=++ B 截面-0Q 0,M F M a b=-=+ 题(c) A 截面-Q 503,F qa M ==C 截面-2Q 5736,F qa M qa ==B 截面-Q 103,F qa M =-=题(d) A 截面-2Q 1328,F ql M qa ==-C 截面-2Q 1128,F ql M qa ==-D 截面-2Q 1128,F ql M qa ==-B 截面-Q 00,F M ==题(e ) A 截面-Q P P 2,F F M F l =-=C 截面-Q P 20,F F M =-=B 截面-Q P 0,F F M ==题(f ) A 截面-P Q 02,F lF M ==C 截面-P Q 02,F l F M ==D 截面-P Q P 2,F l F F M =-=B 截面-Q P 0,F F M =-=2 试建立图示各梁的剪力方程和弯矩方程,试画出图示各梁的剪力图和弯矩图解:qaaqaF MF FaF(完整word 版)南京工业大学工程力学弯曲内力习题答案解:a qa 2aqFF MF qa22F ql(完整word 版)南京工业大学工程力学弯曲内力习题答案解:解:q2qaqa 2a aaFF2F F(完整word版)南京工业大学工程力学弯曲内力习题答案解:FF。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
第四章弯曲内力习题
一、填空题
1、梁纯弯曲时,横截面上的正应力沿高度方向呈分布,横截面上距中性轴愈远的点处应力的绝对值,中性轴上的各点应力为。
2、如果一段梁内各横截面上的剪力Q为零,而弯矩M为常量,则该段梁的弯曲称为;如果该梁各横截面上同时存在剪力Q和弯矩M,则这种弯曲为。
3、根据梁弯曲的平面假设,梁上其间存在一层既不伸长也不缩短的纤维,这一层纤维称为;该层与梁横截面的交线称为。
4、求梁变形的基本方法是和。
二、计算题
1、作下列两梁的弯矩图。
求出支座处的约束反力、弯矩的最大绝对值,并把该值标注在弯矩图上。
2
弯矩图上。
3、作下列梁的弯矩图。
求出支座处的约束反力、弯矩的最大绝对值,并把该值标注在弯矩图上
4、作下列梁的弯矩图。
5、作下列梁的弯矩图。
