计算齿轮侧隙
侧隙计算

1、曲轴齿轮与惰齿轮A啮合时的法向侧隙计算曲轴齿轮、惰齿轮A均是变位斜齿轮,其标准中心距计算如下:a=m n(z1+z2)/(2cosβ),已知m n=2.5,z1=21,z2=31,β=18°计算得a=68.35mm设计图纸给定安装中心距为69.77~69.82mm,查阅资料得法向侧隙计算公式为:Cn= m n(z v1+z v2)cosαn(invαn′- invαn0′)当量齿数z v1= z1/cos3β=24.42,z v2= z2/cos3β=36.05法向压力角αn=15°αn0′为两齿轮无侧隙安装时的啮合角invαn0′=2tanαn(x t1+ x t2)/(z v1+z v2)+ invαn端面变位系数x t1= x n1cosβ,x t2= x n2cosβ,已知法面变位系数x n1=0.417,x n2=0.176,则,x t1=0.397,x t2=0.167,计算得invαn0′=0.01115αn′为实际安装后的啮合角,设实际安装后的中心距为a′,有这样一个公式:a′cosαn′=a cosαn取a′=69.77mm时,αn′=18.87°,Cn=0.1853mm取a′=69.82mm时,αn′=18.99°,Cn=0.2234mm所以该对齿轮安装后的法向侧隙范围是0.1853~0.2234mm经验公式:J nbmin=2(0.06+0.0005a i+0.03 m n)/3,其中J nbmin为最小法向侧隙,a i为最小安装中心距,计算得J nbmin=0.1133mm2、凸轮轴齿轮与惰齿轮A啮合时的法向侧隙计算凸轮轴齿轮、惰齿轮A均是变位斜齿轮,其标准中心距计算如下:a=m n(z1+z2)/(2cosβ),已知m n=2.5,z1=42,z2=31,β=18°计算得a=95.95mm设计图纸给定安装中心距为96.49~96.54mm,查阅资料得法向侧隙计算公式为:Cn= m n(z v1+z v2)cosαn(invαn′- invαn0′)当量齿数z v1= z1/cos3β=48.84,z v2= z2/cos3β=36.05法向压力角αn=15°αn0′为两齿轮无侧隙安装时的啮合角invαn0′=2tanαn(x t1+ x t2)/(z v1+z v2)+ invαn端面变位系数x t1= x n1cosβ,x t2= x n2cosβ,已知法面变位系数x n1=0.002,x n2=0.176,则,x t1=0.0019,x t2=0.167,计算得invαn0′=0.00722αn′为实际安装后的啮合角,设实际安装后的中心距为a′,有这样一个公式:a′cosαn′=a cosαn取a′=96.49mm时,αn′=16.15°,Cn=0.1005mm取a′=96.54mm时,αn′=16.26°,Cn=0.1357mm所以该对齿轮安装后的法向侧隙范围是0.1005~0.1357mm经验公式:J nbmin=2(0.06+0.0005a i+0.03 m n)/3,其中J nbmin为最小法向侧隙,a i为最小安装中心距,计算得J nbmin=0.1222mm3、惰齿轮B与惰齿轮A啮合时的法向侧隙计算惰齿轮B不是变位齿轮,但可以看成是法面变位系数x n1=0的变位斜齿轮,惰齿轮A是变位斜齿轮,其标准中心距计算如下:a=m n(z1+z2)/(2cosβ),已知m n=2.5,z1=29,z2=31,β=18°计算得a=78.86mm设计图纸给定安装中心距为79.29~79.34mm,查阅资料得法向侧隙计算公式为:Cn= m n(z v1+z v2)cosαn(invαn′- invαn0′)当量齿数z v1= z1/cos3β=33.72,z v2= z2/cos3β=36.05法向压力角αn=15°αn0′为两齿轮无侧隙安装时的啮合角invαn0′=2tanαn(x t1+ x t2)/(z v1+z v2)+ invαn端面变位系数x t1= x n1cosβ,x t2= x n2cosβ,已知法面变位系数x n1=0,x n2=0.176,则,x t1=0,x t2=0.167,计算得invαn0′=0.00743αn′为实际安装后的啮合角,设实际安装后的中心距为a′,有这样一个公式:a′cosαn′=a cosαn取a′=79.29mm时,αn′=16.12°,Cn=0.0390mm取a′=79.34mm时,αn′=16.24°,Cn=0.0678mm所以该对齿轮安装后的法向侧隙范围是0.0390~0.0678mm经验公式:J nbmin=2(0.06+0.0005a i+0.03 m n)/3,其中J nbmin为最小法向侧隙,a i为最小安装中心距,计算得J nbmin=0.1164mm。
齿轮副最大与最小侧隙的计算

Ts1、Ts2—分别为小齿轮、大齿轮的齿厚公差(μm);
Ta—齿轮副的中心距公差(μm);
αn’—齿轮压力角(0)。
≤10
>10-25
>25-60
>60
喷油润滑
10
20
30
30-50
油池润滑
5-10
2.齿轮副最大法向侧隙值的计算
计算齿轮副的最大法向侧隙时,主要考虑齿轮的加工精度。其计算公式如下
Jnmax=Jmin+【(Ts12+Ts22)Xcos2αn+(TaX2Xsinαn)】(1/2)
式中 Jnmax—最大法向侧隙(μm);
式中Jnmin—最小法向侧隙(μm);
a—齿轮副中心距(μm);
α1
△t1、△t2—分别为齿轮、箱体温度与标准温度(200C)之差(0C);
αn’—齿轮副法向啮合角(0);
δ—润滑状况系数(检附表);
mn—齿轮模数。
δ表值
润滑方式
齿轮节圆圆周速度v(m/s)
齿轮副侧隙探讨
一、由最小侧隙推导大小齿轮齿厚上偏差:
二、齿轮副最大侧隙计算
齿轮副最小和最大法向侧隙值计算
2010-04-28 12:16
1.齿轮副最小法向侧隙值的计算
计算齿轮副的最小法向侧隙时,主要考虑齿轮副的热变形和润滑状况的工作条件。其计算公式如下:
Jnmin=2a·(α1△t1-α2△t2)sinαn’+δmn
计算齿轮侧隙

无侧隙啮合参数未知参数齿厚、齿距侧隙参数符号主动齿轮(小)从动齿轮(大)齿数z 2140法向模数m n 法向压力角αn 螺旋角β法向变位系数x n 0.047-0.465齿宽b 齿顶圆直径d a 54.396.5齿根圆直径d f 42.3584.55任意圆直径d x 54.396.5中心距a 当量齿数zv 32.8290359262.53149699当量模数m n 当量压力角αn 当量螺旋角β当量变位系数x n 0.047-0.465当量分度圆直径d 65.66125.06当量基圆直径d b 61.89117.89任意圆压力角α29.3023.61任意圆直径d'70.97128.66当量齿轮任意圆直径dx 70.97128.66任意圆直径d 54.0696.44曹德义 2008年11月14.570齿 轮 计 算2.0019.530.52.0019.50啮合压力角渐开线函数a b c 啮合压力角弧度端面啮合角理论中心距离中心距变动系数y 中心距变动系数y 中心距变动系数yn 中心距变动系数yn 齿顶高变动系数△y 齿顶高系数ha* 1.428 1.464顶隙系数c*0.2180.145理论啮合线长度端面变位系数x t 0.040-0.401齿顶高h a 2.778 1.826齿根高h f 3.197 4.149齿根圆直径d f 42.3584.55端面模数m t 端面压力角αt 齿顶圆端面压力角αat 33.8727.14任意圆端面压力角αxt 33.8727.14齿顶圆螺旋角βa 33.2731.48任意圆螺旋角βx 33.2731.48分度圆直径d 48.7448792.85节圆直径 d'48.2091.80节圆螺旋角β'30.2230.22基圆直径d b 45.08685.877齿顶圆曲率半径ρa 15.1322.01任意圆曲率半径ρx 15.1322.01理论啮合线长度l 渐开线起始圆直径45.41688.002导程259.974495.189基圆螺旋角βb 端面啮合角αt 法向啮合角αn 三角函数invαn 齿顶圆压力角αa 33.8727.14任意圆压力角αx 33.8727.14端面重合度εα轴向重合度εβ总重合度εγ法向齿距p n -0.374-0.374-0.434-0.43420.54169.92733781.840.016系 数0.3590.3750.1410.35924.5360.0743.016.2832.321.1722.3424.7428.58320.7018.0330.0108端面齿距p t 基圆齿距p bt 基圆法向齿距p bn 法向齿厚s n 3.208 2.483端面齿厚s t 3.723 2.882齿顶圆端面齿厚s at 0.943 1.271齿顶圆法向齿厚s an 0.788 1.084任意圆端面齿厚s xt 0.943 1.271任意圆法向齿厚s xn 0.788 1.084基圆端面齿厚s bt 4.3927 4.4726基圆法向齿厚s bn 3.8573 3.9276节圆端面齿厚s t' 3.8966 3.2589节圆法向齿厚s n' 3.3671 2.8161当量齿数z v 32.8362.53节圆端面齿距p t'节圆法向齿距p n'圆周侧隙j wt 法向侧隙j bn 法向侧隙j bn 圆周侧隙j wt 7.2926.7455.9237.21026.23050.05470.044940.044940.0547备注输入端面法向考虑倒棱考虑倒棱根据节圆齿厚计算根据基圆齿厚计算。
齿轮侧隙计算公式

齿轮侧隙计算公式齿轮是机械传动中常用的一种元件,它通过齿间啮合的方式来传递动力和扭矩。
齿轮的侧隙是指两个相邻齿面之间的距离,它对齿轮传动的精度和可靠性有着非常重要的影响。
因此,在进行齿轮设计和制造时,需要准确计算齿轮的侧隙。
齿轮侧隙的计算可以通过以下公式来实现:S=Kt(bm+bf+ΔF)其中,S表示齿轮侧隙,Kt表示齿轮侧隙系数,bm表示模数,bf表示齿宽系数,ΔF表示两轮啮合产生的变形力。
首先,我们需要确定齿轮侧隙系数Kt。
对于各种齿轮传动方式(平行轴齿轮、斜齿轮、锥齿轮等),都有相应的侧隙系数值。
在平行轴齿轮啮合时,Kt一般为0.05~0.15;在斜齿轮啮合时,Kt一般为0.07~0.20;在锥齿轮啮合时,Kt一般为0.10~0.20。
接下来,通过计算齿宽系数bf,可以确定齿轮侧隙计算中的第二个参数。
bf分为全齿宽系数和有效齿宽系数两种,通常取全齿宽系数。
bf的计算方法是bf=b/(z*cosα),其中b表示齿宽,z表示齿数,α表示齿轮齿面斜角。
最后,我们需要考虑啮合变形力的影响。
在齿轮啮合过程中,由于齿轮齿面形状、变形等因素,会在齿面产生一定的变形力。
啮合变形力ΔF的计算可以采用有限元法、试验法等方法,在具体的设计中需要根据实际情况进行确定。
通过以上公式和参数计算,我们可以得到准确的齿轮侧隙值。
齿轮侧隙对于齿轮的传动精度和可靠性有着非常重要的作用,因此在齿轮设计和制造过程中,必须非常注重齿轮侧隙的准确计算。
同时,在实际生产中也需要进行严格的监测和测量,保证齿轮的稳定性和可靠性。
浅谈机械设计中齿轮传动侧隙的解决方法

浅谈机械设计中齿轮传动侧隙的解决方法发表时间:2019-08-29T15:18:22.920Z 来源:《知识-力量》2019年10月40期作者:金孝燮[导读] 齿轮在世界各个国家的应用历史较早,其在众多机械设备中的应用非常广泛,并具有十分关键的作用。
齿轮能够起到传递动力,对运动速度与方向做出改变的作用,随着制造技术水平的快速提升与发展,对齿轮生产制造提出更为严格的标准要求。
基于此,本文对机械设计中齿轮传动侧隙的解决方法做出分析与探讨,旨在为相关设计人员提供帮助与参考。
(齐齐哈尔工程学院,161005)摘要:齿轮在世界各个国家的应用历史较早,其在众多机械设备中的应用非常广泛,并具有十分关键的作用。
齿轮能够起到传递动力,对运动速度与方向做出改变的作用,随着制造技术水平的快速提升与发展,对齿轮生产制造提出更为严格的标准要求。
基于此,本文对机械设计中齿轮传动侧隙的解决方法做出分析与探讨,旨在为相关设计人员提供帮助与参考。
关键词:机械设计;齿轮传动侧隙;解决办法前言:齿轮最早在中国古代就被人们广泛应用,历经千百年来的发展,齿轮形势与作用均发生重大的变化与发展。
有齿,且彼此啮合的机械零部件称之为齿轮。
针对机械设计,尽管齿轮传动侧隙对齿轮稳定可靠工作状态具有关键作用,不过齿轮彼此侧隙并未越大或越小越好,需要对侧隙做出系统精准的计算以及补偿等,获取最适宜、精准的齿轮传动侧隙,为齿轮的稳定可靠工作状态提供可靠保障。
一、齿轮传动侧隙优缺点齿轮侧隙主要是一对齿轮处于啮合状态下,其中一个齿轮单个齿同另一个齿轮单个齿齿面发生接触过程中,前一个齿的其他齿面同第二个齿轮彼此啮合的齿相邻的齿在分度圆上存在的间隙。
基于理论层面分析,齿轮侧隙需等于零,不过齿轮具体运行阶段,齿形会由于温度的变化产生相应的变化。
不过如处于常温环境条件下,若不存在侧隙则会发生咬死的情况,并且可以位于侧隙中空出储存的有效空间,因此,存在侧隙情况属于整张现象。
齿轮副侧隙计算方法

润滑方式 油池润滑
喷油润滑
齿 轮 线 速 度%&&+:"
1#"% "%#1#(* (*#1#.%
1$.%
/-8%#& #*""%$0-
"%0(%0’%0#’%"*%$0-
注’0- 为法向模数
#($/-9是考虑齿轮传 动 的 温 度 变 化! 这 时 由 于 齿 轮 和箱体的材料不同!温度不同以及材料的线膨胀系数不 同!而使原侧隙/-8发 生 减 小 #或 增 大$! 所 以! 除 前 述 /-8外! 还需加上/-9的补偿" 所以
;%!$"&&! "理论值# 最 大 法 向 侧 隙/-&8F;/E&8F<=+!;%!.$6<=+(%1&&
;%!.%&&! "理论值# 若考虑加工及安装产生的基节$轴向$轴线平行度 和中心距偏差%则有! 最小法向侧隙/-&,-;%!$":%38% (+,-!-:4
;%!’$" "&&# 最大法向侧隙/-&8F;%!.%7%38% (+,-!-74
%!%"#
3B
% ! 基节极限偏差 3C9
?%!%(%
3C9
&!齿向公差 :’ 接触斑点 按齿高不小于
%!%(% *%D
:’ *%D
按齿长不小于 /%D
%!%"# ?%!%(% %!%(%
/%D
%!%$";%!’$* "&&# /-&8F; "%2+," 72+,( % #<=+"<=+!- 7 %38% (+,-!-
直齿圆柱齿轮变位系数、公法线长度、齿厚、最小法向侧隙的计算

外啮合直齿圆柱齿轮变位系数、公法线长度、齿厚、最小法向侧隙的计算1,直齿圆柱齿轮变位系数计算:Case1:a,此处例子仅计算用齿条型刀具加工时的情况(插齿刀加工见相关手册公式):小结:由此可知本例选取的齿数在不变位的情况也不会产生根切现象。
b,根据下图选择大小齿轮的变位系数和x∑。
本例在P6-P7区间取值。
即齿根及齿面承载能力较高区,进行选择。
因大小齿轮的齿数和为18+19=37。
所以本例选择的变位系数和x∑=0.8。
本例我们的两个齿轮在工作时属于减速运动,所以按减速运动的变位系数分配线图,进行2个齿轮的变位系数的选择。
先按(z1+z1)/2=18.5,作为横坐标,做一条垂线(图中蓝色的线),再按x∑/2=0.4,作为纵坐标,做一条水平线(图中橙色的线),接着沿着L线的趋势,穿过上面2条线的交点做一条射线(图中红色的线)最后按大小齿轮的齿数做相应的垂线(图中紫色的线),即得到需要的各自变位系数。
最后我们选择的变位系数即为:小齿轮x1=0.42,大齿轮x2=0.38。
【基本保障其和与之前x ∑一致,即可】。
c,验算变位后的齿顶厚度:注:一般要求齿顶厚Sa≥0.25m;对于表面淬火的齿轮要求Sa≥0.4m下表中的da的计算见后面的计算表格中的计算公式(因为当齿轮变位后,齿顶圆的计算和未变位齿轮的计算稍有差别-涉及到变位系数和中心距变位系数。
)。
分度圆直径db mm 73.8 77.9齿轮的齿顶圆直径da mm 83.027 86.799齿轮的齿顶压力角αa °27.27 26.17中间值invα0.0215 0.0215中间值invαa 0.0587 0.0347齿顶厚Sα 5.77 7.47判断值0.25m 1.025 1.025判断值0.4m 1.64 1.64小结:计算发现变位后的齿轮齿顶厚满足设计需求。
根据上面确定的变位系数,计算齿轮的中心距变位系数和节圆直径、齿根圆直径、齿顶圆直径。
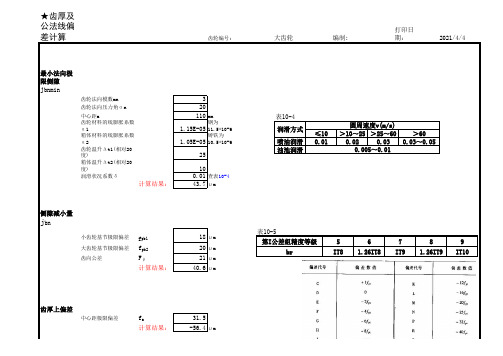
齿轮侧隙及齿厚偏差自动计算表
Ess
-66.0 μm
Esi
-176.0 μm
Ess*cosα n0.72Fr*sin αn
计算结果: Esi*cosα n+0.72Fr*s inαn 计算结果:
-75.80997 μm -151.5956 μm
Ewms/(sin αMt*cosβ b) 计算结果 Ewms/(sin αMt*cosβ b)*cos(π /2z)
★齿厚及 公法线偏 差计算
最小法向极 限侧隙
jbnmin
jnmin=1000* a(α1*Δ
t1-α2*Δ
t2)*2*sin
αn+δ
*mn*1000
齿轮法向模数mn
齿轮法向压力角αn
中心距a 齿轮材料的线膨胀系数 α1 箱体材料的线膨胀系数 α2 齿轮温升Δt1(相对20 度) 箱体温升Δt2(相对20 度)
>60
喷油润滑 0.01
0.02
0.03 0.03~0.05
油池润滑
0.005~0.01
表10-5 第I公差组精度等级 br
5
6
7
8
9
IT8 1.26IT8 IT9 1.26IT9 IT10
齿厚公差
齿圈径向跳动公差
径向切深公差
齿厚下偏差
齿距极限偏差Fpt 齿厚上偏差/Fpt 齿厚下偏差/Fpt
Ts=2*tanα n*(Fr^2+br ^2)^0.5 Fr
-180.9787
偶数齿
本表不属 于国家标 准,仅供 注:1 参考.
2 αMt1= 25 3 螺旋角β 8.1094
见标准齿轮 参数计算
4
βb= 0.132949
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
无侧隙啮合参数未知参数
齿厚、齿距侧隙
参数
符号主动齿轮(小)从动齿轮(大)齿数
z 2140法向模数
m n 法向压力角
αn 螺旋角
β法向变位系数
x n 0.047-0.465齿宽
b 齿顶圆直径
d a 54.396.5齿根圆直径
d f 42.3584.55任意圆直径
d x 54.396.5中心距
a 当量齿数
zv 32.8290359262.53149699当量模数
m n 当量压力角
αn 当量螺旋角
β当量变位系数
x n 0.047-0.465当量分度圆直径
d 65.66125.06当量基圆直径
d b 61.89117.89任意圆压力角
α29.3023.61任意圆直径
d'70.97128.66当量齿轮任意圆直径
dx 70.97128.66
任意圆直径d 54.0696.44
曹德义 2008年11月14.570齿 轮 计 算 2.0019.530.52.0019.500
啮合压力角渐开线函数a b c 啮合压力角弧度端面啮合角理论中心距离中心距变动系数y 中心距变动系数y 中心距变动系数yn 中心距变动系数yn 齿顶高变动系数△y 齿顶高系数ha* 1.428 1.464顶隙系数c*0.2180.145理论啮合线长度端面变位系数x t 0.040-0.401齿顶高h a 2.778 1.826齿根高h f 3.197 4.149齿根圆直径d f 42.3584.55端面模数m t 端面压力角αt 齿顶圆端面压力角αat 33.8727.14任意圆端面压力角αxt 33.8727.14齿顶圆螺旋角βa 33.2731.48任意圆螺旋角βx 33.2731.48分度圆直径d 48.7448792.85节圆直径 d'48.2091.80节圆螺旋角β'30.2230.22基圆直径d b 45.08685.877齿顶圆曲率半径ρa 15.1322.01任意圆曲率半径ρx 15.1322.01理论啮合线长度l 渐开线起始圆直径
45.41688.002导程
259.974495.189基圆螺旋角βb 端面啮合角αt 法向啮合角αn 三角函数invαn 齿顶圆压力角αa 33.8727.14任意圆压力角αx 33.8727.14端面重合度εα轴向重合度εβ总重合度εγ法向齿距p n -0.374-0.374-0.434-0.43420.54169.92733781.840.016
系 数0.3590.3750.1410.35924.5360.0743.016.2832.321.1722.3424.7428.58320.7018.0330.0108
端面齿距p t 基圆齿距p bt 基圆法向齿距p bn 法向齿厚s n 3.208 2.483端面齿厚s t 3.723 2.882齿顶圆端面齿厚s at 0.943 1.271齿顶圆法向齿厚s an 0.788 1.084任意圆端面齿厚s xt 0.943 1.271任意圆法向齿厚s xn 0.788 1.084基圆端面齿厚s bt 4.3927 4.4726基圆法向齿厚s bn 3.8573 3.9276节圆端面齿厚s t' 3.8966 3.2589节圆法向齿厚s n' 3.3671 2.8161当量齿数z v 32.8362.53
节圆端面齿距p t'节圆法向齿距p n'圆周侧隙j wt 法向侧隙j bn 法向侧隙j bn 圆周侧隙j wt 7.2926.7455.9237.21026.23050.05470.044940.044940.0547
备注输入
端面法向
考虑倒棱考虑倒棱
根据节圆齿厚计算根据基圆齿厚计算。
